Non-Invasive Composition Identification in Organic Solar Cells via Deep Learning
Abstract
1. Introduction
2. Experimental
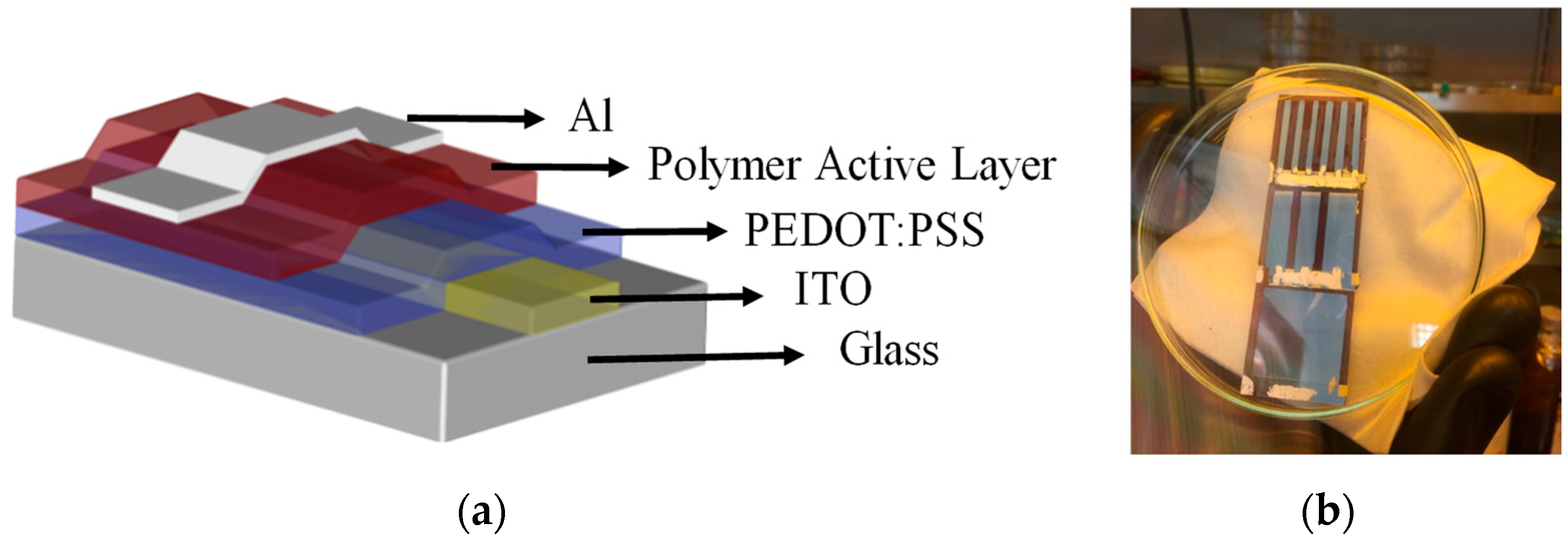
2.1. Device Fabrication
2.2. Optical Simulation
2.3. Data Processing Using Deep Learning
3. Results and Discussion
3.1. Absorption Spectra Analysis
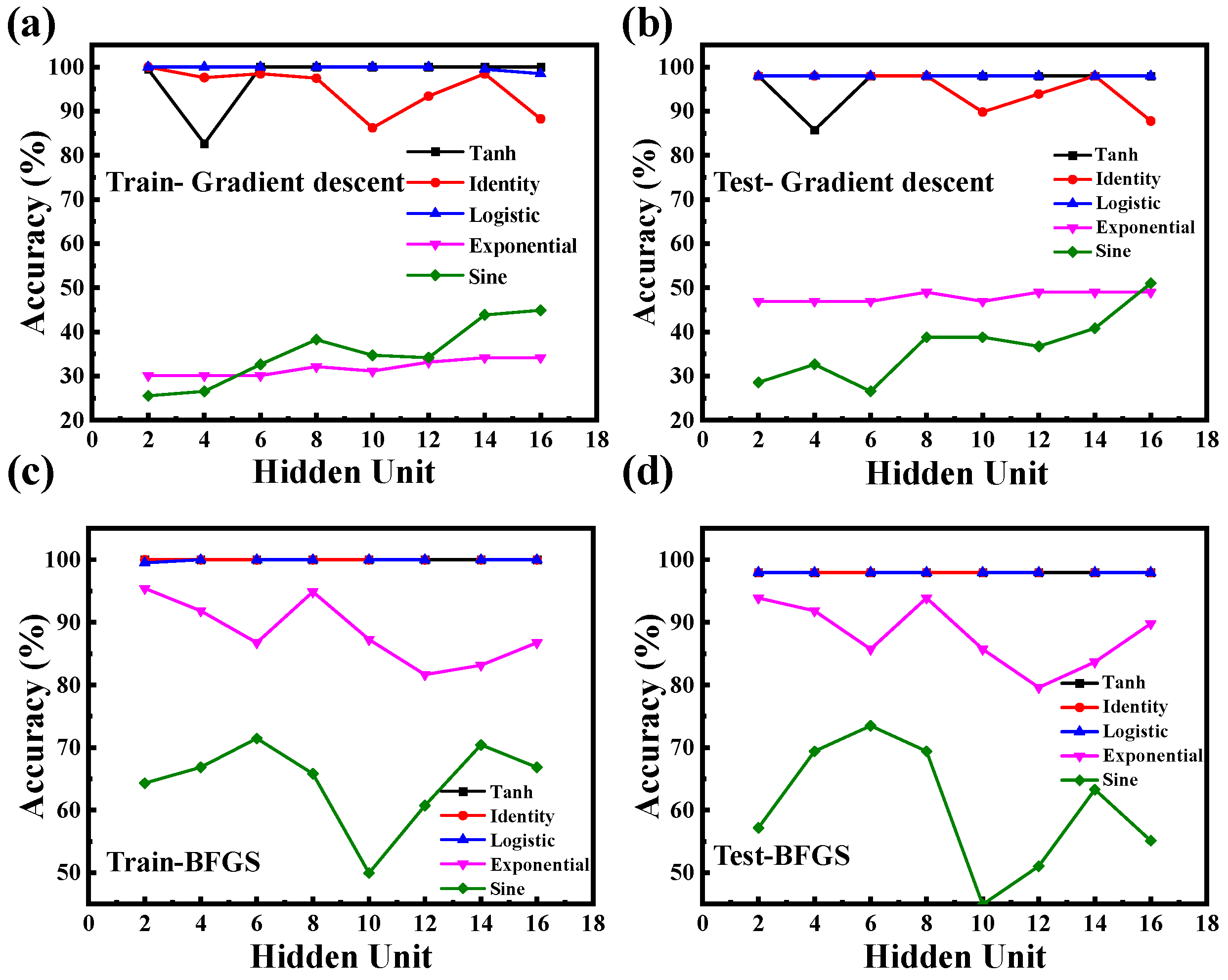
3.2. Deep Learning Analysis
3.3. Confusion Matrix Analysis
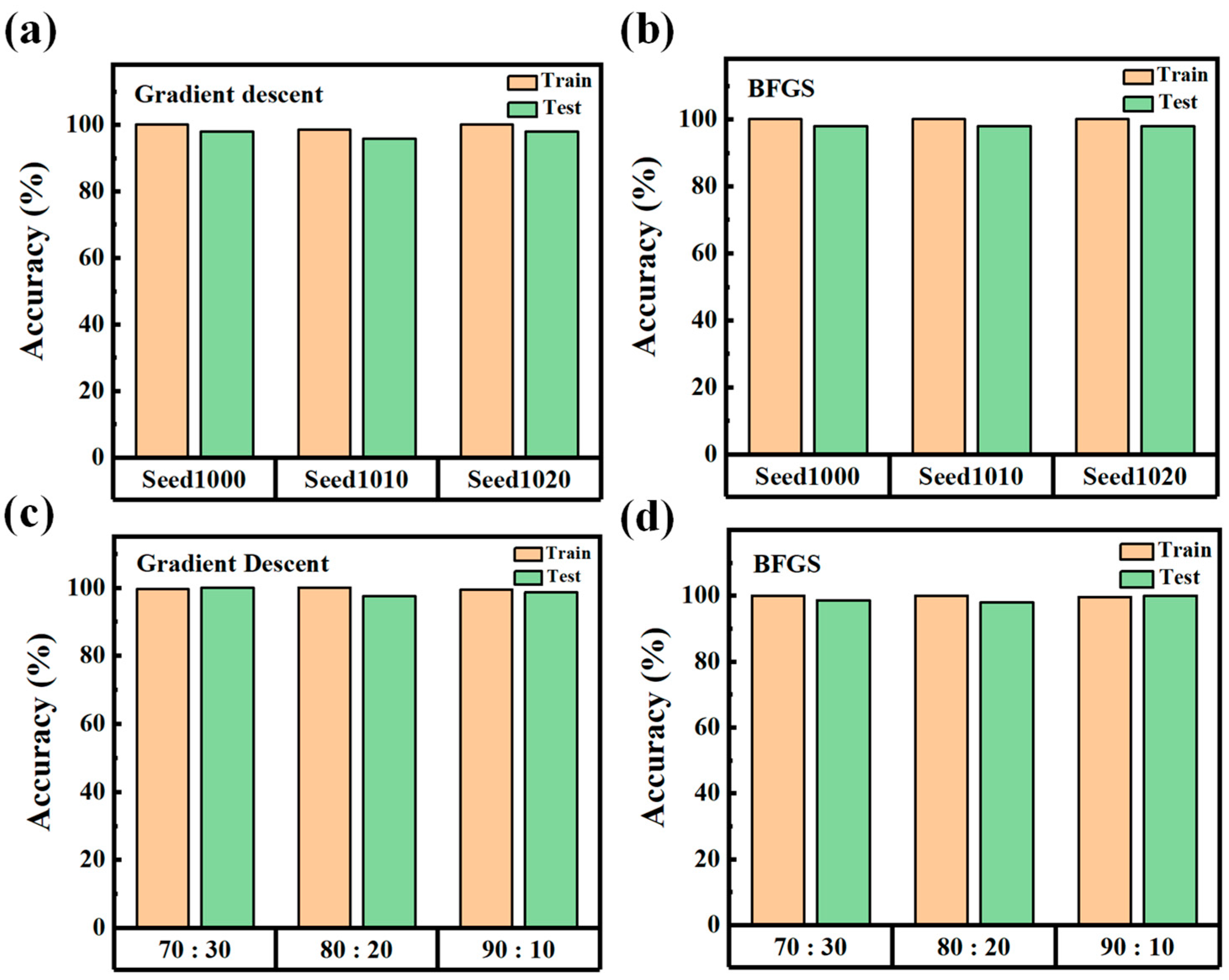
3.4. Robustness Evaluation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Choi, Y.; Kim, D.; Ryu, S.U.; Kim, H.; Kim, S.; Kim, M.; Park, T. Stability of Organic Photovoltaics: From Root Causes to Advanced Analytical Techniques. Adv. Energy Mater. 2025, 2501340, early view. [Google Scholar] [CrossRef]
- Kong, Y.; Chen, H.; Zuo, L. Understanding the Nonradiative Charge Recombination in Organic Photovoltaics: From Molecule to Device. Adv. Funct. Mater. 2025, 35, 2413864. [Google Scholar] [CrossRef]
- Zhang, S.; Li, S.; Song, S.; Zhao, Y.; Gao, L.; Chen, H.; Li, H.; Lin, J. Deep Learning-Assisted Design of Novel Donor–Acceptor Combinations for Organic Photovoltaic Materials with Enhanced Efficiency. Adv. Mater. 2025, 37, 2407613. [Google Scholar] [CrossRef] [PubMed]
- Mazzio, K.A.; Luscombe, C.K. The future of organic photovoltaics. Chem. Soc. Rev. 2015, 44, 78–90. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Zhang, M.; Zhou, Z.; Zhong, W.; Hao, T.; Xu, S.; Zeng, R.; Zhuang, J.; Xue, X.; Jing, H.; et al. Progress of organic photovoltaics towards 20% efficiency. Nat. Rev. Electr. Eng. 2024, 1, 581–596. [Google Scholar] [CrossRef]
- Chen, L.; Ma, R.; Yi, J.; Dela Peña, T.A.; Li, H.; Wei, Q.; Yan, C.; Wu, J.; Li, M.; Cheng, P.; et al. Exploiting the donor-acceptor-additive interaction’s morphological effect on the performance of organic solar cells. Aggregate 2024, 5, e455. [Google Scholar] [CrossRef]
- Bin, H.; Zhang, Z.G.; Gao, L.; Chen, S.; Zhong, L.; Xue, L.; Yang, C.; Li, Y. Non-fullerene polymer solar cells based on alkylthio and fluorine substituted 2D-conjugated polymers reach 9.5% efficiency. J. Am. Chem. Soc. 2016, 138, 4657–4664. [Google Scholar] [CrossRef] [PubMed]
- Bin, H.; Gao, L.; Zhang, Z.G.; Yang, Y.; Zhang, Y.; Zhang, C.; Chen, S.; Xue, L.; Yang, C.; Xiao, M.; et al. 11.4% Efficiency non-fullerene polymer solar cells with trialkylsilyl substituted 2D-conjugated polymer as donor. Nat. Commun. 2016, 7, 13651. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Moss, B.; Clarke, T.M. Quantifying triplet formation in conjugated polymer/non-fullerene acceptor blends. J. Mater. Chem. A 2022, 10, 20874–20885. [Google Scholar] [CrossRef]
- Rodríguez-Martínez, X.; Pascual-San-José, E.; Campoy-Quiles, M. Accelerating organic solar cell material’s discovery: High-throughput screening and big data. Energy Environ. Sci. 2021, 14, 3301–3322. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Lüer, L.; Heumueller, T.; Wagner, J.; Berger, C.; Osterrieder, T.; Wortmann, J.; Langner, S.; Vongsaysy, U.; Bertrand, M.; et al. Elucidating the full potential of OPV materials utilizing a high-throughput robot-based platform and machine learning. Joule 2021, 5, 495–506. [Google Scholar] [CrossRef]
- Treat, N.D.; Campos, L.M.; Dimitriou, M.D.; Ma, B.; Chabinyc, M.L.; Hawker, C.J. Nanostructured hybrid solar cells: Dependence of the open circuit voltage on the interfacial composition. Adv. Mater. 2010, 22, 4982–4986. [Google Scholar] [CrossRef] [PubMed]
- Jacoutot, P.; Scaccabarozzi, A.D.; Zhang, T.; Qiao, Z.; Aniés, F.; Neophytou, M.; Bristow, H.; Kumar, R.; Moser, M.; Nega, A.D.; et al. Infrared organic photodetectors employing ultralow bandgap polymer and non-fullerene acceptors for biometric monitoring. Small 2022, 18, 2200580. [Google Scholar] [CrossRef] [PubMed]
- Gambhir, A.; Sandwell, P.; Nelson, J. The future costs of OPV–A bottom-up model of material and manufacturing costs with uncertainty analysis. Sol. Energy Mater. Sol. Cells 2016, 156, 49–58. [Google Scholar] [CrossRef]
- Bernardo, G.; Lopes, T.; Lidzey, D.G.; Mendes, A. Progress in upscaling organic photovoltaic devices. Adv. Energy Mater. 2021, 11, 2100342. [Google Scholar] [CrossRef]
- Ukawa, T.; Takayanagi, T.; Morimoto, H.; Higashi, Y.; Idei, N.; Yoshizumi, M.; Tsuji, T. Novel non-invasive method of measurement of endothelial function: Enclosed-zone flow-mediated dilatation (ezFMD). Med. Biol. Eng. Comput. 2012, 50, 1239–1247. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.F.; Tseng, Z.C.; Hsueh, W.J.; Chen, J.H.; Huang, C.Y. Room-Temperature Gas Identification via Photochemically Activated p-type CuCrO2 Nanostructured Films Using Machine Learning. ACS Appl. Nano Mater. 2025, 8, 189–199. [Google Scholar] [CrossRef]
- Lin, P.T.; Tseng, Z.C.; Huang, C.Y. Machine Learning Assisted Wavelength Recognition in Cu2O/Si Self-Powered Photodetector Arrays for Advanced Image Sensing Applications. ACS Appl. Electron. Mater. 2025, 7, 225–235. [Google Scholar]
- Bayram, S.; Ocal, M.E.; Laptali Oral, E.; Atis, C.D. Comparison of multi layer perceptron (MLP) and radial basis function (RBF) for construction cost estimation: The case of Turkey. J. Civ. Eng. Manag. 2016, 22, 480–490. [Google Scholar] [CrossRef]
- Wu, T.H.; Tseng, Z.C.; Huang, C.Y. Recognition of NO2 and O3 gases using patterned Cu2O nanoparticles on IGZO thin films through machine learning. J. Mater. Chem. C 2024, 12, 18427–18434. [Google Scholar] [CrossRef]
- Parini, A.; Bellanca, G.; Trillo, S.; Saccomandi, L.; Bassi, P. Transfer matrix and full Maxwell time domain analysis of nonlinear gratings. Opt. Quant. Electron. 2004, 36, 189–199. [Google Scholar] [CrossRef]
- Kerremans, R.; Kaiser, C.; Li, W.; Zarrabi, N.; Meredith, P.; Armin, A. The optical constants of solution-processed semiconductors—New challenges with perovskites and non-fullerene acceptors. Adv. Opt. Mater. 2020, 8, 2000319. [Google Scholar] [CrossRef]
- Lin, M.Y.; Wu, S.H.; Hsiao, L.J.; Budiawan, W.; Boopathi, K.M.; Tu, W.C.; Chang, Y.C.; Chu, C.W. Enhance the light-harvesting capability of the ITO-free inverted small molecule solar cell by ZnO nanorods. Opt. Express 2016, 24, 17910–17915. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.Y.; Kang, Y.L.; Chen, Y.C.; Tsai, T.H.; Lin, S.C.; Huang, Y.H.; Chen, Y.J.; Lu, C.Y.; Lin, H.Y.; Wang, L.A. Plasmonic ITO-free polymer solar cell. Opt. Express 2014, 22, A438–A445. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Li, Y.; Xiao, L.; Qiao, Q.; Dhakal, R.; Zhang, Z.; Gong, Q.; Galipeau, D.; Yan, X. Femtosecond time-resolved fluorescence study of P3HT/PCBM blend films. J. Phys. Chem. C 2010, 114, 14590–14600. [Google Scholar] [CrossRef]
- Geng, Y.; Li, T.; Zhang, Z.; Lin, Y. To Maximize Luminescence for an Efficient Organic Solar Cell. Chin. J. Chem. 2024, 42, 3157–3168. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, H.; Jain, S.C.; Venkatesu, P.; Chand, S.; Kumar, V. Effect of active layer thickness on open circuit voltage in organic photovoltaic devices. Jpn. J. Appl. Phys. 2009, 48, 121501. [Google Scholar] [CrossRef]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation functions in deep learning: A comprehensive survey and benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar] [CrossRef]
- Schittenkopf, C.; Deco, G.; Brauer, W. Two strategies to avoid overfitting in feedforward networks. Neural Netw. 1997, 10, 505–516. [Google Scholar] [CrossRef]
- Badem, H.; Basturk, A.; Caliskan, A.; Yuksel, M.E. A new efficient training strategy for deep neural networks by hybridization of artificial bee colony and limited–memory BFGS optimization algorithms. Neurocomputing 2017, 266, 506–526. [Google Scholar] [CrossRef]
- Wei, Z.; Yu, G.; Yuan, G.; Lian, Z. The superlinear convergence of a modified BFGS-type method for unconstrained optimization. Comput. Optim. Appl. 2004, 29, 315–332. [Google Scholar] [CrossRef]
- Huang, C.Y.; Huang, B.L.; Liao, S.Y.; Huang, Y.Y.; Ma, Y.L.; Lin, P.T.; Chen, J.H.; Hsu, C.J.; Huang, C.Y. High-precision liquid crystal cell gap estimation via machine learning. Optik 2025, 327, 172314. [Google Scholar] [CrossRef]
- Lin, P.T.; Tseng, Z.C.; Huang, C.Y. Optical fingerprint for gas identification at room temperature using light-activated a-IGZO thin films and machine learning. Sens. Actuators A Phys. 2025, 388, 116482. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.-H.; Zhang, Y.-L.; Cheng, C.-H.; Wu, S.-H.; Li, C.-H.; Liao, S.-Y.; Tseng, Z.-C.; Lin, M.-Y.; Huang, C.-Y. Non-Invasive Composition Identification in Organic Solar Cells via Deep Learning. Nanomaterials 2025, 15, 1112. https://doi.org/10.3390/nano15141112
Chang Y-H, Zhang Y-L, Cheng C-H, Wu S-H, Li C-H, Liao S-Y, Tseng Z-C, Lin M-Y, Huang C-Y. Non-Invasive Composition Identification in Organic Solar Cells via Deep Learning. Nanomaterials. 2025; 15(14):1112. https://doi.org/10.3390/nano15141112
Chicago/Turabian StyleChang, Yi-Hsun, You-Lun Zhang, Cheng-Hao Cheng, Shu-Han Wu, Cheng-Han Li, Su-Yu Liao, Zi-Chun Tseng, Ming-Yi Lin, and Chun-Ying Huang. 2025. "Non-Invasive Composition Identification in Organic Solar Cells via Deep Learning" Nanomaterials 15, no. 14: 1112. https://doi.org/10.3390/nano15141112
APA StyleChang, Y.-H., Zhang, Y.-L., Cheng, C.-H., Wu, S.-H., Li, C.-H., Liao, S.-Y., Tseng, Z.-C., Lin, M.-Y., & Huang, C.-Y. (2025). Non-Invasive Composition Identification in Organic Solar Cells via Deep Learning. Nanomaterials, 15(14), 1112. https://doi.org/10.3390/nano15141112







