Abstract
This work explores the physical properties of the MAX-phase material Cr3AlC2 through the application of density functional theory (DFT). The refined lattice parameters were determined through the minimization of the total energy. In order to explore the electronic properties and bonding features, we carried out computations on the band structure and charge density distribution. The calculated elastic constants (Cij) validated the mechanical stability of Cr3AlC2. To assess the material’s ductility or brittleness, we calculated Pugh’s ratio, Poisson’s ratio, and Cauchy pressure. The hardness was determined. This study examined the anisotropic behavior of Cr3AlC2 using directional analyses of its elastic properties and by computing relevant anisotropy indicators. We examined several key properties of Cr3AlC2, including the Grüneisen parameter, acoustic characteristics, Debye temperature, thermal conductivity, melting point, heat capacity, Helmholtz free energy, entropy, and internal energy. Phonon dispersion spectra were analyzed to assess the dynamic stability of Cr3AlC2.
1. Introduction
Cr3AlC2, which belongs to the renowned MAX-phase family, exhibits unique attributes that combine the advantages of both metals and ceramics. The material is distinguished by its reduced density, superior resistance to oxidation, notable ductility, efficient electrical conductivity, self-lubricating properties, and favorable machinability [1,2,3,4,5]. These exceptional characteristics make Ti3AlC2 a material of significant technological interest, with great potential for applications at high temperatures. As a result, both Ti3AlC2 and its structurally analogous compound Ti3SiC2 have been extensively investigated [6]. These results are emphasized in a recent review article [7], focusing on layered, electrically conductive Ti2AlC and Ti3AlC2, as well as in another study by Barsoum [8]. Much of the prior research has focused on comprehending and modeling M2AX materials [9,10,11,12]. For M3AX2 phases, only a limited number of compounds have been examined, with Ti3SiC2 and Ti3AlC2 being notable exceptions [13]. However, as mentioned earlier, many M3AX2 compounds have recently been synthesized. For example, Ta3AlC2 was synthesized from metallic melts [14], whereas Ti3SnC2 was discovered by Dubois and colleagues [15]. Thus, a theoretical study of M3AX2 phases is both pertinent and essential for gaining insights into their characteristics. To date, it is commonly acknowledged that Ti3AlC2 and Ti2AlC exhibit superior oxidation resistance compared to Ti3SiC2 [16,17]. This exceptional oxidation resistance is believed to result from the development of a protective, dense Al2O3 surface layer. Given the assumption that other M3AlC2 compounds might also exhibit oxidation resistance similarly to Ti3AlC2, studying them would prove beneficial. To the best of our knowledge, apart from the significant case of Ti3AlC2, the properties of M3AlC2 compounds have not been thoroughly explored. The purpose of this study is to fill this research gap. The overall characteristics of the crystal structure, electronic properties, and elastic behavior of Cr3AlC2 were thoroughly examined.
2. Theoretical Methods
The characteristics of Cr3AlC2 were investigated by employing the DFT method, utilizing the Vienna ab initio simulation code [18]. The electron–nucleus interaction was modeled using pseudopotentials created through the projector-augmented wave (PAW) approach [19]. The exchange–correlation energy was calculated based on the generalized gradient approximation (GGA) in conjunction with the Perdew–Burke–Ernzerhof (PBE) functional [20]. Convergence tests indicated that a cutoff energy of 480 eV and k-point mesh of 8 × 8 × 10 were appropriate for achieving accurate results. An energy convergence criterion of 10−4 eV/cell was used, together with a force convergence threshold of 0.001 eV/Å for minimizing Hellmann–Feynman forces. Furthermore, the dynamic stability of Cr3AlC2 was assessed through phonon frequency analysis. Phonon computations were performed utilizing a 2 × 1 × 2 supercell, employing the Phonopy package [21,22].
3. Results and Discussion
3.1. Structural Properties
As shown in Figure 1, Cr3AlC2 adopts a hexagonal crystal structure belonging to the P63/mmc (194) space group. Table 1 presents the calculation results of this study as well as the relevant reference data [23]. The resulting values show reasonable consistency when contrasted with theoretical predictions. Notably, the difference between the computed lattice parameters and the theoretical values remains below 0.69%. Furthermore, Table 1 also provides the pressure-dependent lattice parameters, density, and volume.
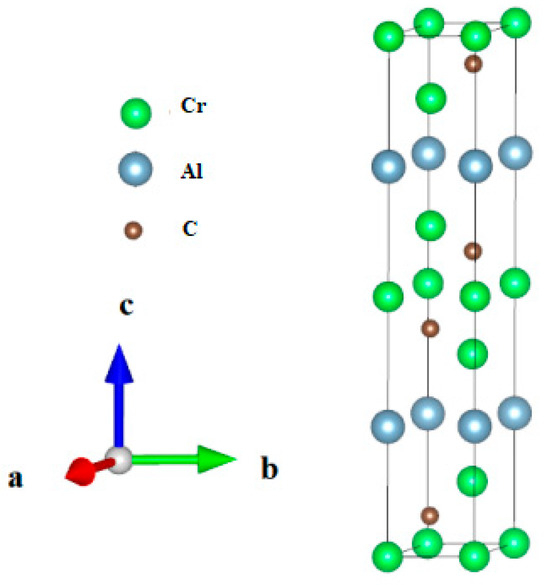
Figure 1.
The crystal model of Cr3AlC2.

Table 1.
The optimized lattice parameters a and c (Å), density ρ (g/cm3), and volume V (Å3) of Cr3AlC2.
3.2. Electronic Properties
In Figure 2, the band structure of Cr3AlC2 is presented. At EF (Fermi energy level), the conduction and valence bands overlap, confirming the metallic nature of Cr3AlC2. Additionally, we calculated the density of states for Cr3AlC2 to analyze the bonding properties and contributions of various electronic states. The valence band is divided into two distinct sub-bands. (i) The lowest valence band spans from −15.0 to −10 eV for Cr3AlC2, where most of the states in this total density of states region are attributed to C-s orbitals, with minor contributions from Cr-s and Cr-p states. (ii) The upper valence band of Cr3AlC2 lies between −10 and 0.0 eV. It should be emphasized that the hybridization peak between Cr-d and C-p states appears in the lower-energy region, whereas the Cr-d peak is situated in the higher-energy range, close to the Fermi level (EF) (Figure 3).
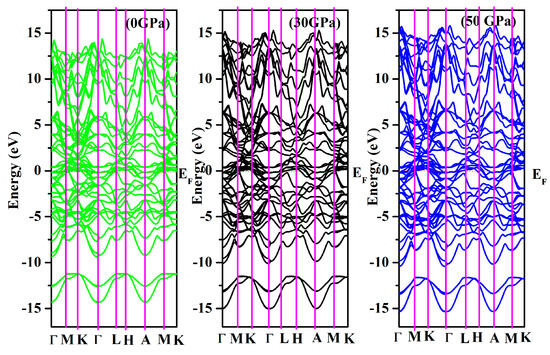
Figure 2.
The band structure of Cr3AlC2 under various pressures.
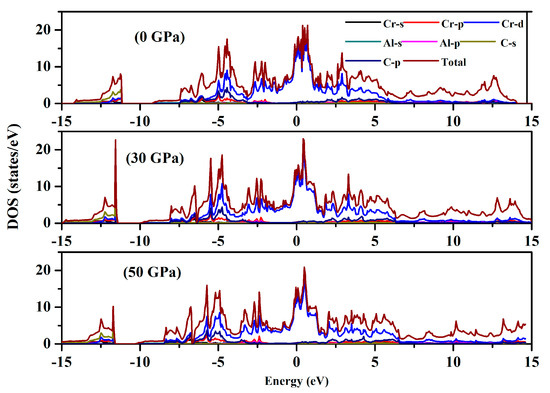
Figure 3.
Density of states of Cr3AlC2 under various pressures.
Figure 4 displays the charge density mapping (CDM) on the (101) plane, which provides insights into the bonding interactions among different atoms. With increasing pressure from 0 to 50 GPa, a significant enhancement in charge density is evident at specific locations. This elevated charge density enhances the bonding between Cr and C atoms, attributed to the overlapping of their electronic states. The CDM results indicate that the Cr-C bond exhibits greater strength compared to the Al-C bond.
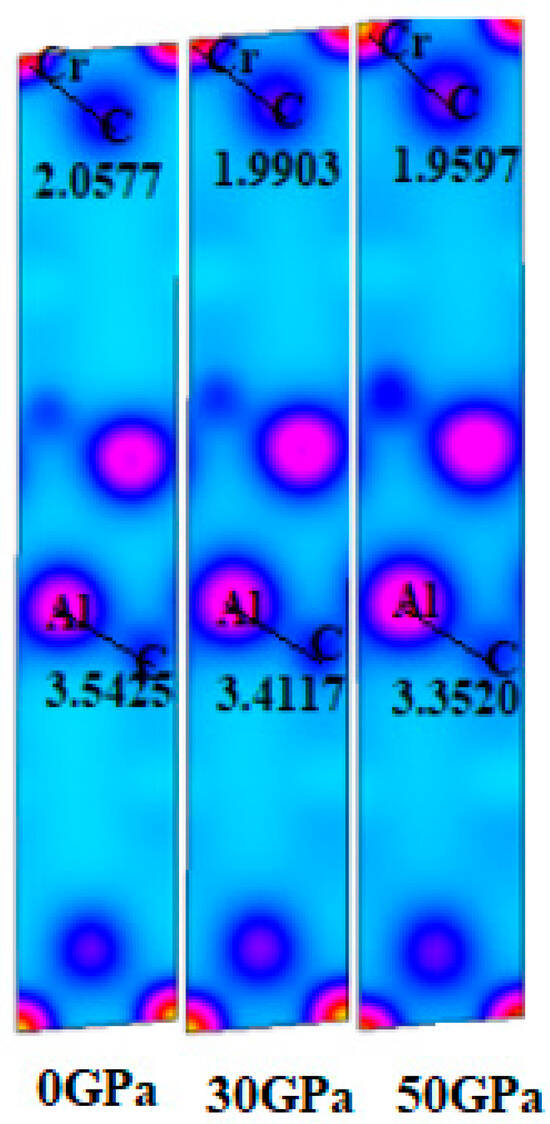
Figure 4.
CDM of Cr3AlC2 under various pressures.
3.3. Mechanical Properties
The elastic constants Cij of Cr3AlC2 under various pressure conditions are presented in Table 2. Based on the Born criteria, the mechanical stability requirements at equilibrium are influenced by different crystal symmetries [24]:
C44 > 0; C11 + C12 − 2C132/C33 > 0; and C11 − C12 > 0

Table 2.
Calculated Cij (GPa), elastic moduli (GPa), and E (GPa) of Cr3AlC2.
As shown in Table 2, the calculated Cij values for Cr3AlC2 align well with the corresponding theoretical values [23], suggesting that the current computational results are accurate. Based on the Voigt [25] and Reuss [26] methods, we calculated the values of bulk modulus (B) and shear modulus (G) using Hill’s approximation [27]. The computed values are summarized in Table 2, together with other previously reported results [23]. As shown in Table 2, the calculated B, G, and Young’s modulus (E) of Cr3AlC2 at 0 GPa are 207.0 GPa, 118.6 GPa, and 298.8 GPa, respectively, which align well with earlier findings. Table 3 presents Poisson’s ratio (v), G/B ratio, C13–C44, and C12–C66 values for Cr3AlC2 [28]. The mechanical behavior of brittleness or ductility can be evaluated using these parameters. A material is considered brittle if ν < 0.33, G/B > 0.57, C13–C44 < 0, and C12–C66 < 0; otherwise, it is classified as ductile. In Table 3, it is clear that Cr3AlC2 exhibits Poisson’s ratios (ν) below 0.33, G/B < 0.57, negative C13–C44 values, and negative C12-C66 values. These results indicate that Cr3AlC2 demonstrates brittle characteristics.

Table 3.
Calculated G/B, Poisson’s ratio v, C13–C44, and C12–C66 of Cr3AlC2.
According to the literature [29,30,31], we can calculate various anisotropic parameters of the material such as three shear anisotropic factors, A1, A2, and A3, percentage anisotropy in compressibility (AB) and shear (AG), and the universal anisotropic index AU. As shown in Table 4, the Cr3AlC2 under consideration exhibits anisotropic behavior since the values of A1, A2, and A3 differ from unity. The non-zero values of AB, AG, and AU (as shown in Table 4) confirm the anisotropic nature of Cr3AlC2.

Table 4.
Calculated elastic anisotropic factors of Cr3AlC2.
To offer more distinct and thorough insight into the anisotropic properties of the investigated materials, we employed both two-dimensional (2D) and three-dimensional (3D) graphical representations of linear compressibility β, E, and G by ELATE software [32,33,34]. Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 present the 2D and 3D visualizations produced. A perfect sphere represents complete isotropy in solids, while deviations from this spherical shape indicate varying degrees of anisotropy (Figure 5, Figure 6 and Figure 7). Figure 8 illustrates the anisotropy in β, where the xy-plane shows isotropic behavior, and the xz- and yz-planes show anisotropic behavior. E also demonstrates anisotropic behavior, as depicted in Figure 9. This figure reveals that E exhibits isotropic properties within the xy-plane but displays anisotropic characteristics in the xz- and yz-planes. The graphs indicate that for Cr3AlC2, the blue line achieves its peak values along the axes in both the xz- and yz-planes, while it reaches its lowest value at a 45-degree angle relative to these axes. The shear modulus presents two surfaces in both 2D and 3D representations, as shown in Figure 10. Additionally, Table 5 provides the βmax/βmin, Gmax/Gmin, and Emax/Emin values of β, E, and G for Cr3AlC2, confirming its significant anisotropic properties. As the pressure increases, the anisotropy also strengthens.

Figure 5.
The β (TPa−1) surface characteristics of Cr3AlC2 under various pressures.
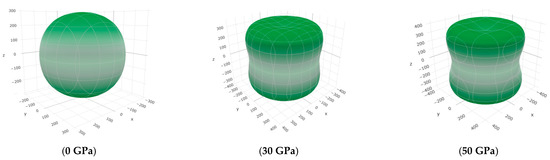
Figure 6.
The E (GPa) surface characteristics of Cr3AlC2 under various pressures.
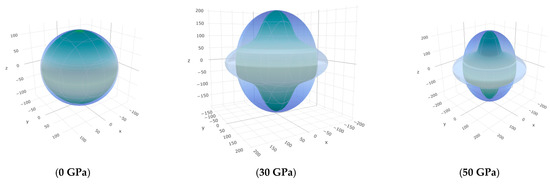
Figure 7.
The G (GPa) surface characteristics of Cr3AlC2 under various pressures.
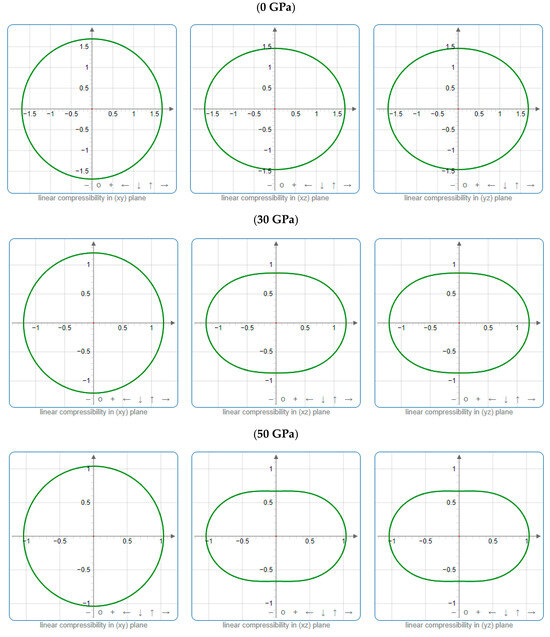
Figure 8.
Projections of β (TPa−1) in different planes of Cr3AlC2 under various pressures.
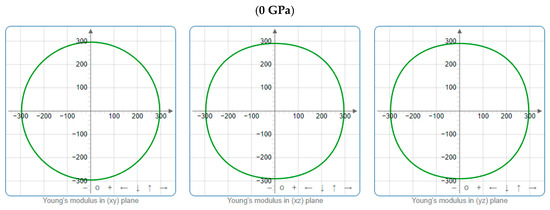
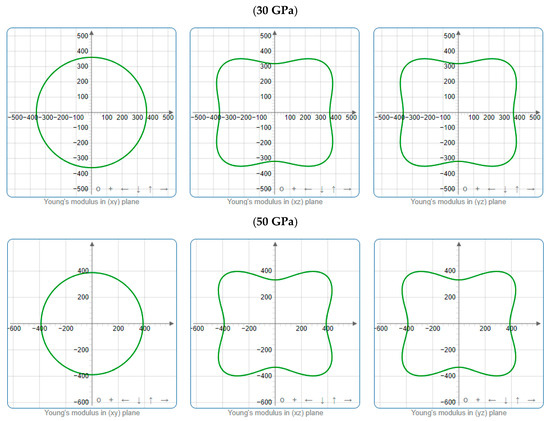
Figure 9.
Projections of E (GPa) in different planes of Cr3AlC2 under various pressures.
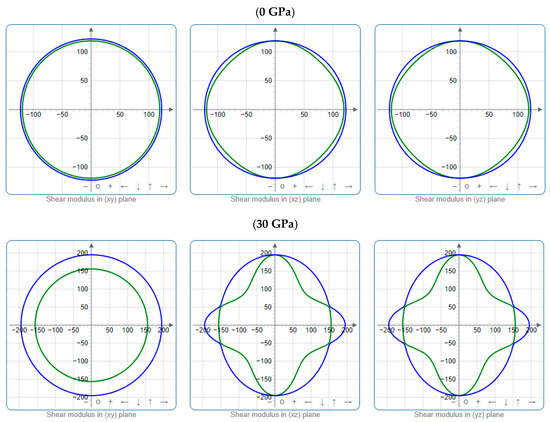
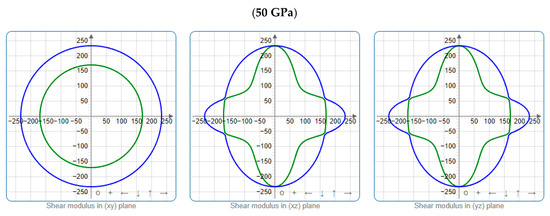
Figure 10.
Projections of G (GPa) in different planes of Cr3AlC2 under various pressures.

Table 5.
The values of βmax/βmin, Gmax/Gmin, and Emax/Emin of Cr3AlC2 under various pressures.
In this study, we computed both the Chen hardness (Hchen) and the Miao hardness (Hmiao) [35,36].
Fine’s principle establishes the criteria for defining the melting point of a solid [37,38].
Tm = 354 + 4.5(2C11 + C33)/3
The thermal conductivity κ of the material is obtained from the Clarke model [39]:
Here, kB is Boltzmann’s constant, ρ is the density, Ma is the average mass per atom, and Young’s modulus (E).
Furthermore, based on a method in the literature, we were able to calculate the average sound velocity vm, the longitudinal velocity (vl), the transverse velocity (vt), and the Debye temperature θ [40]. In addition, the Grüneisen γa can be described by vl and vt [41]:
The changes in vl, vt, vm, and θ under various pressures are summarized in Table 6. The θ, vl, vt, and vm at 0 GPa are determined to be 702.4 K, 7.1182 km/s, 3.8357 km/s, and 4.2820 km/s, respectively. The values for HV, Tm, γa, and κ of Cr3AlC2 are provided in Table 6. The melting point of Cr3AlC2 is recorded as 1985.9 K under 0 GPa. If the maximum operational temperature is estimated as 0.8 Tm, then the maximum service temperature of Cr3AlC2 approaches approximately 1300 °C, suggesting that Cr3AlC2 possesses favorable thermal stability for practical applications. As shown in Table 6, when the pressure increases, HV, Tm, γa, and k tend to rise. Furthermore, the hardness values for Cr3AlC2 obtained using Chen’s and Miao’s models at 0 GPa are 11.189 and 15.455 GPa, respectively. And our hardness is slightly greater than that of materials of the same type (Ti3AlC2 and Ti3SiC2) [13]. The hardness values calculated using the two methods are presented in Table 6. It has been observed that there is strong concurrence between them, suggesting the accuracy of the computation.

Table 6.
The hardness (HChen and HMiao) (GPa), wave velocity (vl, vt, vm) (km/s), Debye temperature θ (K), Grüneisen constant γa, melting point Tm (K), and thermal conductivity k (W.m−1 K−1) of Cr3AlC2.
3.4. Dynamical Properties
To ensure that the dynamical stability is thoroughly examined, it becomes imperative to conduct an analysis of the phonon dispersion of Cr3AlC2, when subjected to elevated pressure. The phonon dispersion and phonon density of state for Cr3AlC2 were calculated at 0 GPa, 30 GPa, and 50 GPa, as depicted in Figure 11 and Figure 12. It is clear that Cr3AlC2 exhibits dynamical stability, as no imaginary phonon frequencies are detected in this crystal structure. In correlation with the representation of the phonon density of state illustrated in Figure 12, the frequency range of 0–15 THz primarily corresponds to Cr and Al vibrations, while the frequency range of 15–25 THz predominantly corresponds to C vibrations.
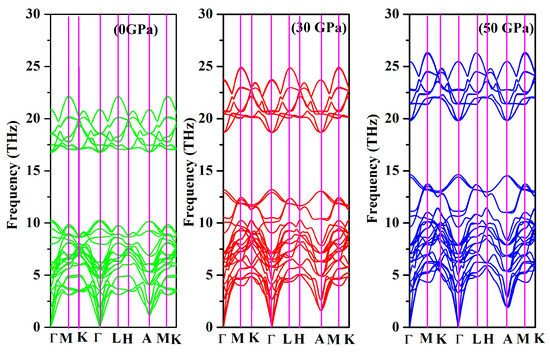
Figure 11.
Phonon dispersion of Cr3AlC2 under various pressures.
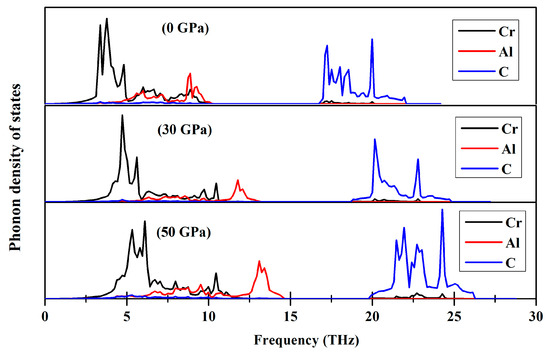
Figure 12.
Phonon density of states of Cr3AlC2 under various pressures.
3.5. Thermal Properties
The thermodynamic potential functions of Cr3AlC2 were calculated based on the phonon density of states obtained using the quasi-harmonic approximation [42]. These functions include the internal energy E, Helmholtz free energy F, and entropy S. Figure 13 shows S and CV as functions of temperature. Below 50 K, the S values are nearly zero, as shown in Figure 13a. Above 100 K, there is a noticeable nonlinear increase, a trend that is quite common and becomes increasingly evident with increasing temperature as natural processes evolve. Figure 13b depicts CV for Cr3AlC2 across the temperature interval from 0 to 1000 K. At T < 300 K, CV follows the Debye T3 power law, while at T > 800 K, it closely aligns with the Dulong–Petit model. Table 7 presents F and E at various temperatures and pressures. These thermodynamic results are expected to provide a valuable reference for the practical utilization of Cr3AlC2.
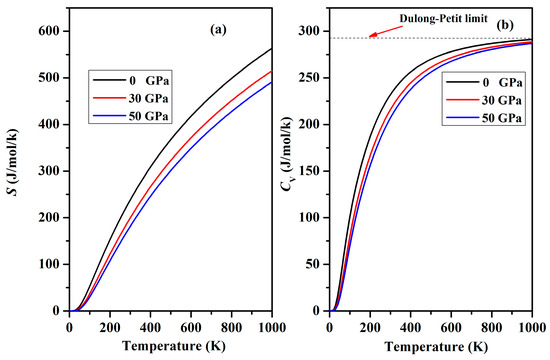
Figure 13.
Changes in heat capacity CV and entropy S with temperature under various pressures. (a) Heat capacity CV (b) Entropy S.

Table 7.
The calculated F (KJ/mol) and E (KJ/mol) of Cr3AlC2 under various pressures.
4. Conclusions
In this study, a thorough investigation of Cr3AlC2 was conducted based on DFT. The mechanical properties were examined in detail under varying pressure conditions. Additionally, the calculated phonon dispersion further validates the material’s dynamical stability. This compound demonstrates a reasonable level of mechanical anisotropy alongside sufficient hardness. All thermal properties exhibit distinctive behavior across the pressure range from 0 to 50 GPa. However, these properties (θ, γa, Tm, and k) gradually increase as pressure rises to 50 GPa. We believe that these results will encourage researchers to delve deeper into this material, both through theoretical modeling and experimental exploration.
Author Contributions
Software, Q.F.; Formal analysis, Q.F.; Investigation, H.H.; Writing—original draft, J.Y. and Q.F.; Supervision, S.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (52262042), Leshan Normal University (grant nos. 2021SSDJS013, KYPY2023-0028, KYPY2024-0008), and the Opening Project of Crystalline Silicon Photovoltaic New Energy Research Institute (grant nos. 2022CHXK009, 2022CHXK013); Key Laboratory of Sichuan Province for Bamboo Pests Control and Resource Development (ZLKF202307); and Science and Technology Bureau of Leshan City (grant nos. 23GZD023, 23SZD044).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Barsoum, M.W.; Brodkin, D.; El-Raghy, T. Layered machinable ceramics for high temperature applications. Scr. Mater. 1997, 36, 535. [Google Scholar] [CrossRef]
- Barsoum, M.W. Thermodynamically stable nanolaminates. Prog. Solid State Chem. Prog. Solid State Chem. 2000, 28, 201. [Google Scholar] [CrossRef]
- Tzenovm, N.V.; Barsoum, M.W. Synthesis and Characterization of Ti3AlC2. J. Am. Ceram. Soc. 2000, 83, 825. [Google Scholar] [CrossRef]
- Sun, Z.; Zhou, Y.; Li, M. High temperature oxidation behavior of Ti3SiC2-based material in air. Acta Mater. 2001, 49, 4347–4353. [Google Scholar] [CrossRef]
- Palmquist, J.P.; Li, S.; Persson, P.O.A.; Emmerlich, J.; Wilhelmsson, O.; Hogberg, H.; Katsnelson, M.I.; Johansson, B.; Ahuja, O.; Eriksson, L.; et al. Mn+1AXn phases in the Ti-Si-C system studied by thin-film synthesis and ab initio calculations. Phys. Rev. B 2004, 70, 165401. [Google Scholar] [CrossRef]
- Xie, X.; Li, X.Q.; Jia, Q.; Bai, C.G.; Malzbende, J.; Cui, Y.Y.; Yang, R. Mechanical properties and toughening mechanisms of highly textured Ti3AlC2 composite material. J. Am. Ceram. Soc. 2022, 42, 5493–5504. [Google Scholar] [CrossRef]
- Wang, J.Y.; Zhou, Y.C. First-principles study of equilibrium properties and electronic structure of Ti3Si0.75Al0.25C2 solid solution. J. Phys. Condens. Matter 2003, 15, 5959. [Google Scholar] [CrossRef]
- Barsoum, M.W.; El-Raghy, T. Synthesis and Characterization of a Remarkable Ceramic: Ti3SiC2. J. Am. Ceram. Soc. 1996, 79, 1953–1956. [Google Scholar] [CrossRef]
- Sun, Z.M.; Music, D.; Ahuja, R.; Schneider, J.M. Theoretical investigation of the bonding and elastic properties of nanolayered ternary nitrides. Phys. Rev. B 2005, 71, 193402. [Google Scholar] [CrossRef]
- Hug, G. Electronic structures of and composition gaps among the ternary carbides Ti2MC. Phys. Rev. B 2006, 74, 184113. [Google Scholar] [CrossRef]
- Daoudi, B.; Yakoubi, A.; Beldi, L.; Bouhafs, B. Full-potential electronic structure of Hf2AlC and Hf2AlN. Acta Mater. 2007, 55, 4161–4165. [Google Scholar] [CrossRef]
- Bai, Y.; He, X.; Li, M.; Sun, Y.; Zhu, C.; Li, Y. Chemical bonding and elastic properties of Ti3AC2 phases (A = Si, Ge, and Sn): A first-principle study. Solid State Sci. 2009, 12, 144–147. [Google Scholar] [CrossRef]
- Ali, M.S.; Islam, A.K.M.A.; Hossain, M.M.; Parvin, F. Phase stability, elastic, electronic, thermal and optical properties of Ti3Al1-xSixC2 (0≤ x ≤1): First principle study. Phys. B 2012, 407, 4221–4228. [Google Scholar] [CrossRef]
- Etzkorn, J.; Ade, M.; Hillebrecht, H. Ta3AlC2 and Ta4AlC3-Single-Crystal Investigations of Two New Ternary Carbides of Tantalum Synthesized by the Molten Metal Technique. Inorg. Chem. 2007, 46, 1410–1418. [Google Scholar] [CrossRef]
- Dubois, S.; Cabioch, T.; Chartier, P.; Gauthier, V.; Jaouen, M. A New Ternary Nanolaminate Carbide: Ti3SnC2. J. Am. Ceram. Soc. 2007, 90, 2642–2644. [Google Scholar] [CrossRef]
- Wang, X.H.; Zhou, Y.C. Oxidation behavior of Ti3AlC2 powders in flowing air. J. Mater. Chem. 2002, 12, 2781–2785. [Google Scholar] [CrossRef]
- Lee, D.B. High-temperature oxidation of Ti3AlC2 between 1173 and 1473 K in air. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2006, 434, 147–154. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K. Ernzerhof, Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Togo, A.; Oba, F.; Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and -type at high pressures. Phys. Rev. B 2008, 78, 134106. [Google Scholar] [CrossRef]
- Fan, Q.; Hou, H.J.; Yang, J.H. Effect of pressures on the structural, electronic, optical, elastic, dynamical properties and thermal properties of Mo2C: A study explored by theoretical simulation. Int. J. Refract. Met. H. 2024, 119, 106522. [Google Scholar] [CrossRef]
- He, X.D.; Bai, Y.L.; Zhu, C.C.; Sun, Y.; Li, M.; Barsoum, M.W. General trends in the structural, electronic and elastic properties of the M3AlC2 phases (M = transition metal): A first-principle study. Comp. Mate. Sci. 2010, 49, 691–698. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. ZAMM J. Appl. Math. Mech. Zeitschrif Für Angew. Math. Mech. 1929, 9, 49. [Google Scholar] [CrossRef]
- Brazhkin, V.V. High-pressure synthesized materials: Treasures and hints. High Press. Res. 2007, 27, 333. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823. [Google Scholar] [CrossRef]
- Vasilyev, D.; Ikhsanov, R.S.; Zheleznyi, M.; Kartsev, A. Calculations of elastic and thermal properties of the strengthening C14 Fe6Nb4Al2 Laves phase using the density functional theory. J. Mater. Sci. 2025, 60, 5427. [Google Scholar] [CrossRef]
- Chung, D.H.; Buessem, W.R.; Vahldiek, F.W.; Mersol, S.A. Anisotropy in Single Crystal Refractory Compound; Plenum: New York, NY, USA, 1968. [Google Scholar]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 1010, 55504. [Google Scholar] [CrossRef]
- Fan, Q.; Zhang, S.R.; Hou, H.J.; Yang, J.H. First-Principles to Explore the Pressure on the Structural, Mechanical, Electronic Structure and Thermodynamic Properties of Nb2C. Int. J. Quantum Chem. 2025, 125, e70040. [Google Scholar] [CrossRef]
- Fan, Q.; Zhang, S.R.; Hou, H.J.; Yang, J.H. Predictions of structural stability, elastic anisotropy and thermodynamic properties of TM5Si3C (TM = Cr, Mo, and W). Vacuum 2023, 208, 111648. [Google Scholar] [CrossRef]
- Gaillac, R.; Pullumbi, P.; Coudert, F.-X. ELATE: An open-source online application for analysis and visualization of elastic tensors. J. Phys. Condens. Matter 2016, 28, 275201. [Google Scholar] [CrossRef] [PubMed]
- Qureshi, M.W.; Ma, X.X.; Tang, G.Z.; Paude, R. Ab initio predictions of structure and physical properties of the Zr2GaC and Hf2GaC MAX phases under pressure. Sci. Rep. 2021, 11, 3260. [Google Scholar] [CrossRef]
- Kabir, M.H.; Hossain, M.M.; Ali, M.A.; Uddin, M.M.; Ali, M.L.; Hasan, M.Z.; Islam, A.K.M.A.; Naqib, S.H. First principles study of mechanical, thermal, electronic, optical and superconducting properties of C40-type germanide-based MGe2 (M = V, Nb and Ta). Results Phys. 2023, 51, 106701. [Google Scholar] [CrossRef]
- Ali, M.A.; Hossain, M.M.; Uddin, M.M.; Islam, A.K.M.A.; Naqib, S.H. Understanding the improvement of thermo-mechanical and optical properties of 212 MAX phase borides Zr2AB2 (A = In, Tl). J. Mater. Res. Technol. 2021, 15, 2227. [Google Scholar] [CrossRef]
- Rana, M.R.; Islam, S.; Hoque, K.; Biswas, G.G.; Hossain, M.E.; Naqib, S.H.; Ali, M.A. DFT prediction of the stability and physical properties of M2GaB (M = Sc, V, Nb, Ta). J. Mater. Res. Technol. 2023, 24, 7795. [Google Scholar] [CrossRef]
- Ali, M.A. Muhammad Waqas Qureshi, DFT insights into the new Hf-based chalcogenide MAX phase Hf2SeC. Vacuum 2022, 201, 111072. [Google Scholar] [CrossRef]
- Ali, M.A.; Hossain, M.M.; Uddin, M.M.; Hossain, M.A.; Islam, A.K.M.A.; Naqib, S.H. Physical properties of new MAX phase borides M2SB (M = Zr, Hf and Nb) in comparison with conventional MAX phase carbides M2SC (M = Zr, Hf and Nb): Comprehensive insights. J. Mater. Res. Technol. 2021, 11, 1000. [Google Scholar] [CrossRef]
- Arab, F.; Sahraoui, F.A.; Haddadi, K.; Bouhemadou, A.; Louail, L. Phase stability, mechanical and thermodynamic properties of orthorhombic and trigonal MgSiN2: An ab initio study. Phase Transit. 2016, 89, 480. [Google Scholar] [CrossRef]
- Lee, C.; Gonze, X. Ab initio calculation of the thermodynamic properties and atomic temperature factors of SiO2 α-quartz and stishovite. Phys. Rev. B 1995, 51, 8610. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).