Insights into the Adsorption of Carbon Dioxide in Zeolites ITQ-29 and 5A Based on Kinetic Measurements and Molecular Simulations
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup and Procedure
2.2. Adsorption Isotherm Models and Isosteric Heat
2.3. Modeling and Simulation Techniques
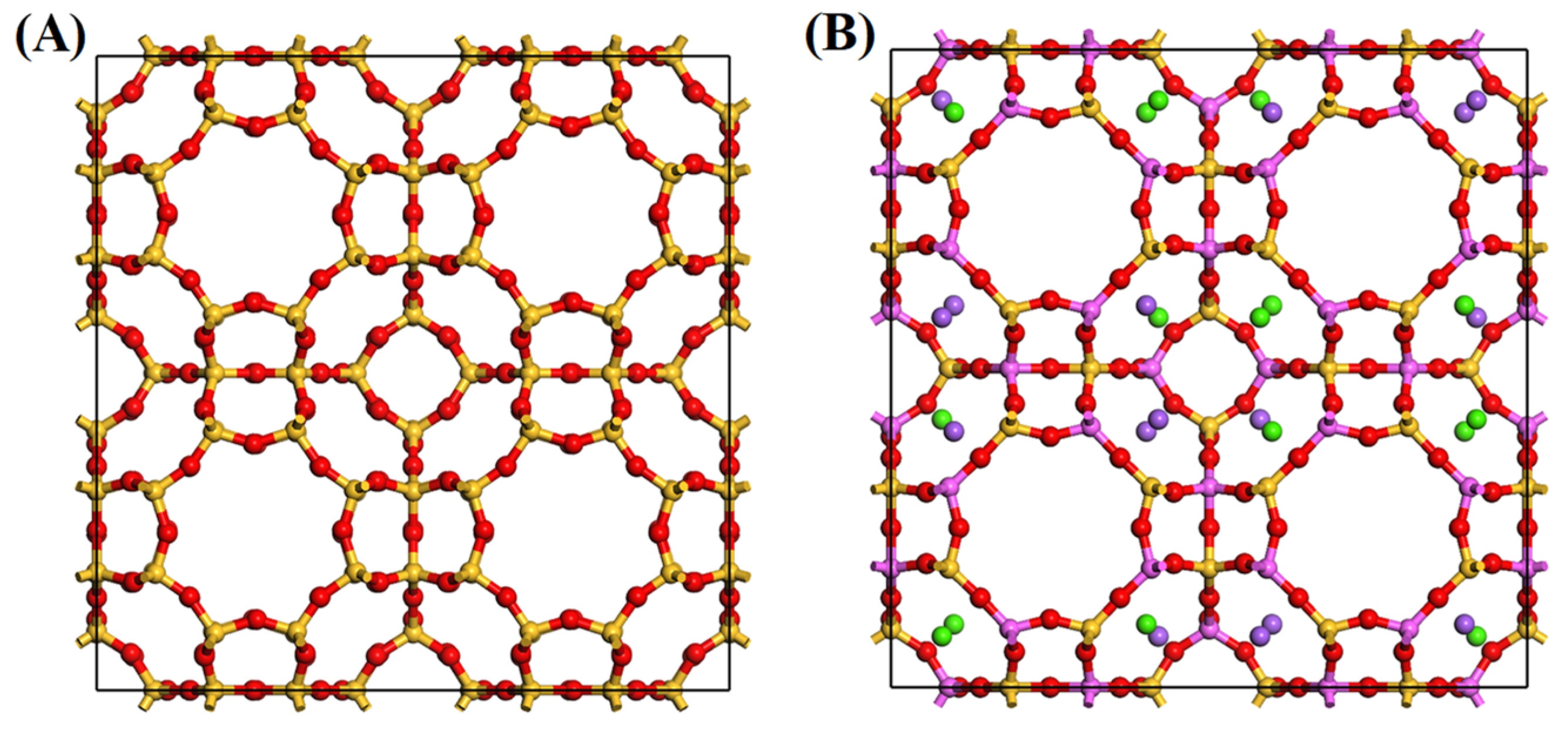
2.3.1. Optimized Structural Modeling and Density Functional Theory Calculations
2.3.2. Grand Canonical Monte Carlo Simulations
2.3.3. Diffusion Behavior
3. Results and Discussion
3.1. Laboratory Experiments Output
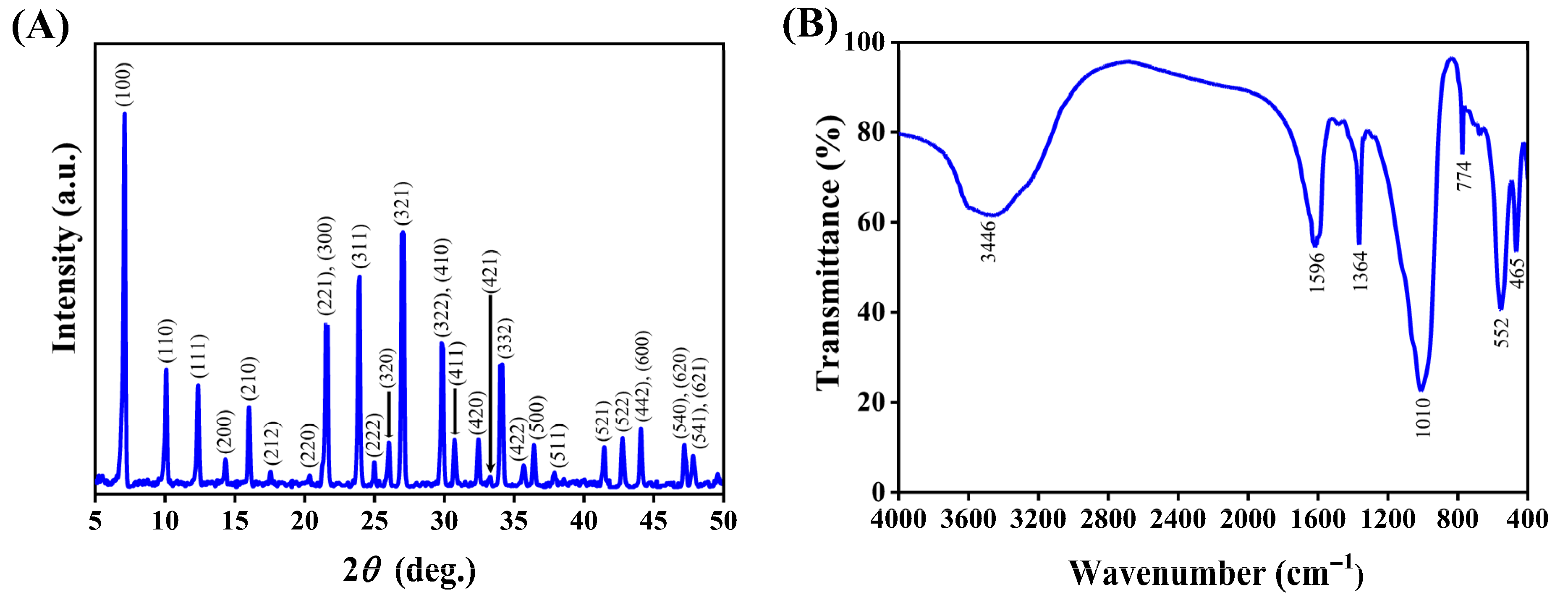
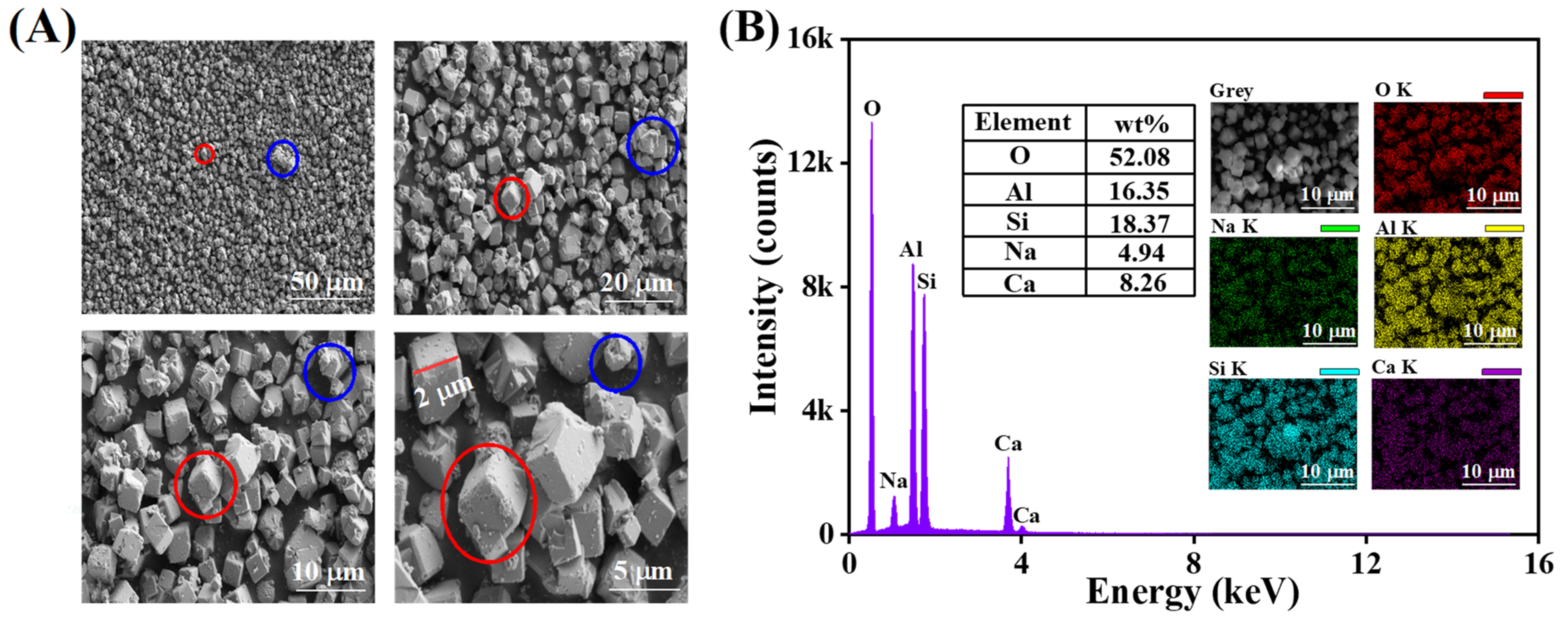
3.1.1. Characterization
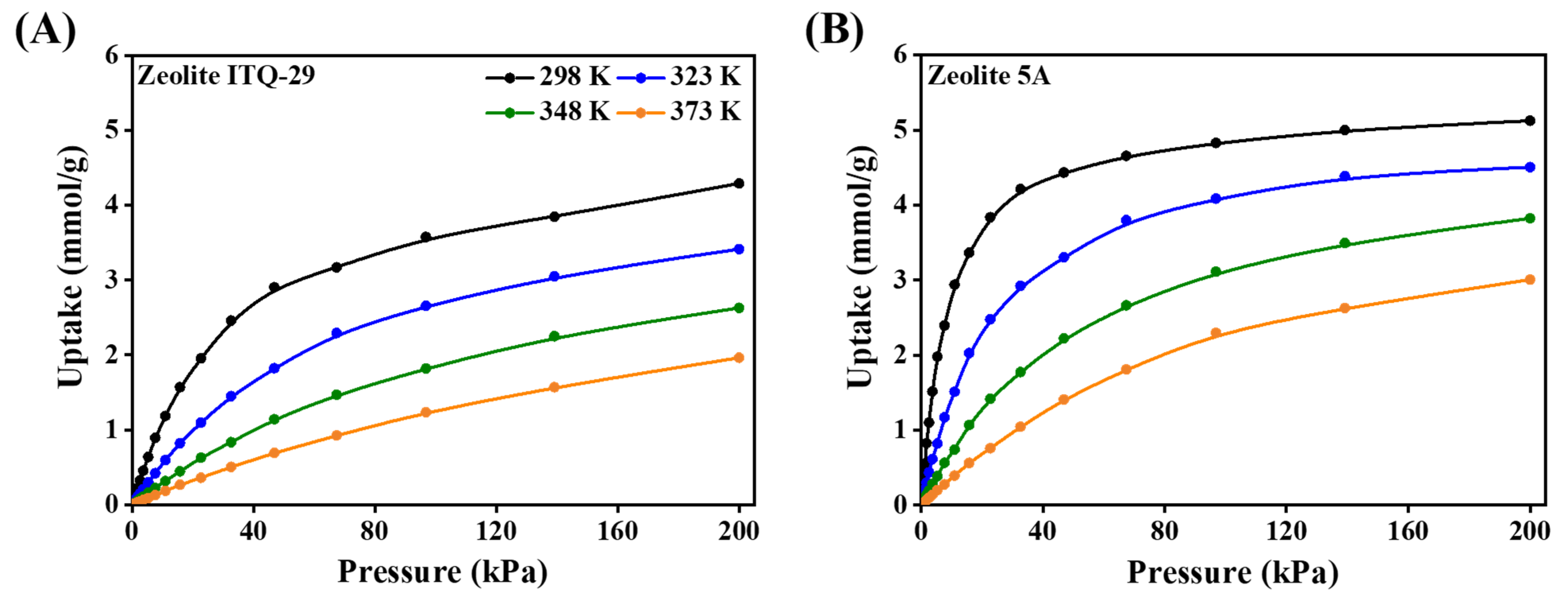
3.1.2. Adsorption Isotherms
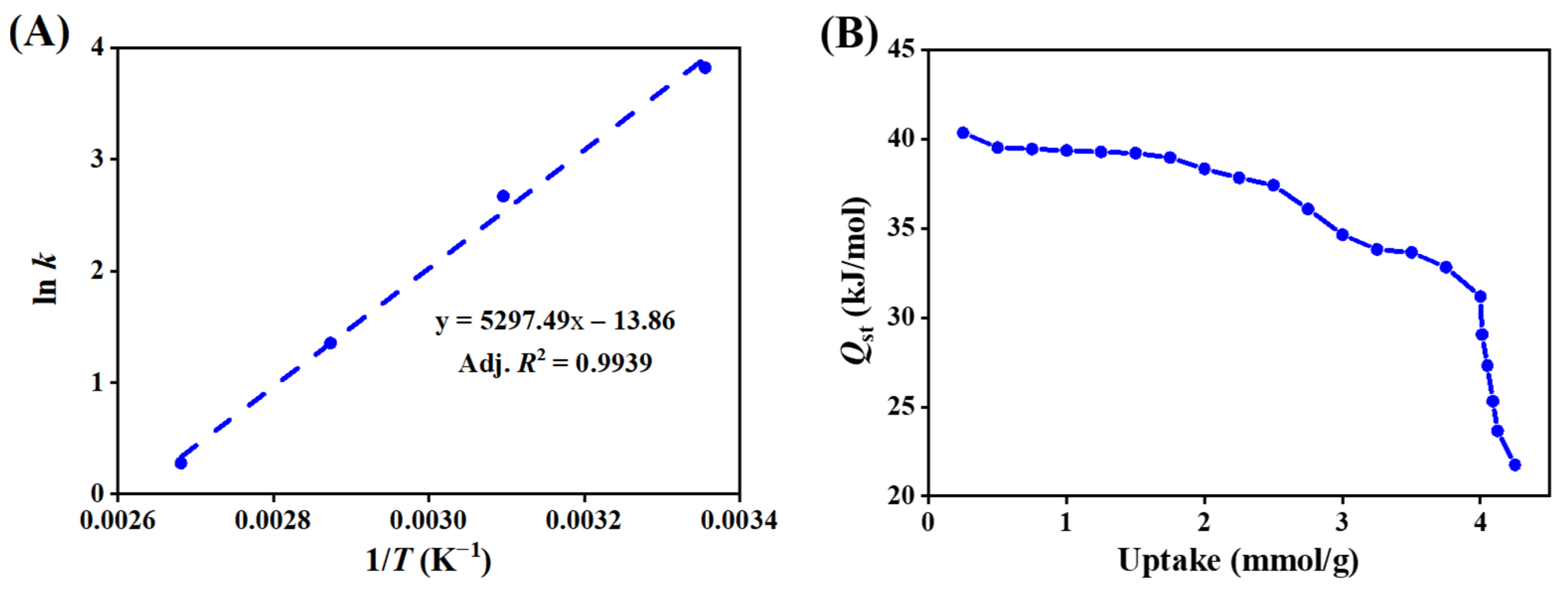
3.1.3. Adsorption Thermodynamics
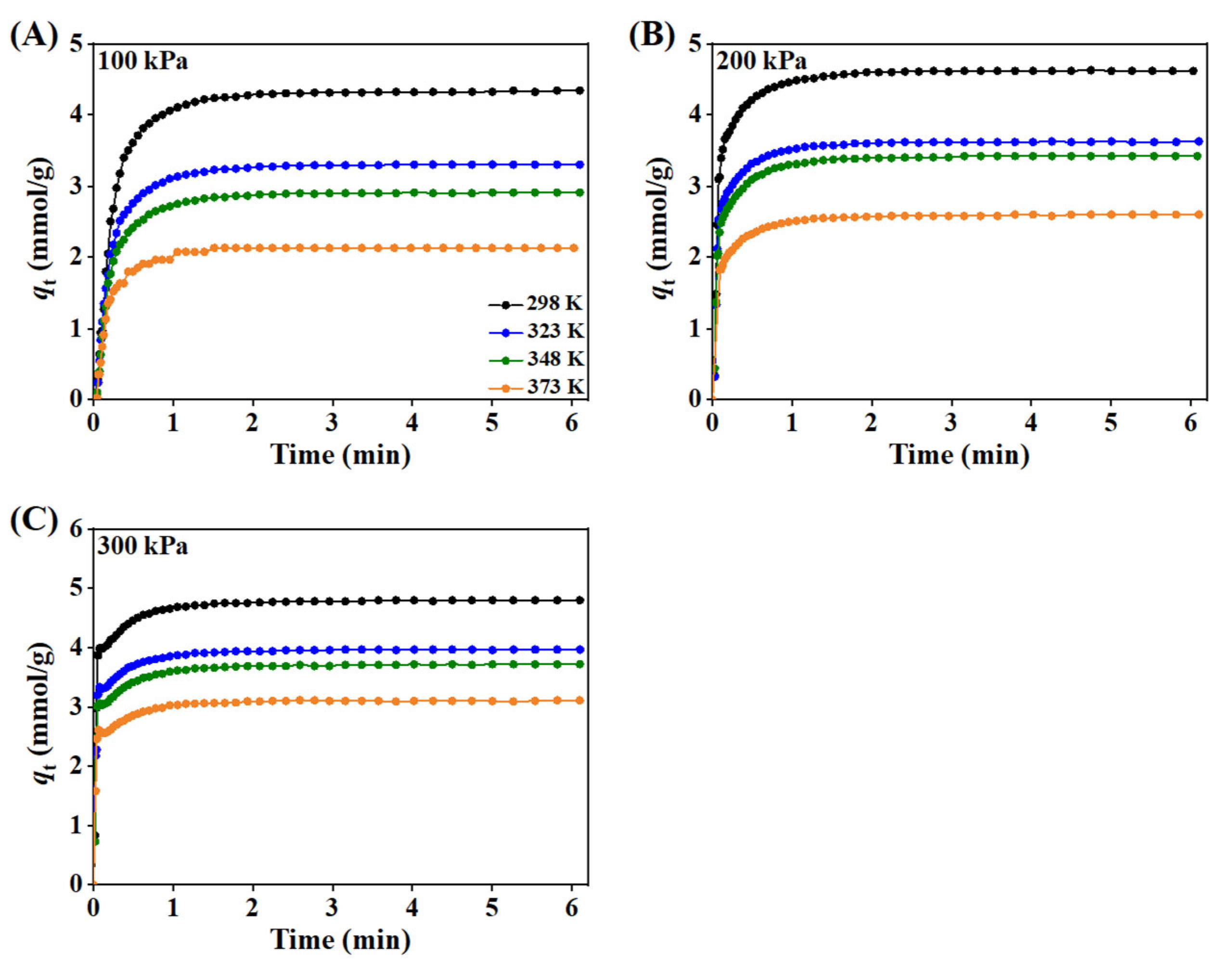
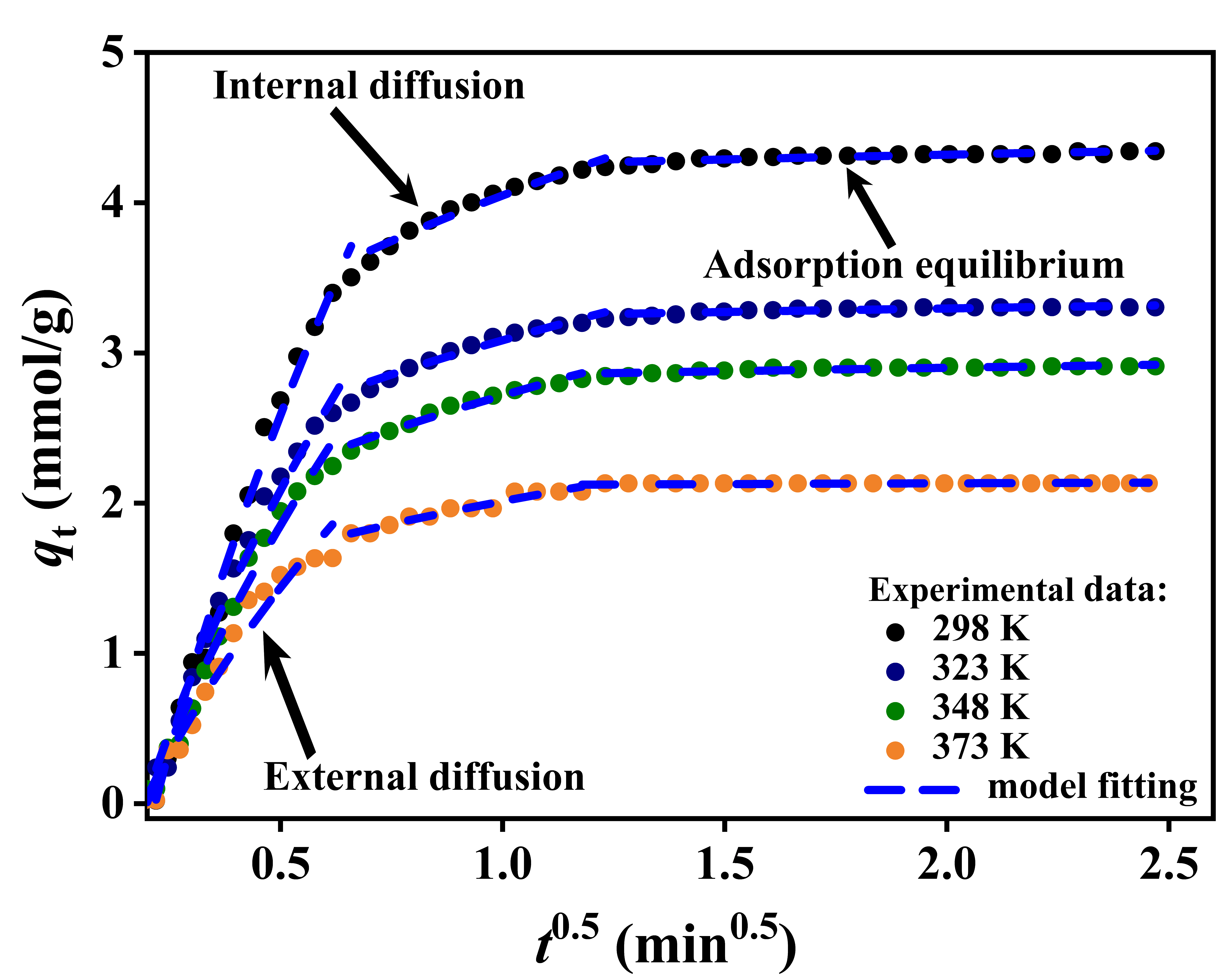
3.1.4. Adsorption Kinetics
3.2. Simulation Techniques Output
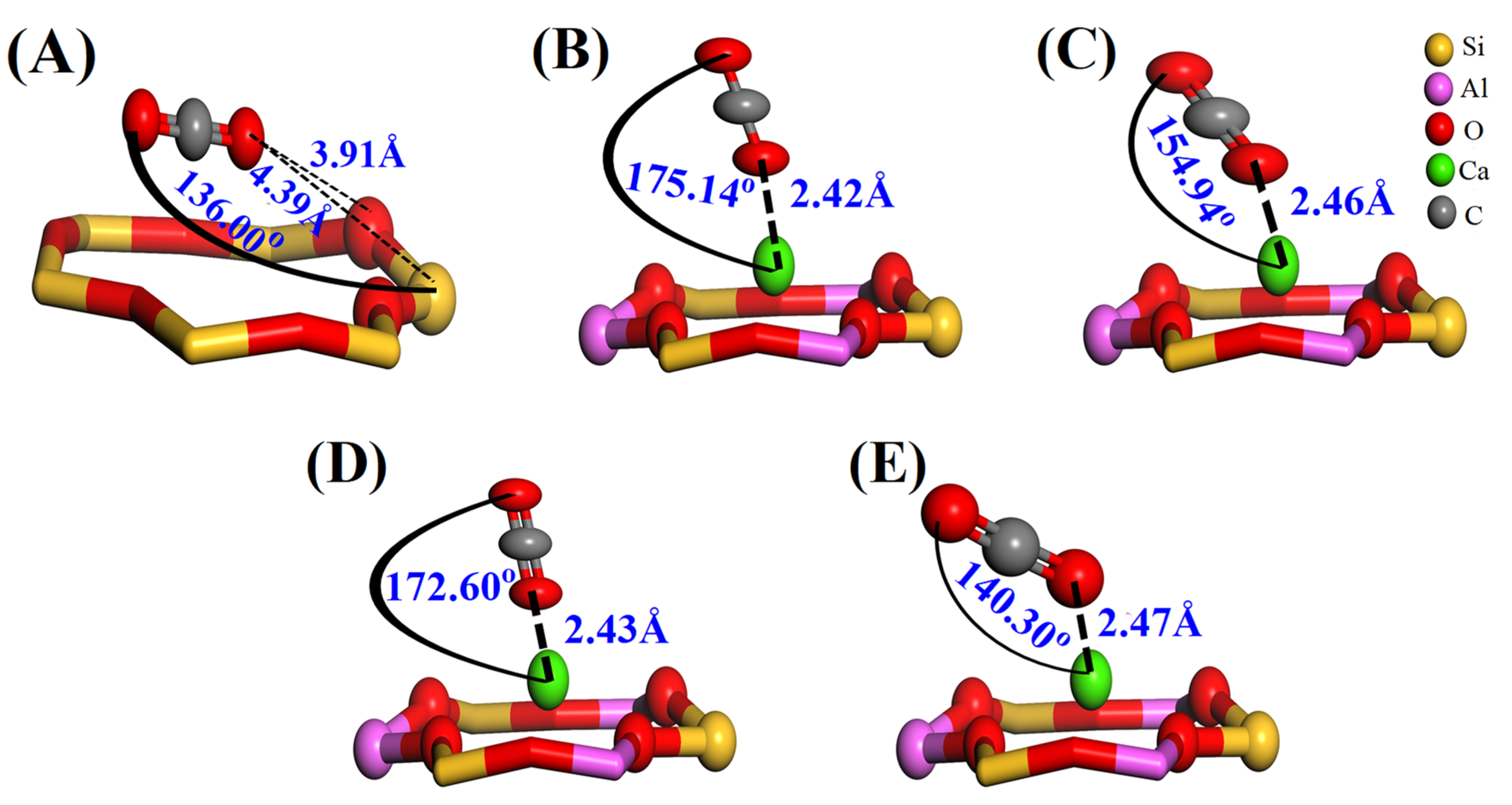
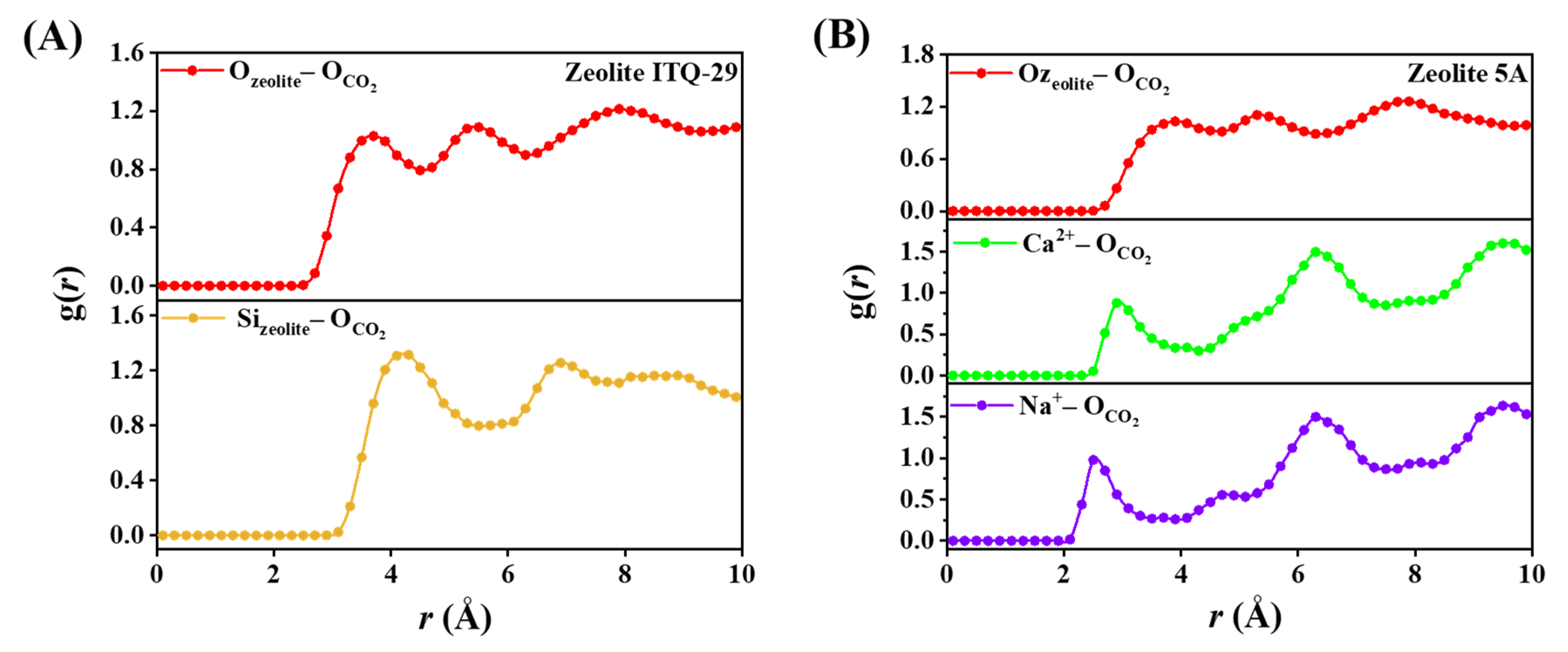
3.2.1. Adsorption Structures and Adsorption Energies
3.2.2. Adsorption Isotherm Simulations
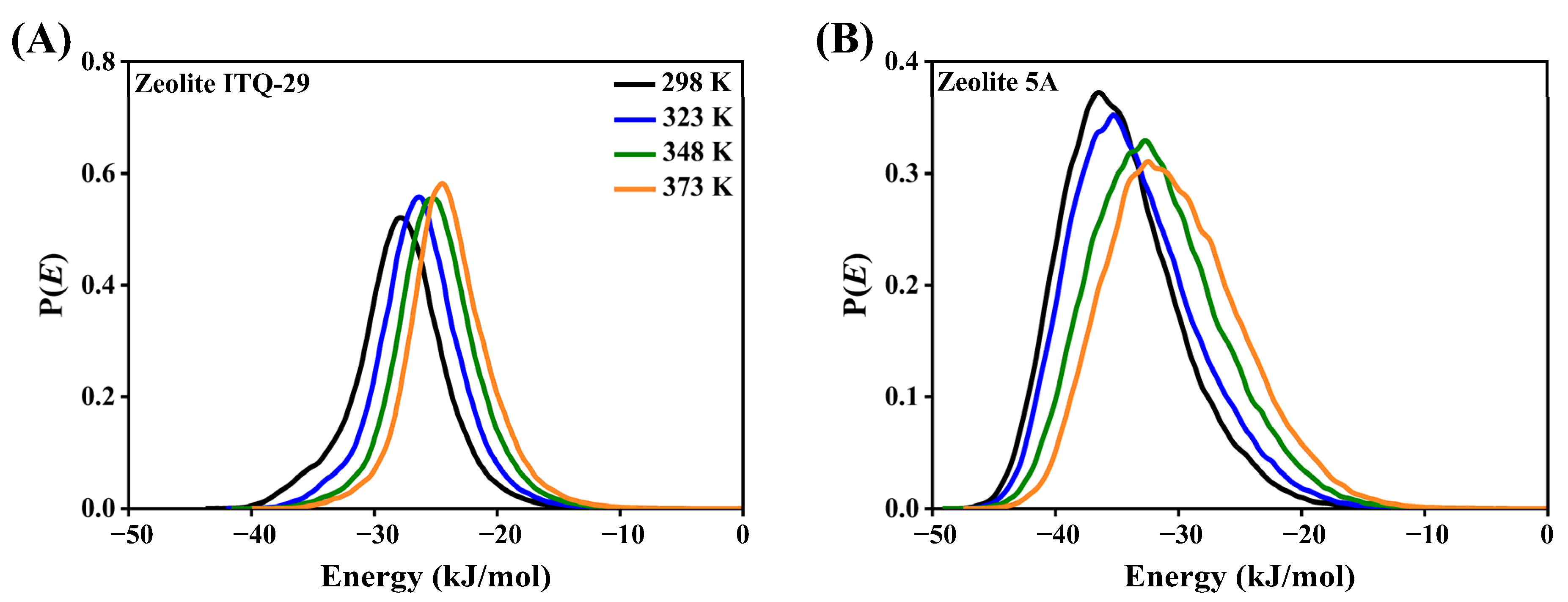
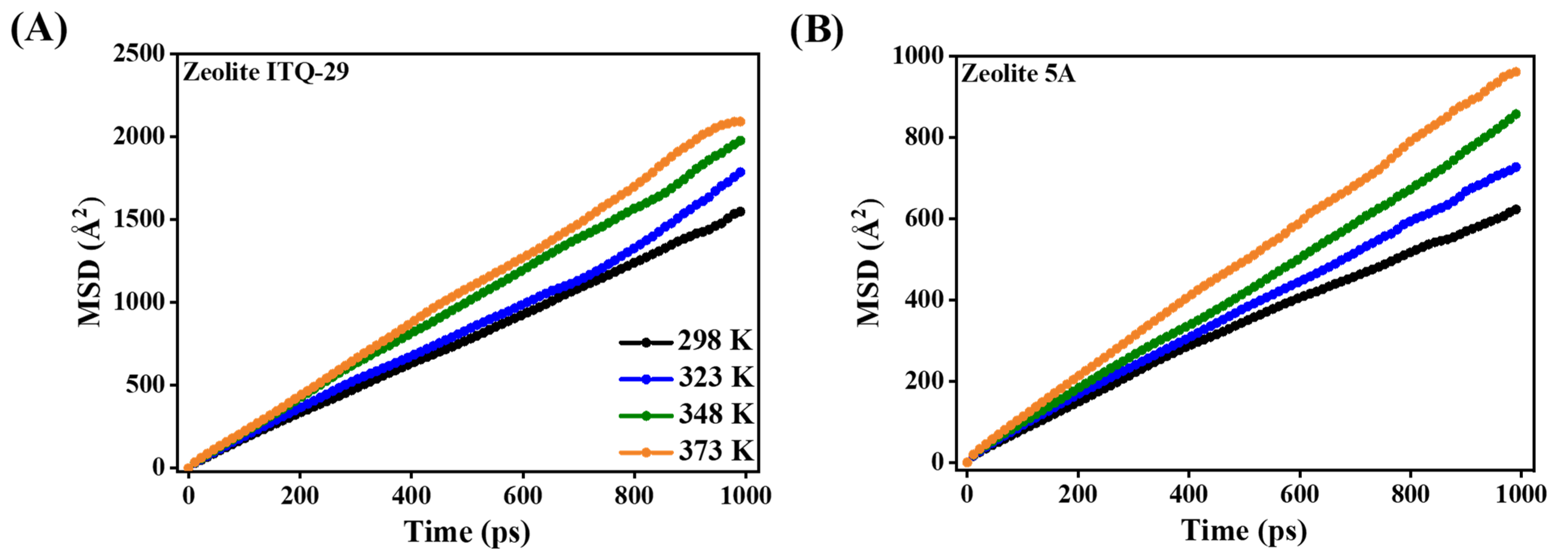
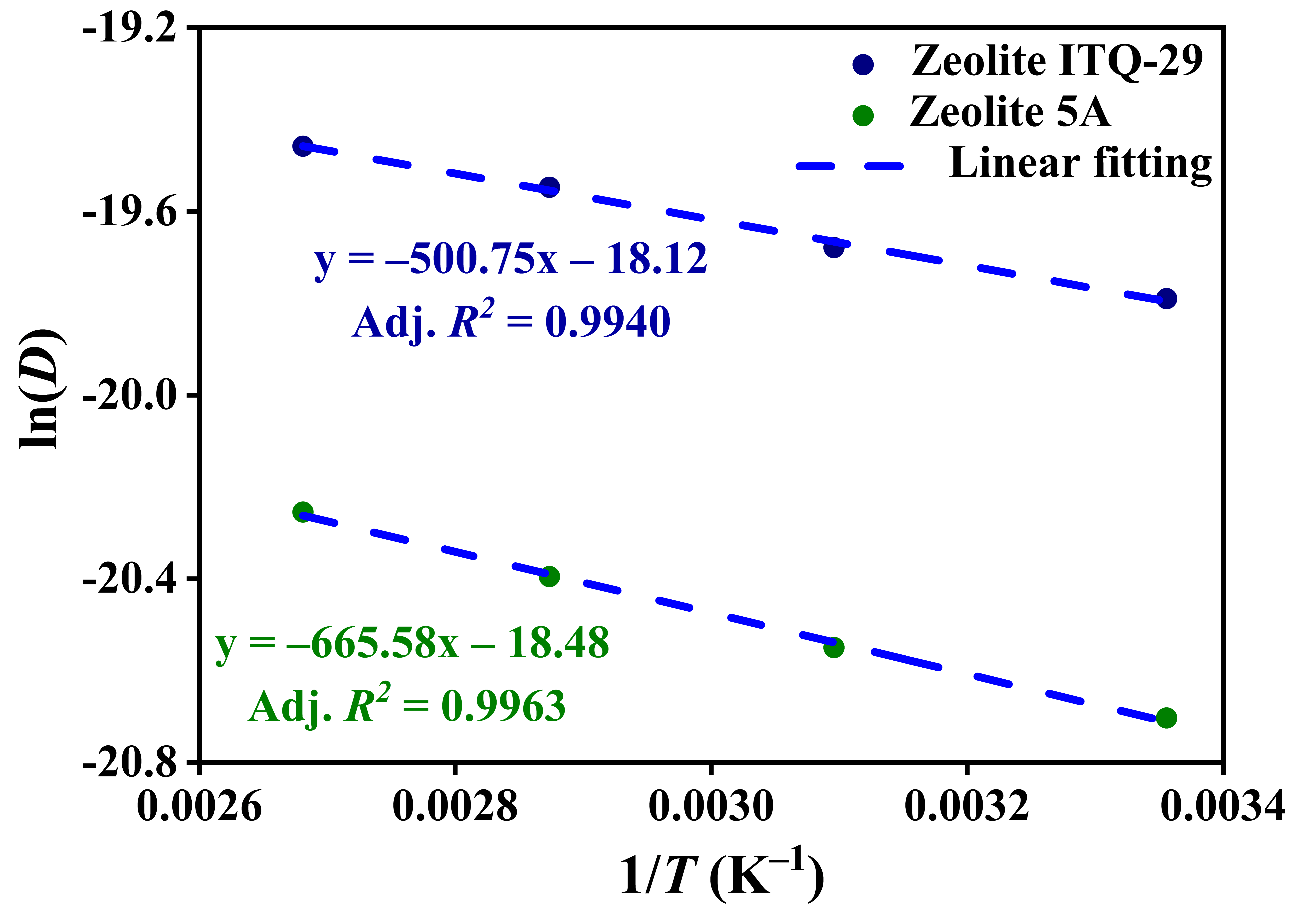
3.2.3. Diffusion Coefficients and Activation Energies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | activated carbon |
| MOFs | metal organic frameworks |
| COF | covalent organic frameworks |
| XRD | X-ray diffraction |
| FTIR | Fourier transform infrared spectroscopy |
| SEM | scanning electron microscope |
| EDS | energy-dispersive X-ray spectroscopy |
| DFT | density functional theory |
| GCMC | Grand Conical Monto Carlo |
| MD | molecular dynamics |
| D | diffusion coefficient |
| Ea | activation energy |
References
- Liu, Z.; Deng, Z.; Davis, S.J.; Ciais, P. Global carbon emissions in 2023. Nat. Rev. Earth Environ. 2024, 5, 253–254. [Google Scholar] [CrossRef]
- Nagireddi, S.; Agarwal, J.R.; Vedapuri, D. Carbon Dioxide Capture, Utilization, and Sequestration: Current Status, Challenges, and Future Prospects for Global Decarbonization. ACS Eng. Au 2024, 4, 22–48. [Google Scholar] [CrossRef]
- Geweda, A.E.; Zayed, M.E.; Khan, M.Y.; Alquaity, A.B.S. Mitigating CO2 emissions: A review on emerging technologies/strategies for CO2 capture. J. Energy Inst. 2025, 118, 101911. [Google Scholar] [CrossRef]
- Das, A.; Peu, S.D.; Hossain, M.S.; Nahid, M.M.A.; Karim, F.R.B.; Chowdhury, H.; Porag, M.H.; Argha, D.B.P.; Saha, S.; Islam, A.R.M.T.; et al. Advancements in adsorption-based carbon dioxide capture technologies- A comprehensive review. Heliyon 2023, 9, e22341. [Google Scholar] [CrossRef]
- Nema, A.; Kumar, A.; Warudkar, V. An in-depth critical review of different carbon capture techniques: Assessing their effectiveness and role in reducing climate change emissions. Energy Convers. Manag. 2025, 323, 119244. [Google Scholar] [CrossRef]
- Sai Bhargava Reddy, M.; Ponnamma, D.; Sadasivuni, K.K.; Kumar, B.; Abdullah, A.M. Carbon dioxide adsorption based on porous materials. RSC Adv. 2021, 1121, 12658–12681. [Google Scholar] [CrossRef]
- Ilkaeva, M.; Vieira, R.; Pereira, J.M.P.; Sardo, M.; Marin-Montesinos, I.; Mafra, L. Assessing CO2 Capture in Porous Sorbents via Solid-State NMR-Assisted Adsorption Techniques. J. Am. Chem. Soc. 2023, 145, 8764–8769. [Google Scholar] [CrossRef]
- Pereira, D.; Fonseca, R.; Marin-Montesinos, I.; Sardo, M.; Mafra, L. Understanding CO2 adsorption mechanisms in porous adsorbents: A solid-state NMR survey. Curr. Opin. Colloid Interface Sci. 2023, 64, 101690. [Google Scholar] [CrossRef]
- Jedli, H.; Almonnef, M.; Rabhi, R.; Mbarek, M.; Abdessalem, J.; Slimi, K. Activated Carbon as an Adsorbent for CO2 Capture: Adsorption, Kinetics, and RSM Modeling. ACS Omega 2024, 9, 2080–2087. [Google Scholar] [CrossRef]
- Abuelnoor, N.; AlHajaj, A.; Khaleel, M.; Vega, L.F.; Abu-Zahra, M.R.M. (2021). Activated carbons from biomass-based sources for CO2 capture applications. Chemosphere 2021, 282, 131111. [Google Scholar] [CrossRef]
- Mahajan, S.; Lahtinen, M. Recent progress in metal-organic frameworks (MOFs) for CO2 capture at different pressures. J. Environ. Chem. Eng. 2022, 10, 108930. [Google Scholar] [CrossRef]
- Pettinari, C.; Tombesi, A. Metal–organic frameworks for carbon dioxide capture. MRS Energy Sustain. 2020, 7, 35. [Google Scholar] [CrossRef]
- Zhou, Z.; Ma, T.; Zhang, H.; Chheda, S.; Li, H.; Wang, K.; Ehrling, S.; Giovine, R.; Li, C.; Alawadhi, A.H.; et al. Carbon dioxide capture from open air using covalent organic frameworks. Nature 2024, 635, 96–101. [Google Scholar] [CrossRef]
- Sharma, V.; De, D. CO2 adsorption with covalent organic framework (COF). In Nanomaterials for CO2 Capture, Storage, Conversion and Utilization; Elsevier: Amsterdam, The Netherlands, 2021; pp. 53–86. [Google Scholar] [CrossRef]
- Kumar, S.; Srivastava, R.; Koh, J. Utilization of zeolites as CO2 capturing agents: Advances and future perspectives. J. CO2 Util. 2020, 41, 101251. [Google Scholar] [CrossRef]
- Zhou, X.; Falconer, J.L.; Medlin, J.W. Competitive adsorption between propylene and propane on zeolite 5A and the influence of organic phosphonic acid coatings. Sep. Purif. Technol. 2024, 346, 127435. [Google Scholar] [CrossRef]
- Tao, Z.; Tian, Y.; Wu, W.; Liu, Z.; Fu, W.; Wei Kung, C.; Shang, J. Development of zeolite adsorbents for CO2 separation in achieving carbon neutrality. NPJ Mater. Sustain. 2024, 2, 20. [Google Scholar] [CrossRef]
- Zhou, X.; Falconer, J.L.; Medlin, J.W. Mechanism of selectivity control for zeolites modified with organic monolayers. Microporous Mesoporous Mater. 2022, 337, 111913. [Google Scholar] [CrossRef]
- Breck, D.W.; Skeels, G.W. Silicon Substituted Zeolite Compositions and Process for Preparing Same. U.S. Patent 4503023A, 5 March 1985. [Google Scholar]
- Combariza, A.F.; Gomez, D.A.; Sastre, G. Simulating the Properties of Small Pore Silica Zeolites Using Interatomic Potentials. Chem. Soc. Rev. 2013, 42, 114–127. [Google Scholar] [CrossRef]
- Antúnez-García, J.; Galván, D.H.; Petranovskii, V.; Murrieta-Rico, F.N.; Yocupicio-Gaxiola, R.I.; Shelyapina, M.G.; Fuentes-Moyado, S. The effect of chemical composition on the properties of LTA zeolite: A theoretical study. Comput. Mater. Sci. 2021, 196, 110557. [Google Scholar] [CrossRef]
- Corma, A.; Rey, F.; Rius, J.; Sabater, M.J.; Valencia, S. Supramolecular self-assembled molecules as organic directing agent for synthesis of zeolites. Nature 2004, 431, 287–290. [Google Scholar] [CrossRef]
- Gramlich, V.; MEIER, W.M. The crystal structure of hydrated NaA: A detailed refinement of a pseudosymmetric zeolite structure. Z. Für Krist. Cryst. Mater. 1971, 133, 134–149. [Google Scholar] [CrossRef]
- Mofarahi, M.; Seyyedi, M. Pure and Binary Adsorption Isotherms of Nitrogen and Oxygen on Zeolite 5A. J. Chem. Eng. Data 2009, 54, 916–921. [Google Scholar] [CrossRef]
- Mofarahi, M.; Gholipour, F. Gas adsorption separation of CO2/CH4 system using zeolite 5A. Microporous Mesoporous Mater. 2014, 200, 1–10. [Google Scholar] [CrossRef]
- Boonchuay, A.; Worathanakul, P. The Diffusion Behavior of CO2 Adsorption from a CO2/CH4 Gas Mixture on Zeolite 5A in a Fixed-Bed Column. Atmosphere 2022, 13, 513. [Google Scholar] [CrossRef]
- Saha, D.; Bao, Z.; Jia, F.; Deng, S. Adsorption of CO2, CH4, N2O, and N2 on MOF-5, MOF-177, and Zeolite 5A. Environ. Sci. Technol. 2010, 44, 1820–1826. [Google Scholar] [CrossRef] [PubMed]
- Khoramzadeh, E.; Mofarahi, M.; Lee, C.-H. Equilibrium Adsorption Study of CO2 and N2 on Synthesized Zeolites 13X, 4A, 5A, and Beta. J. Chem. Eng. Data 2019, 64, 5648–5664. [Google Scholar] [CrossRef]
- Wang, J.; Guo, X. Adsorption isotherm models: Classification, physical meaning, application and solving method. Chemosphere 2020, 258, 127279. [Google Scholar] [CrossRef]
- Tran, H.N.; Lima, E.C.; Juang, R.-S.; Bollinger, J.-C.; Chao, H.-P. Thermodynamic parameters of liquid–phase adsorption process calculated from different equilibrium constants related to adsorption isotherms: A comparison study. J. Environ. Chem. Eng. 2021, 9, 106674. [Google Scholar] [CrossRef]
- Gautam Sah, R.P.; Sahoo, S. A review on adsorption isotherms and kinetics of CO2 and various adsorbent pairs suitable for carbon capture and green refrigeration applications. Sādhanā 2023, 48, 27. [Google Scholar] [CrossRef]
- Revellame, E.D.; Fortela, D.L.; Sharp, W.; Hernandez, R.; Zappi, M.E. Adsorption kinetic modeling using pseudo-first order and pseudo-second order rate laws: A review. Clean. Eng. Technol. 2020, 1, 100032. [Google Scholar] [CrossRef]
- Sangsuradet, S.; Worathanakul, P. Mass transport, kinetic model, and application of CO2 adsorption on zeolite 5A granules. CLEAN—Soil Air Water 2024, 52, e2200406. [Google Scholar] [CrossRef]
- Rashidi, N.A.; Bokhari, A.; Yusup, S. Evaluation of kinetics and mechanism properties of CO2 adsorption onto the palm kernel shell activated carbon. Environ. Sci. Pollut. Res. 2021, 28, 33967–33979. [Google Scholar] [CrossRef]
- Paudel, H.P.; Shi, W.; Hopkinson, D.; Steckel, J.A.; Duan, Y. Computational modelling of adsorption and diffusion properties of CO2 and CH4 in ZIF-8 for gas separation applications: A density functional theory approach. React. Chem. Eng. 2021, 6, 990–1001. [Google Scholar] [CrossRef]
- Cai, S.; Yu, L.; Huo, E.; Ren, Y.; Liu, X.; Chen, Y. Adsorption and Diffusion Properties of Functionalized MOFs for CO2 Capture: A Combination of Molecular Dynamics Simulation and Density Functional Theory Calculation. Langmuir 2024, 40, 6869–6877. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, X.; Wang, Y.; Liu, J.; Qiu, X.; Liu, L.; Gao, S.; Yang, X.; Ma, J.; Zhang, C. Molecular Simulation of Adsorption of CO2 from a Combustion Exhaust Mixture of Zeolites with Different Topological Structures. Processes 2024, 12, 2730. [Google Scholar] [CrossRef]
- Golchoobi, A.; Pahlavanzadeh, H. Molecular simulation, experiments and modelling of single adsorption capacity of 4A molecular sieve for CO2–CH4 separation. Sep. Sci. Technol. 2016, 51, 2318–2325. [Google Scholar] [CrossRef]
- Akten, E.D.; Siriwardane, R.; Sholl, D.S. Monte Carlo Simulation of Single- and Binary-Component Adsorption of CO2, N2, and H2 in Zeolite Na-4A. Energy Fuels 2003, 17, 977–983. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, X.; Yang, X.; Wang, S.; Qiu, X.; Liu, L.; Gao, S.; Li, Z.; Zhang, C. Molecular Simulation of Adsorption Separation of CO2 from Combustion Exhaust Mixture of Commercial Zeolites. Processes 2023, 11, 2987. [Google Scholar] [CrossRef]
- Okello, F.O.; Tizhe Fidelis, T.; Agumba, J.; Manda, T.; Ochilo, L.; Mahmood, A.; Pembere, A. Towards estimation and mechanism of CO2 adsorption on zeolite adsorbents using molecular simulations and machine learning. Mater. Today Commun. 2023, 36, 106594. [Google Scholar] [CrossRef]
- Li, X.; Shen, W.; Sun, H.; Meng, L.; Wang, B.; Zhan, C.; Zhao, B. Theoretical studies on carbon dioxide adsorption in cation-exchanged molecular sieves. RSC Adv. 2020, 10, 32241–32248. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Zhu, M.; Tang, Y.; Fu, Y.; Li, W.; Xiao, B. Molecular simulation and experimental investigation of CO2 capture in a polymetallic cation-exchanged 13X zeolite. J. Mater. Chem. A 2018, 6, 19570–19583. [Google Scholar] [CrossRef]
- Swenson, H.; Stadie, N.P. Langmuir’s Theory of Adsorption: A Centennial Review. Langmuir 2019, 35, 5409–5426. [Google Scholar] [CrossRef]
- Vigdorowitsch, M.; Pchelintsev, A.; Tsygankova, L.; Tanygina, E. Freundlich Isotherm: An Adsorption Model Complete Framework. Appl. Sci. 2021, 11, 8078. [Google Scholar] [CrossRef]
- Tzabar, N.; ter Brake, H.J.M. Adsorption isotherms and Sips models of nitrogen, methane, ethane, and propane on commercial activated carbons and polyvinylidene chloride. Adsorption 2016, 22, 901–914. [Google Scholar] [CrossRef]
- Foo, K.Y.; Hameed, B.H. Insights into the modeling of adsorption isotherm systems. Chem. Eng. J. 2010, 156, 2–10. [Google Scholar] [CrossRef]
- Hameed, B.H.; Tan, I.A.W.; Ahmad, A.L. Adsorption isotherm, kinetic modeling and mechanism of 2,4,6-trichlorophenol on coconut husk-based activated carbon. Chem. Eng. J. 2008, 144, 235–244. [Google Scholar] [CrossRef]
- Jedli, H.; Brahmi, J.; Hedfi, H.; Mbarek, M.; Bouzgarrou, S.; Slimi, K. Adsorption kinetics and thermodynamics properties of Supercritical CO2 on activated clay. J. Pet. Sci. Eng. 2018, 166, 476–481. [Google Scholar] [CrossRef]
- Baerlocher, C.; Meier, W.M.; Olson, D.H. LTA. Atlas of Zeolite Framework Types; Elsevier: Amsterdam, The Netherlands, 2001; Volume 6, pp. 168–169. [Google Scholar] [CrossRef]
- Seff, K.; Shoemaker, D.P. The structures of zeolite sorption complexes. I. The structures of dehydrated zeolite 5A and its iodine sorption complex. Acta Crystallogr. 1967, 22, 162–170. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Seminario, J.M. Energetics using DFT: Comparions to precise ab initio and experiment. Chem. Phys. Lett. 1993, 206, 547–554. [Google Scholar] [CrossRef]
- Fang, H.; Kamakoti, P.; Zang, J.; Cundy, S.; Paur, C.; Ravikovitch, P.I.; Sholl, D.S. Prediction of CO2 Adsorption Properties in Zeolites Using Force Fields Derived from Periodic Dispersion-Corrected DFT Calculations. J. Phys. Chem. C 2012, 116, 10692–10701. [Google Scholar] [CrossRef]
- Ozturk, Z. Hydrogen storage on lithium modified silica based chabazite type zeolite, A computational study. Int. J. Hydrog. Energy. 2018, 43, 22365–22376. [Google Scholar] [CrossRef]
- Krishna, R.; van Baten, J.M. Influence of isotherm inflection on the diffusivities of C5–C8 linear alkanes in MFI zeolite. Chem. Phys. Lett. 2005, 407, 159–165. [Google Scholar] [CrossRef]
- Ghosh, A.; Ma, L.; Gao, C. Zeolite molecular sieve 5A acts as a reinforcing filler, altering the morphological, mechanical, and thermal properties of chitosan. J. Mater. Sci. 2013, 48, 3926–3935. [Google Scholar] [CrossRef]
- Liang, T.; Wang, B.; Fan, Z.; Liu, Q. A facile fabrication of superhydrophobic and superoleophilic adsorption material 5A zeolite for oil–water separation with potential use in floating oil. Open Phys. 2021, 19, 486–493. [Google Scholar] [CrossRef]
- Wang, P.; Cao, J.; Zhang, Y.; Sun, Q. Controllable Preparation of Cubic Zeolite A and Application of Langmuir Model in Carbon Dioxide Adsorption. Nanomaterials 2021, 11, 3375. [Google Scholar] [CrossRef]
- Crupi, V.; Majolino, D.; Venuti, V. Diffusional and vibrational dynamics of water in NaA zeolites by neutron and Fourier transform infrared spectroscopy. J. Phys. Condens. Matter 2004, 16, S5297–S5316. [Google Scholar] [CrossRef]
- Zhang, Y.; Cui, B.; Zhao, C.; Lin, H.; Li, J. Co–Ni layered double hydroxides for water oxidation in neutral electrolyte. Phys. Chem. Chem. Phys. 2013, 15, 7363. [Google Scholar] [CrossRef]
- Valdez, R.; Grotjahn, D.B.; Smith, D.K.; Quintana, J.M.; Olivas, A. Nanosheets of Co-(Ni and Fe) Layered Double Hydroxides for Electrocatalytic Water Oxidation Reaction. Int. J. Electrochem. Sci. 2015, 10, 909–918. [Google Scholar] [CrossRef]
- Hauchhum, L.; Mahanta, P. Carbon dioxide adsorption on zeolites and activated carbon by pressure swing adsorption in a fixed bed. Int. J. Energy Environ. Eng. 2014, 5, 349–356. [Google Scholar] [CrossRef]
- Armandi, M.; Garrone, E.; Areán, C.O.; Bonelli, B. Thermodynamics of Carbon Dioxide Adsorption on the Protonic Zeolite H-ZSM-5. ChemPhysChem 2009, 10, 3316–3319. [Google Scholar] [CrossRef]
- Saha, P.; Chowdhury, S. Insight Into Adsorption Thermodynamics. Thermodynamics 2011, 16, 350–364. [Google Scholar] [CrossRef]
- Maceiras, R.; Feijoo, J.; Perez-Rial, L.; Alfonsin, V.; Falcon, P. Study of natural zeolites for hydrogen purification: CO2 adsorption capacity and kinetic mechanism. Fuel 2024, 376, 132732. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, X.; Wang, J.; Zhong, L.; Othman, R.M.; Lithoxoos, G.P.; Shakhs, A.N.; Almansour, F.; Zeng, X.; Sun, X.; et al. High-temperature ammonia treatment of zeolite-template carbon for enhanced CO2 adsorption: A study on diffusion behaviors and adsorption mechanisms. Chem. Eng. J. 2025, 505, 159168. [Google Scholar] [CrossRef]
- Wang, J.; Guo, X. Rethinking of the intraparticle diffusion adsorption kinetics model: Interpretation, solving methods and applications. Chemosphere 2022, 309, 136732. [Google Scholar] [CrossRef]
- Guo, X.; Wang, J. A general kinetic model for adsorption: Theoretical analysis and modeling. J. Mol. Liq. 2019, 288, 111100. [Google Scholar] [CrossRef]
- Kumar, K.V.; Porkodi, K. Mass transfer, kinetics and equilibrium studies for the biosorption of methylene blue using Paspalum notatum. J. Hazard. Mater. 2007, 146, 214–226. [Google Scholar] [CrossRef]
- Korablev, G.A. Calculations of activation energy of diffusion and self-diffusion. Eur. Chem. Bull. 2018, 7, 23. [Google Scholar] [CrossRef]
- Palomino, M.; Corma, A.; Rey, F.; Valencia, S. New Insights on CO2−Methane Separation Using LTA Zeolites with Different Si/Al Ratios and a First Comparison with MOFs. Langmuir 2010, 26, 1910–1917. [Google Scholar] [CrossRef]
- Dirar, Q.H.; Loughlin, K.F. Intrinsic adsorption properties of CO2 on 5A and 13X zeolite. Adsorption 2013, 19, 1149–1163. [Google Scholar] [CrossRef]
- Krishna, R.; van Baten, J.M. A molecular dynamics investigation of a variety of influences of temperature on diffusion in zeolites. Microporous Mesoporous Mater. 2009, 125, 126–134. [Google Scholar] [CrossRef]




| Zeolite 5A | BET Surface Area (m2/g) | Pore Volume (cm3/g) | Average Pore Width (nm) |
|---|---|---|---|
| Measured | 743 | 0.239 | 0.47 |
| Simulated | 758 | 0.260 | 0.46 |
| Temperature (K) | Pseudo-First-Order | Pseudo-Second-Order | ||||
|---|---|---|---|---|---|---|
| qe (mmol/g) | k1 (min−1) | Adj. R2 | qe (mmol/g) | k2 (g/mmol·min) | Adj. R2 | |
| 298 | 3.39 | 2.08 | 0.978 | 5.22 | 0.25 | 0.509 |
| 323 | 2.53 | 2.43 | 0.986 | 3.46 | 0.82 | 0.995 |
| 348 | 2.28 | 2.77 | 0.983 | 3.10 | 1.23 | 0.983 |
| 373 | 1.56 | 3.04 | 0.978 | 2.41 | 1.53 | 0.827 |
| Temperature (K) | External Film Diffusion | Intraparticle Diffusion | Surface Adsorption at Equilibrium | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Kdiff1 | C | Adj. R2 | Kdiff2 | C | Adj. R2 | Kdiff3 | C | Adj. R2 | |
| 298 | 10.75 | −5.02 | 0.988 | 2.26 | 1.79 | 0.960 | 0.167 | 4.084 | 0.806 |
| 323 | 7.79 | −3.43 | 0.980 | 1.70 | 1.38 | 0.956 | 0.126 | 3.119 | 0.738 |
| 348 | 7.08 | −3.16 | 0.982 | 1.73 | 0.99 | 0.967 | 0.116 | 2.728 | 0.743 |
| 373 | 5.35 | −2.34 | 0.961 | 1.14 | 0.87 | 0.935 | 0.027 | 2.094 | 0.937 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elsayed, M.A.; Zhou, S.; Zhao, X.; Manggada, G.W.; Chen, Z.; Wang, F.; Tang, Z. Insights into the Adsorption of Carbon Dioxide in Zeolites ITQ-29 and 5A Based on Kinetic Measurements and Molecular Simulations. Nanomaterials 2025, 15, 1077. https://doi.org/10.3390/nano15141077
Elsayed MA, Zhou S, Zhao X, Manggada GW, Chen Z, Wang F, Tang Z. Insights into the Adsorption of Carbon Dioxide in Zeolites ITQ-29 and 5A Based on Kinetic Measurements and Molecular Simulations. Nanomaterials. 2025; 15(14):1077. https://doi.org/10.3390/nano15141077
Chicago/Turabian StyleElsayed, Magdy Abdelghany, Shixue Zhou, Xiaohui Zhao, Gumawa Windu Manggada, Zhongyuan Chen, Fang Wang, and Zhijuan Tang. 2025. "Insights into the Adsorption of Carbon Dioxide in Zeolites ITQ-29 and 5A Based on Kinetic Measurements and Molecular Simulations" Nanomaterials 15, no. 14: 1077. https://doi.org/10.3390/nano15141077
APA StyleElsayed, M. A., Zhou, S., Zhao, X., Manggada, G. W., Chen, Z., Wang, F., & Tang, Z. (2025). Insights into the Adsorption of Carbon Dioxide in Zeolites ITQ-29 and 5A Based on Kinetic Measurements and Molecular Simulations. Nanomaterials, 15(14), 1077. https://doi.org/10.3390/nano15141077





