From Theory to Experiment: Reviewing the Role of Graphene in Li-Ion Batteries Through Density Functional Theory
Abstract
1. Introduction
2. Density Functional Theory in Lithium-Ion Batteries
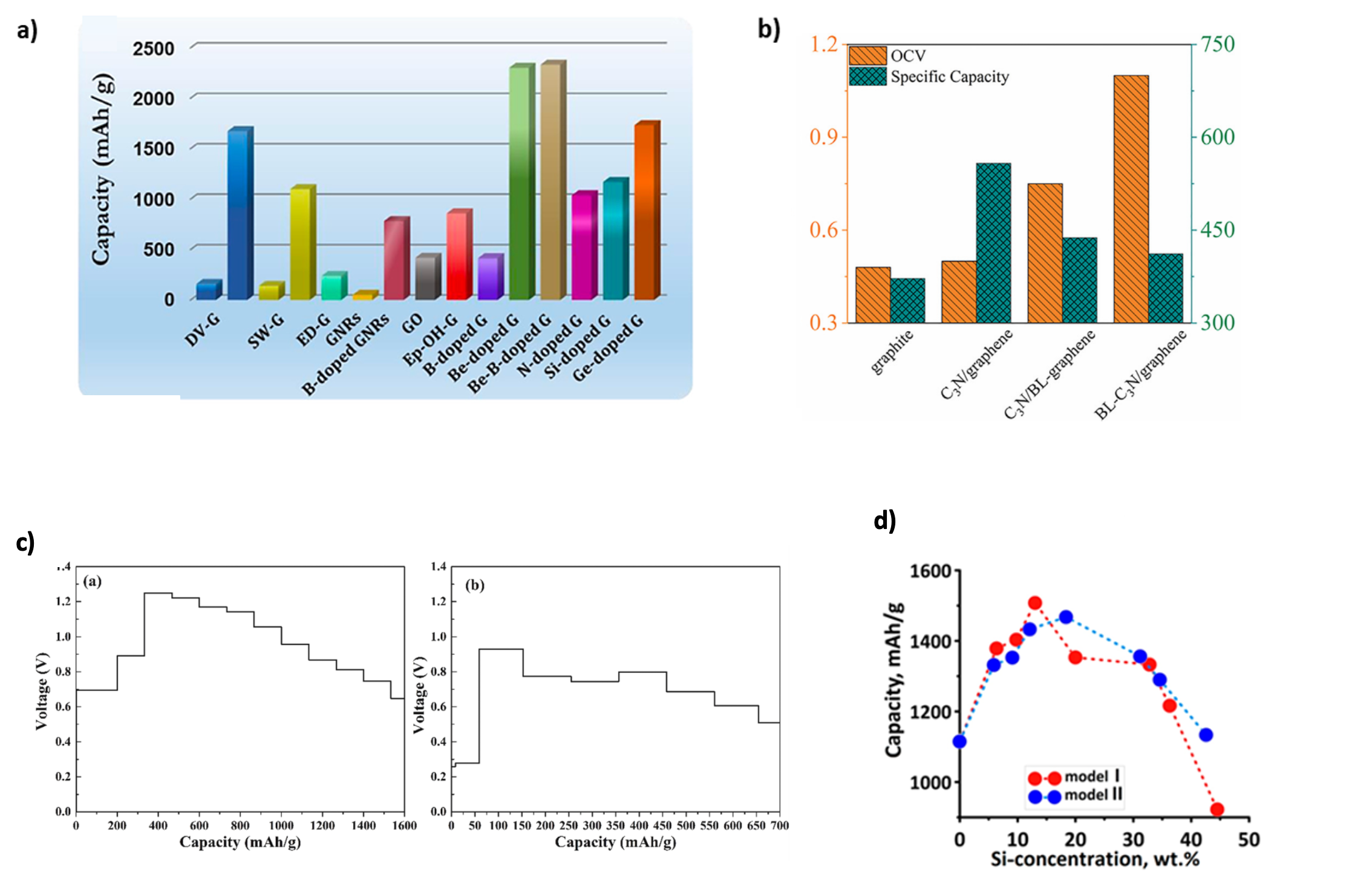
2.1. Open Circuit Voltage and Theoretical Capacity
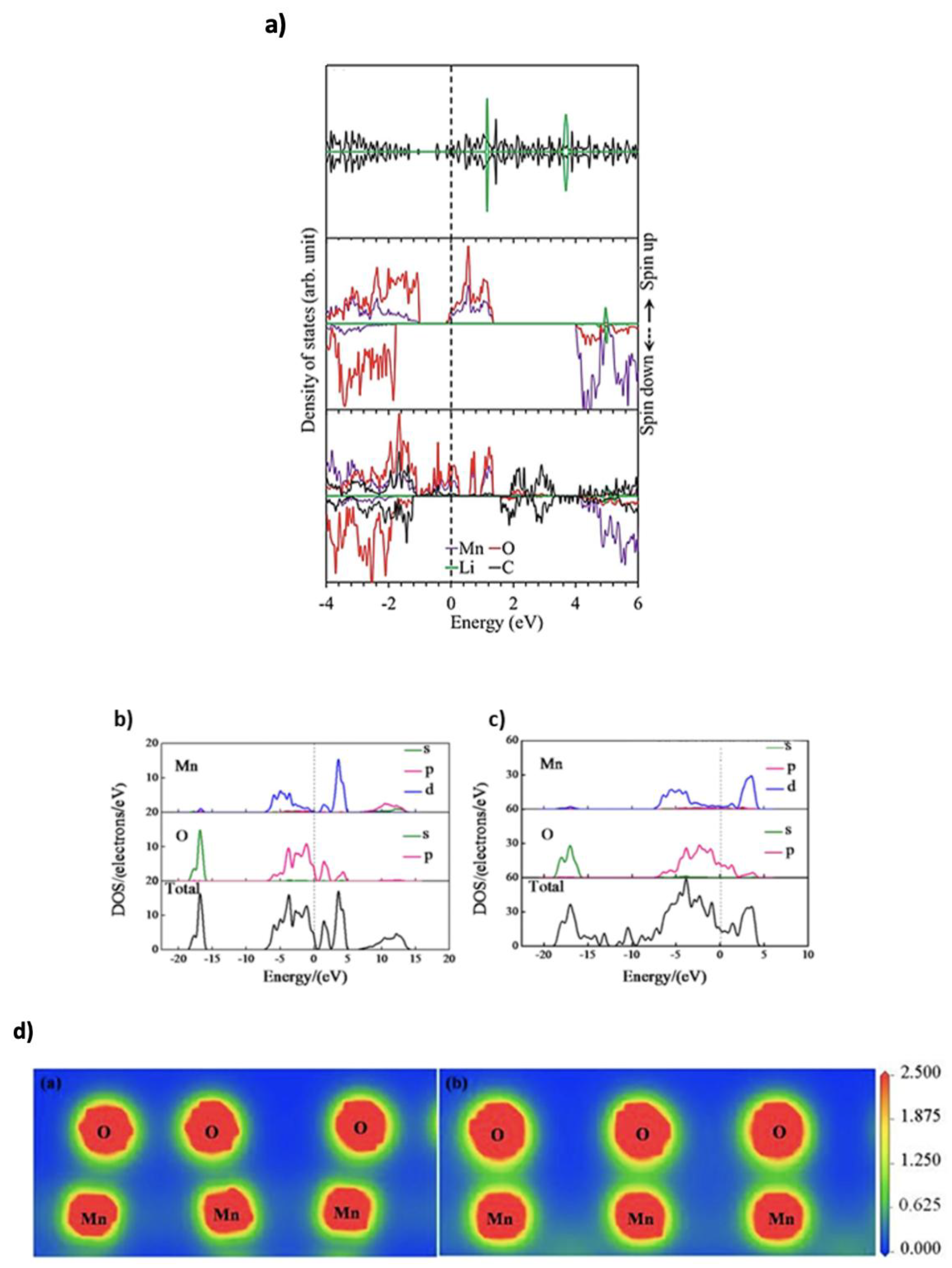
2.2. Electronic Structure
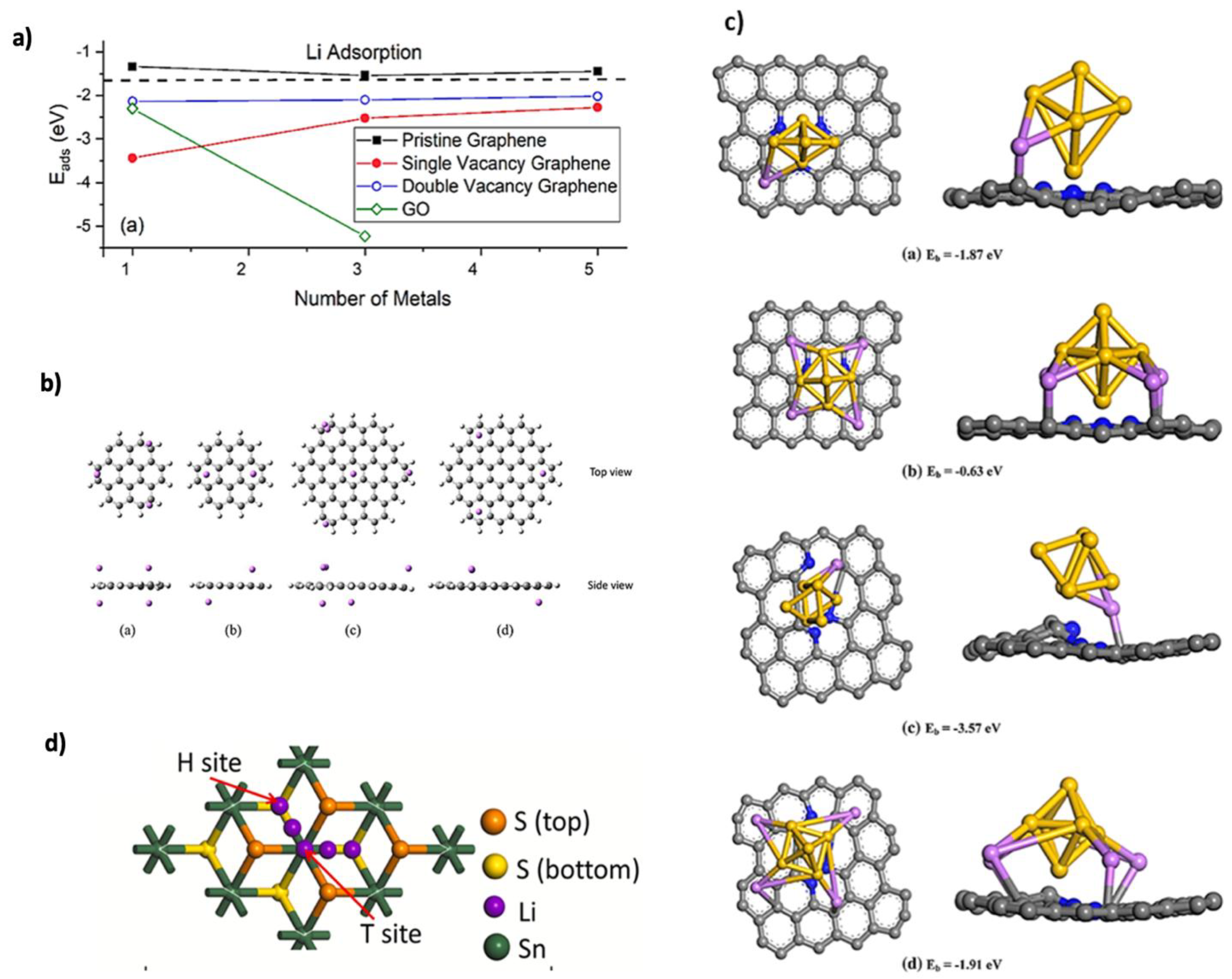
2.3. Adsorption Kinetics
2.4. Diffusion Kinetics
2.5. Challenges
3. Graphene-Based Anode Materials for Lithium-Ion Batteries (LIBs)
3.1. Overview of Lithium-Ion Batteries and the Role of Graphene
3.2. Engineering Graphene for High-Performance Anode Materials in LIBs
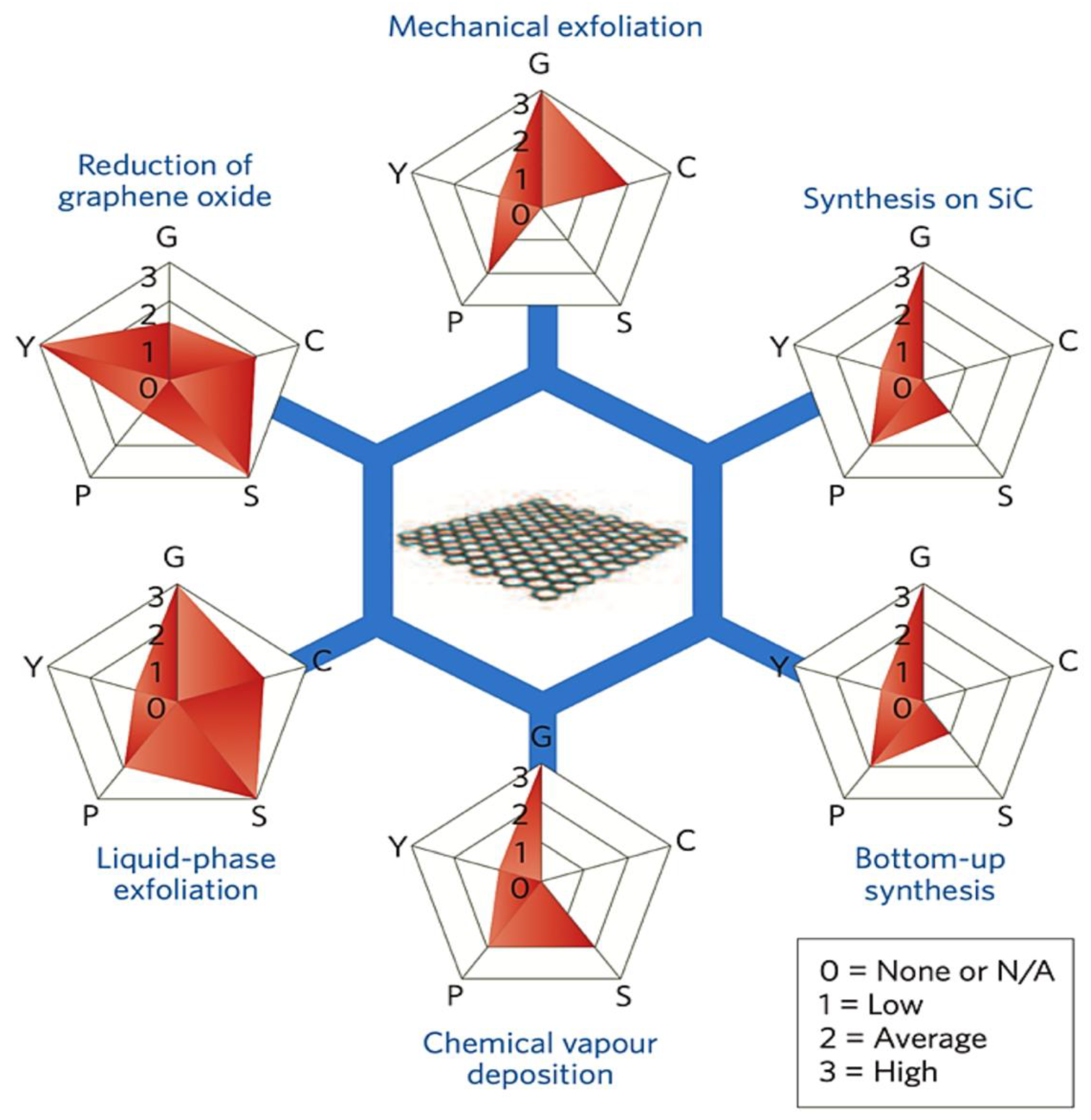
3.2.1. Graphene Synthesis
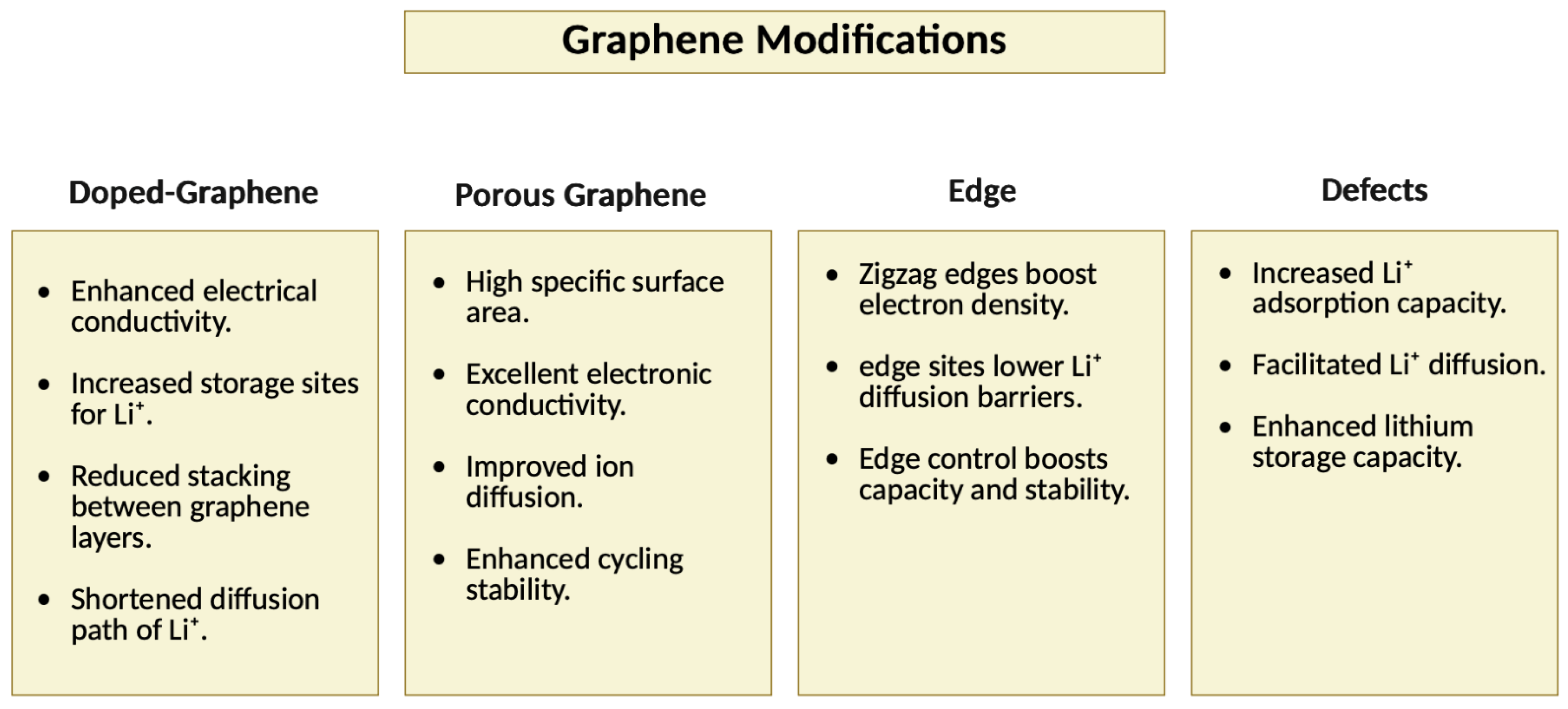
3.2.2. Functionalization of Graphene
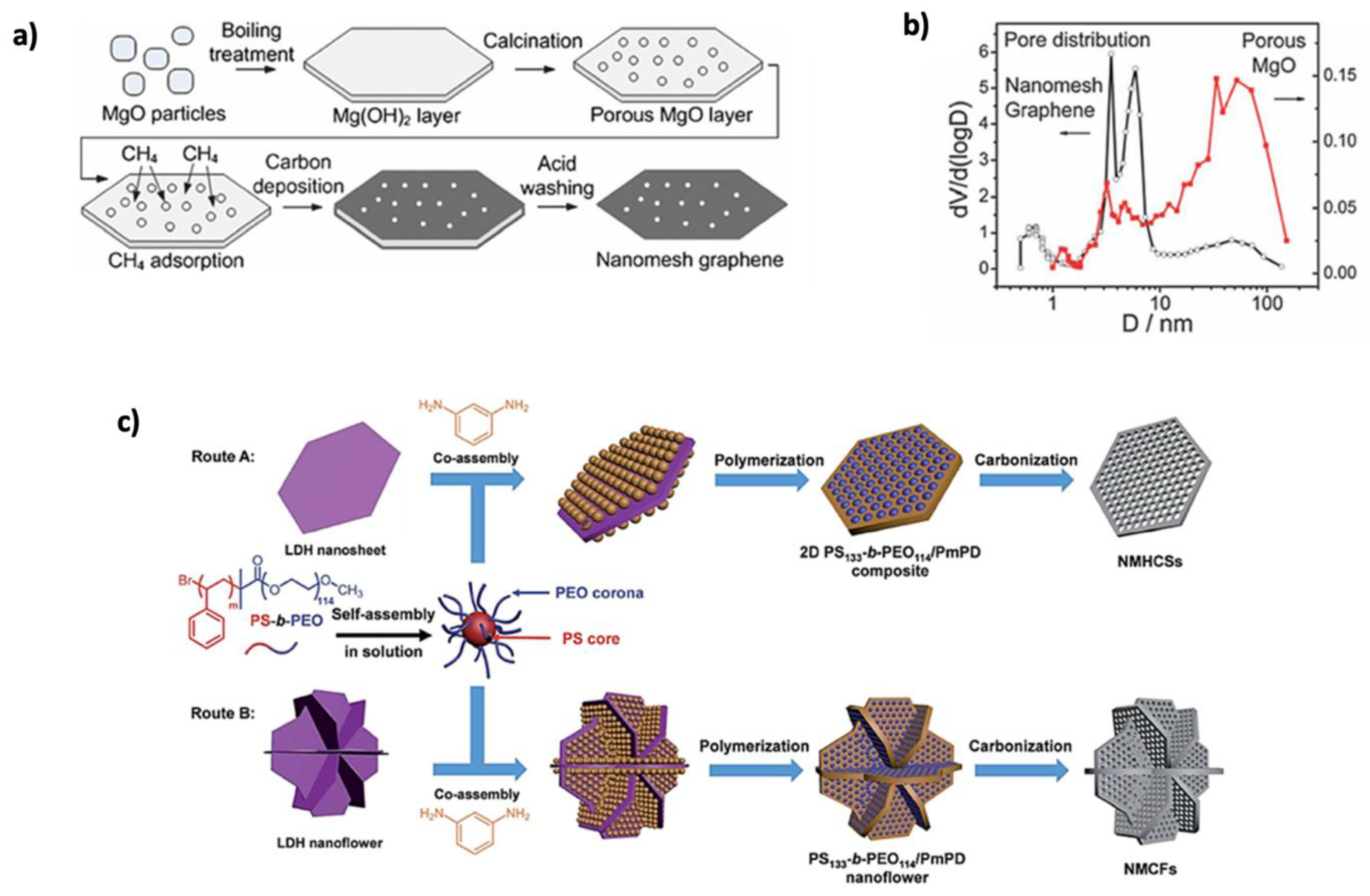
Porous Graphene
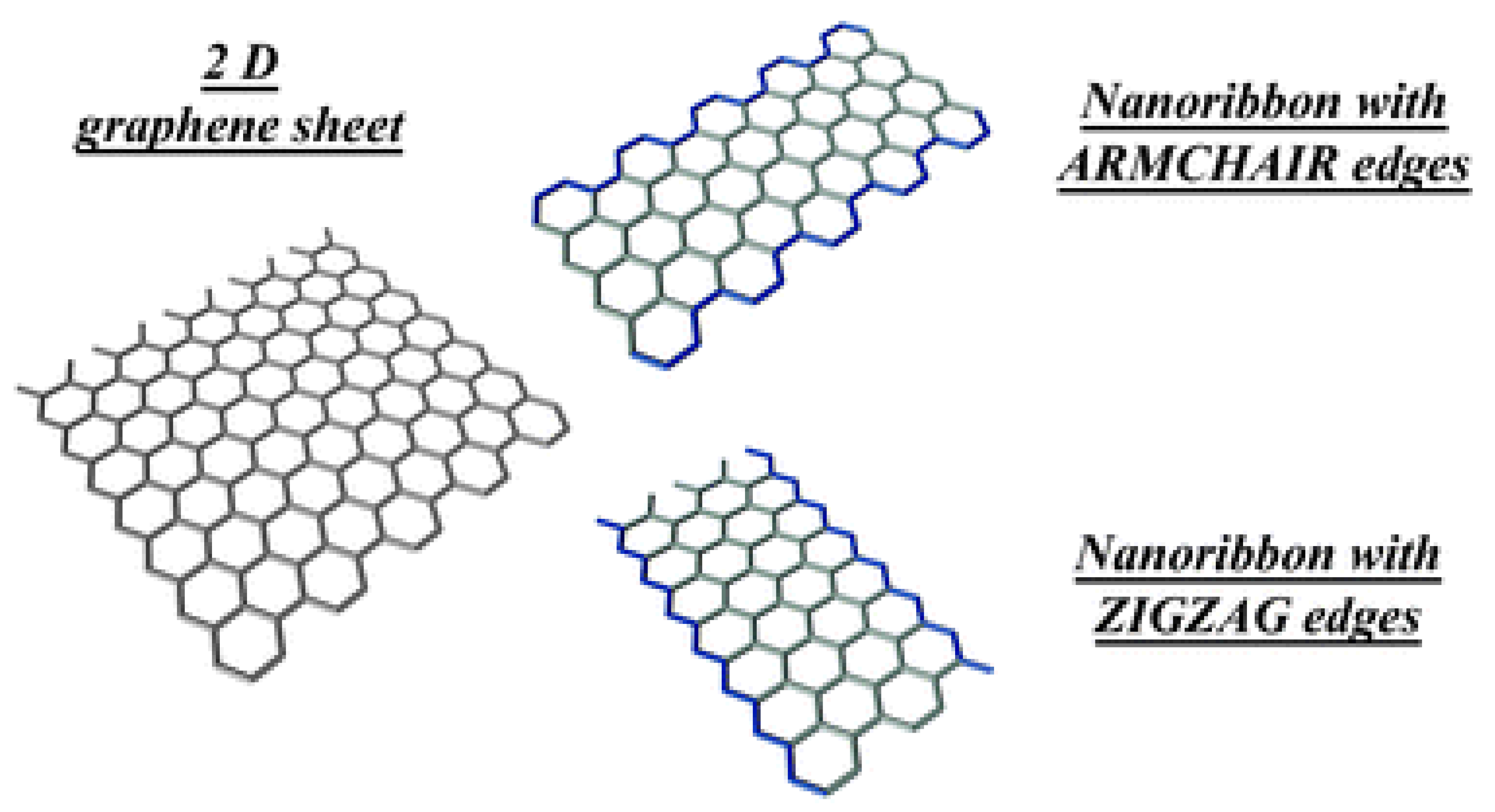
Edge
Defects
3.3. Graphene-Based Anodes: Materials and Composites
3.3.1. Pristine Graphene
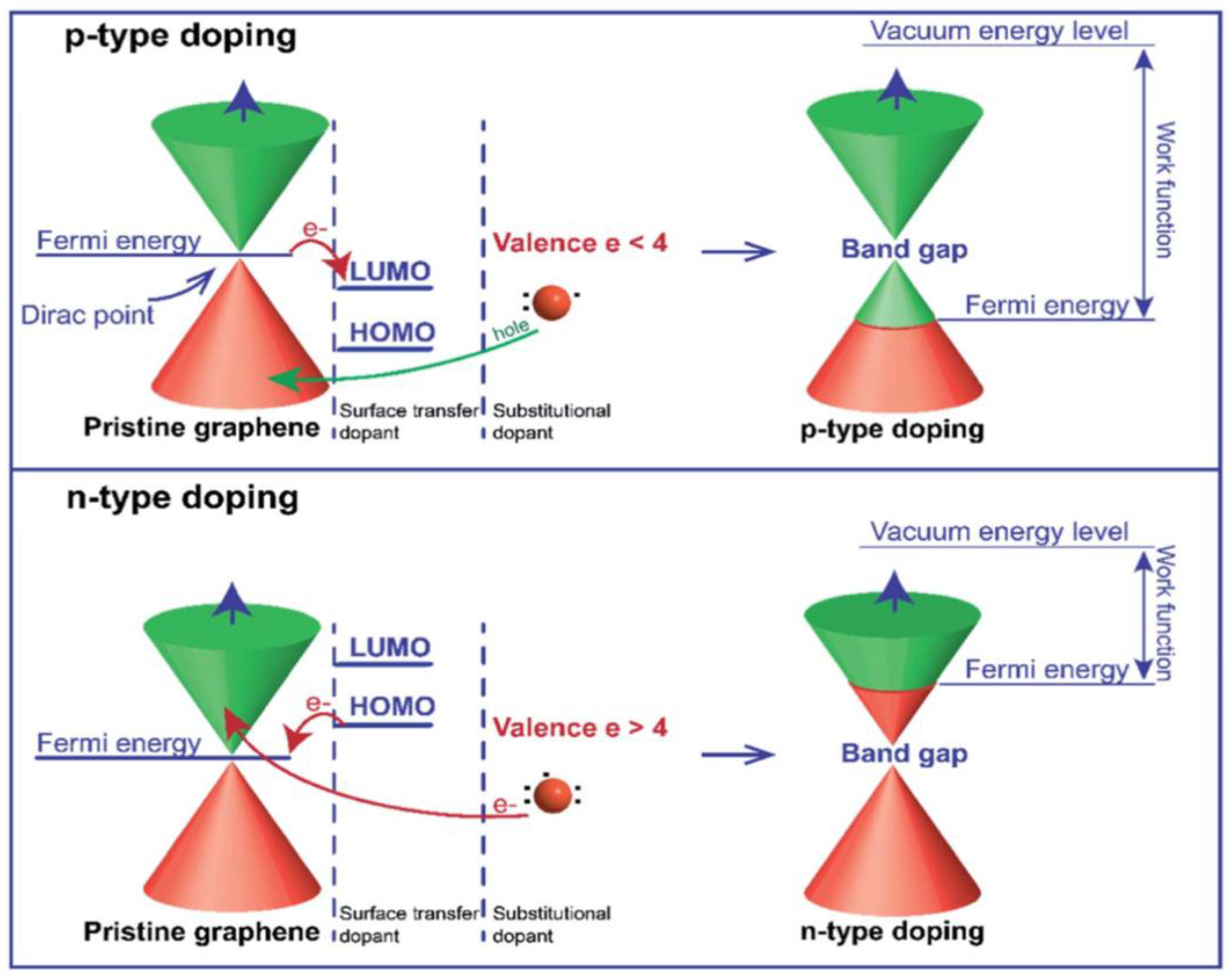
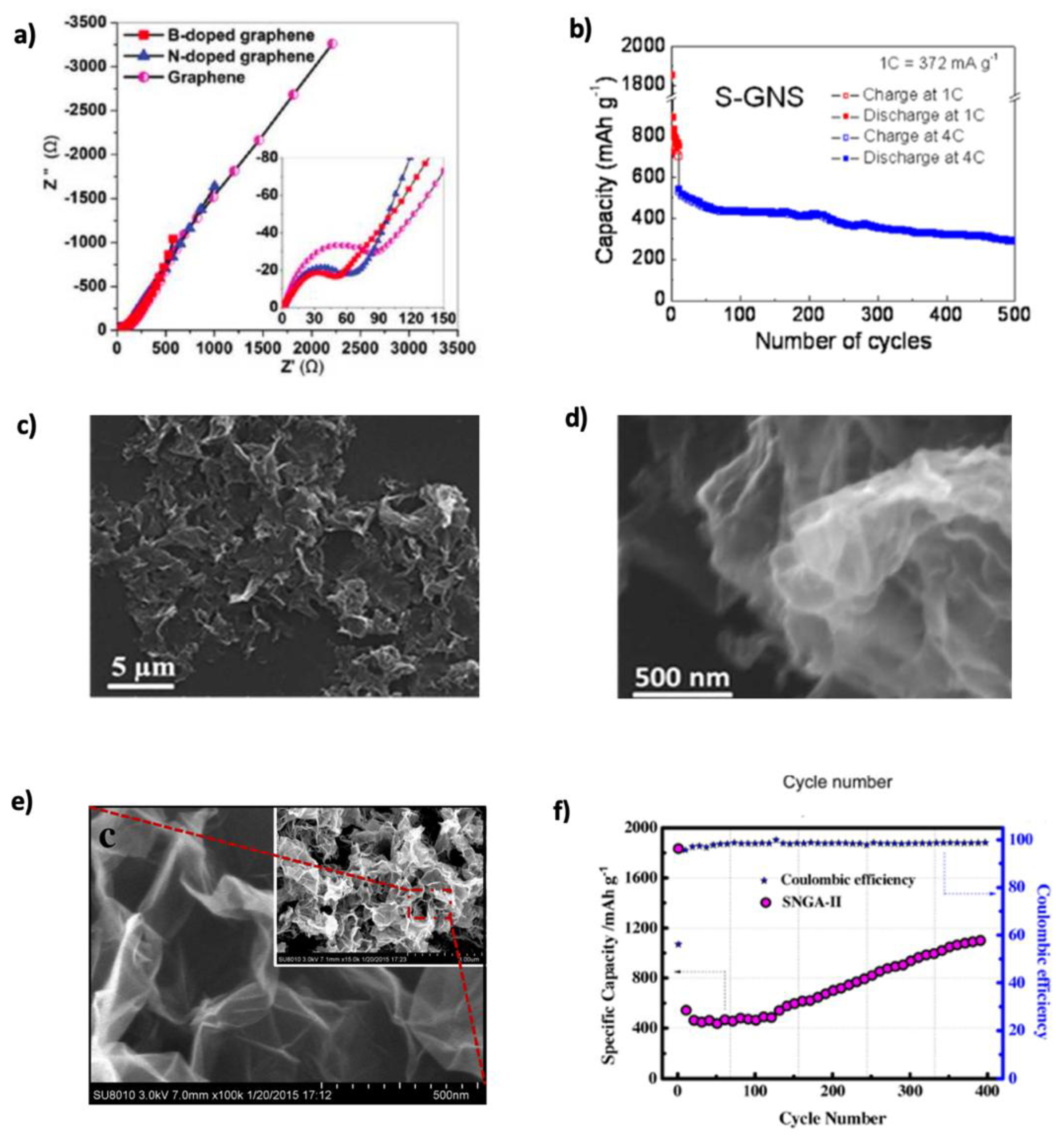
3.3.2. Doped Graphene
3.3.3. Graphene-Based Composite Materials
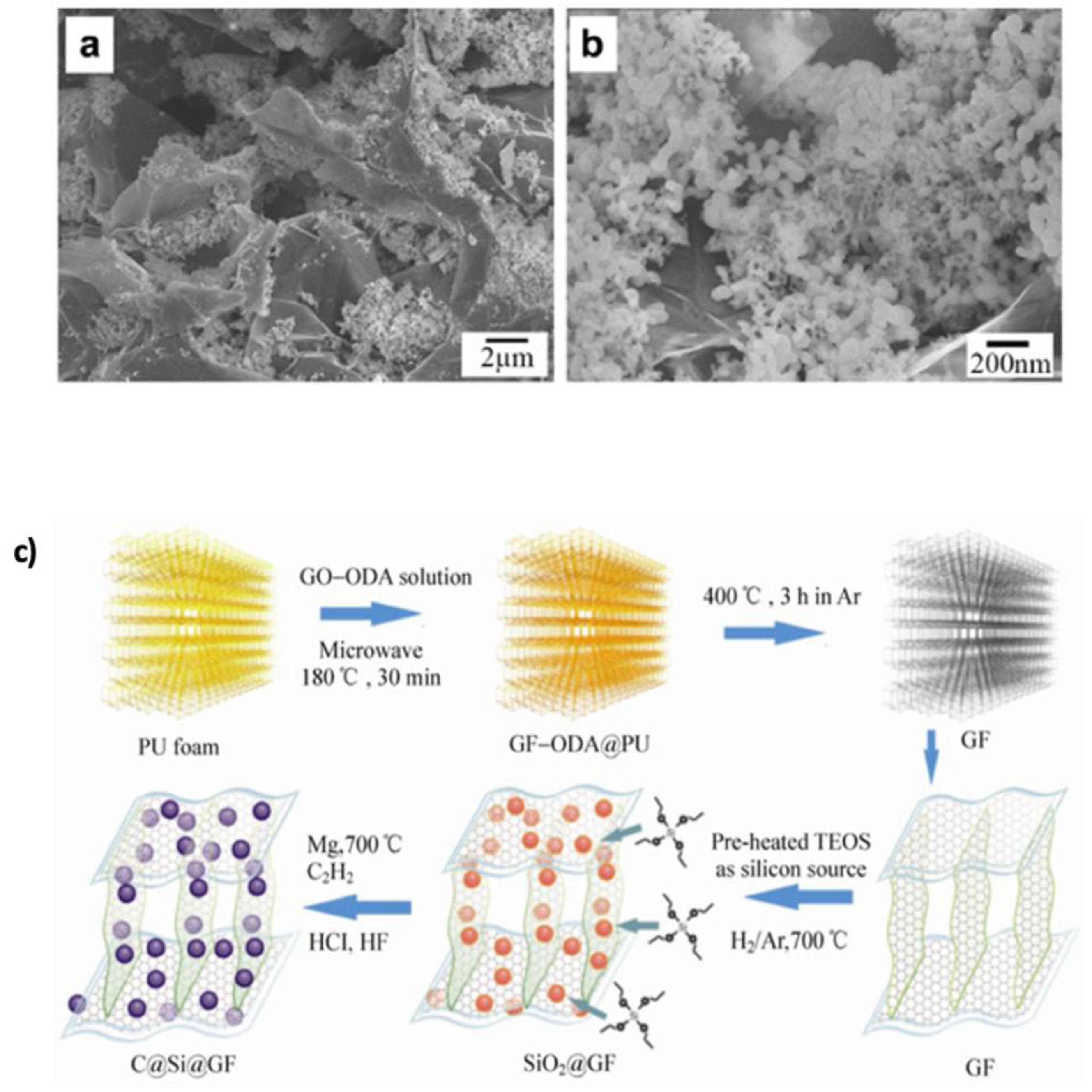
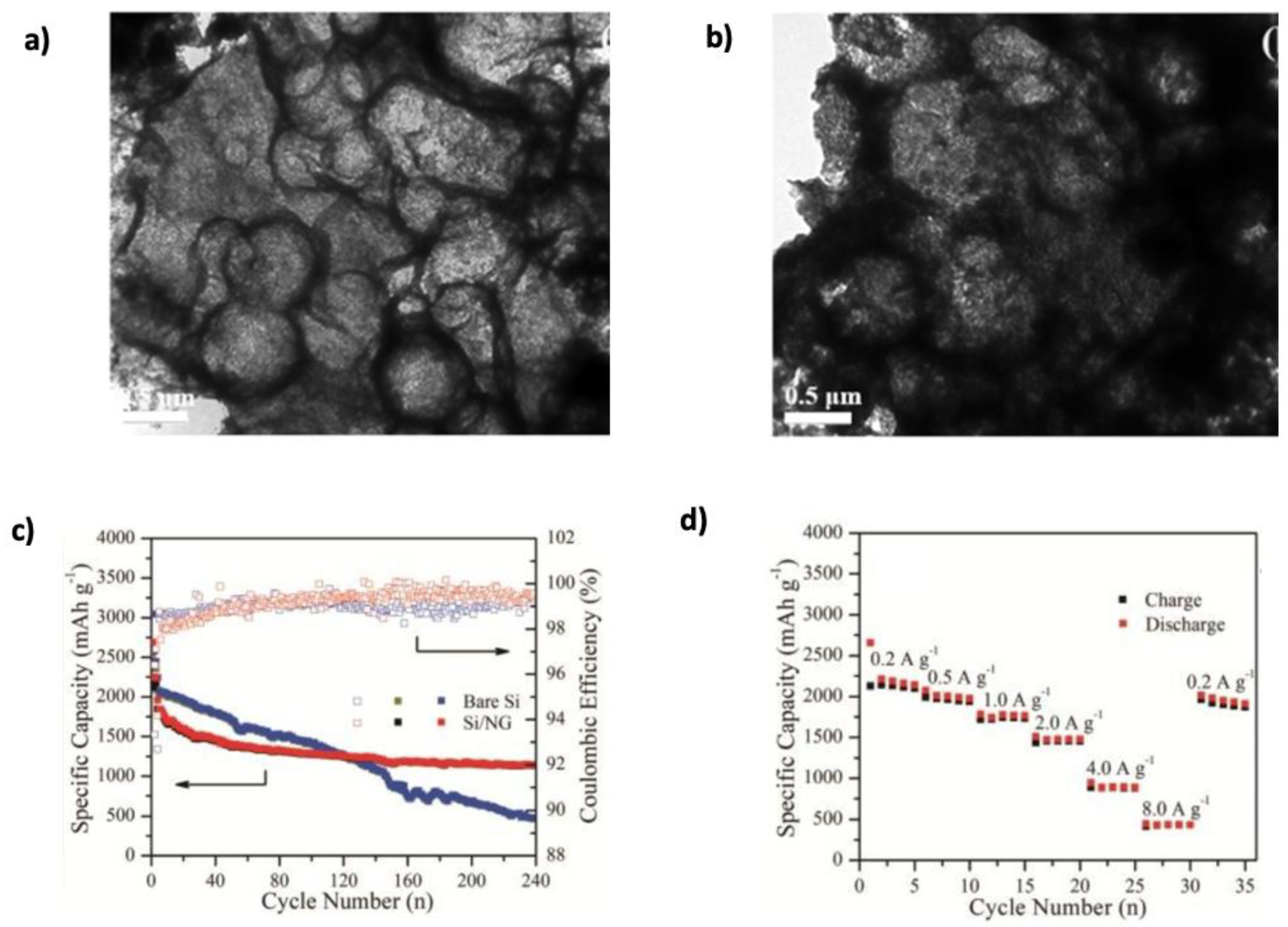
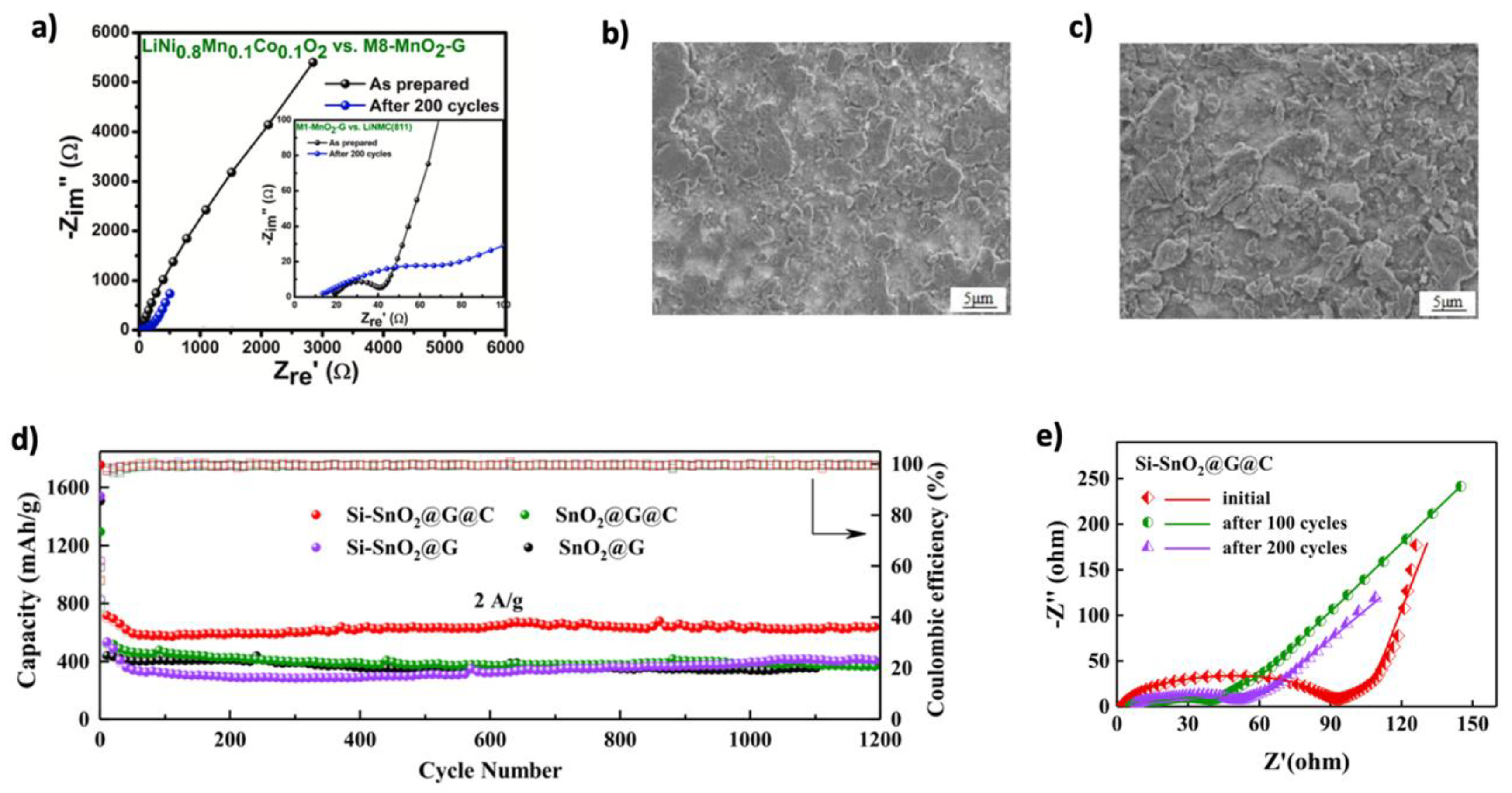
Si–Graphene Composites
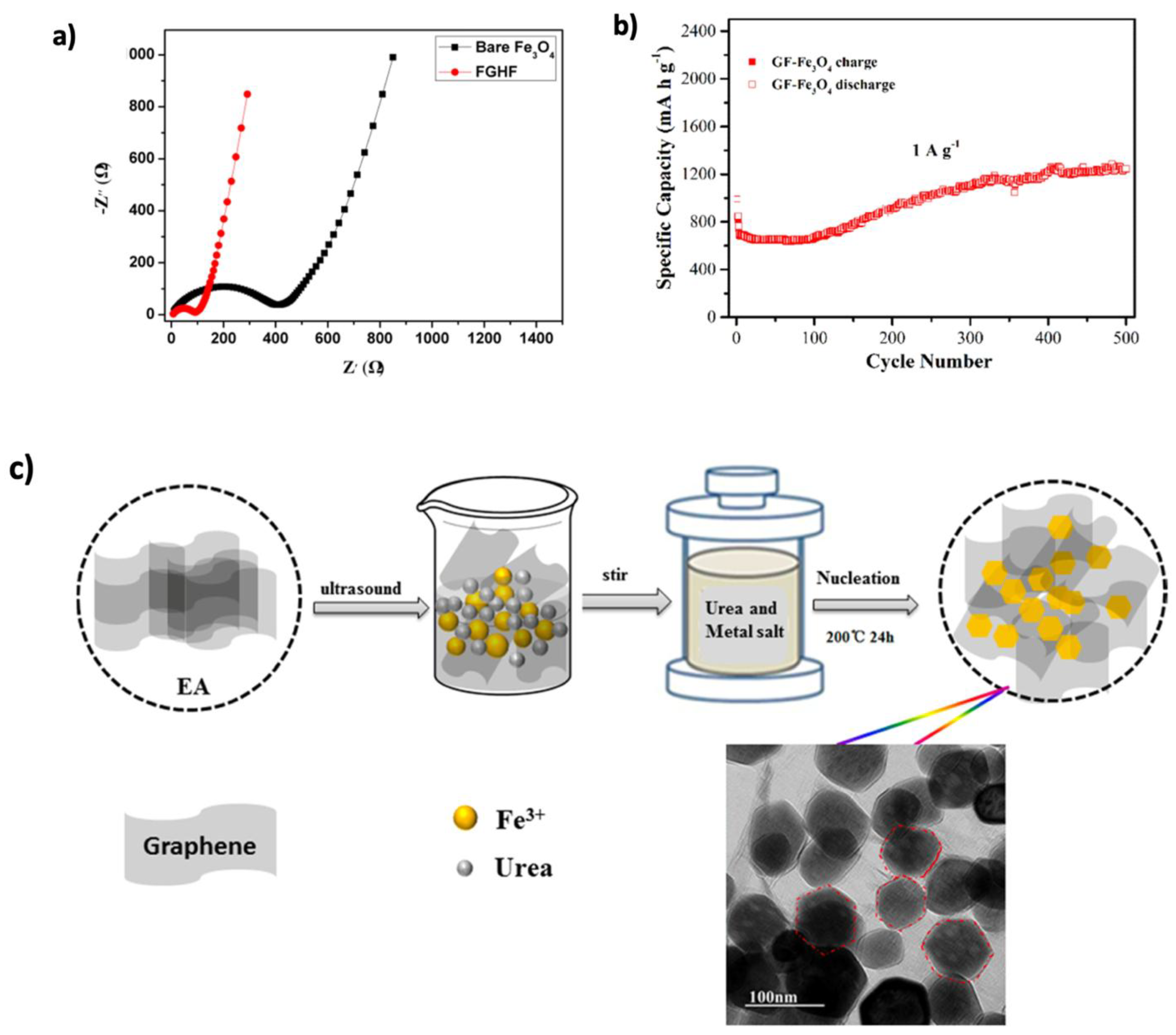
Transition Metal Oxide–Graphene Composites
Metal Sulfide–Graphene Composites
4. Conclusions and Future Prospects
Author Contributions
Funding
Conflicts of Interest
References
- Divakaran, A.M.; Minakshi, M.; Bahri, P.A.; Paul, S.; Kumari, P.; Divakaran, A.M.; Manjunatha, K.N. Rational Design on Materials for Developing next Generation Lithium-Ion Secondary Battery. Prog. Solid State Chem. 2021, 62, 100298. [Google Scholar] [CrossRef]
- Ayyanusamy, P.; Swathi Tharani, D.; Alphonse, R.; Minakshi, M.; Sivasubramanian, R. Synthesis of Amorphous Nickel-Cobalt Hydroxides for Ni−Zn Batteries. Chem. A Eur. J. 2024, 30, e202402325. [Google Scholar] [CrossRef] [PubMed]
- Mahmud, S.; Rahman, M.; Kamruzzaman, M.; Ali, M.O.; Emon, M.S.A.; Khatun, H.; Ali, M.R. Recent Advances in Lithium-Ion Battery Materials for Improved Electrochemical Performance: A Review. Results Eng. 2022, 15, 100472. [Google Scholar] [CrossRef]
- Xu, J.; Cai, X.; Cai, S.; Shao, Y.; Hu, C.; Lu, S.; Ding, S. High-Energy Lithium-Ion Batteries: Recent Progress and a Promising Future in Applications. Energy Environ. Mater. 2023, 6, e12450. [Google Scholar] [CrossRef]
- Bi, J.; Du, Z.; Sun, J.; Liu, Y.; Wang, K.; Du, H.; Ai, W.; Huang, W. On the Road to the Frontiers of Lithium-Ion Batteries: A Review and Outlook of Graphene Anodes. Adv. Mater. 2023, 35, 2210734. [Google Scholar] [CrossRef]
- Joy, R.; Balakrishnan, N.T.M.; Das, A.; Shafeek, S.; Thakur, V.K.; Zaghib, K.; Jaffarali, J.F.M.; Reddy, M.V.V.; Raghavan, P. Graphene: Chemistry and Applications for Lithium-Ion Batteries. Electrochem 2022, 3, 143–183. [Google Scholar] [CrossRef]
- Trihutomo, P.; Sulaiman, F.; Mahardika, R. Improvement of Boron-Doped Graphene Material as an Anode Candidate for Sustainable Energy Storage Based Lithium Batteries. Eureka Phys. Eng. 2024, 2024, 128–136. [Google Scholar] [CrossRef]
- Mand Khan, B.; Chun Oh, W.; Nuengmatch, P.; Ullah, K. Role of Graphene-Based Nanocomposites as Anode Material for Lithium-Ion Batteries. Mater. Sci. Eng. B 2023, 287, 116141. [Google Scholar] [CrossRef]
- Tian, J.; Xing, F.; Gao, Q. Graphene-Based Nanomaterials as the Cathode for Lithium-Sulfur Batteries. Molecules 2021, 26, 2507. [Google Scholar] [CrossRef]
- Raccichini, R.; Varzi, A.; Passerini, S.; Scrosati, B. The Role of Graphene for Electrochemical Energy Storage. Nat. Mater. 2015, 14, 271–279. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, M.; He, W.; Guo, T.; Tong, W.; Kan, E.; Ouyang, X.; Qiao, F.; Wang, J.; Sun, X.; et al. Unveiling the Autocatalytic Growth of Li2S Crystals at the Solid-Liquid Interface in Lithium-Sulfur Batteries. Nat. Commun. 2024, 15, 9535. [Google Scholar] [CrossRef] [PubMed]
- Yildirim, H.; Kinaci, A.; Zhao, Z.J.; Chan, M.K.Y.; Greeley, J.P. First-Principles Analysis of Defect-Mediated Li Adsorption on Graphene. ACS Appl. Mater. Interfaces 2014, 6, 21141–21150. [Google Scholar] [CrossRef] [PubMed]
- Loghavi, M.M.; Mohammadi-Manesh, H.; Eqra, R.; Ghasemi, A.; Babaiee, M. DFT Study of Adsorption of Lithium on Si, Ge-Doped Divacancy Defected Graphene as Anode Material of Li-Ion Battery. Phys. Chem. Res. 2018, 6, 871–878. [Google Scholar] [CrossRef]
- Wang, T.; Qi, Y.; Li, M.; Zhao, X.; Xia, C.; An, Y.; Wei, S. First-Principles Study of Penta-Graphene/MoS2 VdW Heterostructure as Anode Material for Lithium-Ion Batteries. Diam. Relat. Mater. 2023, 136, 109928. [Google Scholar] [CrossRef]
- Zhang, M.; Cui, Z.; Wang, Y.; Jiang, H. Hybrid Functionals with System-dependent Parameters: Conceptual Foundations and Methodological Developments. WIREs Comput. Mol. Sci. 2020, 10, e1476. [Google Scholar] [CrossRef]
- Vogiatzis, K.D.; Polynski, M.V.; Kirkland, J.K.; Townsend, J.; Hashemi, A.; Liu, C.; Pidko, E.A. Computational Approach to Molecular Catalysis by 3d Transition Metals: Challenges and Opportunities. Chem. Rev. 2019, 119, 2453–2523. [Google Scholar] [CrossRef]
- Chelikowsky, J.R.; Fan, D.; Lee, A.J.; Sakai, Y. Simulating Noncontact Atomic Force Microscopy Images. Phys. Rev. Mater. 2019, 3, 110302. [Google Scholar] [CrossRef]
- Kotsonis, G.N.; Almishal, S.S.I.; Marques dos Santos Vieira, F.; Crespi, V.H.; Dabo, I.; Rost, C.M.; Maria, J. High-entropy Oxides: Harnessing Crystalline Disorder for Emergent Functionality. J. Am. Ceram. Soc. 2023, 106, 5587–5611. [Google Scholar] [CrossRef]
- Young, J.; Smeu, M. Applications of Ab Initio Molecular Dynamics for Modeling Batteries. In Computational Design of Battery Materials; Springer International Publishing: Cham, Switzerland, 2024; pp. 329–365. [Google Scholar]
- Liu, M.; Wu, Z.; Liu, S.; Guo, T.; Chen, P.; Cao, X.; Pan, S.; Zhou, T.; Pompizii, L.; Najafov, M.; et al. Accelerated Reversible Conversion of Li 2 S 2 to Li 2 S by Spidroin Regulated Li + Flux for High-performance Li-Sulfur Batteries. Angew. Chem. Int. Ed. 2025, 64, e202417624. [Google Scholar] [CrossRef]
- Adekoya, D.; Qian, S.; Gu, X.; Wen, W.; Li, D.; Ma, J.; Zhang, S. DFT-Guided Design and Fabrication of Carbon-Nitride-Based Materials for Energy Storage Devices: A Review. Nano-Micro Lett. 2021, 13, 13. [Google Scholar] [CrossRef]
- Liu, H.; Dong, H.; Ji, Y.; Wang, L.; Hou, T.; Li, Y. The Adsorption, Diffusion and Capacity of Lithium on Novel Boron-Doped Graphene Nanoribbon: A Density Functional Theory Study. Appl. Surf. Sci. 2019, 466, 737–745. [Google Scholar] [CrossRef]
- Gao, J.; Shi, S.Q.; Li, H. Brief Overview of Electrochemical Potential in Lithium Ion Batteries. Chin. Phys. B 2015, 25, 115–138. [Google Scholar] [CrossRef]
- He, Q.; Yu, B.; Li, Z.; Zhao, Y. Density Functional Theory for Battery Materials. Energy Environ. Mater. 2019, 2, 264–279. [Google Scholar] [CrossRef]
- Fernández-Gamboa, J.R.; Tielens, F.; Zulueta, Y.A. Impact of Li Disorder on the Open Cell Voltage Profile of LixTi6O13 Anodes: A Theoretical Study. Mater. Sci. Semicond. Process. 2024, 173, 108144. [Google Scholar] [CrossRef]
- Ullah, S.; Denis, P.A.; Sato, F. Beryllium Doped Graphene as an Efficient Anode Material for Lithium-Ion Batteries with Significantly Huge Capacity: A DFT Study. Appl. Mater. Today 2017, 9, 333–340. [Google Scholar] [CrossRef]
- Gavali, D.S.; Kawazoe, Y.; Thapa, R. First-Principles Identification of Interface Effect on Li Storage Capacity of C3N/Graphene Multilayer Heterostructure. J. Colloid Interface Sci. 2022, 610, 80–88. [Google Scholar] [CrossRef]
- Kong, C.P.; Hu, Y.Y.; Bai, F.Q.; Zhang, H.X.; Jia, R. F-GDY and F-GDY/Graphene as Anodes in Lithium-Ion Batteries: A First-Principle Investigation. Appl. Surf. Sci. 2022, 595, 153543. [Google Scholar] [CrossRef]
- Kolosov, D.A.; Glukhova, O.E. Theoretical Study of a New Porous 2D Silicon-Filled Composite Based on Graphene and Single-Walled Carbon Nanotubes for Lithium-Ion Batteries. Appl. Sci. 2020, 10, 5786. [Google Scholar] [CrossRef]
- Mousavi-Khoshdel, M.; Targholi, E.; Momeni, M.J. First-Principles Calculation of Quantum Capacitance of Codoped Graphenes as Supercapacitor Electrodes. J. Phys. Chem. C 2015, 119, 26290–26295. [Google Scholar] [CrossRef]
- Lu, Y.; Hou, X.; Miao, L.; Li, L.; Shi, R.; Liu, L.; Chen, J. Cyclohexanehexone with Ultrahigh Capacity as Cathode Materials for Lithium-Ion Batteries. Angew. Chem. 2019, 131, 7094–7098. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Ren, W.; Zhang, D.; Yang, Y.; Yang, J.; Wang, J.; Zeng, X.; NuLi, Y. Challenges and Prospects of Mg-Air Batteries: A Review. Energy Mater. 2022, 2, 200024. [Google Scholar] [CrossRef]
- Hymel, J.H.; Khan, S.N.; Pederson, J.P.; McDaniel, J.G. Computational Electrosynthesis Study of Anodic Intramolecular Olefin Coupling: Elucidating the Role of the Electrical Double Layer. J. Phys. Chem. C 2023, 127, 19489–19508. [Google Scholar] [CrossRef]
- Bahari, Y.; Mortazavi, B.; Rajabpour, A.; Zhuang, X.; Rabczuk, T. Application of Two-Dimensional Materials as Anodes for Rechargeable Metal-Ion Batteries: A Comprehensive Perspective from Density Functional Theory Simulations. Energy Storage Mater. 2021, 35, 203–282. [Google Scholar] [CrossRef]
- Yu, L.; Chen, X.; Yao, N.; Gao, Y.; Yuan, Y.; Gao, Y.; Tang, C.; Zhang, Q. Advanced Carbon as Emerging Energy Materials in Lithium Batteries: A Theoretical Perspective. InfoMat 2025, 7, e12653. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Yang, D.; Zhu, B.; Lin, H.; Ma, T.; Jia, B. Doping Mechanism Directed Graphene Applications for Energy Conversion and Storage. J. Mater. Chem. A Mater. 2021, 9, 7366–7395. [Google Scholar] [CrossRef]
- Liu, M.; Bai, W.; Guo, H.; Sun, J.; Liu, Y.; Fang, M.; Guo, T.; Yang, S.; Vasiliev, A.L.; Kulesza, P.J.; et al. A Permselective and Multifunctional 3D N-Doped Carbon Nanotubes Interlayer for High-Performance Lithium-Sulfur Batteries. Electrochim. Acta 2022, 421, 140430. [Google Scholar] [CrossRef]
- Muchuweni, E.; Mombeshora, E.T.; Muiva, C.M.; Sathiaraj, T.S. Lithium-Ion Batteries: Recent Progress in Improving the Cycling and Rate Performances of Transition Metal Oxide Anodes by Incorporating Graphene-Based Materials. J. Energy Storage 2023, 73, 109013. [Google Scholar] [CrossRef]
- Zheng, J.; Ren, Z.; Guo, P.; Fang, L.; Fan, J. Diffusion of Li + Ion on Graphene: A DFT Study. Appl. Surf. Sci. 2011, 258, 1651–1655. [Google Scholar] [CrossRef]
- Daula Shamim, S.U.; Hossain, M.K.; Hasan, S.M.; Hossain, A.; Ahmed, F. Ab Initio Study of N-Doped Graphene Oxide (NDGO) as a Promising Anode Material for Li-Ion Rechargeable Battery. Mol. Simul. 2020, 46, 1135–1145. [Google Scholar] [CrossRef]
- Zaidi, S.Z.J.; Hassan, S.; Raza, M.; Walsh, F.C. Transition Metal Oxide as Possible Electrode Materials for Li-Ion Batteries: A DFT Analysis. Int. J. Electrochem. Sci. 2021, 16, 210322. [Google Scholar] [CrossRef]
- Wu, S.; Fan, K.; Wu, M.; Yin, G. Two-Dimensional MnO2/Graphene Hybrid Nanostructures as Anode for Lithium Ion Batteries. Int. J. Mod. Phys. B 2016, 30, 1650208. [Google Scholar] [CrossRef]
- Zhang, H.; Du, X.; Ding, S.; Wang, Q.; Chang, L.; Ma, X.; Hao, X.; Pen, C. DFT Calculations of the Synergistic Effect of λ-MnO2/Graphene Composites for Electrochemical Adsorption of Lithium Ions. Phys. Chem. Chem. Phys. 2019, 21, 8133–8140. [Google Scholar] [CrossRef] [PubMed]
- De Souza, L.A.; Monteiro de Castro, G.; Marques, L.F.; Belchior, J.C. A DFT Investigation of Lithium Adsorption on Graphenes as a Potential Anode Material in Lithium-Ion Batteries. J. Mol. Graph. Model. 2021, 108, 107998. [Google Scholar] [CrossRef]
- Dimakis, N.; Salas, I.; Gonzalez, L.; Vadodaria, O.; Ruiz, K.; Bhatti, M.I. Li and Na Adsorption on Graphene and Graphene Oxide Examined by Density Functional Theory, Quantum Theory of Atoms in Molecules, and Electron Localization Function. Molecules 2019, 24, 754. [Google Scholar] [CrossRef]
- Zhang, F.; Fang, W.; Wu, X.; Lu, X. Enhanced Stability and the Lithium Storage Mechanism of Oxygen Vacancy-Induced Heterogeneous Li 4 Ti 5 O 12/TiO 2 (B) Anolytes. J. Mater. Chem. A Mater. 2024, 12, 18393–18403. [Google Scholar] [CrossRef]
- Mlotshwa, T.M.; Jhamba, L.; Maluta, N.E.; Kirui, J.K. Computational Analyses of Graphene Quantum Dots for Anode Material in Lithium-Ion Batteries. In Proceedings of the 66th annual conference of the South African Institute of Physics (SAIP), Gqeberha, South Africa, 1–8 July 2022. [Google Scholar]
- Shaker, M.; Shahalizade, T.; Mumtaz, A.; Hemmati Saznaghi, M.; Javanmardi, S.; Gaho, M.A.; Cao, W.; Hu, W.; Jin, Z.; Ge, Q.; et al. A Review on the Role of Graphene Quantum Dots and Carbon Quantum Dots in Secondary-Ion Battery Electrodes. FlatChem 2023, 40, 100516. [Google Scholar] [CrossRef]
- Pattarapongdilok, N.; Parasuk, V. Adsorptions of Lithium Ion/Atom and Packing of Li Ions on Graphene Quantum Dots: Application for Li-Ion Battery. Comput. Theor. Chem. 2020, 1177, 112779. [Google Scholar] [CrossRef]
- Hu, R.; Zhou, J. A DFT Study of Li Adsorption on Surface of Si Clusters Anchored N-Doped Defective Graphene Composite. Appl. Surf. Sci. 2018, 457, 789–796. [Google Scholar] [CrossRef]
- Bijoy, T.K.; Sudhakaran, S.; Lee, S.C. WS2-Graphene van Der Waals Heterostructure as Promising Anode Material for Lithium-Ion Batteries: A First-Principles Approach. ACS Omega 2024, 9, 6482–6491. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, X.; Qian, Y.; Wu, H.; Kan, E. First-Principles Study on S and N Doping Graphene/SnS2 Heterostructure for Lithium-Ion Battery. Chem. Phys. Lett. 2021, 769, 138391. [Google Scholar] [CrossRef]
- Wan, W.; Wang, H. First-Principles Investigation of Adsorption and Diffusion of Ions on Pristine, Defective and B-Doped Graphene. Materials 2015, 8, 6163–6178. [Google Scholar] [CrossRef]
- Wasalathilake, K.C.; Ayoko, G.A.; Yan, C. Effects of Heteroatom Doping on the Performance of Graphene in Sodium-Ion Batteries: A Density Functional Theory Investigation. Carbone N. Y. 2018, 140, 276–285. [Google Scholar] [CrossRef]
- Yang, G.; Fan, X.; Liang, Z.; Xu, Q.; Zheng, W. Density Functional Theory Study of Li Binding to Graphene. RSC Adv. 2016, 6, 26540–26545. [Google Scholar] [CrossRef]
- Ji, Z.; Contreras-Torres, F.F.; Jalbout, A.F.; Ramírez-Treviño, A. Surface Diffusion and Coverage Effect of Li Atom on Graphene as Studied by Several Density Functional Theory Methods. Appl. Surf. Sci. 2013, 285, 846–852. [Google Scholar] [CrossRef]
- Fan, X.; Zheng, W.T.; Kuo, J.L. Adsorption and Diffusion of Li on Pristine and Defective Graphene. ACS Appl. Mater. Interfaces 2012, 4, 2432–2438. [Google Scholar] [CrossRef]
- Murugesan, V.; Hu, J. Exploring the Interaction between Lithium Ion and Defective Graphene Surface Using Dispersion Corrected DFT Studies. ECS Trans. 2013, 53, 23–32. [Google Scholar] [CrossRef]
- Uthaisar, C.; Barone, V. Edge Effects on the Characteristics of Li Diffusion in Graphene. Nano Lett. 2010, 10, 2838–2842. [Google Scholar] [CrossRef]
- Kong, X. Metal-Free Si-Doped Graphene: A New and Enhanced Anode Material for Li Ion Battery. J. Alloys Compd. 2016, 687, 534–540. [Google Scholar] [CrossRef]
- Tran, T.N.; Anh Duy, N.V.; Hieu, N.H.; Nguyen, T.A.; Van, N.T.; Bac Phung, T.V.; Zulueta, Y.A.; Nguyen, M.T.; Schall, P.; Dang, M.T. Electric Field Enhances the Electronic and Diffusion Properties of Penta-Graphene Nanoribbon Anodes in Lithium-Ion Batteries. RSC Adv. 2024, 14, 33524–33535. [Google Scholar] [CrossRef]
- Obrovac, M.N.; Chevrier, V.L. Alloy Negative Electrodes for Li-Ion Batteries. Chem. Rev. 2014, 114, 11444–11502. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Lu, G. Subspace Formulation of Time-Dependent Density Functional Theory for Large-Scale Calculations. J. Chem. Phys. 2015, 143, 64110. [Google Scholar] [CrossRef] [PubMed]
- Ajeel, F.N.; Mohammed, M.H.; Khudhair, A.M. Effects of Lithium Impurities on Electronic and Optical Properties of Graphene Nanoflakes: A DFT–TDDFT Study. Chin. J. Phys. 2019, 58, 109–116. [Google Scholar] [CrossRef]
- Ardakani, Y.S.; Moradi, M. DFT/TDDFT Investigation of Electronic, Magnetic, and Optical Properties of Graphene Containing Different Values of Se Impurity. Phys. Solid State 2020, 62, 1262–1270. [Google Scholar] [CrossRef]
- Urban, A.; Seo, D.-H.; Ceder, G. Computational Understanding of Li-Ion Batteries. NPJ Comput. Mater. 2016, 2, 16002. [Google Scholar] [CrossRef]
- Chen, R.; Luo, J.; Yang, A.; Xie, Z.; Elnaggar, A.Y.; Liu, B.; El-Bahy, S.M.; Guo, Z. Electronic Structure and Delithiation Mechanism of Vanadium and Nickel Doped Li2MnPO4F Cathode Material for Lithium-Ion Batteries. J. Mater. Sci. Mater. Electron. 2024, 35, 1342. [Google Scholar] [CrossRef]
- Harun, K.; Salleh, N.A.; Deghfel, B.; Yaakob, M.K.; Mohamad, A.A. DFT + U Calculations for Electronic, Structural, and Optical Properties of ZnO Wurtzite Structure: A Review. Results Phys. 2020, 16, 102829. [Google Scholar] [CrossRef]
- Yu, M.; Yang, S.; Wu, C.; Marom, N. Machine Learning the Hubbard U Parameter in DFT+U Using Bayesian Optimization. NPJ Comput. Mater. 2020, 6, 180. [Google Scholar] [CrossRef]
- Kowalski, P.M.; Bornhake, T.; Cheong, O.; Dohrmann, N.; Koch Liston, A.L.; Potts, S.K.; Shad, A.; Tesch, R.; Ting, Y.Y. Fundamentals of Energy Storage from First Principles Simulations: Challenges and Opportunities. Front. Energy Res. 2023, 10, 1096190. [Google Scholar] [CrossRef]
- Ting, Y.-Y.; Kowalski, P.M. Refined DFT+U Method for Computation of Layered Oxide Cathode Materials. Electrochim. Acta 2023, 443, 141912. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, B.; Xiao, J.; Zhou, L.; Chen, M. Application of First Principles Computations Based on Density Functional Theory (DFT) in Cathode Materials of Sodium-Ion Batteries. Batteries 2023, 9, 86. [Google Scholar] [CrossRef]
- Morgan, B.J.; Watson, G.W. GGA+U Description of Lithium Intercalation into Anatase TiO2. Phys. Rev. B Condens. Matter Mater. Phys. 2010, 82, 144119. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Y.; Gao, W.; Lin, Y.; Zhao, X.; Wang, Q.; Yao, X.; He, M.; Ye, X.; Liu, Y. Sizable Bandgaps of Graphene in 3d Transition Metal Intercalated Defective Graphene/WSe2 Heterostructures. RSC Adv. 2019, 9, 18157–18164. [Google Scholar] [CrossRef] [PubMed]
- Devi, R.; Singh, B.; Canepa, P.; Sai Gautam, G. Effect of Exchange-Correlation Functionals on the Estimation of Migration Barriers in Battery Materials. NPJ Comput. Mater. 2022, 8, 160. [Google Scholar] [CrossRef]
- Yang, J.H.; Kitchaev, D.A.; Ceder, G. Rationalizing Accurate Structure Prediction in the Meta-GGA SCAN Functional. Phys. Rev. B 2019, 100, 35132. [Google Scholar] [CrossRef]
- Grimme, S. Density Functional Theory with London Dispersion Corrections. WIREs Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 36402. [Google Scholar] [CrossRef]
- Sokolovskiy, V.; Baigutlin, D.; Miroshkina, O.; Buchelnikov, V. Meta-GGA SCAN Functional in the Prediction of Ground State Properties of Magnetic Materials: Review of the Current State. Metals 2023, 13, 728. [Google Scholar] [CrossRef]
- Peng, H.; Yang, Z.-H.; Perdew, J.P.; Sun, J. Versatile van Der Waals Density Functional Based on a Meta-Generalized Gradient Approximation. Phys. Rev. X 2016, 6, 41005. [Google Scholar] [CrossRef]
- Ladha, D.G. A Review on Density Functional Theory–Based Study on Two-Dimensional Materials Used in Batteries. Mater. Today Chem. 2019, 11, 94–111. [Google Scholar] [CrossRef]
- Bulusheva, L.G.; Stolyarova, S.G.; Chuvilin, A.L.; Shubin, Y.V.; Asanov, I.P.; Sorokin, A.M.; Mel’Gunov, M.S.; Zhang, S.; Dong, Y.; Chen, X.; et al. Creation of Nanosized Holes in Graphene Planes for Improvement of Rate Capability of Lithium-Ion Batteries. Nanotechnology 2018, 29, 134001. [Google Scholar] [CrossRef] [PubMed]
- Datta, D.; Li, J.; Koratkar, N.; Shenoy, V.B. Enhanced Lithiation in Defective Graphene. Carbone N. Y. 2014, 80, 305–310. [Google Scholar] [CrossRef]
- Wu, Z.S.; Ren, W.; Xu, L.; Li, F.; Cheng, H.M. Doped Graphene Sheets as Anode Materials with Superhigh Rate and Large Capacity for Lithium Ion Batteries. ACS Nano 2011, 5, 5463–5471. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zeng, Z.; Ahn, H.; Wang, G. First-Principles Study on the Enhancement of Lithium Storage Capacity in Boron Doped Graphene. Appl. Phys. Lett. 2009, 95, 183103. [Google Scholar] [CrossRef]
- Ma, C.; Shao, X.; Cao, D. Nitrogen-Doped Graphene Nanosheets as Anode Materials for Lithium Ion Batteries: A First-Principles Study. J. Mater. Chem. 2012, 22, 8911. [Google Scholar] [CrossRef]
- Xiang, H.; Zhang, K.; Ji, G.; Lee, J.Y.; Zou, C.; Chen, X.; Wu, J. Graphene/Nanosized Silicon Composites for Lithium Battery Anodes with Improved Cycling Stability. Carbone N. Y. 2011, 49, 1787–1796. [Google Scholar] [CrossRef]
- Tang, Q.; Shan, Z.; Wang, L.; Qin, X. MoO2–Graphene Nanocomposite as Anode Material for Lithium-Ion Batteries. Electrochim. Acta 2012, 79, 148–153. [Google Scholar] [CrossRef]
- Ma, J.; Fu, J.; Niu, M.; Quhe, R. MoO2 and Graphene Heterostructure as Promising Flexible Anodes for Lithium-Ion Batteries. Carbone N. Y. 2019, 147, 357–363. [Google Scholar] [CrossRef]
- Youn, D.H.; Jo, C.; Kim, J.Y.; Lee, J.; Lee, J.S. Ultrafast Synthesis of MoS2 or WS2-Reduced Graphene Oxide Composites via Hybrid Microwave Annealing for Anode Materials of Lithium Ion Batteries. J. Power Sources 2015, 295, 228–234. [Google Scholar] [CrossRef]
- Wang, Q.; Nie, Y.-X.; He, B.; Xing, L.-L.; Xue, X.-Y. SnS2–Graphene Nanocomposites as Anodes of Lithium-Ion Batteries. Solid State Sci. 2014, 31, 81–84. [Google Scholar] [CrossRef]
- Li, G. Regulating Mass Transport Behavior for High-Performance Lithium Metal Batteries and Fast-Charging Lithium-Ion Batteries. Adv. Energy Mater. 2021, 11, 2002891. [Google Scholar] [CrossRef]
- Huang, G.; Cai, B.; Zhan, C.; Sun, P. Two-Dimensional Material as Anode for Lithium Ion Batteries: Recent Progress. Int. J. Electrochem. Sci. 2020, 15, 5416–5429. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.; Yang, M.; Chen, W. High-Safety Separators for Lithium-Ion Batteries and Sodium-Ion Batteries: Advances and Perspective. Energy Storage Mater. 2021, 41, 522–545. [Google Scholar] [CrossRef]
- Kumar, N.; Salehiyan, R.; Chauke, V.; Joseph Botlhoko, O.; Setshedi, K.; Scriba, M.; Masukume, M.; Sinha Ray, S. Top-down Synthesis of Graphene: A Comprehensive Review. FlatChem 2021, 27, 100224. [Google Scholar] [CrossRef]
- Ali, A.; Liang, F.; Zhu, J.; Shen, P.K. The Role of Graphene in Rechargeable Lithium Batteries: Synthesis, Functionalisation, and Perspectives. Nano Mater. Sci. 2022. [Google Scholar] [CrossRef]
- Kumar, R.; Sahoo, S.; Joanni, E.; Singh, R.K.; Tan, W.K.; Kar, K.K.; Matsuda, A. Recent Progress in the Synthesis of Graphene and Derived Materials for next Generation Electrodes of High Performance Lithium Ion Batteries. Prog. Energy Combust. Sci. 2019, 75, 100786. [Google Scholar] [CrossRef]
- Ahmad, F.; Zahid, M.; Jamil, H.; Khan, M.A.; Atiq, S.; Bibi, M.; Shahbaz, K.; Adnan, M.; Danish, M.; Rasheed, F.; et al. Advances in Graphene-Based Electrode Materials for High-Performance Supercapacitors: A Review. J. Energy Storage 2023, 72, 108731. [Google Scholar] [CrossRef]
- Safian, M.T.; Umar, K.; Mohamad Ibrahim, M.N. Synthesis and Scalability of Graphene and Its Derivatives: A Journey towards Sustainable and Commercial Material. J. Clean Prod. 2021, 318, 128603. [Google Scholar] [CrossRef]
- Chen, K.; Shi, L.; Zhang, Y.; Liu, Z. Scalable Chemical-Vapour-Deposition Growth of Three-Dimensional Graphene Materials towards Energy-Related Applications. Chem. Soc. Rev. 2018, 47, 3018–3036. [Google Scholar] [CrossRef]
- Ramezani, M.J.; Rahmani, O. A Review of Recent Progress in the Graphene Syntheses and Its Applications. Mech. Adv. Mater. Struct. 2024, 1–33. [Google Scholar] [CrossRef]
- Muthoosamy, K.; Geetha Bai, R.; Abubakar, I.B.; Sudheer, S.M.; Lim, H.N.; Loh, H.S.; Huang, N.M.; Chia, C.H.; Manickam, S. Exceedingly Biocompatible and Thin-Layered Reduced Graphene Oxide Nanosheets Using an Eco-Friendly Mushroom Extract Strategy. Int. J. Nanomed. 2015, 10, 1505–1519. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, Z.X.; Yin, J. Facile Synthesis of Soluble Graphene via a Green Reduction of Graphene Oxide in Tea Solution and Its Biocomposites. ACS Appl. Mater. Interfaces 2011, 3, 1127–1133. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.; Al-Marri, A.H.; Khan, M.; Shaik, M.R.; Mohri, N.; Adil, S.F.; Kuniyil, M.; Alkhathlan, H.Z.; Al-Warthan, A.; Tremel, W.; et al. Green Approach for the Effective Reduction of Graphene Oxide Using Salvadora Persica L. Root (Miswak) Extract. Nanoscale Res. Lett. 2015, 10, 281. [Google Scholar] [CrossRef]
- Kartick, B.; Srivastava, S.K.; Srivastava, I. Green Synthesis of Graphene. J. Nanosci. Nanotechnol. 2013, 13, 4320–4324. [Google Scholar] [CrossRef]
- Kuila, T.; Bose, S.; Khanra, P.; Mishra, A.K.; Kim, N.H.; Lee, J.H. A Green Approach for the Reduction of Graphene Oxide by Wild Carrot Root. Carbone N. Y. 2012, 50, 914–921. [Google Scholar] [CrossRef]
- Thakur, S.; Karak, N. Green Reduction of Graphene Oxide by Aqueous Phytoextracts. Carbon 2012, 50, 5331–5339. [Google Scholar] [CrossRef]
- Tavakoli, F.; Salavati-Niasari, M.; Badiei, A.; Mohandes, F. Green Synthesis and Characterization of Graphene Nanosheets. Mater. Res. Bull. 2015, 63, 51–57. [Google Scholar] [CrossRef]
- Haghighi, B.; Tabrizi, M.A. Green-Synthesis of Reduced Graphene Oxide Nanosheets Using Rose Water and a Survey on Their Characteristics and Applications. RSC Adv. 2013, 3, 13365–13371. [Google Scholar] [CrossRef]
- De Silva, K.K.H.; Huang, H.H.; Joshi, R.K.; Yoshimura, M. Chemical Reduction of Graphene Oxide Using Green Reductants. Carbon N. Y. 2017, 119, 190–199. [Google Scholar] [CrossRef]
- Ismail, Z. Green Reduction of Graphene Oxide by Plant Extracts: A Short Review. Ceram. Int. 2019, 45, 23857–23868. [Google Scholar] [CrossRef]
- Shang, T.; Feng, G.; Li, Q.; Zheng, Y. Production of Graphene Nanosheets by Supercritical CO2 Process Coupled with Micro-Jet Exfoliation. Fuller. Nanotub. Carbon Nanostruct. 2017, 25, 691–698. [Google Scholar] [CrossRef]
- Shu, K.; Tian, S.; Wang, Y.; Fei, G.; Sun, L.; Niu, H.; Duan, Y.; Hu, G.; Wang, H. Graphene Composite via Bacterial Cellulose Assisted Liquid Phase Exfoliation for Sodium-Ion Batteries. Polymer 2023, 15, 203. [Google Scholar] [CrossRef] [PubMed]
- Bhaskar, A.; Deepa, M.; Rao, T.N.; Varadaraju, U.V. Enhanced Nanoscale Conduction Capability of a MoO2/Graphene Composite for High Performance Anodes in Lithium Ion Batteries. J. Power Sources 2012, 216, 169–178. [Google Scholar] [CrossRef]
- Mahmood, N.; Zhang, C.; Jiang, J.; Liu, F.; Hou, Y. Multifunctional Co 3 S 4/Graphene Composites for Lithium Ion Batteries and Oxygen Reduction Reaction. Chem. A Eur. J. 2013, 19, 5183–5190. [Google Scholar] [CrossRef]
- Han, S.; Wu, D.; Li, S.; Zhang, F.; Feng, X. Porous Graphene Materials for Advanced Electrochemical Energy Storage and Conversion Devices. Adv. Mater. 2014, 26, 849–864. [Google Scholar] [CrossRef]
- Huang, H.; Shi, H.; Das, P.; Qin, J.; Li, Y.; Wang, X.; Su, F.; Wen, P.; Li, S.; Lu, P.; et al. The Chemistry and Promising Applications of Graphene and Porous Graphene Materials. Adv. Funct. Mater. 2020, 30, 1909035. [Google Scholar] [CrossRef]
- Russo, P.; Hu, A.; Compagnini, G. Synthesis, Properties and Potential Applications of Porous Graphene: A Review. Nanomicro. Lett. 2013, 5, 260–273. [Google Scholar] [CrossRef]
- Ning, G.; Fan, Z.; Wang, G.; Gao, J.; Qian, W.; Wei, F. Gram-Scale Synthesis of Nanomesh Graphene with High Surface Area and Its Application in Supercapacitor Electrodes. Chem. Commun. 2011, 47, 5976–5978. [Google Scholar] [CrossRef]
- Dutta, S.; Bhaumik, A.; Wu, K.C.W. Hierarchically Porous Carbon Derived from Polymers and Biomass: Effect of Interconnected Pores on Energy Applications. Energy Environ. Sci. 2014, 7, 3574–3592. [Google Scholar] [CrossRef]
- Kukułka, W.; Kierzek, K.; Stankiewicz, N.; Chen, X.; Tang, T.; Mijowska, E. Well-Designed Porous Graphene Flakes for Lithium-Ion Batteries with Outstanding Rate Performance. Langmuir 2019, 35, 12613–12619. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, L.; Yu, P.; Zhao, L.; Tian, C.; Zhou, W.; Zhang, L.; Fu, H. From Graphite to Porous Graphene-like Nanosheets for High Rate Lithium-Ion Batteries. Nano Res. 2015, 8, 2998–3010. [Google Scholar] [CrossRef]
- He, Y.; Zhuang, X.; Lei, C.; Lei, L.; Hou, Y.; Mai, Y.; Feng, X. Porous Carbon Nanosheets: Synthetic Strategies and Electrochemical Energy Related Applications. Nano Today 2019, 24, 103–119. [Google Scholar] [CrossRef]
- Tian, H.; Wang, N.; Xu, F.; Zhang, P.; Hou, D.; Mai, Y.; Feng, X. Nitrogen-Doped Carbon Nanosheets and Nanoflowers with Holey Mesopores for Efficient Oxygen Reduction Catalysis. J. Mater. Chem. A Mater. 2018, 6, 10354–10360. [Google Scholar] [CrossRef]
- Fang, Y.; Lv, Y.; Che, R.; Wu, H.; Zhang, X.; Gu, D.; Zheng, G.; Zhao, D. Two-Dimensional Mesoporous Carbon Nanosheets and Their Derived Graphene Nanosheets: Synthesis and Efficient Lithium Ion Storage. J. Am. Chem. Soc. 2013, 135, 1524–1530. [Google Scholar] [CrossRef]
- Jia, X.; Campos-Delgado, J.; Terrones, M.; Meunier, V.; Dresselhaus, M.S. Graphene Edges: A Review of Their Fabrication and Characterization. Nanoscale 2011, 3, 86–95. [Google Scholar] [CrossRef]
- Kim, Y.A.; Hayashi, T.; Kim, J.H.; Endo, M. Important Roles of Graphene Edges in Carbon-Based Energy Storage Devices. J. Energy Chem. 2013, 22, 183–194. [Google Scholar] [CrossRef]
- Sonia, F.J.; Aslam, M.; Mukhopadhyay, A. Understanding the Processing-Structure-Performance Relationship of Graphene and Its Variants as Anode Material for Li-Ion Batteries: A Critical Review. Carbon N. Y. 2020, 156, 130–165. [Google Scholar] [CrossRef]
- Acik, M.; Chabal, Y.J. Nature of Graphene Edges: A Review. Jpn. J. Appl. Phys. 2011, 50, 70101. [Google Scholar] [CrossRef]
- Bhardwaj, T.; Antic, A.; Pavan, B.; Barone, V.; Fahlman, B.D. Enhanced Electrochemical Lithium Storage by Graphene Nanoribbons. J. Am. Chem. Soc. 2010, 132, 12556–12558. [Google Scholar] [CrossRef] [PubMed]
- Xiao, B.; Li, X.; Li, X.; Wang, B.; Langford, C.; Li, R.; Sun, X. Graphene Nanoribbons Derived from the Unzipping of Carbon Nanotubes: Controlled Synthesis and Superior Lithium Storage Performance. J. Phys. Chem. C 2014, 118, 881–890. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, X.; Zhang, H.; Liu, H.; Yu, X.; Dai, X.; Liu, G.; Chen, G. Large Vacancy-Defective Graphene for Enhanced Lithium Storage. Carbon. Trends 2023, 10, 100237. [Google Scholar] [CrossRef]
- Dong, S.; Song, Y.; Su, M.; Wang, G.; Gao, Y.; Zhu, K.; Cao, D. Flash Joule Heating Induced Highly Defective Graphene towards Ultrahigh Lithium Ion Storage. Chem. Eng. J. 2024, 481, 147988. [Google Scholar] [CrossRef]
- Kucinskis, G.; Bajars, G.; Kleperis, J. Graphene in Lithium Ion Battery Cathode Materials: A Review. J. Power Sources 2013, 240, 66–79. [Google Scholar] [CrossRef]
- Yoo, E.J.; Kim, J.; Hosono, E.; Zhou, H.S.; Kudo, T.; Honma, I. Large Reversible Li Storage of Graphene Nanosheet Families for Use in Rechargeable Lithium Ion Batteries. Nano Lett. 2008, 8, 2277–2282. [Google Scholar] [CrossRef]
- Vargas, O.; Caballero, Á.; Morales, J.; Elia, G.A.; Scrosati, B.; Hassoun, J. Electrochemical Performance of a Graphene Nanosheets Anode in a High Voltage Lithium-Ion Cell. Phys. Chem. Chem. Phys. 2013, 15, 20444–20446. [Google Scholar] [CrossRef]
- Li, X.; Hu, Y.; Liu, J.; Lushington, A.; Li, R.; Sun, X. Structurally Tailored Graphene Nanosheets as Lithium Ion Battery Anodes: An Insight to Yield Exceptionally High Lithium Storage Performance. Nanoscale 2013, 5, 12607–12615. [Google Scholar] [CrossRef]
- Yang, J.; Jia, K.; Wang, M.; Liu, S.; Hu, C.; Zhang, K.; Zhang, Y.; Qiu, J. Fabrication of Nitrogen-Doped Porous Graphene Hybrid Nanosheets from Metal-Organic Frameworks for Lithium-Ion Batteries. Nanotechnology 2020, 31, 145402. [Google Scholar] [CrossRef] [PubMed]
- Xing, Z.; Ju, Z.; Zhao, Y.; Wan, J.; Zhu, Y.; Qiang, Y.; Qian, Y. One-Pot Hydrothermal Synthesis of Nitrogen-Doped Graphene as High-Performance Anode Materials for Lithium Ion Batteries. Sci. Rep. 2016, 6, 26146. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, J.; Guo, S.; Pinna, N. Graphene/N-Doped Carbon Sandwiched Nanosheets with Ultrahigh Nitrogen Doping for Boosting Lithium-Ion Batteries. J. Mater. Chem. A Mater. 2016, 4, 1423–1431. [Google Scholar] [CrossRef]
- Huang, Y.; Li, K.; Yang, G.; Aboud, M.F.A.; Shakir, I.; Xu, Y. Ultrathin Nitrogen-Doped Carbon Layer Uniformly Supported on Graphene Frameworks as Ultrahigh-Capacity Anode for Lithium-Ion Full Battery. Small 2018, 14, 1703969. [Google Scholar] [CrossRef]
- Yun, Y.S.; Le, V.D.; Kim, H.; Chang, S.J.; Baek, S.J.; Park, S.; Kim, B.H.; Kim, Y.H.; Kang, K.; Jin, H.J. Effects of Sulfur Doping on Graphene-Based Nanosheets for Use as Anode Materials in Lithium-Ion Batteries. J. Power Sources 2014, 262, 79–85. [Google Scholar] [CrossRef]
- Liu, H.; Yang, W.; Che, S.; Li, Y.; Xu, C.; Wang, X.; Ma, G.; Huang, G.; Li, Y. Silicon Doped Graphene as High Cycle Performance Anode for Lithium-Ion Batteries. Carbone N. Y. 2022, 196, 633–638. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, L.; Zhu, J.; Jiang, S.P.; Shen, P.K. Crumpled Nitrogen- and Boron-Dual-Self-Doped Graphene Sheets as an Extraordinary Active Anode Material for Lithium Ion Batteries. J. Mater. Chem. A Mater. 2016, 4, 14155–14162. [Google Scholar] [CrossRef]
- Cai, D.; Wang, C.; Shi, C.; Tan, N. Facile Synthesis of N and S Co-Doped Graphene Sheets as Anode Materials for High-Performance Lithium-Ion Batteries. J. Alloys Compd. 2018, 731, 235–242. [Google Scholar] [CrossRef]
- Shan, H.; Li, X.; Cui, Y.; Xiong, D.; Yan, B.; Li, D.; Lushington, A.; Sun, X. Sulfur/Nitrogen Dual-Doped Porous Graphene Aerogels Enhancing Anode Performance of Lithium Ion Batteries. Electrochim. Acta 2016, 205, 188–197. [Google Scholar] [CrossRef]
- Sungur, B.; Bayram, E.; Kömür, A.İ. Enhanced Performance for Li & Na Ion Battery Anodes by Charge Modulation of Interface Through SiC4 and SiN1C3 Active Centers on Silicon Nitrogen Co-Doped Graphene. ChemElectroChem 2024, 11, e202400401. [Google Scholar] [CrossRef]
- Chen, S.; Bao, P.; Huang, X.; Sun, B.; Wang, G. Hierarchical 3D Mesoporous Silicon@graphene Nanoarchitectures for Lithium Ion Batteries with Superior Performance. Nano Res. 2014, 7, 85–94. [Google Scholar] [CrossRef]
- Jamaluddin, A.; Umesh, B.; Chen, F.; Chang, J.K.; Su, C.Y. Facile Synthesis of Core-Shell Structured Si@graphene Balls as a High-Performance Anode for Lithium-Ion Batteries. Nanoscale 2020, 12, 9616–9627. [Google Scholar] [CrossRef]
- Liu, X.; Lu, J.; Jiang, J.; Jiang, Y.; Gao, Y.; Li, W.; Zhao, B.; Zhang, J. Enhancing Lithium Storage Performance by Strongly Binding Silicon Nanoparticles Sandwiching between Spherical Graphene. Appl. Surf. Sci. 2021, 539, 148191. [Google Scholar] [CrossRef]
- Nie, P.; Le, Z.; Chen, G.; Liu, D.; Liu, X.; Wu, H.B.; Xu, P.; Li, X.; Liu, F.; Chang, L.; et al. Graphene Caging Silicon Particles for High-Performance Lithium-Ion Batteries. Small 2018, 14, 1800635. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Zhu, R.; He, Q.; Liu, S.; Wu, D.; Fu, H.; Du, J.; Zhu, J.; He, H. In Situ Synthesis of a Silicon Flake/Nitrogen-Doped Graphene-like Carbon Composite from Organoclay for High-Performance Lithium-Ion Battery Anodes. Chem. Commun. 2019, 55, 2644–2647. [Google Scholar] [CrossRef] [PubMed]
- Fang, H.; Meng, F.; Chen, G.; Wang, L.; Zhang, S.; Yan, J.; Zhang, Y.; Zhang, L. Sandwich-Structured Fe3O4/Graphene Hybrid Film for High-Performance Lithium-Ion Batteries. Int. J. Electrochem. Sci. 2019, 14, 7937–7946. [Google Scholar] [CrossRef]
- Li, L.; Wang, H.; Xie, Z.; An, C.; Jiang, G.; Wang, Y. 3D Graphene-Encapsulated Nearly Monodisperse Fe3O4 Nanoparticles as High-Performance Lithium-Ion Battery Anodes. J. Alloys Compd. 2020, 815, 152337. [Google Scholar] [CrossRef]
- Gao, X.; Xiao, Z.; Jiang, L.; Wang, C.; Lin, X.; Sheng, L. Yolk-Shell Porous Fe3O4@C Anchored on Graphene as Anode for Li-Ion Half/Full Batteries with High Rate Capability and Long Cycle Life. J. Colloid. Interface Sci. 2023, 641, 820–830. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, Z.; Mai, J.; Lau, T.K.; Lu, X.; Hsu, Y.J.; Chen, Y.; Lee, A.C.; Hou, Y.; Meng, Y.S.; et al. Revisiting the Origin of Cycling Enhanced Capacity of Fe3O4 Based Nanostructured Electrode for Lithium Ion Batteries. Nano Energy 2017, 41, 426–433. [Google Scholar] [CrossRef]
- Qin, G.T.; Ding, L.; Zeng, M.; Zhang, K.B.; Zhang, Y.Q.; Bai, Y.; Wen, J.W.; Li, J. Mesoporous Fe2O3/N-Doped Graphene Composite as an Anode Material for Lithium Ion Batteries with Greatly Enhanced Electrochemical Performance. J. Electroanal. Chem. 2020, 866, 114176. [Google Scholar] [CrossRef]
- Tian, L.; Xie, Y.; Lu, J.; Hu, Q.; Xiao, Y.; Liu, T.; Davronbek, B.; Zhu, X.; Su, X. Self-Assembled 3D Fe3O4/N-Doped Graphene Aerogel Composite for Large and Fast Lithium Storage with an Excellent Cycle Performance. J. Electroanal. Chem. 2022, 922, 116763. [Google Scholar] [CrossRef]
- Ette, P.M.; Bosubabu, D.; Ramesha, K. Graphene Anchored Mesoporous MnO2 Nanostructures as Stable and High-Performance Anode Materials for Li-Ion Batteries. Electrochim. Acta 2022, 414, 140164. [Google Scholar] [CrossRef]
- Xu, T.; Meng, Q.; Fan, Q.; Yang, M.; Zhi, W.; Cao, B. Electrophoretic Deposition of Binder-Free MnO2/Graphene Films for Lithium-Ion Batteries. Chin. J. Chem. 2017, 35, 1575–1585. [Google Scholar] [CrossRef]
- Chen, J.; Hu, X.; Gao, H.; Yan, S.; Chen, S.; Liu, X. Graphene-Wrapped MnCO3/Mn3O4 Nanocomposite as an Advanced Anode Material for Lithium-Ion Batteries: Synergistic Effect and Electrochemical Performances. J. Mater. Sci. Technol. 2022, 99, 9–17. [Google Scholar] [CrossRef]
- Liu, L.; An, M.; Yang, P.; Zhang, J. Superior Cycle Performance and High Reversible Capacity of SnO2/Graphene Composite as an Anode Material for Lithium-Ion Batteries. Sci. Rep. 2015, 5, 9055. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Huang, X.; Wei, Z.; Xia, L.; Pan, H.; Zhang, T.; Wang, H.; Duan, X.; Jia, D.; Zhou, Y.; et al. Orderly Stacked Graphene Sheets Supporting SnO2 Nanoparticles as an Anode Material for Lithium-Ion Batteries with Incremental Capacity. Appl. Surf. Sci. 2021, 564, 150265. [Google Scholar] [CrossRef]
- Ao, L.; Wu, C.; Wang, X.; Xu, Y.; Jiang, K.; Shang, L.; Li, Y.; Zhang, J.; Hu, Z.; Chu, J. Superior and Reversible Lithium Storage of SnO2/Graphene Composites by Silicon Doping and Carbon Sealing. ACS Appl. Mater. Interfaces 2020, 12, 20824–20837. [Google Scholar] [CrossRef]
- Gao, C.; Jiang, Z.; Wang, P.; Jensen, L.R.; Zhang, Y.; Yue, Y. Optimized Assembling of MOF/SnO2/Graphene Leads to Superior Anode for Lithium Ion Batteries. Nano Energy 2020, 74, 104868. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; He, X.; Zhang, X.; Yan, B.; Hou, X.; Du, L.; Placke, T.; Winter, M.; Li, J. A Three-Dimensional TiO2-Graphene Architecture with Superior Li Ion and Na Ion Storage Performance. J. Power Sources 2020, 461, 228129. [Google Scholar] [CrossRef]
- Li, L.; Zhou, G.; Shan, X.Y.; Pei, S.; Li, F.; Cheng, H.M. Co3O4 Mesoporous Nanostructures@graphene Membrane as an Integrated Anode for Long-Life Lithium-Ion Batteries. J. Power Sources 2014, 255, 52–58. [Google Scholar] [CrossRef]
- Ou, J.; Wu, S.; Yang, L.; Wang, H. Facile Preparation of NiO@graphene Nanocomposite with Superior Performances as Anode for Li-Ion Batteries. Acta Metall. Sin. 2022, 35, 212–222. [Google Scholar] [CrossRef]
- Teng, Y.; Zhao, H.; Zhang, Z.; Li, Z.; Xia, Q.; Zhang, Y.; Zhao, L.; Du, X.; Du, Z.; Lv, P.; et al. MoS2 Nanosheets Vertically Grown on Graphene Sheets for Lithium-Ion Battery Anodes. ACS Nano 2016, 10, 8526–8535. [Google Scholar] [CrossRef]
- Xiao, Z.; Sheng, L.; Jiang, L.; Zhao, Y.; Jiang, M.; Zhang, X.; Zhang, M.; Shi, J.; Lin, Y.; Fan, Z. Nitrogen-Doped Graphene Ribbons/MoS2 with Ultrafast Electron and Ion Transport for High-Rate Li-Ion Batteries. Chem. Eng. J. 2021, 408, 127269. [Google Scholar] [CrossRef]
- Liu, S.; Jia, K.; Yang, J.; He, S.; Liu, Z.; Wang, X.; Qiu, J. Encapsulating Flower-like MoS2 Nanosheets into Interlayer of Nitrogen-Doped Graphene for High-Performance Lithium-Ion Storage. Chem. Eng. J. 2023, 475, 146181. [Google Scholar] [CrossRef]
- Jiang, Y.; Song, D.; Wu, J.; Wang, Z.; Huang, S.; Xu, Y.; Chen, Z.; Zhao, B.; Zhang, J. Sandwich-like SnS2/Graphene/SnS2 with Expanded Interlayer Distance as High-Rate Lithium/Sodium-Ion Battery Anode Materials. ACS Nano 2019, 13, 9100–9111. [Google Scholar] [CrossRef] [PubMed]
- He, C.J.; Wang, Y.Q.; Meng, W.J.; Zhang, J.; Xie, Y.; Hou, Y.L.; Zhao, D.L. Hierarchical Microspheres Constructed by SnS2 Nanosheets and S-Doped Graphene for High Performance Lithium/Sodium-Ion Batteries. J. Alloys Compd. 2022, 889, 161648. [Google Scholar] [CrossRef]
- Gao, D.; Wang, Y.; Liu, Y.; Sun, H.; Wu, M.; Zhang, H. Interfacial Engineering of 0D/2D SnS2 Heterostructure onto Nitrogen-Doped Graphene for Boosted Lithium Storage Capability. J. Colloid. Interface Sci. 2019, 538, 116–124. [Google Scholar] [CrossRef]
- Sheng, Y.; Zhang, X.; Lan, B.; Wei, C.; Wang, Y.; Wen, G. MoS2/SnS2 Synergistically Cooperate with Graphene to Construct High-Quality Lithium Storage Anode Materials. Colloids Surf. A Physicochem. Eng. Asp. 2023, 659, 130798. [Google Scholar] [CrossRef]
- Yin, S.; Wang, Y.; Zhang, X.; Wei, C.; Huang, X.; Wen, G. External and Internal Cultivation: Design for Mo-Doped SnS2/SnO2 Heterostructure on N-Doped Graphene Achieves Kinetics-Enhanced and Superior-Lithium Storage Performance. Appl. Surf. Sci. 2023, 609, 155435. [Google Scholar] [CrossRef]
- Xu, X.; Ji, S.; Gu, M.; Liu, J. In Situ Synthesis of MnS Hollow Microspheres on Reduced Graphene Oxide Sheets as High-Capacity and Long-Life Anodes for Li- and Na-Ion Batteries. ACS Appl. Mater. Interfaces 2015, 7, 20957–20964. [Google Scholar] [CrossRef]
- He, J.; Chen, Y.; Li, P.; Fu, F.; Wang, Z.; Zhang, W. Self-Assembled CoS2 Nanoparticles Wrapped by CoS2-Quantum-Dots-Anchored Graphene Nanosheets as Superior-Capability Anode for Lithium-Ion Batteries. Electrochim. Acta 2015, 182, 424–429. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, W.; Ye, J.; Wang, Z.; Lee, J.Y. L-Cysteine-Assisted Hydrothermal Synthesis of Nickel Disulfide/Graphene Composite with Enhanced Electrochemical Performance for Reversible Lithium Storage. J. Power Sources 2015, 294, 51–58. [Google Scholar] [CrossRef]
- Aghamohammadi, H.; Hassanzadeh, N.; Eslami-Farsani, R. A Review Study on the Recent Advances in Developing the Heteroatom-Doped Graphene and Porous Graphene as Superior Anode Materials for Li-Ion Batteries. Ceram. Int. 2021, 47, 22269–22301. [Google Scholar] [CrossRef]
- Sun, D.; Tan, Z.; Tian, X.; Ke, F.; Wu, Y.; Zhang, J. Graphene: A Promising Candidate for Charge Regulation in High-Performance Lithium-Ion Batteries. Nano Res. 2021, 14, 4370–4385. [Google Scholar] [CrossRef]
- Wu, D.H.; Li, Y.F.; Zhou, Z. First-Principles Studies on Doped Graphene as Anode Materials in Lithium-Ion Batteries. Theor. Chem. Acc. 2011, 130, 209–213. [Google Scholar] [CrossRef]
- Hardikar, R.P.; Das, D.; Han, S.S.; Lee, K.-R.; Singh, A.K. Boron Doped Defective Graphene as a Potential Anode Material for Li-Ion Batteries. Phys. Chem. Chem. Phys. 2014, 16, 16502. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Hou, Z.F.; Gao, B.; Frauenheim, T. Doped Graphenes as Anodes with Large Capacity for Lithium-Ion Batteries. J. Mater. Chem. A Mater. 2016, 4, 13407–13413. [Google Scholar] [CrossRef]
- Masood, K.B.; Kumar, P.; Singh, R.A.; Singh, J. Odyssey of Thermoelectric Materials: Foundation of the Complex Structure. J. Phys. Commun. 2018, 2, 62001. [Google Scholar] [CrossRef]
- Denis, P.A. Heteroatom Codoped Graphene: The Importance of Nitrogen. ACS Omega 2022, 7, 45935–45961. [Google Scholar] [CrossRef]
- Feng, Q.; Li, T.; Sui, Y.; Xiao, B.; Wang, T.; Sun, Z.; Qi, J.; Wei, F.; Meng, Q.; Ren, Y.; et al. Facile Synthesis and First-Principles Study of Nitrogen and Sulfur Dual-Doped Porous Graphene Aerogels/Natural Graphite as Anode Materials for Li-Ion Batteries. J. Alloys Compd. 2021, 884, 160923. [Google Scholar] [CrossRef]
- Sehrawat, P.; Shabir, A.; Abid; Julien, C.M.; Islam, S.S. Recent Trends in Silicon/Graphene Nanocomposite Anodes for Lithium-Ion Batteries. J. Power Sources 2021, 501, 229709. [Google Scholar] [CrossRef]
- Chou, C.Y.; Hwang, G.S. Role of Interface in the Lithiation of Silicon-Graphene Composites: A First Principles Study. J. Phys. Chem. C 2013, 117, 9598–9604. [Google Scholar] [CrossRef]
- Kolosov, D.A.; Glukhova, O.E. Ab Initio Study of Porous Graphene–CNT Silicon Composite for Li-Ion and Na-Ion Batteries. C 2021, 7, 57. [Google Scholar] [CrossRef]
- Yang, Y.; Yuan, W.; Zhang, X.; Wang, C.; Yuan, Y.; Huang, Y.; Ye, Y.; Qiu, Z.; Tang, Y. A Review on FexOy-Based Materials for Advanced Lithium-Ion Batteries. Renew. Sustain. Energy Rev. 2020, 127, 109884. [Google Scholar] [CrossRef]
- Bashir, T.; Ismail, S.A.; Song, Y.; Irfan, R.M.; Yang, S.; Zhou, S.; Zhao, J.; Gao, L. A Review of the Energy Storage Aspects of Chemical Elements for Lithium-Ion Based Batteries. Energy Mater. 2022, 1, 100019. [Google Scholar] [CrossRef]
- Glibo, A.; Reda, M.; Surace, Y.; Kahr, J.; Flandorfer, H.; Cupid, D.M. Influence of Transition-Metal Order of Lnmo Spinel on Li Ion Diffusion and Thermodynamics of LNMO. ECS Meet. Abstr. 2024, MA2024-02, 247. [Google Scholar] [CrossRef]
- Ubale, A.U.; Waghmare, M.A.; Iqbal, K.S.; Pathan, H.M. Manganese Oxides: Promising Electrode Materials for Li-Ion Batteries and Supercapacitors. J. Mater. Sci. Mater. Electron. 2020, 31, 14003–14021. [Google Scholar] [CrossRef]
- Choi, Y.J.; Kim, Y.H.; Kim, H.K.; Kim, K.B. Synergistic Effect of Graphene Nanoperforation on the Reversibility of the Conversion Reaction of a SnO2/Nanoperforated Graphene Composite. Chem. Eng. J. 2021, 417, 128542. [Google Scholar] [CrossRef]
- Srivastava, M.; Singh, J.; Kuila, T.; Layek, R.K.; Kim, N.H.; Lee, J.H. Recent Advances in Graphene and Its Metal-Oxide Hybrid Nanostructures for Lithium-Ion Batteries. Nanoscale 2015, 7, 4820–4868. [Google Scholar] [CrossRef]
- Duhan, N.; Dhilip Kumar, T.J. Ab Initio Study of Li-Shrouded Si-Doped γ-Graphyne Nanosheet as Propitious Anode in Li-Ion Batteries. Appl. Surf. Sci. 2024, 642, 158553. [Google Scholar] [CrossRef]
- Yin, S.; Zhang, X.; Huang, X.; Zhou, F.; Wang, Y.; Wen, G. SnO/SnO2 Heterojunction Nanoparticles Anchored on Graphene Nanosheets for Lithium Storage. ACS Appl. Nano Mater. 2024, 7, 14419–14430. [Google Scholar] [CrossRef]
- Dharmalingam, S.T.; Dar, M.A.; Gul, R.; Minakshi Sundaram, M.; Alnaser, I.A.; Sivasubramanian, R. Nano-Octahedron Cobalt Oxide Decorated Graphene Nanocomposites for the Selective/Simultaneous Detection of Dopamine. Adv. Mater. Interfaces 2025, 2400981. [Google Scholar] [CrossRef]
- Yu, X.Y.; Lou, X.W. Mixed Metal Sulfides for Electrochemical Energy Storage and Conversion. Adv. Energy Mater. 2018, 8, 1701592. [Google Scholar] [CrossRef]
- Lv, Y.; Chen, B.; Zhao, N.; Shi, C.; He, C.; Li, J.; Liu, E. Interfacial Effect on the Electrochemical Properties of the Layered Graphene/Metal Sulfide Composites as Anode Materials for Li-Ion Batteries. Surf. Sci. 2016, 651, 10–15. [Google Scholar] [CrossRef]
- Wang, H.; Tran, D.; Qian, J.; Ding, F.; Losic, D. MoS2/Graphene Composites as Promising Materials for Energy Storage and Conversion Applications. Adv. Mater. Interfaces 2019, 6, 1900915. [Google Scholar] [CrossRef]
- Shao, X.; Wang, K.; Pang, R.; Shi, X. Lithium Intercalation in Graphene/MoS2 Composites: First-Principles Insights. J. Phys. Chem. C 2015, 119, 25860–25867. [Google Scholar] [CrossRef]
- Mahmud, S.T.; Mia, R.; Mahmud, S.; Sha, S.; Zhang, R.; Deng, Z.; Yanilmaz, M.; Luo, L.; Zhu, J. Recent Developments of Tin (II) Sulfide/Carbon Composites for Achieving High-Performance Lithium Ion Batteries: A Critical Review. Nanomaterials 2022, 12, 1246. [Google Scholar] [CrossRef]
- Idisi, D.O.; Benecha, E.M.; Mwakikunga, B.; Asante, J.K.O. Effect of Interlayer Spacing on the Electronic and Optical Properties of SnS2/Graphene/SnS2 Sandwich Heterostructure: A Density Functional Theory Study. J. Comput. Electron. 2024, 23, 1029–1038. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Z.; Li, D.; Guo, P.; Liu, D.; Shang, X.; Lv, M.; He, D. Nanoscale α-MnS Crystallites Grown on N-S Co-Doped RGO as a Long-Life and High-Capacity Anode Material of Li-Ion Batteries. Appl. Surf. Sci. 2017, 416, 858–867. [Google Scholar] [CrossRef]
- Wang, H.; Lu, S.; Chen, Y.; Han, L.; Zhou, J.; Wu, X.; Qin, W. A Graphene/Co9S8 Nanocomposite Paper as a Binder-Free and Free-Standing Anode for Lithium-Ion Batteries. J. Mater. Chem. A Mater. 2015, 3, 23677–23683. [Google Scholar] [CrossRef]



| Graphene Modification | Experimental Capacity (mAh g−1) | Theoretical Capacity (mAh g−1) | Li+ Adsorption (eV) | Li+ Diffusion (eV) | Ref. |
|---|---|---|---|---|---|
| Porous graphene | 910 * | 2857.7 ** | 1.80 ** | 0.37–0.39 ** | [60,61] *, ** |
| Defective graphene | 210 * | 1675 ** | 0.028 to 0.052 ** | _____ | [83,84] *, ** |
| B-doped graphene | 1549 * | 2271 ** | 0.759 ** | 0.454 ** | [85,86] *, ** |
| N-doped graphene | 1043 * | 1262 ** | 1.26–1.19 | _____ | [85,87] *, ** |
| Si/graphene | 2753 * | 2896 ** | −3.80 ** | _____ | [29,88] **, * |
| MoO2/graphene | 1037 * | 1411 ** | −0.87 ** | 0.077 ** | [89,90] *, ** |
| WS2/graphene | 421 * | 588.16 ** | −2.33 to −1.99 ** | 0.24−0.28 ** | [51,91] *, ** |
| SnS2/graphene | 766.3 * | 1330 ** | 1.97 to 3.22 ** | 0.21 ** | [52,92] **, * |
| Material | Theoretical Capacity (mAh g−1) | Main Limitations | Key Advantages |
|---|---|---|---|
| Graphene | ~744 | Moderate storage capacity as a pure material | High electrical conductivity, large surface area, mechanical flexibility, stable SEI formation, and long cycle life |
| Si | ~4200 | Severe volume expansion (~300%), unstable SEI formation, and rapid capacity fading | Extremely high theoretical capacity, earth abundance, low cost, environmentally friendly, and high melting points suitable for thermal stability |
| Transition Metal Oxides | ~1000–1200 (e.g., Fe3O4, MnO2) | Significant volume expansion, poor electrical conductivity, and low cycling stability | High theoretical capacities, natural abundance, non-toxicity, corrosion resistance, and conversion-type lithiation mechanism |
| Metal Sulfides | ~600–1200 (e.g., MoS2, SnS2) | Poor cycling stability and slow Li+ diffusion kinetics | Layered structure for Li+ intercalation, moderate to high capacities, and tunable electrochemical properties |
| Materials | Reversible Capacity (mAh g−1) at Current Density (A g−1) | Cycling Performance | Rate Performance | Ref. |
|---|---|---|---|---|
| Capacity (mAh g−1) at Current Density (A g−1) | ||||
| Pristine Graphene | ||||
| GNSs | 540 @ 0.05 | 290 mAh g−1 after 20 cycles | ______ | [136] |
| GNSs+CNTs | 730 @ 0.05 | 480 mAh g−1 after 20 cycles | ______ | [136] |
| GNSs+C60 | 784 @ 0.05 | 600 mAh g−1 after 20 cycles | ______ | [136] |
| GNSs | 600 @ 74.5 | 500 mAh g−1 after 50 cycles | ______ | [137] |
| GNS-I | 407 @ 0.1 | 269 mAh g−1 after 100 cycles | ______ | [138] |
| GNS-II | 723 @ 0.1 | 400 mAh g−1 after 100 cycles | ______ | [138] |
| GNS-III | 1348 @ 0.1 | 691 mAh g−1 after 100 cycles | ______ | [138] |
| Doped Graphene | ||||
| N-doped graphene | 1040 @ 0.05 | 872 mAh g−1 after 30 cycles | 199 @ 25 | [85] |
| B-doped graphene | 1549 @ 0.05 | 1227 mAh g−1 after 30 cycles | 235 @ 25 | [85] |
| N-doped Porous Graphene Hybrid Nanosheets | 1971.2 @ 0.1 | 90.38% after 1000 cycles | 374.2 @ 2 | [139] |
| N-doped graphene | 950 @ 0.1 | >500 mAh g−1 after 150 cycles | 150 @ 5 | [140] |
| N-doped carbon/rGO | 1100 @ 0.1 | 535 mAh g−1 after 1200 cycles | 45 @ 20 | [141] |
| N-doped carbon graphene framework | 2018 @ 0.5 | 93% after 10,000 cycles | 340 @ 40 | [142] |
| Sulfur-doped graphene nanosheets (S-GNSs) | 870 @ 0.374 | 290 mAh g−1 after 500 cycles | 285 @ 11.16 | [143] |
| Si-doped graphene | ______ | 86% after 400 cycles | ~100 @ 4 | [144] |
| 3D crumpled B- and N-co-doped graphene nanosheets (NBGs-1000) | 909 @ 0.05 | 877 mAh g−1 after 125 cycles | 318 @ 2 | [145] |
| N and S co-doped graphene | 1016 @ 0.1 | 788.2 mAh g−1 after 50 cycles | 250.1 @ 20 | [146] |
| S/N co-doped aerogels (SNGA-II) | 981.4 @ 0.1 | 1109.8 mAh g−1 after 400 cycles | ~350 @ 0.8 | [147] |
| Si-N co-doped graphene | 644 @ 0.1 | 578.75 mAh g−1 after 500 cycles | 240 @ 5 | [148] |
| Graphene-Based Composites | ||||
| graphene/Si nanocomposites (SGE) | 2753 @ 0.3 | 800 mAh g−1 after 30 cycles | ______ | [88] |
| 3D Mesoporous Si@graphene | 1480 @ 0.1 | 89.1% after 200 cycles | 659 @ 10 | [149] |
| Si@graphene | ______ | 1063.2 mAh g−1 after 100 cycles | 1360.9 @ 3 | [150] |
| Sandwich-graphene/Si | 1575.5 @ 0.1 | 1085.6 mAh g−1 after 500 cycles | 258.4 @ 5 | [151] |
| Si@N-doped Graphene Cages | 2350 @ 0.1 | 900 mAh g−1 after 200 cycles | 890 @ 5 | [152] |
| Si/N-doped Graphene | 1533 @ 0.2 | 97% after 50 cycles | 200 @ 10 | [153] |
| Sandwich Fe3O4/Graphene film | 896 @ 2 | 798 mAh g−1 after 300 cycles | 598 @ 20 | [154] |
| 3D Fe3O4@rGO | ~1000 @ 0.4 | 1139 mAh g−1 after 100 cycles | 786 @ 3.2 | [155] |
| Yolk–shell Fe3O4@C | 1143 @ 0.1 | 579 mAh g−1 after 1800 cycles | 358 @ 10.0 | [156] |
| 3D graphene foam (GF– Fe3O4) | ______ | ~1220 mAh g−1 after 500 cycles | ~500 @ 5 | [157] |
| porous Fe3O4/N-rGO | 1094.9 @ 0.1C | 905.2 mAh g−1 After 250 cycles | 884.7 @ 1C | [158] |
| 3D Fe3O4/N-doped rGO | ______ | 1184.8 mAh g−1 after 500 cycles | 455.1 @ 2 | [159] |
| Mesoporous MnO2/3D graphene | 1512 @ 0.24 | 1496.7 mAh g−1 after 500 cycles | 780 @ 12.3 | [160] |
| MnO2/Graphene Films | ~800 @ 0.1 | 1652.2 mAh g−1 after 200 cycles | 616.8 @ 4 | [161] |
| Graphene-wrapped MnCO3/Mn3O4 | ~1300 @ 0.5 | 1522.8 mAh g−1 after 200 cycles | 605.5 @ 5 | [162] |
| SnO2/graphene | ~800 @ 1 | 677 mAh g−1 after 1000 cycles | 790 @ 1 | [163] |
| SnO2/stacked graphene | ~366 @ − | 1080 mAh g−1 after 500 cycles | ~400 @ 5 | [164] |
| Si–SnO₂ nanorods/rGO @ C | 1127 @ 0.1 | 654 mAh g−1 after 1200 cycles | ~600 @ 5 | [165] |
| SnO2@ metal–organic framework (MOF)/graphene | ______ | 450 mAh g−1 after 1000 cycles | 324 @ 2 | [166] |
| 3D TiO2-graphene | 271 @ 0.017 | 264 mAh g−1 after 500 cycles | 158 @ 1.7 | [167] |
| Co3O4 nanowall@graphene | ~800 @ 0.1 | >600 mAh g−1 after 500 cycles | ______ | [168] |
| NiO@graphene | 886 @ 0.05 | 205 mAh g−1 after 500 cycles | 742 @ 5 | [169] |
| MoS2/graphene | 1077 @ 0.1 | 907 mAh g−1 after 400 cycles | 890 @ 1 | [170] |
| N-doped graphene ribbons/MoS2 | 1151 @ 0.1 | 92.6% after 600 cycles | 499.3 @ 8 | [171] |
| Flower-like MoS2/N-doped graphene | 1202 @ 0.2 | 78% after 800 cycles | 835 @ 5 | [172] |
| SnS2/rGO/SnS2 | 1295 @ 0.1 | 909 mAh g−1 after 400 cycles | 844 @ 10 | [173] |
| SnS2/S-doped rGO | 1630.9 @ 0.1 | 1177.2 mAh g−1 after 400 cycles | 1050.0 @ 2 | [174] |
| SnS2/N-doped graphene | 1101.3 @ 0.1 | fading of 0.04% per cycle for 200 cycles | 656.3 @ 2 | [175] |
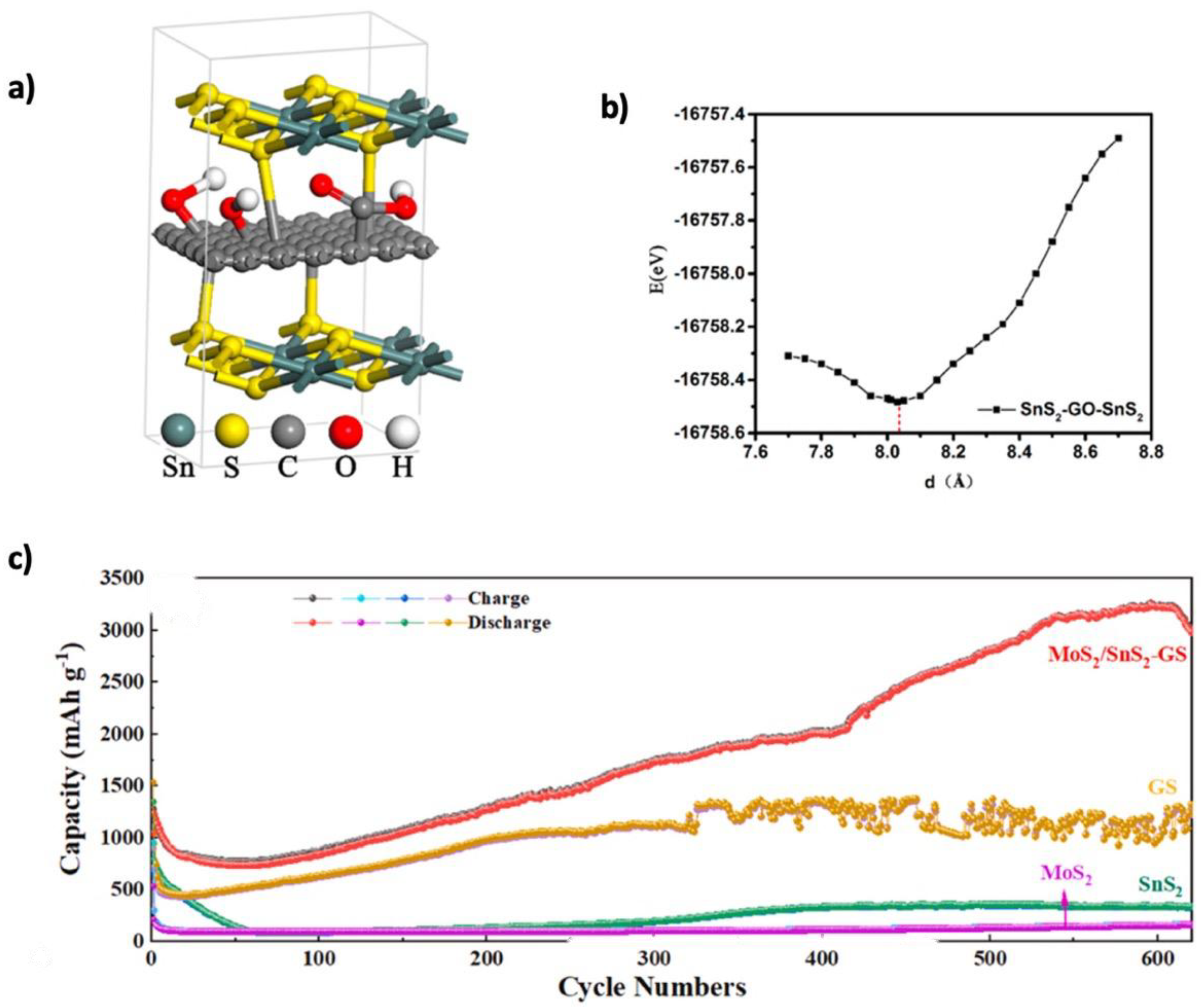
| Three-layer MoS2/SnS2 on S-doped graphene | 1100 @ 0.1 | 3224.3 mAh g−1 after 600 cycles | 1062.8 @ 3 | [176] |
| 3D Mo–SnS₂/SnO₂–N-doped graphene composite | ______ | 2052.4 mAh g−1 after 600 cycles | 617.33 @ 3 | [177] |
| MnS/rGO | 800 @ 1 | 640 mAh g−1 after 400 cycles | 580 @ 2 | [178] |
| CoS2-quantum-dots anchored graphene GNSs | 1025.5 @ 0.1 | 831 mAh g−1 after 300 cycles | 411 @ 10 | [179] |
| NiS2/graphene | 1200 @ 0.1 | 810 mAh g−1 after 1000 cycles | 740 @ 1 | [180] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AlJaber, G.; AlShammari, B.; AlOtaibi, B. From Theory to Experiment: Reviewing the Role of Graphene in Li-Ion Batteries Through Density Functional Theory. Nanomaterials 2025, 15, 992. https://doi.org/10.3390/nano15130992
AlJaber G, AlShammari B, AlOtaibi B. From Theory to Experiment: Reviewing the Role of Graphene in Li-Ion Batteries Through Density Functional Theory. Nanomaterials. 2025; 15(13):992. https://doi.org/10.3390/nano15130992
Chicago/Turabian StyleAlJaber, Ghada, Basheer AlShammari, and Bandar AlOtaibi. 2025. "From Theory to Experiment: Reviewing the Role of Graphene in Li-Ion Batteries Through Density Functional Theory" Nanomaterials 15, no. 13: 992. https://doi.org/10.3390/nano15130992
APA StyleAlJaber, G., AlShammari, B., & AlOtaibi, B. (2025). From Theory to Experiment: Reviewing the Role of Graphene in Li-Ion Batteries Through Density Functional Theory. Nanomaterials, 15(13), 992. https://doi.org/10.3390/nano15130992






