MRE Encapsulating MRG: Synergistic Improvement in Modulus Tunability and Energy Dissipation
Abstract
1. Introduction
2. Materials and Methods
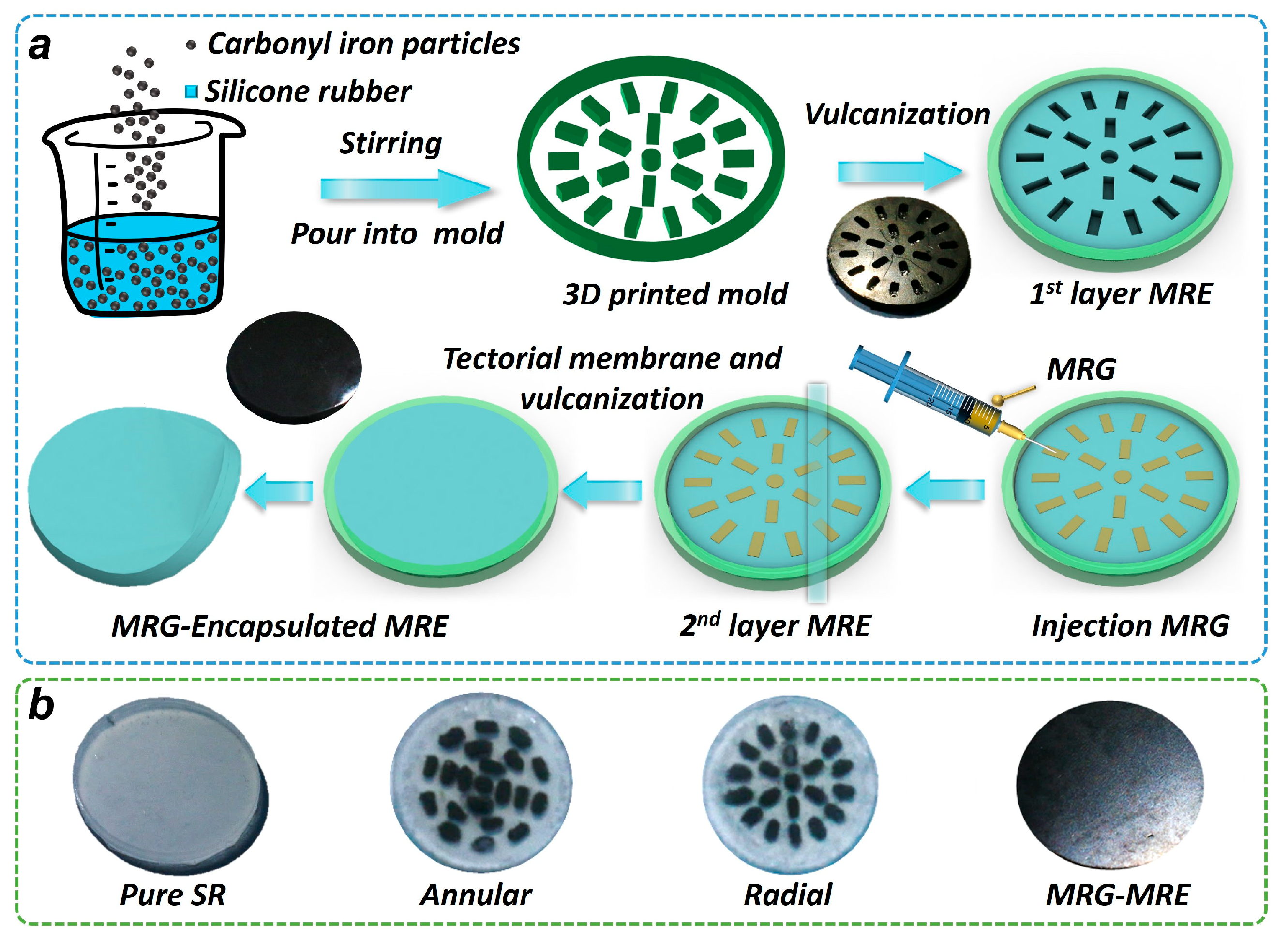
2.1. Preparation of MRE Encapsulating MRG Samples
2.1.1. Raw Materials
2.1.2. Preparation of MRE and MRG Mixtures
2.1.3. Preparation of Composite Samples
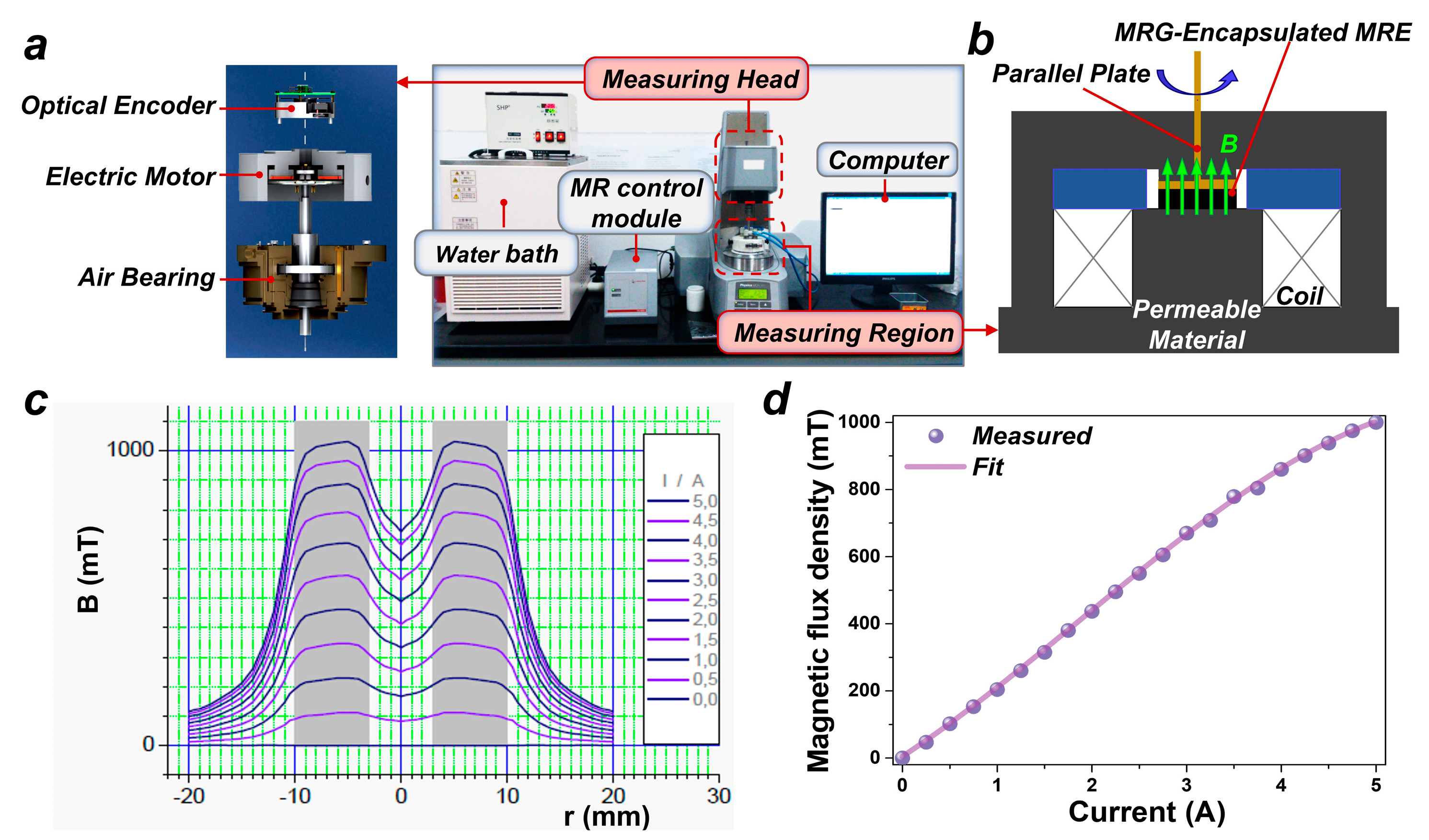
2.2. Characterization of MRE Encapsulating MRG Samples
3. Results and Discussion
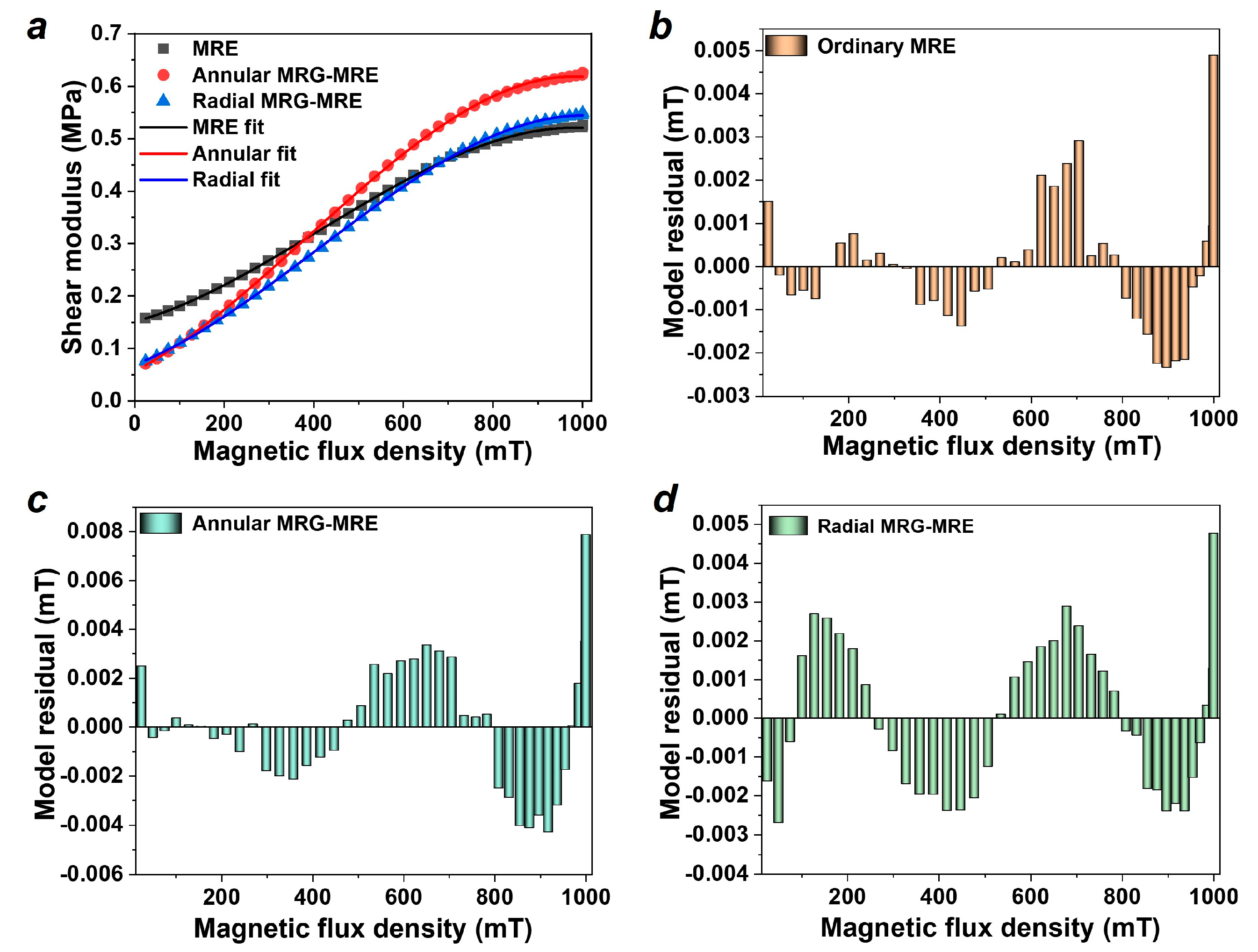
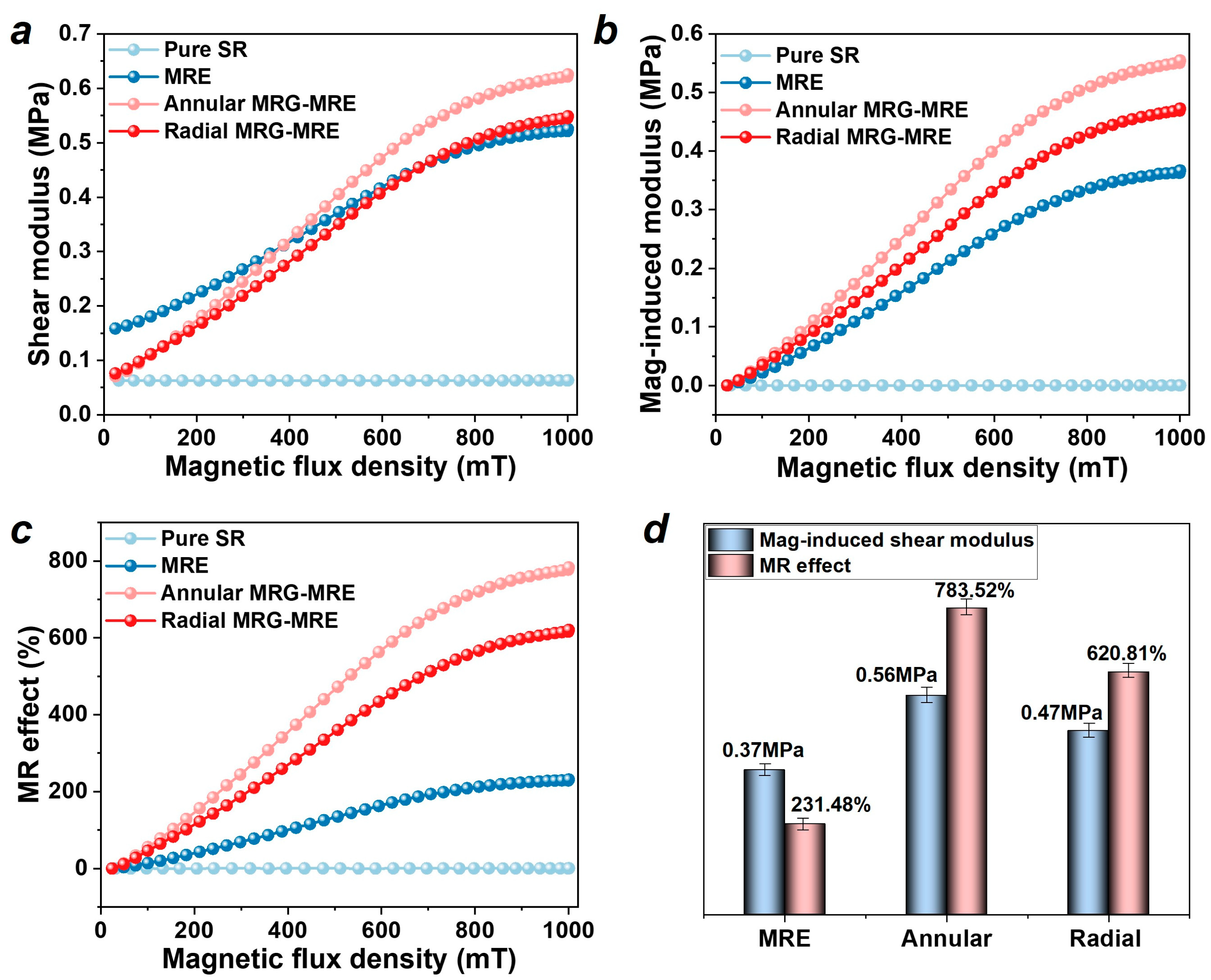
3.1. Storage Modulus Results and Analysis
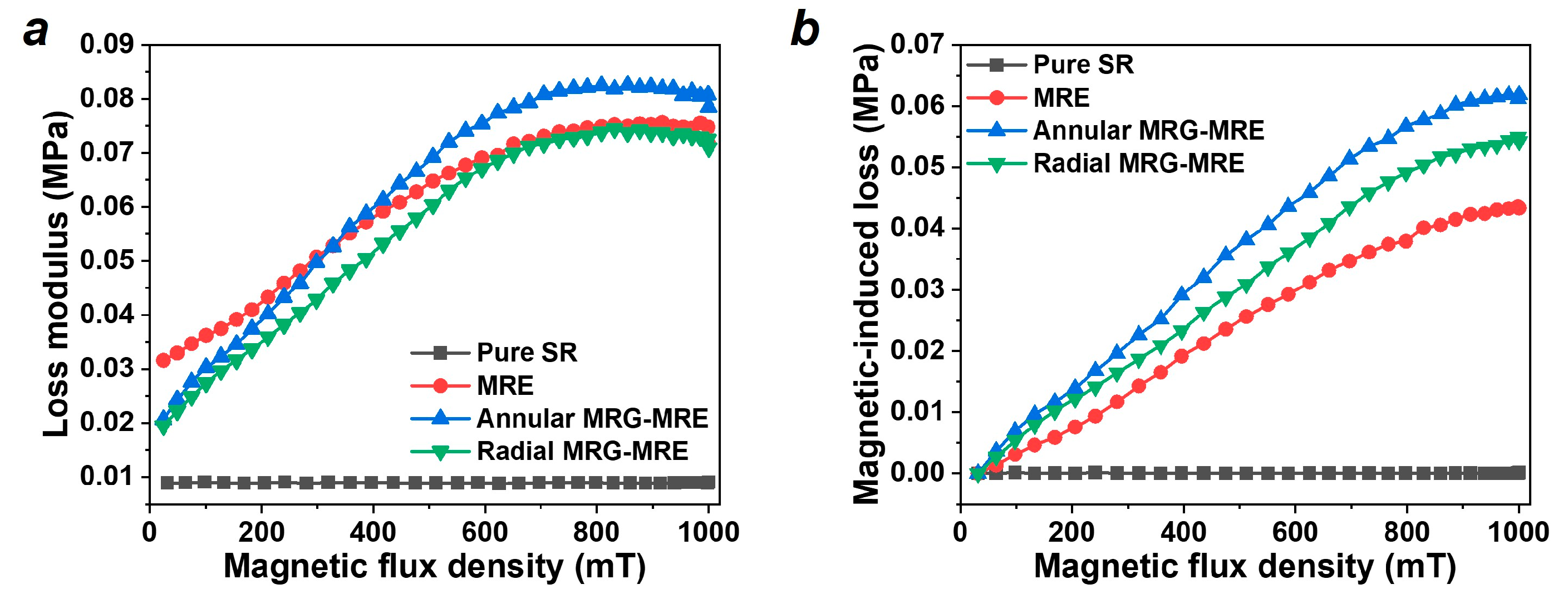
3.2. Loss Modulus Results and Analysis
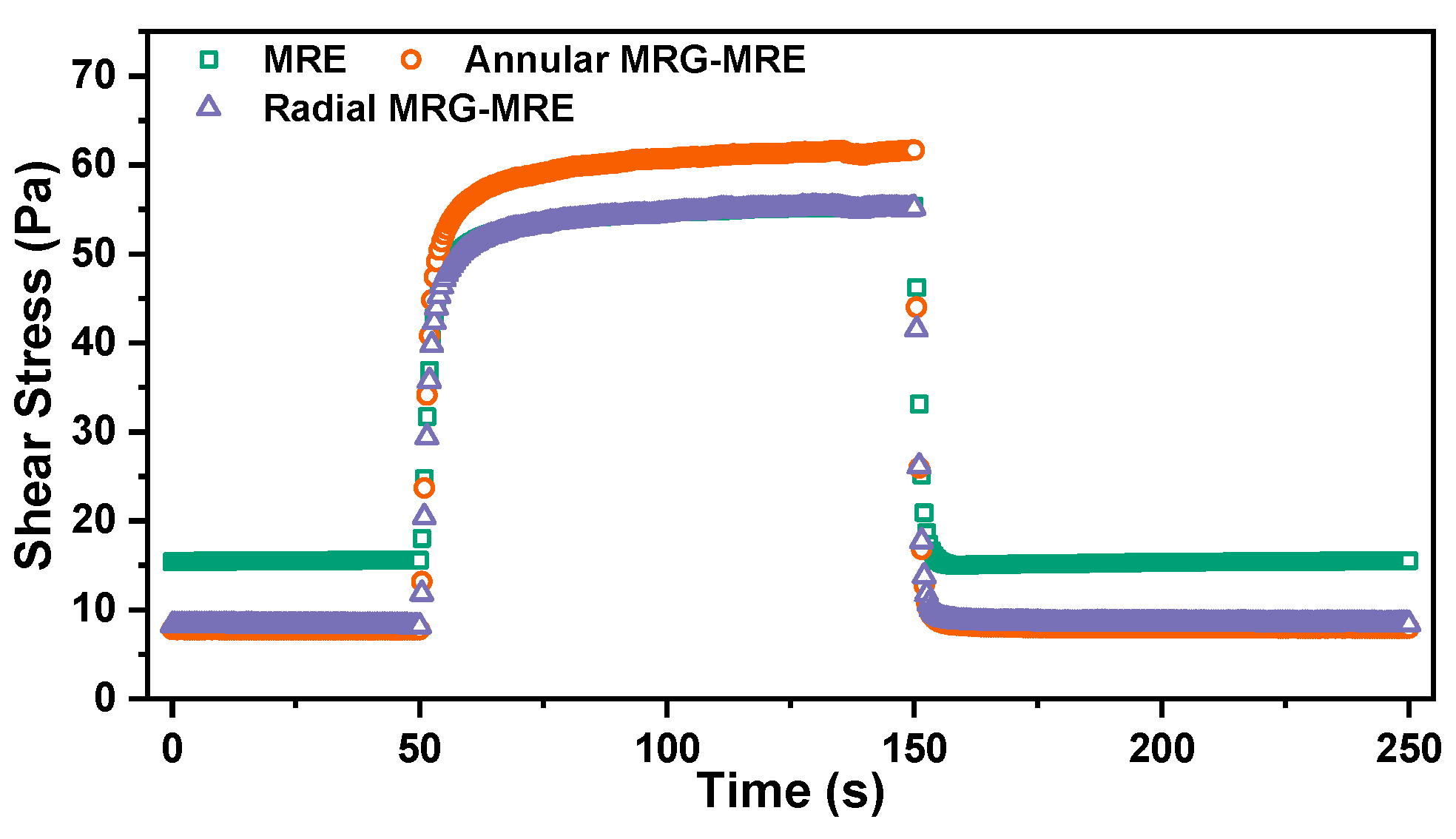
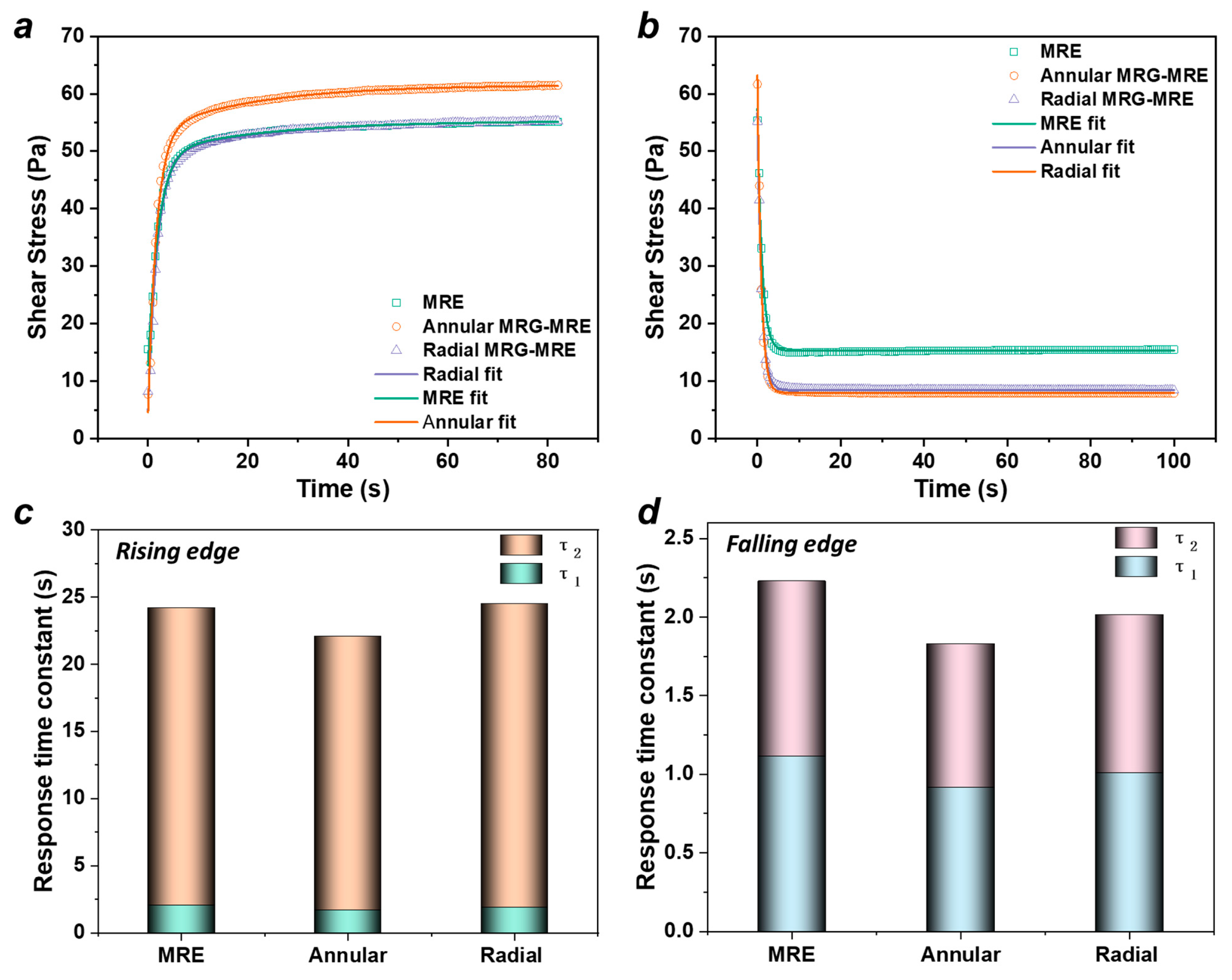
3.3. Dynamic Magnetic-Induced Response Time Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, D.P.; Zhao, C.Y.; Yang, J.J.; Lai, S.Y.; Wang, X.Y.; Gong, X.L. Enhanced Mechanical-Magnetic Coupling and Bioinspired Structural Design of Magnetorheological Elastomers. Adv. Funct. Mater. 2025, 35, 2419111. [Google Scholar] [CrossRef]
- Bastola, A.K.; Paudel, M.; Li, L.; Li, W.H. Recent progress of magnetorheological elastomers: A review. Smart Mater. Struct. 2020, 29, 123002. [Google Scholar] [CrossRef]
- Zhu, Z.S.; Wang, Z.; Dai, K.R.; Wang, X.F.; Zhang, H.; Zhang, W.L. An adaptive and space-energy efficiency vibration absorber system using a self-sensing and tunable magnetorheological elastomer. Nano Energy 2023, 117, 108927. [Google Scholar] [CrossRef]
- Fu, J.; Huang, Z.; Li, W.; Wang, W.; Zhong, C.; Qi, S.; Yu, M. A bidirectional-controllable magnetorheological elastomer-based quasi-zero-stiffness isolator. Smart Mater. Struct. 2024, 33, 085009. [Google Scholar] [CrossRef]
- Zhu, M.; Fu, J.; Li, W.; Xia, D.B.; Qi, S.; Yu, M. Design and co-optimization of a laminated isolation bearing based on magnetorheological elastomer. Mech. Syst. Signal Process. 2021, 159, 107843. [Google Scholar] [CrossRef]
- Choi, Y.; Wereley, N.M. Vibration Isolation Performance of an Adaptive Magnetorheological Elastomer-Based Dynamic Vibration Absorber. Actuators 2022, 11, 157. [Google Scholar] [CrossRef]
- Erenchun, A.; Kari, L.; Blanco, B.; Wang, B.C.; Irazu, L.; Gil-Negrete, N. Modeling and design of magnetorheological elastomer isolator system for an active control solution to reduce the vibration transmission in elevator context. Intell. Mater. Syst. Struct. 2024, 35, 29–48. [Google Scholar] [CrossRef]
- Jin, S.D.; Sun, S.S.; Yang, J.; Deng, L.; Du, H.P.; Li, W.H. A hybrid MRE isolation system integrated with ball-screw inerter for vibration control. Smart Mater. Struct. 2022, 31, 025009. [Google Scholar] [CrossRef]
- Fu, J.; Li, P.D.; Liao, G.Y.; Lai, J.J.; Yu, M. Development and Dynamic Characterization of a Mixed Mode Magnetorheological Elastomer Isolator. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Li, W.W.; Liu, S.; Lou, C.C.; Sang, M.; Gong, X.L.; Leung, K.C.F.; Xuan, S.H. Magneto-induced self-stratifying liquid metal-elastomer composites with high thermal conductivity for soft actuator. Cell Rep. Phys. Sci. 2023, 4, 101209. [Google Scholar] [CrossRef]
- Ding, W.J.; Zhou, Y.S.; Sun, M.; Fu, H.N.; Chen, Y.J.; Zhang, Z.; Pei, Z.; Chai, H. Magnetorheological elastomer actuated multi-stable gripper reinforced stiffness with twisted and coiled polymer. Thin-Wall. Struct. 2023, 193, 111223. [Google Scholar] [CrossRef]
- Zhang, T.T.; Manshaii, F.; Bowen, C.R.; Zhang, M.Y.; Qian, W.Q.; Hu, C.S.; Bai, Y.N.; Huang, Z.J.; Yang, Y.; Chen, J. A flexible pressure sensor array for self-powered identity authentication during typing. Sci. Adv. 2025, 11, eads2297. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.Q.; Qin, Q.H.; Lu, Y.; Mi, Y.J.; Meng, J.J.; Zhao, Z.Q.; Wu, H.; Cao, X.; Wang, N. Smart Triboelectric Nanogenerators Based on Stimulus-Response Materials: From Intelligent Applications to Self-Powered Systems. Nanomaterials 2023, 13, 1316. [Google Scholar] [CrossRef] [PubMed]
- Bica, I.; Anitas, E.M.; Chirigiu, L. Hybrid Magnetorheological Composites for Electric and Magnetic Field Sensors and Transducers. Nanomaterials 2020, 10, 2060. [Google Scholar] [CrossRef]
- Li, Z.M.; Wang, S.; Liu, S.; Wang, W.H.; Wu, J.P.; Xuan, T.T.; Zhang, Z.T.; Li, D.Y.; Ma, Y.Q.; Gong, X.L. Photothermally-Induced Reversible Rigidity of Nacre-Mimetic Composites Toward Semi-Active Personal Safeguard. Adv. Funct. Mater. 2025, 35, 2414780. [Google Scholar] [CrossRef]
- He, X.K.; Wu, J.P.; Xuan, S.H.; Sun, S.S.; Gong, X.L. Stretchable and Recyclable Liquid Metal Droplets Embedded Elastomer Composite with High Mechanically Sensitive Conductivity. Acs Appl. Mater. Inter. 2022, 14, 9597–9607. [Google Scholar] [CrossRef]
- Zhou, S.; Li, Y.H.; Wang, Q.Q.; Lyu, Z. Integrated Actuation and Sensing: Toward Intelligent Soft Robots. Cyborg Bionic Syst. 2024, 5, 0105. [Google Scholar] [CrossRef]
- Qi, S.; Guo, H.Y.; Fu, J.; Xie, Y.P.; Zhu, M.; Yu, M. 3D printed shape-programmable magneto-active soft matter for biomimetic applications. Compos. Sci. Technol. 2020, 188, 107973. [Google Scholar] [CrossRef]
- Sun, T.L.; Gong, X.L.; Jiang, W.Q.; Li, J.F.; Xu, Z.B.; Li, W.H. Study on the damping properties of magnetorheological elastomers based on cis-polybutadiene rubber. Polym. Test. 2008, 27, 520–526. [Google Scholar] [CrossRef]
- Chiu, W.T.; Tahara, M.; Hosoda, H. A facile fabrication for the magnetorheological elastomer composed of Fe particles and silicone rubber matrix. Mater. Lett. 2025, 379, 137635. [Google Scholar] [CrossRef]
- Zhang, Q.S.; Chen, G.Q.; Xu, J.T.; Wen, P.; Peng, B. Experimental and theoretical investigations on Magnetostrictive stresses of PDMS based magnetorheological elastomer films. Polym. Compos. 2024, 45, 12421–12433. [Google Scholar] [CrossRef]
- Huang, X.W.; Li, L.; Ruan, X.H. Theoretical and experimental research on the mechanical properties of magnetorheological elastomers based on PDMS. Front. Mater. 2023, 10, 1253055. [Google Scholar] [CrossRef]
- Gowda, D.K.; Odenbach, S. Investigation of quasistatic and dynamic mechanical properties of thermoplastic polyurethane magnetorheological elastomers. J. Magn. Magn. Mater. 2023, 579, 170856. [Google Scholar] [CrossRef]
- Hu, D.; Long, H.T.; Lu, J.B.; Li, H.L.; Zeng, J.; Yan, Q.S. Preparation and performance study of silicon modified polyurethane-based magnetorheological elastomeric polishing pad. Smart Mater. Struct. 2024, 33, 105005. [Google Scholar] [CrossRef]
- Rahim, M.I.S.A.; Kamaruddin, S.; Ismail, N.I.N.; Yahya, N.Z.N.; Ahmad, N. Dynamic properties of isotropic natural rubber-based magnetorheological elastomers. J. Rubber Res. 2025, 28, 27–38. [Google Scholar] [CrossRef]
- Alam, M.N.; Kumar, V.; Ryu, S.R.; Choi, J.; Lee, D.J. Anisotropic magnetorheological elastomers with carbonyl iron particles in natural rubber and acrylonitrile butadiene rubber: A comparative study. J. Intell. Mater. Syst. Struct. 2021, 32, 1604–1613. [Google Scholar] [CrossRef]
- Gao, T.M.; Chen, J.; Hui, Y.H.; Wang, S.; Choi, H.J.; Chung, K. Role of calcium carbonate as an interfacial compatibilizer in the magneto-rheological elastomers based on ethylene/acrylic elastomer (AEM) and its magneto-induced properties. Mater. Res. Express 2019, 6, 085320. [Google Scholar] [CrossRef]
- Gao, T.; Xie, R.H.; Chung, K. Microstructure and dynamic mechanical properties of magnetorheological elastomer based on ethylene/acrylic elastomer prepared using different manufacturing methods. Micro Nano Lett. 2018, 13, 1026–1030. [Google Scholar] [CrossRef]
- Ubaidillah; Choi, H.J.; Mazlan, S.A.; Imaduddin, F.; Harjana. Fabrication and viscoelastic characteristics of waste tire rubber based magnetorheological elastomer. Smart Mater. Struct. 2016, 25, 115026. [Google Scholar] [CrossRef]
- de Souza, C.O.; Salles, B.R.; Escócio, V.A.; Lopes, T.C.; de Almeida, N.C.; Nunes, R.C.R. Production and characterization of magnetic EPDM composites with carbonyl iron powder (CIP) using different curing systems. J. Elastom. Plast. 2025, 57, 457–474. [Google Scholar] [CrossRef]
- Rashid, R.Z.A.; Yunus, N.A.; Mazlan, S.A.; Johari, N.; Aziz, S.A.A.; Nordin, N.A.; Khairi, M.H.A.; Johari, M.A.F. Temperature Dependent on Mechanical and Rheological Properties of EPDM-Based Magnetorheological Elastomers Using Silica Nanoparticles. Materials 2022, 15, 2556. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Yu, M.; Zhu, M.; Qi, S.; Fu, J. Carbonyl iron powder surface modification of magnetorheological elastomers for vibration absorbing application. Smart Mater. Struct. 2016, 25, 115005. [Google Scholar] [CrossRef]
- Zhou, Y.F.; Li, L.L.; Li, W.Y.; Wen, S.P.; Jiang, L.; Jerrams, S.; Ma, J.W.; Chen, S.J. The fabrication and properties of magnetorheological elastomers employing bio-inspired dopamine modified carbonyl iron particles. Smart Mater. Struct. 2020, 29, 055005. [Google Scholar] [CrossRef]
- Yu, M.; Zhu, M.; Fu, J.; Yang, P.A.; Qi, S. A dimorphic magnetorheological elastomer incorporated with Fe nano-flakes modified carbonyl iron particles: Preparation and characterization. Smart Mater. Struct. 2015, 24, 115021. [Google Scholar] [CrossRef]
- Cvek, M.; Mrlik, M.; Sevcik, J.; Sedlacik, M. Tailoring Performance, Damping, and Surface Properties of Magnetorheological Elastomers via Particle-Grafting Technology. Polymers 2018, 10, 1411. [Google Scholar] [CrossRef]
- Yu, M.; Qi, S.; Fu, J.; Yang, P.A.; Zhu, M. Preparation and characterization of a novel magnetorheological elastomer based on polyurethane/epoxy resin IPNs matrix. Smart Mater. Struct. 2015, 24, 045009. [Google Scholar] [CrossRef]
- Tong, Y.; Dong, X.F.; Qi, M. Payne effect and damping properties of flower-like cobalt particles-based magnetorheological elastomers. Compos. Commun. 2019, 15, 120–128. [Google Scholar] [CrossRef]
- Padalka, O.; Song, H.J.; Wereley, N.M.; Filer, J.A.; Bell, R.C. Stiffness and Damping in Fe, Co, and Ni Nanowire-Based Magnetorheological Elastomeric Composites. IEEE Trans. Magn. 2010, 46, 2275–2277. [Google Scholar] [CrossRef]
- Khimi, S.R.; Pickering, K.L. The effect of silane coupling agent on the dynamic mechanical properties of iron sand/ natural rubber magnetorheological elastomers. Compos. Part B-Eng. 2016, 90, 115–125. [Google Scholar] [CrossRef]
- Zhang, W.; Gong, X.L.; Xuan, S.H.; Xu, Y.G. High-Performance Hybrid Magnetorheological Materials: Preparation and Mechanical Properties. Ind. Eng. Chem. Res. 2010, 49, 12471–12476. [Google Scholar] [CrossRef]
- Wang, X.J.; Gordaninejad, F. A new magnetorheological fluid-elastomer mount: Phenomenological modeling and experimental study. Smart Mater. Struct. 2009, 18, 095045. [Google Scholar] [CrossRef]
- Bastola, A.K.; Hoang, V.T.; Li, L. A novel hybrid magnetorheological elastomer developed by 3D printing. Mater. Des. 2017, 114, 391–397. [Google Scholar] [CrossRef]
- Bastola, A.K.; Paudel, M.; Li, L. Development of hybrid magnetorheological elastomers by 3D printing. Polymer 2018, 149, 213–228. [Google Scholar] [CrossRef]
- Cvek, M.; Zahoranova, A.; Mrlik, M.; Sramkova, P.; Minarik, A.; Sedlacik, M. Poly(2-oxazoline)-based magnetic hydrogels: Synthesis, performance and cytotoxicity. Colloid. Surface B 2020, 190, 110912. [Google Scholar] [CrossRef]
- Li, W.; Qi, S.; Zhu, M.; Xia, D.B.; Fu, J.; Yu, M. Improving transient magnetorheological response of magnetorheological elastomer by incorporating CIP@FeNi particles. Smart Mater. Struct. 2021, 30, 024002. [Google Scholar] [CrossRef]
- Yu, M.; Yang, P.A.; Fu, J.; Liu, S.Z.; Choi, S.B. A theoretical model for the field-dependent conductivity of magneto-rheological gels and experimental verification. Sens. Actuators A Phys. 2016, 245, 127–134. [Google Scholar] [CrossRef]
- Yu, M.; Gan, R.Y.; Fu, J.; Qi, S.; Han, J.Y.; Li, H.T. High-velocity micromorphological observation and simulation of magnetorheological gel using programmable magneto-controlled microfluidics system and micro-tube dynamic models. Smart Mater. Struct. 2024, 33, 035001. [Google Scholar] [CrossRef]
- Laeuger, J.; Wollny, K.; Stettin, H.; Huck, S. A new device for the full rheological characterization of magneto-rheological fluids. In Proceedings of the Electrorheological Fluids and Magnetorheological Suspensions (ERMR 2004), Beijing, China, 29 August–3 September 2005; pp. 370–376. [Google Scholar]


| Parameters | (MPa) | (MPa/mT) | (MPa/mT2) | (MPa/mT3) |
|---|---|---|---|---|
| Ordinary MRE | 0.1509 | 2.3936 × 10−4 | 6.6424 × 10−7 | −5.3392 × 10−10 |
| Annular MRG-MRE | 0.0571 | 4.4592 × 10−4 | 8.4374 × 10−7 | −7.2881 × 10−10 |
| Radial MRG-MRE | 0.0694 | 3.3099 × 10−4 | 7.6016 × 10−7 | −6.1639 × 10−10 |
| Sample | Magnetic-Induced Modulus | MR Effect |
|---|---|---|
| Pure SR | / | / |
| Ordinary MRE | 0.3669 ± 0.012 MPa | 231.48 ± 8.5% |
| Annular MRG-MRE | 0.5550 ± 0.019 MPa | 783.52 ± 26.3% |
| Radial MRG-MRE | 0.4728 ± 0.016 MPa | 620.81 ± 21.1% |
| Parameters | (mT−1) | (mT−2) | (mT−3) | (mT−4) | (mT−5) | (mT−6) | |
|---|---|---|---|---|---|---|---|
| Ordinary MRE | 0.19 | 6.27 × 10−4 | −9.70 × 10−6 | 6.39 × 10−8 | −2.28 × 10−10 | 4.77 × 10−13 | −6.02 × 10−16 |
| Annular MRG-MRE | 0.29 | −0.01 | 2.06 × 10−4 | −1.51 × 10−6 | 6.20 × 10−9 | −1.52 × 10−11 | 2.27 × 10−14 |
| Radial MRG-MRE | 0.25 | −0.01 | 1.77 × 10−4 | −1.31 × 10−6 | 5.35 × 10−9 | −1.31 × 10−11 | 1.96 × 10−14 |
| Parameters | |||||
|---|---|---|---|---|---|
| Ordinary MRE | 55.2517 | −36.7373 | −5.7108 | 2.0620 | 22.1336 |
| Annular MRG-MRE | 61.5137 | −48.6466 | −8.2622 | 1.7036 | 20.3842 |
| Radial MRG-MRE | 55.3081 | −44.0505 | −6.2676 | 1.8838 | 22.6456 |
| Parameters | |||||
|---|---|---|---|---|---|
| Ordinary MRE | 15.2875 | 32.4476 | 9.7183 | 1.1140 | 1.1141 |
| Annular MRG-MRE | 7.9952 | 44.5825 | 10.6378 | 0.9158 | 0.9126 |
| Radial MRG-MRE | 8.4923 | 44.4016 | 3.8252 | 1.0066 | 1.0065 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, M.; Li, W.; Hou, Q.; Li, Y. MRE Encapsulating MRG: Synergistic Improvement in Modulus Tunability and Energy Dissipation. Nanomaterials 2025, 15, 1031. https://doi.org/10.3390/nano15131031
Zhu M, Li W, Hou Q, Li Y. MRE Encapsulating MRG: Synergistic Improvement in Modulus Tunability and Energy Dissipation. Nanomaterials. 2025; 15(13):1031. https://doi.org/10.3390/nano15131031
Chicago/Turabian StyleZhu, Mi, Wang Li, Qi Hou, and Yanmei Li. 2025. "MRE Encapsulating MRG: Synergistic Improvement in Modulus Tunability and Energy Dissipation" Nanomaterials 15, no. 13: 1031. https://doi.org/10.3390/nano15131031
APA StyleZhu, M., Li, W., Hou, Q., & Li, Y. (2025). MRE Encapsulating MRG: Synergistic Improvement in Modulus Tunability and Energy Dissipation. Nanomaterials, 15(13), 1031. https://doi.org/10.3390/nano15131031





