Two-Dimensional Porous Beryllium Trinitride Monolayer as Multifunctional Energetic Material
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Calculation Details
3. Results and Discussion
3.1. Structural Search and Energetic Properties of BeN3
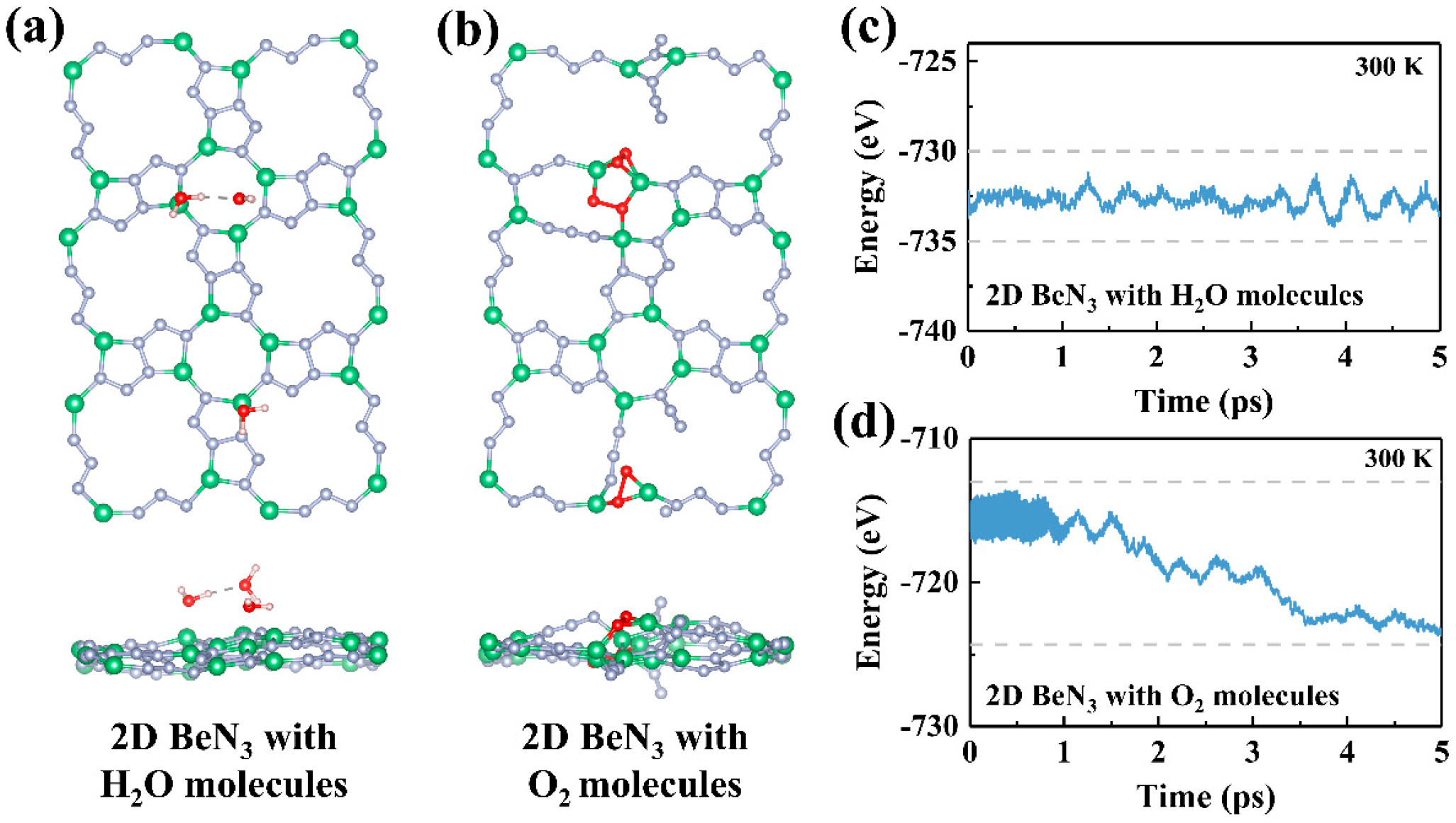
3.2. Bonding Characteristics and Stability of BeN3
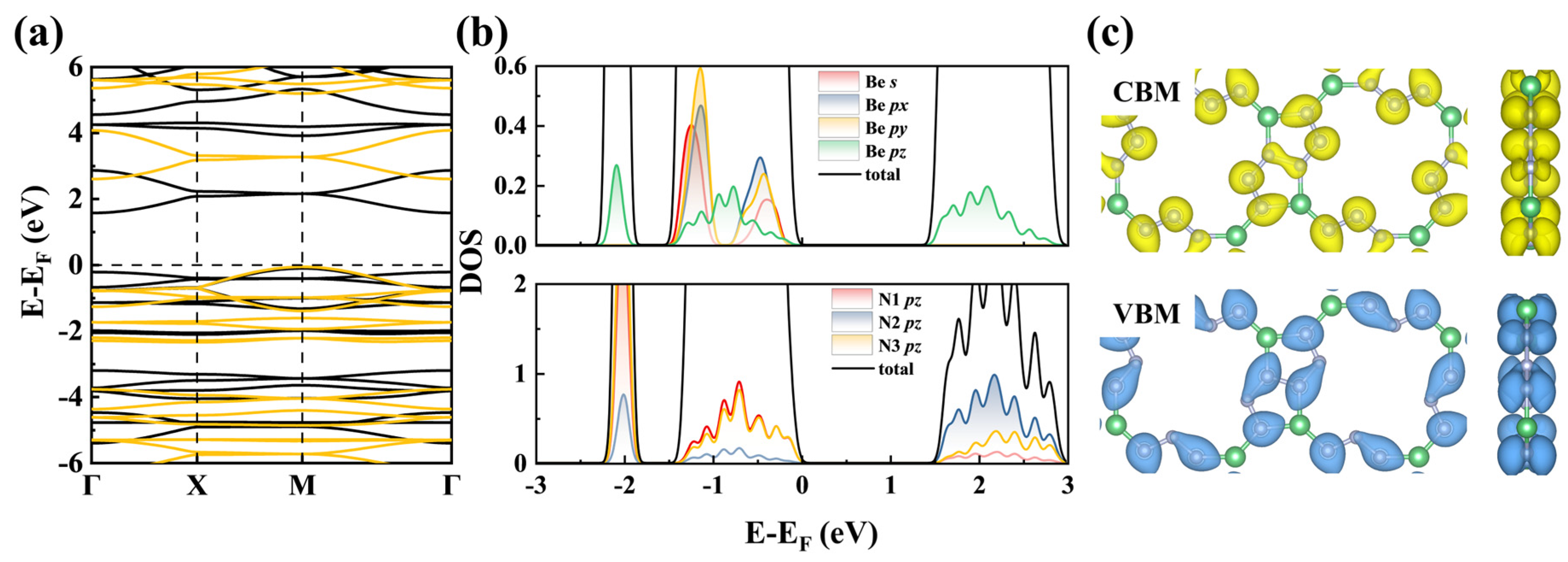
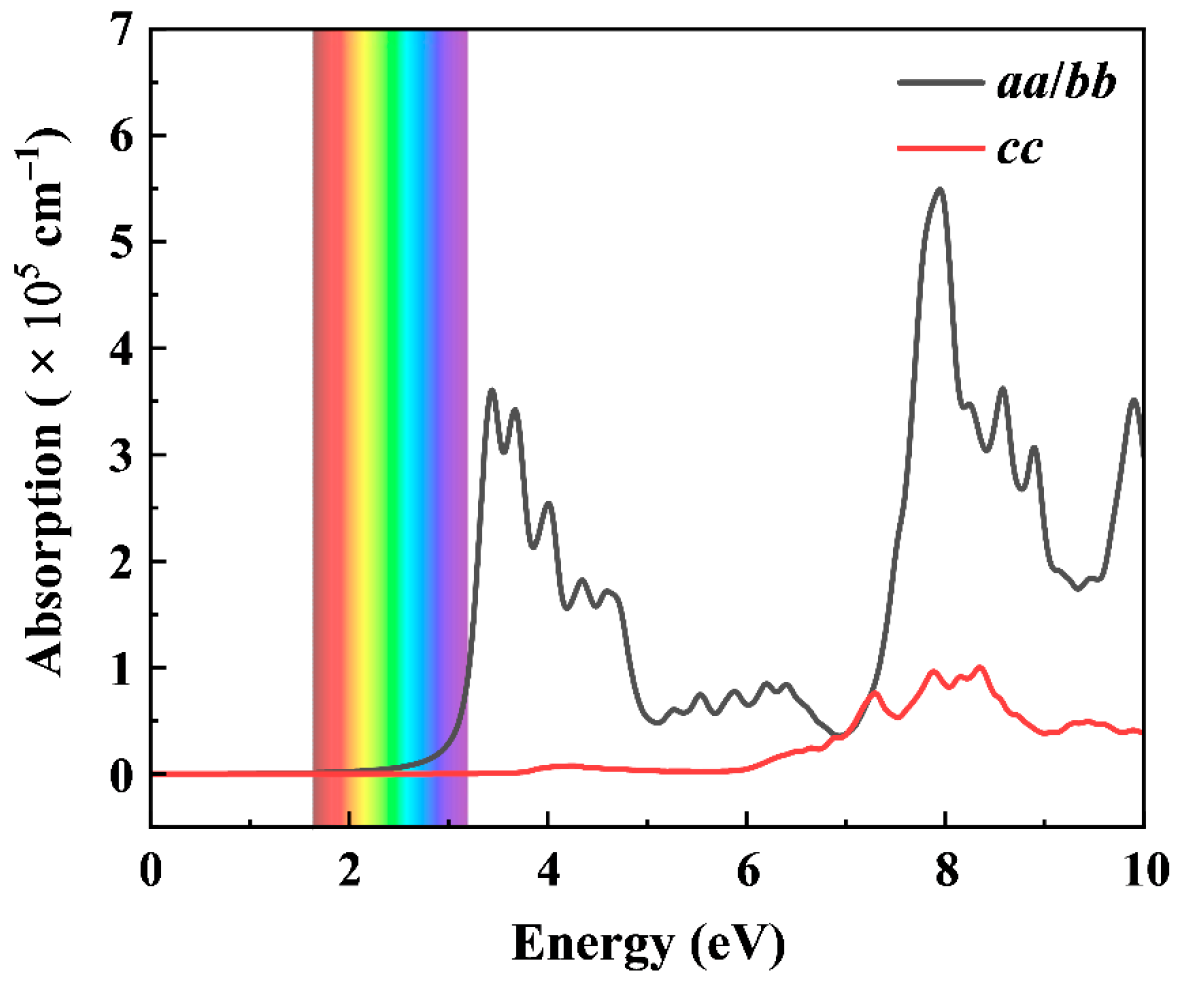
3.3. Mechanical, Electronic, and Optical Properties of BeN3
3.4. Gas Separation Applications of BeN3
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, C.; Sun, C.; Hu, B.; Yu, C.; Lu, M. Synthesis and characterization of the pentazolate anion cyclo-N5ˉ in (N5)6(H3O)3(NH4)4Cl. Science 2017, 355, 374–376. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Shreeve, J.N.M. 3,3’-Dinitroamino-4,4’-azoxyfurazan and Its Derivatives: An Assembly of Diverse N–O Building Blocks for High-Performance Energetic Materials. J. Am. Chem. Soc. 2014, 136, 4437–4445. [Google Scholar] [CrossRef] [PubMed]
- Mailhiot, C.; Yang, L.H.; McMahan, A.K. Polymeric nitrogen. Phys. Rev. B 1992, 46, 14419–14435. [Google Scholar] [CrossRef]
- Laniel, D.; Geneste, G.; Weck, G.; Mezouar, M.; Loubeyre, P. Hexagonal Layered Polymeric Nitrogen Phase Synthesized near 250 GPa. Phys. Rev. Lett. 2019, 122, 066001. [Google Scholar] [CrossRef]
- McMahan, A.K.; LeSar, R. Pressure Dissociation of Solid Nitrogen under 1 Mbar. Phys. Rev. Lett. 1985, 54, 1929–1932. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, Y.; Miao, M.; Zhong, X.; Lv, J.; Cui, T.; Li, J.; Chen, L.; Pickard, C.J.; Ma, Y. Cagelike Diamondoid Nitrogen at High Pressures. Phys. Rev. Lett. 2012, 109, 175502. [Google Scholar] [CrossRef]
- Sun, J.; Martinez-Canales, M.; Klug, D.D.; Pickard, C.J.; Needs, R.J. Stable All-Nitrogen Metallic Salt at Terapascal Pressures. Phys. Rev. Lett. 2013, 111, 175502. [Google Scholar] [CrossRef]
- Glukhovtsev, M.N.; Jiao, H.; Schleyer, P.v.R. Besides N(2), What Is the Most Stable Molecule Composed Only of Nitrogen Atoms? Inorg Chem 1996, 35, 7124–7133. [Google Scholar] [CrossRef]
- Zhou, H.; Wong, N.-B.; Zhou, G.; Tian, A. Theoretical Study on “Multilayer” Nitrogen Cages. J. Phys. Chem. A 2006, 110, 3845–3852. [Google Scholar] [CrossRef]
- Thompson, M.D.; Bledson, T.M.; Strout, D.L. Dissociation Barriers for Odd-Numbered Acyclic Nitrogen Molecules N9 and N11. J. Phys. Chem. A 2002, 106, 6880–6882. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Botana, J.; Zhang, M.; Zhu, H.; Chen, L.; Liu, H.; Cui, T.; Miao, M. Polymerization of nitrogen in lithium azide. J. Chem. Phys. 2013, 139, 164710. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Yin, K.; Zhang, X.; Wang, H.; Li, Q.; Wu, Z. Structural and electronic properties of sodium azide at high pressure: A first principles study. Solid State Commun. 2013, 161, 13–18. [Google Scholar] [CrossRef]
- Steele, B.A.; Oleynik, I.I. Novel Potassium Polynitrides at High Pressures. J. Phys. Chem. A 2017, 121, 8955–8961. [Google Scholar] [CrossRef] [PubMed]
- Peng, F.; Han, Y.; Liu, H.; Yao, Y. Exotic stable cesium polynitrides at high pressure. Sci. Rep. 2015, 5, 16902. [Google Scholar] [CrossRef]
- Wei, S.; Li, D.; Liu, Z.; Li, X.; Tian, F.; Duan, D.; Liu, B.; Cui, T. Alkaline-earth metal (Mg) polynitrides at high pressure as possible high-energy materials. Phys. Chem. Chem. Phys. 2017, 19, 9246–9252. [Google Scholar] [CrossRef]
- Zhu, S.; Peng, F.; Liu, H.; Majumdar, A.; Gao, T.; Yao, Y. Stable Calcium Nitrides at Ambient and High Pressures. Inorg Chem 2016, 55, 7550–7555. [Google Scholar] [CrossRef]
- Shen, Y.; Oganov, A.R.; Qian, G.; Zhang, J.; Dong, H.; Zhu, Q.; Zhou, Z. Novel lithium-nitrogen compounds at ambient and high pressures. Sci. Rep. 2015, 5, 14204. [Google Scholar] [CrossRef]
- Steele, B.A.; Oleynik, I.I. Sodium pentazolate: A nitrogen rich high energy density material. Chem. Phys. Lett. 2016, 643, 21–26. [Google Scholar] [CrossRef]
- Williams, A.S.; Steele, B.A.; Oleynik, I.I. Novel rubidium poly-nitrogen materials at high pressure. J. Chem. Phys. 2017, 147, 234701. [Google Scholar] [CrossRef]
- Xia, K.; Zheng, X.; Yuan, J.; Liu, C.; Gao, H.; Wu, Q.; Sun, J. Pressure-Stabilized High-Energy-Density Alkaline-Earth-Metal Pentazolate Salts. J. Phys. Chem. C 2019, 123, 10205–10211. [Google Scholar] [CrossRef]
- Yi, W.; Zhao, L.; Liu, X.; Chen, X.; Zheng, Y.; Miao, M. Packing high-energy together: Binding the power of pentazolate and high-valence metals with strong bonds. Mater. Des. 2020, 193, 108820. [Google Scholar] [CrossRef]
- Bykov, M.; Fedotenko, T.; Chariton, S.; Laniel, D.; Glazyrin, K.; Hanfland, M.; Smith, J.S.; Prakapenka, V.B.; Mahmood, M.F.; Goncharov, A.F.; et al. High-Pressure Synthesis of Dirac Materials: Layered van der Waals Bonded BeN4 Polymorph. Phys. Rev. Lett. 2021, 126, 175501. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Frapper, G. Barium–Nitrogen Phases Under Pressure: Emergence of Structural Diversity and Nitrogen-Rich Compounds. Chem. Mater. 2018, 30, 7623–7636. [Google Scholar] [CrossRef]
- Wei, S.; Lian, L.; Liu, Y.; Li, D.; Liu, Z.; Cui, T. Pressure-stabilized polymerization of nitrogen in alkaline-earth-metal strontium nitrides. Phys. Chem. Chem. Phys. 2020, 22, 5242–5248. [Google Scholar] [CrossRef] [PubMed]
- Bhadram, V.S.; Kim, D.Y.; Strobel, T.A. High-Pressure Synthesis and Characterization of Incompressible Titanium Pernitride. Chem. Mater. 2016, 28, 1616–1620. [Google Scholar] [CrossRef]
- Niwa, K.; Suzuki, K.; Muto, S.; Tatsumi, K.; Soda, K.; Kikegawa, T.; Hasegawa, M. Discovery of the Last Remaining Binary Platinum-Group Pernitride RuN2. Chem. A Eur. J. 2014, 20, 13885–13888. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, X.; Dong, H.; Zhang, X.; Wu, F.; Mu, Z.; Wen, M. Pressure-Induced High-Energy-Density BeN4 Materials with Nitrogen Chains: First-Principles Study. J. Phys. Chem. C 2021, 125, 25376–25382. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, Z.; Liu, L.; Yang, G. Pressure-induced stable BeN4 as a high-energy density material. J. Power Sources 2017, 365, 155–161. [Google Scholar] [CrossRef]
- Wei, S.; Li, D.; Liu, Z.; Wang, W.; Tian, F.; Bao, K.; Duan, D.; Liu, B.; Cui, T. A Novel Polymerization of Nitrogen in Beryllium Tetranitride at High Pressure. J. Phys. Chem. C 2017, 121, 9766–9772. [Google Scholar] [CrossRef]
- Yu, S.; Huang, B.; Zeng, Q.; Oganov, A.R.; Zhang, L.; Frapper, G. Emergence of Novel Polynitrogen Molecule-like Species, Covalent Chains, and Layers in Magnesium–Nitrogen MgxNy Phases under High Pressure. J. Phys. Chem. C 2017, 121, 11037–11046. [Google Scholar] [CrossRef]
- Yuan, J.; Xia, K.; Wu, J.; Sun, J. High-energy-density pentazolate salts: CaN10 and BaN10. Sci. China Phys. Mech. Astron. 2020, 64, 218211. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, H.; Huang, L.; Long, H.; Zhang, X.; Wu, F.; Mu, Z.; Wen, M. Pressure-Induced High-Energy-Density BeN6 Materials: First-Principles study. Comput. Mater. Sci. 2024, 244, 113272. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, A.; Wang, M.; Zhu, X.; Rodin, A.S.; Su, H.; Castro Neto, A.H. Phosphorene: From theory to applications. Nat. Rev. Mater. 2016, 1, 16061. [Google Scholar] [CrossRef]
- Wang, Z.-Q.; Lü, T.-Y.; Wang, H.-Q.; Feng, Y.P.; Zheng, J.-C. Review of borophene and its potential applications. Front. Phys. 2019, 14, 33403. [Google Scholar] [CrossRef]
- Tiwari, S.K.; Sahoo, S.; Wang, N.; Huczko, A. Graphene research and their outputs: Status and prospect. J. Sci. Adv. Mater. Devices 2020, 5, 10–29. [Google Scholar] [CrossRef]
- Yang, Q.; Zhao, Y.; Jiang, X.; Wang, B.; Zhao, J. Unconventional stoichiometric two-dimensional potassium nitrides with anion-driven metallicity and superconductivity. J. Mater. Chem. C 2024, 12, 103–109. [Google Scholar] [CrossRef]
- Wei, Y.; Ma, Y.; Wei, W.; Li, M.; Huang, B.; Dai, Y. Promising Photocatalysts for Water Splitting in BeN2 and MgN2 Monolayers. J. Phys. Chem. C 2018, 122, 8102–8108. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.; Zhang, C.; Wang, Q. Stabilizing benzene-like planar N6 rings to form a single atomic honeycomb BeN3 sheet with high carrier mobility. Nanoscale 2018, 10, 949–957. [Google Scholar] [CrossRef]
- Mortazavi, B.; Shojaei, F.; Zhuang, X. Ultrahigh stiffness and anisotropic Dirac cones in BeN4 and MgN4 monolayers: A first-principles study. Mater. Today Nano 2021, 15, 100125. [Google Scholar] [CrossRef]
- Zhou, W.; Guo, S.; Zeng, H.; Zhang, S. High-Performance Monolayer BeN2 Transistors With Ultrahigh On-State Current: A DFT Coupled With NEGF Study. IEEE Trans. Electron. Devices 2022, 69, 4501–4506. [Google Scholar] [CrossRef]
- Ding, Y.-M.; Ji, Y.; Dong, H.; Rujisamphan, N.; Li, Y. Electronic properties and oxygen reduction reaction catalytic activity of h-BeN2 and MgN2 by first-principles calculations. Nanotechnology 2019, 30, 465202. [Google Scholar] [CrossRef] [PubMed]
- Ni, S.; Jiang, J.; Wang, W.; Wu, X.; Zhuo, Z.; Wang, Z. Beryllium dinitride monolayer: A multifunctional direct bandgap anisotropic semiconductor containing polymeric nitrogen with oxygen reduction catalysis and potassium-ion storage capability. J. Mater. Chem. A 2025, 13, 10214–10223. [Google Scholar] [CrossRef]
- Filho, M.A.M.; Farmer, W.; Hsiao, C.-L.; dos Santos, R.B.; Hultman, L.; Birch, J.; Ankit, K.; Gueorguiev, G.K. Density Functional Theory-Fed Phase Field Model for Semiconductor Nanostructures: The Case of Self-Induced Core–Shell InAlN Nanorods. Cryst. Growth Des. 2024, 24, 4717–4727. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Cadelano, E.; Palla, P.L.; Giordano, S.; Colombo, L. Elastic properties of hydrogenated graphene. Phys. Rev. B 2010, 82, 235414. [Google Scholar] [CrossRef]
- Bardeen, J.; Shockley, W. Deformation Potentials and Mobilities in Non-Polar Crystals. Phys. Rev. 1950, 80, 72–80. [Google Scholar] [CrossRef]
- Peng, B.; Zhang, H.; Shao, H.; Xu, Y.; Zhang, R.; Zhu, H. The electronic, optical, and thermodynamic properties of borophene from first-principles calculations. J. Mater. Chem. C 2016, 4, 3592–3598. [Google Scholar] [CrossRef]
- Saha, S.; Sinha, T.P.; Mookerjee, A. Electronic structure, chemical bonding, and optical properties of paraelectricBaTiO3. Phys. Rev. B 2000, 62, 8828–8834. [Google Scholar] [CrossRef]
- Jiang, D.-e.; Cooper, V.R.; Dai, S. Porous Graphene as the Ultimate Membrane for Gas Separation. Nano Lett. 2009, 9, 4019–4024. [Google Scholar] [CrossRef]
- Blankenburg, S.; Bieri, M.; Fasel, R.; Müllen, K.; Pignedoli, C.A.; Passerone, D. Porous Graphene as an Atmospheric Nanofilter. Small 2010, 6, 2266–2271. [Google Scholar] [CrossRef]
- Carlotti, M.; Johns, J.W.C.; Trombetti, A. The ν5 Fundamental Bands of N2H2 and N2D2. Can. J. Phys. 1974, 52, 340–344. [Google Scholar] [CrossRef]
- Morino, Y.; Iijima, T.; Murata, Y. An Electron Diffraction Investigation on the Molecular Structure of Hydrazine. Bull. Chem. Soc. Jpn. 1960, 33, 46–48. [Google Scholar] [CrossRef]
- Raza, Z.; Pickard, C.J.; Pinilla, C.; Saitta, A.M. High Energy Density Mixed Polymeric Phase from Carbon Monoxide and Nitrogen. Phys. Rev. Lett. 2013, 111, 235501. [Google Scholar] [CrossRef] [PubMed]
- Peng, F.; Yao, Y.; Liu, H.; Ma, Y. Crystalline LiN5 Predicted from First-Principles as a Possible High-Energy Material. J. Phys. Chem. Lett. 2015, 6, 2363–2366. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Wang, D.; Zhang, S.; Zhang, H. Pressure-stabilized GdN6 with an armchair–antiarmchair structure as a high energy density material. J. Mater. Chem. A 2021, 9, 16751–16758. [Google Scholar] [CrossRef]
- Lu, W.; Hao, K.; Liu, S.; Lv, J.; Zhou, M.; Gao, P. Pressure-stabilized high-energy-density material YN10. J. Phys. Condens. Matter 2022, 34, 135403. [Google Scholar] [CrossRef]
- Liu, L.; Tang, J.; Wang, Q.-Q.; Shi, D.-X.; Zhang, G.-Y. Thermal stability of MoS2 encapsulated by graphene. Acta Phys. Sin. 2018, 67, 226501. [Google Scholar] [CrossRef]
- Liu, F.; Wang, M.; Chen, Y.; Gao, J. Thermal stability of graphene in inert atmosphere at high temperature. J. Solid State Chem. 2019, 276, 100–103. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, Y. Density Functional Theory Study of the Silicene-like SiX and XSi3 (X = B, C, N, Al, P) Honeycomb Lattices: The Various Buckled Structures and Versatile Electronic Properties. J. Phys. Chem. C 2013, 117, 18266–18278. [Google Scholar] [CrossRef]
- Zhuo, Z.; Wu, X.; Yang, J. Two-dimensional silicon crystals with sizable band gaps and ultrahigh carrier mobility. Nanoscale 2018, 10, 1265–1271. [Google Scholar] [CrossRef]
- Zhuo, Z.; Wu, X.; Yang, J. Two-Dimensional Phosphorus Porous Polymorphs with Tunable Band Gaps. J. Am. Chem. Soc. 2016, 138, 7091–7098. [Google Scholar] [CrossRef]
- Li, Y.; Liao, Y.; Chen, Z. Inside Back Cover: Be2C Monolayer with Quasi-Planar Hexacoordinate Carbons: A Global Minimum Structure. Angew. Chem. Int. Ed. 2014, 53, 7369. [Google Scholar] [CrossRef]
- Roy, S.; Zhang, X.; Puthirath, A.B.; Meiyazhagan, A.; Bhattacharyya, S.; Rahman, M.M.; Babu, G.; Susarla, S.; Saju, S.K.; Tran, M.K.; et al. Structure, Properties and Applications of Two-Dimensional Hexagonal Boron Nitride. Adv. Mater. 2021, 33, 2101589. [Google Scholar] [CrossRef]
- Chen, J.; Xi, J.; Wang, D.; Shuai, Z. Carrier Mobility in Graphyne Should Be Even Larger than That in Graphene: A Theoretical Prediction. J. Phys. Chem. Lett. 2013, 4, 1443–1448. [Google Scholar] [CrossRef] [PubMed]
- Qiao, J.; Kong, X.; Hu, Z.-X.; Yang, F.; Ji, W. High-mobility transport anisotropy and linear dichroism in few-layer black phosphorus. Nat. Commun. 2014, 5, 4475. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, G.; Zhang, Y.-W. Polarity-Reversed Robust Carrier Mobility in Monolayer MoS2 Nanoribbons. J. Am. Chem. Soc. 2014, 136, 6269–6275. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Wu, X.; Li, Z.; Yang, J. Helium separation via porous silicene based ultimate membrane. Nanoscale 2013, 5, 9062–9066. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Wu, X.; Li, Z.; Yang, J. Porous silicene as a hydrogen purification membrane. Phys. Chem. Chem. Phys. 2013, 15, 5753–5757. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Hu, Q.; Wang, W.; Guo, H. Two-Dimensional Porous Beryllium Trinitride Monolayer as Multifunctional Energetic Material. Nanomaterials 2025, 15, 1004. https://doi.org/10.3390/nano15131004
Jiang J, Hu Q, Wang W, Guo H. Two-Dimensional Porous Beryllium Trinitride Monolayer as Multifunctional Energetic Material. Nanomaterials. 2025; 15(13):1004. https://doi.org/10.3390/nano15131004
Chicago/Turabian StyleJiang, Jiaxin, Qifan Hu, Weiyi Wang, and Hongyan Guo. 2025. "Two-Dimensional Porous Beryllium Trinitride Monolayer as Multifunctional Energetic Material" Nanomaterials 15, no. 13: 1004. https://doi.org/10.3390/nano15131004
APA StyleJiang, J., Hu, Q., Wang, W., & Guo, H. (2025). Two-Dimensional Porous Beryllium Trinitride Monolayer as Multifunctional Energetic Material. Nanomaterials, 15(13), 1004. https://doi.org/10.3390/nano15131004





