Theoretical Analysis of Contact Angle and Contact Angle Hysteresis of Wenzel Drops on Superhydrophobic Surfaces
Abstract
1. Introduction
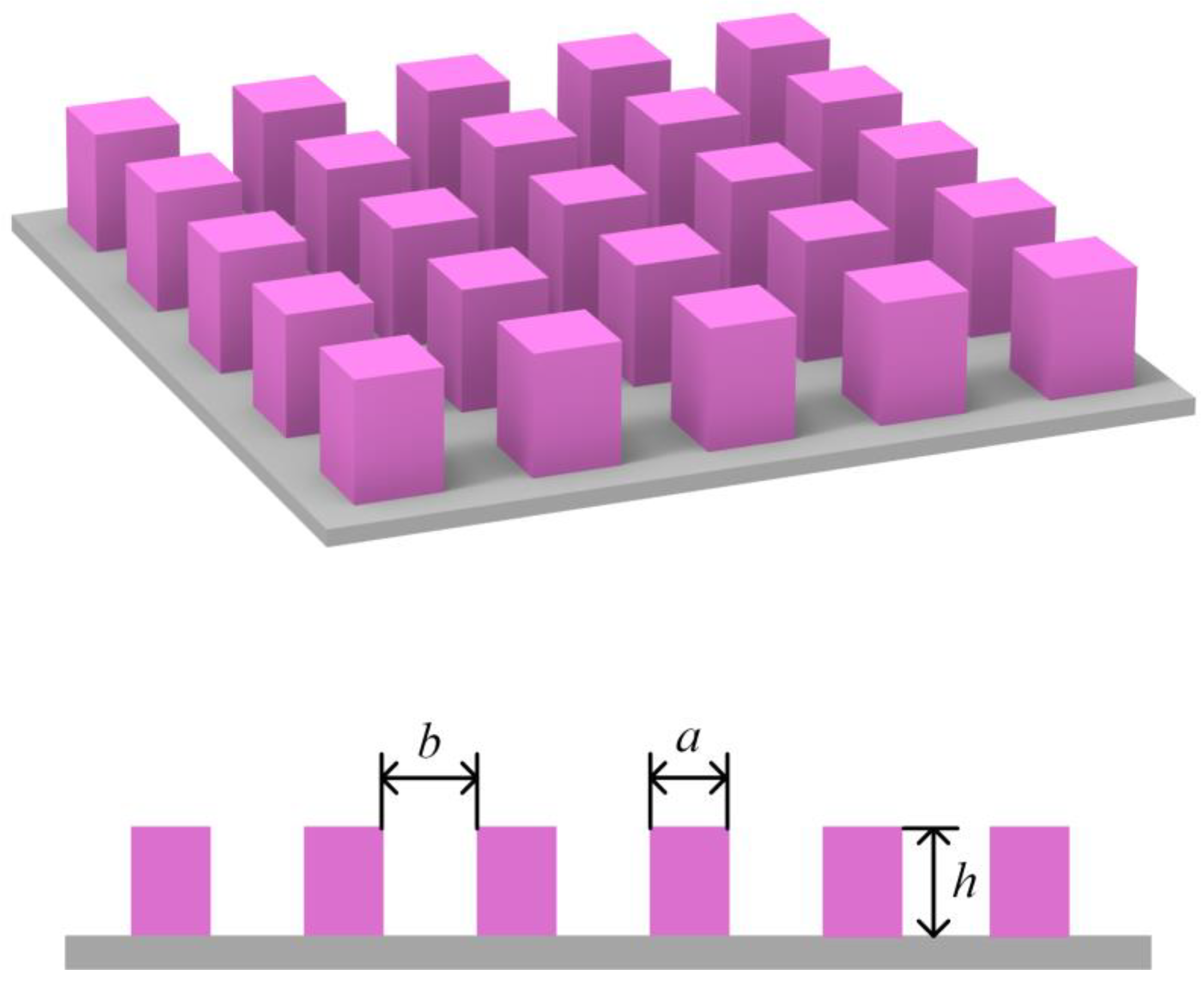
2. Theoretical Model
2.1. Free Energy of the Wenzel Wetting System
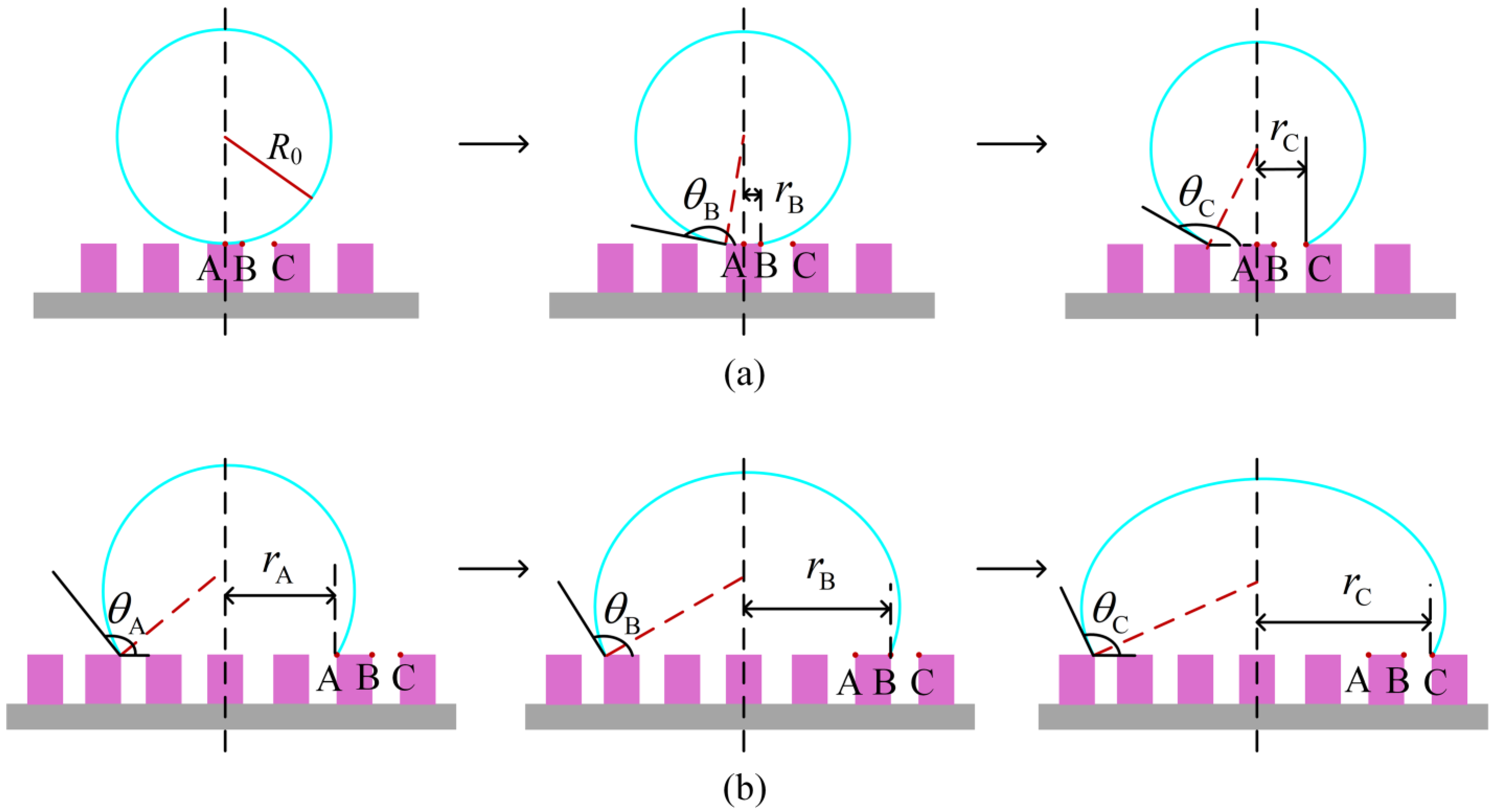
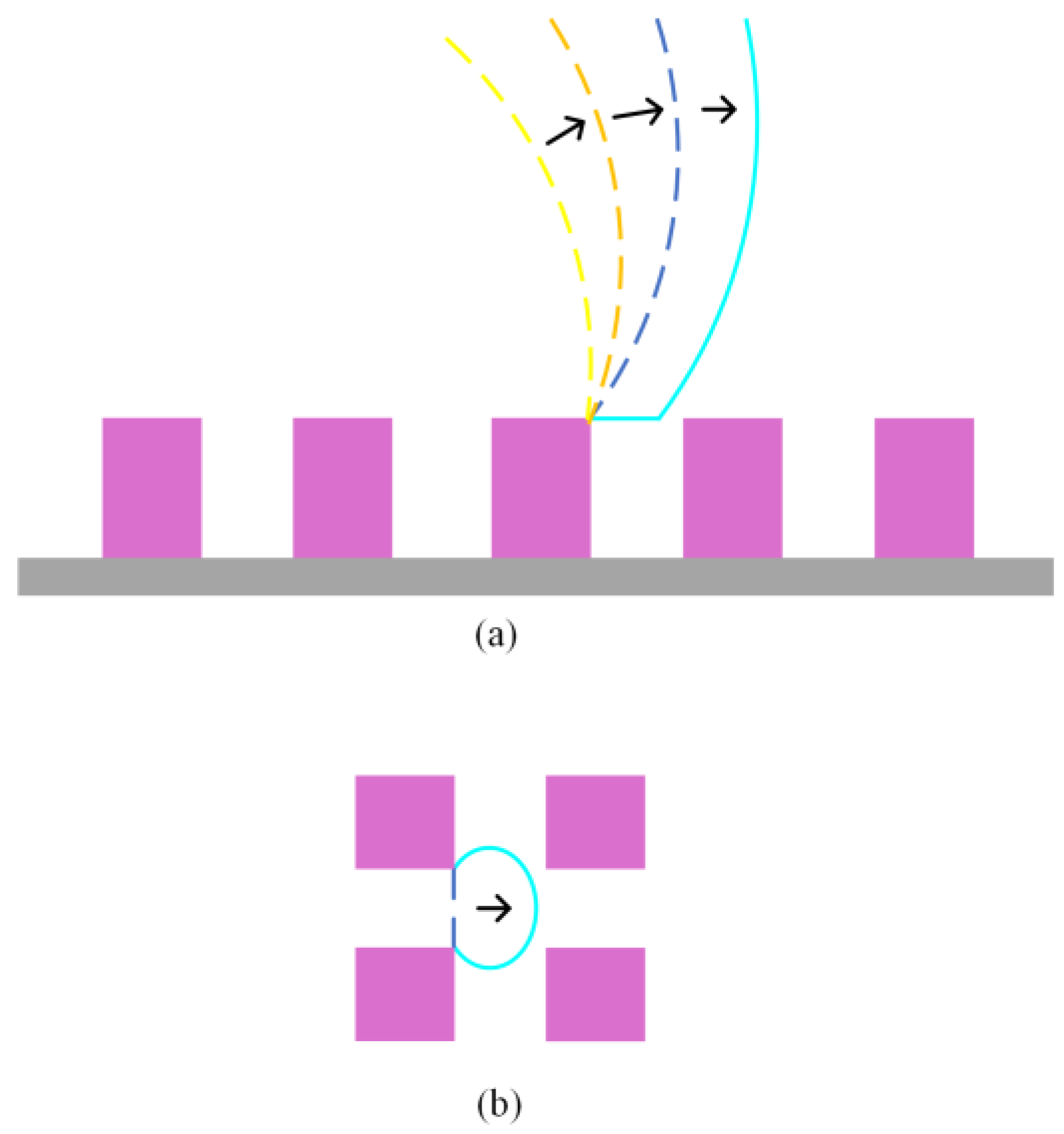
2.2. Analysis of Free Energy Barrier
3. Results and Discussion
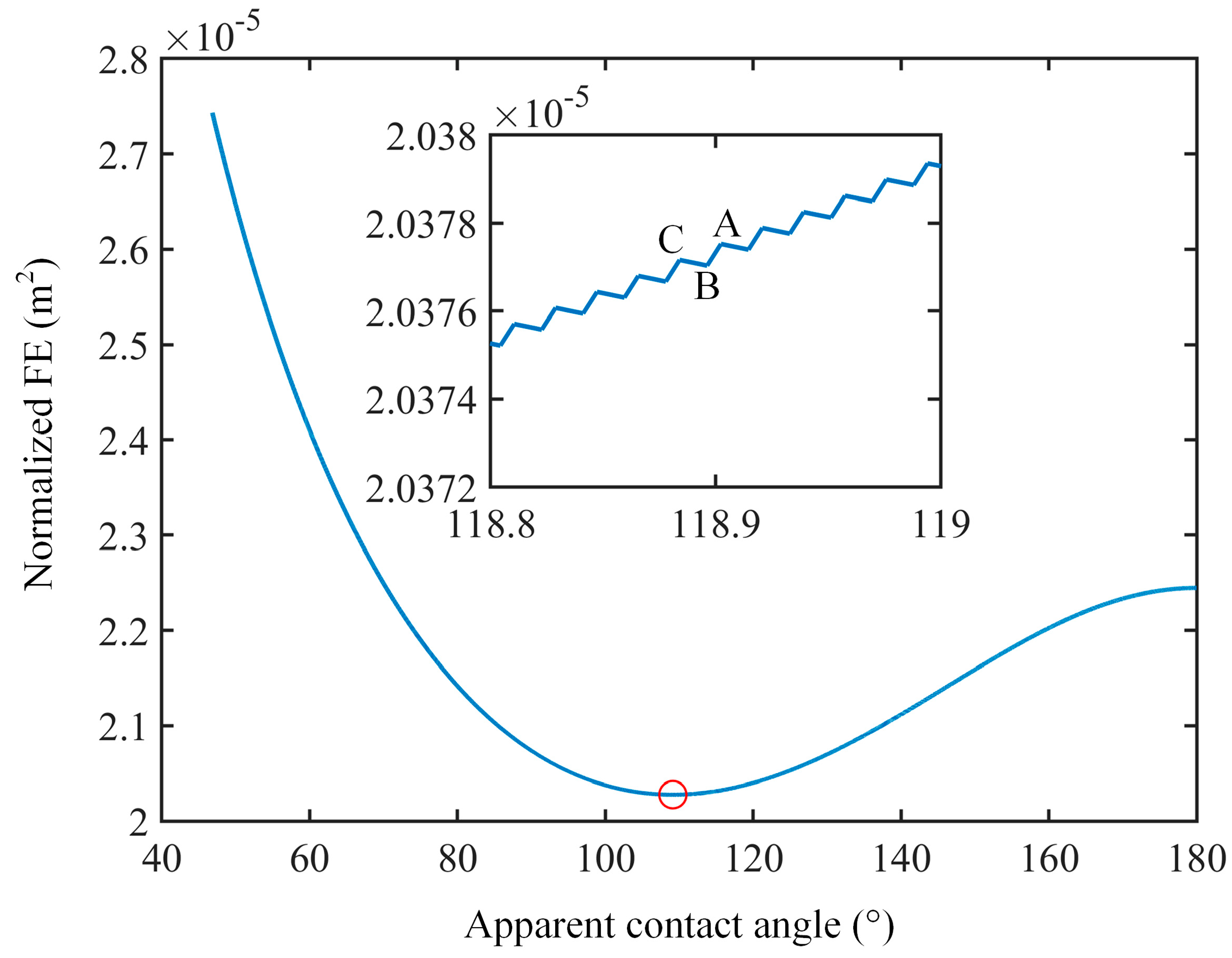
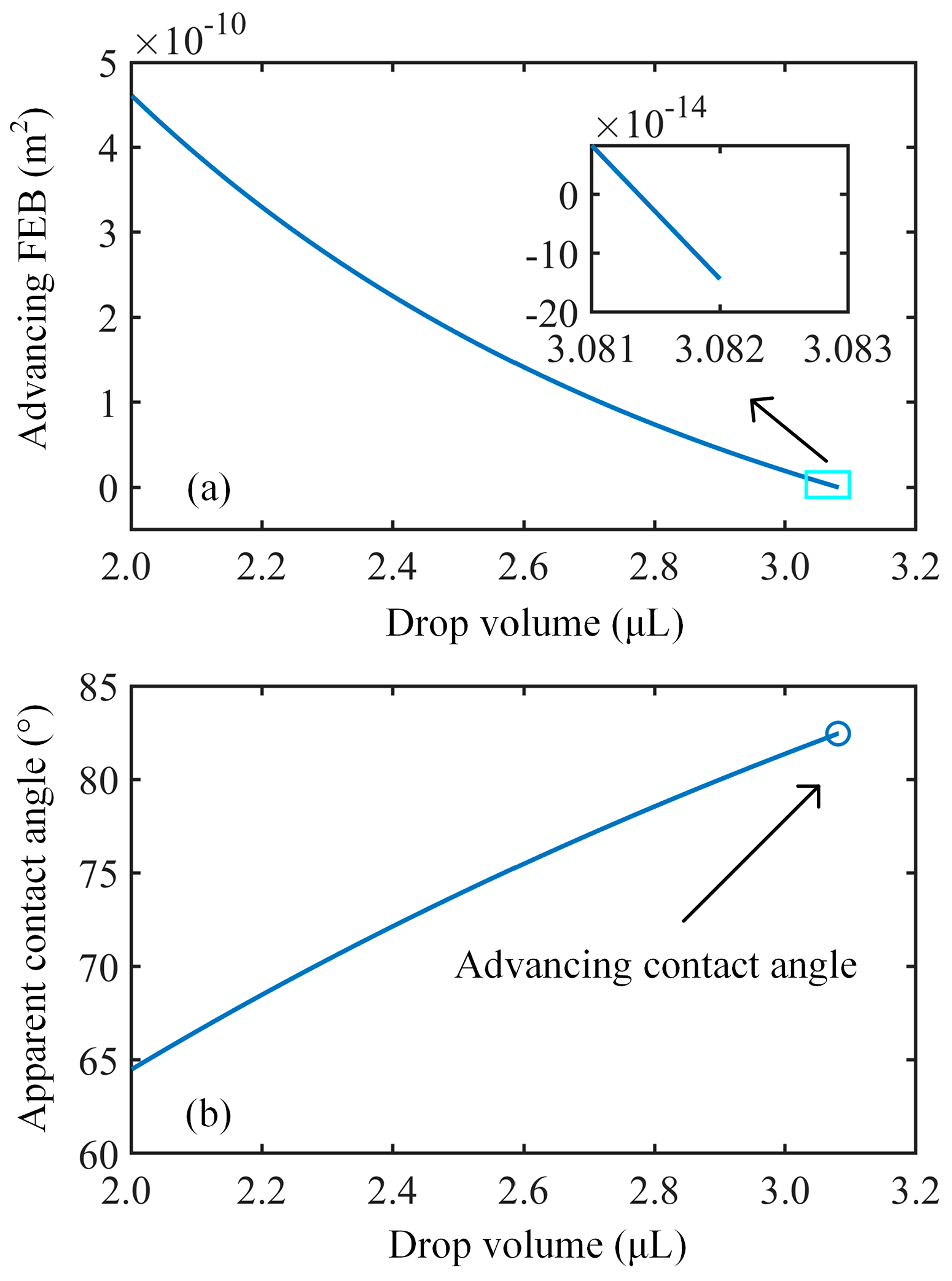
3.1. Analysis of Free Energy and Equilibrium Contact Angle
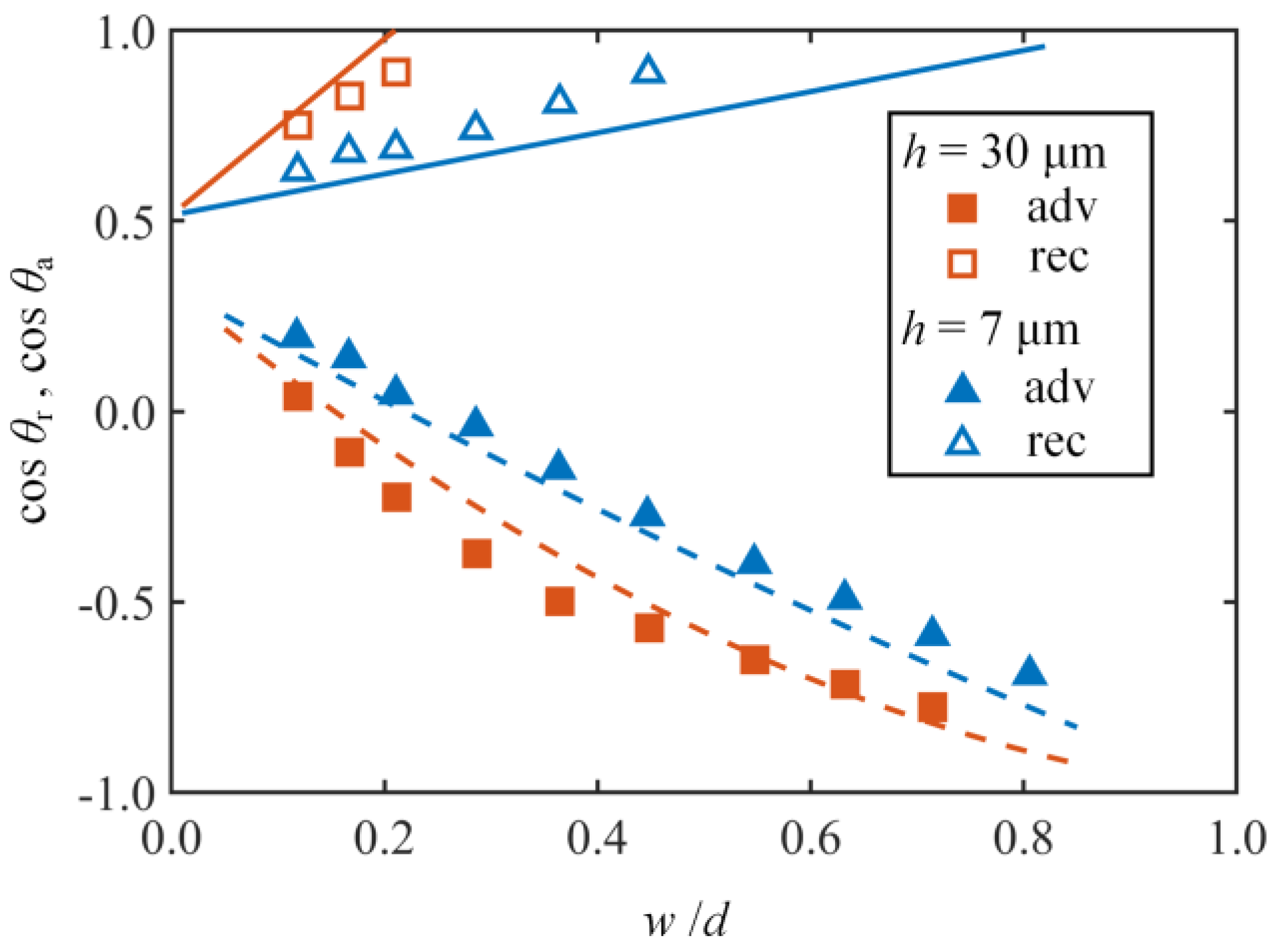
3.2. Analysis of Free Energy Barrier and Contact Angle Hysteresis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, H.; Guo, Z. Recent advances in self-healing superhydrophobic coatings. Nano Today 2023, 51, 101933. [Google Scholar] [CrossRef]
- Shigrekar, M.; Amdoskar, V. A review on recent progress and techniques used for fabricating superhydrophobic coatings derived from biobased materials. RSC Adv. 2024, 14, 32668–32699. [Google Scholar] [CrossRef]
- Luo, J.; Guo, Z. Recent advances in biomimetic superhydrophobic surfaces: Focusing on abrasion resistance, self-healing and anti-icing. Nanoscale 2024, 16, 16404–16419. [Google Scholar] [CrossRef] [PubMed]
- Cai, H.; Duan, C.; Fu, M.; Zhang, J.; Huang, H.; Hu, Y.; Shi, J.; Ye, D. Scalable Fabrication of Superhydrophobic Coating with Rough Coral Reef-Like Structures for Efficient Self-Cleaning and Oil-Water Separation: An Experimental and Molecular Dynamics Simulation Study. Small 2023, 19, 2207118. [Google Scholar] [CrossRef]
- Li, X.; Yang, K.; Yuan, Z.; Liu, S.; Du, J.; Li, C.; Meng, S. Recent Advances on the Abrasion Resistance Enhancements and Applications of Superhydrophobic Materials. Chem. Rec. 2023, 23, e202200298. [Google Scholar] [CrossRef] [PubMed]
- Si, Y.; Li, C.; Hu, J.; Zhang, C.; Dong, Z. Bioinspired Superwetting Open Microfluidics: From Concepts, Phenomena to Applications. Adv. Funct. Mater. 2023, 33, 2301017. [Google Scholar] [CrossRef]
- Zhou, X.; Zang, H.; Guan, Y.; Li, S.; Liu, M. Superhydrophobic Flexible Strain Sensors Constructed Using Nanomaterials: Their Fabrications and Sustainable Applications. Nanomaterials 2023, 13, 2639. [Google Scholar] [CrossRef]
- Hussain, S.; Muangnapoh, T.; Traipattanakul, B.; Lekmuenwai, M. Anti-Icing Property of Superhydrophobic Nanostructured Brass via Deposition of Silica Nanoparticles and Nanolaser Treatment. Nanomaterials 2023, 13, 1139. [Google Scholar] [CrossRef]
- Li, Y.; Jin, H.; Nie, S.; Zhang, P.; Gao, N. Dynamic behavior of water droplets and flashover characteristics on a superhydrophobic silicone rubber surface. Appl. Phys. Lett. 2017, 110, 201602. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, S.; Liu, S.; Zuo, Z.; Gao, Y.; Wu, C.; Liang, X. Super-hydrophobic silicone rubber for outdoor electrical insulation. Nano Today 2024, 58, 102406. [Google Scholar] [CrossRef]
- Makkonen, L. A thermodynamic model of contact angle hysteresis. J. Chem. Phys. 2017, 147, 064703. [Google Scholar] [CrossRef] [PubMed]
- Huhtamäki, T.; Tian, X.; Korhonen, J.T.; Ras, R.H.A. Surface-wetting characterization using contact-angle measurements. Nat. Protoc. 2018, 13, 1521–1538. [Google Scholar] [CrossRef] [PubMed]
- Li, Y. An analytical approach for determining contact angle hysteresis on smooth, micropillared, and micropored homogeneous surfaces. J. Colloid Interface Sci. 2025, 679, 554–565. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Wang, Y.; Zhang, H.; An, K. Recent advances and strategies in mechanical stability of superhydrophobic surfaces. Prog. Org. Coat. 2024, 194, 108595. [Google Scholar] [CrossRef]
- Luo, W.; Li, M. Recent Advances in Fabrication of Durable, Transparent, and Superhydrophobic Surfaces. Nanomaterials 2023, 13, 2359. [Google Scholar] [CrossRef]
- Paxson, A.T.; Varanasi, K.K. Self-similarity of contact line depinning from textured surfaces. Nat. Commun. 2013, 4, 1492. [Google Scholar] [CrossRef]
- Schellenberger, F.; Encinas, N.; Vollmer, D.; Butt, H.-J. How Water Advances on Superhydrophobic Surfaces. Phys. Rev. Lett. 2016, 116, 096101. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, W.; Sarshar, M.A.; Choi, C.-H. Generalized models for advancing and receding contact angles of fakir droplets on pillared and pored surfaces. J. Colloid Interface Sci. 2019, 552, 359–371. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, X. Contact angle hysteresis analysis on superhydrophobic surface based on the design of channel and pillar models. Mater. Des. 2017, 131, 323–333. [Google Scholar] [CrossRef]
- Yao, C.-W.; Tang, S.; Sebastian, D.; Tadmor, R. Sliding of water droplets on micropillar-structured superhydrophobic surfaces. Appl. Surf. Sci. 2020, 504, 144493. [Google Scholar] [CrossRef]
- Li, Y. Theoretical analysis of contact angle hysteresis of suspended drops on micropillared superhydrophobic surfaces. Colloids Surf. Physicochem. Eng. Asp. 2023, 666, 131244. [Google Scholar] [CrossRef]
- Zhu, J.; Dai, X. A new model for contact angle hysteresis of superhydrophobic surface. AIP Adv. 2019, 9, 065309. [Google Scholar] [CrossRef]
- Bai, X.; Gou, X.; Zhang, J.; Liang, J.; Yang, L.; Wang, S.; Hou, X.; Chen, F. A Review of Smart Superwetting Surfaces Based on Shape-Memory Micro/Nanostructures. Small 2023, 19, 2206463. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Cai, Y.; Lu, G.; Hu, J.; Zhao, J.; Zheng, L.; Weng, Z.; Cheng, H.; Lin, J.; Wu, L. Stretchable superhydrophobic elastomers with on-demand tunable wettability for droplet manipulation and multi-stage reaction. J. Mater. Chem. C 2023, 11, 10069–10078. [Google Scholar] [CrossRef]
- Lee, J.; Hwang, S.-H.; Yoon, S.-S.; Khang, D.-Y. Evaporation characteristics of water droplets in Cassie, Wenzel, and mixed states on superhydrophobic pillared Si surface. Colloids Surf. Physicochem. Eng. Asp. 2019, 562, 304–309. [Google Scholar] [CrossRef]
- Wenzel, R.N. Resistance of Solid Surfaces to Wetting by Water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Gao, L.; McCarthy, T.J. How Wenzel and Cassie Were Wrong. Langmuir 2007, 23, 3762–3765. [Google Scholar] [CrossRef]
- Forsberg, P.S.H.; Priest, C.; Brinkmann, M.; Sedev, R.; Ralston, J. Contact Line Pinning on Microstructured Surfaces for Liquids in the Wenzel State. Langmuir 2010, 26, 860–865. [Google Scholar] [CrossRef] [PubMed]
- Barbieri, L.; Wagner, E.; Hoffmann, P. Water Wetting Transition Parameters of Perfluorinated Substrates with Periodically Distributed Flat-Top Microscale Obstacles. Langmuir 2007, 23, 1723–1734. [Google Scholar] [CrossRef]
- Li, W.; Amirfazli, A. Microtextured superhydrophobic surfaces: A thermodynamic analysis. Adv. Colloid Interface Sci. 2007, 132, 51–68. [Google Scholar] [CrossRef]
- Young, T., III. An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 1805, 95, 65–87. [Google Scholar] [CrossRef]
- Dong, Z.; Levkin, P.A. 3D Microprinting of Super-Repellent Microstructures: Recent Developments, Challenges, and Opportunities. Adv. Funct. Mater. 2023, 33, 2213916. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, L.; Yu, M.; Guo, J.; Liu, C.; Zhu, C.; Zhao, M.; Huang, Y.; Zheng, Y. Measurement Methods for Droplet Adhesion Characteristics and Micrometer-Scale Quantification of Contact Angle on Superhydrophobic Surfaces: Challenges and Opportunities. Langmuir 2024, 40, 9873–9891. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Guo, S.; Liu, X.; Guo, Z.; Yu, C.; Ning, Y.; Liu, K.; Jiang, L. Directional liquid dynamics on superwetting interfaces. Appl. Phys. Rev. 2024, 11, 021316. [Google Scholar] [CrossRef]
- Aldhaleai, A.; Tsai, P.A. Evaporation Dynamics of Surfactant-Laden Droplets on a Superhydrophobic Surface: Influence of Surfactant Concentration. Langmuir 2022, 38, 593–601. [Google Scholar] [CrossRef]
- Krishnan, S.R.; Bal, J.; Putnam, S.A. A simple analytic model for predicting the wicking velocity in micropillar arrays. Sci. Rep. 2019, 9, 20074. [Google Scholar] [CrossRef]
- Ruiz-Cabello, F.J.M.; Rodríguez-Valverde, M.A.; Cabrerizo-Vílchez, M.A. Equilibrium contact angle or the most-stable contact angle? Adv. Colloid Interface Sci. 2014, 206, 320–327. [Google Scholar] [CrossRef]
- Bittoun, E.; Marmur, A. Chemical Nano-Heterogeneities Detection by Contact Angle Hysteresis: Theoretical Feasibility. Langmuir 2010, 26, 15933–15937. [Google Scholar] [CrossRef]

| Surface Structural Parameters | θe(°) | θw(°) | ||
|---|---|---|---|---|
| a (nm) | b (nm) | h (nm) | ||
| 100 | 100 | 100 | 110.3208 | 110.3220 |
| 100 | 200 | 100 | 104.5255 | 104.5263 |
| 100 | 300 | 100 | 102.5223 | 102.5364 |
| 100 | 400 | 100 | 101.6156 | 101.6207 |
| 100 | 100 | 200 | 121.3917 | 121.3956 |
| 200 | 100 | 200 | 118.8389 | 118.8394 |
| 300 | 100 | 200 | 115.7313 | 115.7293 |
| 400 | 100 | 200 | 113.3067 | 113.3232 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Liu, J.; Dong, J.; Du, Y.; Han, J.; Niu, Y. Theoretical Analysis of Contact Angle and Contact Angle Hysteresis of Wenzel Drops on Superhydrophobic Surfaces. Nanomaterials 2024, 14, 1978. https://doi.org/10.3390/nano14231978
Li Y, Liu J, Dong J, Du Y, Han J, Niu Y. Theoretical Analysis of Contact Angle and Contact Angle Hysteresis of Wenzel Drops on Superhydrophobic Surfaces. Nanomaterials. 2024; 14(23):1978. https://doi.org/10.3390/nano14231978
Chicago/Turabian StyleLi, Yufeng, Junyan Liu, Jialong Dong, Yufeng Du, Jinchun Han, and Yuanyuan Niu. 2024. "Theoretical Analysis of Contact Angle and Contact Angle Hysteresis of Wenzel Drops on Superhydrophobic Surfaces" Nanomaterials 14, no. 23: 1978. https://doi.org/10.3390/nano14231978
APA StyleLi, Y., Liu, J., Dong, J., Du, Y., Han, J., & Niu, Y. (2024). Theoretical Analysis of Contact Angle and Contact Angle Hysteresis of Wenzel Drops on Superhydrophobic Surfaces. Nanomaterials, 14(23), 1978. https://doi.org/10.3390/nano14231978






