Spontaneous Magnetization Induced by Antiferromagnetic Toroidal Ordering
Abstract
1. Introduction
2. Setup
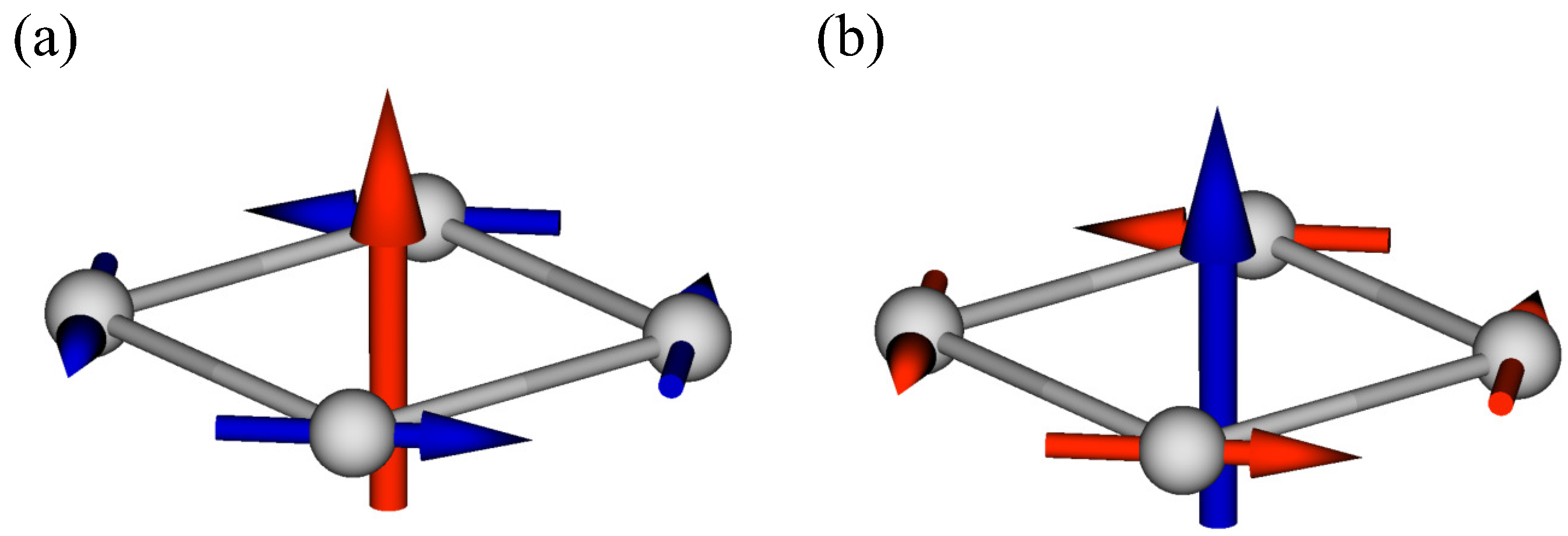
2.1. Symmetry Analysis
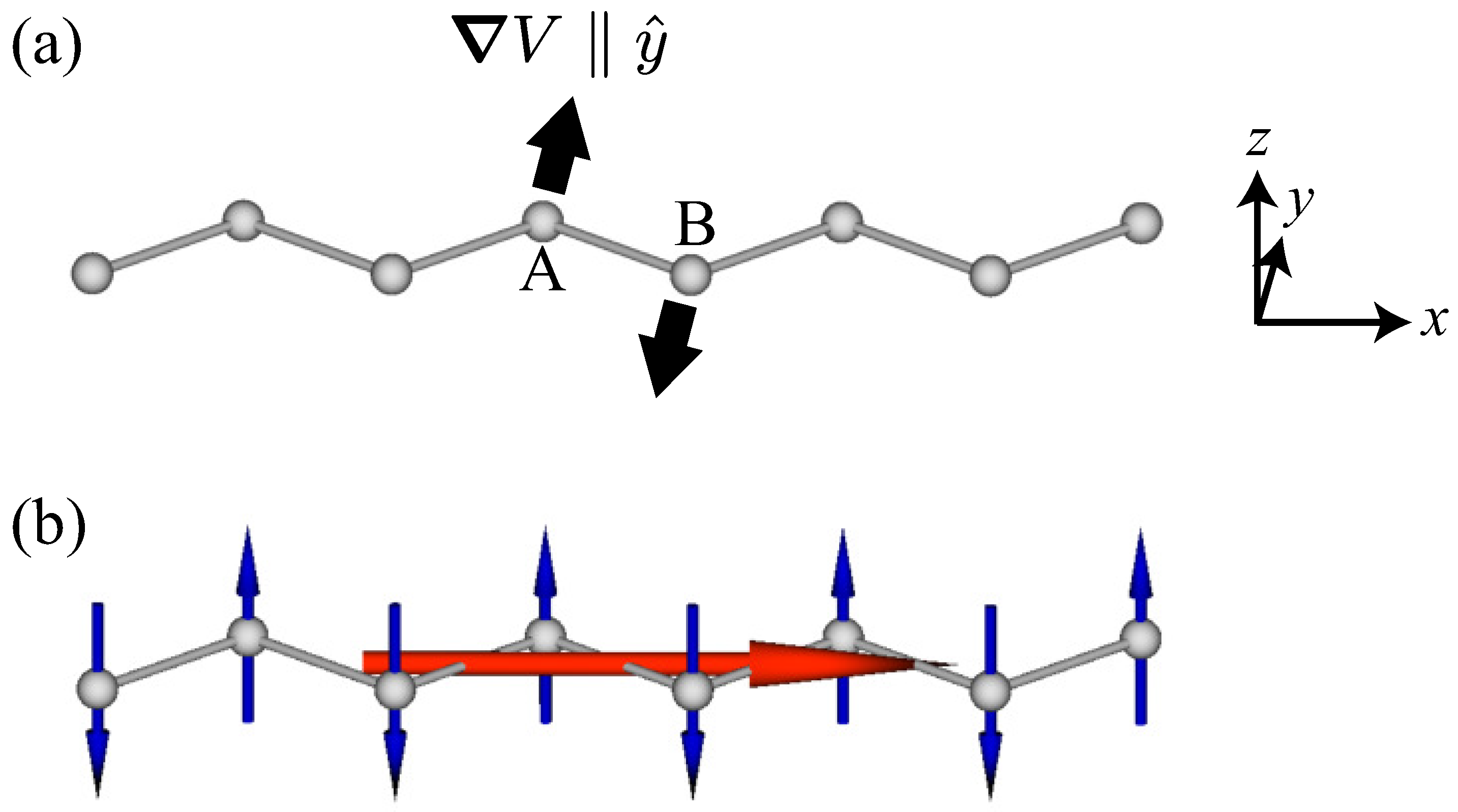
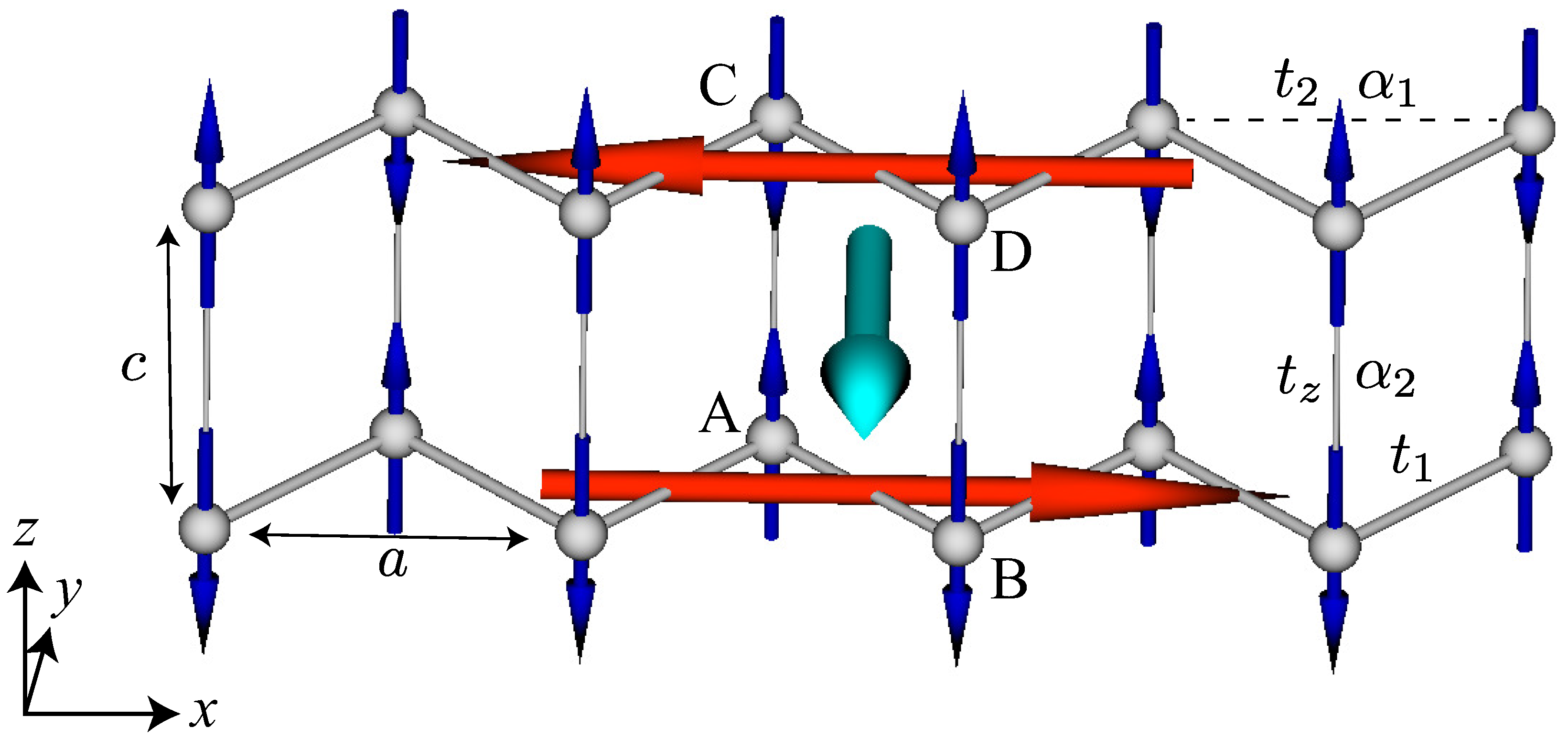
2.2. Model
3. Results
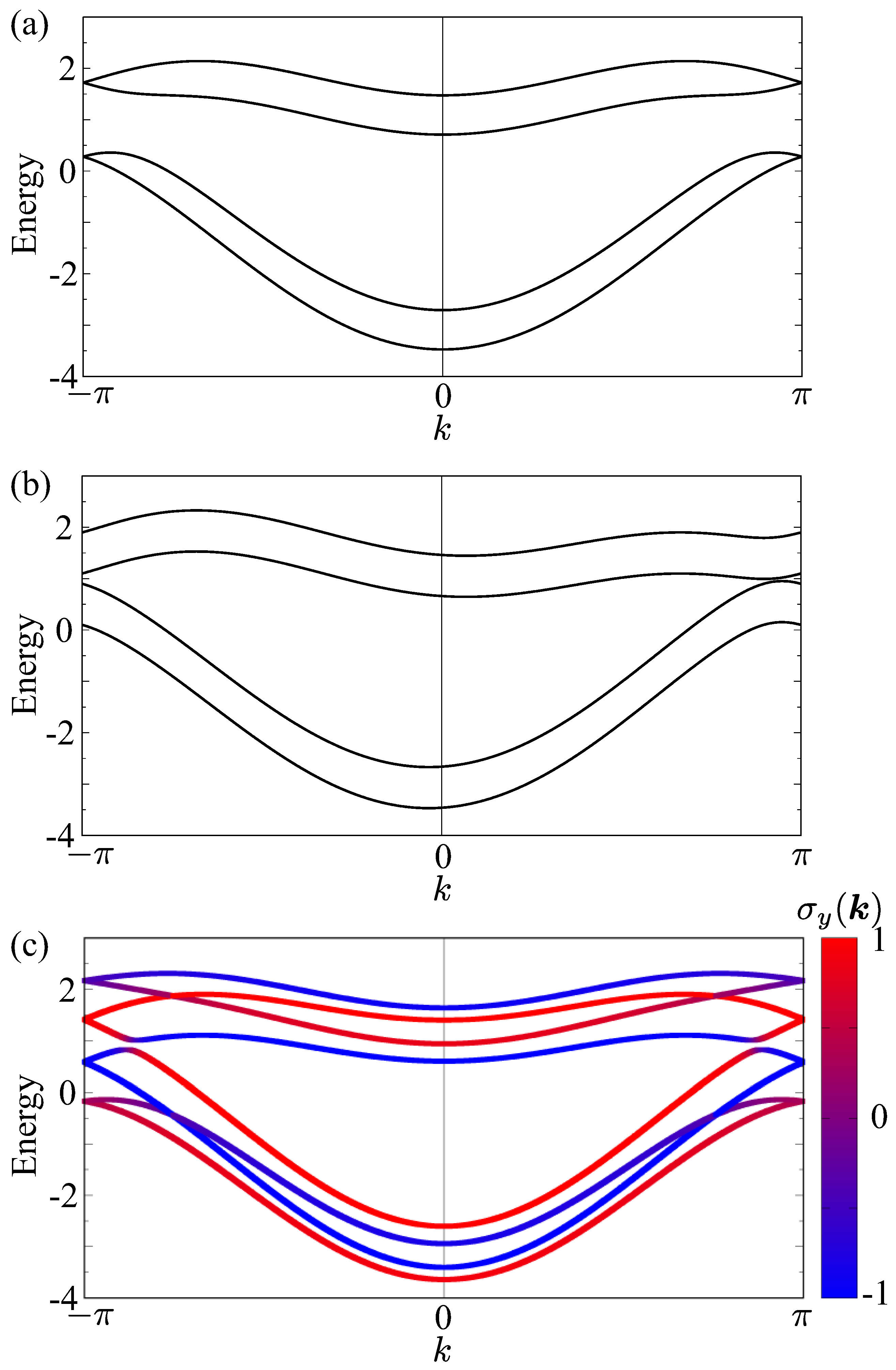
3.1. Electronic Band Structure
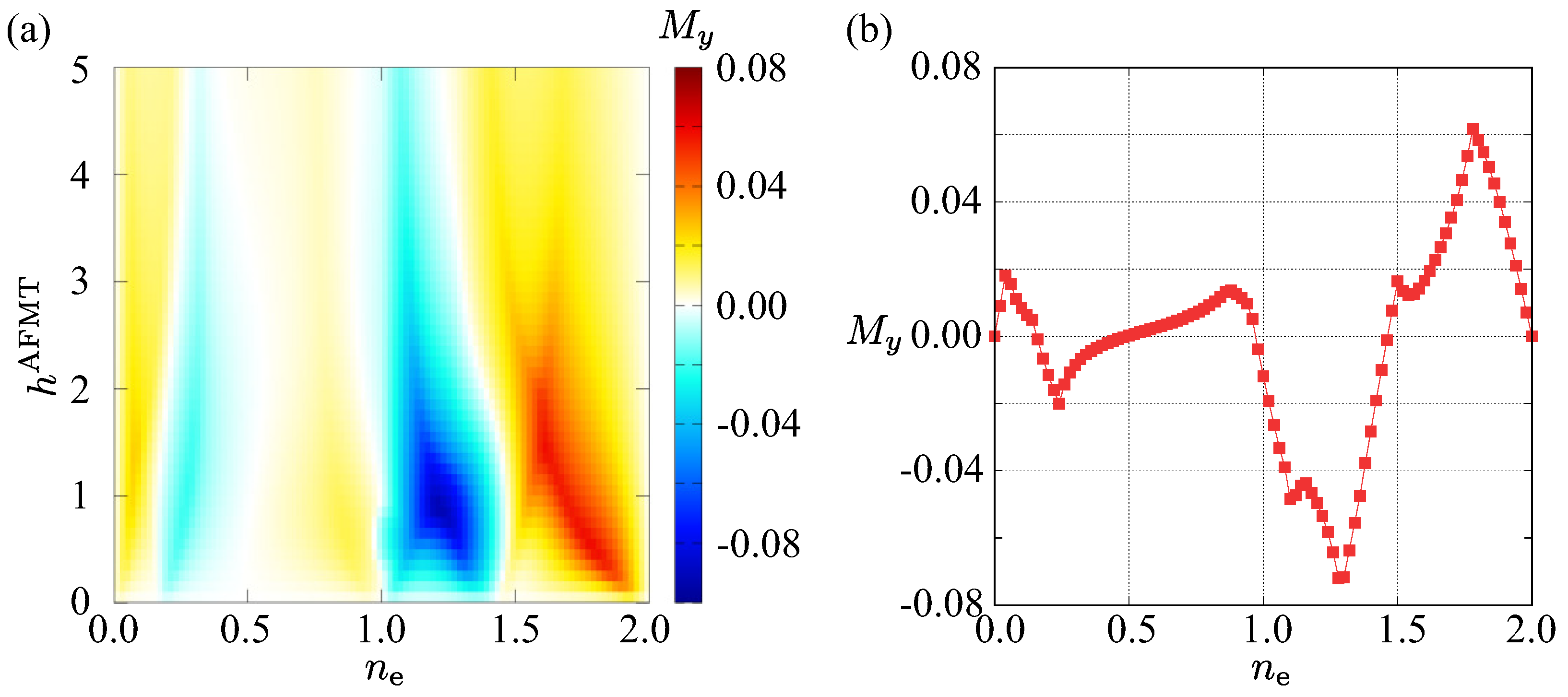
3.2. Spontaneous Magnetization
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dubovik, V.; Cheshkov, A. Multipole expansion in classical and quantum field theory and radiation. Sov. J. Part. Nucl. 1975, 5, 318–337. [Google Scholar]
- Dubovik, V.; Tugushev, V. Toroid moments in electrodynamics and solid-state physics. Phys. Rep. 1990, 187, 145–202. [Google Scholar] [CrossRef]
- Gorbatsevich, A.; Kopaev, Y.V. Toroidal order in crystals. Ferroelectrics 1994, 161, 321–334. [Google Scholar] [CrossRef]
- Kopaev, Y.V. Toroidal ordering in crystals. Physics-Uspekhi 2009, 52, 1111–1125. [Google Scholar] [CrossRef]
- Spaldin, N.A.; Fiebig, M.; Mostovoy, M. The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect. J. Phys. Condens. Matter 2008, 20, 434203. [Google Scholar] [CrossRef]
- Papasimakis, N.; Fedotov, V.; Savinov, V.; Raybould, T.; Zheludev, N. Electromagnetic toroidal excitations in matter and free space. Nat. Mater. 2016, 15, 263. [Google Scholar] [CrossRef]
- Talebi, N.; Guo, S.; van Aken, P.A. Theory and applications of toroidal moments in electrodynamics: Their emergence, characteristics, and technological relevance. Nanophotonics 2018, 7, 93–110. [Google Scholar] [CrossRef]
- Cheong, S.W.; Talbayev, D.; Kiryukhin, V.; Saxena, A. Broken symmetries, non-reciprocity, and multiferroicity. npj Quantum Mater. 2018, 3, 19. [Google Scholar] [CrossRef]
- Kusunose, H.; Hayami, S. Generalization of microscopic multipoles and cross-correlated phenomena by their orderings. J. Phys. Condens. Matter 2022, 34, 464002. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Unified description of electronic orderings and cross correlations by complete multipole representation. J. Phys. Soc. Jpn. 2024, 93, 072001. [Google Scholar] [CrossRef]
- Xu, X.; Huang, F.T.; Cheong, S.W. Magnetic toroidicity. J. Phys. Condens. Matter 2024, 36, 203002. [Google Scholar] [CrossRef]
- Azimi-Mousolou, V.; Bergman, A.; Delin, A.; Eriksson, O.; Pereiro, M.; Thonig, D.; Sjöqvist, E. Quantum spin systems: Toroidal classification and geometric duality. Phys. Rev. B 2024, 110, L140403. [Google Scholar] [CrossRef]
- Popov, Y.F.; Kadomtseva, A.; Belov, D.; Vorob’ev, G.; Zvezdin, A. Magnetic-field-induced toroidal moment in the magnetoelectric Cr2O3. J. Exp. Theor. Phys. Lett. 1999, 69, 330–335. [Google Scholar] [CrossRef]
- Schmid, H. On ferrotoroidics and electrotoroidic, magnetotoroidic and piezotoroidic effects*. Ferroelectrics 2001, 252, 41–50. [Google Scholar] [CrossRef]
- Ederer, C.; Spaldin, N.A. Towards a microscopic theory of toroidal moments in bulk periodic crystals. Phys. Rev. B 2007, 76, 214404. [Google Scholar] [CrossRef]
- Yanase, Y. Magneto-Electric Effect in Three-Dimensional Coupled Zigzag Chains. J. Phys. Soc. Jpn. 2014, 83, 014703. [Google Scholar] [CrossRef]
- Thöle, F.; Spaldin, N.A. Magnetoelectric multipoles in metals. Philos. Trans. R. Soc. A 2018, 376, 20170450. [Google Scholar] [CrossRef]
- Miyahara, S.; Furukawa, N. Nonreciprocal Directional Dichroism and Toroidalmagnons in Helical Magnets. J. Phys. Soc. Jpn. 2012, 81, 023712. [Google Scholar] [CrossRef]
- Miyahara, S.; Furukawa, N. Theory of magneto-optical effects in helical multiferroic materials via toroidal magnon excitation. Phys. Rev. B 2014, 89, 195145. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Asymmetric Magnon Excitation by Spontaneous Toroidal Ordering. J. Phys. Soc. Jpn. 2016, 85, 053705. [Google Scholar] [CrossRef]
- Matsumoto, T.; Hayami, S. Nonreciprocal magnons due to symmetric anisotropic exchange interaction in honeycomb antiferromagnets. Phys. Rev. B 2020, 101, 224419. [Google Scholar] [CrossRef]
- Sawada, K.; Nagaosa, N. Optical Magnetoelectric Effect in Multiferroic Materials: Evidence for a Lorentz Force Acting on a Ray of Light. Phys. Rev. Lett. 2005, 95, 237402. [Google Scholar] [CrossRef]
- Kawaguchi, H.; Tatara, G. Effective Hamiltonian theory for nonreciprocal light propagation in magnetic Rashba conductor. Phys. Rev. B 2016, 94, 235148. [Google Scholar] [CrossRef]
- Watanabe, H.; Yanase, Y. Nonlinear electric transport in odd-parity magnetic multipole systems: Application to Mn-based compounds. Phys. Rev. Res. 2020, 2, 043081. [Google Scholar] [CrossRef]
- Watanabe, H.; Yanase, Y. Photocurrent response in parity-time symmetric current-ordered states. Phys. Rev. B 2021, 104, 024416. [Google Scholar] [CrossRef]
- Suzuki, Y. Tunneling spin current in systems with spin degeneracy. Phys. Rev. B 2022, 105, 075201. [Google Scholar] [CrossRef]
- Yatsushiro, M.; Oiwa, R.; Kusunose, H.; Hayami, S. Analysis of model-parameter dependences on the second-order nonlinear conductivity in PT-symmetric collinear antiferromagnetic metals with magnetic toroidal moment on zigzag chains. Phys. Rev. B 2022, 105, 155157. [Google Scholar] [CrossRef]
- Kondo, H.; Akagi, Y. Nonlinear magnon spin Nernst effect in antiferromagnets and strain-tunable pure spin current. Phys. Rev. Res. 2022, 4, 013186. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M.; Kusunose, H. Nonlinear spin Hall effect in PT-symmetric collinear magnets. Phys. Rev. B 2022, 106, 024405. [Google Scholar] [CrossRef]
- Mentink, S.A.M.; Drost, A.; Nieuwenhuys, G.J.; Frikkee, E.; Menovsky, A.A.; Mydosh, J.A. Magnetic Ordering and Frustration in Hexagonal UNi4B. Phys. Rev. Lett. 1994, 73, 1031–1034. [Google Scholar] [CrossRef]
- Oyamada, A.; Kondo, M.; Fukuoka, K.; Itou, T.; Maegawa, S.; Li, D.X.; Haga, Y. NMR studies of the partially disordered state in a triangular antiferromagnet UNi4B. J. Phys. Condens. Matter 2007, 19, 145246. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Matsumori, H.; Saito, H.; Hidaka, H.; Amitsuka, H.; Nakamura, S.; Awaji, S.; Gorbunov, D.I.; Zherlitsyn, S.; Wosnitza, J.; et al. Electric Quadrupolar Contributions in the Magnetic Phases of UNi4B. Phys. Rev. Lett. 2021, 126, 157201. [Google Scholar] [CrossRef]
- Ishitobi, T.; Hattori, K. Triple-Q partial magnetic orders induced by quadrupolar interactions: Triforce order scenario for UNi4B. Phys. Rev. B 2023, 107, 104413. [Google Scholar] [CrossRef]
- Saito, H.; Uenishi, K.; Miura, N.; Tabata, C.; Hidaka, H.; Yanagisawa, T.; Amitsuka, H. Evidence of a New Current-Induced Magnetoelectric Effect in a Toroidal Magnetic Ordered State of UNi4B. J. Phys. Soc. Jpn. 2018, 87, 033702. [Google Scholar] [CrossRef]
- Ota, K.; Shimozawa, M.; Muroya, T.; Miyamoto, T.; Hosoi, S.; Nakamura, A.; Homma, Y.; Honda, F.; Aoki, D.; Izawa, K. Zero-field current-induced Hall effect in ferrotoroidic metal. arXiv 2022, arXiv:2205.05555. [Google Scholar]
- Folen, V.J.; Rado, G.T.; Stalder, E.W. Anisotropy of the Magnetoelectric Effect in Cr2O3. Phys. Rev. Lett. 1961, 6, 607–608. [Google Scholar] [CrossRef]
- Krotov, S.; Kadomtseva, A.; Popov, Y.F.; Zvezdin, A.; Vorob’ev, G.; Belov, D. Magnetoelectric interactions and induced toroidal ordering in Cr2O3. J. Magn. Magn. Mater. 2001, 226, 963–964. [Google Scholar] [CrossRef]
- Arima, T.; Jung, J.H.; Matsubara, M.; Kubota, M.; He, J.P.; Kaneko, Y.; Tokura, Y. Resonant magnetoelectric X-ray scattering in GaFeO3: Observation of ordering of toroidal moments. J. Phys. Soc. Jpn. 2005, 74, 1419–1422. [Google Scholar] [CrossRef]
- Staub, U.; Bodenthin, Y.; Piamonteze, C.; García-Fernández, M.; Scagnoli, V.; Garganourakis, M.; Koohpayeh, S.; Fort, D.; Lovesey, S.W. Parity- and time-odd atomic multipoles in magnetoelectric GaFeO3 as seen via soft x-ray Bragg diffraction. Phys. Rev. B 2009, 80, 140410. [Google Scholar] [CrossRef]
- Staub, U.; Piamonteze, C.; Garganourakis, M.; Collins, S.P.; Koohpayeh, S.M.; Fort, D.; Lovesey, S.W. Ferromagnetic-type order of atomic multipoles in the polar ferrimagnetic GaFeO3. Phys. Rev. B 2012, 85, 144421. [Google Scholar] [CrossRef]
- Nie, Y.m. First-principles approach to investigate toroidal property of magnetoelectric multiferroic GaFeO3. J. Appl. Phys. 2016, 119. [Google Scholar] [CrossRef]
- Van Aken, B.B.; Rivera, J.P.; Schmid, H.; Fiebig, M. Observation of ferrotoroidic domains. Nature 2007, 449, 702–705. [Google Scholar] [CrossRef]
- Zimmermann, A.S.; Meier, D.; Fiebig, M. Ferroic nature of magnetic toroidal order. Nat. Commun. 2014, 5, 4796. [Google Scholar] [CrossRef]
- Fogh, E.; Zaharko, O.; Schefer, J.; Niedermayer, C.; Holm-Dahlin, S.; Sørensen, M.K.; Kristensen, A.B.; Andersen, N.H.; Vaknin, D.; Christensen, N.B.; et al. Dzyaloshinskii-Moriya interaction and the magnetic ground state in magnetoelectric LiCoPO4. Phys. Rev. B 2019, 99, 104421. [Google Scholar] [CrossRef]
- Tóth, B.; Kocsis, V.; Tokunaga, Y.; Taguchi, Y.; Tokura, Y.; Bordács, S. Imaging antiferromagnetic domains in LiCoPO4 via the optical magnetoelectric effect. Phys. Rev. B 2024, 110, L100405. [Google Scholar] [CrossRef]
- Murakawa, H.; Onose, Y.; Miyahara, S.; Furukawa, N.; Tokura, Y. Ferroelectricity Induced by Spin-Dependent Metal-Ligand Hybridization in Ba2CoGe2O7. Phys. Rev. Lett. 2010, 105, 137202. [Google Scholar] [CrossRef]
- Yamauchi, K.; Barone, P.; Picozzi, S. Theoretical investigation of magnetoelectric effects in Ba2CoGe2O7. Phys. Rev. B 2011, 84, 165137. [Google Scholar] [CrossRef]
- Toledano, P.; Khalyavin, D.D.; Chapon, L.C. Spontaneous toroidal moment and field-induced magnetotoroidic effects in Ba2CoGe2O7. Phys. Rev. B 2011, 84, 094421. [Google Scholar] [CrossRef]
- Hutanu, V.; Sazonov, A.; Murakawa, H.; Tokura, Y.; Náfrádi, B.; Chernyshov, D. Symmetry and structure of multiferroic Ba2CoGe2O7. Phys. Rev. B 2011, 84, 212101. [Google Scholar] [CrossRef]
- Baum, M.; Schmalzl, K.; Steffens, P.; Hiess, A.; Regnault, L.P.; Meven, M.; Becker, P.; Bohatý, L.; Braden, M. Controlling toroidal moments by crossed electric and magnetic fields. Phys. Rev. B 2013, 88, 024414. [Google Scholar] [CrossRef]
- Tolédano, P.; Ackermann, M.; Bohatý, L.; Becker, P.; Lorenz, T.; Leo, N.; Fiebig, M. Primary ferrotoroidicity in antiferromagnets. Phys. Rev. B 2015, 92, 094431. [Google Scholar] [CrossRef]
- Lee, C.; Kang, J.; Hong, J.; Shim, J.H.; Whangbo, M.H. Analysis of the difference between the pyroxenes LiFeSi2O6 and LiFeGe2O6 in their spin order, spin orientation, and ferrotoroidal order. Chem. Mater. 2014, 26, 1745–1750. [Google Scholar] [CrossRef]
- Wadley, P.; Novák, V.; Campion, R.; Rinaldi, C.; Martí, X.; Reichlová, H.; Železnỳ, J.; Gazquez, J.; Roldan, M.; Varela, M.; et al. Tetragonal phase of epitaxial room-temperature antiferromagnet CuMnAs. Nat. Commun. 2013, 4, 2322. [Google Scholar] [CrossRef]
- Wadley, P.; Howells, B.; Železnỳ, J.; Andrews, C.; Hills, V.; Campion, R.P.; Novák, V.; Olejník, K.; Maccherozzi, F.; Dhesi, S.; et al. Electrical switching of an antiferromagnet. Science 2016, 351, 587–590. [Google Scholar] [CrossRef]
- Godinho, J.; Reichlová, H.; Kriegner, D.; Novák, V.; Olejník, K.; Kašpar, Z.; Šobáň, Z.; Wadley, P.; Campion, R.; Otxoa, R.; et al. Electrically induced and detected Néel vector reversal in a collinear antiferromagnet. Nat. Commun. 2018, 9, 4686. [Google Scholar] [CrossRef]
- Manchon, A.; Železný, J.; Miron, I.M.; Jungwirth, T.; Sinova, J.; Thiaville, A.; Garello, K.; Gambardella, P. Current-induced spin-orbit torques in ferromagnetic and antiferromagnetic systems. Rev. Mod. Phys. 2019, 91, 035004. [Google Scholar] [CrossRef]
- Wang, C.; Gao, Y.; Xiao, D. Intrinsic Nonlinear Hall Effect in Antiferromagnetic Tetragonal CuMnAs. Phys. Rev. Lett. 2021, 127, 277201. [Google Scholar] [CrossRef]
- Ding, L.; Xu, X.; Jeschke, H.O.; Bai, X.; Feng, E.; Alemayehu, A.S.; Kim, J.; Huang, F.T.; Zhang, Q.; Ding, X.; et al. Field-tunable toroidal moment in a chiral-lattice magnet. Nat. Commun. 2021, 12, 5339. [Google Scholar] [CrossRef]
- Xu, X.; Huang, F.T.; Admasu, A.S.; Kratochvílová, M.; Chu, M.W.; Park, J.G.; Cheong, S.W. Multiple ferroic orders and toroidal magnetoelectricity in the chiral magnet BaCoSiO4. Phys. Rev. B 2022, 105, 184407. [Google Scholar] [CrossRef]
- Nakamura, R.; Aoki, I.; Kimura, K. Ferrotoroidic State Induced by Structural Rotation and Falsely Chiral Antiferromagnetism in PbMn2Ni6Te3O18. J. Phys. Soc. Jpn. 2024, 93, 063703. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous Multipole Ordering by Local Parity Mixing. J. Phys. Soc. Jpn. 2015, 84, 064717. [Google Scholar] [CrossRef]
- Cysne, T.P.; Guimarães, F.S.M.; Canonico, L.M.; Rappoport, T.G.; Muniz, R.B. Orbital magnetoelectric effect in zigzag nanoribbons of p-band systems. Phys. Rev. B 2021, 104, 165403. [Google Scholar] [CrossRef]
- Li, X.; Cao, T.; Niu, Q.; Shi, J.; Feng, J. Coupling the valley degree of freedom to antiferromagnetic order. Proc. Natl. Acad. Sci. USA 2013, 110, 3738–3742. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous parity breaking in spin-orbital coupled systems. Phys. Rev. B 2014, 90, 081115. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent spin-valley-orbital physics by spontaneous parity breaking. J. Phys. Condens. Matter 2016, 28, 395601. [Google Scholar] [CrossRef]
- Yanagi, Y.; Kusunose, H. Optical Selection Rules in Spin–Orbit Coupled Systems on Honeycomb Lattice. J. Phys. Soc. Jpn. 2017, 86, 083703. [Google Scholar] [CrossRef]
- Yanagi, Y.; Hayami, S.; Kusunose, H. Manipulating the magnetoelectric effect: Essence learned from Co4Nb2O9. Phys. Rev. B 2018, 97, 020404. [Google Scholar] [CrossRef]
- Oishi, R.; Umeo, K.; Shimura, Y.; Onimaru, T.; Strydom, A.M.; Takabatake, T. Antiferromagnetic order in the honeycomb Kondo lattice CePt6Al3 induced by Pd substitution. Phys. Rev. B 2021, 104, 104411. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent odd-parity multipoles and magnetoelectric effects on a diamond structure: Implication for the 5d transition metal oxides A OsO4 (A = K, Rb, and Cs). Phys. Rev. B 2018, 97, 024414. [Google Scholar] [CrossRef]
- Ishitobi, T.; Hattori, K. Magnetoelectric Effects and Charge-Imbalanced Solenoids: Antiferro Quadrupole Orders in a Diamond Structure. J. Phys. Soc. Jpn. 2019, 88, 063708. [Google Scholar] [CrossRef]
- Yamaura, J.i.; Hiroi, Z. Crystal structure and magnetic properties of the 5d transition metal oxides A OsO4 (A = K, Rb, Cs). Phys. Rev. B 2019, 99, 155113. [Google Scholar] [CrossRef]
- Paramekanti, A.; Maharaj, D.D.; Gaulin, B.D. Octupolar order in d-orbital Mott insulators. Phys. Rev. B 2020, 101, 054439. [Google Scholar] [CrossRef]
- Maharaj, D.D.; Sala, G.; Stone, M.B.; Kermarrec, E.; Ritter, C.; Fauth, F.; Marjerrison, C.A.; Greedan, J.E.; Paramekanti, A.; Gaulin, B.D. Octupolar versus Néel Order in Cubic 5d2 Double Perovskites. Phys. Rev. Lett. 2020, 124, 087206. [Google Scholar] [CrossRef]
- Winkler, R.; Zülicke, U. Theory of electric, magnetic, and toroidal polarizations in crystalline solids with applications to hexagonal lonsdaleite and cubic diamond. Phys. Rev. B 2023, 107, 155201. [Google Scholar] [CrossRef]
- Hitomi, T.; Yanase, Y. Electric Octupole Order in Bilayer Ruthenate Sr3Ru2O7. J. Phys. Soc. Jpn. 2014, 83, 114704. [Google Scholar] [CrossRef]
- Hitomi, T.; Yanase, Y. Electric octupole order in bilayer Rashba system. J. Phys. Soc. Jpn. 2016, 85, 124702. [Google Scholar] [CrossRef]
- Kirikoshi, A.; Hayami, S. Microscopic mechanism for intrinsic nonlinear anomalous Hall conductivity in noncollinear antiferromagnetic metals. Phys. Rev. B 2023, 107, 155109. [Google Scholar] [CrossRef]
- Yatsushiro, M.; Kusunose, H.; Hayami, S. Multipole classification in 122 magnetic point groups for unified understanding of multiferroic responses and transport phenomena. Phys. Rev. B 2021, 104, 054412. [Google Scholar] [CrossRef]
- Kusunose, H.; Oiwa, R.; Hayami, S. Symmetry-adapted modeling for molecules and crystals. Phys. Rev. B 2023, 107, 195118. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Time-reversal switching responses in antiferromagnets. Phys. Rev. B 2023, 108, L140409. [Google Scholar] [CrossRef]
- Tokura, Y.; Nagaosa, N. Nonreciprocal responses from non-centrosymmetric quantum materials. Nat. Commun. 2018, 9, 3740. [Google Scholar] [CrossRef] [PubMed]
- Baltz, V.; Manchon, A.; Tsoi, M.; Moriyama, T.; Ono, T.; Tserkovnyak, Y. Antiferromagnetic spintronics. Rev. Mod. Phys. 2018, 90, 015005. [Google Scholar] [CrossRef]
- Solovyev, I.V. Magneto-optical effect in the weak ferromagnets LaMO3 (M= Cr, Mn, and Fe). Phys. Rev. B 1997, 55, 8060–8063. [Google Scholar] [CrossRef]
- Chen, H.; Niu, Q.; MacDonald, A.H. Anomalous Hall Effect Arising from Noncollinear Antiferromagnetism. Phys. Rev. Lett. 2014, 112, 017205. [Google Scholar] [CrossRef]
- Chen, H.; Wang, T.C.; Xiao, D.; Guo, G.Y.; Niu, Q.; MacDonald, A.H. Manipulating anomalous Hall antiferromagnets with magnetic fields. Phys. Rev. B 2020, 101, 104418. [Google Scholar] [CrossRef]
- Kurita, K.; Koretsune, T. X-ray Magnetic Circular Dichroism Arising from the Magnetic Dipole Moment in Antiferromagnets. J. Phys. Soc. Jpn. 2024, 93, 024705. [Google Scholar] [CrossRef]
- Nakatsuji, S.; Kiyohara, N.; Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 2015, 527, 212. [Google Scholar] [CrossRef]
- Suzuki, M.T.; Koretsune, T.; Ochi, M.; Arita, R. Cluster multipole theory for anomalous Hall effect in antiferromagnets. Phys. Rev. B 2017, 95, 094406. [Google Scholar] [CrossRef]
- Ikhlas, M.; Tomita, T.; Koretsune, T.; Suzuki, M.T.; Nishio-Hamane, D.; Arita, R.; Otani, Y.; Nakatsuji, S. Large anomalous Nernst effect at room temperature in a chiral antiferromagnet. Nat. Phys. 2017, 13, 1085. [Google Scholar] [CrossRef]
- Kuroda, K.; Tomita, T.; Suzuki, M.T.; Bareille, C.; Nugroho, A.; Goswami, P.; Ochi, M.; Ikhlas, M.; Nakayama, M.; Akebi, S.; et al. Evidence for magnetic Weyl fermions in a correlated metal. Nat. Mater. 2017, 16, 1090. [Google Scholar] [CrossRef]
- Higo, T.; Man, H.; Gopman, D.B.; Wu, L.; Koretsune, T.; van’t Erve, O.M.; Kabanov, Y.P.; Rees, D.; Li, Y.; Suzuki, M.T.; et al. Large magneto-optical Kerr effect and imaging of magnetic octupole domains in an antiferromagnetic metal. Nat. Photonics 2018, 12, 73. [Google Scholar] [CrossRef] [PubMed]
- Kimata, M.; Sasabe, N.; Kurita, K.; Yamasaki, Y.; Tabata, C.; Yokoyama, Y.; Kotani, Y.; Ikhlas, M.; Tomita, T.; Amemiya, K.; et al. X-ray study of ferroic octupole order producing anomalous Hall effect. Nat. Commun. 2021, 12, 5582. [Google Scholar] [CrossRef] [PubMed]
- Gurung, G.; Shao, D.F.; Paudel, T.R.; Tsymbal, E.Y. Anomalous Hall conductivity of noncollinear magnetic antiperovskites. Phys. Rev. Mater. 2019, 3, 044409. [Google Scholar] [CrossRef]
- Zhou, X.; Hanke, J.P.; Feng, W.; Li, F.; Guo, G.Y.; Yao, Y.; Blügel, S.; Mokrousov, Y. Spin-order dependent anomalous Hall effect and magneto-optical effect in the noncollinear antiferromagnets Mn3XN with X = Ga, Zn, Ag, or Ni. Phys. Rev. B 2019, 99, 104428. [Google Scholar] [CrossRef]
- Boldrin, D.; Samathrakis, I.; Zemen, J.; Mihai, A.; Zou, B.; Johnson, F.; Esser, B.D.; McComb, D.W.; Petrov, P.K.; Zhang, H.; et al. Anomalous Hall effect in noncollinear antiferromagnetic Mn3NiN thin films. Phys. Rev. Mater. 2019, 3, 094409. [Google Scholar] [CrossRef]
- Huyen, V.T.N.; Suzuki, M.T.; Yamauchi, K.; Oguchi, T. Topology analysis for anomalous Hall effect in the noncollinear antiferromagnetic states of Mn3 AN (A = Ni, Cu, Zn, Ga, Ge, Pd, In, Sn, Ir, Pt). Phys. Rev. B 2019, 100, 094426. [Google Scholar] [CrossRef]
- You, Y.; Bai, H.; Feng, X.; Fan, X.; Han, L.; Zhou, X.; Zhou, Y.; Zhang, R.; Chen, T.; Pan, F.; et al. Cluster magnetic octupole induced out-of-plane spin polarization in antiperovskite antiferromagnet. Nat. Commun. 2021, 12, 6524. [Google Scholar] [CrossRef]
- Kotegawa, H.; Kuwata, Y.; Huyen, V.T.N.; Arai, Y.; Tou, H.; Matsuda, M.; Takeda, K.; Sugawara, H.; Suzuki, M.T. Large anomalous Hall effect and unusual domain switching in an orthorhombic antiferromagnetic material NbMnP. npj Quantum Mater. 2023, 8, 56. [Google Scholar] [CrossRef]
- Arai, Y.; Hayashi, J.; Takeda, K.; Tou, H.; Sugawara, H.; Kotegawa, H. Intrinsic Anomalous Hall Effect Arising from Antiferromagnetism as Revealed by High-Quality NbMnP. J. Phys. Soc. Jpn. 2024, 93, 063702. [Google Scholar] [CrossRef]
- Tomizawa, T.; Kontani, H. Anomalous Hall effect in the t2g orbital kagome lattice due to noncollinearity: Significance of the orbital Aharonov-Bohm effect. Phys. Rev. B 2009, 80, 100401. [Google Scholar] [CrossRef]
- Kim, W.J.; Oh, T.; Song, J.; Ko, E.K.; Li, Y.; Mun, J.; Kim, B.; Son, J.; Yang, Z.; Kohama, Y.; et al. Strain engineering of the magnetic multipole moments and anomalous Hall effect in pyrochlore iridate thin films. Sci. Adv. 2020, 6, eabb1539. [Google Scholar] [CrossRef] [PubMed]
- Sivadas, N.; Okamoto, S.; Xiao, D. Gate-Controllable Magneto-optic Kerr Effect in Layered Collinear Antiferromagnets. Phys. Rev. Lett. 2016, 117, 267203. [Google Scholar] [CrossRef] [PubMed]
- Naka, M.; Hayami, S.; Kusunose, H.; Yanagi, Y.; Motome, Y.; Seo, H. Anomalous Hall effect in κ-type organic antiferromagnets. Phys. Rev. B 2020, 102, 075112. [Google Scholar] [CrossRef]
- Kotegawa, H.; Tanaka, H.; Takeuchi, Y.; Tou, H.; Sugawara, H.; Hayashi, J.; Takeda, K. Large Anomalous Hall Conductivity Derived from an f-Electron Collinear Antiferromagnetic Structure. Phys. Rev. Lett. 2024, 133, 106301. [Google Scholar] [CrossRef] [PubMed]
- Šmejkal, L.; González-Hernández, R.; Jungwirth, T.; Sinova, J. Crystal time-reversal symmetry breaking and spontaneous Hall effect in collinear antiferromagnets. Sci. Adv. 2020, 6, eaaz8809. [Google Scholar] [CrossRef]
- Yamasaki, Y.; Nakao, H.; Arima, T.h. Augmented Magnetic Octupole in Kagomé 120-degree Antiferromagnets Detectable via X-ray Magnetic Circular Dichroism. J. Phys. Soc. Jpn. 2020, 89, 083703. [Google Scholar] [CrossRef]
- Akiba, K.; Iwamoto, K.; Sato, T.; Araki, S.; Kobayashi, T.C. Anomalous Hall effect triggered by pressure-induced magnetic phase transition in α-Mn. Phys. Rev. Res. 2020, 2, 043090. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Essential role of the anisotropic magnetic dipole in the anomalous Hall effect. Phys. Rev. B 2021, 103, L180407. [Google Scholar] [CrossRef]
- Chen, H. Electronic chiralization as an indicator of the anomalous Hall effect in unconventional magnetic systems. Phys. Rev. B 2022, 106, 024421. [Google Scholar] [CrossRef]
- Lei, C.; Trevisan, T.V.; Heinonen, O.; McQueeney, R.J.; MacDonald, A.H. Quantum anomalous Hall effect in perfectly compensated collinear antiferromagnetic thin films. Phys. Rev. B 2022, 106, 195433. [Google Scholar] [CrossRef]
- Sasabe, N.; Kimata, M.; Nakamura, T. Presence of X-Ray Magnetic Circular Dichroism Signal for Zero-Magnetization Antiferromagnetic State. Phys. Rev. Lett. 2021, 126, 157402. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez Betancourt, R.D.; Zubáč, J.; Gonzalez-Hernandez, R.; Geishendorf, K.; Šobáň, Z.; Springholz, G.; Olejník, K.; Šmejkal, L.; Sinova, J.; Jungwirth, T.; et al. Spontaneous Anomalous Hall Effect Arising from an Unconventional Compensated Magnetic Phase in a Semiconductor. Phys. Rev. Lett. 2023, 130, 036702. [Google Scholar] [CrossRef] [PubMed]
- Sasabe, N.; Mizumaki, M.; Uozumi, T.; Yamasaki, Y. Ferroic Order for Anisotropic Magnetic Dipole Term in Collinear Antiferromagnets of (t2g)4 System. Phys. Rev. Lett. 2023, 131, 216501. [Google Scholar] [CrossRef]
- Attias, L.; Levchenko, A.; Khodas, M. Intrinsic anomalous Hall effect in altermagnets. Phys. Rev. B 2024, 110, 094425. [Google Scholar] [CrossRef]
- Hariki, A.; Dal Din, A.; Amin, O.J.; Yamaguchi, T.; Badura, A.; Kriegner, D.; Edmonds, K.W.; Campion, R.P.; Wadley, P.; Backes, D.; et al. X-Ray Magnetic Circular Dichroism in Altermagnetic α-MnTe. Phys. Rev. Lett. 2024, 132, 176701. [Google Scholar] [CrossRef]
| Irrep. | Multipole | FM Stacking | AFM Stacking | Note |
|---|---|---|---|---|
| − | x | |||
| − | y | |||
| − | z | AFMT | ||
| − | − | |||
| y | − | |||
| x | − | |||
| − | − | |||
| z | − | FMT |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayami, S. Spontaneous Magnetization Induced by Antiferromagnetic Toroidal Ordering. Nanomaterials 2024, 14, 1729. https://doi.org/10.3390/nano14211729
Hayami S. Spontaneous Magnetization Induced by Antiferromagnetic Toroidal Ordering. Nanomaterials. 2024; 14(21):1729. https://doi.org/10.3390/nano14211729
Chicago/Turabian StyleHayami, Satoru. 2024. "Spontaneous Magnetization Induced by Antiferromagnetic Toroidal Ordering" Nanomaterials 14, no. 21: 1729. https://doi.org/10.3390/nano14211729
APA StyleHayami, S. (2024). Spontaneous Magnetization Induced by Antiferromagnetic Toroidal Ordering. Nanomaterials, 14(21), 1729. https://doi.org/10.3390/nano14211729







