Design and Simulation for Minimizing Non-Radiative Recombination Losses in CsGeI2Br Perovskite Solar Cells
Abstract
1. Introduction
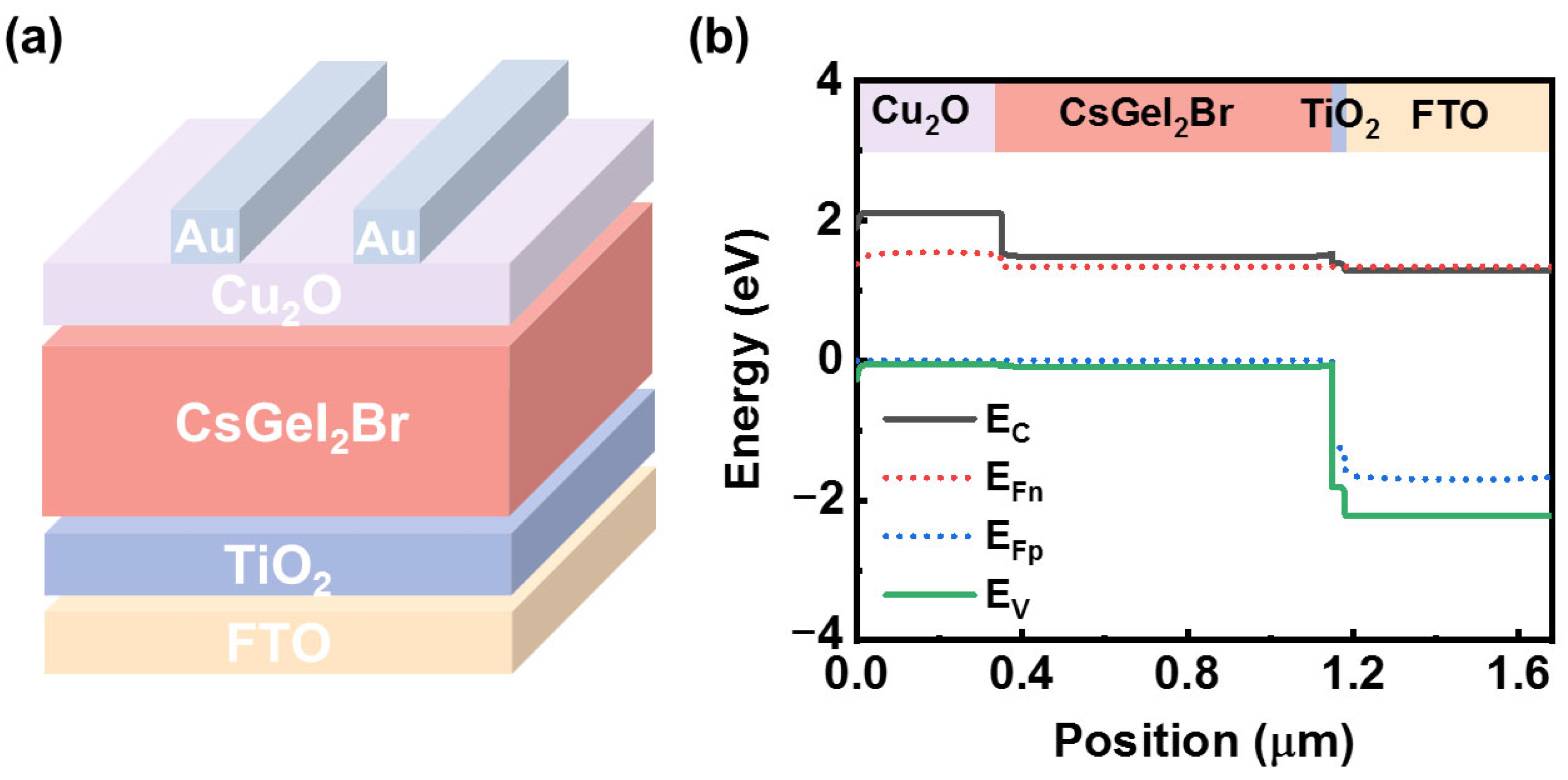
2. Theoretical Methods
3. Results and Discussion
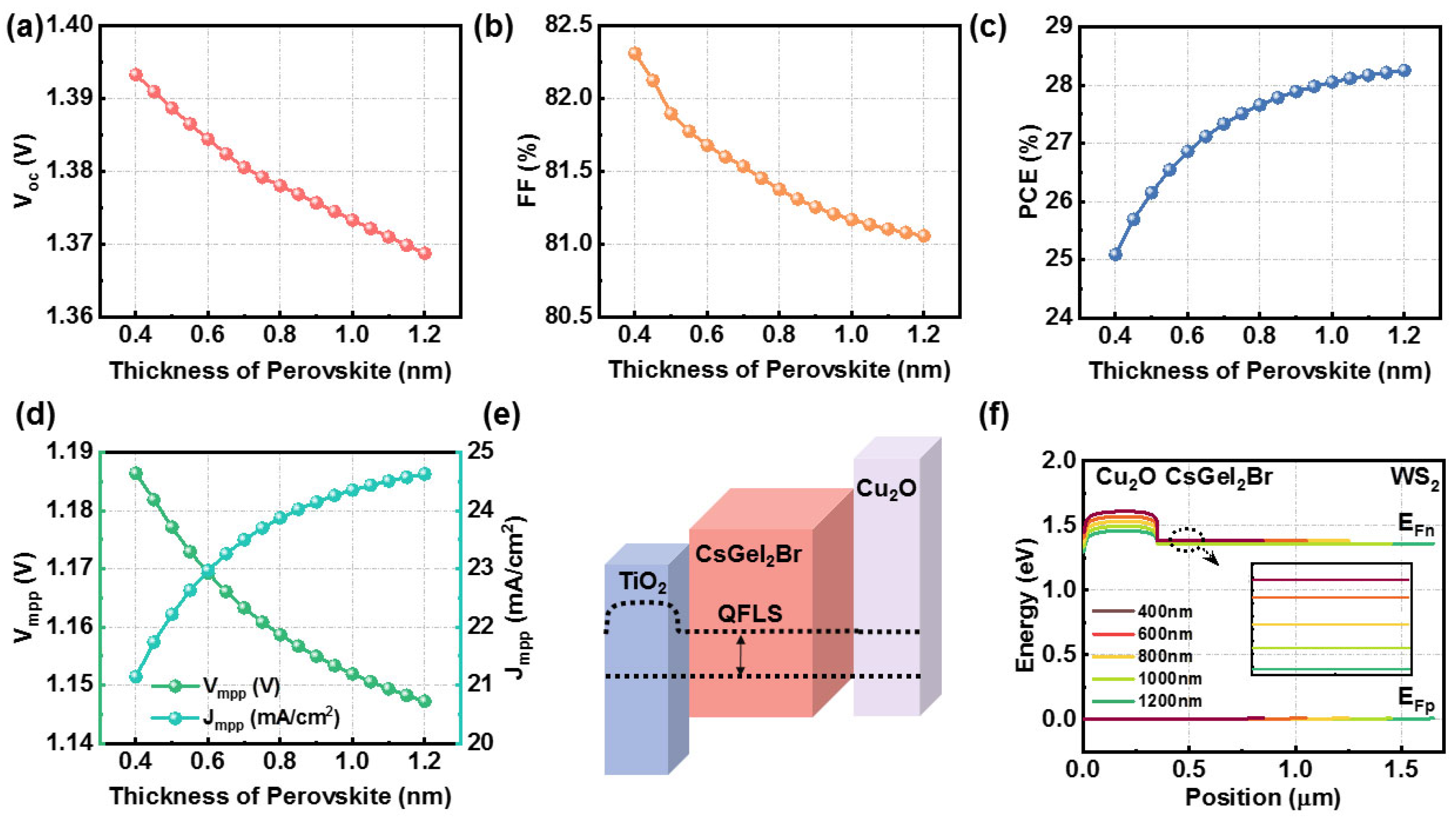
3.1. Dependence of Perovskite Thickness
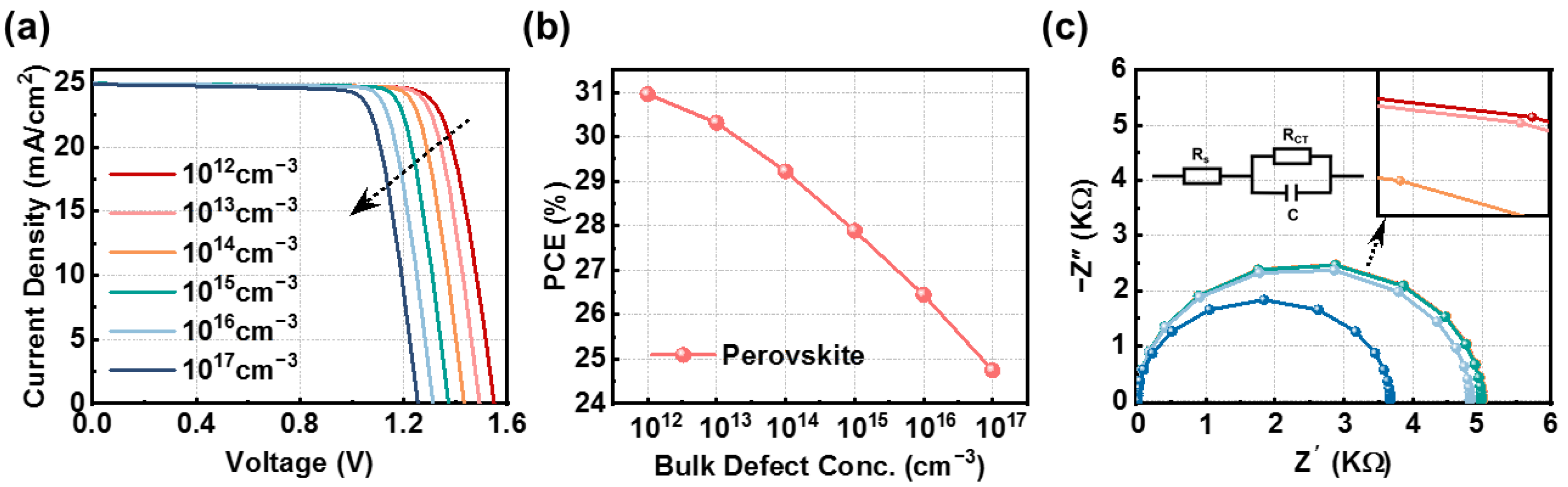
3.2. Dependence of Perovskite Bulk Defect Density
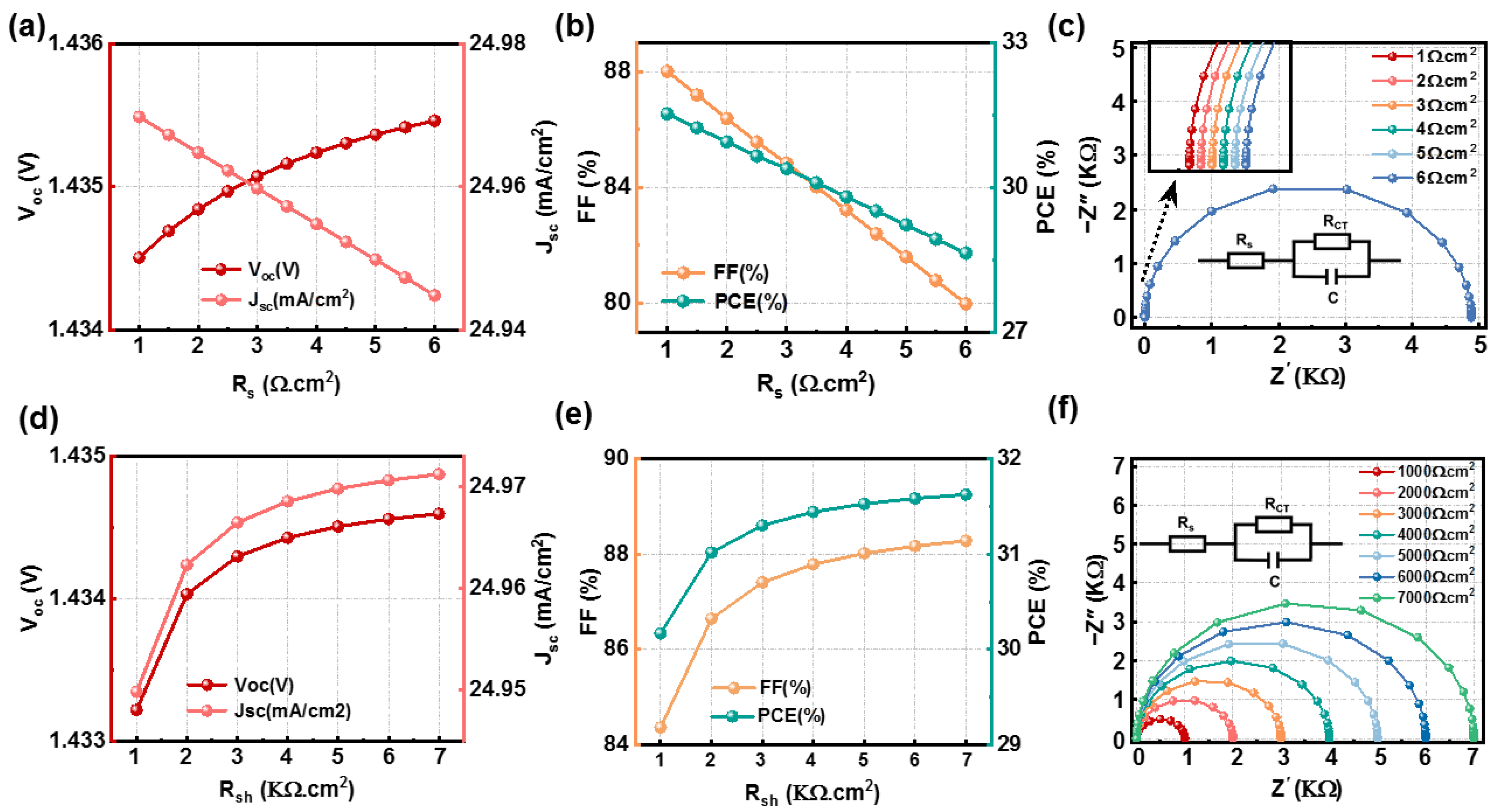
3.3. Dependence of Perovskite Series and Shunt Resistance
3.4. Dependence of Perovskite Auger Recombination
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, M.; Johnston, M.B.; Snaith, H.J. Efficient planar heterojunction perovskite solar cells by vapour deposition. Nature 2013, 501, 395–398. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhou, H.; Hu, J.; Huang, B.; Sun, M.; Dong, B.; Zheng, G.; Huang, Y.; Chen, Y.; Li, L. A Eu3+-Eu2+ ion redox shuttle imparts operational durability to Pb-I perovskite solar cells. Science 2019, 363, 265–270. [Google Scholar] [CrossRef] [PubMed]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef] [PubMed]
- Jeon, N.J.; Na, H.; Jung, E.H.; Yang, T.-Y.; Lee, Y.G.; Kim, G.; Shin, H.-W.; Il Seok, S.; Lee, J.; Seo, J. A fluorene-terminated hole-transporting material for highly efficient and stable perovskite solar cells. Nat. Energy 2018, 3, 682–689. [Google Scholar] [CrossRef]
- Li, Q.; Liu, H.; Hou, C.-H.; Yan, H.; Li, S.; Chen, P.; Xu, H.; Yu, W.-Y.; Zhao, Y.; Sui, Y.; et al. Harmonizing the bilateral bond strength of the interfacial molecule in perovskite solar cells. Nat. Energy 2024, 1–11. [Google Scholar] [CrossRef]
- Zhou, S.; Fu, S.; Wang, C.; Meng, W.; Zhou, J.; Zou, Y.; Lin, Q.; Huang, L.; Zhang, W.; Zeng, G.; et al. Aspartate all-in-one doping strategy enables efficient all-perovskite tandems. Nature 2023, 624, 69–73. [Google Scholar] [CrossRef]
- Liu, J.; He, Y.; Ding, L.; Zhang, H.; Li, Q.; Jia, L.; Yu, J.; Lau, T.W.; Li, M.; Qin, Y. Perovskite-silicon tandem solar cells with bilayer interface passivation. Nature 2024, 1–3. [Google Scholar] [CrossRef]
- Xu, J.; Castriotta, L.A.; Di Carlo, A.; Brown, T.M. Air-stable lead-free antimony-based perovskite inspired solar cells and modules. ACS Energy Lett. 2024, 9, 671–678. [Google Scholar] [CrossRef]
- Abate, A. Perovskite solar cells go lead free. Joule 2017, 1, 659–664. [Google Scholar] [CrossRef]
- Guerrero, A.; Bisquert, J.; Garcia-Belmonte, G. Impedance spectroscopy of metal halide perovskite solar cells from the perspective of equivalent circuits. Chem. Rev. 2021, 121, 14430–14484. [Google Scholar] [CrossRef]
- Sarkar, J.; Talukdar, A.; Debnath, P.; Chatterjee, S. Study of bromine substitution on band gap broadening with consequent blue shift in optical properties and efficiency optimization of lead-free CsGeIXBr3−X based perovskite solar cells. J. Comput. Electron. 2023, 22, 1075–1088. [Google Scholar] [CrossRef]
- Duan, C.; Zou, F.; Wen, Q.; Qin, M.; Li, J.; Chen, C.; Lu, X.; Ding, L.; Yan, K. A bifunctional carbazide additive for durable CsSnI3 perovskite solar cells. Adv. Mater. 2023, 35, 2300503. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Park, N.G. Causes and solutions of recombination in perovskite solar cells. Adv. Mater. 2019, 31, 1803019. [Google Scholar] [CrossRef] [PubMed]
- Tress, W.; Yavari, M.; Domanski, K.; Yadav, P.; Niesen, B.; Baena, J.P.C.; Hagfeldt, A.; Graetzel, M. Interpretation and evolution of open-circuit voltage, recombination, ideality factor and subgap defect states during reversible light-soaking and irreversible degradation of perovskite solar cells. Energy Environ. Sci. 2018, 11, 151–165. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, K. Charge transport and recombination in perovskite (CH3NH3)PbI3 sensitized TiO2 solar cells. J. Phys. Chem. Lett 2013, 4, 2880–2884. [Google Scholar] [CrossRef]
- Agiorgousis, M.L.; Sun, Y.-Y.; Zeng, H.; Zhang, S. Strong covalency-induced recombination centers in perovskite solar cell material CH3NH3PbI3. J. Am. Chem. Soc. 2014, 136, 14570–14575. [Google Scholar] [CrossRef] [PubMed]
- Wolff, C.M.; Zu, F.; Paulke, A.; Toro, L.P.; Koch, N.; Neher, D. Reduced interface-mediated recombination for high open-circuit voltages in CH3NH3PbI3 solar cells. Adv. Mater. 2017, 29, 1700159. [Google Scholar] [CrossRef]
- Liu, Y.; Akin, S.; Pan, L.; Uchida, R.; Arora, N.; Milić, J.V.; Hinderhofer, A.; Schreiber, F.; Uhl, A.R.; Zakeeruddin, S.M. Ultrahydrophobic 3D/2D fluoroarene bilayer-based water-resistant perovskite solar cells with efficiencies exceeding 22%. Sci. Adv. 2019, 5, eaaw2543. [Google Scholar] [CrossRef]
- Aydin, E.; De Bastiani, M.; De Wolf, S. Defect and contact passivation for perovskite solar cells. Adv. Mater. 2019, 31, 1900428. [Google Scholar] [CrossRef]
- Alsalme, A.; Alsaeedi, H. Twenty-two percent efficient Pb-free all-perovskite tandem solar cells using SCAPS-1D. Nanomaterials 2023, 13, 96. [Google Scholar] [CrossRef]
- Gregg, B.A.; Hanna, M.C. Comparing organic to inorganic photovoltaic cells: Theory, experiment, and simulation. J. Appl. Phys. 2003, 93, 3605–3614. [Google Scholar] [CrossRef]
- Shi, M.; Li, M. Semiconductor Devices: Physics and Technology, 3rd ed.; Soochow University Press: Suzhou, China, 2014; pp. 52–60. [Google Scholar]
- Salem, M.S.; Shaker, A.; Othman, M.S.; Al-Bagawia, A.H.; Fedawy, M.; Aleid, G.M. Numerical analysis and design of high performance HTL-free antimony sulfide solar cells by SCAPS-1D. Opt. Mater. 2022, 123, 111880. [Google Scholar] [CrossRef]
- Abdelaziz, S.; Zekry, A.; Shaker, A.; Abouelatta, M. Investigating the performance of formamidinium tin-based perovskite solar cell by SCAPS device simulation. Opt. Mater. 2020, 101, 109738. [Google Scholar] [CrossRef]
- Karthick, S.; Bouclé, J.; Velumani, S. Effect of bismuth iodide (BiI3) interfacial layer with different HTL’s in FAPI based perovskite solar cell–SCAPS–1D study. Sol. Energy 2021, 218, 157–168. [Google Scholar] [CrossRef]
- He, Y.; Xu, L.; Yang, C.; Guo, X.; Li, S. Design and numerical investigation of a lead-free inorganic layered double perovskite Cs4CuSb2Cl12 nanocrystal solar cell by SCAPS-1D. Nanomaterials 2021, 11, 2321. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.Y.; Gangishetty, M.K.; Kelly, T.L. Effect of CH3NH3PbI3 thickness on device efficiency in planar heterojunction perovskite solar cells. J. Mater. Chem. A 2014, 2, 19873–19881. [Google Scholar] [CrossRef]
- Alharbi, S.R.; Darwish, A.A.A.; Al Garni, S.E.; ElSaeedy, H.I.; Abd El-Rahman, K.F. Influence of thickness and annealing on linear and nonlinear optical properties of manganese (III) chloride tetraphenyl porphine (MnTPPCl). Infrared Phys. Technol. 2016, 78, 77–83. [Google Scholar] [CrossRef]
- Mandadapu, U.; Vedanayakam, S.V.; Thyagarajan, K. Simulation and analysis of lead based perovskite solar cell using SCAPS-1D. Indian J. Sci. Technol. 2017, 10, 65–72. [Google Scholar] [CrossRef]
- Caprioglio, P.; Stolterfoht, M.; Wolff, C.M.; Unold, T.; Rech, B.; Albrecht, S.; Neher, D. On the relation between the open-circuit voltage and quasi-fermi level splitting in efficient perovskite solar cells. Adv. Energy Mater. 2019, 9, 1901631. [Google Scholar] [CrossRef]
- He, M.; Li, B.; Cui, X.; Jiang, B.; He, Y.; Chen, Y.; O’Neil, D.; Szymanski, P.; Ei-Sayed, M.A.; Huang, J. Meniscus-assisted solution printing of large-grained perovskite films for high-efficiency solar cells. Nat. Commun. 2017, 8, 16045. [Google Scholar] [CrossRef]
- Liang, Z.; Xu, H.; Zhang, Y.; Liu, G.; Chu, S.; Tao, Y.; Xu, X.; Xu, S.; Zhang, L.; Chen, X. A Selective Targeting Anchor Strategy Affords Efficient and Stable Ideal-Bandgap Perovskite Solar Cells. Adv. Mater. 2022, 34, 2110241. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Yan, G.; Hong, R.; Liang, Z.; Kirchartz, T. Quantifying efficiency limitations in all-inorganic halide perovskite solar cells. Adv. Mater. 2022, 34, 2108132. [Google Scholar] [CrossRef] [PubMed]
- Green, M.A.; Ho-Baillie, A.W.Y. Pushing to the limit: Radiative efficiencies of recent mainstream and emerging solar cells. ACS Energy Lett. 2019, 4, 1639–1644. [Google Scholar] [CrossRef]
- Chang, B.-Y.; Park, S.-M. Electrochemical impedance spectroscopy. Annu. Rev. Anal. Chem. 2010, 3, 207–229. [Google Scholar] [CrossRef]
- Vivier, V.; Orazem, M.E. Impedance analysis of electrochemical systems. Chem. Rev. 2022, 122, 11131–11168. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.S.; Wang, L.C.; Li, D.Z.; Wang, K. State-of-health estimation of lithium-ion batteries based on electrochemical impedance spectroscopy: A review. Prot. Control Mod. Power Syst. 2023, 8, 1–17. [Google Scholar] [CrossRef]
- Yoo, S.M.; Yoon, S.J.; Anta, J.A.; Lee, H.J.; Boix, P.P.; Mora-Seró, I. An equivalent circuit for perovskite solar cell bridging sensitized to thin film architectures. Joule 2019, 3, 2535–2549. [Google Scholar] [CrossRef]
- Galatopoulos, F.; Savva, A.; Papadas, I.T.; Choulis, S.A. The effect of hole transporting layer in charge accumulation properties of pin perovskite solar cells. APL Mater. 2017, 5, 076102. [Google Scholar] [CrossRef]
- Mundhaas, N.; Yu, Z.J.; Bush, K.A.; Wang, H.P.; Häusele, J.; Kavadiya, S.; McGehee, M.D.; Holman, Z.C. Series resistance measurements of perovskite solar cells using Jsc–Voc measurements. Solar RRL 2019, 3, 1800378. [Google Scholar] [CrossRef]
- Bi, Z.; Zhang, S.; Thandapani, M.; Zhu, Y.; Zheng, Y.; Liem, N.Q.; Xiao, X.; Xu, G.; Guerrero, A.; Xu, X. High shunt resistance SnO2-PbO electron transport layer for perovskite solar cells used in low lighting applications. Adv. Sustain. Syst. 2021, 5, 2100120. [Google Scholar] [CrossRef]
- Luo, D.; Su, R.; Zhang, W.; Gong, Q.; Zhu, R. Minimizing non-radiative recombination losses in perovskite solar cells. Nat. Rev. Mater. 2020, 5, 44–60. [Google Scholar] [CrossRef]
- Al-Mousoi, A.K.; Mohammed, M.K.; Kumar, A.; Pandey, R.; Madan, J.; Dastan, D.; Hossain, M.K.; Sakthivel, P.; Yaseen, Z.M. Understanding Auger recombination in perovskite solar cells. Phys. Chem. Chem. Phys. 2023, 25, 16459–16468. [Google Scholar] [CrossRef] [PubMed]

| Material Parameters | FTO [23] | TiO2 [24] | Cu2O [25,26] | CsGeI2Br [11] |
|---|---|---|---|---|
| Thickness (nm) | 500 | 30 | 350 | 800 |
| Band gap, Eg (eV) | 3.5 | 3.2 | 2.17 | 1.579 |
| Electron affinity (eV) | 4.0 | 3.9 | 3.2 | 3.76 |
| Dielectric permittivity (relative) | 9.0 | 9.0 | 7.1 | 18.0 |
| CB effective density of states (1/cm3) | 2.2 × 1018 | 2 × 1018 | 2.02 × 1017 | 9.65 × 1017 |
| VB effective density of states (1/cm3) | 1.8 × 1019 | 1.8 × 1019 | 1.1 × 1019 | 1.04 × 1018 |
| Electron thermal velocity (cm/s) | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| Hole thermal velocity (cm/s) | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| Electron mobility (cm3/Vs)) | 20 | 20 | 200 | 20 |
| Hole mobility (cm3/Vs) | 10 | 10 | 80 | 20 |
| Shallow uniform donor density ND (1/cm3) | 1.8 × 1019 | 9 × 1016 | 0 | 0 |
| Shallow uniform acceptor density NA (1/cm3) Total density (1/cm3) | 0 | 0 | 1 × 1018 | 2 × 1016 |
| 1 × 1015 | 1 × 1015 | 1 × 1015 | 1 × 1015 |
| Interface | Defect Type | Capture Cross Section: Electrons/Holes (cm2) | Energetic Distribution | Reference for Defect Energy Level | Total Density (cm−3) |
|---|---|---|---|---|---|
| ETL/CsGeI2Br | neutral | 1 × 10−19/1 × 10−19 | single | above the VB maximum | 1 × 1010 |
| CsGeI2Br/HTL | neutral | 1 × 10−19/1 × 10−19 | single | above the VB maximum | 1 × 1010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, T.; Huang, X.; Zhang, D.; Liu, W.; Li, X. Design and Simulation for Minimizing Non-Radiative Recombination Losses in CsGeI2Br Perovskite Solar Cells. Nanomaterials 2024, 14, 1650. https://doi.org/10.3390/nano14201650
Zhou T, Huang X, Zhang D, Liu W, Li X. Design and Simulation for Minimizing Non-Radiative Recombination Losses in CsGeI2Br Perovskite Solar Cells. Nanomaterials. 2024; 14(20):1650. https://doi.org/10.3390/nano14201650
Chicago/Turabian StyleZhou, Tingxue, Xin Huang, Diao Zhang, Wei Liu, and Xing’ao Li. 2024. "Design and Simulation for Minimizing Non-Radiative Recombination Losses in CsGeI2Br Perovskite Solar Cells" Nanomaterials 14, no. 20: 1650. https://doi.org/10.3390/nano14201650
APA StyleZhou, T., Huang, X., Zhang, D., Liu, W., & Li, X. (2024). Design and Simulation for Minimizing Non-Radiative Recombination Losses in CsGeI2Br Perovskite Solar Cells. Nanomaterials, 14(20), 1650. https://doi.org/10.3390/nano14201650





