Simulation and Experimental Investigation of the Effect of Pore Shape on Heat Transfer Behavior of Phase Change Materials in Porous Metal Structures
Abstract
1. Introduction
2. Numerical Simulation
2.1. Physical Model
2.2. Governing Equations
2.3. Initial and Boundary Conditions
2.4. Problem Setup
3. Experimental Section
3.1. Materials
3.2. Fabrication of the Porous Metal Structures
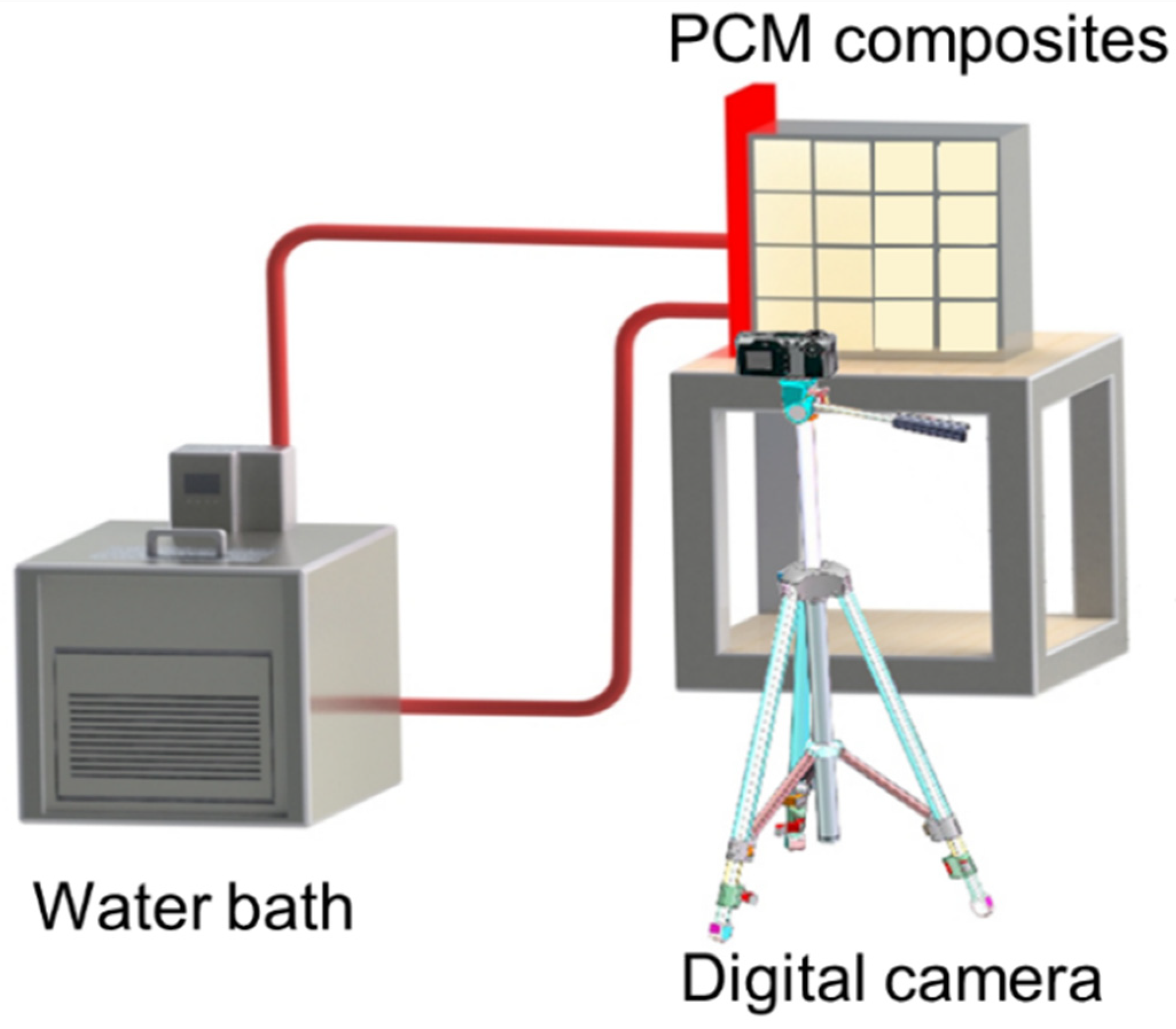
3.3. Experimental System
4. Result and Discussion
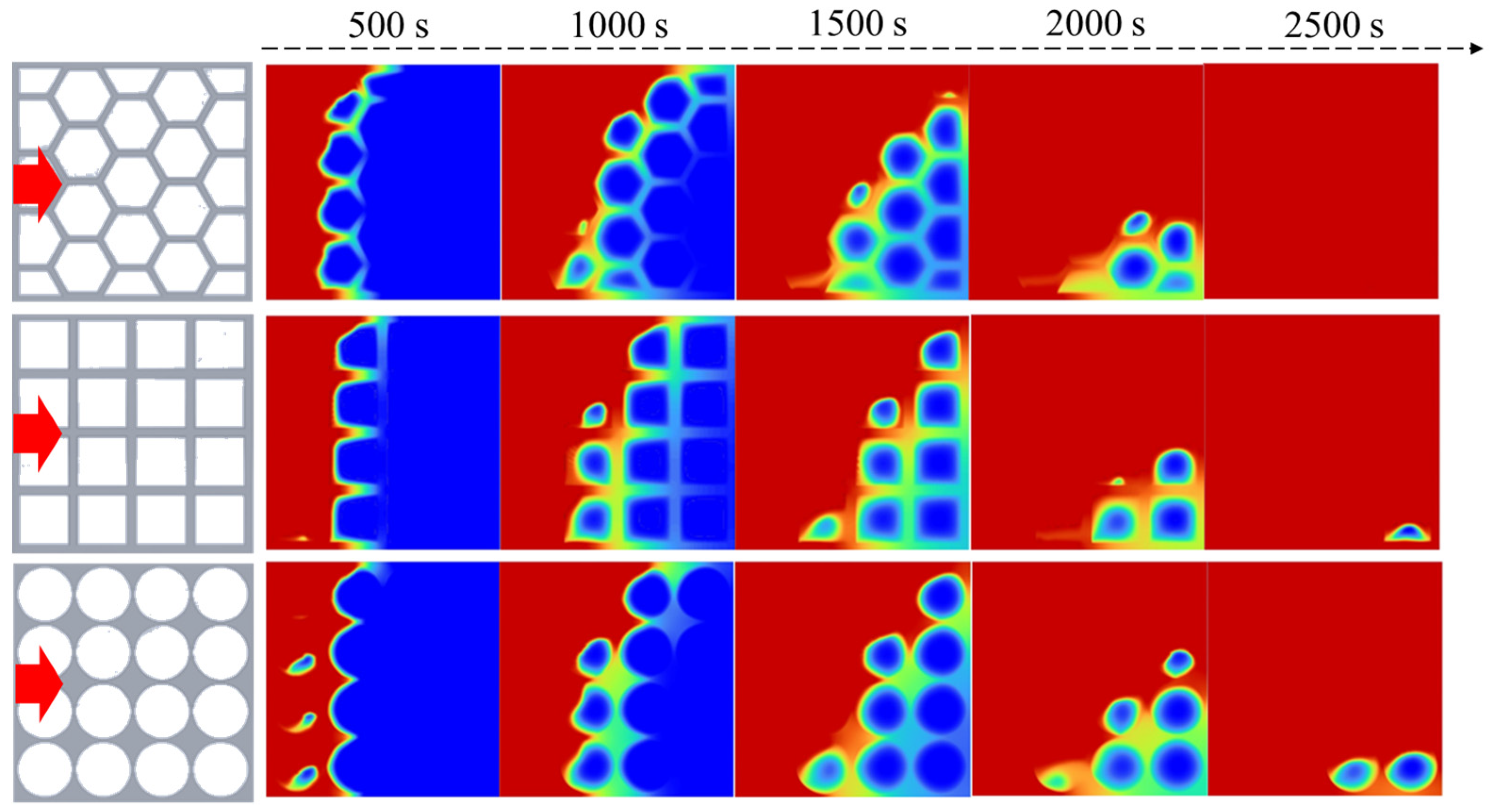
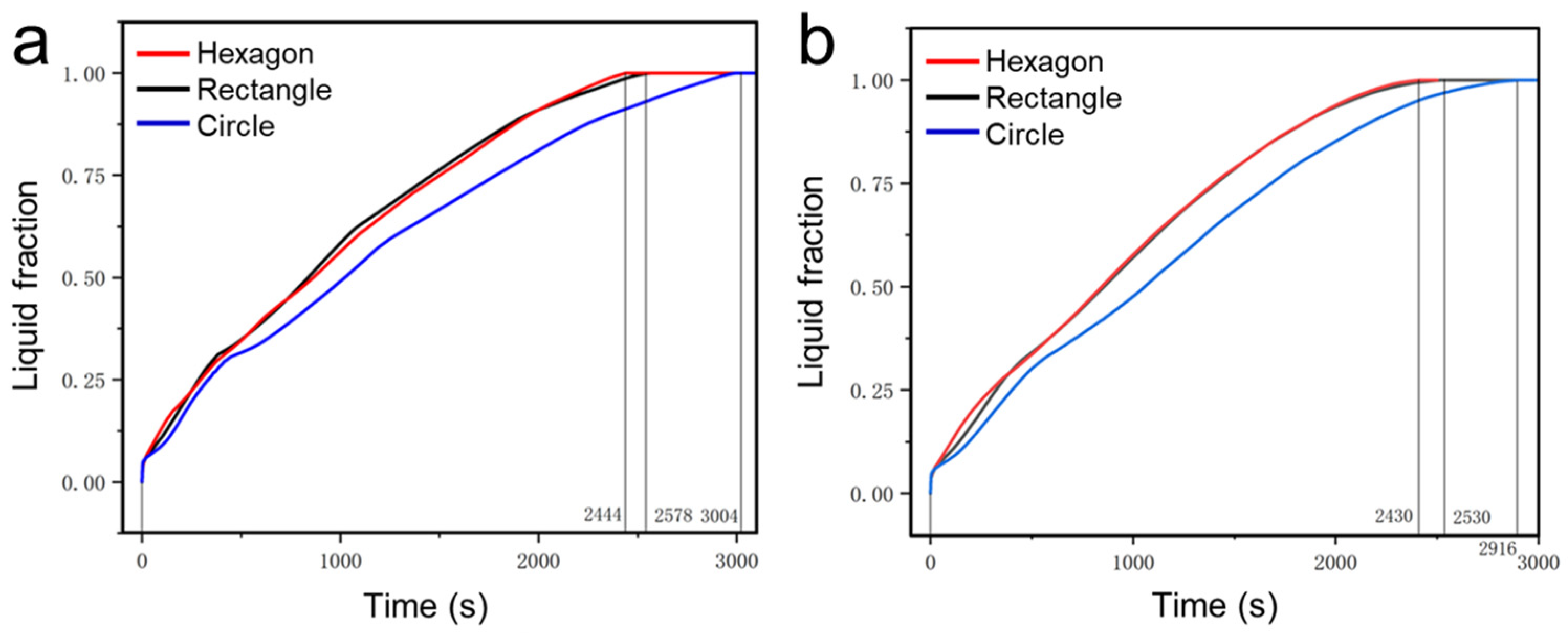
4.1. Simulation of the Melting Process of the PCM within Different Thermal Storage Units
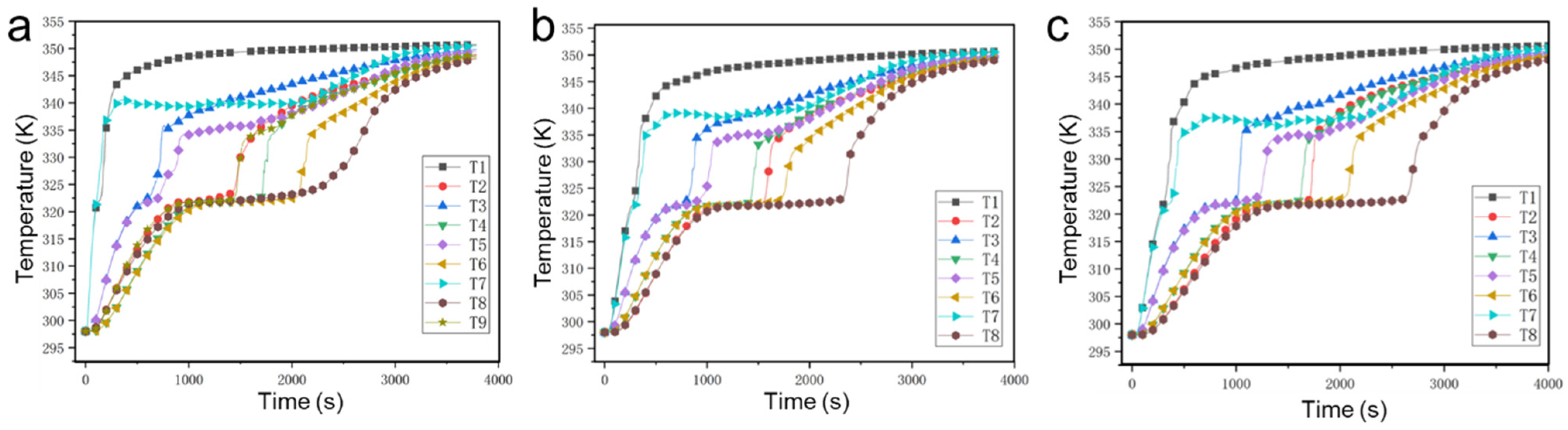
4.2. Visualization Experiments of the PCM within Different Thermal Storage Units
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Interfacial area | |
| Inertial coefficient | |
| Permeability | |
| Interfacial heat transfer coefficient | |
| L | Enthalpy of phase change |
| Solid effective thermal conductivity | |
| Fluid effective thermal conductivity | |
| Thermal dispersion conductivity | |
| Normal direction | |
| p | Pressure |
| t | Time |
| T | Temperature |
| Temperature of the heat source | |
| Velocity along the x axis | |
| Velocity along the y axis | |
| Greek Symbols | |
| Coefficient of expansion | |
| Liquid fraction | |
| Porosity | |
| Viscosity | |
| Density | |
| Subscripts | |
| f | Fluid |
| s | Solid |
References
- Farghali, M.; Osman, A.I.; Mohamed, I.M.; Chen, Z.; Chen, L.; Ihara, I. Strategies to save energy in the context of the energy crisis: A review. Environ. Chem. Lett. 2023, 21, 2003–2039. [Google Scholar] [CrossRef] [PubMed]
- Verduci, R.; Romano, V.; Brunetti, G.; Yaghoobi, N.N.; Di, C.A.; D’Angelo, G.; Ciminelli, C. Solar energy in space applications: Review and technology perspectives. Adv. Energy Mater. 2022, 12, 2200125. [Google Scholar] [CrossRef]
- Li, G.; Li, M.; Taylor, R.; Hao, Y.; Besagni, G.; Markides, C.N. Solar energy utilisation: Current status and roll-out potential. Appl. Therm. Eng. 2022, 209, 118285. [Google Scholar] [CrossRef]
- Suresh, C.; Saini, R.P. Review on solar thermal energy storage technologies and their geometrical configurations. Int. J. Energy Res. 2020, 44, 4163–4195. [Google Scholar] [CrossRef]
- Gautam, A.; Saini, R.P. A review on technical, applications and economic aspect of packed bed solar thermal energy storage system. J. Energy Storage 2020, 27, 101046. [Google Scholar] [CrossRef]
- Palacios, A.; Barreneche, C.; Navarro, M.E.; Ding, Y. Thermal energy storage technologies for concentrated solar power—A review from a materials perspective. Renew. Energy 2020, 156, 1244–1265. [Google Scholar] [CrossRef]
- Javadi, F.S.; Metselaar, H.S.C.; Ganesan, P. Performance improvement of solar thermal systems integrated with phase change materials (PCM), a review. Sol. Energy 2020, 206, 330–352. [Google Scholar] [CrossRef]
- Yuan, K.; Shi, J.; Aftab, W.; Qin, M.; Usman, A.; Zhou, F.; Zou, R. Engineering the thermal conductivity of functional phase-change materials for heat energy conversion, storage, and utilization. Adv. Funct. Mater. 2020, 30, 1904228. [Google Scholar] [CrossRef]
- Khudhair, A.M.; Farid, M.A. Review on energy conservation in building applications with thermal storage by latent heat using phase change materials. In Thermal Energy Storage with Phase Change Materials; CRC Press: Boca Raton, FL, USA, 2021; pp. 162–175. [Google Scholar]
- Jebasingh, B.E.; Arasu, A.V. A comprehensive review on latent heat and thermal conductivity of nanoparticle dispersed phase change material for low-temperature applications. Energy Storage Mater. 2020, 24, 52–74. [Google Scholar] [CrossRef]
- Wu, W.; Wang, X.; Xia, M.; Dou, Y.; Yin, Z.; Wang, J.; Lu, P. A novel composite PCM for seasonal thermal energy storage of solar water heating system. Renew. Energy 2020, 161, 457–469. [Google Scholar] [CrossRef]
- Das, D.; Bordoloi, U.; Muigai, H.H.; Kalita, P. A novel form stable PCM based bio composite material for solar thermal energy storage applications. J. Energy Storage 2020, 30, 101403. [Google Scholar] [CrossRef]
- Lu, X.; Liu, H.; Murugadoss, V.; Seok, I.; Huang, J.; Ryu, J.E.; Guo, Z. Polyethylene glycol/carbon black shape-stable phase change composites for peak load regulating of electric power system and corresponding thermal energy storage. Eng. Sci. 2020, 9, 25–34. [Google Scholar] [CrossRef]
- Wang, S.; Li, F.; Zhang, G.; Yin, C. Analysis of energy storage demand for peak shaving and frequency regulation of power systems with high penetration of renewable energy. Energy 2023, 267, 126586. [Google Scholar] [CrossRef]
- Stalin, P.M.J.; Prasad, K.S.; Kumar, K.P.; Hemadri, G.; Rajesh, M.; Kumar, K.P. Performance improvement of solar PV through the thermal management using a nano-PCM. Mater. Today Proc. 2022, 50, 1553–1558. [Google Scholar] [CrossRef]
- Malik, F.K.; Khan, M.M.; Ahmed, H.F.; Irfan, M.; Ahad, I.U. Performance characteristics of PCM based thermal energy storage system for fluctuating waste heat sources. Case Stud. Therm. 2022, 34, 102012. [Google Scholar] [CrossRef]
- Anagnostopoulos, A.; Navarro, M.E.; Stefanidou, M.; Seferlis, P.; Gaidajis, G.; Ding, Y. Effect of carbon on the performance of red mud-molten salt composites for thermal management and waste heat recovery applications. Energy Storage 2021, 44, 103363. [Google Scholar] [CrossRef]
- Chai, J.; Fan, J. Advanced thermal regulating materials and systems for energy saving and thermal comfort in buildings. Mater. Today Energy 2022, 24, 100925. [Google Scholar] [CrossRef]
- Abdulmunem, A.R.; Hussein, N.F.; Samin, P.M.; Sopian, K.; Hussien, H.A.; Ghazali, H. Integration of recycled waste paper with phase change material in building enclosure. J. Energy Storage 2023, 64, 107140. [Google Scholar] [CrossRef]
- Abdulmunem, A.R.; Hussein, N.F.; Samin, P.M.; Sopian, K.; Hussien, H.A.; Ghazali, H. Investigation of heat transfer of a building wall in the presence of phase change material (PCM). Energy Built Environ. 2020, 1, 199–206. [Google Scholar]
- Wu, S.; Yan, T.; Kuai, Z.; Pan, W. Thermal conductivity enhancement on phase change materials for thermal energy storage: A review. Energy Storage Mater. 2020, 25, 251–295. [Google Scholar] [CrossRef]
- Ren, Q.; Guo, P.; Zhu, J. Thermal management of electronic devices using pin-fin based cascade microencapsulated PCM/expanded graphite composite. Int. J. Heat Mass Transfer. 2020, 149, 119199. [Google Scholar] [CrossRef]
- Rathore, P.K.S.; Kumar Shukla, S. Improvement in thermal properties of PCM/Expanded vermiculite/expanded graphite shape stabilized composite PCM for building energy applications. Renew. Energy 2021, 176, 295–304. [Google Scholar] [CrossRef]
- Zhao, Y.; Jin, L.; Zou, B.; Qiao, G.; Zhang, T.; Cong, L.; Ding, Y. Expanded graphite–Paraffin composite phase change materials: Effect of particle size on the composite structure and properties. Appl Therm. Eng. 2020, 171, 115015. [Google Scholar] [CrossRef]
- Naghdbishi, A.; Yazdi, M.E.; Akbari, G. Experimental investigation of the effect of multi-wall carbon nanotube–Water/glycol based nanofluids on a PVT system integrated with PCM-covered collector. Appl. Therm. Eng. 2020, 178, 115556. [Google Scholar] [CrossRef]
- Fikri, M.A.; Pandey, A.K.; Samykano, M.; Kadirgama, K.; George, M.; Saidur, R.; Tyagi, V.V. Thermal conductivity, reliability, and stability assessment of phase change material (PCM) doped with functionalized multi-wall carbon nanotubes (FMWCNTs). J. Energy Storage 2022, 50, 104676. [Google Scholar] [CrossRef]
- Kumar, M.; Farwaha, H.S.; Kumar, R.; Khan, T.Y.; Javed, S.; Sachdeva, A.K.; Ammarullah, M.I. Thermal performance evaluation of solar collector with rice husk Graphene-PCM: Bioengineering approach. Case Stud. Therm. Eng. 2023, 52, 103773. [Google Scholar] [CrossRef]
- Singh, R.P.; Sze, J.Y.; Kaushik, S.C.; Rakshit, D.; Romagnoli, A. Thermal performance enhancement of eutectic PCM laden with functionalised graphene nanoplatelets for an efficient solar absorption cooling storage system. J. Energy Storage 2021, 33, 102092. [Google Scholar] [CrossRef]
- Chang, C.; Li, B.; Fu, B.; Yang, X.; Ji, Y. Form-Stable Composite Phase Change Materials Based on Porous Copper–Graphene Heterostructures for Solar Thermal Energy Conversion and Storage. Polymers 2023, 15, 4723. [Google Scholar] [CrossRef]
- Huang, S.; Lu, J.; Li, Y. Numerical study on the influence of inclination angle on the melting behaviour of metal foam-PCM latent heat storage units. Energy 2022, 239, 122489. [Google Scholar] [CrossRef]
- Tao, P.; Chang, C.; Tong, Z.; Bao, H.; Song, C.; Wu, J.; Deng, T. Magnetically-accelerated large-capacity solar-thermal energy storage within high-temperature phase-change materials. Energy Environ. Sci. 2019, 12, 1613–1621. [Google Scholar] [CrossRef]
- Li, C.; Zhao, X.; Zhang, B.; Xie, B.; He, Z.; Chen, J.; He, J. Stearic acid/copper foam as composite phase change materials for thermal energy storage. J. Therm. Sci. 2020, 29, 492–502. [Google Scholar] [CrossRef]
- Ye, Q.; Tao, P.; Chang, C.; Zhou, L.; Zeng, X.; Song, C.; Deng, T. Form-stable solar thermal heat packs prepared by impregnating phase-changing materials within carbon-coated copper foams. ACS Appl. Mater. 2018, 11, 3417–3427. [Google Scholar] [CrossRef]
- Chang, C.; Chen, G.; Wu, F.; Han, Z.; Pei, L. Fabrication and thermal performance of 3D copper-mesh-sintered foam/paraffin phase change materials for solar thermal energy storage. Processes 2022, 10, 897. [Google Scholar] [CrossRef]
- Iasiello, M.; Mameli, M.; Filippeschi, S.; Bianco, N. Metal foam/PCM melting evolution analysis: Orientation and morphology effects. Appl. Therm. Eng. 2021, 187, 116572. [Google Scholar] [CrossRef]
- Meng, X.; Yan, L.; Xu, J.; He, F.; Yu, H.; Zhang, M. Effect of porosity and pore density of copper foam on thermal performance of the paraffin-copper foam composite Phase-Change Material. Case Stud. Therm. Eng. 2020, 22, 100742. [Google Scholar] [CrossRef]
- Ying, Q.; Wang, H.; Lichtfouse, E. Numerical simulation on thermal behavior of partially filled metal foam composite phase change materials. Appl. Therm. Eng. 2023, 229, 120573. [Google Scholar] [CrossRef]
- Xiao, T.; Du, Z.; Lu, L.; Li, Y.; Huang, X.; Yang, X.; He, Y.L. Melting of phase change materials inside metal foams with uniform/graded porosity: Pore-scale simulation. Appl. Therm. Eng. 2023, 232, 121082. [Google Scholar] [CrossRef]
- Buonomo, B.; Manca, O.; Nardini, S.; Plomitallo, R.E. Numerical study on latent heat thermal energy storage system with PCM partially filled with aluminum foam in local thermal equilibrium. Renew. Energy 2022, 195, 1368–1380. [Google Scholar] [CrossRef]
- Jiao, K.; Lu, L.; Wen, T.; Wang, Q. A modified mixture theory for one-dimensional melting of pure PCM and PCM/metal foam composite: Numerical analysis and experiment validation. J. Int. J. Heat Mass Transf. 2022, 186, 122461. [Google Scholar] [CrossRef]
- Pu, L.; Zhang, S.; Xu, L.; Ma, Z.; Wang, X. Numerical study on the performance of shell-and-tube thermal energy storage using multiple PCMs and gradient copper foam. Renew. Energy 2021, 174, 573–589. [Google Scholar] [CrossRef]
- Zhang, Z.; He, X. Three-dimensional numerical study on solid-liquid phase change within open-celled aluminum foam with porosity gradient. Appl. Therm. Eng. 2017, 113, 298–308. [Google Scholar] [CrossRef]
- Yu, C.; Ji, Y.; Li, Y.; Liu, Z.; Chu, L.; Kuang, H.; Wang, Z. A three-dimensional oscillating heat pipe filled with liquid metal and ammonia for high-power and high-heat-flux dissipation. Int. J. Heat Mass Transf. 2022, 194, 123096. [Google Scholar] [CrossRef]






| Materials | (kg m−3) | Cp (J kg−1 K−1) | k (W/(mK)) | µ (Pa s) | L (kJ/kg) | Tm (K) | γ (K−1) |
|---|---|---|---|---|---|---|---|
| Paraffin | 900 | 2300 | 0.3 | 0.00324 | 143.3 | 321.75–329.35 | 0.0005 |
| Porous metal structure | 2700 | 880 | 237 | - | - | - | - |
| Material | Manufacturer |
|---|---|
| Paraffin | Sinopharm Chemical Reagent Co., Ltd. (Shanghai, China) |
| AlSi10Mg powder | Wuxi Taichen Metal Materials Co., Ltd. (Wuxi, China) |
| Ar gas (99.99%) | Dalian SPECIAL Gas Co., Ltd. (Dalian, China) |
| Thermal grease | Shenzhen SINWE Materials Co., Ltd. (Shenzhen, China) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.; Li, B.; Fu, B.; Yang, X.; Lou, T.; Ji, Y. Simulation and Experimental Investigation of the Effect of Pore Shape on Heat Transfer Behavior of Phase Change Materials in Porous Metal Structures. Nanomaterials 2024, 14, 1206. https://doi.org/10.3390/nano14141206
Chang C, Li B, Fu B, Yang X, Lou T, Ji Y. Simulation and Experimental Investigation of the Effect of Pore Shape on Heat Transfer Behavior of Phase Change Materials in Porous Metal Structures. Nanomaterials. 2024; 14(14):1206. https://doi.org/10.3390/nano14141206
Chicago/Turabian StyleChang, Chao, Bo Li, Baocai Fu, Xu Yang, Tianyi Lou, and Yulong Ji. 2024. "Simulation and Experimental Investigation of the Effect of Pore Shape on Heat Transfer Behavior of Phase Change Materials in Porous Metal Structures" Nanomaterials 14, no. 14: 1206. https://doi.org/10.3390/nano14141206
APA StyleChang, C., Li, B., Fu, B., Yang, X., Lou, T., & Ji, Y. (2024). Simulation and Experimental Investigation of the Effect of Pore Shape on Heat Transfer Behavior of Phase Change Materials in Porous Metal Structures. Nanomaterials, 14(14), 1206. https://doi.org/10.3390/nano14141206








