Advanced Cellulose–Nanocarbon Composite Films for High-Performance Triboelectric and Piezoelectric Nanogenerators
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Material Preparation
2.3. Film Formation
2.4. Characterization
2.5. Electrical Measurements
3. Results and Discussion
3.1. Morphology of the Starting Materials

3.2. Nanocarbon Dispersions
3.3. Microstructure of the Nanocomposite Films
3.4. Electrical Conductivity
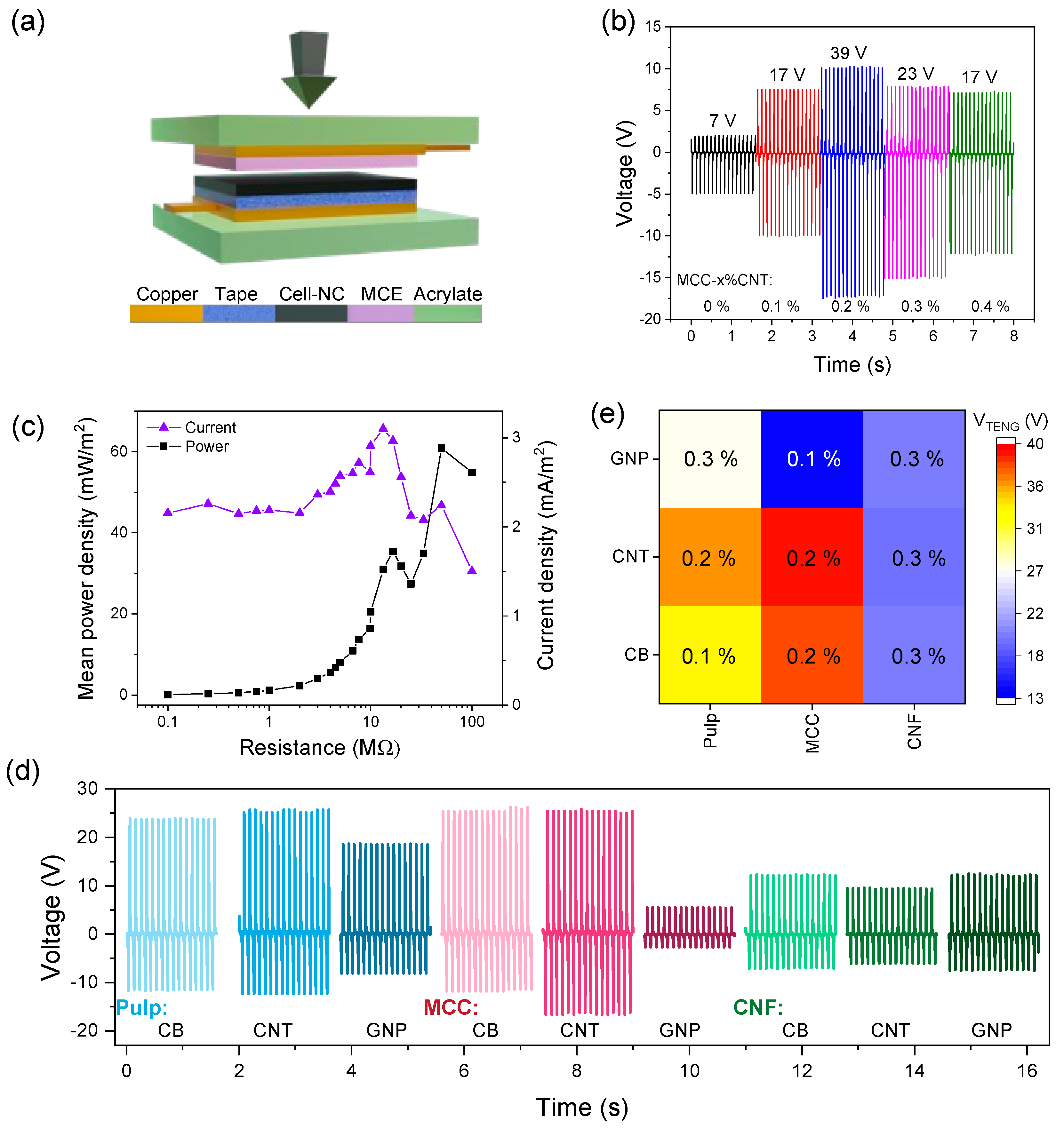
3.5. Triboelectric Properties
3.5.1. Performance Measurements
3.5.2. Film Properties and Performance
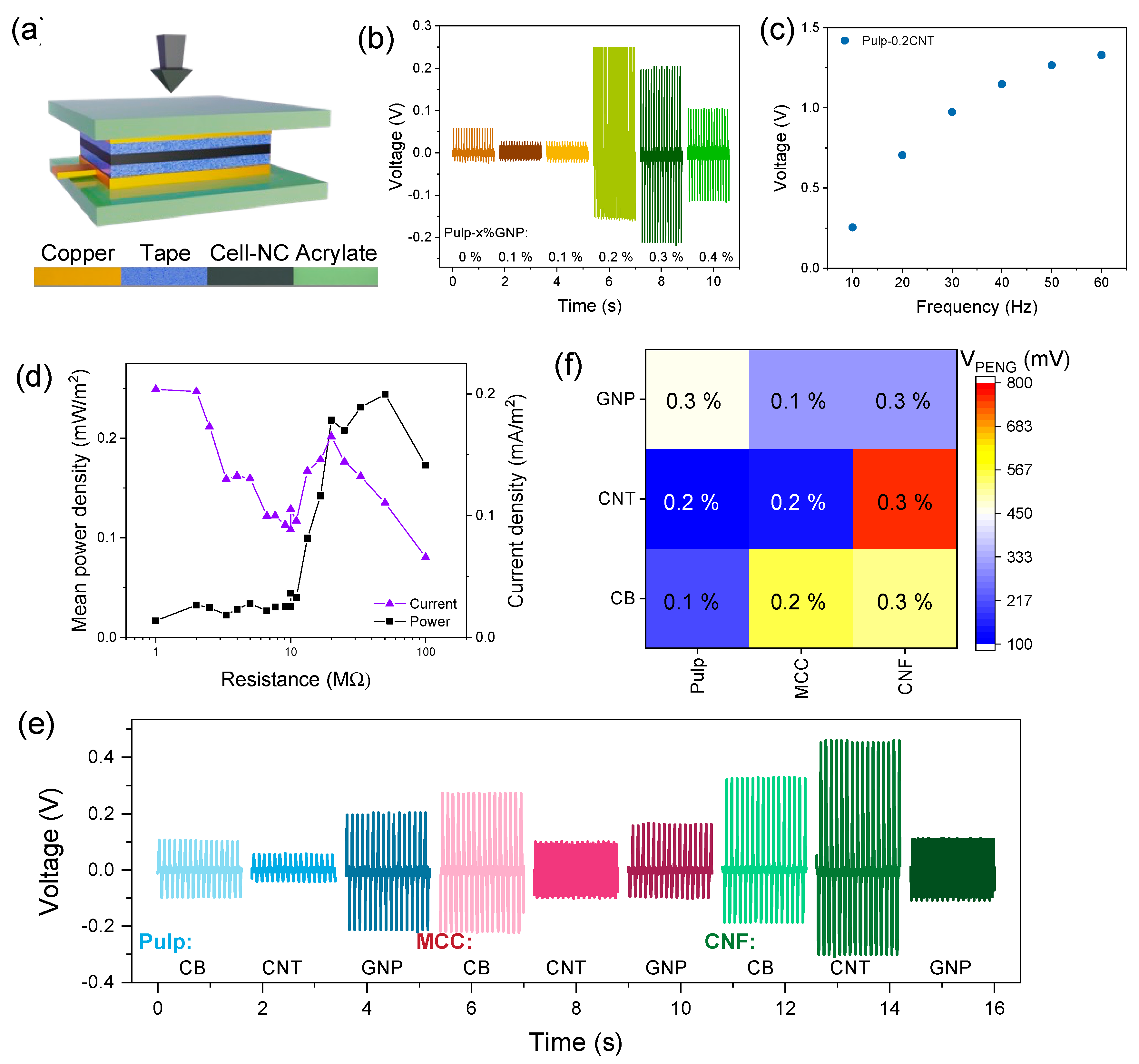
3.6. Piezoelectric Properties
3.6.1. Performance Measurements
3.6.2. Mechanism of Piezoelectricity in Cellulose Nanocomposites
3.6.3. Film Microstructure and Performance
3.6.4. Cellulose Orientation and Piezoresponse
3.7. Piezoelectric Force Microscopy Measurements
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aubin, C.A.; Gorissen, B.; Milana, E.; Buskohl, P.R.; Lazarus, N.; Slipher, G.A.; Keplinger, C.; Bongard, J.; Iida, F.; Lewis, J.A.; et al. Towards Enduring Autonomous Robots via Embodied Energy. Nature 2022, 602, 393–402. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Wang, A.C.; Ding, W.; Guo, H.; Wang, Z.L. Triboelectric Nanogenerator: A Foundation of the Energy for the New Era. Adv. Energy Mater. 2019, 9, 1802906. [Google Scholar] [CrossRef]
- Sezer, N.; Koç, M. A Comprehensive Review on the State-of-the-Art of Piezoelectric Energy Harvesting. Nano Energy 2021, 80, 105567. [Google Scholar] [CrossRef]
- Li, J.; Shepelin, N.A.; Sherrell, P.C.; Ellis, A.V. Poly(Dimethylsiloxane) for Triboelectricity: From Mechanisms to Practical Strategies. Chem. Mater. 2021, 33, 4304–4327. [Google Scholar] [CrossRef]
- Zou, H.; Zhang, Y.; Guo, L.; Wang, P.; He, X.; Dai, G.; Zheng, H.; Chen, C.; Wang, A.C.; Xu, C.; et al. Quantifying the Triboelectric Series. Nat. Commun. 2019, 10, 1427. [Google Scholar] [CrossRef]
- Chen, A.; Zhang, C.; Zhu, G.; Wang, Z.L. Polymer Materials for High-Performance Triboelectric Nanogenerators. Adv. Sci. 2020, 7, 2000186. [Google Scholar] [CrossRef] [PubMed]
- Fang, Z.; Zhang, H.; Qiu, S.; Kuang, Y.; Zhou, J.; Lan, Y.; Sun, C.; Li, G.; Gong, S.; Ma, Z. Versatile Wood Cellulose for Biodegradable Electronics. Adv. Mater. Technol. 2021, 6, 2000928. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Cui, K.; Ge, S.; Cheng, X.; Yan, M.; Yu, J.; Liu, H. Flexible Electronics Based on Micro/Nanostructured Paper. Adv. Mater. 2018, 30, 1801588. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Yao, C.; Wang, F.; Li, Z. Cellulose-Based Nanomaterials for Energy Applications. Small 2017, 13, 1702240. [Google Scholar] [CrossRef]
- Rivadeneyra, A.; Marín-Sánchez, A.; Wicklein, B.; Salmerón, J.F.; Castillo, E.; Bobinger, M.; Salinas-Castillo, A. Cellulose Nanofibers as Substrate for Flexible and Biodegradable Moisture Sensors. Compos. Sci. Technol. 2021, 208, 108738. [Google Scholar] [CrossRef]
- Nandy, S.; Fortunato, E.; Martins, R. Green Economy and Waste Management: An Inevitable Plan for Materials Science. Prog. Nat. Sci. Mater. Int. 2022, 32, 1–9. [Google Scholar] [CrossRef]
- Han, J.; Xu, N.; Liang, Y.; Ding, M.; Zhai, J.; Sun, Q.; Wang, Z.L. Paper-Based Triboelectric Nanogenerators and Their Applications: A Review. Beilstein J. Nanotechnol. 2021, 12, 151–171. [Google Scholar] [CrossRef] [PubMed]
- Torres, F.G.; De-la-Torre, G.E. Polysaccharide-Based Triboelectric Nanogenerators: A Review. Carbohydr. Polym. 2021, 251, 117055. [Google Scholar] [CrossRef]
- Niu, Z.; Cheng, W.; Cao, M.; Wang, D.; Wang, Q.; Han, J.; Long, Y.; Han, G. Recent Advances in Cellulose-Based Flexible Triboelectric Nanogenerators. Nano Energy 2021, 87, 106175. [Google Scholar] [CrossRef]
- Song, Y.; Shi, Z.; Hu, G.-H.; Xiong, C.; Isogai, A.; Yang, Q. Recent Advances in Cellulose-Based Piezoelectric and Triboelectric Nanogenerators for Energy Harvesting: A Review. J. Mater. Chem. A 2021, 9, 1910–1937. [Google Scholar] [CrossRef]
- Song, Y.; Wu, T.; Bao, J.; Xu, M.; Yang, Q.; Zhu, L.; Shi, Z.; Hu, G.-H.; Xiong, C. Porous Cellulose Composite Aerogel Films with Super Piezoelectric Properties for Energy Harvesting. Carbohydr. Polym. 2022, 288, 119407. [Google Scholar] [CrossRef]
- Shi, K.; Zou, H.; Sun, B.; Jiang, P.; He, J.; Huang, X. Dielectric Modulated Cellulose Paper/PDMS-Based Triboelectric Nanogenerators for Wireless Transmission and Electropolymerization Applications. Adv. Funct. Mater. 2020, 30, 1904536. [Google Scholar] [CrossRef]
- Fukada, E. Piezoelectricity of Wood. J. Phys. Soc. Jpn. 1955, 10, 149–154. [Google Scholar] [CrossRef]
- Chae, I.; Jeong, C.K.; Ounaies, Z.; Kim, S.H. Review on Electromechanical Coupling Properties of Biomaterials. ACS Appl. Bio Mater. 2018, 1, 936–953. [Google Scholar] [CrossRef]
- Moon, R.J.; Martini, A.; Nairn, J.; Simonsen, J.; Youngblood, J. Cellulose Nanomaterials Review: Structure, Properties and Nanocomposites. Chem. Soc. Rev. 2011, 40, 3941–3994. [Google Scholar] [CrossRef]
- Tayeb, P.; Tayeb, H.A. Nanocellulose Applications in Sustainable Electrochemical and Piezoelectric Systems: A Review. Carbohydr. Polym. 2019, 224, 115149. [Google Scholar] [CrossRef]
- Yao, C.; Hernandez, A.; Yu, Y.; Cai, Z.; Wang, X. Triboelectric Nanogenerators and Power-Boards from Cellulose Nanofibrils and Recycled Materials. Nano Energy 2016, 30, 103–108. [Google Scholar] [CrossRef]
- Liu, Z.; Muhammad, M.; Cheng, L.; Xie, E.; Han, W. Improved Output Performance of Triboelectric Nanogenerators Based on Polydimethylsiloxane Composites by the Capacitive Effect of Embedded Carbon Nanotubes. Appl. Phys. Lett. 2020, 117, 143903. [Google Scholar] [CrossRef]
- Lee, K.; Mhin, S.; Han, H.; Kwon, O.; Kim, W.-B.; Song, T.; Kang, S.; Kim, K.M. A High-Performance PDMS-Based Triboelectric Nanogenerator Fabricated Using Surface-Modified Carbon Nanotubes via Pulsed Laser Ablation. J. Mater. Chem. A 2022, 10, 1299–1308. [Google Scholar] [CrossRef]
- Wen, R.; Guo, J.; Yu, A.; Zhang, K.; Kou, J.; Zhu, Y.; Zhang, Y.; Li, B.-W.; Zhai, J. Remarkably Enhanced Triboelectric Nanogenerator Based on Flexible and Transparent Monolayer Titania Nanocomposite. Nano Energy 2018, 50, 140–147. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, H.; He, D.; Xu, Y.; Zhang, A.; Liu, Y.; Bai, J. Synergistic Effects of BaTiO3/Multiwall Carbon Nanotube as Fillers on the Electrical Performance of Triboelectric Nanogenerator Based on Polydimethylsiloxane Composite Films. Energy Technol. 2019, 7, 1900101. [Google Scholar] [CrossRef]
- Pusty, M.; Shirage, P.M. Insights and Perspectives on Graphene-PVDF Based Nanocomposite Materials for Harvesting Mechanical Energy. J. Alloys Compd. 2022, 904, 164060. [Google Scholar] [CrossRef]
- Cataldi, P.; Athanassiou, A.; Bayer, I.S. Graphene Nanoplatelets-Based Advanced Materials and Recent Progress in Sustainable Applications. Appl. Sci. 2018, 8, 1438. [Google Scholar] [CrossRef]
- Spahr, M.E.; Rothon, R. Carbon Black as a Polymer Filler. In Polymers and Polymeric Composites: A Reference Series; Palsule, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–31. ISBN 978-3-642-37179-0. [Google Scholar]
- Xiao, J.; Han, J.; Zhang, C.; Ling, G.; Kang, F.; Yang, Q. Dimensionality, Function and Performance of Carbon Materials in Energy Storage Devices. Adv. Energy Mater. 2022, 12, 2100775. [Google Scholar] [CrossRef]
- Hernández-López, S.; Vigueras-Santiago, E.; Mendoza Mora, M.; Farias Mancilla, J.R.; Zaragoza Contreras, E.A. Cellulose-Based Polymer Composite with Carbon Black for Tetrahydrofuran Sensing. Int. J. Polym. Sci. 2013, 2013, 381653. [Google Scholar] [CrossRef][Green Version]
- Esmeryan, K.D.; Fedchenko, Y.I.; Gyoshev, S.D.; Lazarov, Y.; Chaushev, T.A.; Grakov, T. On the Development of Ultradurable Extremely Water-Repellent and Oleophobic Soot-Based Fabrics with Direct Relevance to Sperm Cryopreservation. ACS Appl. Bio Mater. 2022, 5, 3519–3529. [Google Scholar] [CrossRef] [PubMed]
- Cheng, K.; Wallaert, S.; Ardebili, H.; Karim, A. Advanced Triboelectric Nanogenerators Based on Low-Dimension Carbon Materials: A Review. Carbon 2022, 194, 81–103. [Google Scholar] [CrossRef]
- Li, M.; Jie, Y.; Shao, L.-H.; Guo, Y.; Cao, X.; Wang, N.; Wang, Z.L. All-in-One Cellulose Based Hybrid Tribo/Piezoelectric Nanogenerator. Nano Res. 2019, 12, 1831–1835. [Google Scholar] [CrossRef]
- Alam, M.M.; Mandal, D. Native Cellulose Microfiber-Based Hybrid Piezoelectric Generator for Mechanical Energy Harvesting Utility. ACS Appl. Mater. Interfaces 2016, 8, 1555–1558. [Google Scholar] [CrossRef]
- Fillat, Ú.; Wicklein, B.; Martín-Sampedro, R.; Ibarra, D.; Ruiz-Hitzky, E.; Valencia, C.; Sarrión, A.; Castro, E.; Eugenio, M.E. Assessing Cellulose Nanofiber Production from Olive Tree Pruning Residue. Carbohydr. Polym. 2018, 179, 252–261. [Google Scholar] [CrossRef]
- Wicklein, B.; Kocjan, A.; Salazar-Alvarez, G.; Carosio, F.; Camino, G.; Antonietti, M.; Bergström, L. Thermally Insulating and Fire-Retardant Lightweight Anisotropic Foams Based on Nanocellulose and Graphene Oxide. Nat. Nanotechnol. 2015, 10, 277–283. [Google Scholar] [CrossRef]
- Wicklein, B.; Diem, A.M.; Knöller, A.; Cavalcante, M.S.; Bergström, L.; Bill, J.; Burghard, Z. Dual-Fiber Approach toward Flexible Multifunctional Hybrid Materials. Adv. Funct. Mater. 2018, 28, 1704274. [Google Scholar] [CrossRef]
- Lengowski, E.C.; Bonfatti Júnior, E.A.; Kumode, M.M.N.; Carneiro, M.E.; Satyanarayana, K.G. Nanocellulose in the Paper Making. In Sustainable Polymer Composites and Nanocomposites; Inamuddin, T.S., Kumar Mishra, R., Asiri, A.M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 1027–1066. ISBN 978-3-030-05399-4. [Google Scholar]
- Yoon, S.H.; Jin, H.-J.; Kook, M.-C.; Pyun, Y.R. Electrically Conductive Bacterial Cellulose by Incorporation of Carbon Nanotubes. Biomacromolecules 2006, 7, 1280–1284. [Google Scholar] [CrossRef]
- Safari, S.; van de Ven, T.G.M. Effect of Water Vapor Adsorption on Electrical Properties of Carbon Nanotube/Nanocrystalline Cellulose Composites. ACS Appl. Mater. Interfaces 2016, 8, 9483–9489. [Google Scholar] [CrossRef]
- Imai, M.; Akiyama, K.; Tanaka, T.; Sano, E. Highly Strong and Conductive Carbon Nanotube/Cellulose Composite Paper. Compos. Sci. Technol. 2010, 70, 1564–1570. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, F.; Pan, Y.; Jin, L.; Liu, B.; Mao, Y.; Huang, J. Multiwall-Carbon-Nanotube/Cellulose Composite Fibers with Enhanced Mechanical and Electrical Properties by Cellulose Grafting. RSC Adv. 2018, 8, 5678–5684. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ma, P.C.; Chow, W.S.; To, C.K.; Tang, B.Z.; Kim, J.-K. Correlations between Percolation Threshold, Dispersion State, and Aspect Ratio of Carbon Nanotubes. Adv. Funct. Mater. 2007, 17, 3207–3215. [Google Scholar] [CrossRef]
- Rahatekar, S.S.; Shaffer, M.S.P.; Elliott, J.A. Modelling Percolation in Fibre and Sphere Mixtures: Routes to More Efficient Network Formation. Compos. Sci. Technol. 2010, 70, 356–362. [Google Scholar] [CrossRef]
- Shah, Z.M.; Khanday, F.A.; Malik, G.F.A.; Jhat, Z.A. Chapter Fifteen—Fabrication of Polymer Nanocomposite-Based Fractional-Order Capacitor: A Guide. In Fractional-Order Design; Radwan, A.G., Khanday, F.A., Said, L.A., Eds.; Academic Press: Cambridge, MA, USA, 2022; Volume 3, pp. 437–483. ISBN 978-0-323-90090-4. [Google Scholar]
- Han, S.; Wang, P.; Zhou, Y.; Meng, Q.; Aakyiir, M.; Ma, J. Flexible, Mechanically Robust, Multifunctional and Sustainable Cellulose/Graphene Nanocomposite Films for Wearable Human-Motion Monitoring. Compos. Sci. Technol. 2022, 230, 109451. [Google Scholar] [CrossRef]
- Mahmoudian, S.; Reza Sazegar, M.; Afshari, N.; Uzir Wahit, M. Graphene Reinforced Regenerated Cellulose Nanocomposite Fibers Prepared by Lyocell Process. Polym. Compos. 2017, 38, E81–E88. [Google Scholar] [CrossRef]
- Salajkova, M.; Valentini, L.; Zhou, Q.; Berglund, L.A. Tough Nanopaper Structures Based on Cellulose Nanofibers and Carbon Nanotubes. Compos. Sci. Technol. 2013, 87, 103–110. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, X.; Hubbe, M.A.; Pal, L. Highly Conductive Carbon Nanotubes and Flexible Cellulose Nanofibers Composite Membranes with Semi-Interpenetrating Networks Structure. Carbohydr. Polym. 2019, 222, 115013. [Google Scholar] [CrossRef]
- Kocjan, A.; Schmidt, R.; Lazar, A.; Prado-Gonjal, J.; Kovač, J.; Logar, M.; Mompean, F.J.; Garcia-Hernandez, M.; Ruiz-Hitzky, E.; Wicklein, B. In Situ Generation of 3D Graphene-like Networks from Cellulose Nanofibres in Sintered Ceramics. Nanoscale 2018, 10, 10488–10497. [Google Scholar] [CrossRef]
- Fernández-García, L.; Suárez, M.; Menéndez, J.L.; Pecharromán, C.; Menéndez, R.; Santamaría, R. Dielectric Behavior of Ceramic–Graphene Composites around the Percolation Threshold. Nanoscale Res. Lett. 2015, 10, 216. [Google Scholar] [CrossRef]
- Zhu, G.; Pan, C.; Guo, W.; Chen, C.-Y.; Zhou, Y.; Yu, R.; Wang, Z.L. Triboelectric-Generator-Driven Pulse Electrodeposition for Micropatterning. Nano Lett. 2012, 12, 4960–4965. [Google Scholar] [CrossRef]
- Xie, L.; Zhai, N.; Liu, Y.; Wen, Z.; Sun, X. Hybrid Triboelectric Nanogenerators: From Energy Complementation to Integration. Research 2021, 2021, 9143762. [Google Scholar] [CrossRef] [PubMed]
- Cui, P.; Parida, K.; Lin, M.-F.; Xiong, J.; Cai, G.; Lee, P.S. Transparent, Flexible Cellulose Nanofibril–Phosphorene Hybrid Paper as Triboelectric Nanogenerator. Adv. Mater. Interfaces 2017, 4, 1700651. [Google Scholar] [CrossRef]
- Ghaffarinejad, A.; Yavand Hasani, J. Modeling of Triboelectric Charge Accumulation Dynamics at the Metal–Insulator Interface for Variable Capacitive Structures: Application to Triboelectric Nanogenerators. Appl. Phys. A 2019, 125, 259. [Google Scholar] [CrossRef]
- Niu, S.; Wang, S.; Lin, L.; Liu, Y.; Zhou, Y.S.; Hu, Y.; Wang, Z.L. Theoretical Study of Contact-Mode Triboelectric Nanogenerators as an Effective Power Source. Energy Environ. Sci. 2013, 6, 3576–3583. [Google Scholar] [CrossRef]
- Zheng, Q.; Fang, L.; Guo, H.; Yang, K.; Cai, Z.; Meador, M.A.B.; Gong, S. Highly Porous Polymer Aerogel Film-Based Triboelectric Nanogenerators. Adv. Funct. Mater. 2018, 28, 1706365. [Google Scholar] [CrossRef]
- Shi, K.; Huang, X.; Sun, B.; Wu, Z.; He, J.; Jiang, P. Cellulose/BaTiO3 Aerogel Paper Based Flexible Piezoelectric Nanogenerators and the Electric Coupling with Triboelectricity. Nano Energy 2019, 57, 450–458. [Google Scholar] [CrossRef]
- Yu, H.; Huang, T.; Lu, M.; Mao, M.; Zhang, Q.; Wang, H. Enhanced Power Output of an Electrospun PVDF/MWCNTs-Based Nanogenerator by Tuning Its Conductivity. Nanotechnology 2013, 24, 405401. [Google Scholar] [CrossRef]
- Ohya, Y.; Yahata, Y.; Ban, T. Dielectric and Piezoelectric Properties of Dense and Porous PZT Films Prepared by Sol-Gel Method. J. Sol-Gel Sci. Technol. 2007, 42, 397–405. [Google Scholar] [CrossRef]
- Ennawaoui, C.; Hajjaji, A.; Samuel, C.; Sabani, E.; Rjafallah, A.; Najihi, I.; Laadissi, E.M.; Loualid, E.M.; Rguiti, M.; Ballouti, A.E.; et al. Piezoelectric and Electromechanical Characteristics of Porous Poly(Ethylene-Co-Vinyl Acetate) Copolymer Films for Smart Sensors and Mechanical Energy Harvesting Applications. Appl. Syst. Innov. 2021, 4, 57. [Google Scholar] [CrossRef]
- Khan, A.A.; Rana, M.M.; Huang, G.; Mei, N.; Saritas, R.; Wen, B.; Zhang, S.; Voss, P.; Rahman, E.-A.; Leonenko, Z.; et al. Maximizing Piezoelectricity by Self-Assembled Highly Porous Perovskite–Polymer Composite Films to Enable the Internet of Things. J. Mater. Chem. A 2020, 8, 13619–13629. [Google Scholar] [CrossRef]
- Pantea, D.; Darmstadt, H.; Kaliaguine, S.; Roy, C. Electrical Conductivity of Conductive Carbon Blacks: Influence of Surface Chemistry and Topology. Appl. Surf. Sci. 2003, 217, 181–193. [Google Scholar] [CrossRef]
- Chen, B.-Y.; Hwang, K.-S. Comparative Study of Carbon Black and Graphite Powder as Carbon Source for PM Compacts. Powder Metall. 2010, 53, 51–56. [Google Scholar] [CrossRef]
- Lu, S.; Chung, D.D.L. Viscoelastic Behavior of Carbon Black and Its Relationship with the Aggregate Size. Carbon 2013, 60, 346–355. [Google Scholar] [CrossRef]
- Ehrburger-Dolle, F.; Lahaye, J.; Misono, S. Percolation in Carbon Black Powders. Carbon 1994, 32, 1363–1368. [Google Scholar] [CrossRef]
- Dropsens Carbon Nanotubes—Product Information Sheet. Available online: https://www.dropsens.com/en/pdfs_productos/new_brochures/msds/msds_drp_swcnt_mwcnt_en.pdf (accessed on 24 March 2023).
- Deep, N.; Mishra, P. Fabrication and Characterization of Thermally Conductive PMMA/MWCNT Nanocomposites. Mater. Today Proc. 2018, 5, 28328–28336. [Google Scholar] [CrossRef]
- Vozniakovskii, A.A.; Kol’tsova, T.S.; Voznyakovskii, A.P.; Kumskov, A.L.; Kidalov, S.V. Powder Hybrid Nanomaterial: Detonation Nanodiamonds – Carbon Nanotubes and Its Stable Reversible Water Nanofluids. J. Colloid Interface Sci. 2020, 565, 305–314. [Google Scholar] [CrossRef]
- Kim, S.H.; Mulholland, G.W.; Zachariah, M.R. Density Measurement of Size Selected Multiwalled Carbon Nanotubes by Mobility-Mass Characterization. Carbon 2009, 47, 1297–1302. [Google Scholar] [CrossRef]
- KNANO—A Graphene Company KNG-150 Graphene Nanoplatelets, Technical Product Information. Available online: http://en.knano.com.cn/product/14.html (accessed on 24 March 2023).





| Sample | Thickness μm | App. Density mg/mL | Porosity % |
|---|---|---|---|
| CP-0.4CNT | 72 | 0.69 | 52 |
| MCC-2.25CNT | 40 | 0.95 | 35 |
| CNF-1.0GNP | 24 | 1.39 | 5 |
| Cellulose Matrix | Nanocarbon Filler | Percolation Threshold wt% | Conductivity b S/cm |
|---|---|---|---|
| MCC | CNTs | 0.4 | 2.0 × 10−5 |
| MCC | CB | 1.0 | 3.1 × 10−2 |
| MCC | GNPs | 0.5 a | - |
| CP | CNTs | 0.3 | 1.8 × 10−3 |
| CP | CB | 1.0 | 1.0 × 10−2 |
| CP | GNPs | 0.5 a | - |
| CNF | CNTs | 2.5 | 2.5 × 10−1 |
| CNF | CB | 1 a | - |
| CNF | GNPs | 1 a | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González, J.; Ghaffarinejad, A.; Ivanov, M.; Ferreira, P.; Vilarinho, P.M.; Borrás, A.; Amorín, H.; Wicklein, B. Advanced Cellulose–Nanocarbon Composite Films for High-Performance Triboelectric and Piezoelectric Nanogenerators. Nanomaterials 2023, 13, 1206. https://doi.org/10.3390/nano13071206
González J, Ghaffarinejad A, Ivanov M, Ferreira P, Vilarinho PM, Borrás A, Amorín H, Wicklein B. Advanced Cellulose–Nanocarbon Composite Films for High-Performance Triboelectric and Piezoelectric Nanogenerators. Nanomaterials. 2023; 13(7):1206. https://doi.org/10.3390/nano13071206
Chicago/Turabian StyleGonzález, Jaime, Ali Ghaffarinejad, Maxim Ivanov, Paula Ferreira, Paula M. Vilarinho, Ana Borrás, Harvey Amorín, and Bernd Wicklein. 2023. "Advanced Cellulose–Nanocarbon Composite Films for High-Performance Triboelectric and Piezoelectric Nanogenerators" Nanomaterials 13, no. 7: 1206. https://doi.org/10.3390/nano13071206
APA StyleGonzález, J., Ghaffarinejad, A., Ivanov, M., Ferreira, P., Vilarinho, P. M., Borrás, A., Amorín, H., & Wicklein, B. (2023). Advanced Cellulose–Nanocarbon Composite Films for High-Performance Triboelectric and Piezoelectric Nanogenerators. Nanomaterials, 13(7), 1206. https://doi.org/10.3390/nano13071206







