Optical Properties of Concentric Nanorings of Quantum Emitters
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Framework: Bloch Eigenmodes
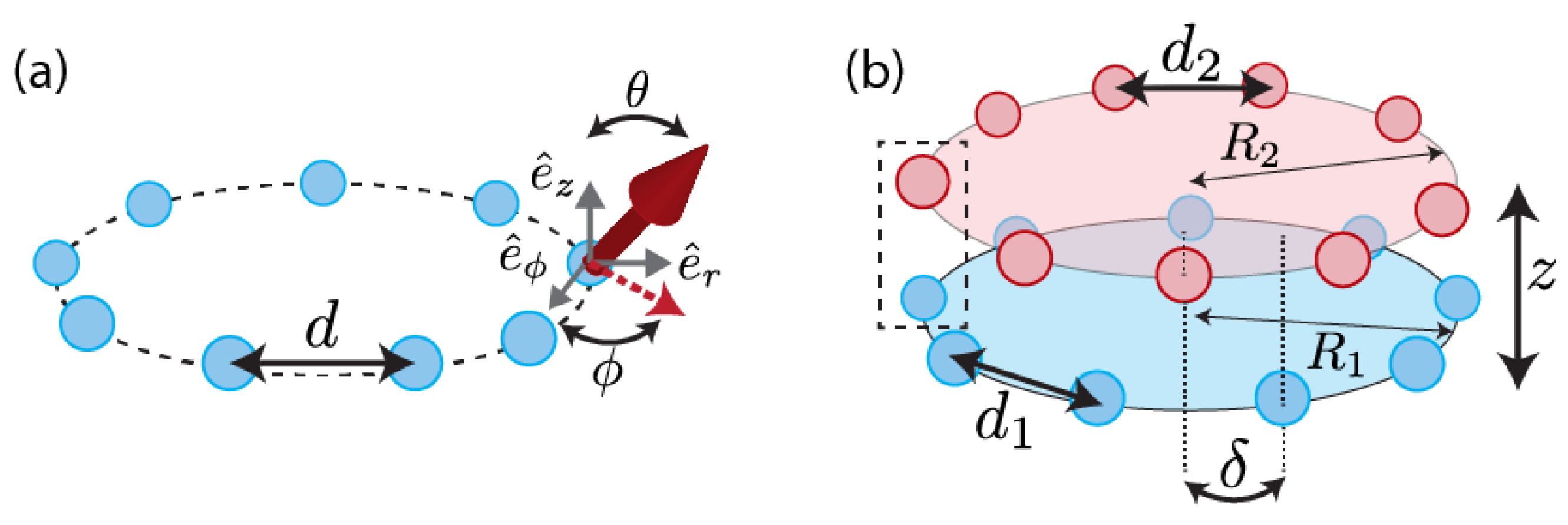
2.2. Bloch Eigenmodes in Rotationally Symmetric Ring Structures
3. Results
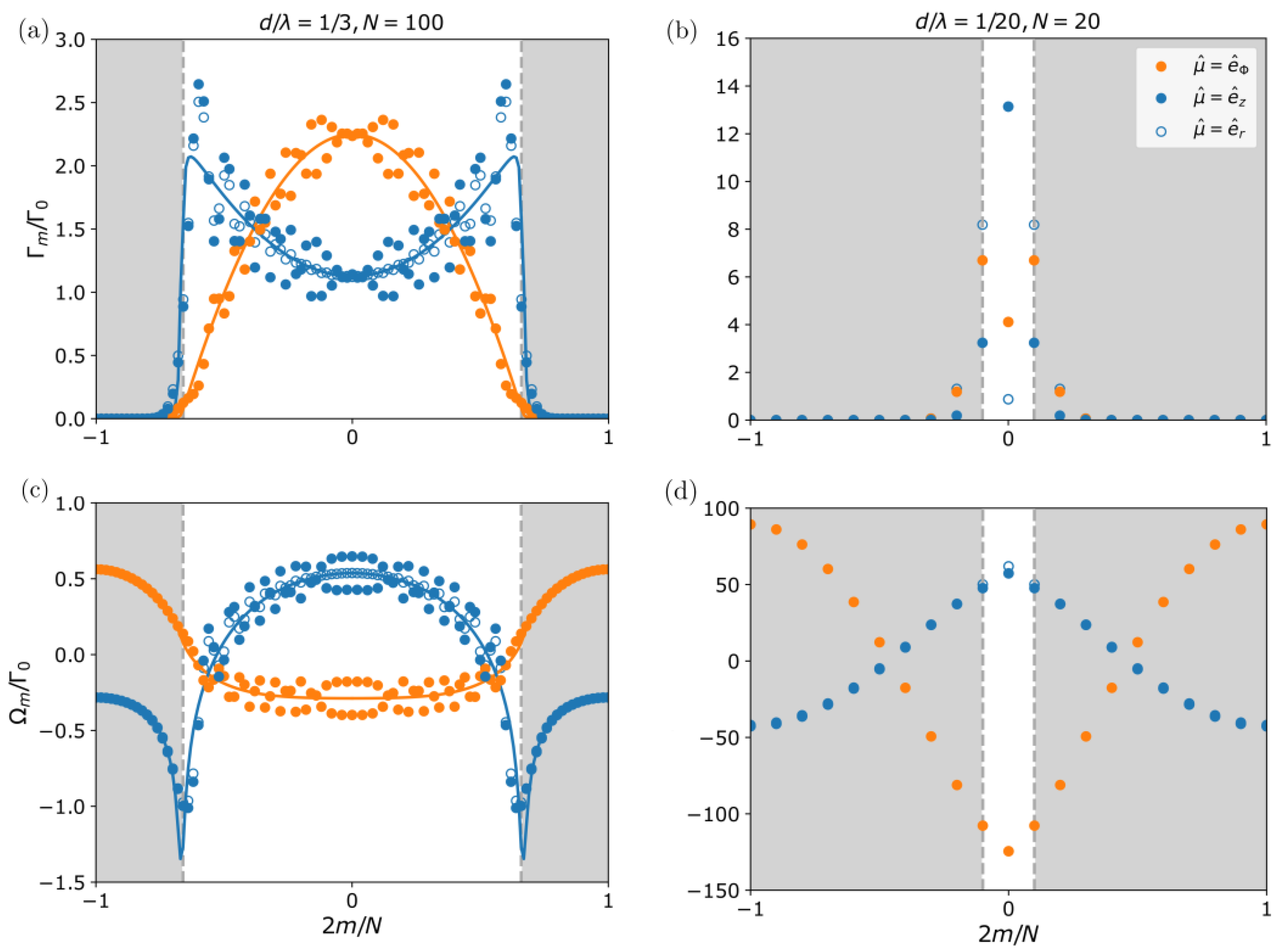
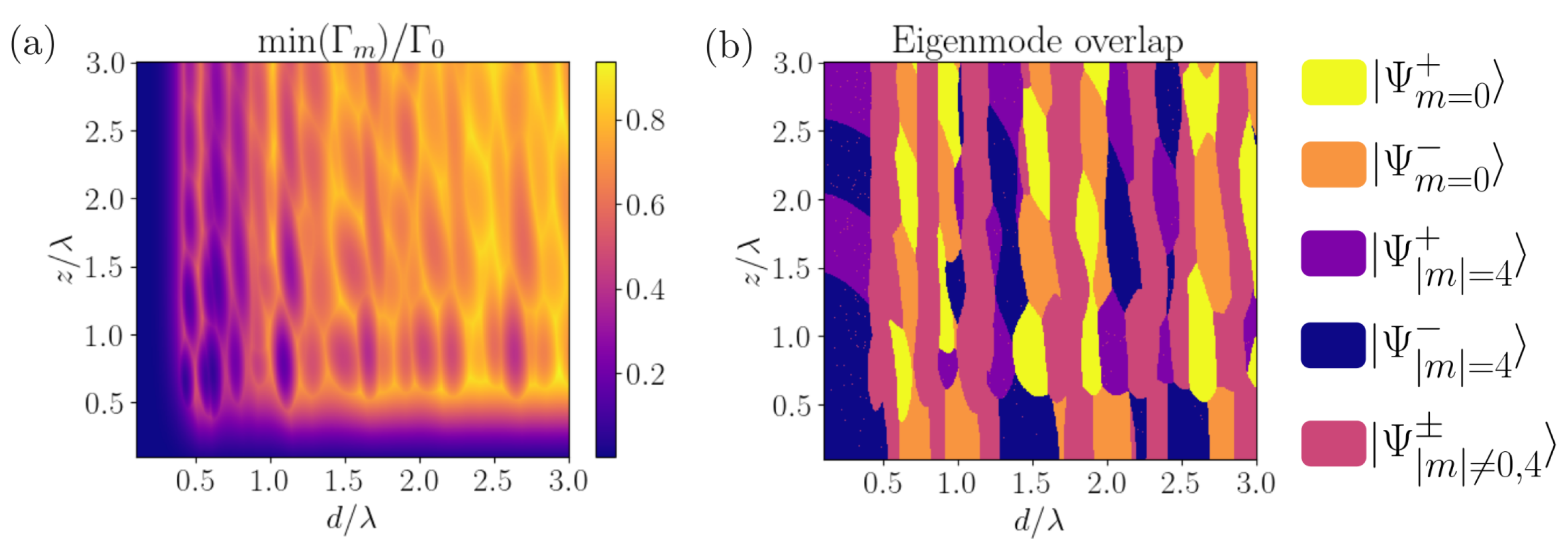
3.1. Optical Properties of a Single Nano-Ring
3.1.1. Dense and Large Ring Case (Quasi-Linear Chain Limit)
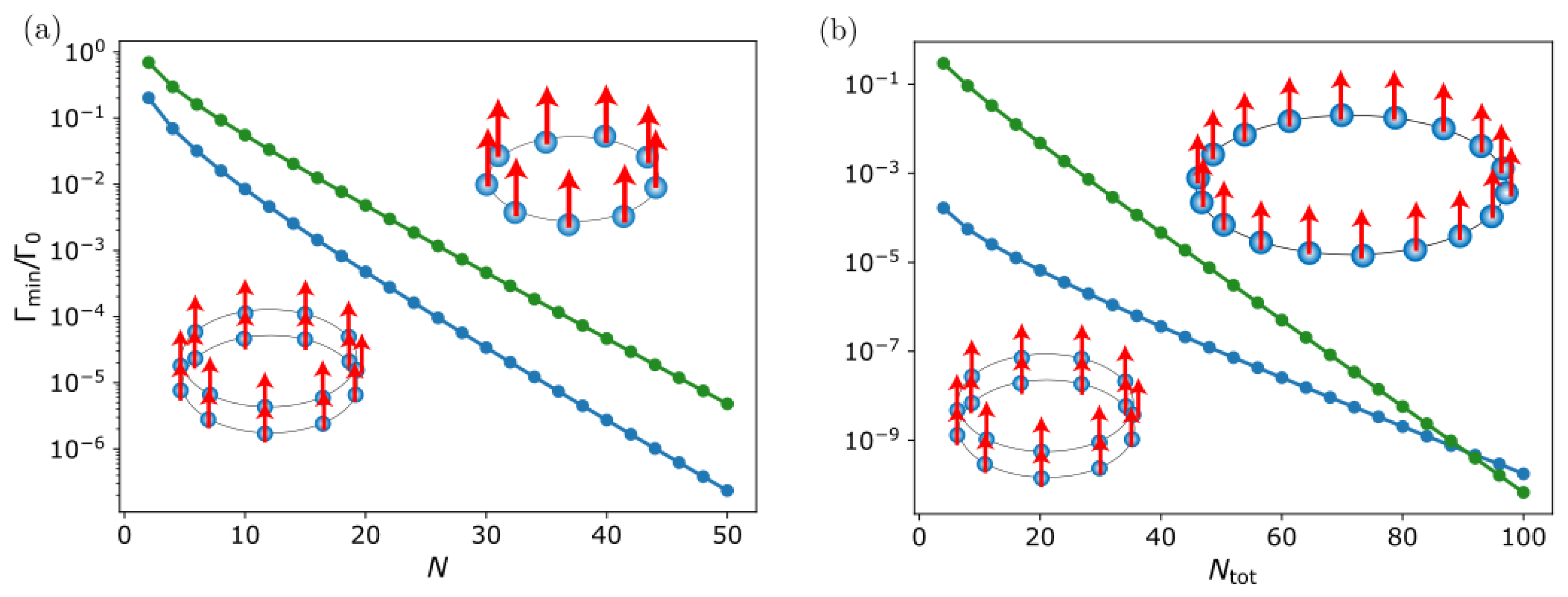
3.1.2. Small Ring Case (Dicke Limit)
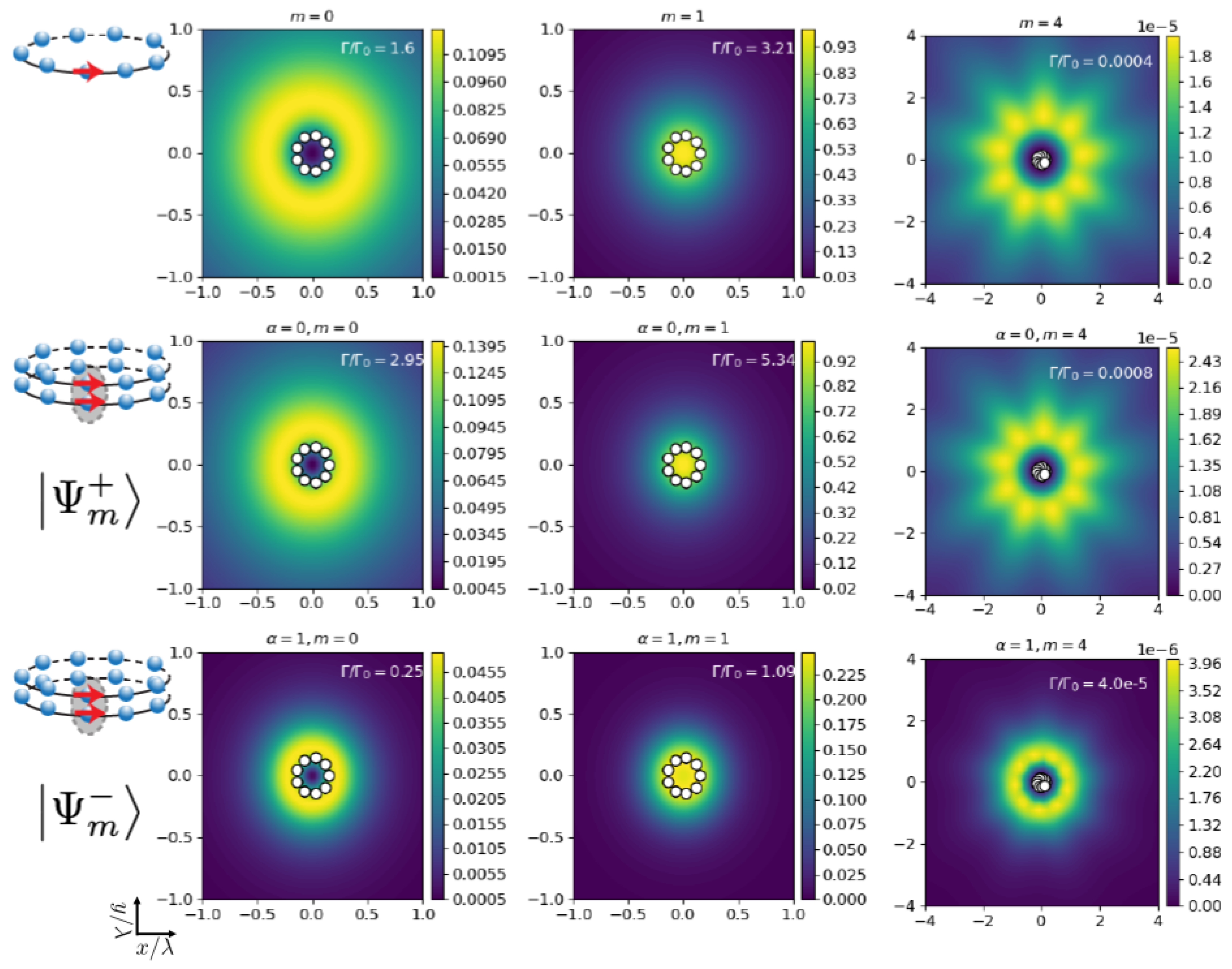
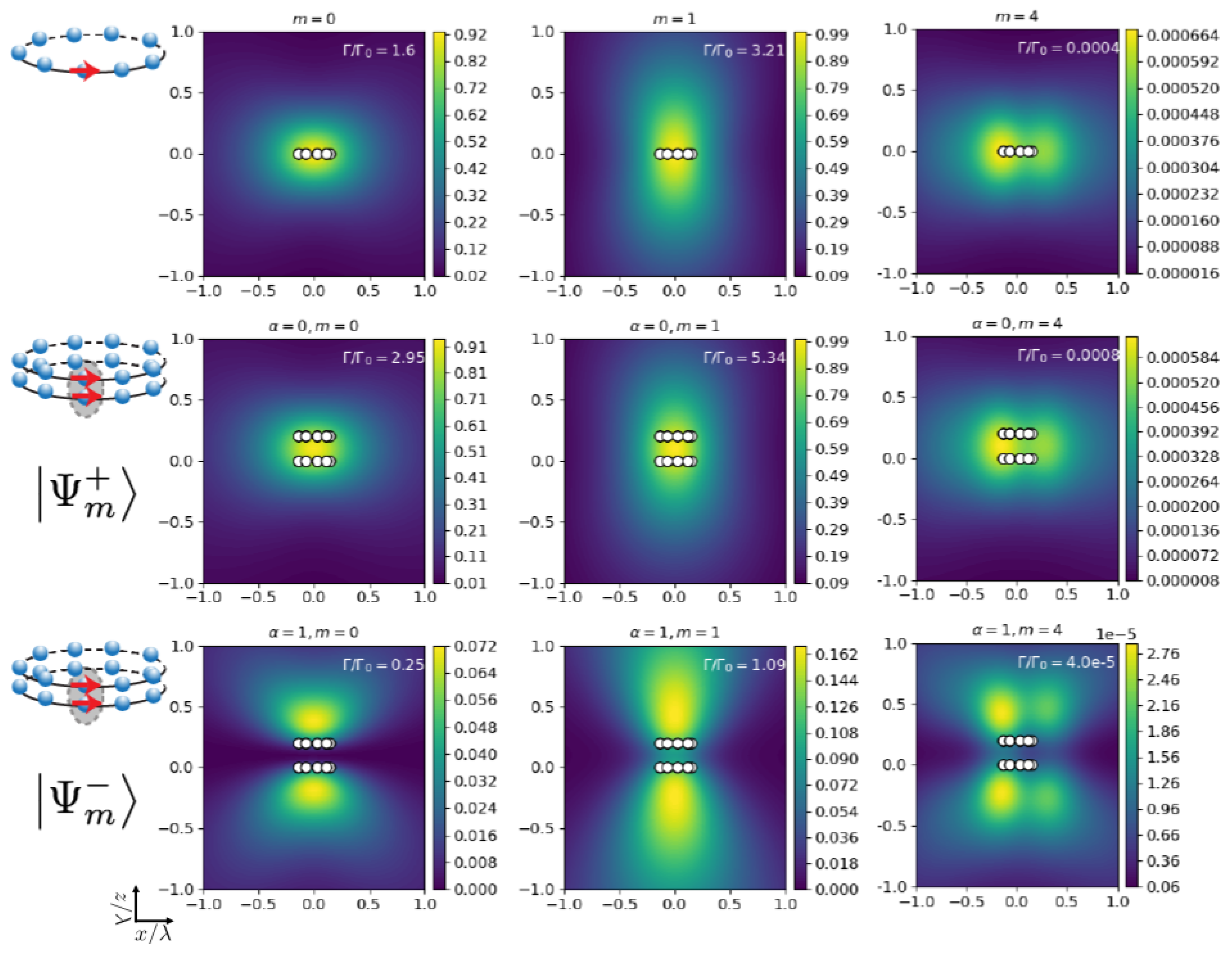
3.2. Optical Properties of Two Coupled Nano-Rings
3.2.1. Coupled Identical Non-Rotated Rings ()
3.2.2. Coupled Unequal Rings with Rotation ()
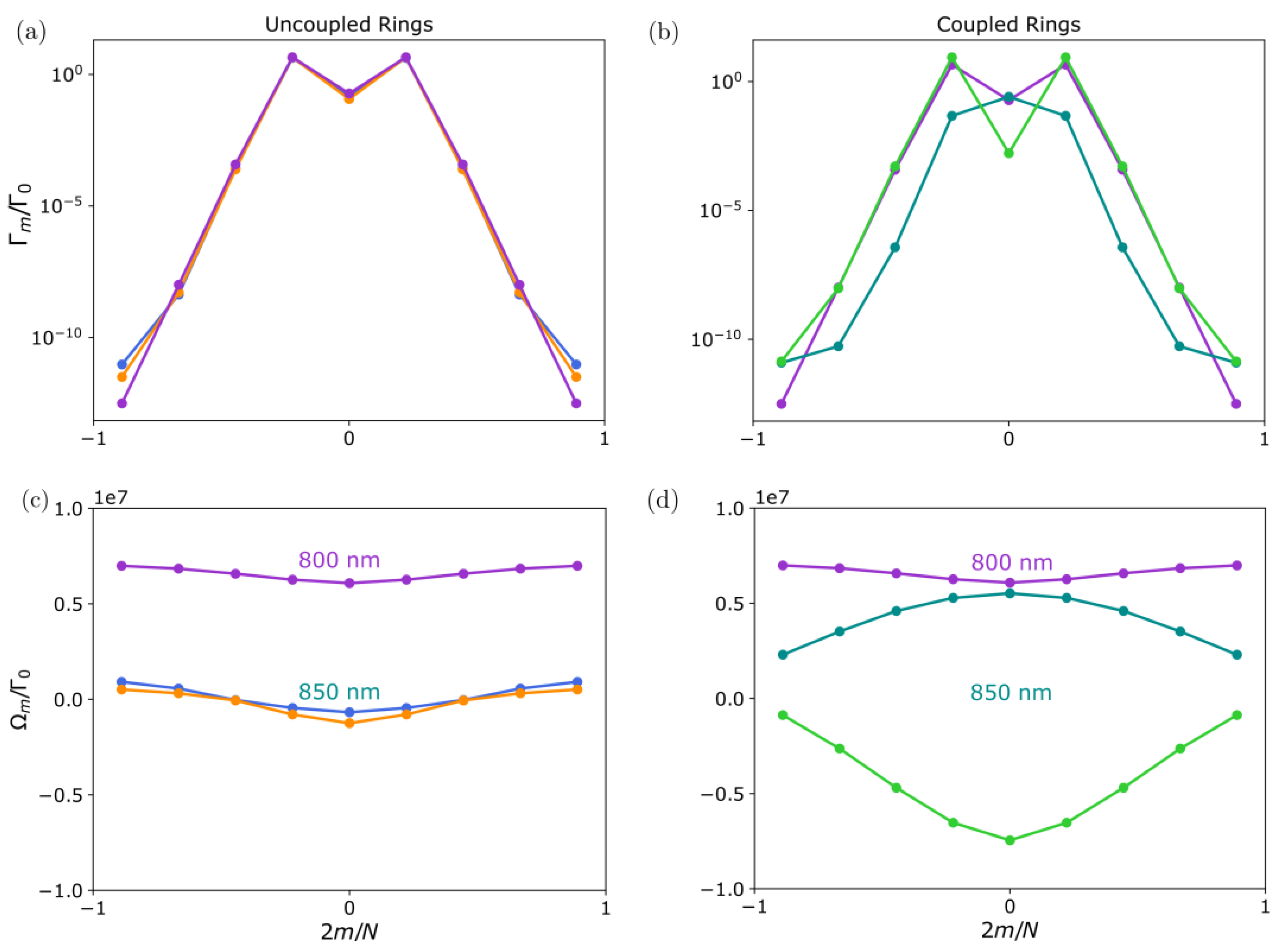
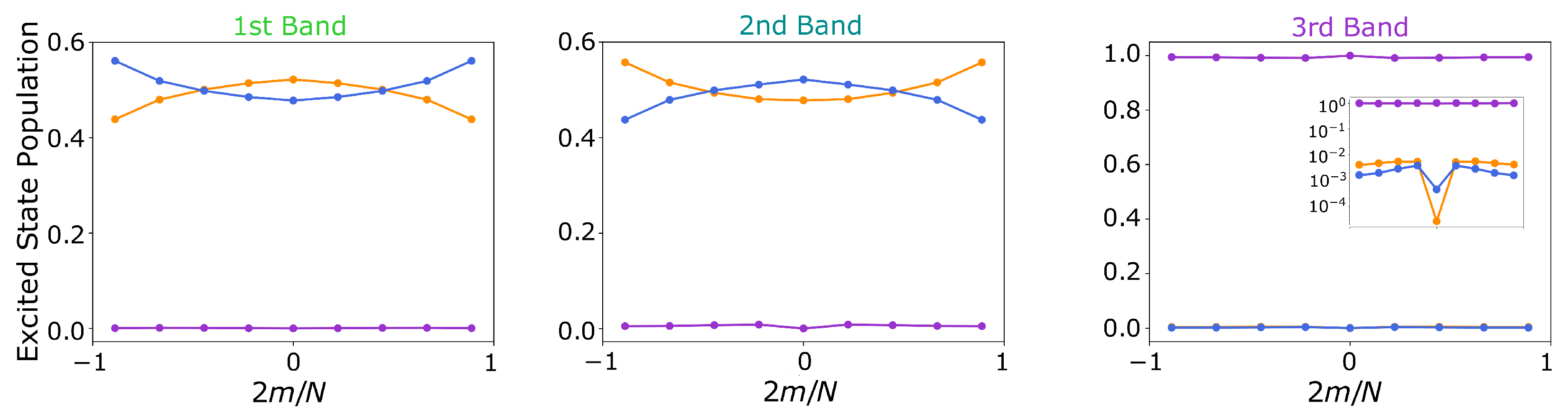
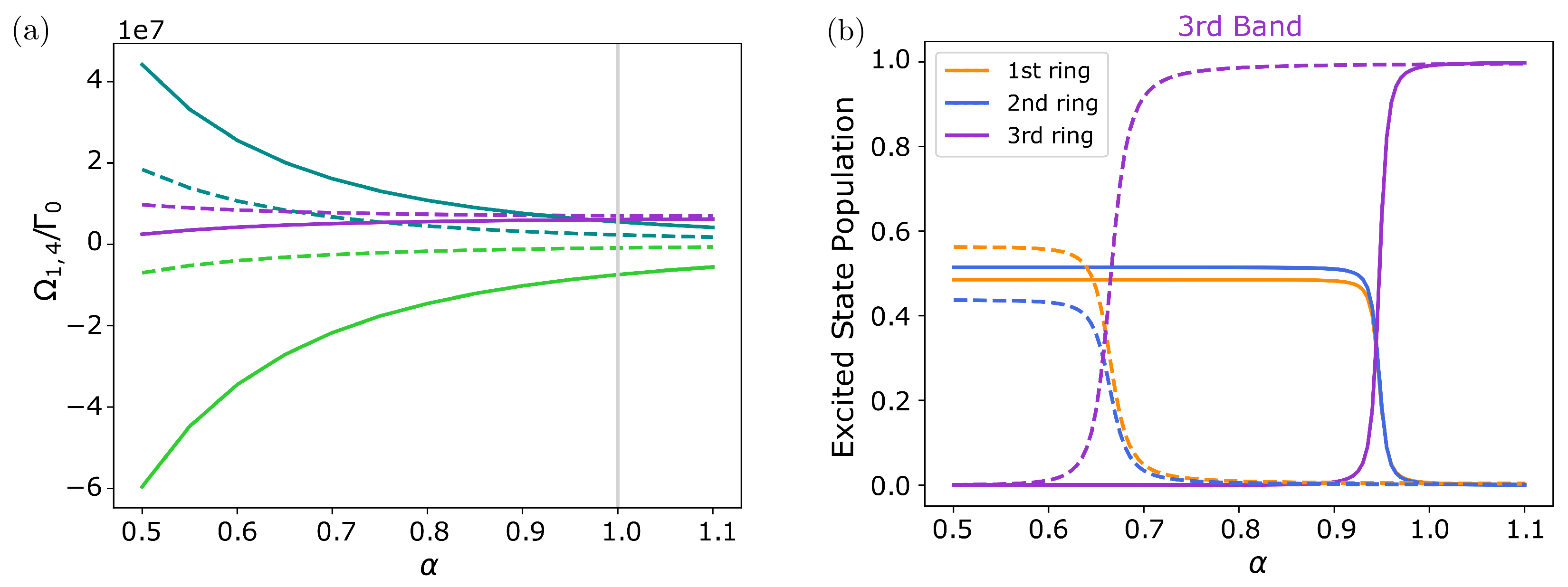
3.3. B850 and B800 Bands in LH2
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef]
- Gross, M.; Haroche, S. Superradiance: An essay on the theory of collective spontaneous emission. Phys. Rep. 1982, 93, 301–396. [Google Scholar] [CrossRef]
- Guerin, W.; Araújo, M.O.; Kaiser, R. Subradiance in a large cloud of cold atoms. Phys. Rev. Lett. 2016, 116, 083601. [Google Scholar] [CrossRef]
- Solano, P.; Barberis-Blostein, P.; Fatemi, F.K.; Orozco, L.A.; Rolston, S.L. Super-radiance reveals infinite-range dipole interactions through a nanofiber. Nat. Commun. 2017, 8, 1–7. [Google Scholar] [CrossRef]
- Porras, D.; Cirac, J.I. Collective generation of quantum states of light by entangled atoms. Phys. Rev. A 2008, 78, 1–14. [Google Scholar] [CrossRef]
- Zoubi, H.; Ritsch, H. Bright and dark excitons in an atom-pair–filled optical lattice within a cavity. EPL Europhys. Lett. 2008, 82, 14001. [Google Scholar] [CrossRef]
- Jenkins, S.D.; Ruostekoski, J. Controlled manipulation of light by cooperative response of atoms in an optical lattice. Phys. Rev. A 2012, 86, 1–5. [Google Scholar] [CrossRef]
- Jenkins, S.D.; Ruostekoski, J. Metamaterial transparency induced by cooperative electromagnetic interactions. Phys. Rev. Lett. 2013, 111, 1–5. [Google Scholar] [CrossRef]
- Plankensteiner, D.; Ostermann, L.; Ritsch, H.; Genes, C. Selective protected state preparation of coupled dissipative quantum emitters. Sci. Rep. 2015, 5, 16231. [Google Scholar] [CrossRef]
- Bettles, R.J.; Gardiner, S.A.; Adams, C.S. Cooperative ordering in lattices of interacting two-level dipoles. Phys. Rev. A 2015, 92, 063822. [Google Scholar] [CrossRef]
- González-Tudela, A.; Hung, C.L.; Chang, D.E.; Cirac, J.I.; Kimble, H.J. Subwavelength vacuum lattices and atom–atom interactions in two-dimensional photonic crystals. Nat. Photonics 2015, 9, 320–325. [Google Scholar] [CrossRef]
- Sutherland, R.; Robicheaux, F. Collective dipole-dipole interactions in an atomic array. Phys. Rev. A 2016, 94, 013847. [Google Scholar] [CrossRef]
- Bettles, R.J.; Gardiner, S.A.; Adams, C.S. Cooperative eigenmodes and scattering in one-dimensional atomic arrays. Phys. Rev. A 2016, 94, 043844. [Google Scholar] [CrossRef]
- Bettles, R.J.; Gardiner, S.A.; Adams, C.S. Enhanced Optical Cross Section via Collective Coupling of Atomic Dipoles in a 2D Array. Phys. Rev. Lett. 2016, 116, 103602. [Google Scholar] [CrossRef] [PubMed]
- Shahmoon, E.; Wild, D.S.; Lukin, M.D.; Yelin, S.F. Cooperative resonances in light scattering from two-dimensional atomic arrays. arXiv 2016, arXiv:1610.00138. [Google Scholar] [CrossRef] [PubMed]
- Asenjo-Garcia, A.; Hood, J.D.; Chang, D.E.; Kimble, H.J. Atom-light interactions in quasi-1D nanostructures: A Green’s function perspective. Phys. Rev. A 2017, 95, 033818. [Google Scholar] [CrossRef]
- Asenjo-Garcia, A.; Moreno-Cardoner, M.; Albrecht, A.; Kimble, H.J.; Chang, D.E. Exponential improvement in photon storage fidelities using subradiance and "selective radiance" in atomic arrays. Phys. Rev. X 2017, 7, 031024. [Google Scholar] [CrossRef]
- Ruostekoski, J.; Javanainen, J. Arrays of strongly coupled atoms in a one-dimensional waveguide. Phys. Rev. A 2017, 96, 033857. [Google Scholar] [CrossRef]
- Hebenstreit, M.; Kraus, B.; Ostermann, L.; Ritsch, H. Subradiance via entanglement in atoms with several independent decay channels. Phys. Rev. Lett. 2017, 118, 143602. [Google Scholar] [CrossRef] [PubMed]
- Chang, D.; Douglas, J.; González-Tudela, A.; Hung, C.L.; Kimble, H. Colloquium: Quantum matter built from nanoscopic lattices of atoms and photons. Rev. Mod. Phys. 2018, 90, 031002. [Google Scholar] [CrossRef]
- Guimond, P.O.; Grankin, A.; Vasilyev, D.; Vermersch, B.; Zoller, P. Subradiant Bell States in Distant Atomic Arrays. Phys. Rev. Lett. 2019, 122, 093601. [Google Scholar] [CrossRef]
- Piñeiro Orioli, A.; Rey, A.M. Dark states of multilevel fermionic atoms in doubly filled optical lattices. Phys. Rev. Lett. 2019, 123, 223601. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Mølmer, K. Theory of Subradiant States of a One-Dimensional Two-Level Atom Chain. Phys. Rev. Lett. 2019, 122, 203605. [Google Scholar] [CrossRef]
- Kornovan, D.; Corzo, N.; Laurat, J.; Sheremet, A. Extremely subradiant states in a periodic one-dimensional atomic array. Phys. Rev. A 2019, 100, 063832. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Yu, C.; Mølmer, K. Subradiant bound dimer excited states of emitter chains coupled to a one dimensional waveguide. Phys. Rev. Res. 2020, 2, 1–9. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Mølmer, K. Subradiant Emission from Regular Atomic Arrays: Universal Scaling of Decay Rates from the Generalized Bloch Theorem. Phys. Rev. Lett. 2020, 125, 253601. [Google Scholar] [CrossRef] [PubMed]
- Piñeiro Orioli, A.; Rey, A.M. Subradiance of multilevel fermionic atoms in arrays with filling N >= 2. Phys. Rev. A 2020, 101, 043816. [Google Scholar] [CrossRef]
- Manzoni, M.T.; Moreno-Cardoner, M.; Asenjo-Garcia, A.; Porto, J.V.; Gorshkov, A.V.; Chang, D.E. Optimization of photon storage fidelity in ordered atomic arrays. New J. Phys. 2018, 20, 083048. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Walther, V.; Mølmer, K.; Pohl, T. Photon-photon interactions in Rydberg-atom arrays. Quantum 2022, 6, 674. [Google Scholar] [CrossRef]
- Moreno-Cardoner, M.; Goncalves, D.; Chang, D.E. Quantum Nonlinear Optics Based on Two-Dimensional Rydberg Atom Arrays. Phys. Rev. Lett. 2021, 127, 263602. [Google Scholar] [CrossRef]
- Bekenstein, R.; Pikovski, I.; Pichler, H.; Shahmoon, E.; Yelin, S.F.; Lukin, M.D. Quantum metasurfaces with atom arrays. Nat. Phys. 2020, 16, 676–681. [Google Scholar] [CrossRef]
- Wei, Z.Y.; Malz, D.; González-Tudela, A.; Cirac, J.I. Generation of photonic matrix product states with Rydberg atomic arrays. Phys. Rev. Res. 2021, 3, 023021. [Google Scholar] [CrossRef]
- Ostermann, L.; Ritsch, H.; Genes, C. Protected State Enhanced Quantum Metrology with Interacting Two-Level Ensembles. Phys. Rev. Lett. 2013, 111, 123601. [Google Scholar] [CrossRef] [PubMed]
- Henriet, L.; Douglas, J.S.; Chang, D.E.; Albrecht, A. Critical open-system dynamics in a one-dimensional optical-lattice clock. Phys. Rev. A 2019, 99, 023802. [Google Scholar] [CrossRef]
- Moreno-Cardoner, M.; Plankensteiner, D.; Ostermann, L.; Chang, D.E.; Ritsch, H. Subradiance-enhanced excitation transfer between dipole-coupled nanorings of quantum emitters. Phys. Rev. A 2019, 100, 023806. [Google Scholar] [CrossRef]
- Cremer, J.; Plankensteiner, D.; Moreno-Cardoner, M.; Ostermann, L.; Ritsch, H. Polarization control of radiation and energy flow in dipole-coupled nanorings. New J. Phys. 2020, 22. [Google Scholar] [CrossRef]
- Mattioni, A.; Caycedo-Soler, F.; Huelga, S.F.; Plenio, M.B. Design Principles for Long-Range Energy Transfer at Room Temperature. Phys. Rev. X 2021, 11, 041003. [Google Scholar] [CrossRef]
- Mattiotti, F.; Sarovar, M.; Giusteri, G.G.; Borgonovi, F.; Celardo, G.L. Efficient light harvesting and photon sensing via engineered cooperative effects. New J. Phys. 2022, 24, 013027. [Google Scholar] [CrossRef]
- Holzinger, R.; Plankensteiner, D.; Ostermann, L.; Ritsch, H. Nanoscale Coherent Light Source. Phys. Rev. Lett. 2020, 124, 253603. [Google Scholar] [CrossRef]
- Moreno-Cardoner, M.; Holzinger, R.; Ritsch, H. Efficient nano-photonic antennas based on dark states in quantum emitter rings. Opt. Express 2022, 30, 10779–10791. [Google Scholar] [CrossRef]
- McDermott, G.; Prince, S.M.; Freer, A.A.; Hawthornthwaite-Lawless, A.M.; Papiz, M.Z.; Cogdell, R.J.; Isaacs, N.W. Crystal structure of an integral membrane light-harvesting complex from photosynthetic bacteria. Nature 1995, 374, 517–521. [Google Scholar] [CrossRef]
- Bourne Worster, S.; Stross, C.; Vaughan, F.M.W.C.; Linden, N.; Manby, F.R. Structure and Efficiency in Bacterial Photosynthetic Light Harvesting. J. Phys. Chem. Lett. 2019, 10, 7383–7390. [Google Scholar] [CrossRef]
- Jang, S.; Newton, M.D.; Silbey, R.J. Multichromophoric Förster Resonance Energy Transfer. Phys. Rev. Lett. 2004, 92, 218301. [Google Scholar] [CrossRef]
- Jang, S.; Cheng, Y.C. Resonance energy flow dynamics of coherently delocalized excitons in biological and macromolecular systems: Recent theoretical advances and open issues. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2013, 3, 84–104. [Google Scholar] [CrossRef]
- Pruchyathamkorn, J.; Kendrick, W.J.; Frawley, A.T.; Mattioni, A.; Caycedo-Soler, F.; Huelga, S.F.; Plenio, M.B.; Anderson, H.L. A Complex Comprising a Cyanine Dye Rotaxane and a Porphyrin Nanoring as a Model Light-Harvesting System. Angew. Chem. Int. Ed. 2020, 59, 16455–16458. [Google Scholar] [CrossRef] [PubMed]
- Rui, J.; Wei, D.; Rubio-Abadal, A.; Hollerith, S.; Zeiher, J.; Stamper-Kurn, D.M.; Gross, C.; Bloch, I. A subradiant optical mirror formed by a single structured atomic layer. Nature 2020, 583, 369–374. [Google Scholar] [CrossRef] [PubMed]
- Bakr, W.S.; Gillen, J.I.; Peng, A.; Fölling, S.; Greiner, M. A quantum gas microscope for detecting single atoms in a Hubbard-regime optical lattice. Nature 2009, 462, 74–77. [Google Scholar] [CrossRef]
- Sherson, J.F.; Weitenberg, C.; Endres, M.; Cheneau, M.; Bloch, I.; Kuhr, S. Single-atom-resolved fluorescence imaging of an atomic Mott insulator. Nature 2010, 467, 68–72. [Google Scholar] [CrossRef] [PubMed]
- Weitenberg, C.; Endres, M.; Sherson, J.F.; Cheneau, M.; Schau, P.; Fukuhara, T.; Bloch, I.; Kuhr, S. Single-spin addressing in an atomic Mott insulator. Nature 2011, 471, 319–325. [Google Scholar] [CrossRef] [PubMed]
- Barredo, D.; De Léséleuc, S.; Lienhard, V.; Lahaye, T.; Browaeys, A. An atom-by-atom assembler of defect-free arbitrary two-dimensional atomic arrays. Science 2016, 354, 1021–1023. [Google Scholar] [CrossRef]
- Endres, M.; Bernien, H.; Keesling, A.; Levine, H.; Anschuetz, E.R.; Krajenbrink, A.; Senko, C.; Vuletic, V.; Greiner, M.; Lukin, M.D. Atom-by-atom assembly of defect-free one-dimensional cold atom arrays. Science 2016, 354, 1024–1027. [Google Scholar] [CrossRef]
- Barredo, D.; Lienhard, V.; de Léséleuc, S.; Lahaye, T.; Browaeys, A. Synthetic three-dimensional atomic structures assembled atom by atom. Nature 2018, 561, 79–82. [Google Scholar] [CrossRef]
- Norcia, M.A.; Young, A.W.; Kaufman, A.M. Microscopic Control and Detection of Ultracold Strontium in Optical-Tweezer Arrays. Phys. Rev. X 2018, 8, 41054. [Google Scholar] [CrossRef]
- Schlosser, M.; Tichelmann, S.; Schäffner, D.; de Mello, D.O.; Hambach, M.; Birkl, G. Large-scale multilayer architecture of single-atom arrays with individual addressability. arXiv 2019, arXiv:1902.05424. [Google Scholar]
- Wang, Z.; Li, H.; Feng, W.; Song, X.; Song, C.; Liu, W.; Guo, Q.; Zhang, X.; Dong, H.; Zheng, D.; et al. Controllable switching between superradiant and subradiant states in a 10-qubit superconducting circuit. Phys. Rev. Lett. 2020, 124, 013601. [Google Scholar] [CrossRef]
- Mirhosseini, M.; Kim, E.; Zhang, X.; Sipahigil, A.; Dieterle, P.B.; Keller, A.J.; Asenjo-Garcia, A.; Chang, D.E.; Painter, O. Cavity quantum electrodynamics with atom-like mirrors. Nature 2019, 569, 692–697. [Google Scholar] [CrossRef]
- van Loo, A.F.; Fedorov, A.; Lalumière, K.; Sanders, B.C.; Blais, A.; Wallraff, A. Photon-Mediated Interactions Between Distant Artificial Atoms. Science 2013, 342, 1494–1496. [Google Scholar] [CrossRef]
- Vukajlovic-Plestina, J.; Kim, W.; Dubrovski, V.G.; Tütüncüoğlu, G.; Lagier, M.; Potts, H.; Friedl, M.; Fontcuberta i Morral, A. Engineering the Size Distributions of Ordered GaAs Nanowires on Silicon. Nano Lett. 2017, 17, 4101–4108. [Google Scholar] [CrossRef]
- Swinkels, M.Y.; Campo, A.; Vakulov, D.; Kim, W.; Gagliano, L.; Steinvall, S.E.; Detz, H.; De Luca, M.; Lugstein, A.; Bakkers, E.; et al. Measuring the Optical Absorption of Single Nanowires. Phys. Rev. Appl. 2020, 14, 024045. [Google Scholar] [CrossRef]
- Holzinger, R.; Oh, S.A.; Reitz, M.; Ritsch, H.; Genes, C. Cooperative subwavelength molecular quantum emitter arrays. Phys. Rev. Res. 2022, 4, 033116. [Google Scholar] [CrossRef]
- Lehmberg, R. Radiation from an N-atom system. I. General formalism. Phys. Rev. A 1970, 2, 883. [Google Scholar] [CrossRef]
- Ostermann, L.; Zoubi, H.; Ritsch, H. Cascaded collective decay in regular arrays of cold trapped atoms. Opt. Express 2012, 20, 29634–29645. [Google Scholar] [CrossRef]
- Cogdell, R.J.; Gall, A.; Köhler, J. The architecture and function of the light-harvesting apparatus of purple bacteria: From single molecules to in vivo membranes. Q. Rev. Biophys. 2006, 39, 227–324. [Google Scholar] [CrossRef] [PubMed]
- Mirkovic, T.; Ostroumov, E.E.; Anna, J.M.; Van Grondelle, R.; Govindjee; Scholes, G.D. Light absorption and energy transfer in the antenna complexes of photosynthetic organisms. Chem. Rev. 2017, 117, 249–293. [Google Scholar] [CrossRef]
- Montemayor, D.; Rivera, E.; Jang, S.J. Computational Modeling of Exciton-Bath Hamiltonians for Light Harvesting 2 and Light Harvesting 3 Complexes of Purple Photosynthetic Bacteria at Room Temperature. J. Phys. Chem. B 2018, 122, 3815–3825. [Google Scholar] [CrossRef]
- Caycedo-Soler, F.; Schroeder, C.A.; Autenrieth, C.; Pick, A.; Ghosh, R.; Huelga, S.F.; Plenio, M.B. Quantum redirection of antenna absorption to photosynthetic reaction centers. J. Phys. Chem. Lett. 2017, 8, 6015–6021. [Google Scholar] [CrossRef]
- Jang, S.J.; Mennucci, B. Delocalized excitons in natural light-harvesting complexes. Rev. Mod. Phys. 2018, 90, 035003. [Google Scholar] [CrossRef]
- Scholes, G.D.; Fleming, G.R. On the Mechanism of Light Harvesting in Photosynthetic Purple Bacteria: B800 to B850 Energy Transfer. J. Phys. Chem. B 2000, 104, 1854–1868. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Silbey, R.J. Coherence in the B800 Ring of Purple Bacteria LH2. Phys. Rev. Lett. 2006, 96, 028103. [Google Scholar] [CrossRef]
- Jang, S.J.; Newton, M.D.; Silbey, R.J. Multichromophoric Förster resonance energy transfer from b800 to b850 in the light harvesting complex 2: Evidence for subtle energetic optimization by purple bacteria. J. Phys. Chem. B 2007, 111 24, 6807–6814. [Google Scholar] [CrossRef]
- Olaya-Castro, A.; Lee, C.F.; Olsen, F.F.; Johnson, N.F. Efficiency of energy transfer in a light-harvesting system under quantum coherence. Phys. Rev. B 2008, 78, 085115. [Google Scholar] [CrossRef]
- Cleary, L.; Chen, H.; Chuang, C.; Silbey, R.J.; Cao, J. Optimal fold symmetry of LH2 rings on a photosynthetic membrane. Proc. Natl. Acad. Sci. USA 2013, 110, 8537–8542. [Google Scholar] [CrossRef]
- Scholes, G.D.; Gould, I.R.; Cogdell, R.J.; Fleming, G.R. Ab Initio Molecular Orbital Calculations of Electronic Couplings in the LH2 Bacterial Light-Harvesting Complex of Rps. Acidophila. J. Phys. Chem. B 1999, 103, 2543–2553. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scheil, V.; Holzinger, R.; Moreno-Cardoner, M.; Ritsch, H. Optical Properties of Concentric Nanorings of Quantum Emitters. Nanomaterials 2023, 13, 851. https://doi.org/10.3390/nano13050851
Scheil V, Holzinger R, Moreno-Cardoner M, Ritsch H. Optical Properties of Concentric Nanorings of Quantum Emitters. Nanomaterials. 2023; 13(5):851. https://doi.org/10.3390/nano13050851
Chicago/Turabian StyleScheil, Verena, Raphael Holzinger, Maria Moreno-Cardoner, and Helmut Ritsch. 2023. "Optical Properties of Concentric Nanorings of Quantum Emitters" Nanomaterials 13, no. 5: 851. https://doi.org/10.3390/nano13050851
APA StyleScheil, V., Holzinger, R., Moreno-Cardoner, M., & Ritsch, H. (2023). Optical Properties of Concentric Nanorings of Quantum Emitters. Nanomaterials, 13(5), 851. https://doi.org/10.3390/nano13050851





