Computer Simulations of EMHD Casson Nanofluid Flow of Blood through an Irregular Stenotic Permeable Artery: Application of Koo-Kleinstreuer-Li Correlations
Abstract
:1. Introduction
- KKL correlations are employed for modeling nanofluid flow through a permeable stenosed artery.
- EMHD Casson fluid flow is considered along with Joule heating, radiation, and viscous dissipation.
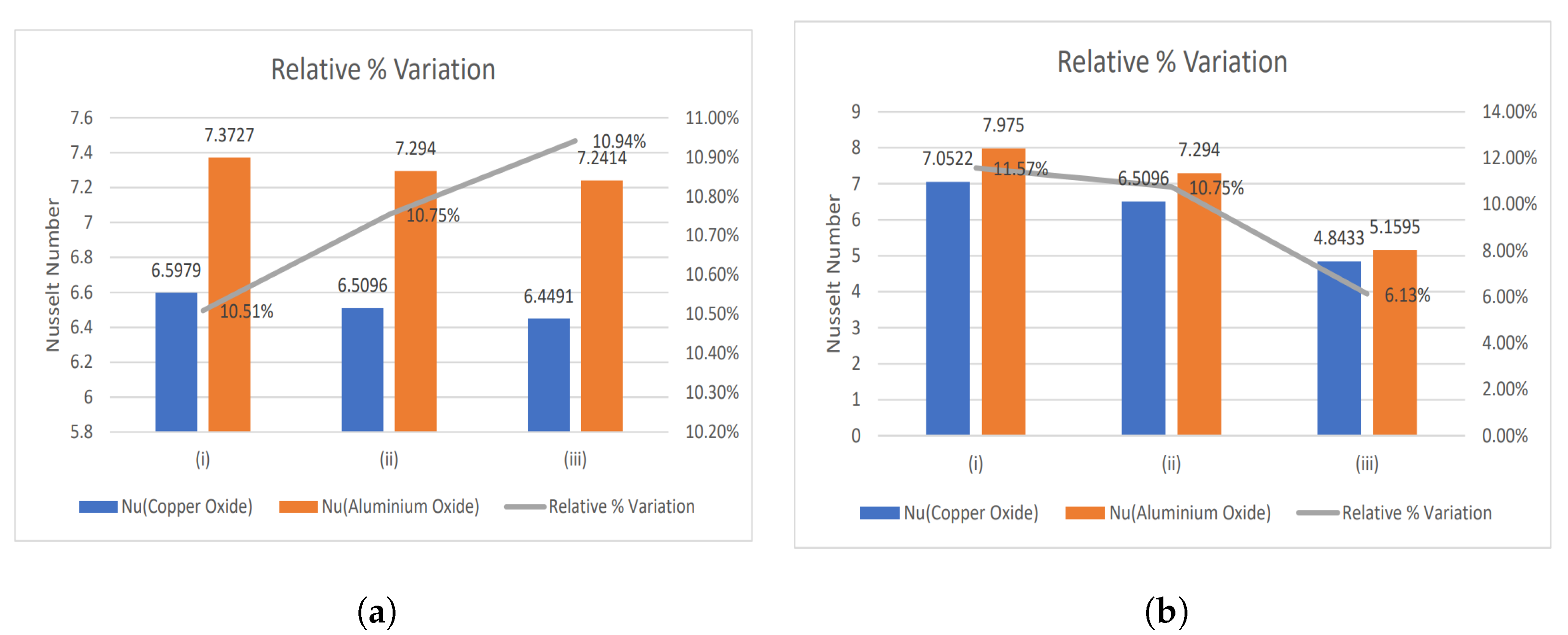
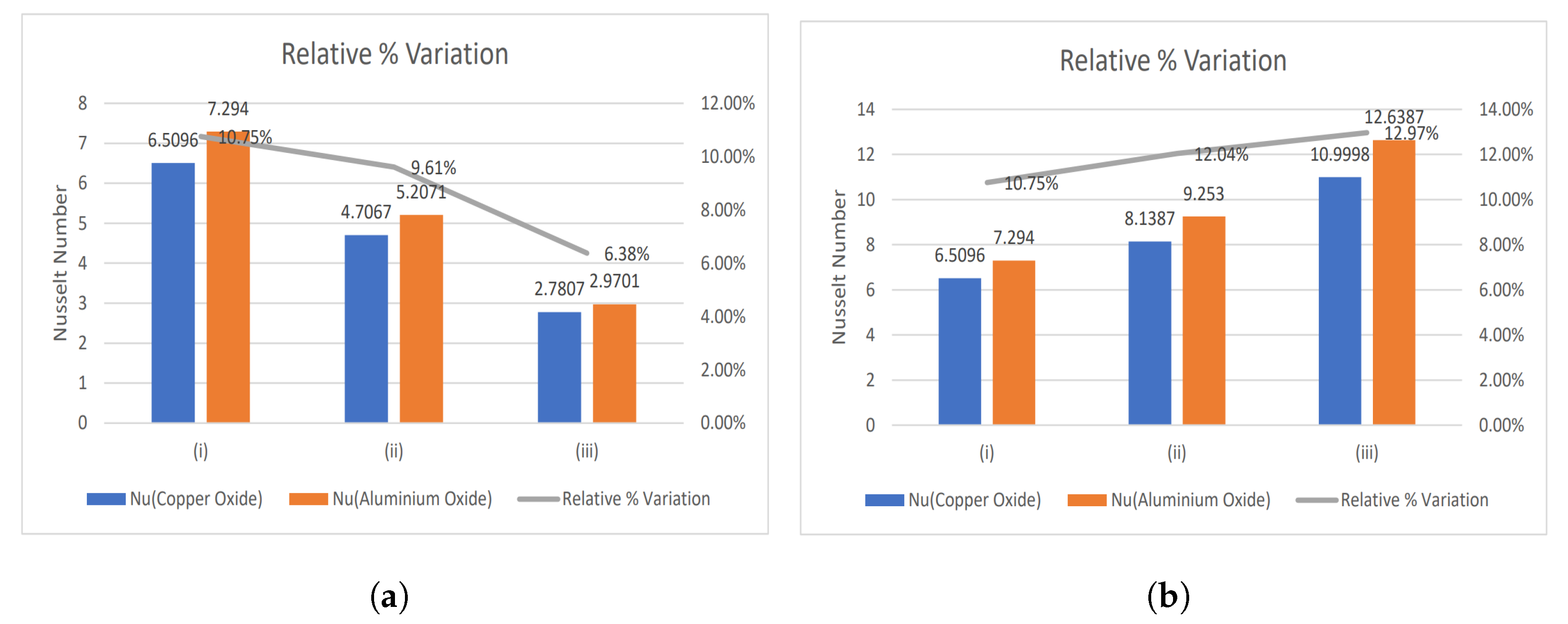
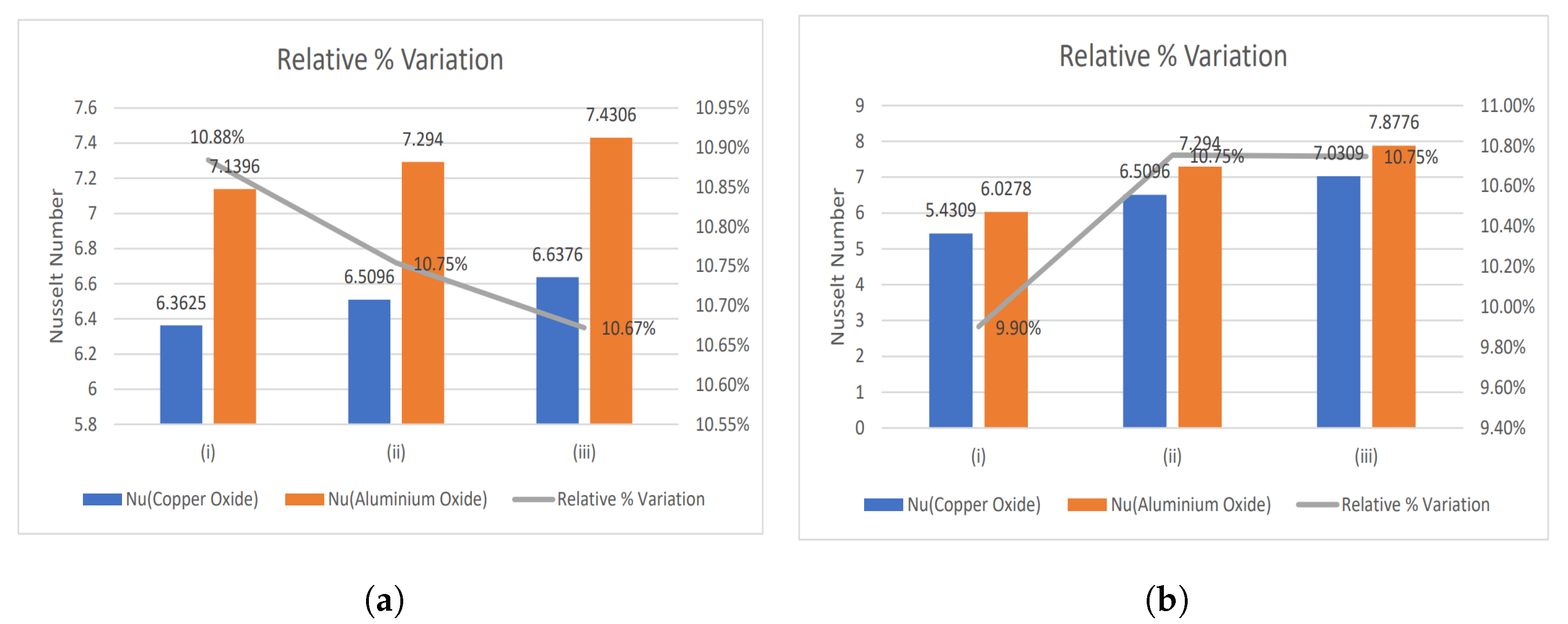
- The relative % variation for the Nusselt number has been calculated and portrayed using bar graphs.
2. Mathematical Formulation
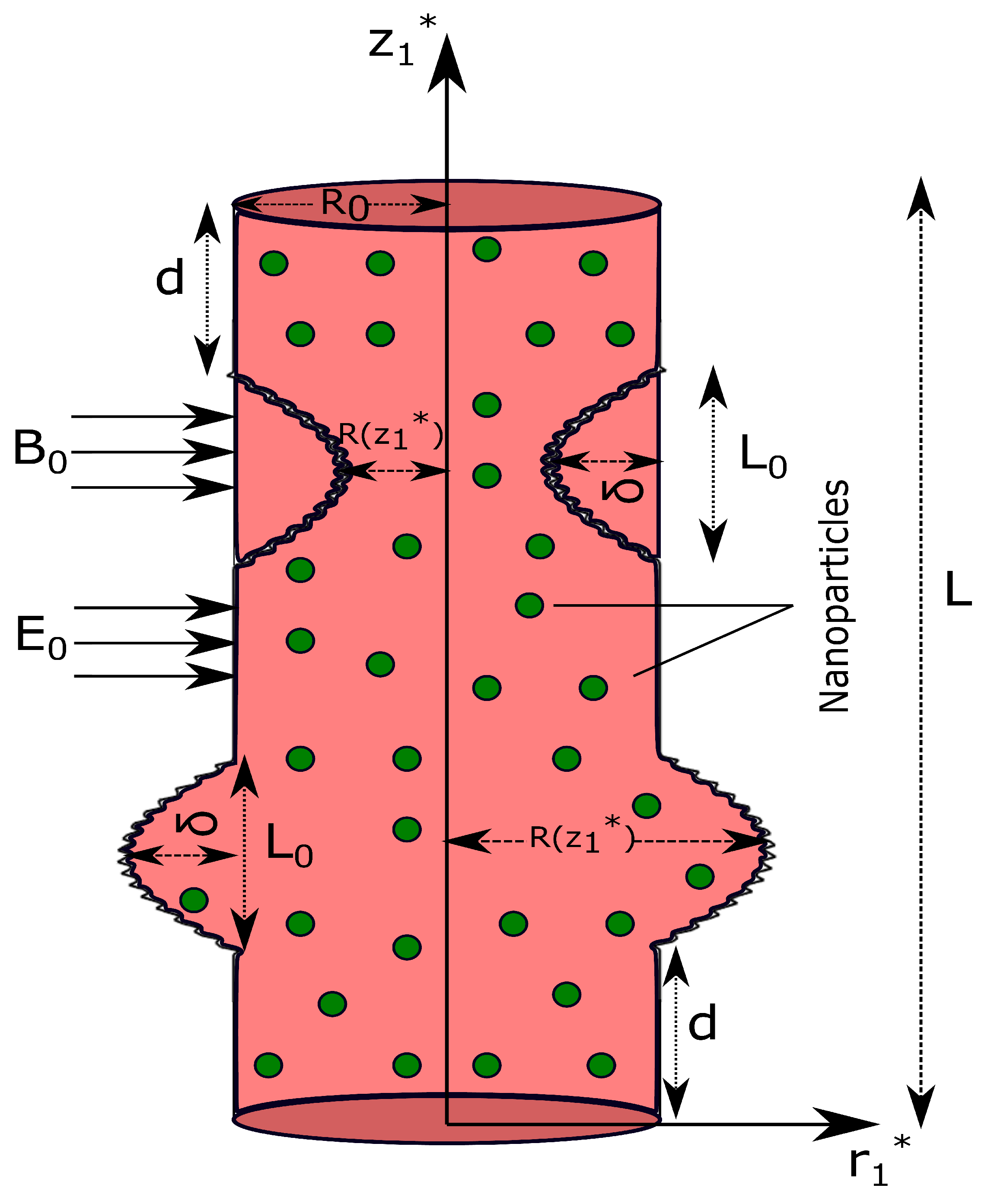
2.1. Mathematical Representation of the Stenosis and Aneursym
2.2. Governing Equations
2.3. Koo-Kleinstreuer-Li (KKL) Correlation for Nanofluid Simulation
2.4. Nanoparticle and Base Fluid Features
2.5. Non-Dimensional Analysis
2.6. Radial Coordinate Transformation
3. Numerical Procedure
3.1. Discretization
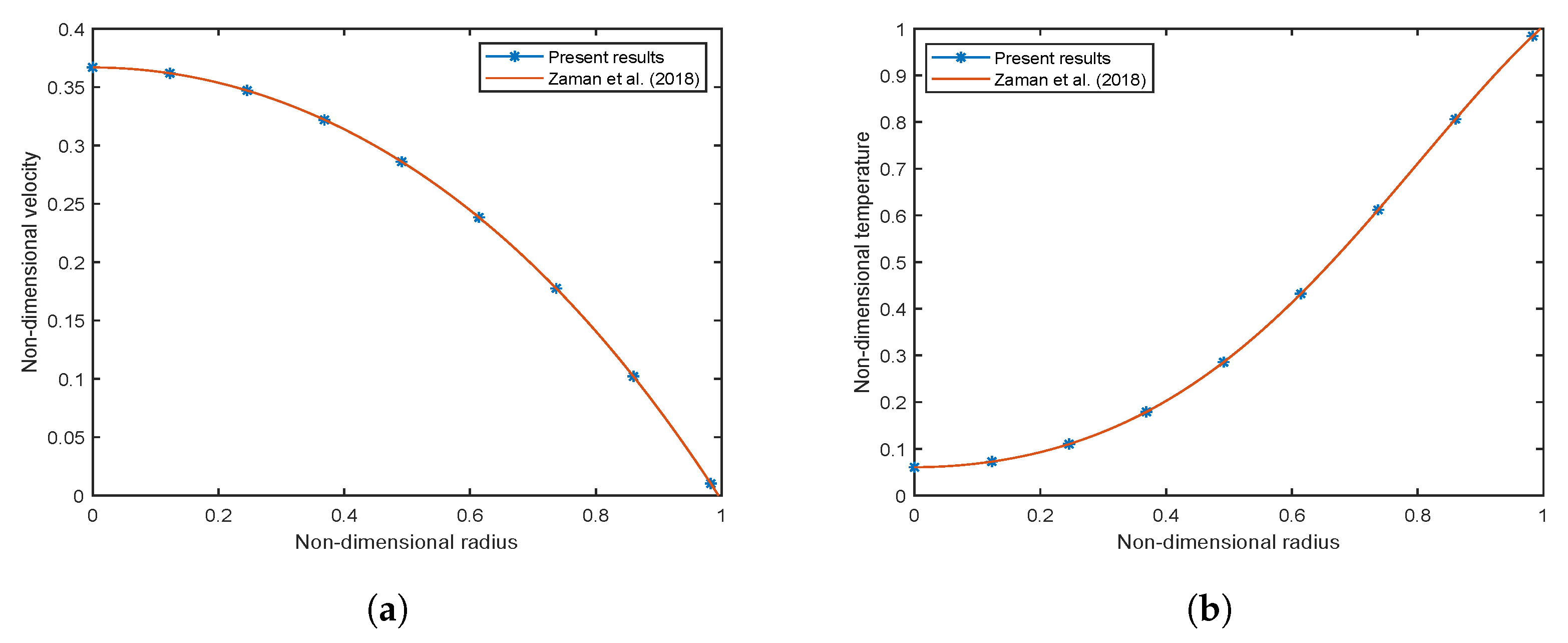
3.2. Validation of the Employed Numerical Scheme
3.2.1. Mesh Independence
3.2.2. Validation with Existing Literature
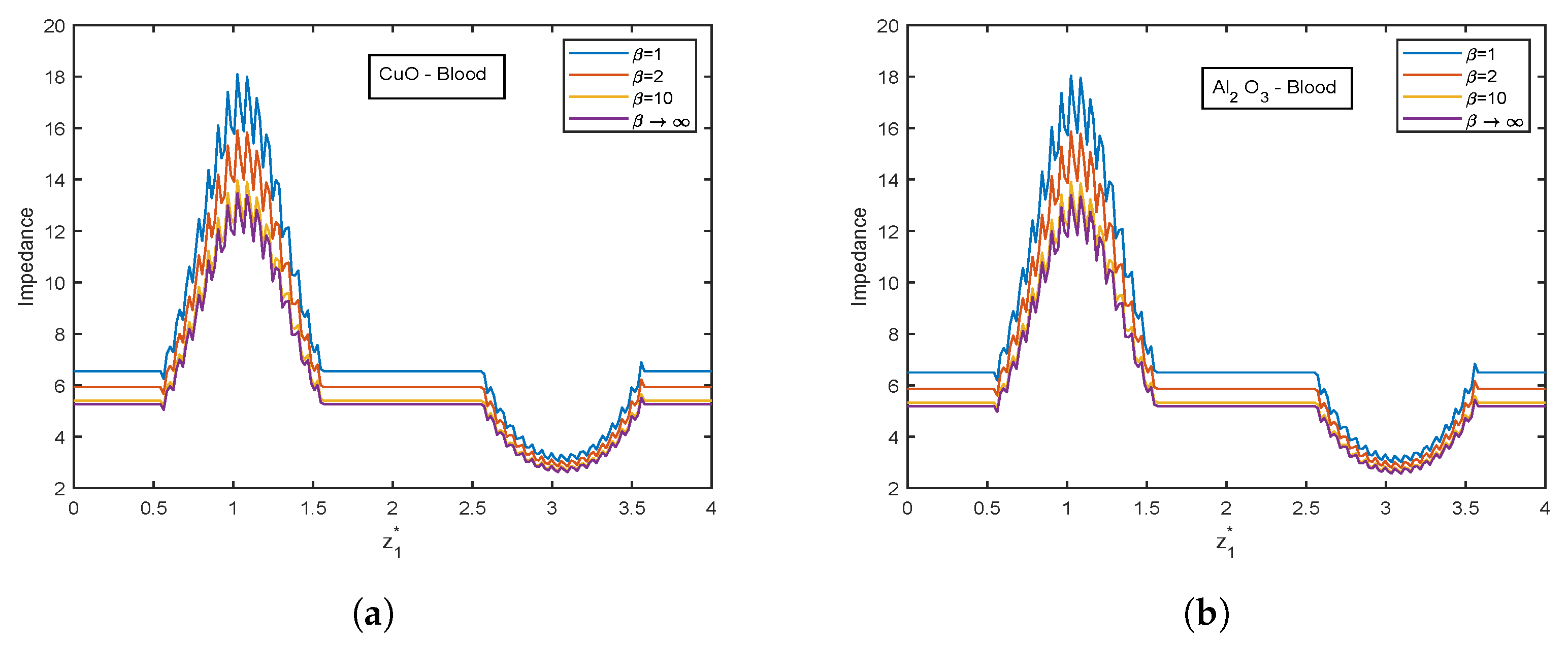
4. Results and Graphical Analysis
4.1. Nusselt Number and Enhancement Ratio
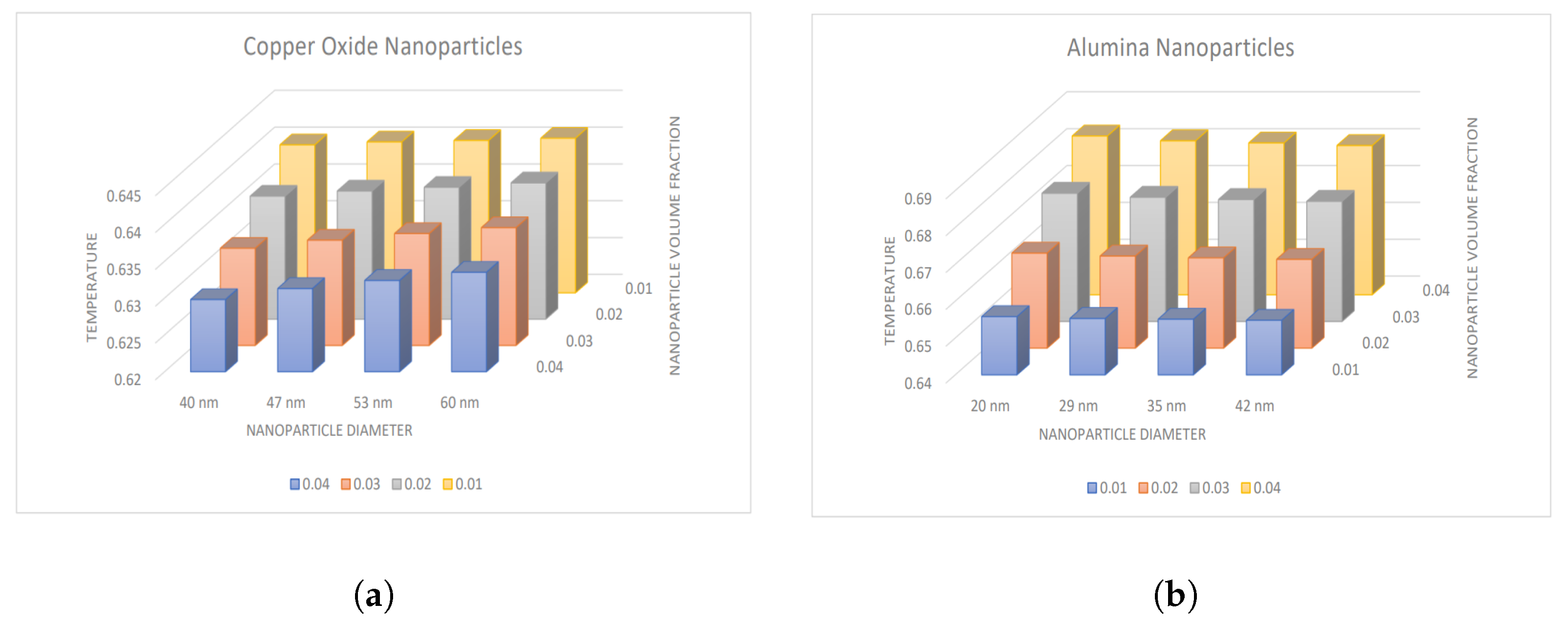
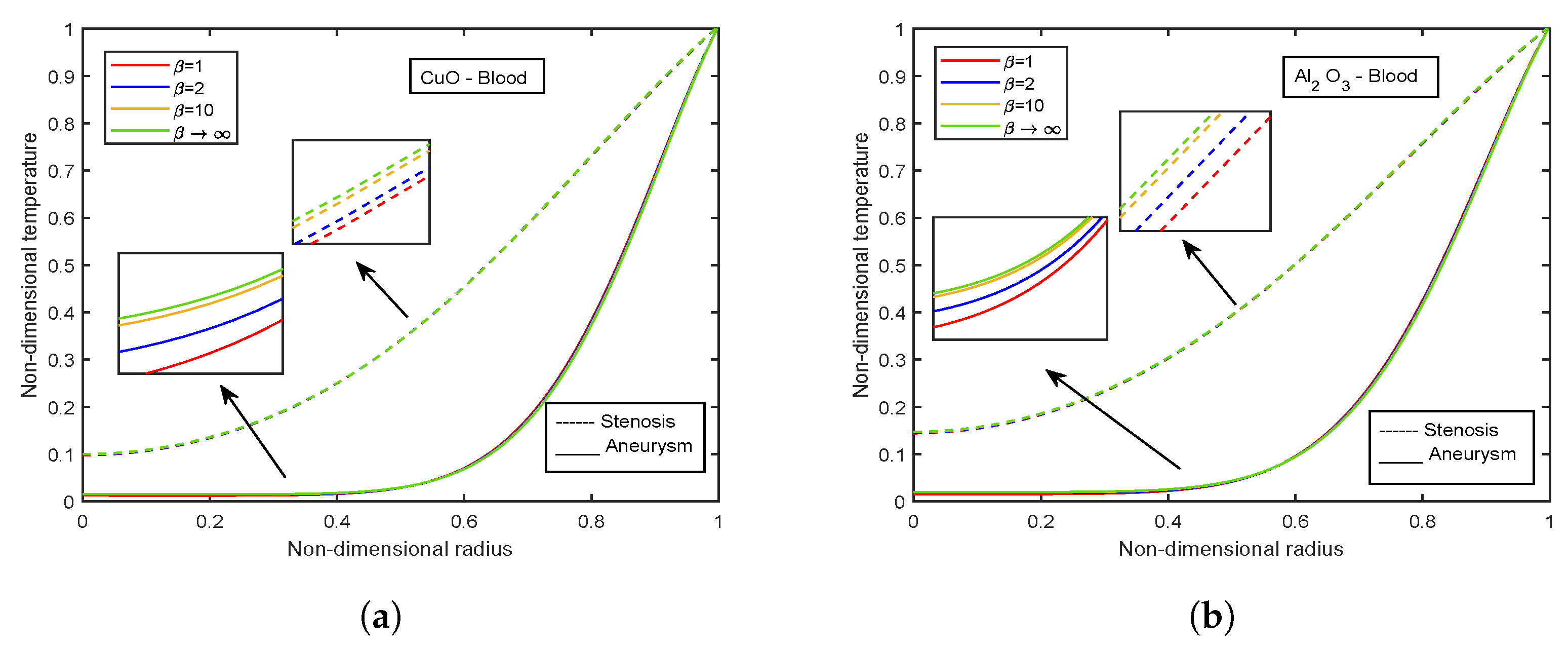
4.2. Influence of Nanoparticle Diameter and Volume Fraction
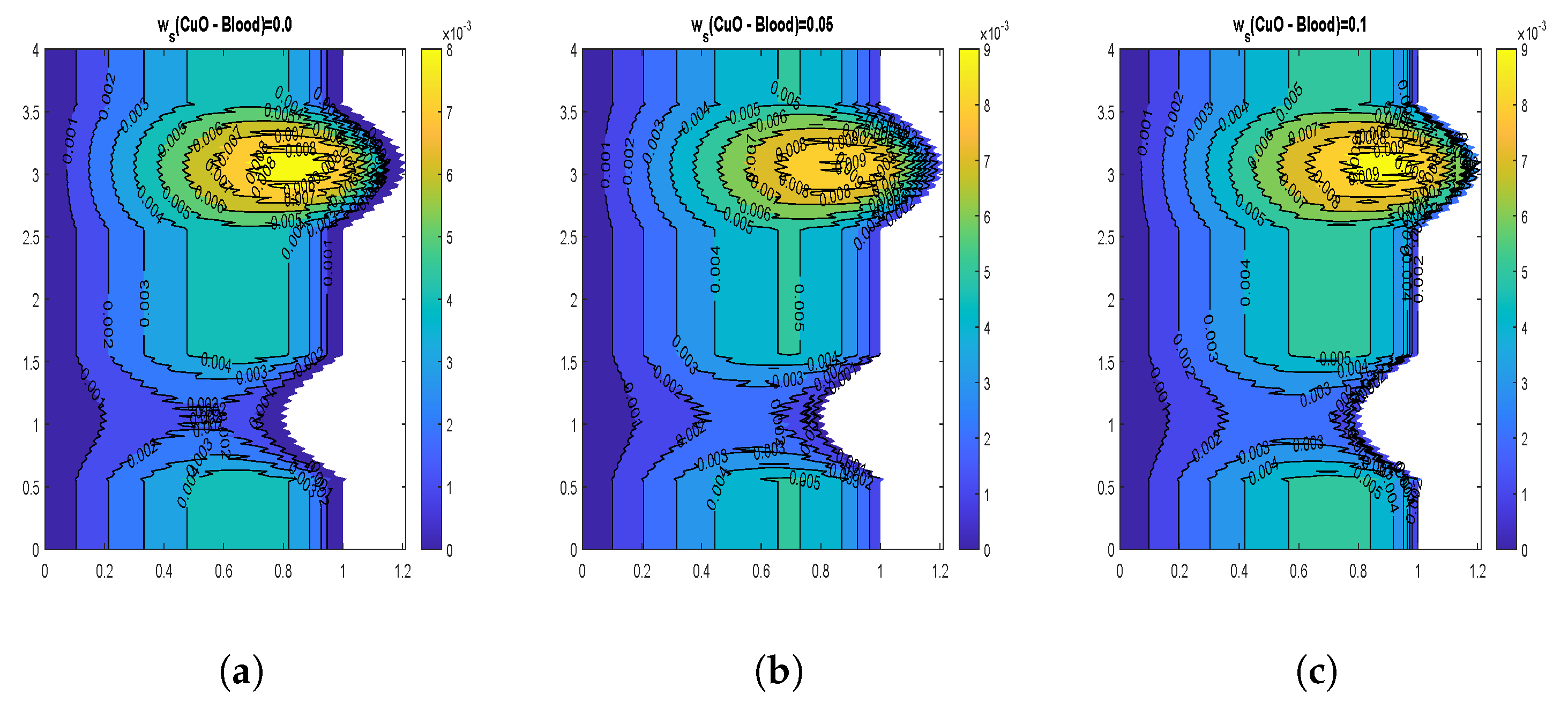
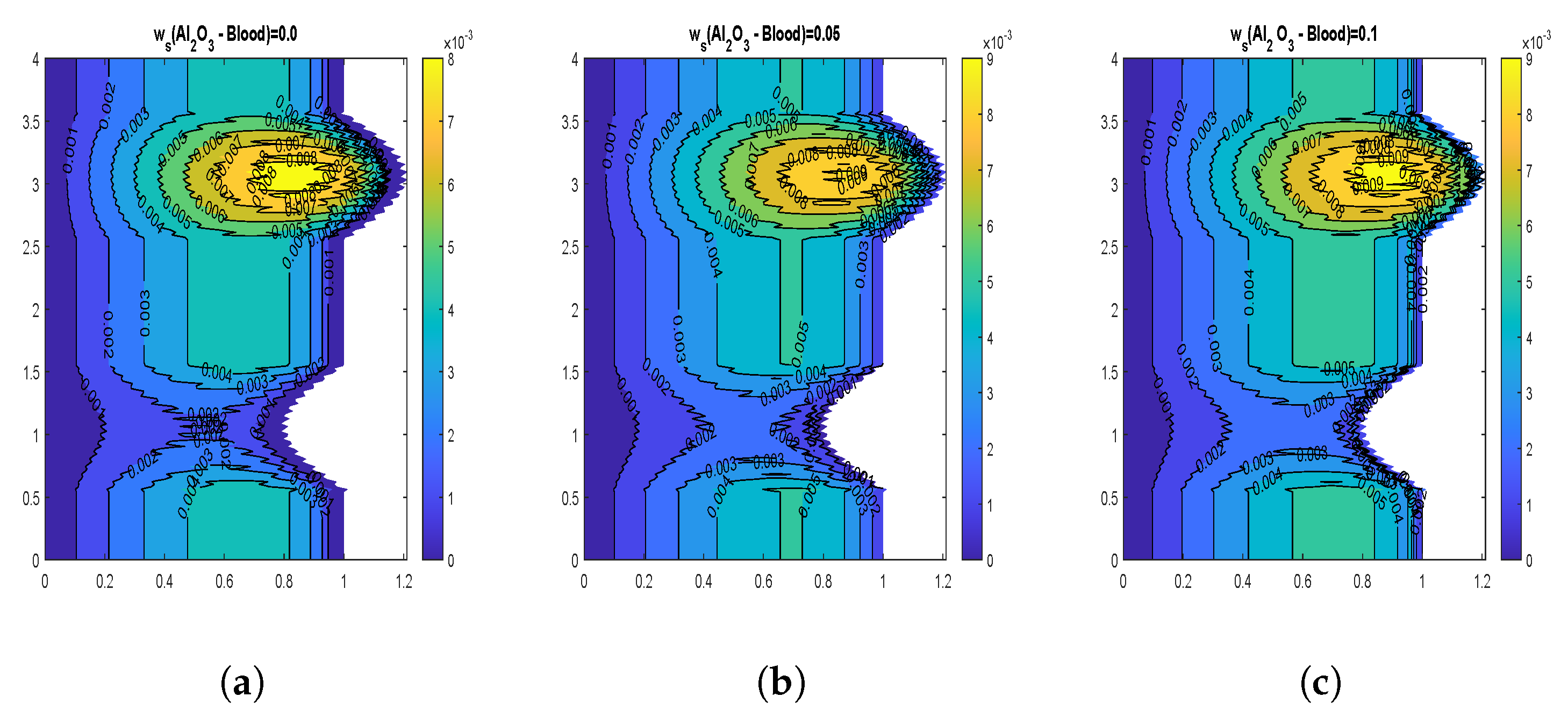
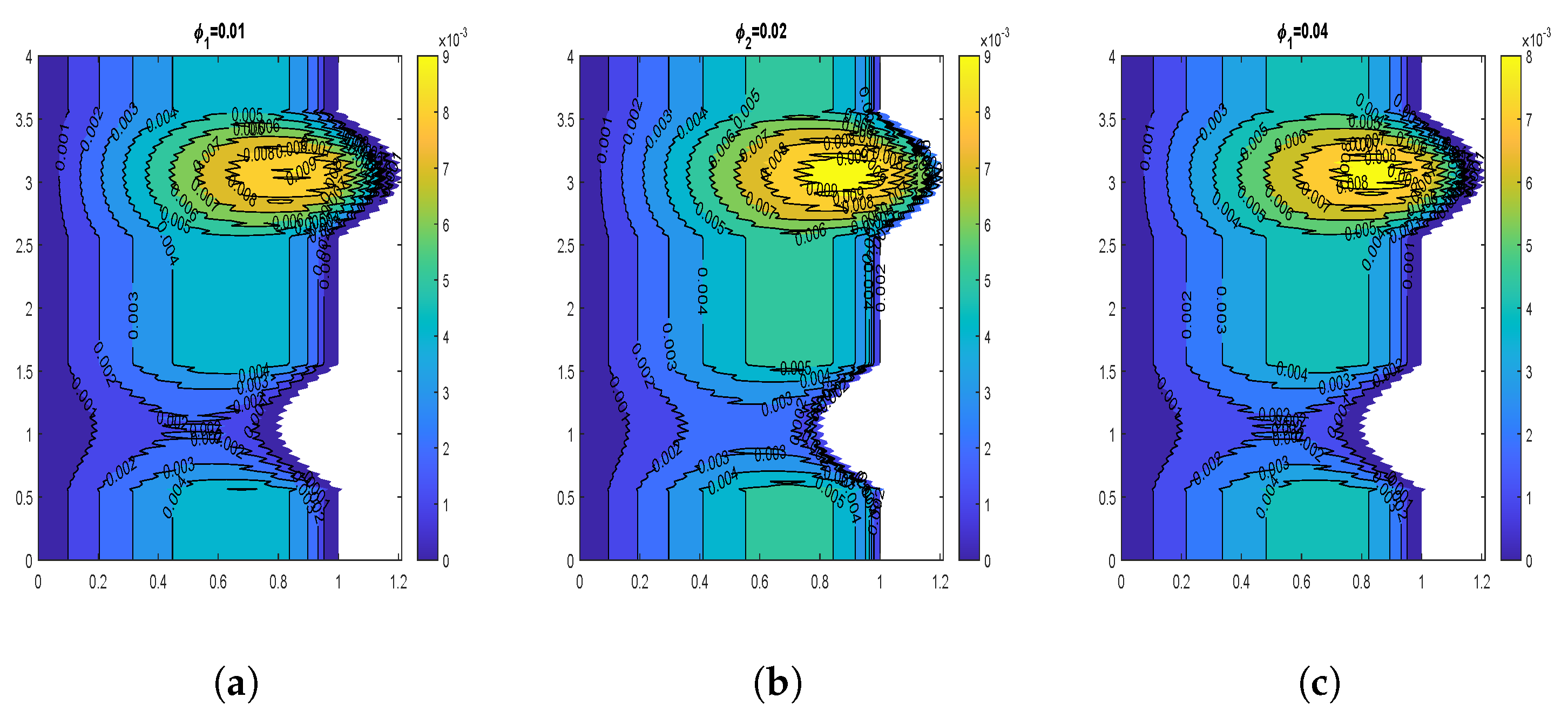
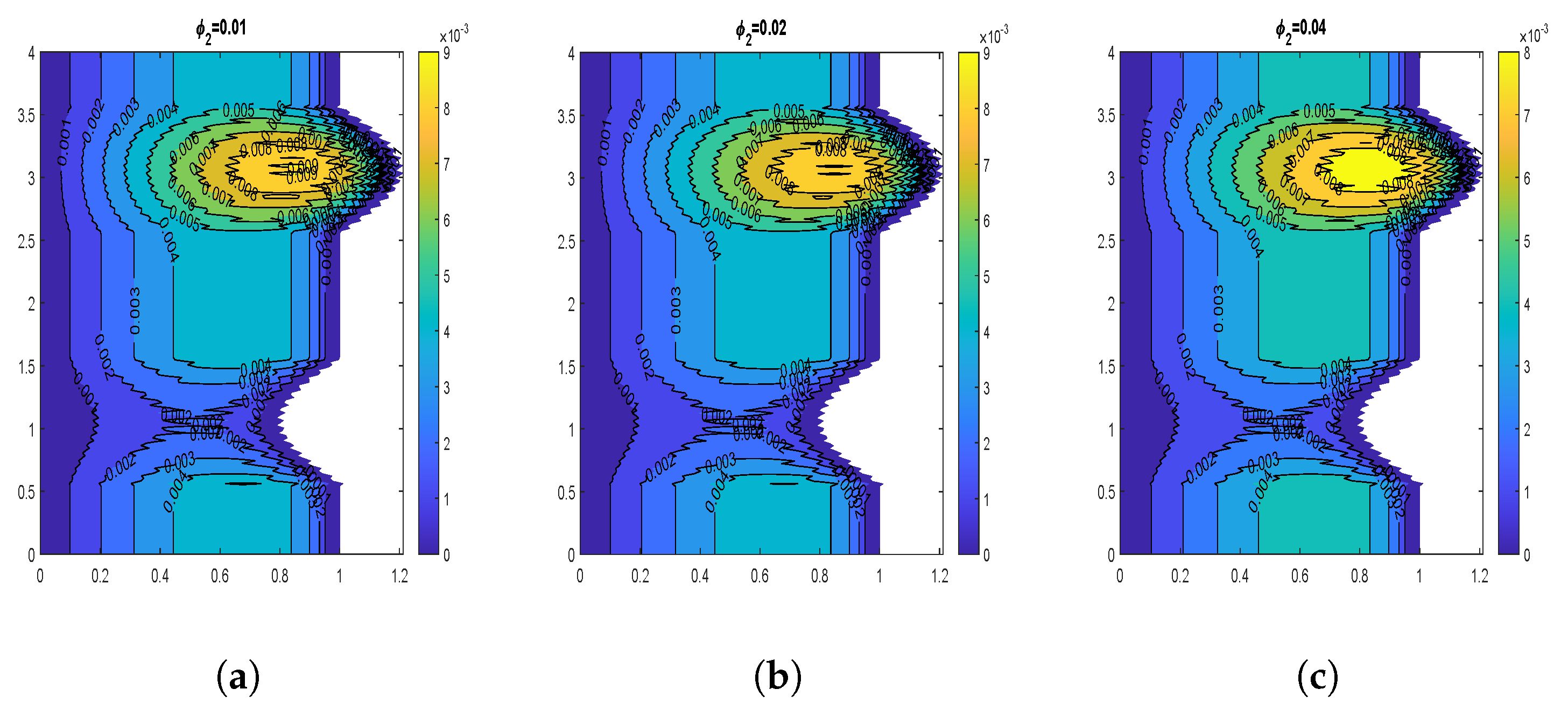
4.3. Velocity Contours
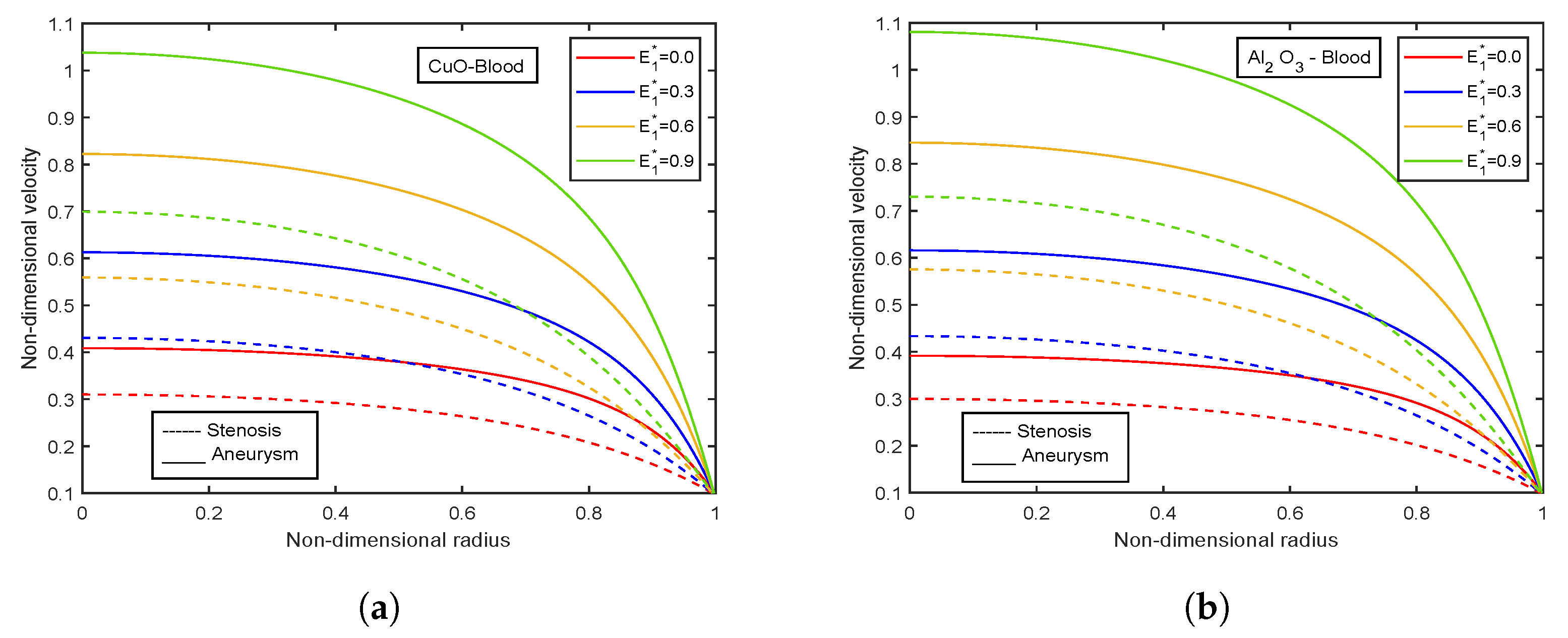
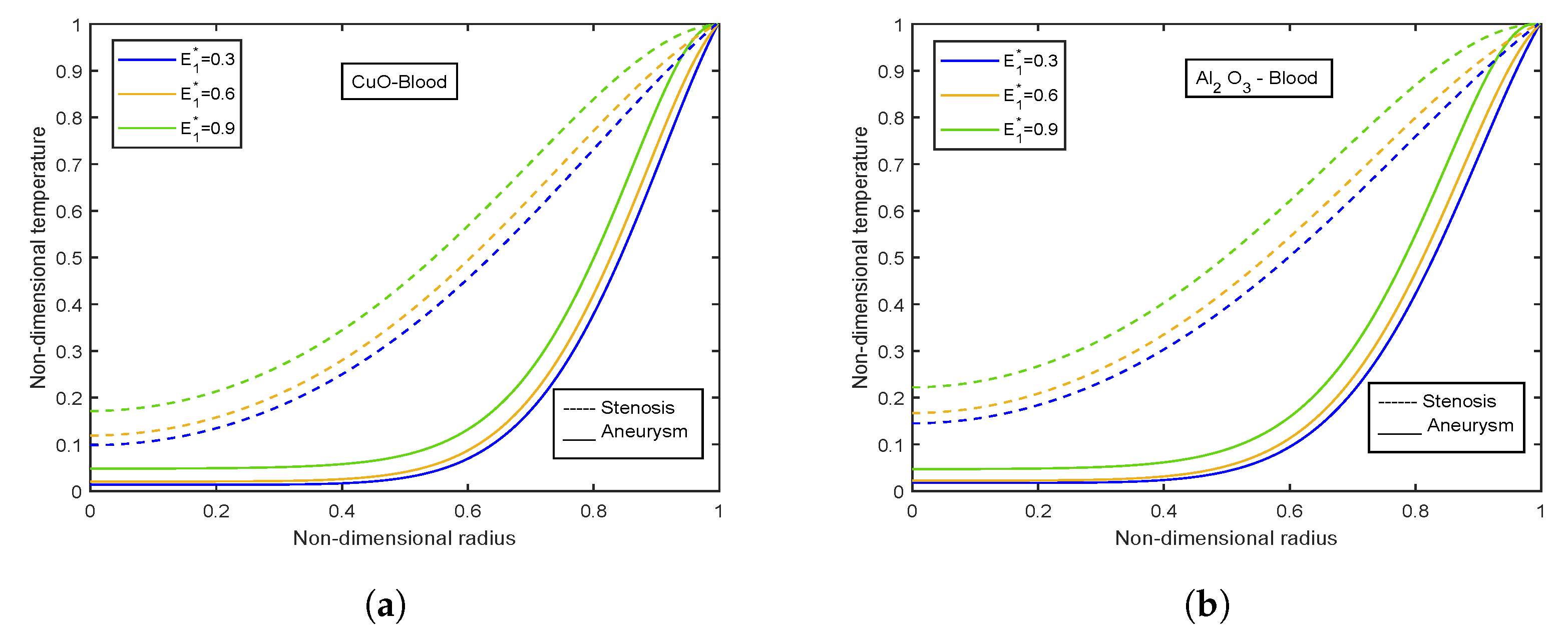
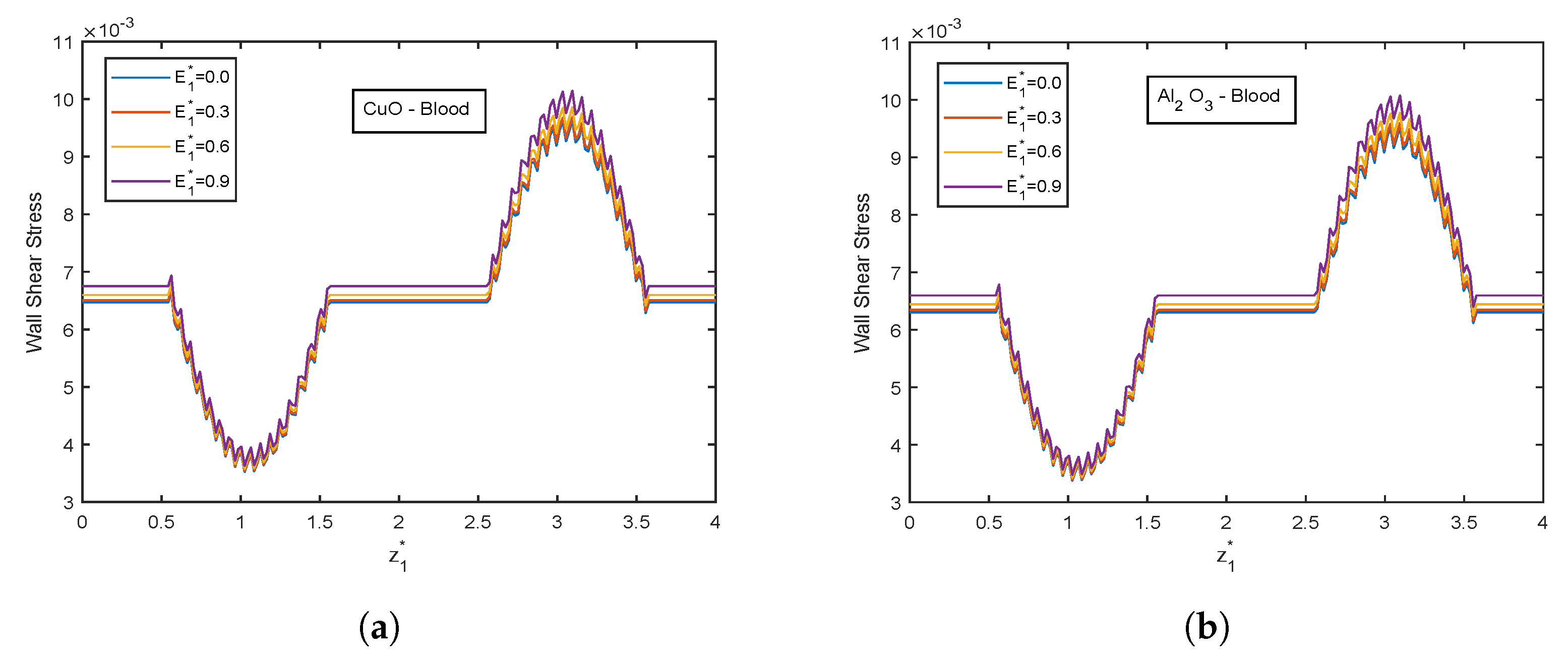
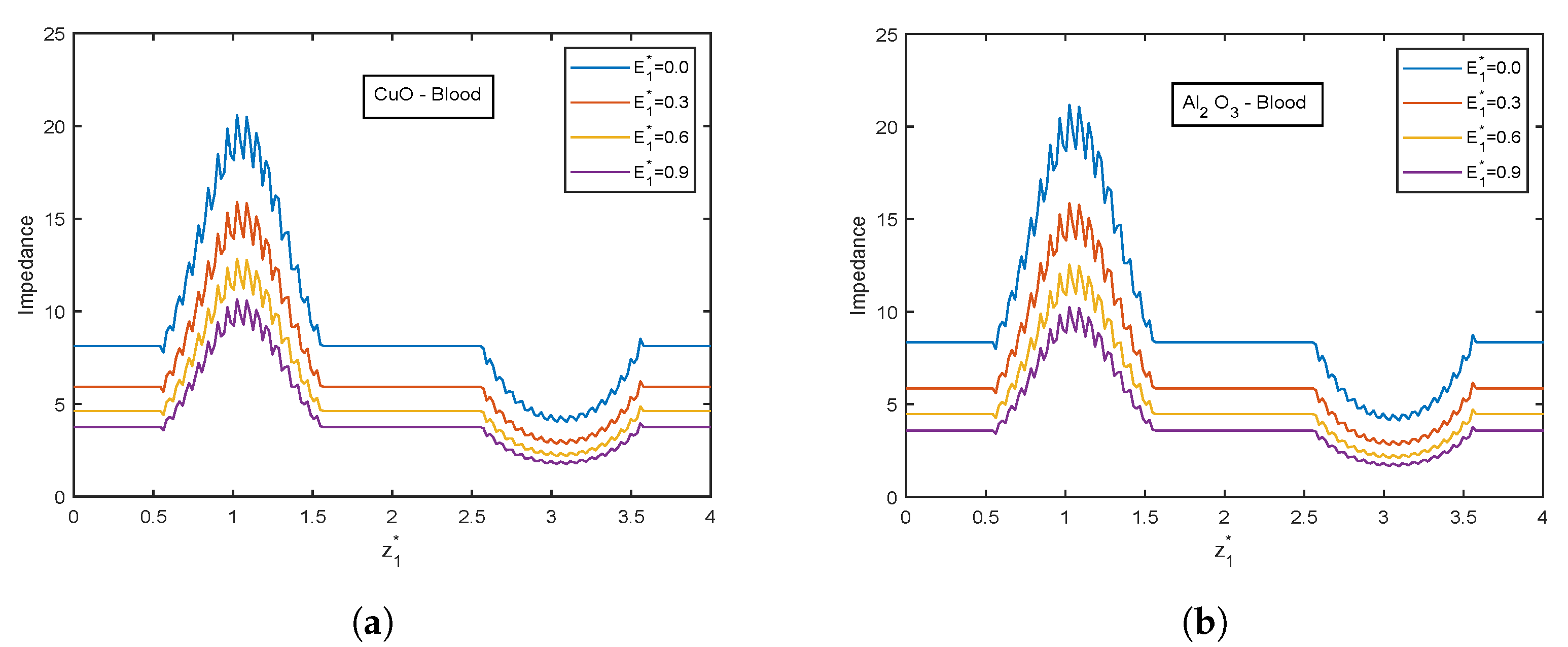
4.4. Impact of Electric Field Parameter
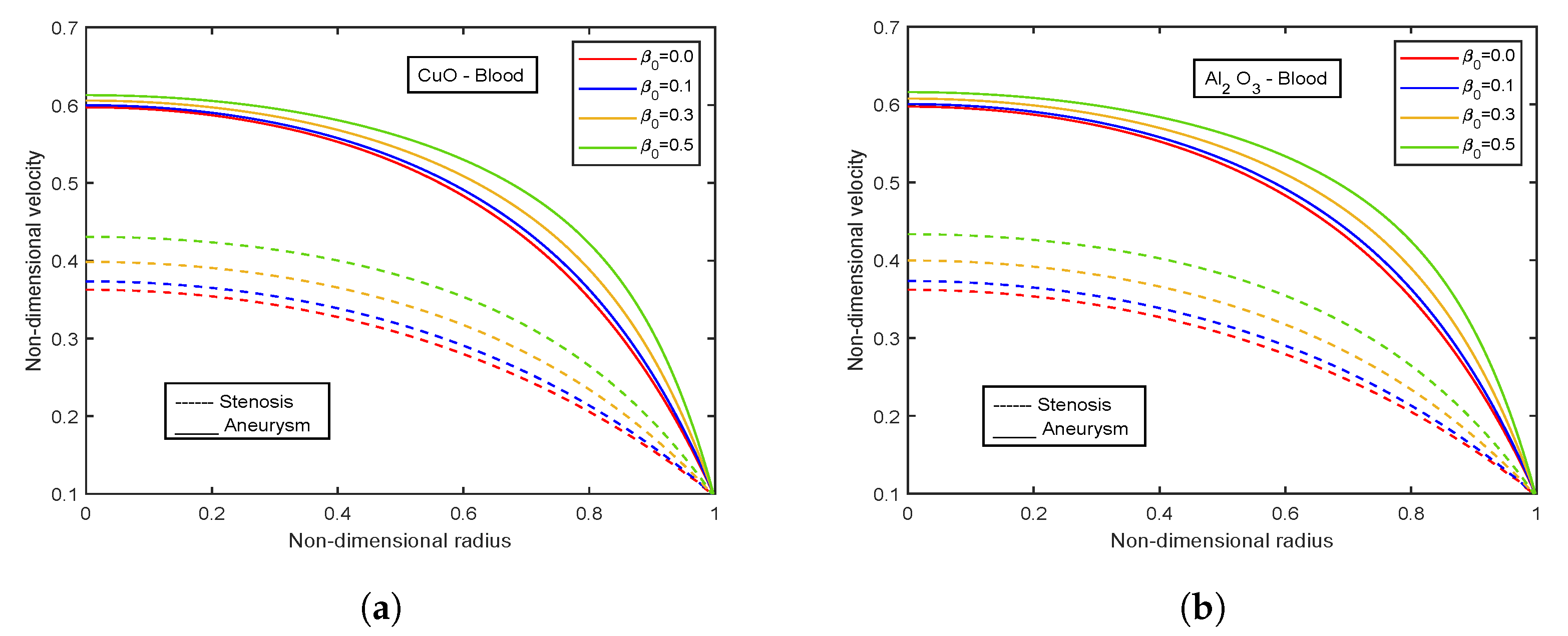
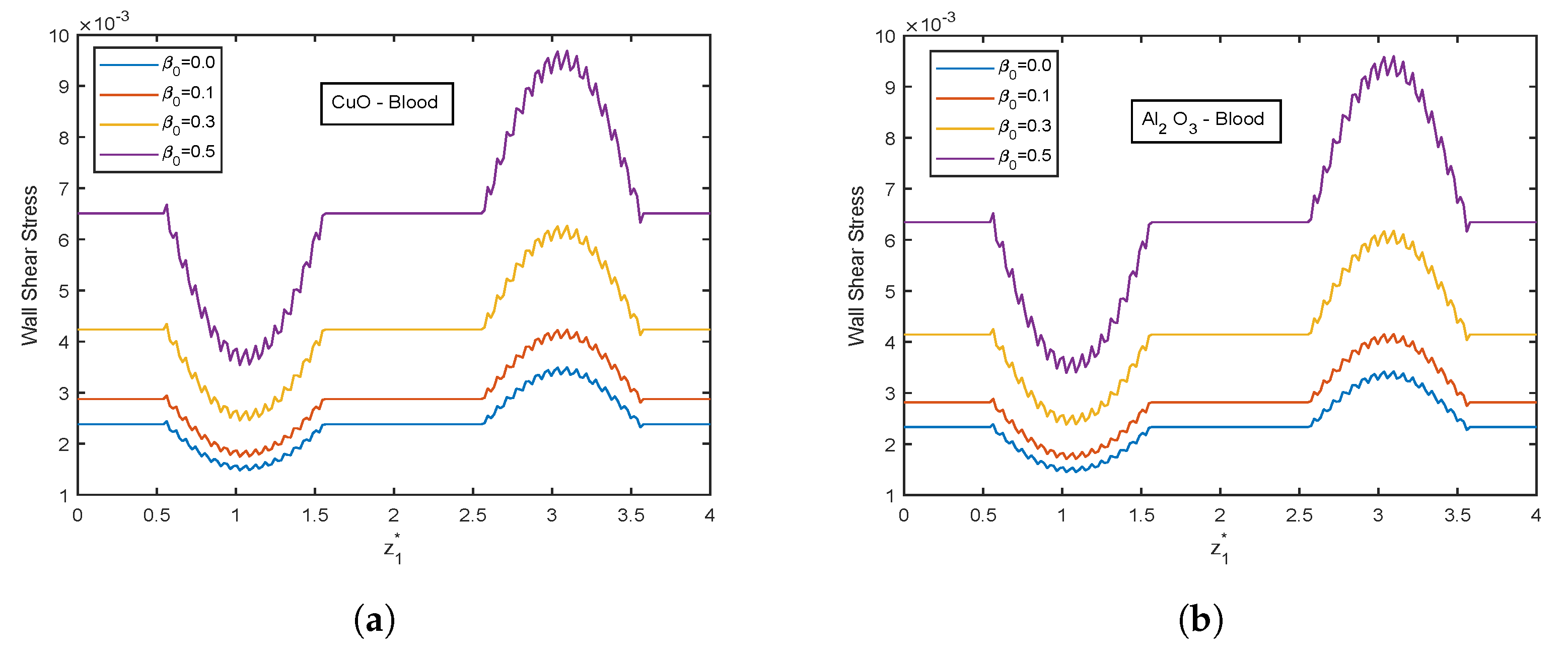
4.5. Effect of Viscosity Parameter
4.6. Impact of Volume Fraction of Nanoparticles
4.7. Effect of Casson Fluid Parameter
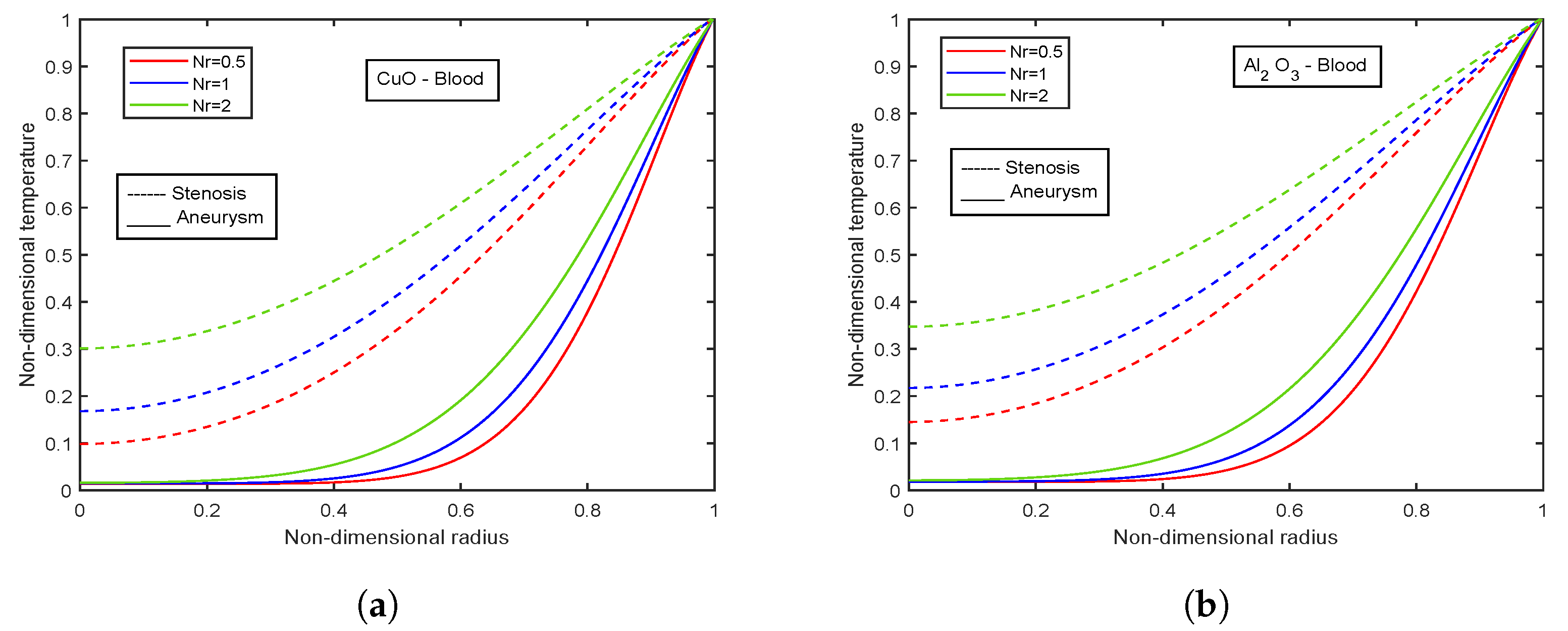
4.8. Effect of Radiation Parameter
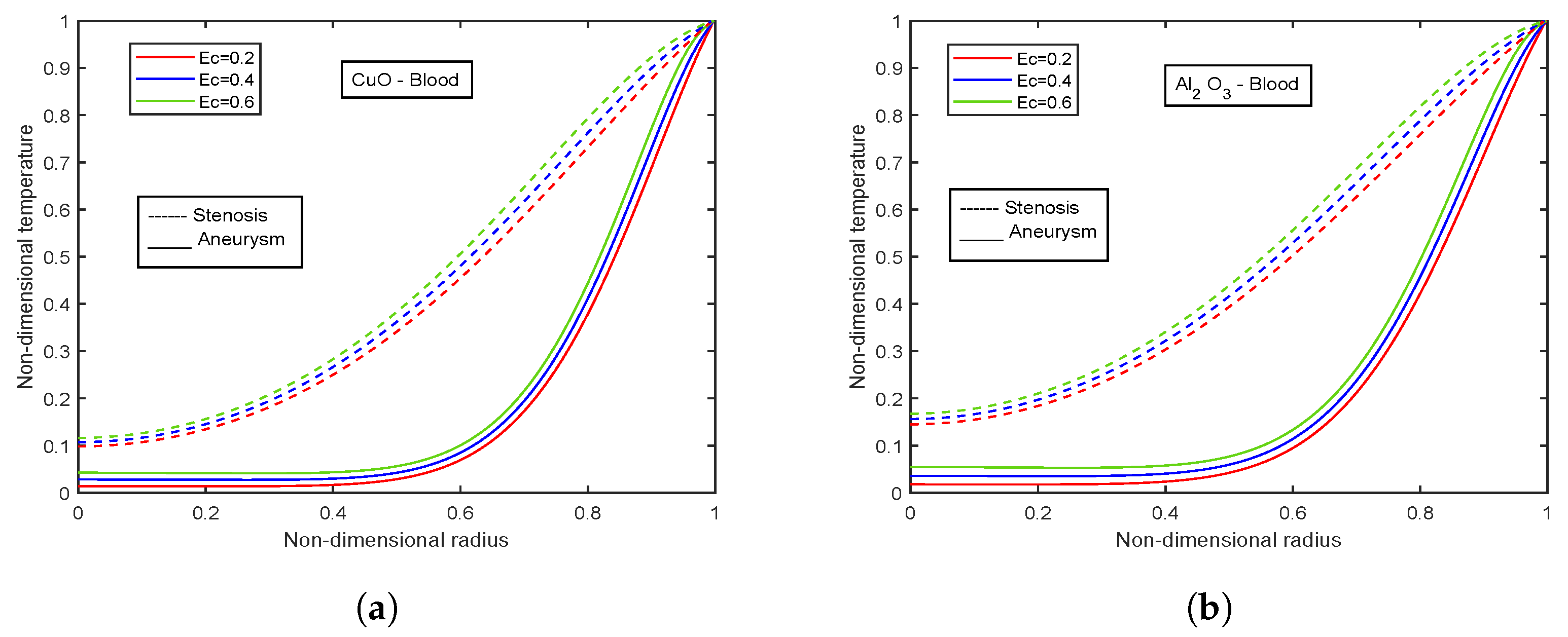
4.9. Impact of Eckert Number
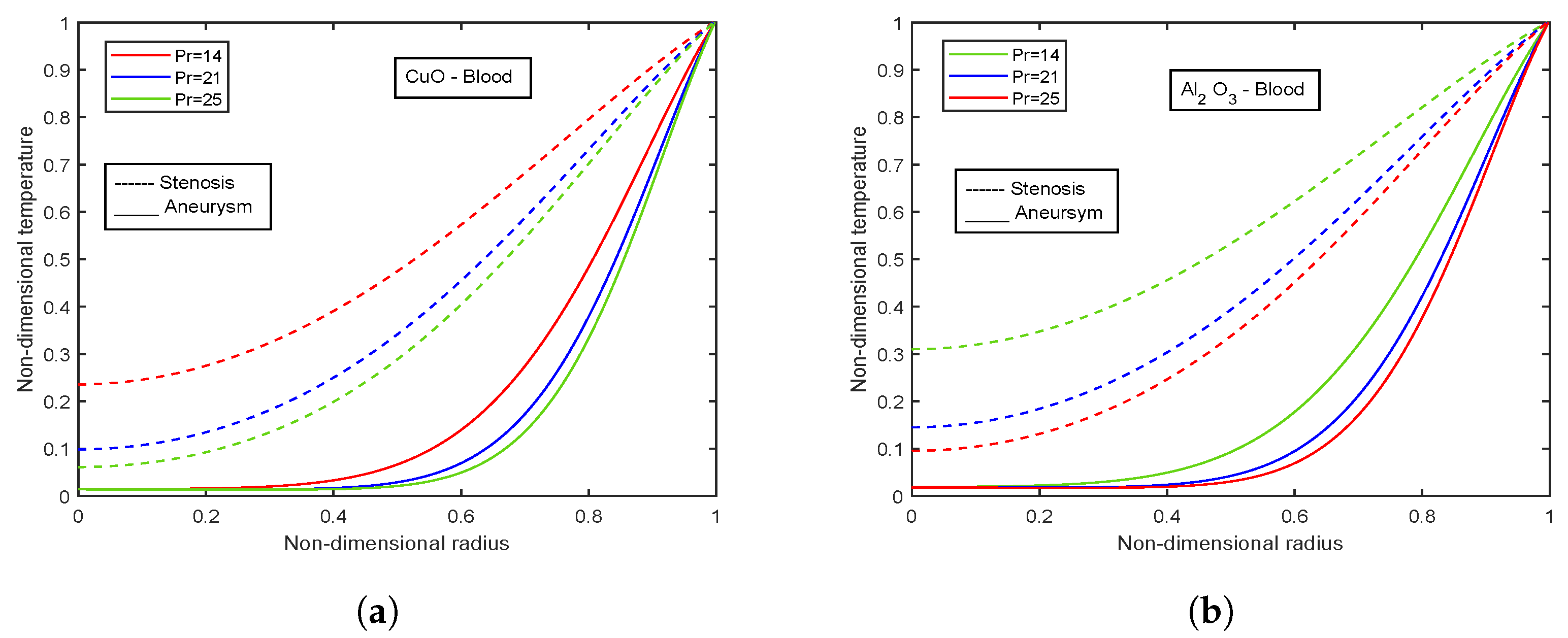
4.10. Effect of Prandtl Number
5. Conclusions
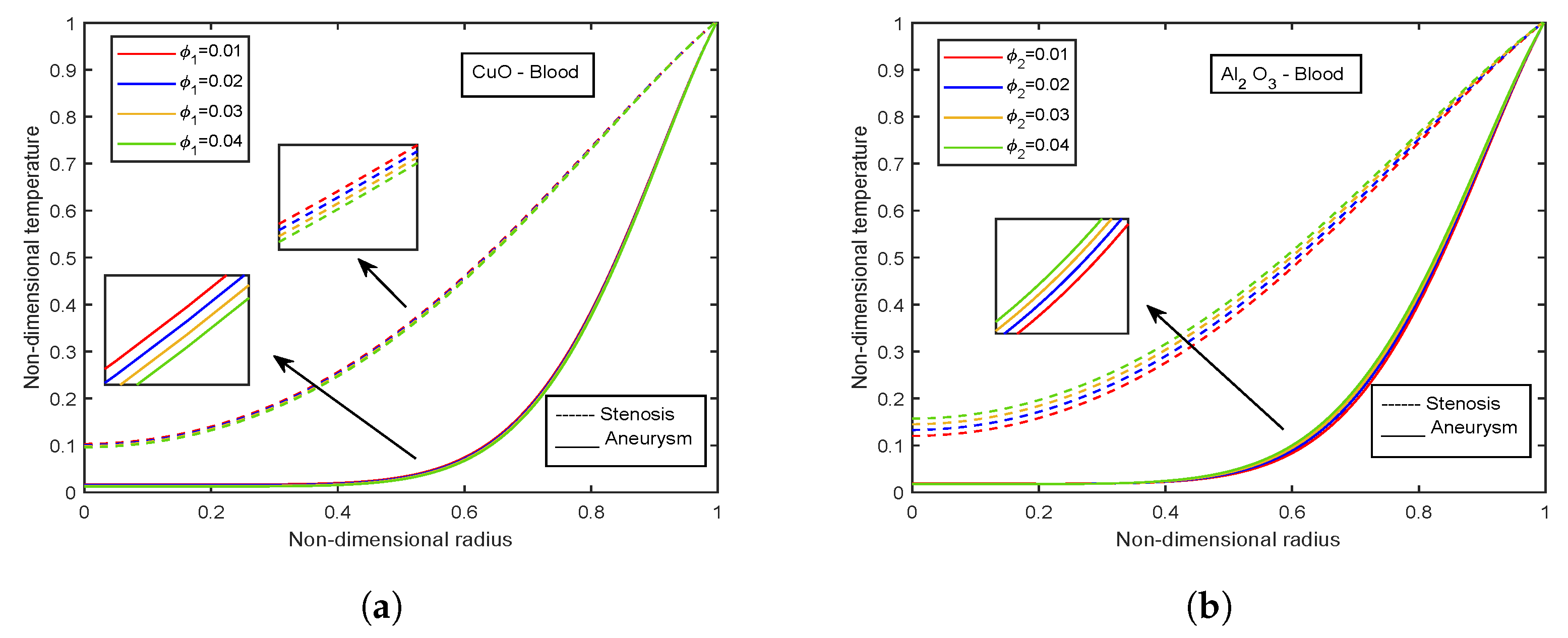
- The temperature and Nusselt number boost with enhancing diameter of CuO nanoparticles and decreasing diameter of AlO nanoparticles.
- Velocity and temperature profiles show inclination with increasing electric field parameter .
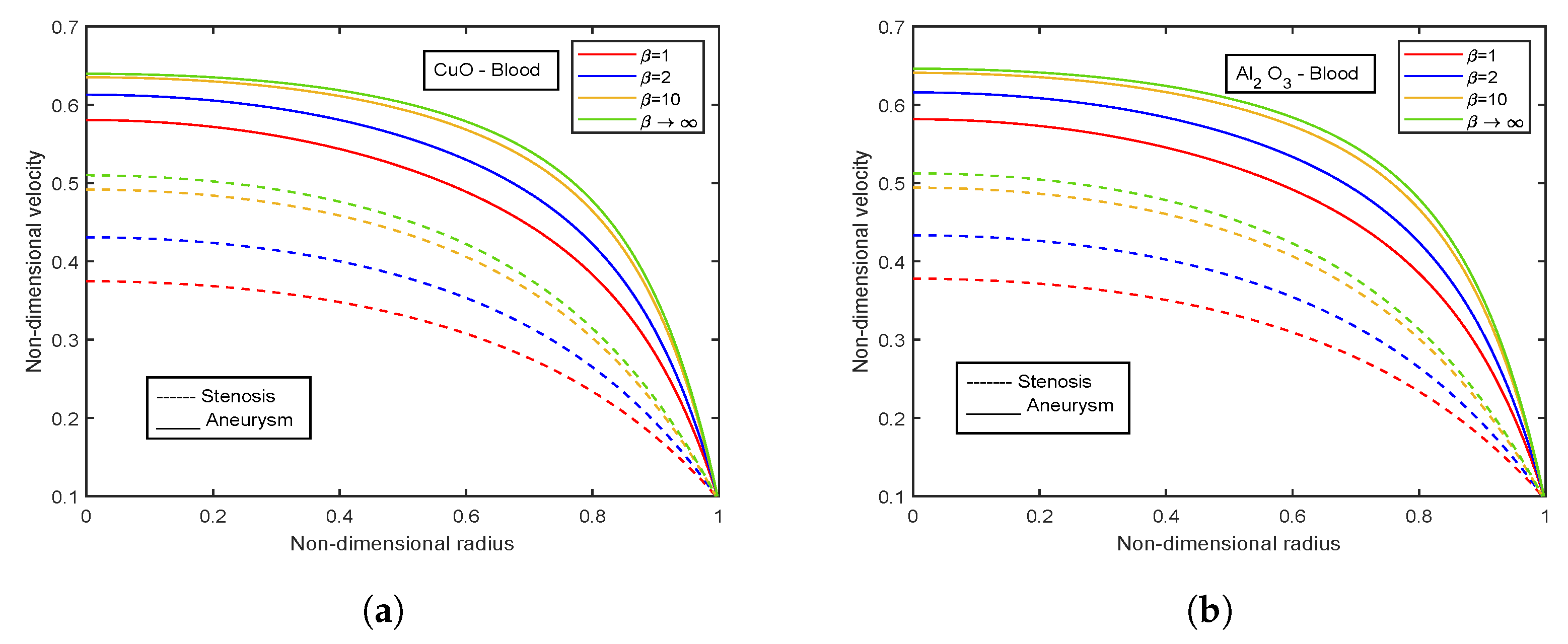
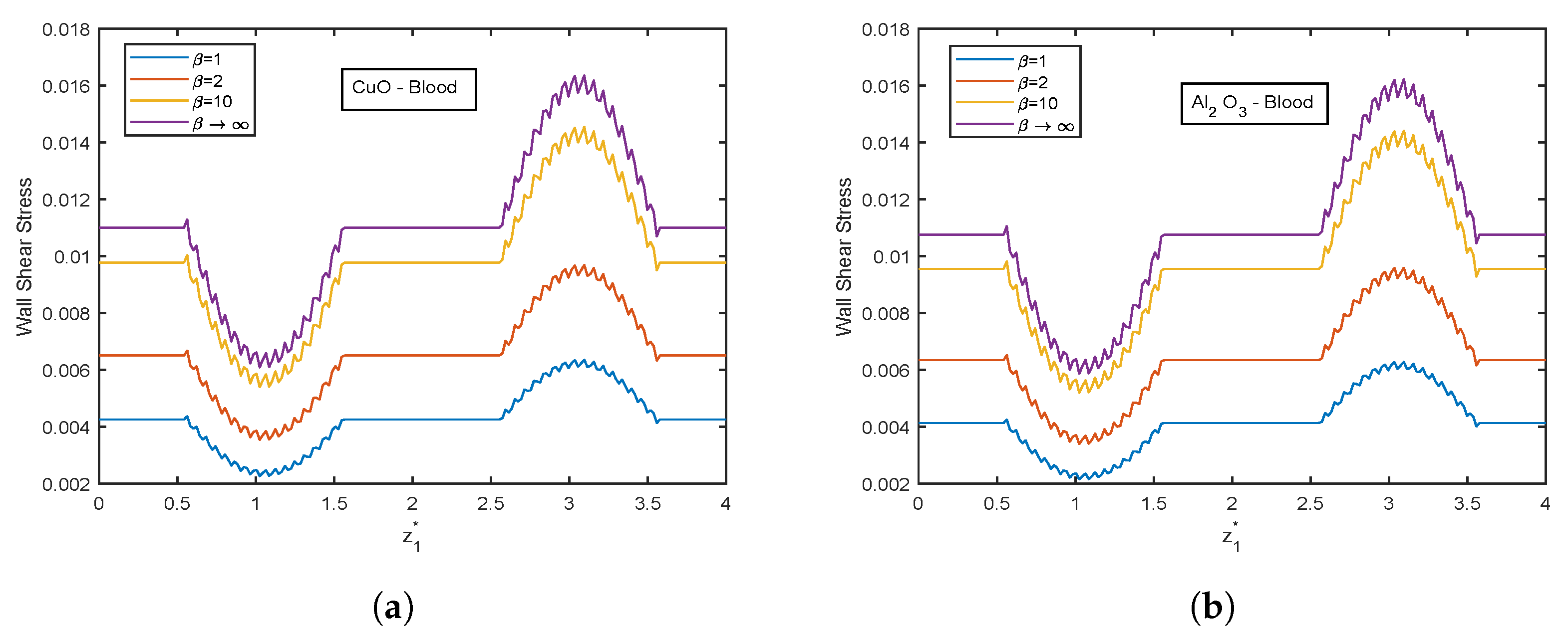
- There is an escalation in velocity and wall shear stress profiles with viscosity parameter .
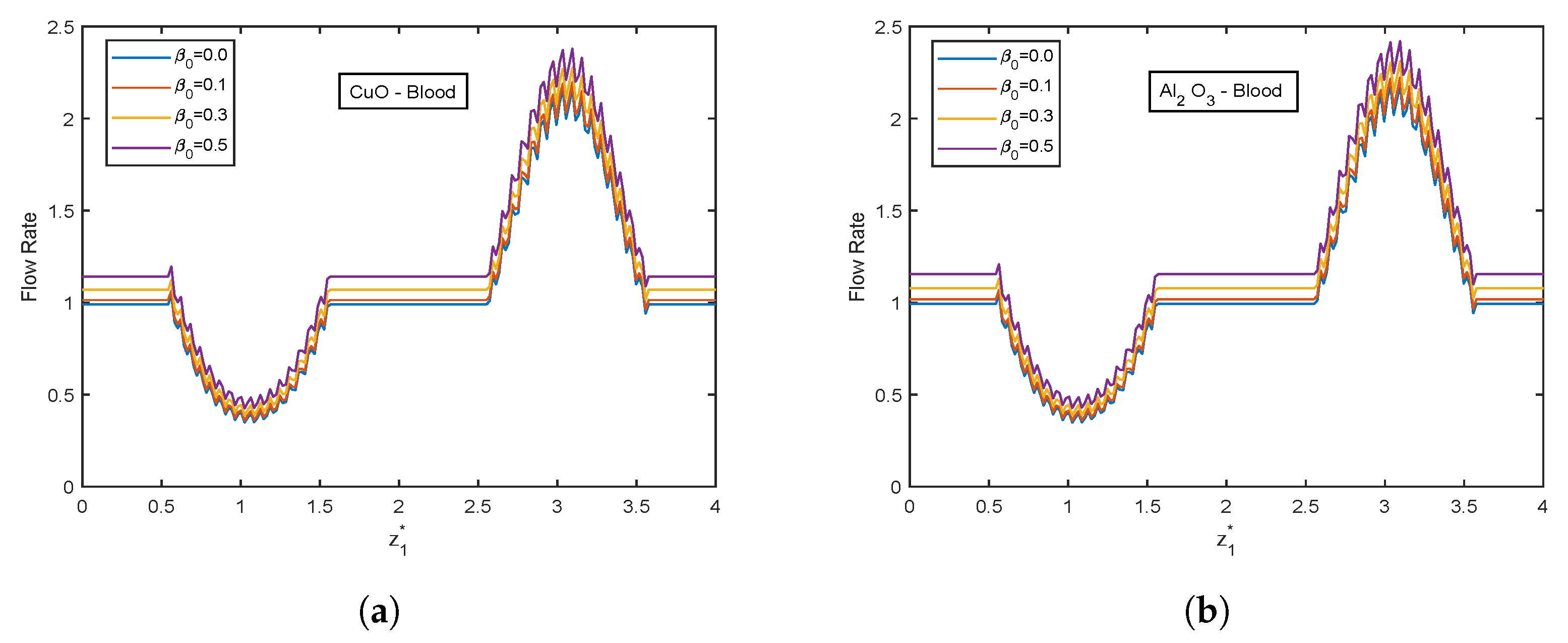
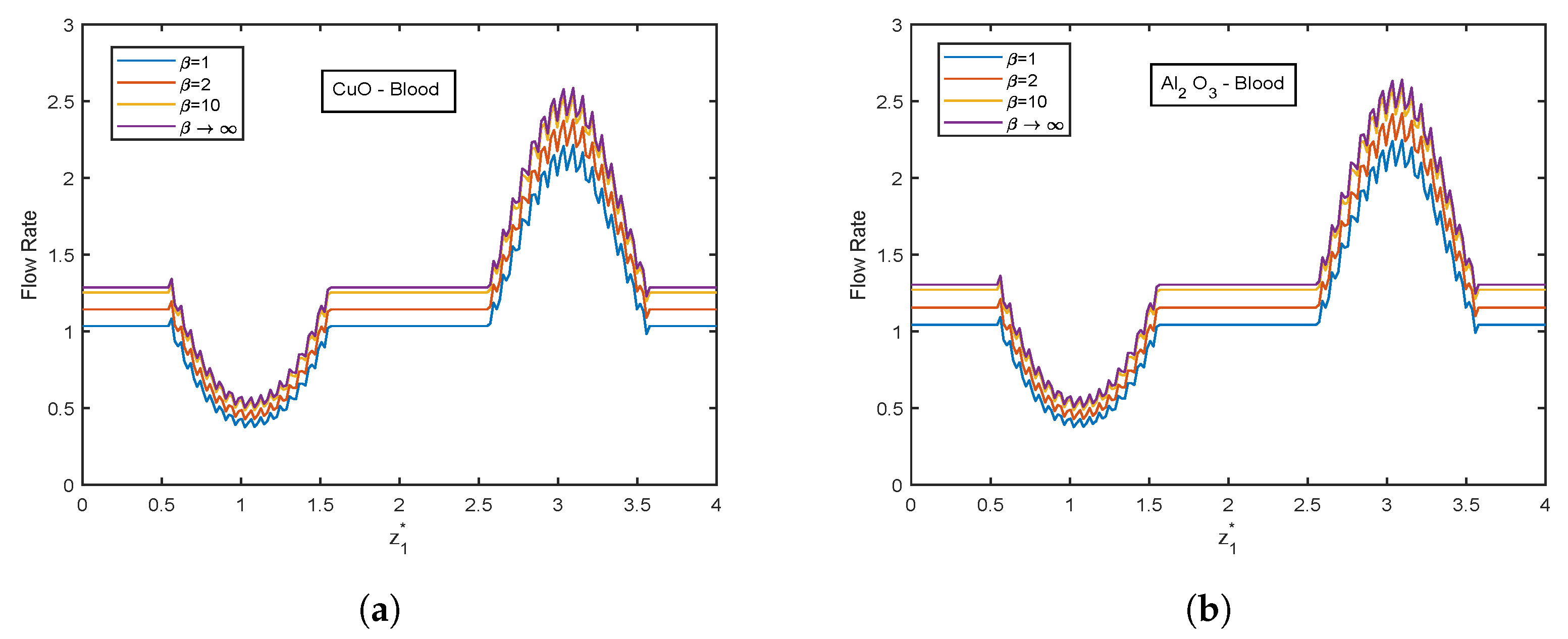
- Flow rate ascends with increment in Casson fluid parameter .
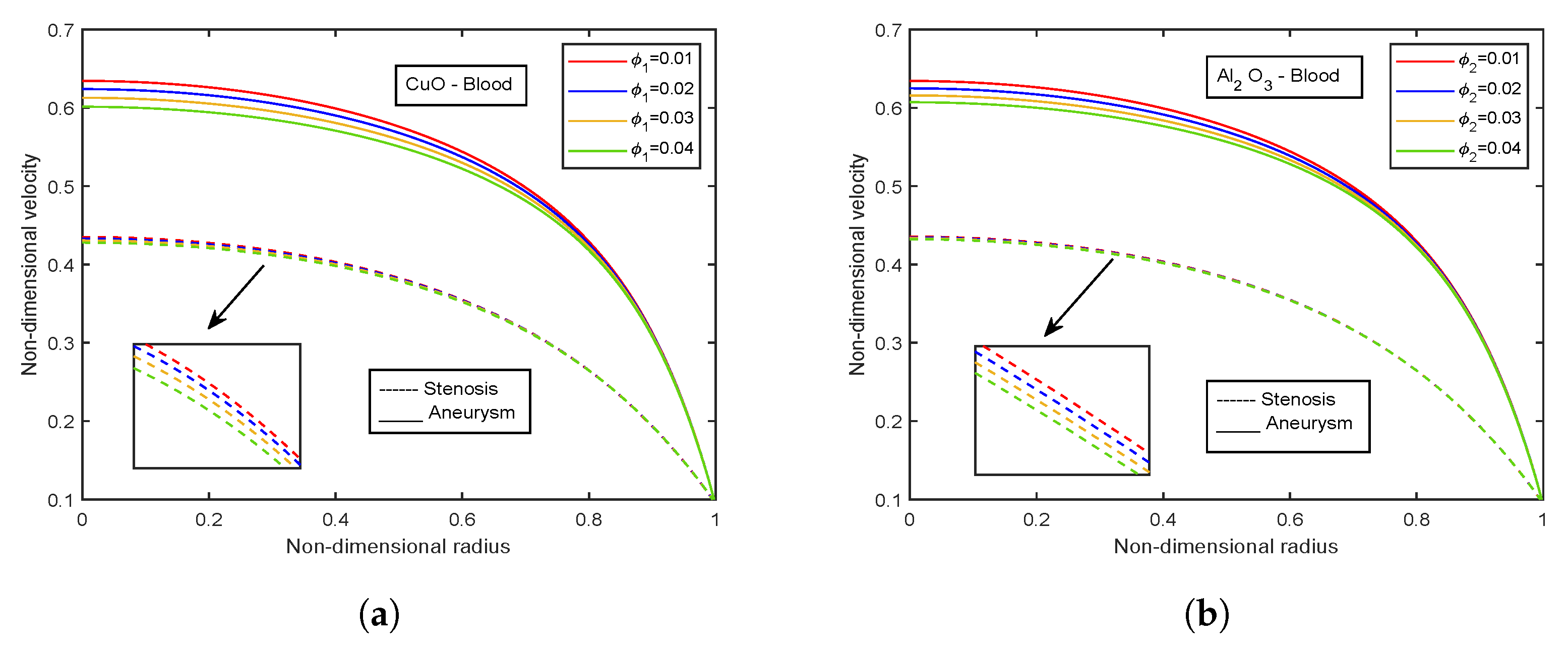
- Velocity descends with rising volume fraction of both CuO and AlO nanoparticles.
- Temperature profiles elevate with volume fraction of AlO nanoparticles, whereas declination is observed for CuO nanoparticles volume fraction.
- With increasing magnetic number, the relative % variation in the Nusselt number rises, but a decreasing trend is analyzed for the electric field parameter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Radial direction | |
| Ec | Eckert Number |
| Axial direction | |
| Pr | Prandtl Number |
| Time | |
| Nr | Radiation parameter |
| Velocity component in radial direction | |
| Nu | Nusselt number |
| Velocity component in axial direction | |
| Da | Darcy number |
| Reference velocity | |
| Re | Reynold’s Number |
| R | Radius of artery in stenotic/aneurysm region |
| Gr | Grashof Number |
| Radius of artery in non-stenotic region | |
| Flow Rate | |
| g | Acceleration by virtue of gravity |
| Greek Letters | |
| Temperature of the base fluid | |
| Stenotic depth/Aneurysm height | |
| Reference temperature | |
| Non-dimensional temperature | |
| Temperature at the wall | |
| Density | |
| Uniform Magnetic Field | |
| Volume fraction of CuO NPs | |
| Specific heat at constant pressure | |
| Volume fraction of AlO NPs | |
| Uniform Electric field | |
| Viscosity constant | |
| Thermal conductivity | |
| Resistance Impedance | |
| Pressure | |
| Blood’s viscosity | |
| Wall slip velocity | |
| Reference viscosity | |
| Pressure gradient parameter | |
| d | Location of stenosis/aneurysm |
| Electrical conductivity | |
| Length of stenosis/aneurysm | |
| Shear stress at the wall | |
| L | Length of the artery |
| Slip parameter | |
| Permeability of the medium | |
| Casson fluid parameter | |
| Magnetic Number | |
| Thermal expansion coefficient |
References
- Ponalagusamy, R. Blood flow through an artery with mild stenosis: A two-layered model, different shapes of stenoses and slip velocity at the wall. J. Appl. Sci. 2007, 7, 1071–1077. [Google Scholar] [CrossRef]
- Shaw, S.; Gorla, R.S.R.; Murthy, P.; Ng, C.O. Pulsatile Casson fluid flow through a stenosed bifurcated artery. Int. J. Fluid Mech. Res. 2009, 36, 43–63. [Google Scholar] [CrossRef]
- Layek, G.; Mukhopadhyay, S.; Gorla, R.S.R. Unsteady viscous flow with variable viscosity in a vascular tube with an overlapping constriction. Int. J. Eng. Sci. 2009, 47, 649–659. [Google Scholar] [CrossRef]
- Riahi, D.N.; Roy, R.; Cavazos, S. On arterial blood flow in the presence of an overlapping stenosis. Math. Comput. Model. 2011, 54, 2999–3006. [Google Scholar] [CrossRef]
- Shaw, S.; Pradhan, S.; Murthy, P. A FSI model on the Casson fluid flow through an elastic stenosed artery. Int. J. Fluid Mech. Res. 2012, 39, 521–534. [Google Scholar] [CrossRef]
- Shit, G.; Majee, S. Pulsatile flow of blood and heat transfer with variable viscosity under magnetic and vibration environment. J. Magn. Magn. Mater. 2015, 388, 106–115. [Google Scholar] [CrossRef]
- Zaman, A.; Ali, N.; Sajid, M. Numerical simulation of pulsatile flow of blood in a porous-saturated overlapping stenosed artery. Math. Comput. Simul. 2017, 134, 1–16. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Mekheimer, K.S.; Zaher, A. Alterations in blood stream by electroosmotic forces of hybrid nanofluid through diseased artery: Aneurysmal/stenosed segment. Chin. J. Phys. 2020, 67, 314–329. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, E.; Ma, L.; Shu, C.; Zheng, L. Analysis of hemodynamics and heat transfer of nanoparticle-injected atherosclerotic patient: Considering the drag force and slip between phases of different particle shapes and volume fractions. Int. J. Therm. Sci. 2021, 159, 106637. [Google Scholar] [CrossRef]
- Poonam; Sharma, B.; Kumawat, C.; Vafai, K. Computational biomedical simulations of hybrid nanoparticles (Au-Al2O3/blood-mediated) transport in a stenosed and aneurysmal curved artery with heat and mass transfer: Hematocrit dependent viscosity approach. Chem. Phys. Lett. 2022, 800, 139666. [Google Scholar] [CrossRef]
- Basha, H.T.; Rajagopal, K.; Ahammad, N.A.; Sathish, S.; Gunakala, S.R. Finite Difference Computation of Au-Cu/Magneto-Bio-Hybrid Nanofluid Flow in an Inclined Uneven Stenosis Artery. Complexity 2022, 2022. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Hassan, A.; Liu, D.; Noreen, S.; Makki, R.; Imran, M.; Ali, M.R. Numerical and Computational simulation of blood flow on hybrid nanofluid with heat transfer through a stenotic artery: Silver and gold nanoparticles. Results Phys. 2023, 44, 106152. [Google Scholar] [CrossRef]
- Badfar, H.; Yekani Motlagh, S.; Sharifi, A. Numerical simulation of magnetic drug targeting to the stenosis vessel using Fe3O4 magnetic nanoparticles under the effect of magnetic field of wire. Cardiovasc. Eng. Technol. 2020, 11, 162–175. [Google Scholar] [CrossRef]
- Varmazyar, M.; Habibi, M.; Amini, M.; Pordanjani, A.H.; Afrand, M.; Vahedi, S.M. Numerical simulation of magnetic nanoparticle-based drug delivery in presence of atherosclerotic plaques and under the effects of magnetic field. Powder Technol. 2020, 366, 164–174. [Google Scholar] [CrossRef]
- Ramadan, S.F.; Mekheimer, K.S.; Bhatti, M.M.; Moawad, A. Phan-Thien-Tanner nanofluid flow with gold nanoparticles through a stenotic electrokinetic aorta: A study on the cancer treatment. Heat Transf. Res. 2021, 52, 87–99. [Google Scholar] [CrossRef]
- Saeed, A.; Khan, N.; Gul, T.; Kumam, W.; Alghamdi, W.; Kumam, P. The flow of blood-based hybrid nanofluids with couple stresses by the convergent and divergent channel for the applications of drug delivery. Molecules 2021, 26, 6330. [Google Scholar] [CrossRef]
- Sharma, B.; Gandhi, R.; Bhatti, M. Entropy analysis of thermally radiating MHD slip flow of hybrid nanoparticles (Au-Al2O3/Blood) through a tapered multi-stenosed artery. Chem. Phys. Lett. 2022, 790, 139348. [Google Scholar] [CrossRef]
- Mekheimer, K.S.; Abo-Elkhair, R.; Abdelsalam, S.; Ali, K.K.; Moawad, A. Biomedical simulations of nanoparticles drug delivery to blood hemodynamics in diseased organs: Synovitis problem. Int. Commun. Heat Mass Transf. 2022, 130, 105756. [Google Scholar] [CrossRef]
- Khanduri, U.; Sharma, B.K. Hall and ion slip effects on hybrid nanoparticles (Au-GO/blood) flow through a catheterized stenosed artery with thrombosis. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 09544062221136710. [Google Scholar] [CrossRef]
- Sharma, B.K.; Poonam; Chamkha, A.J. Effects of heat transfer, body acceleration and hybrid nanoparticles (Au–Al2O3) on MHD blood flow through a curved artery with stenosis and aneurysm using hematocrit-dependent viscosity. Waves Random Complex Media 2022, 1–31. [Google Scholar] [CrossRef]
- Dolui, S.; Bhaumik, B.; De, S. Combined effect of induced magnetic field and thermal radiation on ternary hybrid nanofluid flow through an inclined catheterized artery with multiple stenosis. Chem. Phys. Lett. 2023, 811, 140209. [Google Scholar] [CrossRef]
- Karmakar, P.; Ali, A.; Das, S. Circulation of blood loaded with trihybrid nanoparticles via electro-osmotic pumping in an eccentric endoscopic arterial canal. Int. Commun. Heat Mass Transf. 2023, 141, 106593. [Google Scholar] [CrossRef]
- Walawender, W.P.; Chen, T.Y.; Cala, D.F. An approximate Casson fluid model for tube flow of blood. Biorheology 1975, 12, 111–119. [Google Scholar] [CrossRef] [PubMed]
- Chakravarty, S.; Mandal, P.K. Numerical simulation of Casson fluid flow through differently shaped arterial stenoses. Z. Angew. Math. Phys. 2014, 65, 767–782. [Google Scholar]
- Debnath, S.; Saha, A.K.; Mazumder, B.; Roy, A.K. Transport of a reactive solute in a pulsatile non-Newtonian liquid flowing through an annular pipe. J. Eng. Math. 2019, 116, 1–22. [Google Scholar] [CrossRef]
- Ali, A.; Farooq, H.; Abbas, Z.; Bukhari, Z.; Fatima, A. Impact of Lorentz force on the pulsatile flow of a non-Newtonian Casson fluid in a constricted channel using Darcy’s law: A numerical study. Sci. Rep. 2020, 10, 10629. [Google Scholar] [CrossRef]
- Das, P.; Sarifuddin; Rana, J.; Mandal, P.K. Solute dispersion in transient Casson fluid flow through stenotic tube with exchange between phases. Phys. Fluids 2021, 33, 61907. [Google Scholar] [CrossRef]
- Padma, R.; Tamil Selvi, R.; Ponalagusamy, R. Electromagnetic control of non-Newtonian fluid (blood) suspended with magnetic nanoparticles in the tapered constricted inclined tube. Proc. AIP Conf. Proc. 2021, 2336, 20008. [Google Scholar]
- Beavers, G.S.; Joseph, D.D. Boundary conditions at a naturally permeable wall. J. Fluid Mech. 1967, 30, 197–207. [Google Scholar] [CrossRef]
- Mishra, S.; Siddiqui, S.; Medhavi, A. Blood flow through a composite stenosis in an artery with permeable wall. Appl. Appl. Math. Int. J. AAM 2011, 6, 5. [Google Scholar]
- Ijaz, S.; Nadeem, S. Examination of nanoparticles as a drug carrier on blood flow through catheterized composite stenosed artery with permeable walls. Comput. Methods Programs Biomed. 2016, 133, 83–94. [Google Scholar] [CrossRef]
- Akbar, N.S.; Tripathi, D.; Bég, O.A. Variable-viscosity thermal hemodynamic slip flow conveying nanoparticles through a permeable-walled composite stenosed artery. Eur. Phys. J. Plus 2017, 132, 1–11. [Google Scholar] [CrossRef]
- Shahzadi, I.; Bilal, S. A significant role of permeability on blood flow for hybrid nanofluid through bifurcated stenosed artery: Drug delivery application. Comput. Methods Programs Biomed. 2020, 187, 105248. [Google Scholar] [CrossRef]
- Gandhi, R.; Sharma, B.; Kumawat, C.; Bég, O.A. Modeling and analysis of magnetic hybrid nanoparticle (Au-Al2O3/blood) based drug delivery through a bell-shaped occluded artery with joule heating, viscous dissipation and variable viscosity effects. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 236, 09544089221080273. [Google Scholar] [CrossRef]
- Sharma, B.; Kumawat, C.; Makinde, O. Hemodynamical analysis of MHD two phase blood flow through a curved permeable artery having variable viscosity with heat and mass transfer. Biomech. Model. Mechanobiol. 2022, 1–29. [Google Scholar] [CrossRef]
- Kumawat, C.; Sharma, B.; Al-Mdallal, Q.M.; Rahimi-Gorji, M. Entropy generation for MHD two phase blood flow through a curved permeable artery having variable viscosity with heat and mass transfer. Int. Commun. Heat Mass Transf. 2022, 133, 105954. [Google Scholar] [CrossRef]
- Sharma, B.; Gandhi, R. Combined effects of Joule heating and non-uniform heat source/sink on unsteady MHD mixed convective flow over a vertical stretching surface embedded in a Darcy-Forchheimer porous medium. Propuls. Power Res. 2022, 11, 276–292. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. Viscous dissipation effects in microtubes and microchannels. Int. J. Heat Mass Transf. 2004, 47, 3159–3169. [Google Scholar] [CrossRef]
- Koo, J. Computational Nanofluid Flow and Heat Transfer Analyses Applied to Micro-Systems; North Carolina State University: Raleigh, NC, USA, 2005. [Google Scholar]
- Li, J. Computational Analysis of Nanofluid Flow in Microchannels with Applications to Micro-Heat Sinks and Bio-MEMS. Ph.D. Thesis, Graduate Faculty of North Carolina State University, Raleigh, NC, USA, 2008. [Google Scholar]
- Kandelousi, M.S. KKL correlation for simulation of nanofluid flow and heat transfer in a permeable channel. Phys. Lett. A 2014, 378, 3331–3339. [Google Scholar] [CrossRef]
- Mehmood, K.; Hussain, S.; Sagheer, M. Numerical simulation of MHD mixed convection in alumina–water nanofluid filled square porous cavity using KKL model: Effects of non-linear thermal radiation and inclined magnetic field. J. Mol. Liq. 2017, 238, 485–498. [Google Scholar] [CrossRef]
- Rana, S.; Nawaz, M. Investigation of enhancement of heat transfer in Sutterby nanofluid using Koo–Kleinstreuer and Li (KKL) correlations and Cattaneo–Christov heat flux model. Phys. Scr. 2019, 94, 115213. [Google Scholar] [CrossRef]
- Malik, Z.U.; Mallawi, F.O.; Haq, R.U. Thermal energy performance of nanofluid flow and heat transfer based upon KKL correlation in a rotating vertical channel with permeable surface. Case Stud. Therm. Eng. 2021, 28, 101447. [Google Scholar] [CrossRef]
- Shahzad, F.; Bouslimi, J.; Gouadria, S.; Jamshed, W.; Eid, M.R.; Safdar, R.; Shamshuddin, M.; Nisar, K.S. Hydrogen energy storage optimization in solar-HVAC using Sutterby nanofluid via Koo-Kleinstreuer and Li (KKL) correlations model: A solar thermal application. Int. J. Hydrogen Energy 2022, 47, 18877–18891. [Google Scholar] [CrossRef]
- Ramzan, M.; Shahmir, N.; Ghazwani, H.A.S.; Elmasry, Y.; Kadry, S. A numerical study of nanofluid flow over a curved surface with Cattaneo–Christov heat flux influenced by induced magnetic field. Numer. Heat Transf. Part A Appl. 2023, 83, 197–212. [Google Scholar] [CrossRef]
- Ahmed, A.; Nadeem, S. Effects of magnetohydrodynamics and hybrid nanoparticles on a micropolar fluid with 6-types of stenosis. Results Phys. 2017, 7, 4130–4139. [Google Scholar] [CrossRef]
- Gandhi, R.; Sharma, B.K.; Makinde, O.D. Entropy analysis for MHD blood flow of hybrid nanoparticles (Au–Al2O3/blood) of different shapes through an irregular stenosed permeable walled artery under periodic body acceleration: Hemodynamical applications. ZAMM J. Appl. Math. Mech./Z. Angew. Math. Mech. 2022, e202100532. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. Laminar nanofluid flow in microheat-sinks. Int. J. Heat Mass Transf. 2005, 48, 2652–2661. [Google Scholar] [CrossRef]
- Ellahi, R.; Raza, M.; Vafai, K. Series solutions of non-Newtonian nanofluids with Reynolds’ model and Vogel’s model by means of the homotopy analysis method. Math. Comput. Model. 2012, 55, 1876–1891. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Modeling and optimization of MHD mixed convection in a lid-driven trapezoidal cavity filled with alumina–water nanofluid: Effects of electrical conductivity models. Int. J. Mech. Sci. 2018, 136, 264–278. [Google Scholar] [CrossRef]
- Burton, A.C. Physiology and Biophysics of the Circulation. Acad. Med. 1965, 40, xxx–xxxvi. [Google Scholar]
- Anderson, J.D.; Wendt, J. Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1995; Volume 206. [Google Scholar]
- Zaman, A.; Ali, N.; Kousar, N. Nanoparticles (Cu, TiO2, Al2O3) analysis on unsteady blood flow through an artery with a combination of stenosis and aneurysm. Comput. Math. Appl. 2018, 76, 2179–2191. [Google Scholar] [CrossRef]




| Thermophysical Properties | Blood | CuO | AlO |
|---|---|---|---|
| Density [(kg/m)] | 1060 | 6500 | 3970 |
| Thermal Conductivity [K(W/mK)] | 0.492 | 18 | 25 |
| Electrical Conductivity [(S/m)] | 0.667 | 1 | 3.5 |
| Thermal Expansion Coefficient [(K] | 0.18 | 0.5 | 0.85 |
| Heat Capacitance [(J/kgK)] | 3770 | 540 | 765 |
| – | 47 | 29 |
| Coefficient | CuO | AlO |
|---|---|---|
| −26.593310846 | 52.813488759 | |
| −0.403818333 | 6.115637295 | |
| −33.3516805 | 1 0.6955745084 | |
| −1.915825591 | 4.17455552786 × | |
| 6.42185846658 × | 0.176919300241 | |
| 48.40336955 | −298.19819084 | |
| −9.787756683 | −34.532716906 | |
| 190.245610009 | −3.9225289283 | |
| 10.9285386565 | −0.2354329626 | |
| −0.72009983664 | −0.999063481 |
| Grid Size | Wall Shear Stress () |
|---|---|
| 25 × 25 | 0.0082 |
| 50 × 50 | 0.0035 |
| 70 × 70 | 0.0022 |
| 100 × 100 | 0.0018 |
| 200 × 200 | 0.0018 |
| Time Step Size (dt) | Wall Shear Stress () |
|---|---|
| 0.1 | 0.0035 |
| 0.08 | 0.0038 |
| 0.05 | 0.0042 |
| 0.02 | 0.0045 |
| 0.01 | 0.0044 |
| Parameters | d | e | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | 0.03 | 0.03 | 0.56 | 1.41 | 1 | 0.2 | 0.1 | 0.5 | 0.1 | 2 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gandhi, R.; Sharma, B.K.; Mishra, N.K.; Al-Mdallal, Q.M. Computer Simulations of EMHD Casson Nanofluid Flow of Blood through an Irregular Stenotic Permeable Artery: Application of Koo-Kleinstreuer-Li Correlations. Nanomaterials 2023, 13, 652. https://doi.org/10.3390/nano13040652
Gandhi R, Sharma BK, Mishra NK, Al-Mdallal QM. Computer Simulations of EMHD Casson Nanofluid Flow of Blood through an Irregular Stenotic Permeable Artery: Application of Koo-Kleinstreuer-Li Correlations. Nanomaterials. 2023; 13(4):652. https://doi.org/10.3390/nano13040652
Chicago/Turabian StyleGandhi, Rishu, Bhupendra Kumar Sharma, Nidhish Kumar Mishra, and Qasem M. Al-Mdallal. 2023. "Computer Simulations of EMHD Casson Nanofluid Flow of Blood through an Irregular Stenotic Permeable Artery: Application of Koo-Kleinstreuer-Li Correlations" Nanomaterials 13, no. 4: 652. https://doi.org/10.3390/nano13040652
APA StyleGandhi, R., Sharma, B. K., Mishra, N. K., & Al-Mdallal, Q. M. (2023). Computer Simulations of EMHD Casson Nanofluid Flow of Blood through an Irregular Stenotic Permeable Artery: Application of Koo-Kleinstreuer-Li Correlations. Nanomaterials, 13(4), 652. https://doi.org/10.3390/nano13040652







