Dynamics of Vacancy Formation and Distribution in Semiconductor Heterostructures: Effect of Thermally Generated Intrinsic Electrons
Abstract
1. Introduction
- (1)
- In the general case, vacancies are formed in different ways. The main paths are generation at the surface (Schottky defect formation) and generation in the volume (Frenkel pair formation). In the first case, to consider the vacancy formation, it is necessary to take into account the state of the surface (e.g., the coating type and structure [34,35,36,37,38]) and the free surface exchange by atoms and molecules with the environment [39,40,41,42]. For most semiconductor materials, spontaneous Frenkel pair formation is considered an unlikely source of vacancies thanks to the high energy of forming two defects as a tight pair. However, here we focus on the processes occurring deep in the material volume only. Therefore, we neglect the defect formation and recombination at the surface (Schottky defects) and the defect diffusion from and to the surface. Thus, in our case, the vacancy concentration is determined by the temperature-activated formation of Frenkel pairs (vacancy + interstitial atom).
- (2)
- The recombination of Frenkel pairs occurs only when the interstitial atom is located in the nearest internode to the vacancy (short-range interaction limit).
- (3)
- Vacancies can be neutral or have different charge states (negative for certainty), while the interstitial atom is neutral. The general case, where both the vacancy and interstitial atom have charge states, is discussed in Appendix A.
- (4)
- We neglect the vacancy participation in the complex defect formation, such as bi-vacancies and other complexes of point defects.
- (5)
- We also neglect a change of the vacancy formation and migration energies with a change in the composition of semiconductor alloys that takes place in the QW vicinity during diffusion [43]. Thus, we have a similar probability for the jump of vacancy to the host and the impurity atom states.
2. Vacancy in Uniform Crystals
2.1. Neutral Vacancy Formation
2.2. Charged Vacancy Formation
2.3. Vacancy Recharging
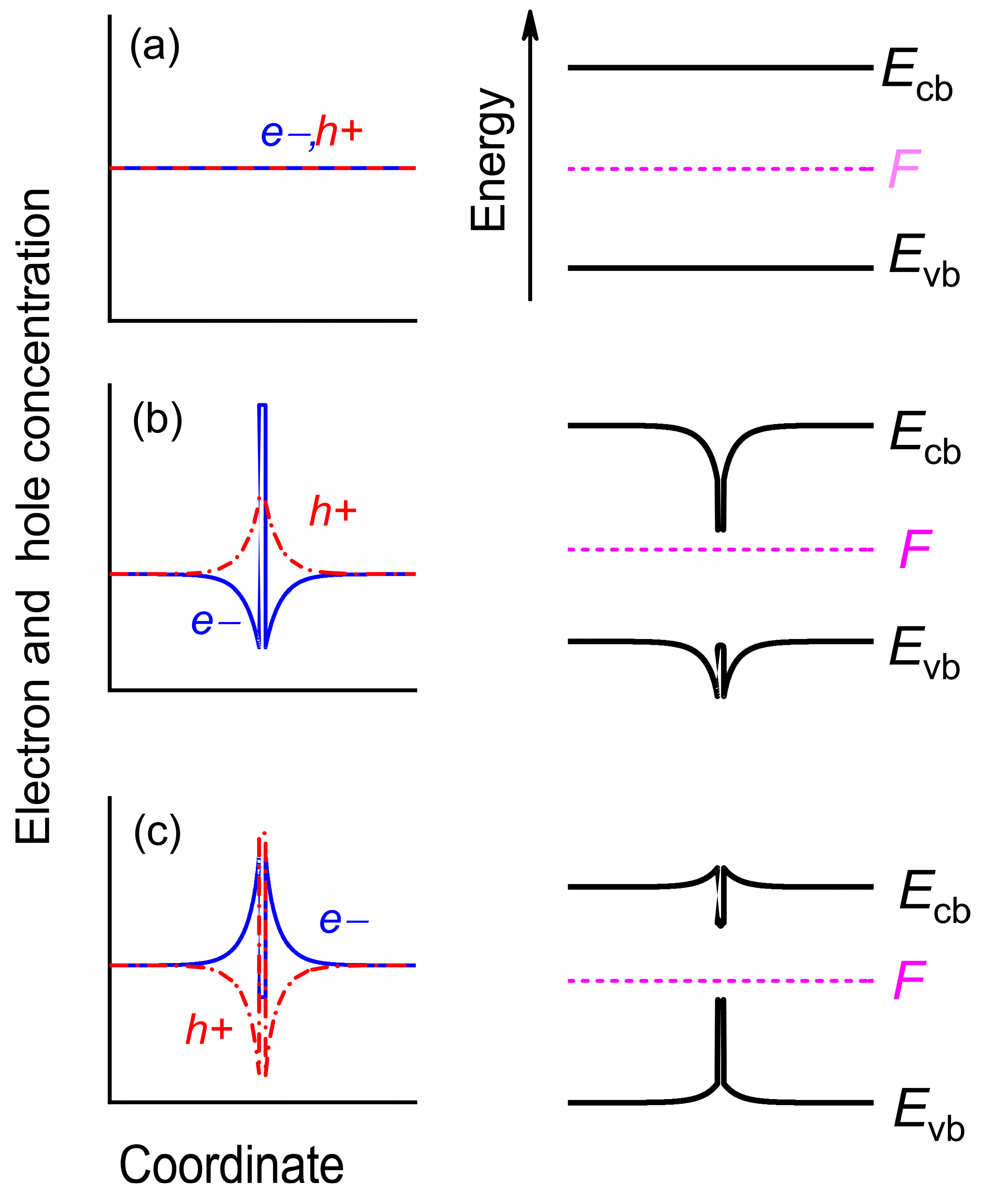
3. Spatial Distribution of Vacancies in a Heterostructure with QWs
4. Diffusion in a Model Heterostructure with a QW
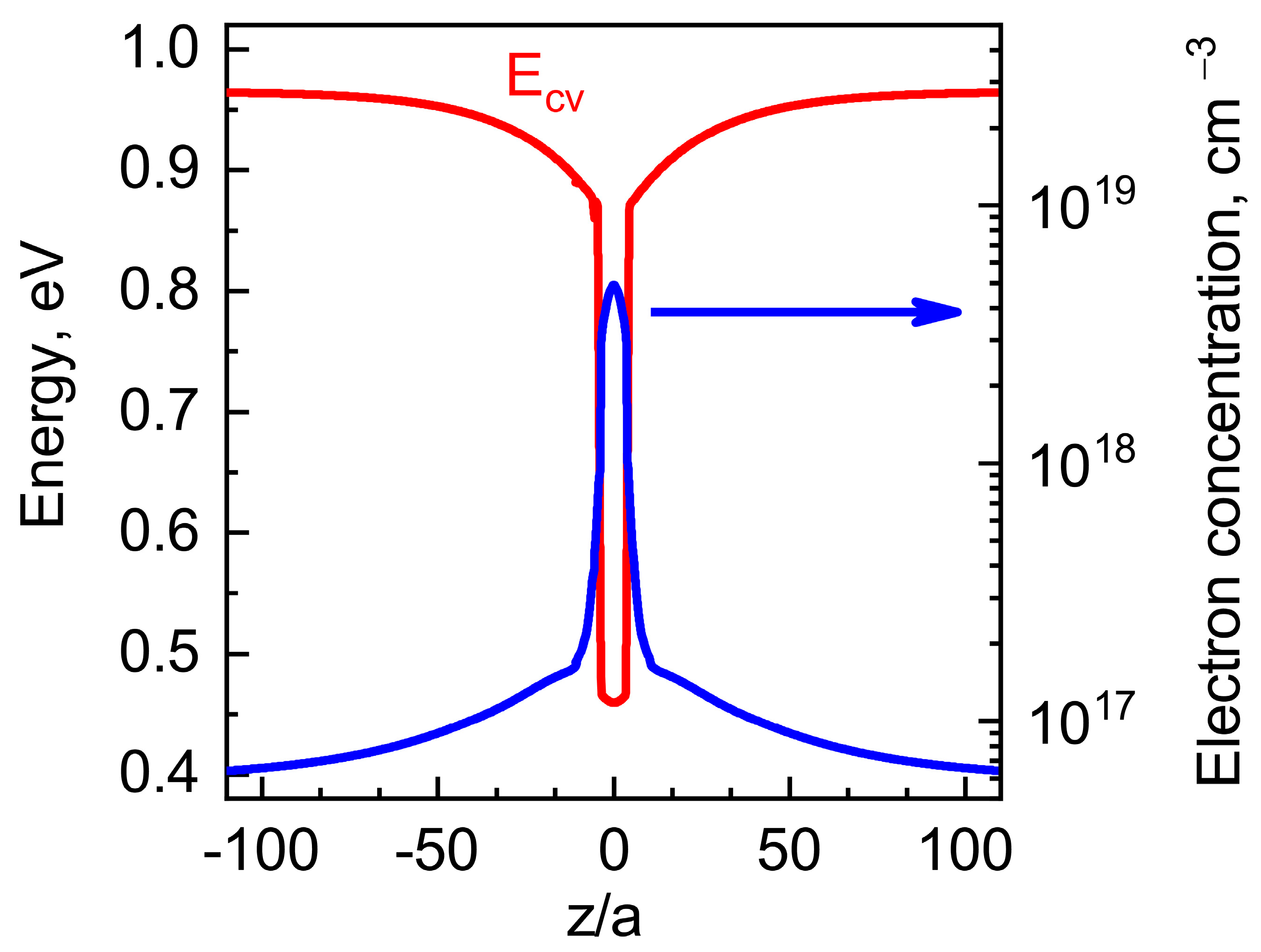
4.1. Effect of Carrier Distribution on the QW Band Structure
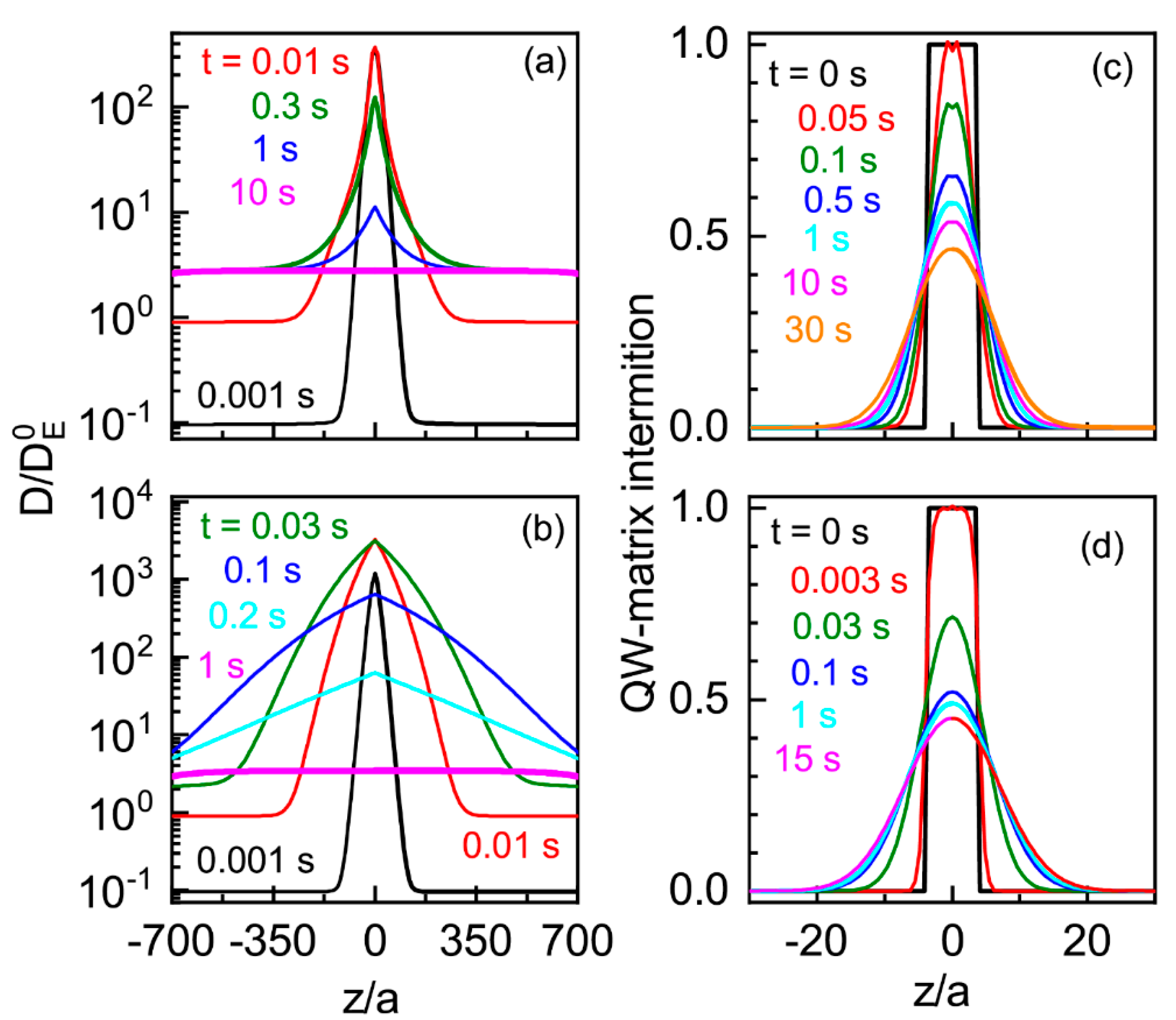
4.2. Diffusivity of QW Material
4.2.1. Approximation of Flat Bands
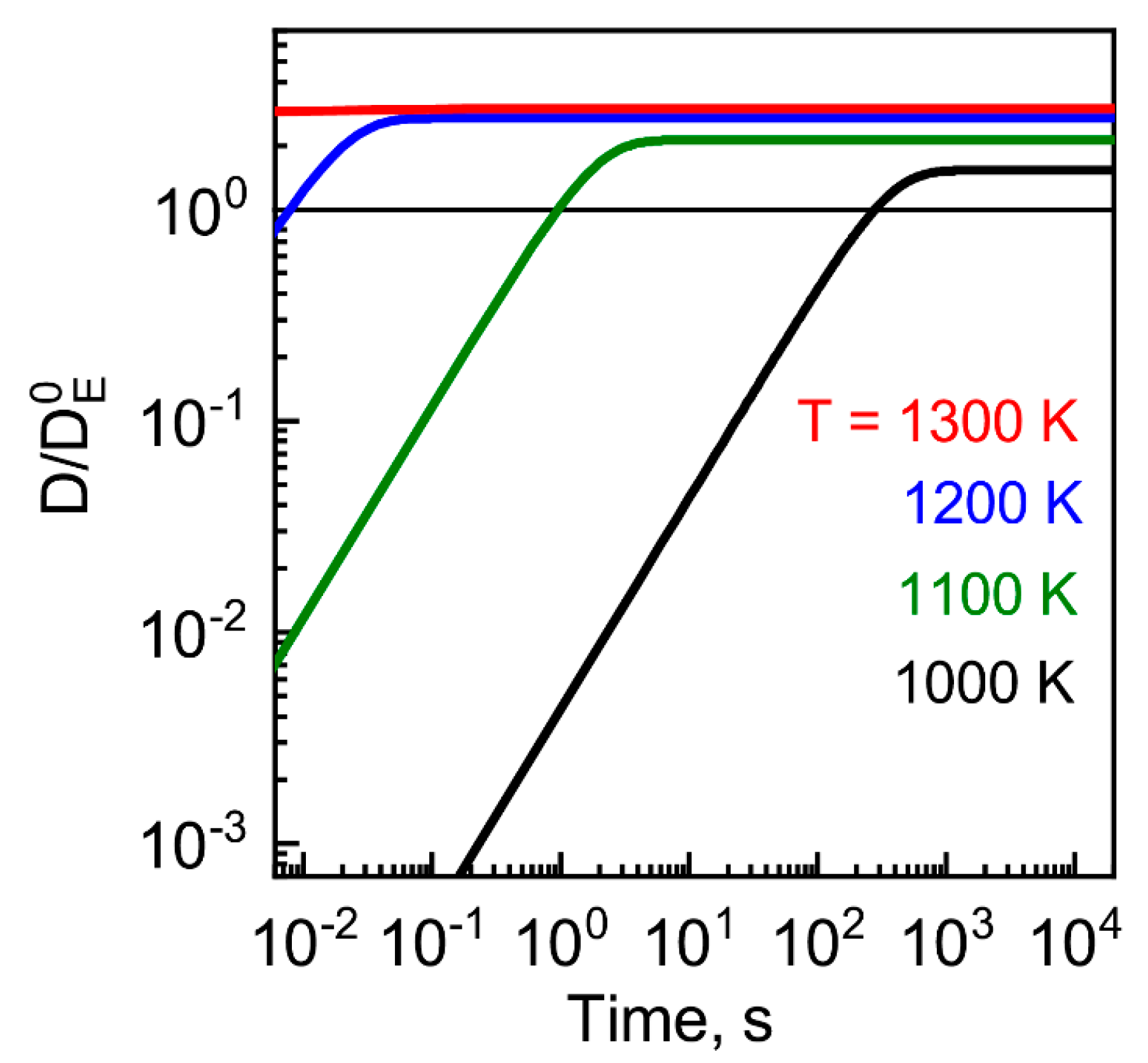
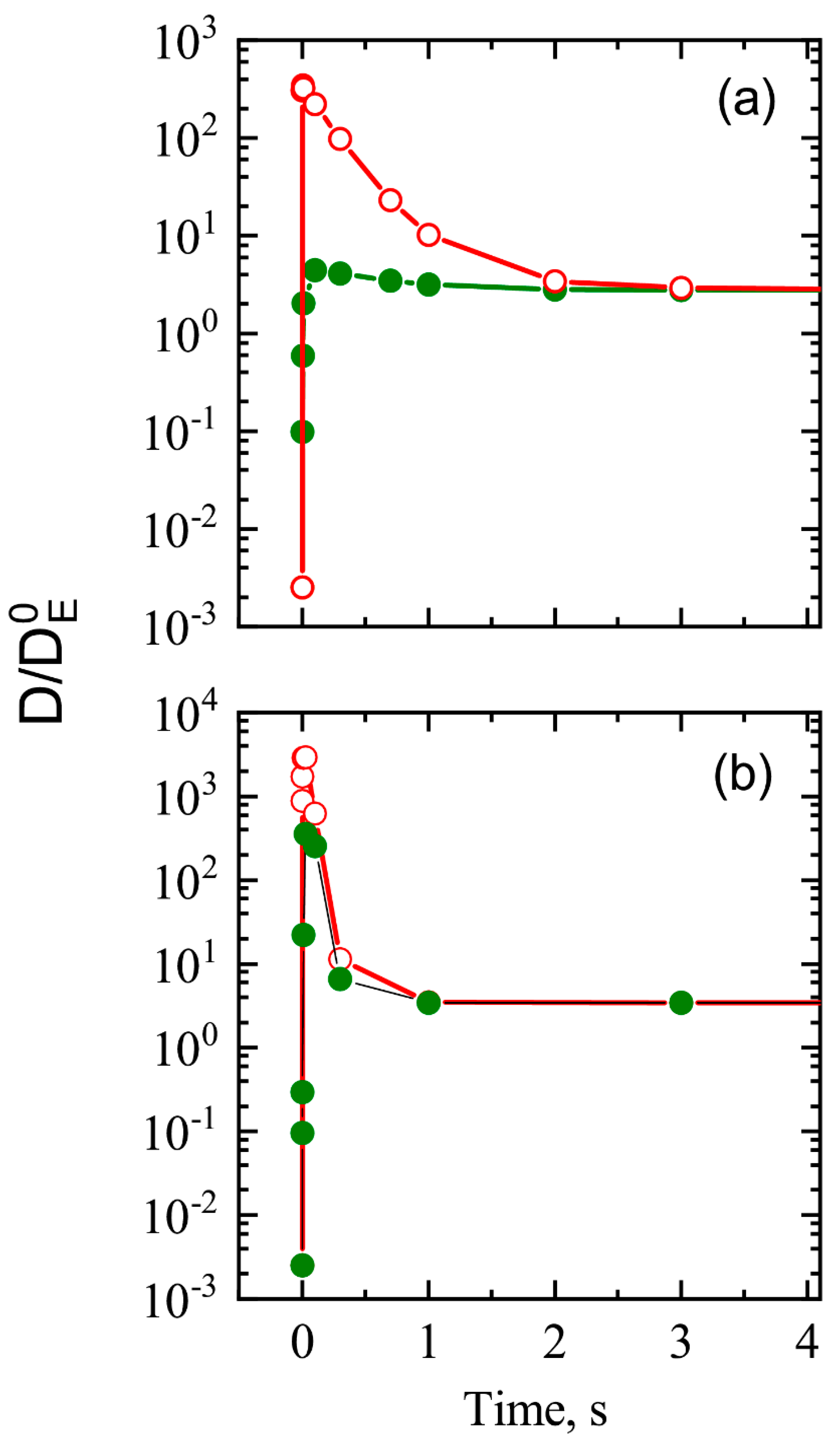
4.2.2. Effect of Thermally Generated Electron Concentration and Distribution
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
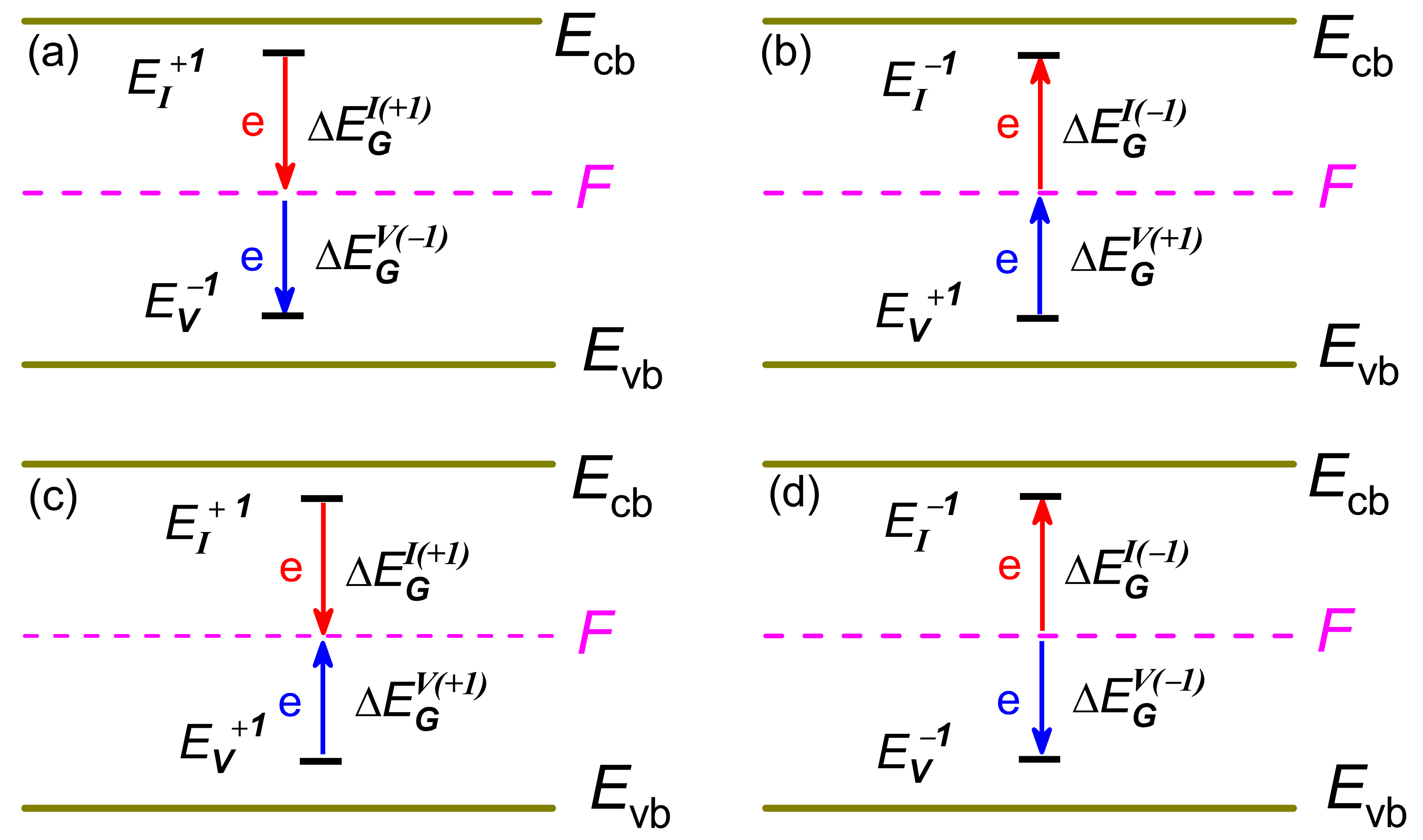
Appendix B
References
- Deppe, D.G.; Holonyak, N., Jr. Atom diffusion and impurity-induced layer disordering in quantum well III-V semiconductor heterostructures. J. Appl. Phys. 1988, 64, R93–R113. [Google Scholar] [CrossRef]
- Marsh, J.H. Quantum well intermixing. Semicond. Sci. Technol. 1993, 8, 1136. [Google Scholar]
- Li, E.H. Semiconductor Quantum Wells Intermixing; Gordon and Breach: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Gupta, D. (Ed.) Diffusion Processes in Advanced Technological Materials; Springer-Verlag: New York, NY, USA, 2005. [Google Scholar]
- Shamirzaev, T.S.; Debus, J.; Abramkin, D.S.; Dunker, D.; Yakovlev, D.R.; Dmitriev, D.V.; Gutakovskii, A.K.; Braginsky, L.S.; Zhuravlev, K.S.; Bayer, M. Exciton recombination dynamics in an ensemble of (In,Al)As/AlAs quantum dots with indirect band-gap and type-I band alignment. Phys. Rev. B 2011, 84, 155318. [Google Scholar] [CrossRef]
- Sinha, S.S.K.; Kumar, S.; Das, M.K. Dot size variability induced changes in the optical absorption spectra of interdiffused quantum dot systems. Appl. Phys. A 2019, 125, 774. [Google Scholar] [CrossRef]
- Tartakovskii, A.I.; Makhonin, M.N.; Sellers, I.R.; Cahill, J.; Andreev, A.D.; Whittaker, D.M.; Wells, J.-P.R.; Fox, A.M.; Mowbray, D.J.; Skolnick, M.S.; et al. Effect of thermal annealing and strain engineering on the fine structure of quantum dot excitons. Phys. Rev. B 2004, 70, 193303. [Google Scholar] [CrossRef]
- Zhao, H.-Q.; Mao, X.; Zhou, D.; Feng, S.; Shi, X.; Ma, Y.; Wei, X.; Mao, Y. Bandgap modulation of MoS2 monolayer by thermal annealing and quick cooling. Nanoscale 2016, 8, 18995–19003. [Google Scholar] [CrossRef]
- Mao, Y.; Mao, X.; Zhao, H.; Zhang, N.; Shi, X.; Yuan, J. Enhancement of photoluminescence efficiency in GeSe ultrathin slab by thermal treatment and annealing: Experiment and first-principles molecular dynamics simulations. Sci. Rep. 2018, 8, 17671. [Google Scholar] [CrossRef]
- Braun, T.; Betzold, S.; Lundt, N.; Kamp, M.; Hцfling, S.; Schneider, C. Impact of ex situ rapid thermal annealing on magneto-optical properties and oscillator strength of In(Ga)As quantum dots. Phys. Rev. B 2016, 93, 155307. [Google Scholar] [CrossRef]
- Loo, V.; Lanco, L.; Lemaitre, A.; Sagnes, I.; Krebs, O.; Voisin, P.; Senellart, P. Quantum dot-cavity strong-coupling regime measured through coherent reflection spectroscopy in a very high-Q micropillar. Appl. Phys. Lett. 2010, 97, 241110. [Google Scholar] [CrossRef]
- Petrov, M.Y.; Ignatiev, I.; Poltavtsev, S.; Greilich, A.; Bauschulte, A.; Yakovlev, D.; Bayer, M. Effect of thermal annealing on the hyperfine interaction in InAs/GaAs quantum dots. Phys. Rev. B 2008, 78, 045315. [Google Scholar] [CrossRef]
- Langbein, W.; Borri, P.; Woggon, U.; Stavarache, V.; Reuter, D.; Wieck, A.D. Radiatively limited dephasing in InAs quantum dots. Phys. Rev. B 2004, 70, 033301. [Google Scholar] [CrossRef]
- Rogers, C.; Gray, D.; Bogdanowicz, N.; Mabuchi, H. Laser annealing for radiatively broadened MoSe2 grown by chemical vapor deposition. Phys. Rev. Mater. 2018, 2, 094003. [Google Scholar] [CrossRef]
- Hruszkewycz, S.O.; Maddali, S.; Anderson, C.P.; Cha, W.; Miao, K.C.; Highland, M.J.; Ulvestad, A.; Awschalom, D.D.; Heremans, F.J. Strain annealing of SiC nanoparticles revealed through Bragg coherent diffraction imaging for quantum technologies. Phys. Rev. Mater. 2018, 2, 086001. [Google Scholar] [CrossRef]
- Petrushkov, M.O.; Abramkin, D.S.; Emelyanov, E.A.; Putyato, M.A.; Komkov, O.S.; Firsov, D.D.; Vasev, A.V.; Yesin, M.Y.; Bakarov, A.K.; Loshkarev, I.D.; et al. Dislocation Filter Based on LT-GaAs Layers for Monolithic GaAs/Si Integration. Nanomaterials 2022, 12, 4449. [Google Scholar] [CrossRef]
- Ivanov, V.Y.; Shamirzaev, T.S.; Yakovlev, D.R.; Gutakovskii, A.K.; Owczarczyk, Ł.; Bayer, M. Optically detected magnetic resonance of photoexcited electrons in (In,Al)As/AlAs quantum dots with indirect band gap and type-I band alignment. Phys. Rev. B 2018, 97, 245306. [Google Scholar] [CrossRef]
- Abramkin, D.S.; Atuchin, V.V. Novel InGaSb/AlP Quantum Dots for Non-Volatile Memories. Nanomaterials 2022, 12, 3794. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Kalagin, A.K.; Toropov, A.I.; Gutakovskii, A.K.; Zhuravlev, K.S. Narrowing of ground energy level distribution in an array of InAs/AlAs QDs by post grown annealing. Phys. Status Solidi C 2006, 3, 3932–3934. [Google Scholar] [CrossRef]
- Tuck, B. Mechanisms of atomic diffusion in the III-V semiconductors. J. Phys. D Appl. Phys. 1985, 18, 557–584. [Google Scholar] [CrossRef]
- Khreis, O.M.; Gillin, W.P.; Homewood, K.P. Interdiffusion: A probe of vacancy diffusion in III-V materials. Phys. Rev. B 1997, 55, 15813–15818. [Google Scholar] [CrossRef]
- El-Mellouhi, F.; Mousseau, N. Self-vacancies in gallium arsenide: An ab initio calculation. Phys. Rev. B 2005, 71, 125207. [Google Scholar] [CrossRef]
- Baraff, G.A.; Schliiter, M. Electronic Structure, Total Energies, and Abundances of the Elementary Point Defects in GaAs. Phys. Rev. Lett. 1985, 55, 1327. [Google Scholar] [CrossRef] [PubMed]
- Walukiewicz, W. Amphoteric native defects in semiconductors. Appl. Phys. Lett. 1989, 54, 2094–2096. [Google Scholar] [CrossRef]
- Seebauer, E.G.; Kratzer, M.C. Charged point defects in semiconductors. Mater. Sci. Eng. R Rep. 2006, 55, 57–149. [Google Scholar] [CrossRef]
- Gebauer, J.; Lausmann, M.; Redmann, F.; Krause-Rehberg, R.; Leipner, H.S.; Weber, E.R.; Ebert, P. Determination of the Gibbs free energy of formation of Ga vacancies in GaAs by positron annihilation. Phys. Rev. B 2003, 67, 235207. [Google Scholar] [CrossRef]
- Tahini, H.A.; Chroneos, A.; Murphy, S.; Schwingenschlogl, U.; Grimes, R.W. Vacancies and defect levels in III–V semiconductors. J. Appl. Phys. 2013, 114, 063517. [Google Scholar] [CrossRef]
- Zhang, S.B.; Northrup, J.E. Chemical potential dependence of defect formation energies in GaAs: Application to Ga self-diffusion. Phys. Rev. Lett. 1991, 67, 2339–2342. [Google Scholar] [CrossRef]
- Vinetskii, V.L.; Kholodar, G.A. The Statistical Interaction of Electrons and Defects in Semiconductors; Naukova Dumka: Kiev, Ukraine, 1969. (In Russian) [Google Scholar]
- Sky, T.N.; Johansen, K.M.; Venkatachalapathy, V.; Svensson, B.G.; Vines, L.; Tuomisto, F. Influence of Fermi level position on vacancy-assisted diffusion of aluminum in zinc oxide. Phys. Rev. B 2018, 98, 245204. [Google Scholar] [CrossRef]
- Babar, R.; Kabir, M. Gate-dependent vacancy diffusion in graphene. Phys. Rev. B 2018, 98, 075439. [Google Scholar] [CrossRef]
- Crawford, J.H., Jr.; Slifkin, L.M. (Eds.) Point defects in solids. In Semiconductors and Molecular Crystals; Plenum Press: New York, NY, USA, 1975; Volume 2. [Google Scholar]
- Drabold, D.A.; Estreicher, S.K. (Eds.) Theory of Defects in Semiconductors; Springer-Verlag: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Djie, H.S.; Gunawan, O.; Wang, D.-N.; Ooi, B.S.; Hwang, J.C.M. Group-III vacancy induced InxGa1−xAs quantum dot interdiffusion. Phys. Rev. B 2006, 73, 155324. [Google Scholar] [CrossRef]
- Wang, Y.; Djie, H.S.; Ooi, B.S. Group-III intermixing in InAs∕InGaAlAs quantum dots-in-well. Appl. Phys. Lett. 2006, 88, 111110. [Google Scholar] [CrossRef]
- Alahmadi, Y.; LiKamW, P. Effects of selective area intermixing on InAlGaAs multiple quantum well laser diode. Semicond. Sci. Technol. 2019, 34, 025010. [Google Scholar] [CrossRef]
- Lever, P.; Tan, H.H.; Jagadish, C. Impurity free vacancy disordering of InGaAs quantum dots. J. Appl. Phys. 2004, 96, 7544–7548. [Google Scholar] [CrossRef]
- McKerracher, I.; Fu, L.; Tan, H.H.; Jagadish, C. Intermixing of InGaAs/GaAs quantum wells and quantum dots using sputter-deposited silicon oxynitride capping layers. J. Appl. Phys. 2012, 112, 113511. [Google Scholar] [CrossRef]
- Rouviere, J.-L.; Kim, Y.; Cunningham, J.; Rentschler, J.A.; Bourret, A.; Ourmazd, A. Measuring properties of point defects by electron microscopy: The Ga vacancy in GaAs. Phys. Rev. Lett. 1992, 68, 2798–2801. [Google Scholar] [CrossRef]
- Hurle, D.T.J. A comprehensive thermodynamic analysis of native point defect and dopant solubilities in gallium arsenide. J. Appl. Phys. 1999, 85, 6957–7022. [Google Scholar] [CrossRef]
- Freysoldt, C.; Neugebauer, J. First-principles calculations for charged defects at surfaces, interfaces, and two-dimensional materials in the presence of electric fields. Phys. Rev. B 2018, 97, 205425. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Sokolov, A.L.; Zhuravlev, K.S.; Kobitski, A.Y.; Wagner, H.P.; Zahn, D.R. Changes in the density of nonradiative recombination centers in GaAs/AlGaAs quantum-well structures as a result of treatment in CF4 plasma. Semiconductors 2002, 36, 81–84. [Google Scholar] [CrossRef]
- Ma, J.; Wei, S.-H. Bowing of the defect formation energy in semiconductor alloys. Phys. Rev. B 2013, 87, 241201. [Google Scholar] [CrossRef]
- Freysoldt, C.; Grabowski, B.; Hickel, T.; Neugebauer, J.; Kresse, G.; Janotti, A.; Van de Walle, C.G. First-principles calculations for point defects in solids. Rev. Mod. Phys. 2014, 86, 253–305. [Google Scholar] [CrossRef]
- Wright, A.F.; Modine, N.A. Migration processes of the As interstitial in GaAs. J. Appl. Phys. 2016, 120, 215705. [Google Scholar] [CrossRef]
- Grundmann, M. The Physics of Semiconductors; Springer-Verlag: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Mitev, P.; Seshadri, S.; Guido, L.J.; Schaafsma, D.T.; Christensen, D.H. Cation vacancy formation and migration in the AlGaAs heterostructure system. Appl. Phys. Lett. 1998, 73, 3718–3720. [Google Scholar] [CrossRef]
- Lahiri, I.; Nolte, D.D.; Melloch, M.R.; Woodall, J.M.; Walukiewicz, W. Enhanced diffusion in nonstoichiometric quantum wells and the decay of supersaturated vacancy concentrations. Appl. Phys. Lett. 1996, 69, 239–241. [Google Scholar] [CrossRef]
- Geursen, R.; Lahiri, I.; Dinu, M.; Melloch, M.R.; Nolte, D.D. Transient enhanced intermixing of arsenic-rich nonstoichiometric AlAs/GaAs quantum wells. Phys. Rev. B 1999, 60, 10926–10934. [Google Scholar] [CrossRef]
- Bert, N.A.; Chaldyshev, V.V.; Musikhin, Y.G.; Suvorova, A.A.; Preobrazhenskii, V.V.; Putyato, M.A.; Semyagin, B.R.; Werner, P. In–Ga intermixing in low-temperature grown GaAs delta doped with In. Appl. Phys. Lett. 1999, 74, 1442–1444. [Google Scholar] [CrossRef]
- Tan, T.Y.; Gosele, U.; Yu, S. Point defects, diffusion mechanisms, and superlattice disordering on Gallium Arsenide-based materials. Crit. Rev. Solid State Mater. Sci. 1991, 17, 47. [Google Scholar] [CrossRef]
- Van Vechten, J.A. Handbook on Semiconductors; Moss, T.S., Ed.; North-Holland: Amsterdam, The Netherlands, 1980; Chapter 1; Volume 3. [Google Scholar]
- Bockstedte, M.; Schefer, M. Theory of Self-Diffusion in GaAs. Z. Phys. Chem. 1997, 200, 195. [Google Scholar] [CrossRef]
- Jia, Y.Q.; Bardeleben, H.J.V.; Stienvard, D.; Delerue, C. Electron-paramagnetic-resonance observation of gallium vacancy in electron-irradiated p-type GaAs. Phys. Rev. B 1992, 45, 1645. [Google Scholar] [CrossRef]
- Vurgaftman, I.; Meyer, J.R.; Ram-Mohan, L.R. Band parameters for III–V compound semiconductors and their alloys. J. Appl. Phys. 2001, 89, 5815–5875. [Google Scholar] [CrossRef]
- Haysom, J.E.; Aers, G.C.; Raymond, S.; Poole, P.J. Study of quantum well intermixing caused by grown-in defects. J. Appl. Phys. 2000, 88, 3090–3092. [Google Scholar] [CrossRef]
- Dion, C.; Desjardins, P.; Shtinkov, N.; Schiettekatte, F.; Poole, P.J.; Raymond, S. Effects of grown-in defects on interdiffusion dynamics in InAs∕InP(001) quantum dots subjected to rapid thermal annealing. J. Appl. Phys. 2008, 103, 083526. [Google Scholar] [CrossRef]
- Fiset-Cyr, A.; Dalacu, D.; Haffouz, S.; Poole, P.J.; Lapointe, J.; Aers, G.C.; Williams, R.L. In-situ tuning of individual position-controlled nanowire quantum dots via laser-induced intermixing. Appl. Phys. Lett. 2018, 113, 053105. [Google Scholar] [CrossRef]
- Zibold, T. Semiconductor based quantum information devices:Theory and simulations. Ph.D. Thesis, Technische Universitдt München, Munich, Germany, 2007. [Google Scholar]
- Shamirzaev, T.S.; Gilinsky, A.M.; Kalagin, A.K.; Nenashev, A.V.; Zhuravlev, K.S. Energy spectrum and structure of thin pseudomorphic InAs quantum wells in an AlAs matrix: Photoluminescence spectra and band-structure calculations. Phys. Rev. B 2007, 76, 155309. [Google Scholar] [CrossRef]
- Shamirzaev, T.S. Type-I semiconductor heterostructures with an indirect-gap conduction band. Semiconductors 2011, 45, 96–102. [Google Scholar] [CrossRef]
- Shamirzaev, T.S.; Yakovlev, D.R.; Kopteva, N.E.; Kudlacik, D.; Glazov, M.M.; Krechetov, A.G.; Gutakovskii, A.K.; Bayer, M. Spin dynamics of charged excitons in ultrathin (In,Al)(Sb,As)/AlAs and Al(Sb,As)/AlAs quantum wells with an indirect band gap. Phys. Rev. B 2022, 106, 075407. [Google Scholar] [CrossRef]
- Gillin, W.; Dunstan, D.J.; Homewood, K.P.; Howard, L.K.; Sealy, B.J. Interdiffusion in InGaAs/GaAs quantum well structures as a function of depth. J. Appl. Phys. 1993, 73, 3782–3786. [Google Scholar] [CrossRef]
- Gillin, W.P. Effect of strain on the interdiffusion of InGaAs/GaAs heterostructures. J. Appl. Phys. 1999, 85, 790–793. [Google Scholar] [CrossRef]

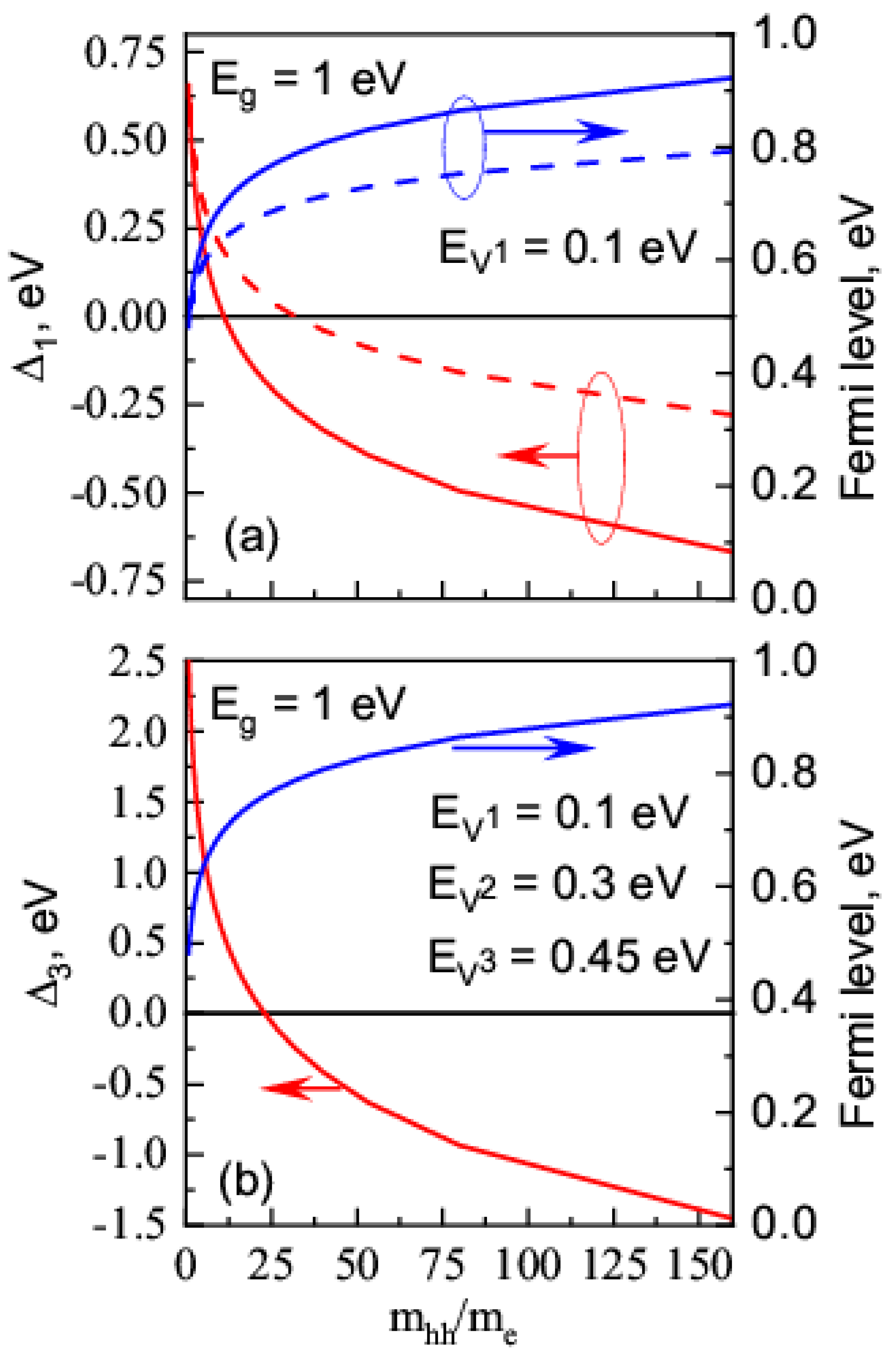
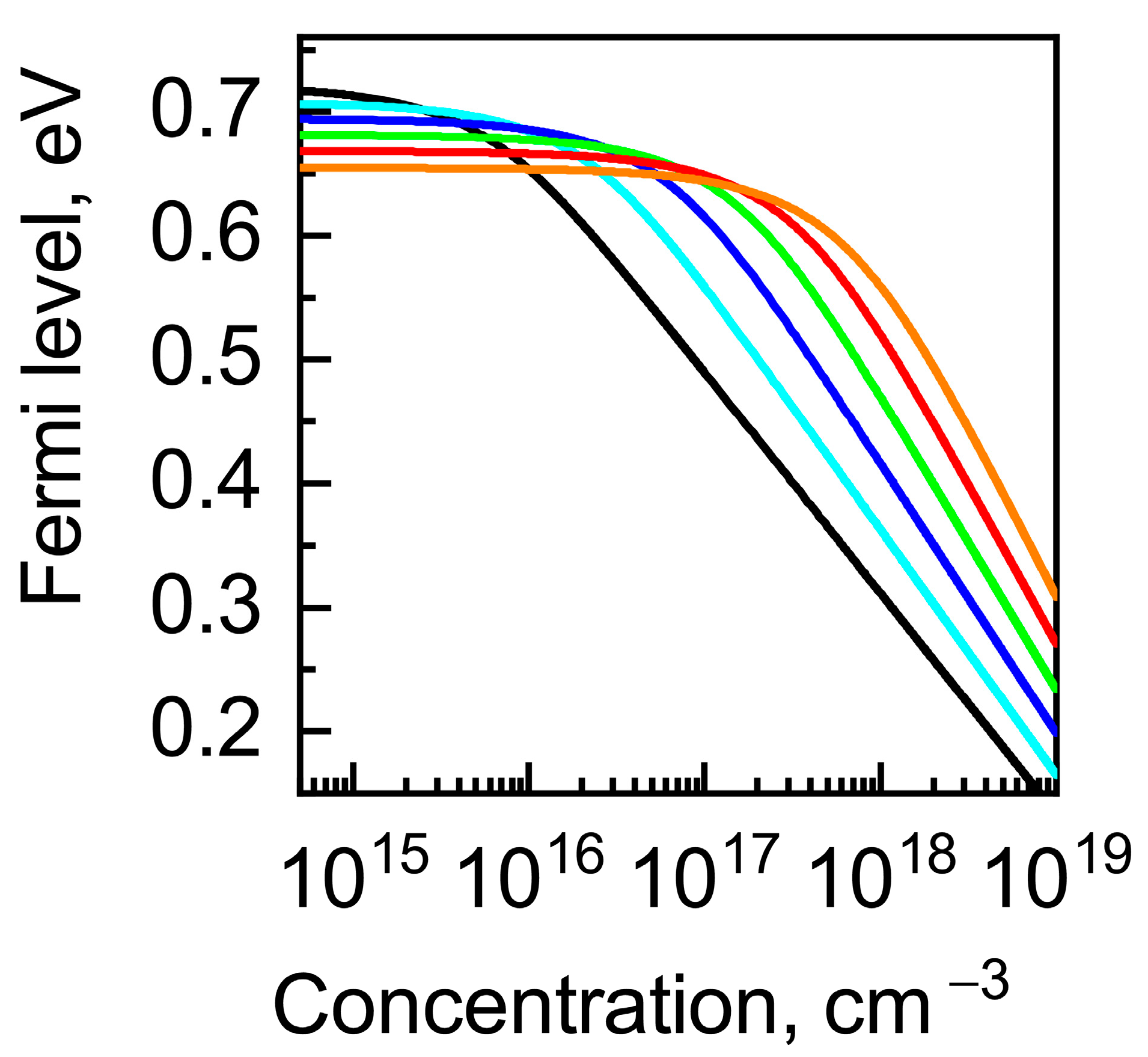
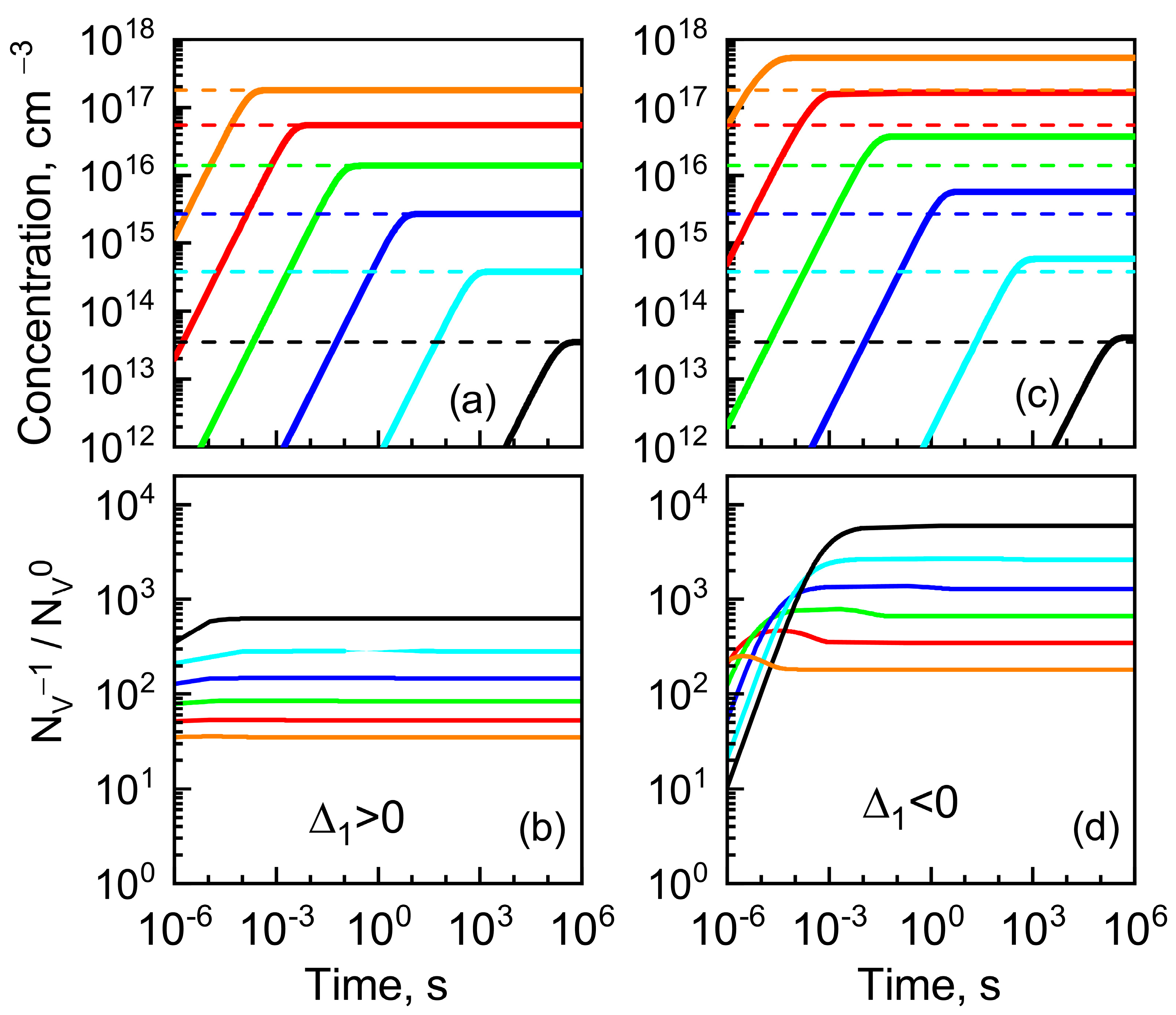

| Parameter | Value |
|---|---|
| (eV) | 2.8 [53], 3.2 [26], 3.7 [54] |
| (eV) | 0.8 [50], 1.8 [48], 2.7 [52], 3.3 [47] |
| 7.3 × k [53] | |
| 11.3 × k [47] | |
| ν (Hz) | 1013 [44] |
| 0.13 × [23,26] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shamirzaev, T.S.; Atuchin, V.V.; Zhilitskiy, V.E.; Gornov, A.Y. Dynamics of Vacancy Formation and Distribution in Semiconductor Heterostructures: Effect of Thermally Generated Intrinsic Electrons. Nanomaterials 2023, 13, 308. https://doi.org/10.3390/nano13020308
Shamirzaev TS, Atuchin VV, Zhilitskiy VE, Gornov AY. Dynamics of Vacancy Formation and Distribution in Semiconductor Heterostructures: Effect of Thermally Generated Intrinsic Electrons. Nanomaterials. 2023; 13(2):308. https://doi.org/10.3390/nano13020308
Chicago/Turabian StyleShamirzaev, Timur S., Victor V. Atuchin, Vladimir E. Zhilitskiy, and Alexander Yu. Gornov. 2023. "Dynamics of Vacancy Formation and Distribution in Semiconductor Heterostructures: Effect of Thermally Generated Intrinsic Electrons" Nanomaterials 13, no. 2: 308. https://doi.org/10.3390/nano13020308
APA StyleShamirzaev, T. S., Atuchin, V. V., Zhilitskiy, V. E., & Gornov, A. Y. (2023). Dynamics of Vacancy Formation and Distribution in Semiconductor Heterostructures: Effect of Thermally Generated Intrinsic Electrons. Nanomaterials, 13(2), 308. https://doi.org/10.3390/nano13020308






