Heat-Mode Excitation in a Proximity Superconductor
Abstract
1. Introduction
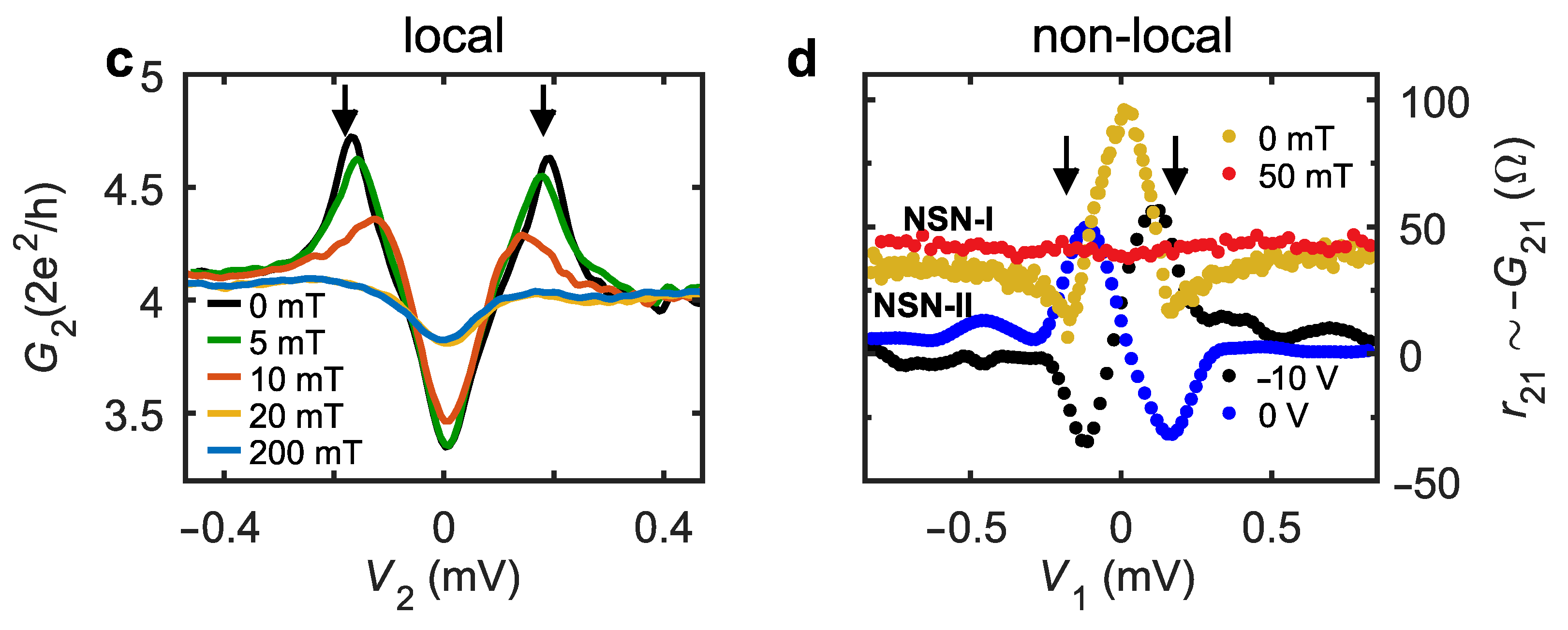
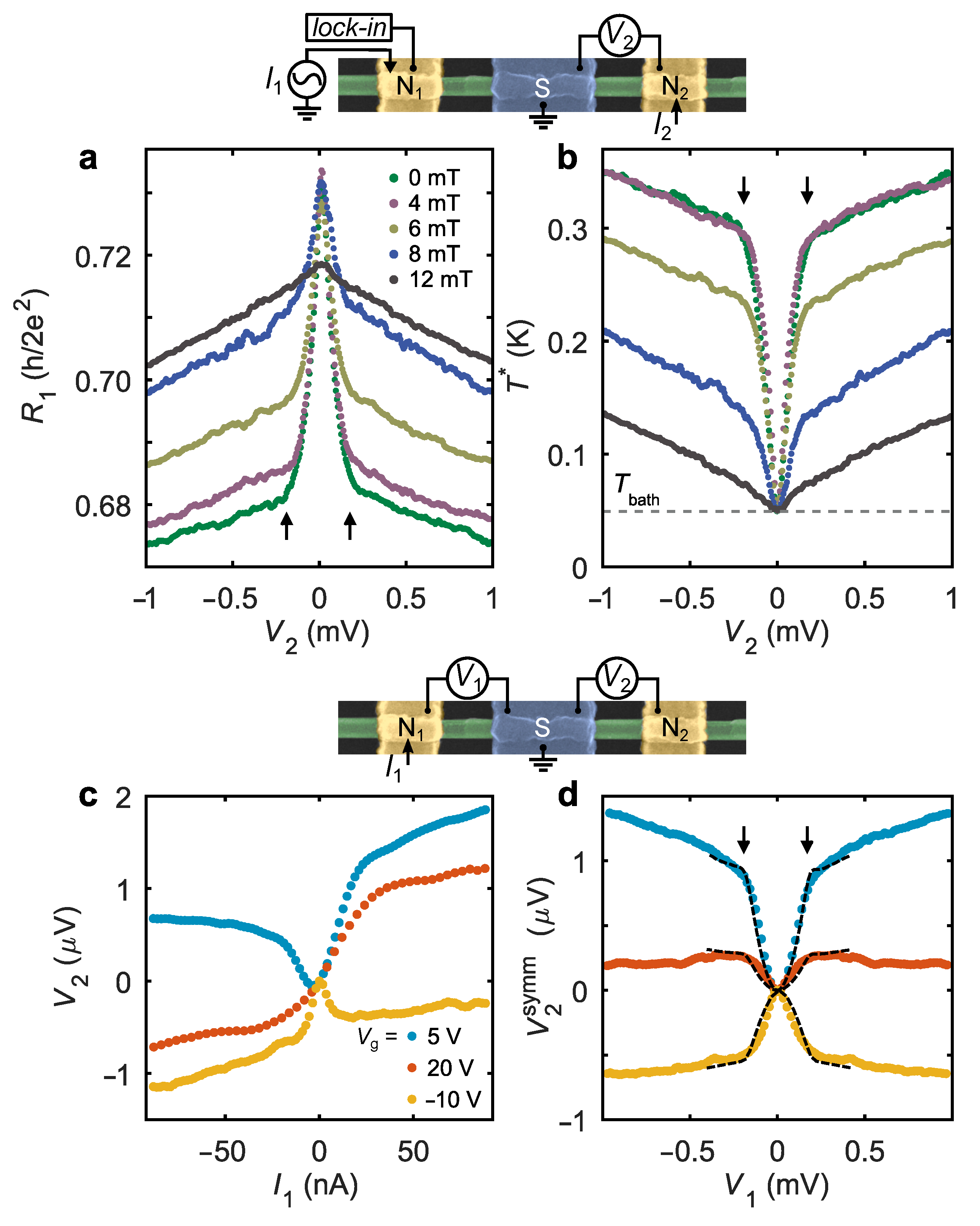
2. Results: Devices and Transport Response
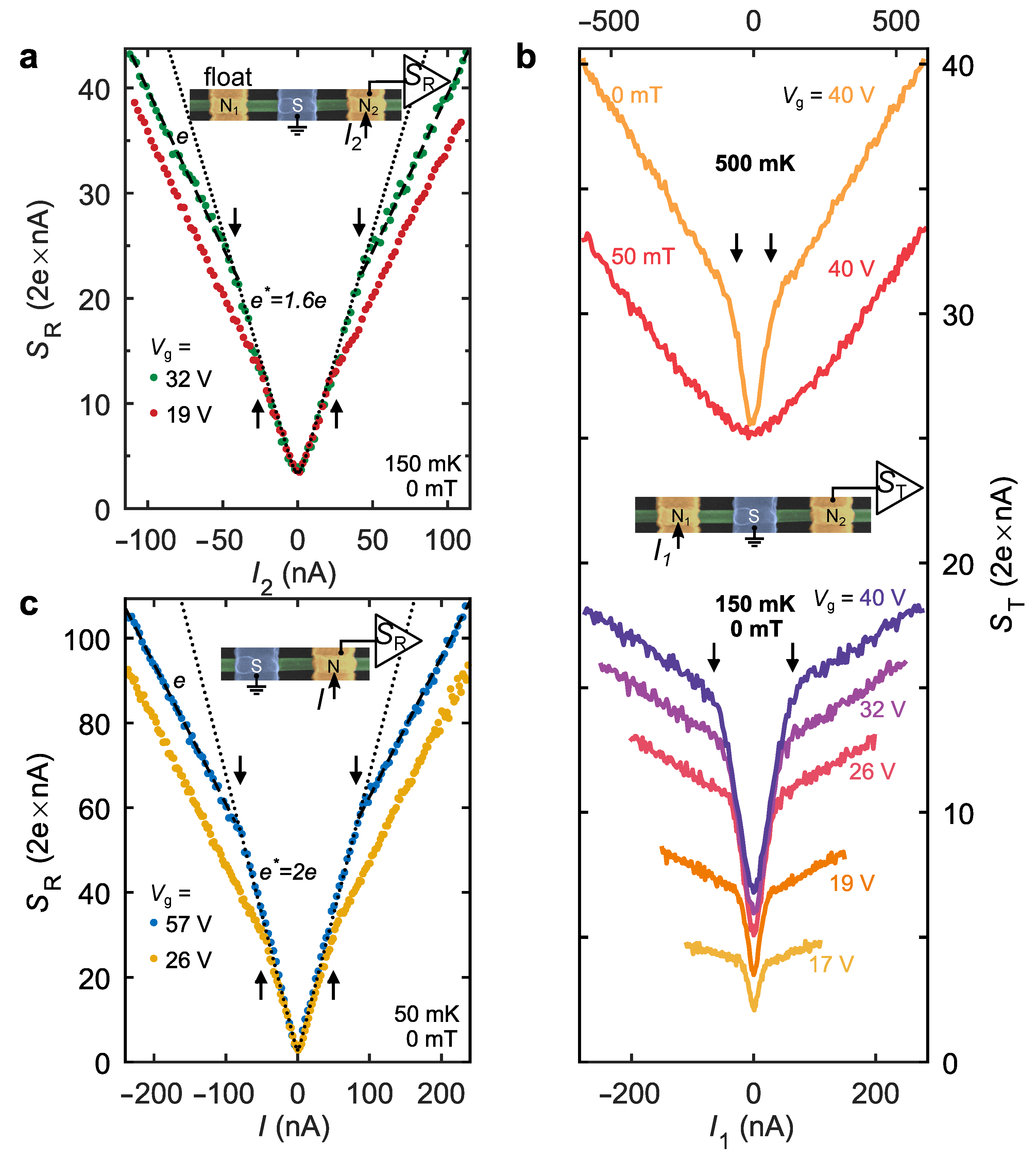
3. Results: Shot Noise Response
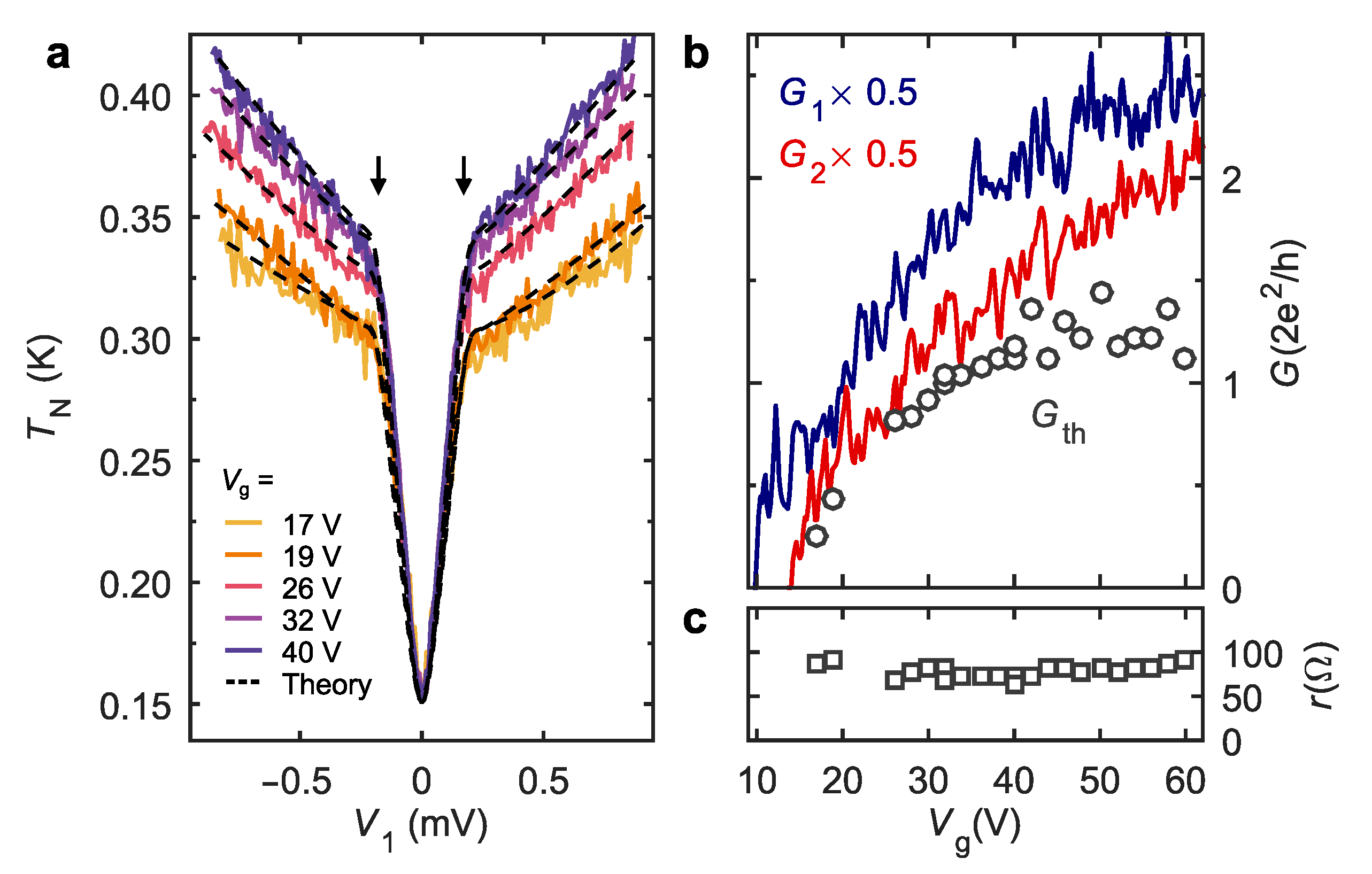
4. Results: Non-Equilibrium DC Transport
5. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Andreev, A.F. Thermal Conductivity of the Intermediate State of Superconductors. JETP Lett. 1964, 46, 1823–1828. [Google Scholar]
- Giazotto, F.; Heikkilä, T.T.; Luukanen, A.; Savin, A.M.; Pekola, J.P. Opportunities for mesoscopics in thermometry and refrigeration: Physics and applications. Rev. Mod. Phys. 2006, 78, 217–274. [Google Scholar] [CrossRef]
- Caroli, C.; Gennes, P.D.; Matricon, J. Bound Fermion states on a vortex line in a type II superconductor. Phys. Lett. 1964, 9, 307–309. [Google Scholar] [CrossRef]
- Titov, M.; Ossipov, A.; Beenakker, C.W.J. Excitation gap of a graphene channel with superconducting boundaries. Phys. Rev. B 2007, 75, 045417. [Google Scholar] [CrossRef]
- Lee, G.H.; Huang, K.F.; Efetov, D.K.; Wei, D.S.; Hart, S.; Taniguchi, T.; Watanabe, K.; Yacoby, A.; Kim, P. Inducing superconducting correlation in quantum Hall edge states. Nat. Phys. 2017, 13, 693–698. [Google Scholar] [CrossRef]
- Zhao, L.; Arnault, E.G.; Bondarev, A.; Seredinski, A.; Larson, T.F.Q.; Draelos, A.W.; Li, H.; Watanabe, K.; Taniguchi, T.; Amet, F.; et al. Interference of chiral Andreev edge states. Nat. Phys. 2020, 16, 862–867. [Google Scholar] [CrossRef]
- Kurilovich, V.D.; Raines, Z.M.; Glazman, L.I. Disorder in Andreev reflection of a quantum Hall edge. arXiv 2022, arXiv:2201.00273. [Google Scholar]
- Banerjee, M.; Heiblum, M.; Rosenblatt, A.; Oreg, Y.; Feldman, D.E.; Stern, A.; Umansky, V. Observed quantization of anyonic heat flow. Nature 2017, 545, 75–79. [Google Scholar] [CrossRef]
- Beenakker, C.W.J. Specular Andreev Reflection in Graphene. Phys. Rev. Lett. 2006, 97, 067007. [Google Scholar] [CrossRef]
- Kopnin, N.B.; Mel’nikov, A.S.; Vinokur, V.M. Reentrant localization of single-particle transport in disordered Andreev wires. Phys. Rev. B 2004, 70, 075310. [Google Scholar] [CrossRef]
- Tinkham, M. Introduction to Superconductivity; Dover Books on Physics Series; Dover Publications: College Park, MD, USA, 2004. [Google Scholar]
- Artemenko, S.N.; Volkov, A.F. Electric fields and collective oscillations in superconductors. Sov. Phys. Uspekhi 1979, 22, 295–310. [Google Scholar] [CrossRef]
- Hofstetter, L.; Csonka, S.; Nygård, J.; Schönenberger, C. Cooper pair splitter realized in a two-quantum-dot Y-junction. Nature 2009, 461, 960–963. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, L.G.; Portier, F.; Roche, P.; Yeyati, A.L.; Kontos, T.; Strunk, C. Carbon Nanotubes as Cooper-Pair Beam Splitters. Phys. Rev. Lett. 2010, 104, 026801. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Ronen, Y.; Heiblum, M.; Mahalu, D.; Kretinin, A.V.; Shtrikman, H. High-efficiency Cooper pair splitting demonstrated by two-particle conductance resonance and positive noise cross-correlation. Nat. Commun. 2012, 3, 1165. [Google Scholar] [CrossRef] [PubMed]
- Lutchyn, R.M.; Sau, J.D.; Das Sarma, S. Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures. Phys. Rev. Lett. 2010, 105, 077001. [Google Scholar] [CrossRef] [PubMed]
- Oreg, Y.; Refael, G.; von Oppen, F. Helical Liquids and Majorana Bound States in Quantum Wires. Phys. Rev. Lett. 2010, 105, 177002. [Google Scholar] [CrossRef]
- Albrecht, S.M.; Higginbotham, A.P.; Madsen, M.; Kuemmeth, F.; Jespersen, T.S.; Nygård, J.; Krogstrup, P.; Marcus, C.M. Exponential protection of zero modes in Majorana islands. Nature 2016, 531, 206–209. [Google Scholar] [CrossRef]
- Deng, M.T.; Vaitiekenas, S.; Hansen, E.B.; Danon, J.; Leijnse, M.; Flensberg, K.; Nygård, J.; Krogstrup, P.; Marcus, C.M. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science 2016, 354, 1557–1562. [Google Scholar] [CrossRef]
- Yu, P.; Chen, J.; Gomanko, M.; Badawy, G.; Bakkers, E.P.A.M.; Zuo, K.; Mourik, V.; Frolov, S.M. Non-Majorana states yield nearly quantized conductance in proximatized nanowires. Nat. Phys. 2021, 17, 482–488. [Google Scholar] [CrossRef]
- Wang, G.; Dvir, T.; van Loo, N.; Mazur, G.P.; Gazibegovic, S.; Badawy, G.; Bakkers, E.P.A.M.; Kouwenhoven, L.P.; de Lange, G. Non-local measurement of quasiparticle distribution in proximitized semiconductor nanowires using quantum dots. arXiv 2021, arXiv:2110.05373. [Google Scholar]
- Vaitiekėnas, S.; Winkler, G.W.; van Heck, B.; Karzig, T.; Deng, M.T.; Flensberg, K.; Glazman, L.I.; Nayak, C.; Krogstrup, P.; Lutchyn, R.M.; et al. Flux-induced topological superconductivity in full-shell nanowires. Science 2020, 367, eaav3392. [Google Scholar] [CrossRef] [PubMed]
- Kopasov, A.A.; Mel’nikov, A.S. Multiple topological transitions driven by the interplay of normal scattering and Andreev scattering. Phys. Rev. B 2020, 101, 054515. [Google Scholar] [CrossRef]
- Denisov, A.O.; Bubis, A.V.; Piatrusha, S.U.; Titova, N.A.; Nasibulin, A.G.; Becker, J.; Treu, J.; Ruhstorfer, D.; Koblmüller, G.; Tikhonov, E.S.; et al. Charge-neutral nonlocal response in superconductor-InAs nanowire hybrid devices. Semicond. Sci. Technol. 2021, 36, 09LT04. [Google Scholar] [CrossRef]
- Keizer, R.S.; Flokstra, M.G.; Aarts, J.; Klapwijk, T.M. Critical Voltage of a Mesoscopic Superconductor. Phys. Rev. Lett. 2006, 96, 147002. [Google Scholar] [CrossRef]
- Hübler, F.; Lemyre, J.C.; Beckmann, D.; Löhneysen, H.V. Charge imbalance in superconductors in the low-temperature limit. Phys. Rev. B 2010, 81, 184524. [Google Scholar] [CrossRef]
- Vercruyssen, N.; Verhagen, T.G.A.; Flokstra, M.G.; Pekola, J.P.; Klapwijk, T.M. Evanescent states and nonequilibrium in driven superconducting nanowires. Phys. Rev. B 2012, 85, 224503. [Google Scholar] [CrossRef]
- Golikova, T.E.; Wolf, M.J.; Beckmann, D.; Batov, I.E.; Bobkova, I.V.; Bobkov, A.M.; Ryazanov, V.V. Nonlocal supercurrent in mesoscopic multiterminal SNS Josephson junction in the low-temperature limit. Phys. Rev. B 2014, 89, 104507. [Google Scholar] [CrossRef]
- Bergeret, F.S.; Silaev, M.; Virtanen, P.; Heikkilä, T.T. Colloquium: Nonequilibrium effects in superconductors with a spin-splitting field. Rev. Mod. Phys. 2018, 90, 041001. [Google Scholar] [CrossRef]
- Kuzmanović, M.; Wu, B.Y.; Weideneder, M.; Quay, C.H.L.; Aprili, M. Evidence for spin-dependent energy transport in a superconductor. Nat. Commun. 2020, 11, 4336. [Google Scholar] [CrossRef]
- Bubis, A.V.; Shpagina, E.V.; Nasibulin, A.G.; Khrapai, V.S. Thermal conductance and nonequilibrium superconductivity in a diffusive NSN wire probed by shot noise. Phys. Rev. B 2021, 104, 125409. [Google Scholar] [CrossRef]
- Nagaev, K.E.; Büttiker, M. Semiclassical theory of shot noise in disordered superconductor–normal-metal contacts. Phys. Rev. B 2001, 63, 081301. [Google Scholar] [CrossRef]
- Kozhevnikov, A.A.; Schoelkopf, R.J.; Prober, D.E. Observation of Photon-Assisted Noise in a Diffusive Normal Metal–Superconductor Junction. Phys. Rev. Lett. 2000, 84, 3398–3401. [Google Scholar] [CrossRef] [PubMed]
- Jehl, X.; Sanquer, M.; Calemczuk, R.; Mailly, D. Detection of doubled shot noise in short normal-metal/superconductor junctions. Nature 2000, 405, 50–53. [Google Scholar] [CrossRef] [PubMed]
- Courtois, H.; Charlat, P.; Gandit, P.; Mailly, D.; Pannetier, B. The Spectral Conductance of a Proximity Superconductor and the Reentrance Effect. J. Low Temp. Phys. 1999, 116, 187–213. [Google Scholar] [CrossRef]
- Eom, J.; Chien, C.J.; Chandrasekhar, V. Phase Dependent Thermopower in Andreev Interferometers. Phys. Rev. Lett. 1998, 81, 437–440. [Google Scholar] [CrossRef]
- Rosdahl, T.O.; Vuik, A.; Kjaergaard, M.; Akhmerov, A.R. Andreev rectifier: A nonlocal conductance signature of topological phase transitions. Phys. Rev. B 2018, 97, 045421. [Google Scholar] [CrossRef]
- Anantram, M.P.; Datta, S. Current fluctuations in mesoscopic systems with Andreev scattering. Phys. Rev. B 1996, 53, 16390–16402. [Google Scholar] [CrossRef]
- Steinbach, A.H.; Martinis, J.M.; Devoret, M.H. Observation of Hot-Electron Shot Noise in a Metallic Resistor. Phys. Rev. Lett. 1996, 76, 3806–3809. [Google Scholar] [CrossRef] [PubMed]
- Henny, M.; Oberholzer, S.; Strunk, C.; Schönenberger, C. 1/3-shot-noise suppression in diffusive nanowires. Phys. Rev. B 1999, 59, 2871–2880. [Google Scholar] [CrossRef]
- Tikhonov, E.S.; Shovkun, D.V.; Ercolani, D.; Rossella, F.; Rocci, M.; Sorba, L.; Roddaro, S.; Khrapai, V.S. Local noise in a diffusive conductor. Sci. Rep. 2016, 6, 30621. [Google Scholar] [CrossRef]
- Ronen, Y.; Cohen, Y.; Kang, J.H.; Haim, A.; Rieder, M.T.; Heiblum, M.; Mahalu, D.; Shtrikman, H. Charge of a quasiparticle in a superconductor. Proc. Natl. Acad. Sci. USA 2016, 113, 1743–1748. [Google Scholar] [CrossRef] [PubMed]
- Tikhonov, E.S.; Shovkun, D.V.; Snelder, M.; Stehno, M.P.; Huang, Y.; Golden, M.S.; Golubov, A.A.; Brinkman, A.; Khrapai, V.S. Andreev Reflection in an s-Type Superconductor Proximized 3D Topological Insulator. Phys. Rev. Lett. 2016, 117, 147001. [Google Scholar] [CrossRef] [PubMed]
- Nagaev, K. On the shot noise in dirty metal contacts. Phys. Lett. A 1992, 169, 103–107. [Google Scholar] [CrossRef]
- Das, A.; Ronen, Y.; Most, Y.; Oreg, Y.; Heiblum, M.; Shtrikman, H. Zero-bias peaks and splitting in an Al–InAs nanowire topological superconductor as a signature of Majorana fermions. Nat. Phys. 2012, 8, 887–895. [Google Scholar] [CrossRef]
- Wu, P.M.; Gooth, J.; Zianni, X.; Svensson, S.F.; Gluschke, J.G.; Dick, K.A.; Thelander, C.; Nielsch, K.; Linke, H. Large Thermoelectric Power Factor Enhancement Observed in InAs Nanowires. Nano Lett. 2013, 13, 4080–4086. [Google Scholar] [CrossRef]
- Tikhonov, E.S.; Shovkun, D.V.; Ercolani, D.; Rossella, F.; Rocci, M.; Sorba, L.; Roddaro, S.; Khrapai, V.S. Noise thermometry applied to thermoelectric measurements in InAs nanowires. Semicond. Sci. Technol. 2016, 31, 104001. [Google Scholar] [CrossRef]
- Hofstetter, L.; Csonka, S.; Baumgartner, A.; Fülöp, G.; d’Hollosy, S.; Nygård, J.; Schönenberger, C. Finite-Bias Cooper Pair Splitting. Phys. Rev. Lett. 2011, 107, 136801. [Google Scholar] [CrossRef] [PubMed]
- Ménard, G.C.; Anselmetti, G.L.R.; Martinez, E.A.; Puglia, D.; Malinowski, F.K.; Lee, J.S.; Choi, S.; Pendharkar, M.; Palmstrøm, C.J.; Flensberg, K.; et al. Conductance-Matrix Symmetries of a Three-Terminal Hybrid Device. Phys. Rev. Lett. 2020, 124, 036802. [Google Scholar] [CrossRef]
- Puglia, D.; Martinez, E.A.; Ménard, G.C.; Pöschl, A.; Gronin, S.; Gardner, G.C.; Kallaher, R.; Manfra, M.J.; Marcus, C.M.; Higginbotham, A.P.; et al. Closing of the induced gap in a hybrid superconductor-semiconductor nanowire. Phys. Rev. B 2021, 103, 235201. [Google Scholar] [CrossRef]
- Tikhonov, E.S.; Denisov, A.O.; Piatrusha, S.U.; Khrapach, I.N.; Pekola, J.P.; Karimi, B.; Jabdaraghi, R.N.; Khrapai, V.S. Spatial and energy resolution of electronic states by shot noise. Phys. Rev. B 2020, 102, 085417. [Google Scholar] [CrossRef]
- Linder, J.; Robinson, J.W.A. Superconducting spintronics. Nat. Phys. 2015, 11, 307–315. [Google Scholar] [CrossRef]
- Schaibley, J.R.; Yu, H.; Clark, G.; Rivera, P.; Ross, J.S.; Seyler, K.L.; Yao, W.; Xu, X. Valleytronics in 2D materials. Nat. Rev. Mater. 2016, 1, 16055. [Google Scholar] [CrossRef]
- Meair, J.; Stano, P.; Jacquod, P. Measuring spin accumulations with current noise. Phys. Rev. B 2011, 84, 073302. [Google Scholar] [CrossRef]
- Arakawa, T.; Shiogai, J.; Ciorga, M.; Utz, M.; Schuh, D.; Kohda, M.; Nitta, J.; Bougeard, D.; Weiss, D.; Ono, T.; et al. Shot Noise Induced by Nonequilibrium Spin Accumulation. Phys. Rev. Lett. 2015, 114, 016601. [Google Scholar] [CrossRef]
- Khrapai, V.S.; Nagaev, K.E. Current noise generated by spin imbalance in presence of spin relaxation. JETP Lett. 2017, 105, 18–20. [Google Scholar] [CrossRef][Green Version]
- Ludwig, T.; Burmistrov, I.S.; Gefen, Y.; Shnirman, A. Current noise geometrically generated by a driven magnet. Phys. Rev. Res. 2020, 2, 023221. [Google Scholar] [CrossRef]
- Read, N.; Green, D. Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect. Phys. Rev. B 2000, 61, 10267–10297. [Google Scholar] [CrossRef]
- Wang, Z.; Qi, X.L.; Zhang, S.C. Topological field theory and thermal responses of interacting topological superconductors. Phys. Rev. B 2011, 84, 014527. [Google Scholar] [CrossRef]
- Akhmerov, A.R.; Dahlhaus, J.P.; Hassler, F.; Wimmer, M.; Beenakker, C.W.J. Quantized Conductance at the Majorana Phase Transition in a Disordered Superconducting Wire. Phys. Rev. Lett. 2011, 106, 057001. [Google Scholar] [CrossRef]
- Bagrets, D.; Altland, A.; Kamenev, A. Sinai Diffusion at Quasi-1D Topological Phase Transitions. Phys. Rev. Lett. 2016, 117, 196801. [Google Scholar] [CrossRef]
- Kasahara, Y.; Ohnishi, T.; Mizukami, Y.; Tanaka, O.; Ma, S.; Sugii, K.; Kurita, N.; Tanaka, H.; Nasu, J.; Motome, Y.; et al. Majorana quantization and half-integer thermal quantum Hall effect in a Kitaev spin liquid. Nature 2018, 559, 227–231. [Google Scholar] [CrossRef] [PubMed]
- Kejriwal, A.; Muralidharan, B. Nonlocal conductance and the detection of Majorana zero modes: Insights from von Neumann entropy. Phys. Rev. B 2022, 105, L161403. [Google Scholar] [CrossRef]
- Blanter, Y.; Büttiker, M. Shot noise in mesoscopic conductors. Phys. Rep. 2000, 336, 1. [Google Scholar] [CrossRef]
- Bubis, A.V.; Denisov, A.O.; Piatrusha, S.U.; Batov, I.E.; Khrapai, V.S.; Becker, J.; Treu, J.; Ruhstorfer, D.; Koblmüller, G. Proximity effect and interface transparency in al/InAs-nanowire/al diffusive junctions. Semicond. Sci. Technol. 2017, 32, 094007. [Google Scholar] [CrossRef]
- Hertenberger, S.; Rudolph, D.; Bichler, M.; Finley, J.J.; Abstreiter, G.; Koblmüller, G. Growth kinetics in position-controlled and catalyst-free InAs nanowire arrays on Si(111) grown by selective area molecular beam epitaxy. J. Appl. Phys. 2010, 108, 114316. [Google Scholar] [CrossRef]
- Becker, J.; Morkötter, S.; Treu, J.; Sonner, M.; Speckbacher, M.; Döblinger, M.; Abstreiter, G.; Finley, J.J.; Koblmüller, G. Carrier trapping and activation at short-period wurtzite/zinc-blende stacking sequences in polytypic inas nanowires. Phys. Rev. B 2018, 97, 115306. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Denisov, A.; Bubis, A.; Piatrusha, S.; Titova, N.; Nasibulin, A.; Becker, J.; Treu, J.; Ruhstorfer, D.; Koblmüller, G.; Tikhonov, E.; et al. Heat-Mode Excitation in a Proximity Superconductor. Nanomaterials 2022, 12, 1461. https://doi.org/10.3390/nano12091461
Denisov A, Bubis A, Piatrusha S, Titova N, Nasibulin A, Becker J, Treu J, Ruhstorfer D, Koblmüller G, Tikhonov E, et al. Heat-Mode Excitation in a Proximity Superconductor. Nanomaterials. 2022; 12(9):1461. https://doi.org/10.3390/nano12091461
Chicago/Turabian StyleDenisov, Artem, Anton Bubis, Stanislau Piatrusha, Nadezhda Titova, Albert Nasibulin, Jonathan Becker, Julian Treu, Daniel Ruhstorfer, Gregor Koblmüller, Evgeny Tikhonov, and et al. 2022. "Heat-Mode Excitation in a Proximity Superconductor" Nanomaterials 12, no. 9: 1461. https://doi.org/10.3390/nano12091461
APA StyleDenisov, A., Bubis, A., Piatrusha, S., Titova, N., Nasibulin, A., Becker, J., Treu, J., Ruhstorfer, D., Koblmüller, G., Tikhonov, E., & Khrapai, V. (2022). Heat-Mode Excitation in a Proximity Superconductor. Nanomaterials, 12(9), 1461. https://doi.org/10.3390/nano12091461






