Constrained DFT for Molecular Junctions
Abstract
1. Introduction
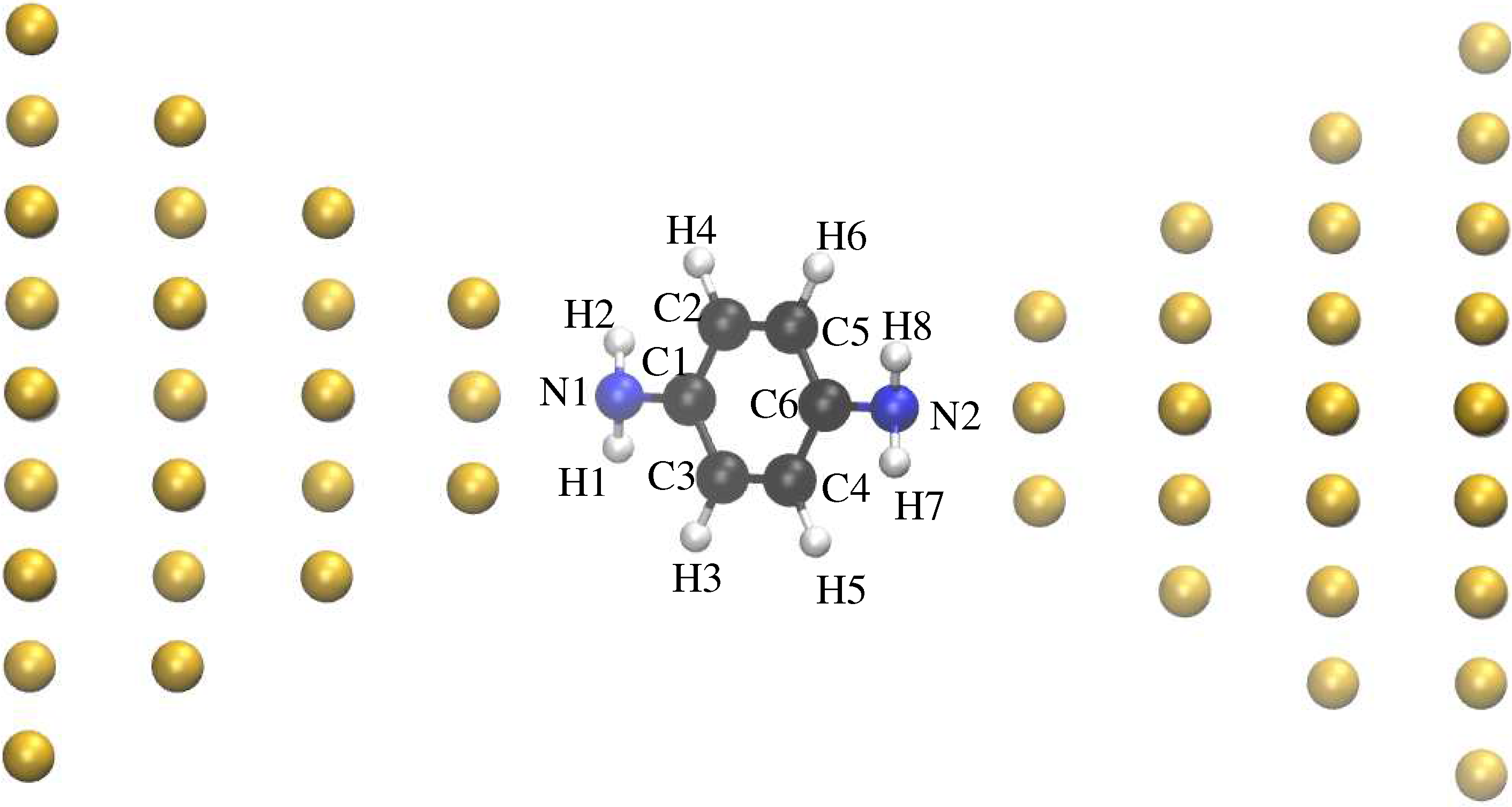
2. Methods
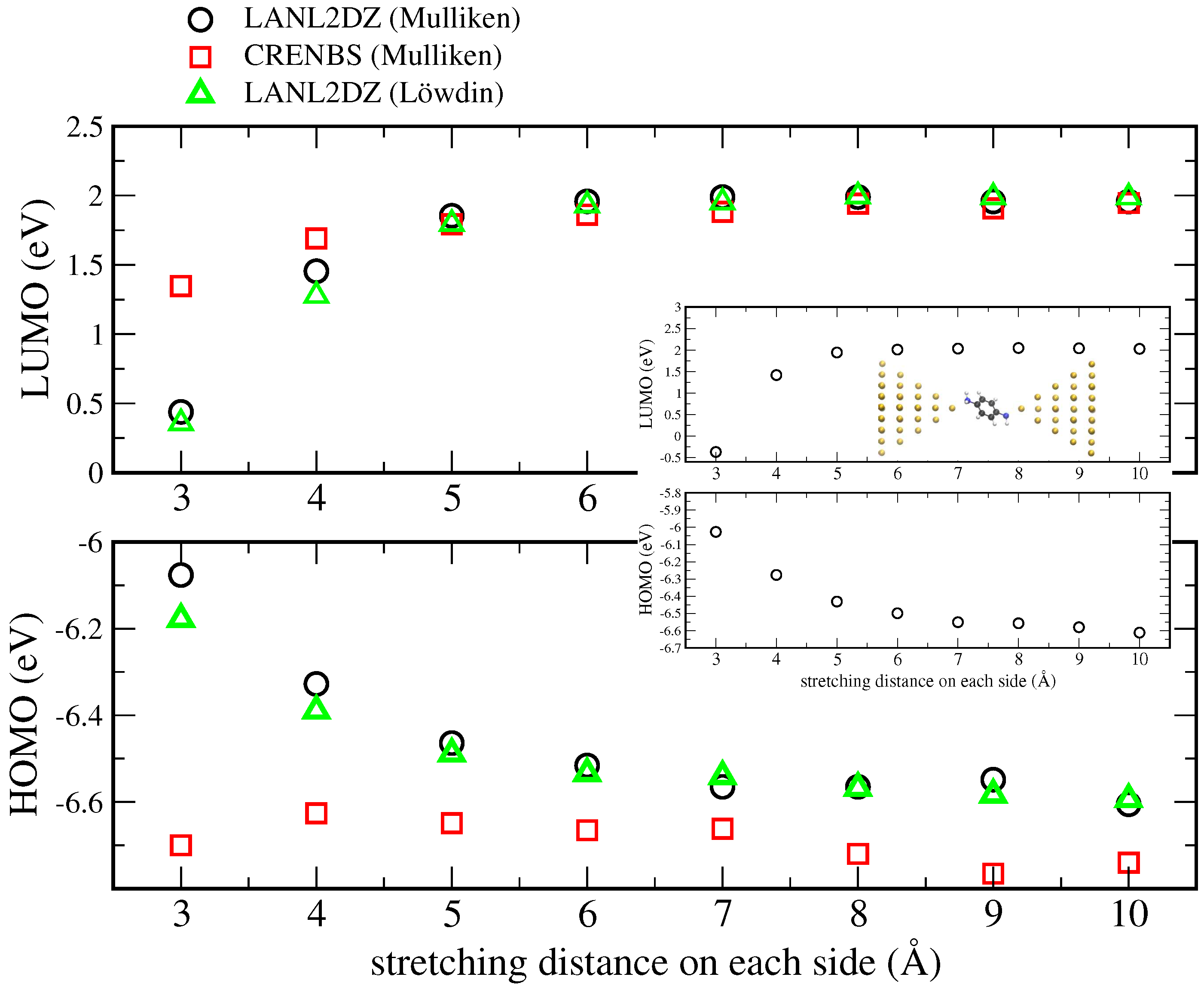
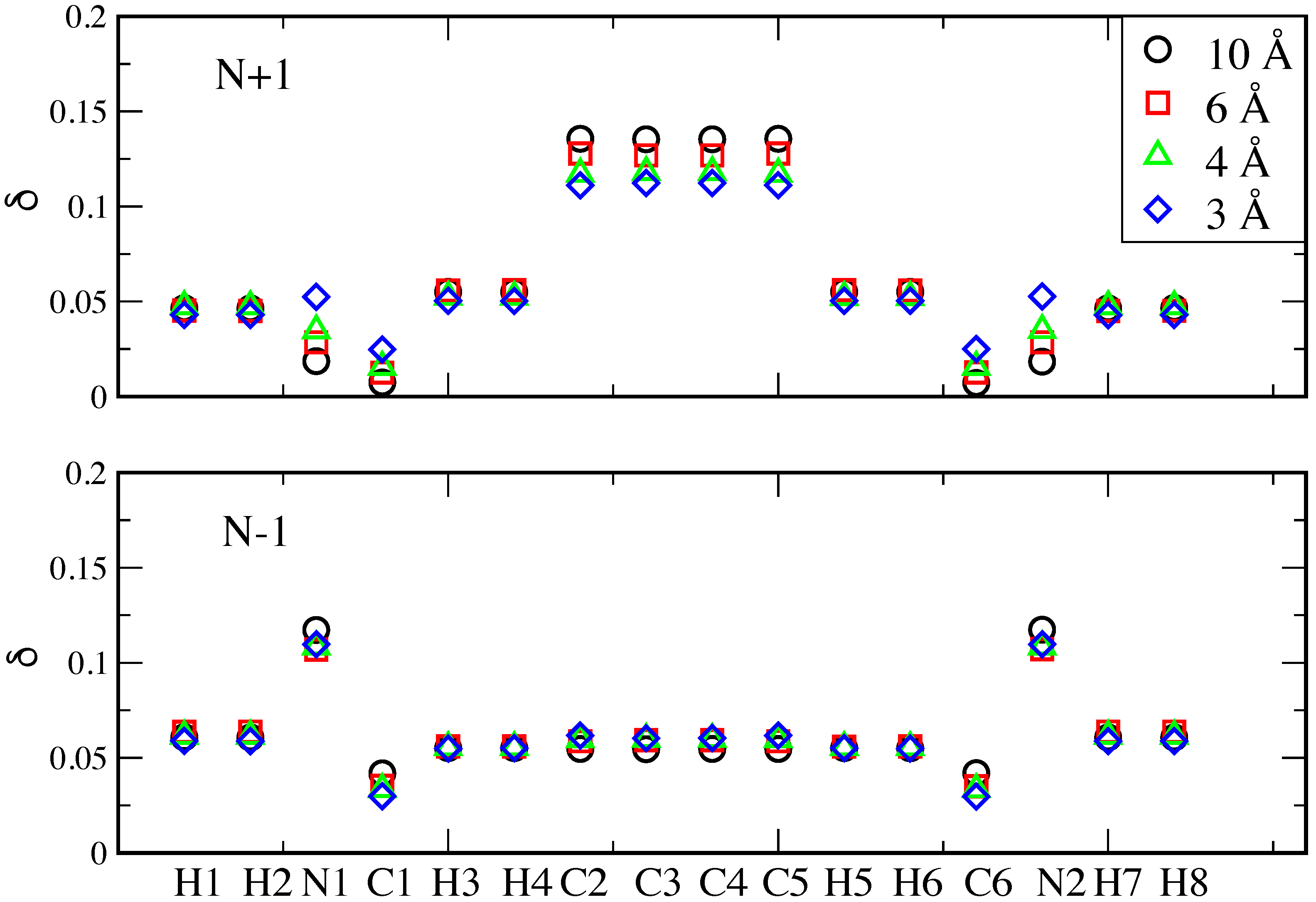
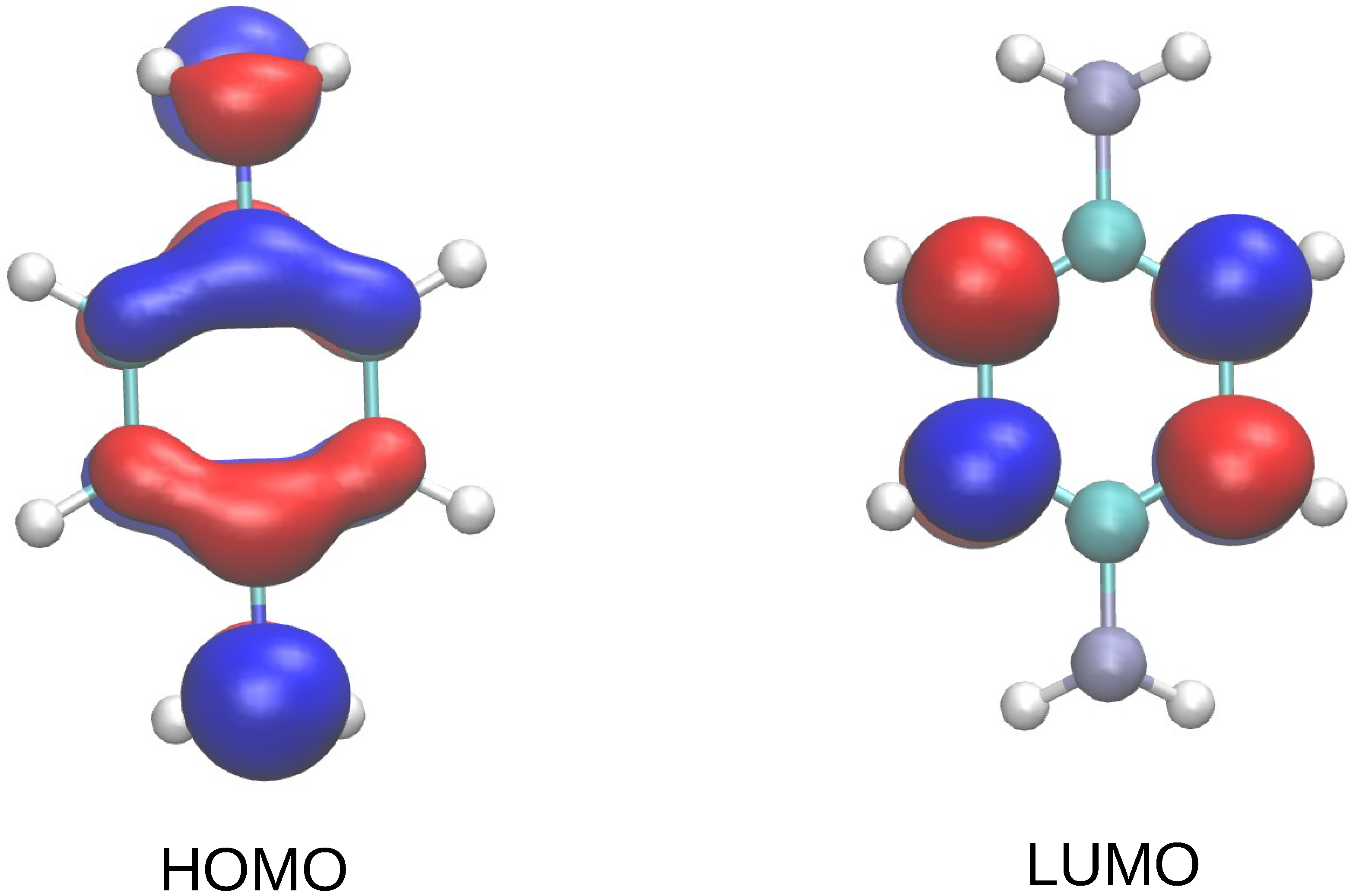
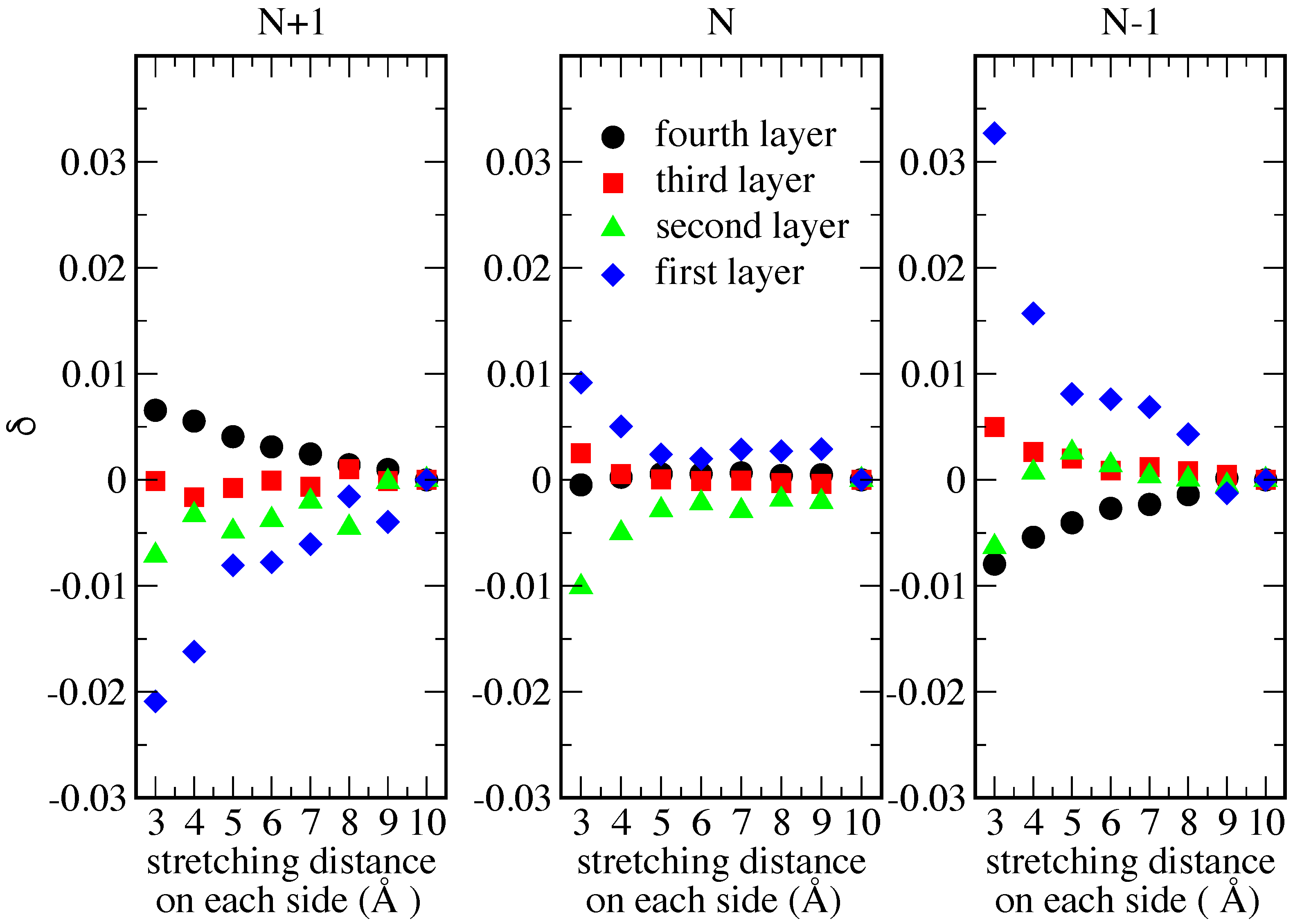
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BDA | benzene diamine |
| cDFT | constrained density functional theory |
| HOMO | highest occupied molecular orbital |
| LUMO | lowest occupied molecular orbital |
References
- Blumberger, J.; McKenna, K.P. Constrained density functional theory applied to electron tunnelling between defects in MgO. Phys. Chem. Chem. Phys. 2013, 15, 2184–2196. [Google Scholar] [CrossRef] [PubMed]
- Difley, S.; Beljonne, D.; Van Voorhis, T. On the singlet-triplet splitting of geminate electron-hole pairs in organic semiconductors. J. Am. Chem. Soc. 2008, 130, 3420–3427. [Google Scholar] [CrossRef] [PubMed]
- Cedillo, A.; Neck, D.V.; Bultinck, P. Self-consistent methods constrained to a fixed number of particles in a given fragment and its relation to the electronegativity equalization method. In Theoretical Chemistry in Belgium; Springer: Berlin/Heidelberg, Germany, 2014; pp. 27–33. [Google Scholar]
- Kaduk, B.; Kowalczyk, T.; Van Voorhis, T. Constrained Density Functional Theory. Chem. Rev. 2012, 112, 321–370. [Google Scholar] [CrossRef] [PubMed]
- Hong, G.; Rosta, E.; Warshel, A. Using the constrained DFT approach in generating diabatic surfaces and off diagonal empirical valence bond terms for modeling reactions in condensed phases. J. Phys. Chem. B 2006, 110, 19570–19574. [Google Scholar] [CrossRef]
- Behler, J.; Delley, B.; Reuter, K.; Scheffler, M. Nonadiabatic potential-energy surfaces by constrained density-functional theory. Phys. Rev. B 2007, 75, 115409. [Google Scholar] [CrossRef]
- Cioslowski, J.; Stefanov, B.B. Electron flow and electronegativity equalization in the process of bond formation. J. Chem. Phys. 1993, 99, 5151–5162. [Google Scholar] [CrossRef]
- Dederichs, P.H.; Blügel, S.; Zeller, R.; Akai, H. Ground States of Constrained Systems: Application to Cerium Impurities. Phys. Rev. Lett. 1984, 53, 2512–2515. [Google Scholar] [CrossRef]
- Shao, Y.; Molnar, L.F.; Jung, Y.; Kussmann, J.; Ochsenfeld, C.; Brown, S.T.; Gilbert, A.T.; Slipchenko, L.V.; Levchenko, S.V.; O’Neill, D.P.; et al. Advances in methods and algorithms in a modern quantum chemistry program package. Phys. Chem. Chem. Phys. 2006, 8, 3172–3191. [Google Scholar] [CrossRef]
- Sena, A.M.P.; Miyazaki, T.; Bowler, D.R. Linear Scaling Constrained Density Functional Theory in CONQUEST. J. Chem. Theory Comput. 2011, 7, 884–889. [Google Scholar] [CrossRef]
- Oberhofer, H.; Blumberger, J. Charge constrained density functional molecular dynamics for simulation of condensed phase electron transfer reactions. J. Chem. Phys. 2009, 131, 064101. [Google Scholar] [CrossRef]
- O’Regan, D.D.; Teobaldi, G. Optimization of constrained density functional theory. Phys. Rev. B 2016, 94, 035159. [Google Scholar] [CrossRef]
- Brooke, C.; Vezzoli, A.; Higgins, S.J.; Zotti, L.A.; Palacios, J.J.; Nichols, R.J. Resonant Transport and Electrostatic Effects in Single-Molecule Electrical Junctions. Phys. Rev. B 2015, 91, 195438. [Google Scholar] [CrossRef]
- Palacios, J.J.; Jacob, D.; Perez-Jimenez, A.J.; Fabian, E.S.; Louis, E.; Verges, J.A.; Soriano, M.; Zotti, L.A.; Dednam, W. Available online: https://www.simuneatomistics.com/; https://github.com/juanjosepalacios/ANT.Gaussian (accessed on 1 May 2021).
- Jacob, D.; Palacios, J.J. Critical comparison of electrode models in density functional theory based quantum transport calculations. J. Chem. Phys. 2011, 134, 044118. [Google Scholar] [CrossRef]
- Palacios, J.J.; Pérez-Jiménez, A.J.; Louis, E.; Vergés, J.A. Fullerene-based molecular nanobridges: A first-principles study. Phys. Rev. B 2001, 64, 115411. [Google Scholar] [CrossRef]
- Palacios, J.J.; Pérez-Jiménez, A.J.; Louis, E.; SanFabián, E.; Vergés, J.A. First-principles approach to electrical transport in atomic-scale nanostructures. Phys. Rev. B 2002, 66, 035322. [Google Scholar] [CrossRef]
- Palacios, J.J.; Pérez-Jiménez, A.J.; Louis, E.; Vergés, J.A. Electronic transport through C60 molecules. Nanotechnology 2001, 12, 160. [Google Scholar] [CrossRef]
- Souza, A.M.; Rungger, I.; Pemmaraju, C.D.; Schwingenschloegl, U.; Sanvito, S. Constrained-DFT method for accurate energy-level alignment of metal/molecule interfaces. Phys. Rev. B 2013, 88, 165112. [Google Scholar] [CrossRef]
- Koch, N. Organic electronic devices and their functional interfaces. ChemPhysChem 2007, 8, 1438–1455. [Google Scholar] [CrossRef]
- Repp, J.; Meyer, G.; Stojković, S.M.; Gourdon, A.; Joachim, C. Molecules on Insulating Films: Scanning-Tunneling Microscopy Imaging of Individual Molecular Orbitals. Phys. Rev. Lett. 2005, 94, 026803. [Google Scholar] [CrossRef]
- Greiner, M.T.; Helander, M.G.; Tang, W.M.; Wang, Z.B.; Qiu, J.; Lu, Z.H. Universal energy-level alignment of molecules on metal oxides. Nat. Mater. 2011, 11, 76–81. [Google Scholar] [CrossRef]
- Lu, X.; Grobis, M.; Khoo, K.H.; Louie, S.G.; Crommie, M.F. Charge transfer and screening in individual C60 molecules on metal substrates: A scanning tunneling spectroscopy and theoretical study. Phys. Rev. B 2004, 70, 115418. [Google Scholar] [CrossRef]
- Perrin, M.L.; Verzijl, C.J.; Martin, C.A.; Shaikh, A.J.; Eelkema, R.; van Esch, J.H.; van Ruitenbeek, J.M.; Thijssen, J.M.; van der Zant, H.S.; Dulić, D. Large tunable image-charge effects in single-molecule junctions. Nat. Nanotechnol. 2013, 8, 282–287. [Google Scholar] [CrossRef] [PubMed]
- Thygesen, K.S.; Rubio, A. Renormalization of Molecular Quasiparticle Levels at metal–molecule Interfaces: Trends across Binding Regimes. Phys. Rev. Lett. 2009, 102, 046802. [Google Scholar] [CrossRef] [PubMed]
- Myöhänen, P.; Tuovinen, R.; Korhonen, T.; Stefanucci, G.; van Leeuwen, R. Image charge dynamics in time-dependent quantum transport. Phys. Rev. B 2012, 85, 075105. [Google Scholar] [CrossRef]
- Tamblyn, I.; Darancet, P.; Quek, S.Y.; Bonev, S.A.; Neaton, J.B. Electronic energy level alignment at metal–molecule interfaces with a GW approach. Phys. Rev. B 2011, 84, 201402. [Google Scholar] [CrossRef]
- Durrant, T.R.; Murphy, S.T.; Watkins, M.B.; Shluger, A.L. Relation between image charge and potential alignment corrections for charged defects in periodic boundary conditions. J. Chem. Phys. 2018, 149, 024103. [Google Scholar] [CrossRef]
- Quek, S.Y.; Choi, H.J.; Louie, S.G.; Neaton, J.B. Length Dependence of Conductance in Aromatic Single-Molecule Junctions. Nano Lett. 2009, 9, 3949–3953. [Google Scholar] [CrossRef]
- Darancet, P.; Widawsky, J.R.; Choi, H.J.; Venkataraman, L.; Neaton, J.B. Quantitative Current–Voltage Characteristics in Molecular Junctions from First Principles. Nano Lett. 2012, 12, 6250–6254. [Google Scholar] [CrossRef]
- Brisendine, J.M.; Refaely-Abramson, S.; Liu, Z.F.; Cui, J.; Ng, F.; Neaton, J.B.; Koder, R.L.; Venkataraman, L. Probing Charge Transport through Peptide Bonds. J. Phys. Chem. Lett. 2018, 9, 763–767. [Google Scholar] [CrossRef]
- Markussen, T.; Jin, C.; Thygesen, K.S. Quantitatively accurate calculations of conductance and thermopower of molecular junctions. Phys. Status Solidi (B) 2013, 250, 2394–2402. [Google Scholar] [CrossRef]
- Neaton, J.B.; Hybertsen, M.S.; Louie, S.G. Renormalization of Molecular Electronic Levels at metal–molecule Interfaces. Phys. Rev. Lett. 2006, 97, 216405. [Google Scholar] [CrossRef] [PubMed]
- Kaasbjerg, K.; Flensberg, K. Strong Polarization-Induced Reduction of Addition Energies in Single-Molecule Nanojunctions. Nano Lett. 2008, 8, 3809–3814. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Frish, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. GAUSSIAN 03, Revision B.01; Gaussian, Inc.: Pittsburg, PA, USA, 2003. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Wadt, W.R.; Hay, P.J. Ab initio effective core potentials for molecular calculations. Potentials for main group elements Na to Bi. J. Chem. Phys. 1985, 82, 284–298. [Google Scholar] [CrossRef]
- Ross, R.B.; Powers, J.M.; Atashroo, T.; Ermler, W.C.; LaJohn, L.A.; Christiansen, P.A. Ab initio relativistic effective potentials with spin–orbit operators. IV. Cs through Rn. J. Chem. Phys. 1990, 93, 6654–6670. [Google Scholar] [CrossRef]
- Dell’Angela, M.; Kladnik, G.; Cossaro, A.; Verdini, A.; Kamenetska, M.; Tamblyn, I.; Quek, S.Y.; Neaton, J.B.; Cvetko, D.; Morgante, A.; et al. Relating Energy Level Alignment and Amine-Linked Single Molecule Junction Conductance. Nano Lett. 2010, 10, 2470–2474. [Google Scholar] [CrossRef]
- Biller, A.; Tamblyn, I.; Neaton, J.B.; Kronik, L. Electronic level alignment at a metal–molecule interface from a short-range hybrid functional. J. Chem. Phys. 2011, 135, 164706. [Google Scholar] [CrossRef]
- Zotti, L.A.; Bürkle, M.; Pauly, F.; Lee, W.; Kim, K.; Jeong, W.; Asai, Y.; Reddy, P.; Cuevas, J.C. Heat dissipation and its relation to thermopower in single-molecule junctions. New J. Phys. 2014, 16, 015004. [Google Scholar] [CrossRef]
- Quek, S.Y.; Venkataraman, L.; Choi, H.J.; Louie, S.G.; Hybertsen, M.S.; Neaton, J.B. Amine–Gold Linked Single-Molecule Circuits: Experiment and Theory. Nano Lett. 2007, 7, 3477–3482. [Google Scholar] [CrossRef]
- Soriano, M.; Palacios, J.J. Theory of projections with nonorthogonal basis sets: Partitioning techniques and effective Hamiltonians. Phys. Rev. B 2014, 90, 075128. [Google Scholar] [CrossRef]
- Wang, B.; Li, S.L.; Truhlar, D.G. Modeling the Partial Atomic Charges in Inorganometallic Molecules and Solids and Charge Redistribution in Lithium-Ion Cathodes. J. Chem. Theory Comput. 2014, 10, 5640–5650. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zotti, L.A.; Dednam, W.; Lombardi, E.B.; Palacios, J.J. Constrained DFT for Molecular Junctions. Nanomaterials 2022, 12, 1234. https://doi.org/10.3390/nano12071234
Zotti LA, Dednam W, Lombardi EB, Palacios JJ. Constrained DFT for Molecular Junctions. Nanomaterials. 2022; 12(7):1234. https://doi.org/10.3390/nano12071234
Chicago/Turabian StyleZotti, Linda Angela, Wynand Dednam, Enrico B. Lombardi, and Juan Jose Palacios. 2022. "Constrained DFT for Molecular Junctions" Nanomaterials 12, no. 7: 1234. https://doi.org/10.3390/nano12071234
APA StyleZotti, L. A., Dednam, W., Lombardi, E. B., & Palacios, J. J. (2022). Constrained DFT for Molecular Junctions. Nanomaterials, 12(7), 1234. https://doi.org/10.3390/nano12071234






