Reconfigurable Light Imaging in Photonic Higher-Order Topological Insulators
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Numerical Simulations
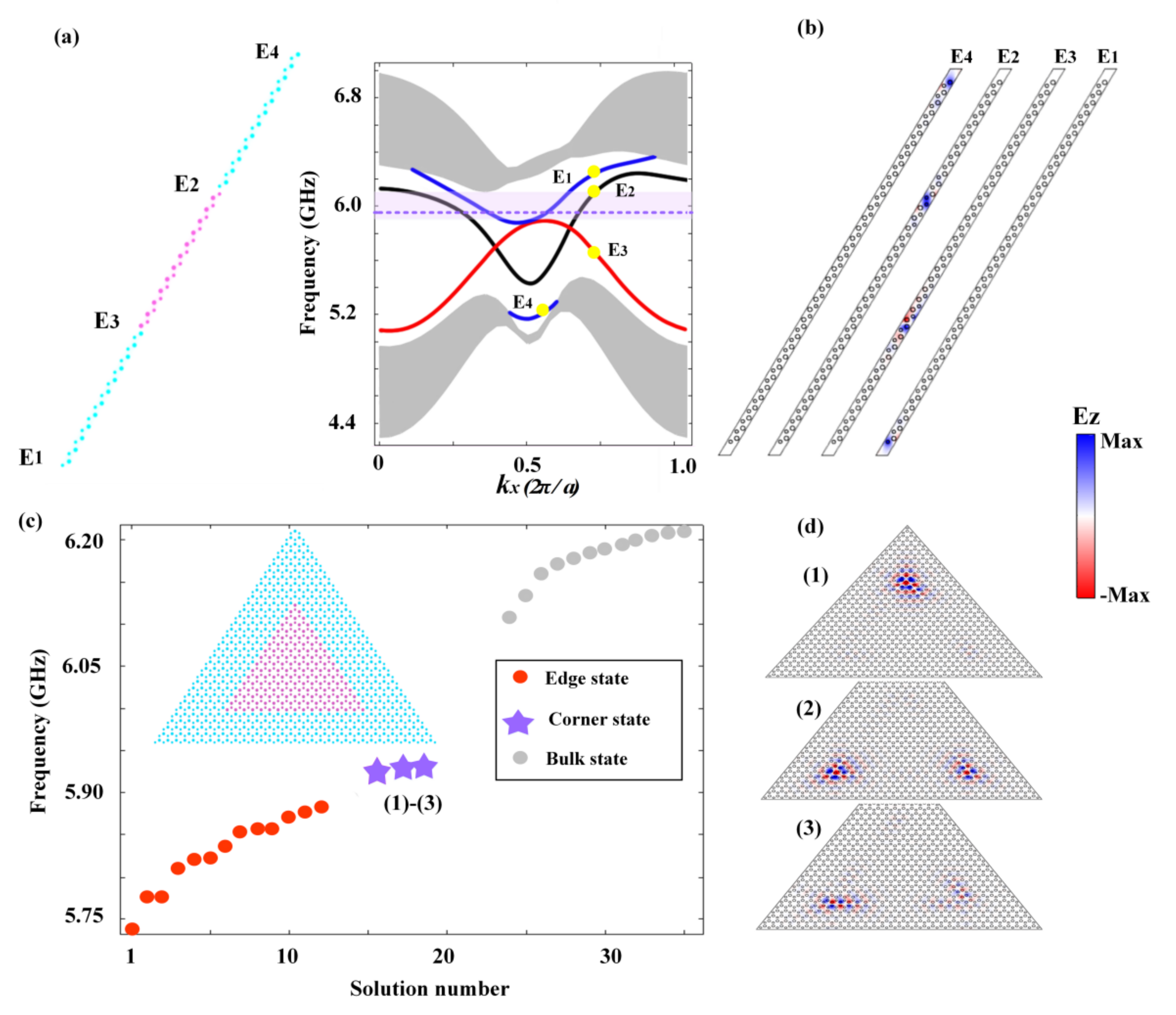
3. Topological Properties of the Proposed HOTI
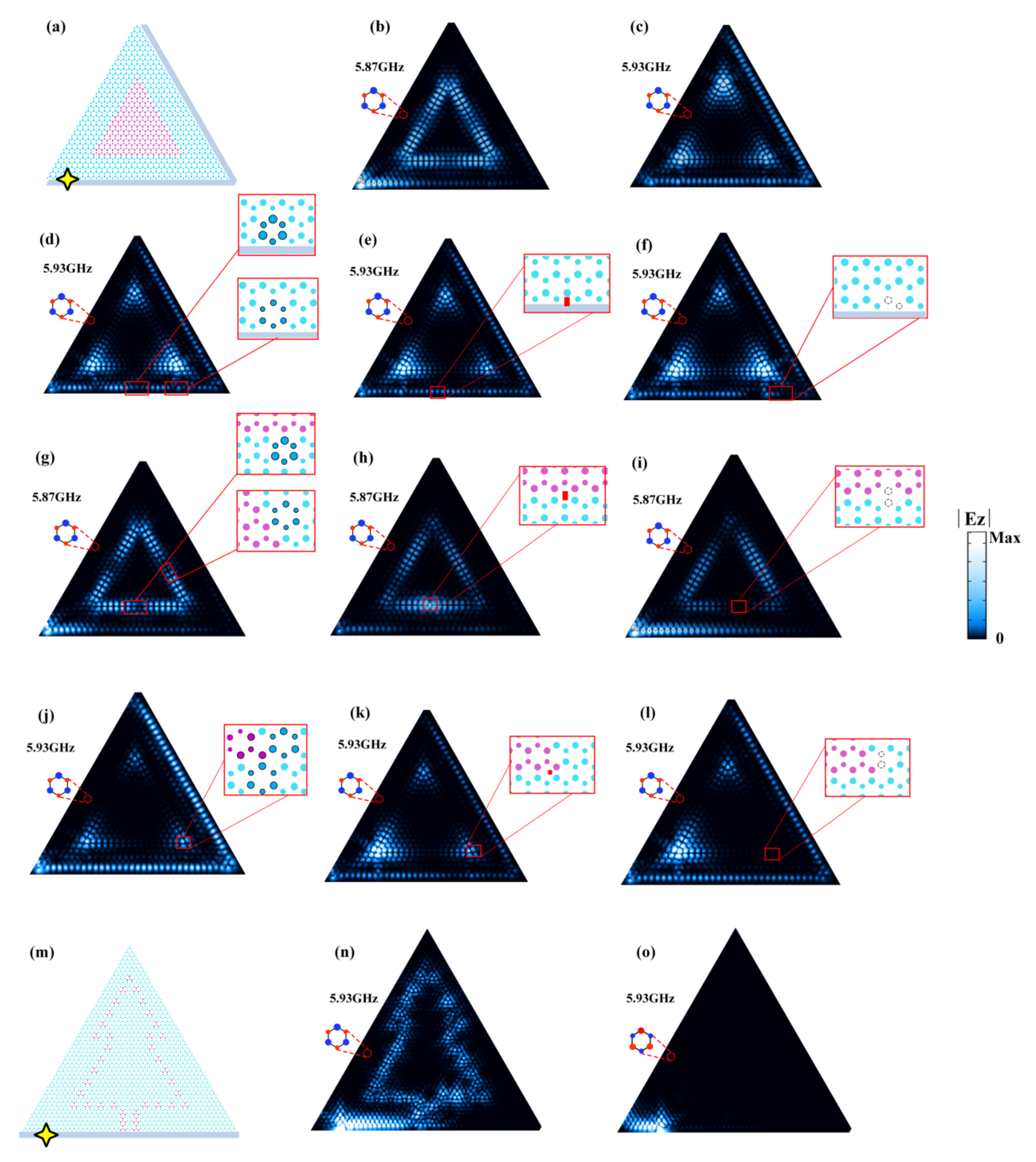
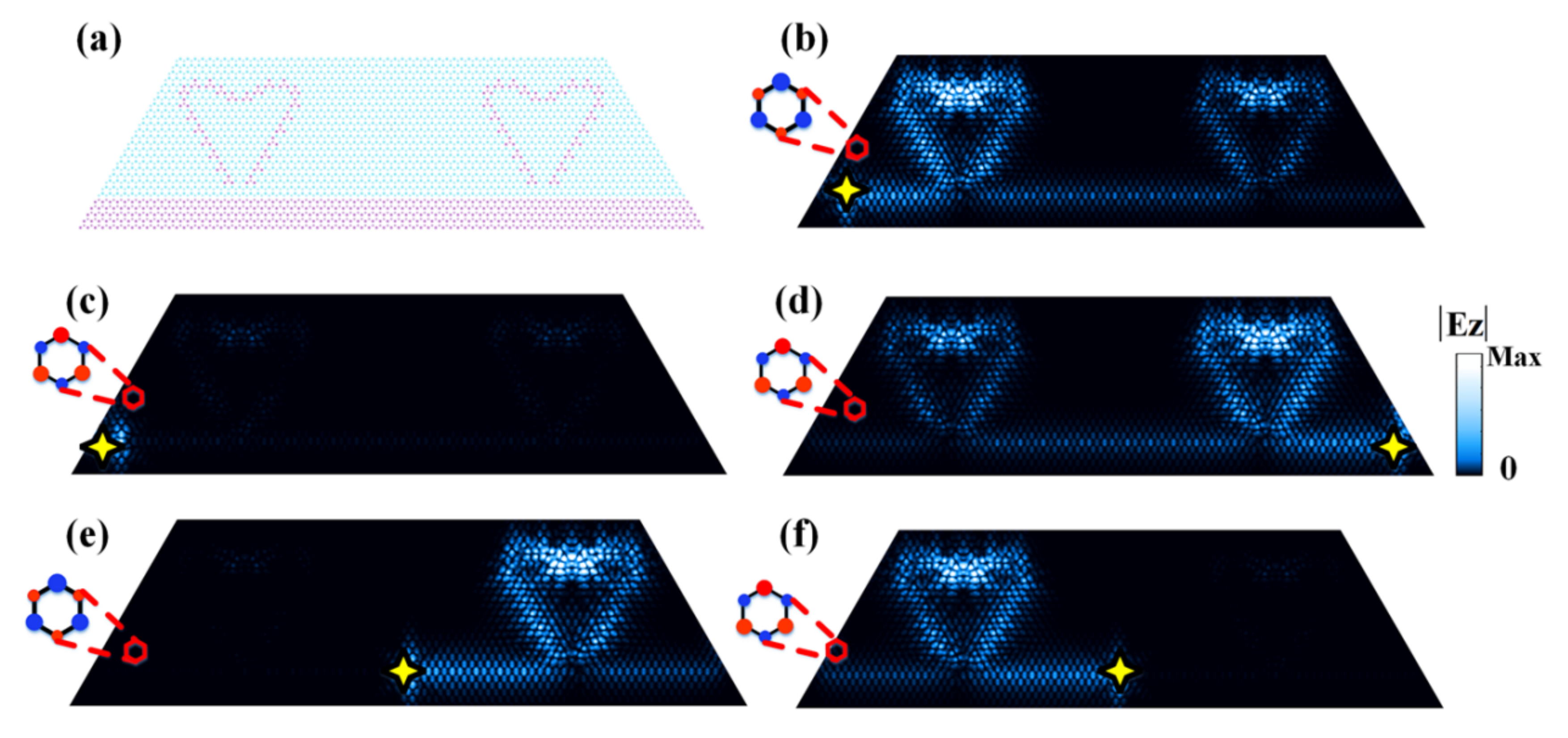
4. Reconfigurable Light Imaging
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kane, C.L.; Mele, E.J. Quantum Spin Hall Effect in Graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bernevig, B.A.; Zhang, S.-C. Quantum Spin Hall Effect. Phys. Rev. Lett. 2006, 96, 106802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.-Z.; Zhang, J.; Feng, X.; Shen, J.; Zhang, Z.; Guo, M.; Li, K.; Ou, Y.; Wei, P.; Wang, L.-L.; et al. Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator. Science 2013, 340, 167–170. [Google Scholar] [CrossRef] [Green Version]
- Laughlin, R.B. Quantized Hall conductivity in two dimensions. Phys. Rev. B 1981, 23, 5632–5633. [Google Scholar] [CrossRef]
- Wang, Z.; Chong, Y.; Joannopoulos, J.D.; Soljačić, M. Reflection-free one-way edge modes in a gyromagnetic photonic crystal. Phys. Rev. Lett. 2008, 100, 013905. [Google Scholar] [CrossRef]
- Wang, Z.; Chong, Y.; Joannopoulos, J.D.; Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 2009, 461, 772–775. [Google Scholar] [CrossRef] [Green Version]
- He, C.; Sun, X.-C.; Liu, X.-P.; Lu, M.-H.; Chen, Y.; Feng, L.; Chen, Y.-F. Photonic topological insulator with broken time-reversal symmetry. Proc. Natl. Acad. Sci. USA 2016, 113, 4924–4928. [Google Scholar] [CrossRef] [Green Version]
- Bahari, B.; Ndao, A.; Vallini, F.; El Amili, A.; Fainman, Y.; Kanté, B. Nonreciprocal lasing in topological cavities of arbitrary geometries. Science 2017, 358, 636–640. [Google Scholar] [CrossRef] [Green Version]
- Lu, L.; Gao, H.; Wang, Z. Topological one-way fiber of second Chern number. Nat. Commun. 2018, 9, 5384. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Liang, W.; Li, Z.-Y. Revealing photonic Lorentz force as the microscopic origin of topological photonic states. Nanophotonics 2020, 9, 3217–3226. [Google Scholar] [CrossRef] [Green Version]
- Colomes, E.; Franz, M. Antichiral Edge States in a Modified Haldane Nanoribbon. Phys. Rev. Lett. 2018, 120, 086603. [Google Scholar] [CrossRef] [Green Version]
- Mandal, S.; Ge, R.; Liew, T.C.H. Antichiral edge states in an exciton polariton strip. Phys. Rev. B 2019, 99, 115423. [Google Scholar] [CrossRef] [Green Version]
- Bhowmick, D.; Sengupta, P. Antichiral edge states in Heisenberg ferromagnet on a honeycomb lattice. Phys. Rev. B 2020, 101, 195133. [Google Scholar] [CrossRef]
- Chen, J.; Liang, W.; Li, Z.-Y. Antichiral one-way edge states in a gyromagnetic photonic crystal. Phys. Rev. B 2020, 101, 214102. [Google Scholar] [CrossRef]
- Zhou, P.; Liu, G.G.; Yang, Y.; Hu, Y.H.; Ma, S.; Xue, H.; Wang, Q.; Deng, L.; Zhang, B. Observation of Photonic Antichiral Edge States. Phys. Rev. Lett. 2020, 125, 263603. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, D.; Hang, Z.; Chong, Y. Observation of antichiral edge states in a circuit lattice. Sci. China Phys. Mech. Astron. 2021, 64, 257011. [Google Scholar] [CrossRef]
- Yu, L.; Xue, H.; Zhang, B. Antichiral edge states in an acoustic resonator lattice with staggered air flow. J. Appl. Phys. 2021, 129, 235103. [Google Scholar] [CrossRef]
- Benalcazar, W.A.; Bernevig, B.A.; Hughes, T.L. Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators. Phys. Rev. B 2017, 96, 245115. [Google Scholar] [CrossRef] [Green Version]
- Benalcazar, W.A.; Bernevig, B.A.; Hughes, T.L. Quantized electric multipole insulators. Science 2017, 357, 61–66. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Imhof, S.; Berger, C.; Bayer, F.; Brehm, J.; Molenkamp, L.W.; Kiessling, T.; Schindler, F.; Lee, C.H.; Greiter, M.; Neupert, T. Topolectrical-circuit realization of topological corner modes. Nat. Phys. 2018, 14, 925–929. [Google Scholar] [CrossRef]
- Serra-Garcia, M.; Peri, V.; Süsstrunk, R.; Bilal, O.R.; Larsen, T.; Villanueva, L.G.; Huber, S. Observation of a phononic quadrupole topological insulator. Nature 2018, 555, 342–345. [Google Scholar] [CrossRef]
- Xie, B.-Y.; Wang, H.-F.; Wang, H.-X.; Zhu, X.-Y.; Jiang, J.-H.; Lu, M.-H.; Chen, Y.-F. Second-order photonic topological insulator with corner states. Phys. Rev. B 2018, 98, 205147. [Google Scholar] [CrossRef] [Green Version]
- Fan, H.; Xia, B.; Tong, L.; Zheng, S.; Yu, D. Elastic higher-order topological insulator with topologically protected corner states. Phys. Rev. Lett. 2019, 122, 204301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.; Wang, H.-X.; Lin, Z.-K.; Tian, Y.; Xie, B.; Lu, M.-H.; Chen, Y.-F.; Jiang, J.-H. Second-order topology and multidimensional topological transitions in sonic crystals. Nat. Phys. 2019, 15, 582–588. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.R.; Hwang, M.S.; Smirnova, D.; Jeong, K.Y.; Kivshar, Y.; Park, H.G. Multipolar lasing modes from topological corner states. Nat. Commun. 2020, 11, 5758. [Google Scholar] [CrossRef] [PubMed]
- Xie, B.; Su, G.; Wang, H.-F.; Liu, F.; Hu, L.; Yu, S.-Y.; Zhan, P.; Lu, M.-H.; Wang, Z.; Chen, Y.-F. Higher-order quantum spin Hall effect in a photonic crystal. Nat. Commun. 2020, 11, 3768. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Y.; Lin, Z.K.; Qin, P.; Chen, Q.; Gao, F.; Li, E.; Jiang, J.H.; Zhang, B.; Chen, H. Higher-Order Topological States in Surface-Wave Photonic Crystals. Adv. Sci. 2020, 7, 1902724. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.; Lin, Z.-K.; Wang, H.-X.; Xiong, Z.; Tian, Y.; Lu, M.-H.; Chen, Y.-F.; Jiang, J.-H. Symmetry-protected hierarchy of anomalous multipole topological band gaps in nonsymmorphic metacrystals. Nat. Commun. 2020, 11, 65. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yue, Z.; Liao, D.; Zhang, Z.; Xiong, W.; Cheng, Y.; Liu, X. Experimental demonstration of a reconfigurable acoustic second-order topological insulator using condensed soda cans array. Appl. Phys. Lett. 2021, 118, 203501. [Google Scholar] [CrossRef]
- Fan, H.; Xia, B.; Zheng, S.; Tong, L. Elastic phononic topological plate with edge and corner sates based on pseudospin-valley-coupling. J. Phys. D Appl. Phys. 2020, 53, 395304. [Google Scholar] [CrossRef]
- Li, Y.; Yu, Y.; Liu, F.; Zhang, B.; Shvets, G. Topology-controlled photonic cavity based on the near-conservation of the valley degree of freedom. Phys. Rev. Lett. 2020, 125, 213902. [Google Scholar] [CrossRef]
- Phan, H.T.; Liu, F.; Wakabayashi, K. Valley-dependent corner states in honeycomb photonic crystals without inversion symmetry. Opt. Express 2021, 29, 18277–18290. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.; Lu, M.-H.; Chen, Y.-F. Valley-Selective Topological Corner States in Sonic Crystals. Phys. Rev. Lett. 2021, 126, 156401. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.P.; Jia, D.; Sun, H.X.; Yuan, S.Q.; Ge, Y.; Si, Q.R.; Liu, X.J. Programmable coding acoustic topological insulator. Adv. Mater. 2018, 30, 1805002. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Long, H.; Liu, C.; Shao, C.; Cheng, Y.; Liu, X.; Christensen, J. Deep-Subwavelength Holey Acoustic Second-Order Topological Insulators. Adv. Mater. 2019, 31, 1904682. [Google Scholar] [CrossRef] [Green Version]
- You, J.W.; Ma, Q.; Lan, Z.; Xiao, Q.; Panoiu, N.C.; Cui, T.J. Reprogrammable plasmonic topological insulators with ultrafast control. Nat. Commun. 2021, 12, 5468. [Google Scholar] [CrossRef]
- Zangeneh-Nejad, F.; Fleury, R. Nonlinear second-order topological insulators. Phys. Rev. Lett. 2019, 123, 053902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, W.; Hu, J.; Wen, S.; Xiang, Y. Dynamically reconfigurable topological states in photonic crystals with liquid crystals. Opt. Lett. 2021, 46, 2589–2592. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Xu, S.; Xiang, Y. Tunable and Reconfigurable Higher-Order Topological Insulators in Photonic Crystals with Phase Change Materials. Ann. Phys. 2022, 534, 2100293. [Google Scholar] [CrossRef]
- Liu, G.-G.; Zhou, P.; Yang, Y.; Xue, H.; Ren, X.; Lin, X.; Sun, H.-x.; Bi, L.; Chong, Y.; Zhang, B. Observation of an unpaired photonic Dirac point. Nat. Commun. 2020, 11, 1873. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.-Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.; Sankar, R.; Chang, G.; Yuan, Z.; Lee, C.-C. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 2015, 349, 613–617. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jia, S.; Xu, S.-Y.; Hasan, M.Z. Weyl semimetals, Fermi arcs and chiral anomalies. Nat. Mater. 2016, 15, 1140–1144. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Sun, H.-X.; Xia, J.-P.; Xue, H.; Gao, Z.; Ge, Y.; Jia, D.; Yuan, S.-Q.; Chong, Y.; Zhang, B. Topological triply degenerate point with double Fermi arcs. Nat. Phys. 2019, 15, 645–649. [Google Scholar] [CrossRef] [Green Version]
- Marino, E.; Nascimento, L.O.; Alves, V.S.; Smith, C.M. Interaction induced quantum valley Hall effect in graphene. Phys. Rev. X 2015, 5, 011040. [Google Scholar] [CrossRef] [Green Version]
- Komatsu, K.; Morita, Y.; Watanabe, E.; Tsuya, D.; Watanabe, K.; Taniguchi, T.; Moriyama, S. Observation of the quantum valley Hall state in ballistic graphene superlattices. Sci. Adv. 2018, 4, eaaq0194. [Google Scholar] [CrossRef] [Green Version]
- Vollmer, F.; Braun, D.; Libchaber, A.; Khoshsima, M.; Teraoka, I.; Arnold, S. Protein detection by optical shift of a resonant microcavity. Appl. Phys. Lett. 2002, 80, 4057–4059. [Google Scholar] [CrossRef]
- Yu, S.-Y.; He, C.; Wang, Z.; Liu, F.-K.; Sun, X.-C.; Li, Z.; Lu, H.-Z.; Lu, M.-H.; Liu, X.-P.; Chen, Y.-F. Elastic pseudospin transport for integratable topological phononic circuits. Nat. Commun. 2018, 9, 3072. [Google Scholar] [CrossRef]
- Zeng, Y.; Chattopadhyay, U.; Zhu, B.; Qiang, B.; Li, J.; Jin, Y.; Li, L.; Davies, A.G.; Linfield, E.H.; Zhang, B.; et al. Electrically pumped topological laser with valley edge modes. Nature 2020, 578, 246–250. [Google Scholar] [CrossRef]
- Wei, G.; Liu, Y.; Liu, Z.; Zhang, D.; Xiao, J. Realization of hierarchical topological transitions and high-Q-response corner states in second-order topological photonic crystals. J. Phys. D Appl. Phys. 2020, 53, 435104. [Google Scholar] [CrossRef]
- Shi, A.; Yan, B.; Ge, R.; Xie, J.; Peng, Y.; Li, H.; Wei, E.; Liu, J. Coupled cavity-waveguide based on topological corner state and edge state. Opt. Lett. 2021, 46, 1089–1092. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhou, Y.; Sun, X.; Zhang, X.; Lu, M.-H.; Chen, Y.-F. Reconfigurable Light Imaging in Photonic Higher-Order Topological Insulators. Nanomaterials 2022, 12, 819. https://doi.org/10.3390/nano12050819
Zhang X, Zhou Y, Sun X, Zhang X, Lu M-H, Chen Y-F. Reconfigurable Light Imaging in Photonic Higher-Order Topological Insulators. Nanomaterials. 2022; 12(5):819. https://doi.org/10.3390/nano12050819
Chicago/Turabian StyleZhang, Xiaomeng, Yuyu Zhou, Xiaochen Sun, Xiujuan Zhang, Ming-Hui Lu, and Yan-Feng Chen. 2022. "Reconfigurable Light Imaging in Photonic Higher-Order Topological Insulators" Nanomaterials 12, no. 5: 819. https://doi.org/10.3390/nano12050819
APA StyleZhang, X., Zhou, Y., Sun, X., Zhang, X., Lu, M.-H., & Chen, Y.-F. (2022). Reconfigurable Light Imaging in Photonic Higher-Order Topological Insulators. Nanomaterials, 12(5), 819. https://doi.org/10.3390/nano12050819






