Engineering the Exchange Spin Waves in Graded Thin Ferromagnetic Films
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of Samples and Research Methods
- Films with a fixed iron concentration gradient from 2 at.% to 10 at.%—linear, with thicknesses in the range of 50–400 nm;
- Bilayer and trilayer structures with different iron concentrations in each layer and a total thickness in the range of 20–220 nm. Each individual layer was epitaxial and uniform in composition. The layers were deposited on top of each other in a single run. Several concentrations of iron were chosen in the bilayer and trilayer samples: 4 at.% and 8 at.% in the bilayer and 2 at.% and 10 at.% in the trilayer ones;
- Films with non-linear composition distributions across the thickness—Lorentzian, sine and cosine, with thicknesses in the range of 200–400 nm.
2.2. Simulations of Thermomagnetic Curves and Spin Waves
3. Results and Discussion
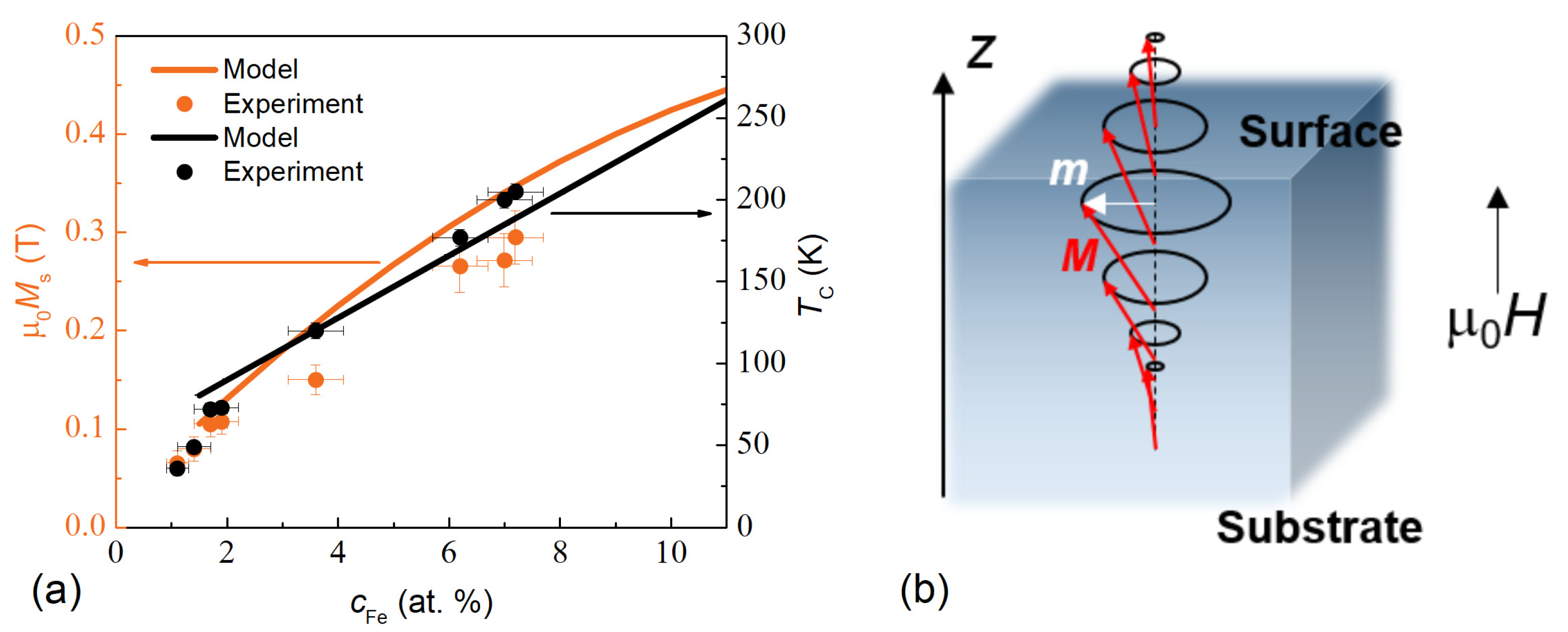
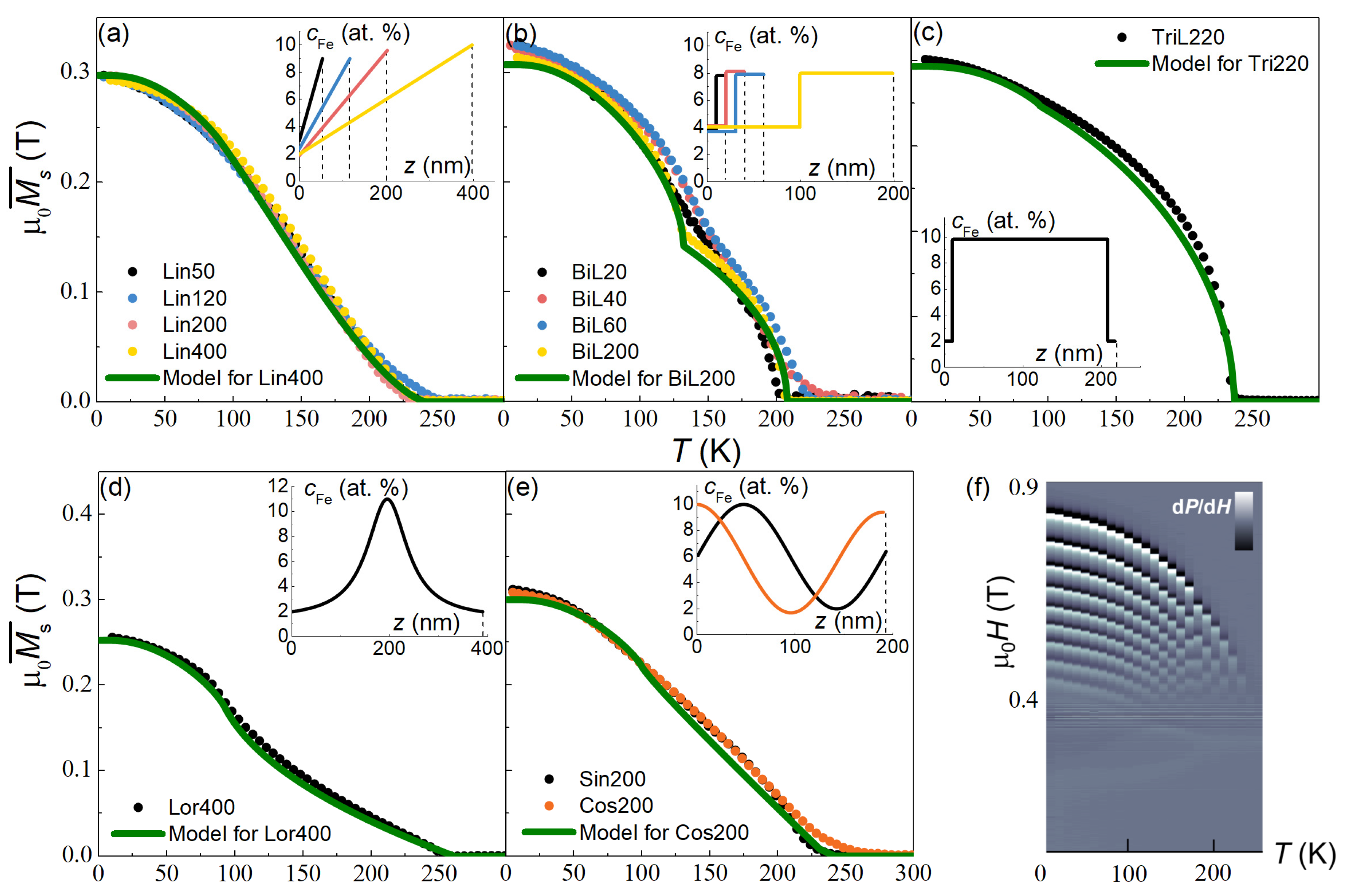
3.1. Temperature Dependences
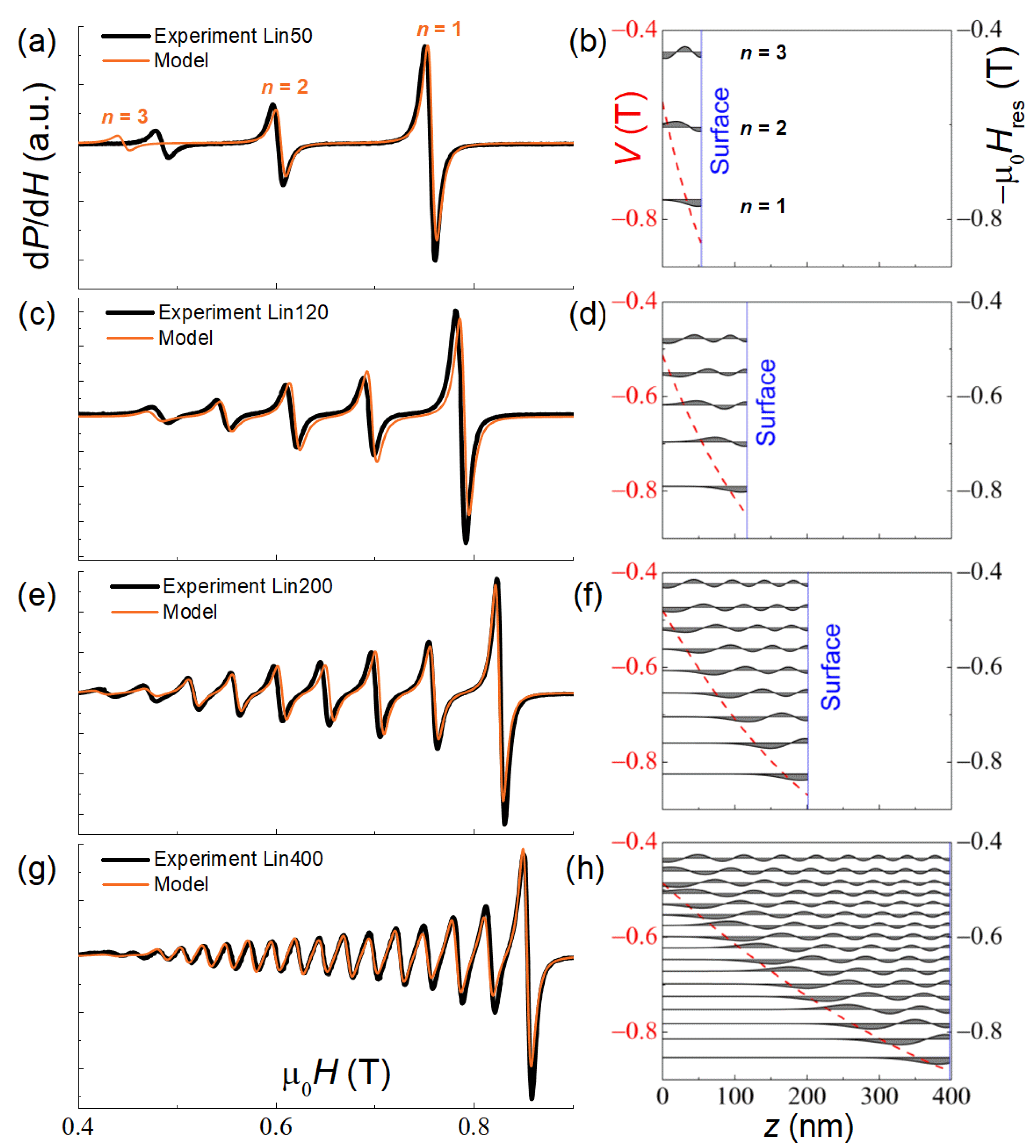
3.2. SSW Resonance Spectra of Linear-Profile Samples Lin50–400
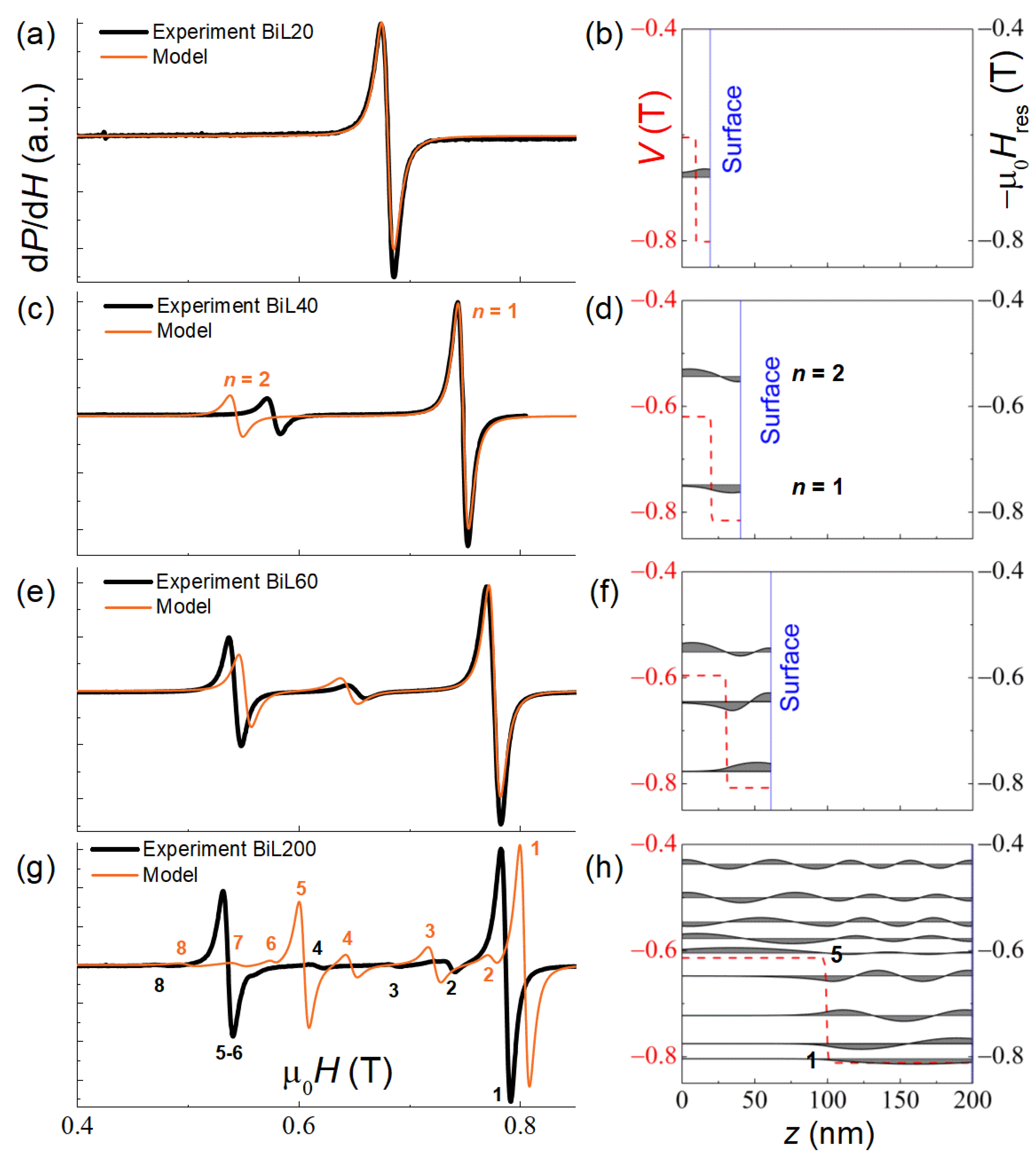
3.3. SSW in Bilayer Samples BiL20–200
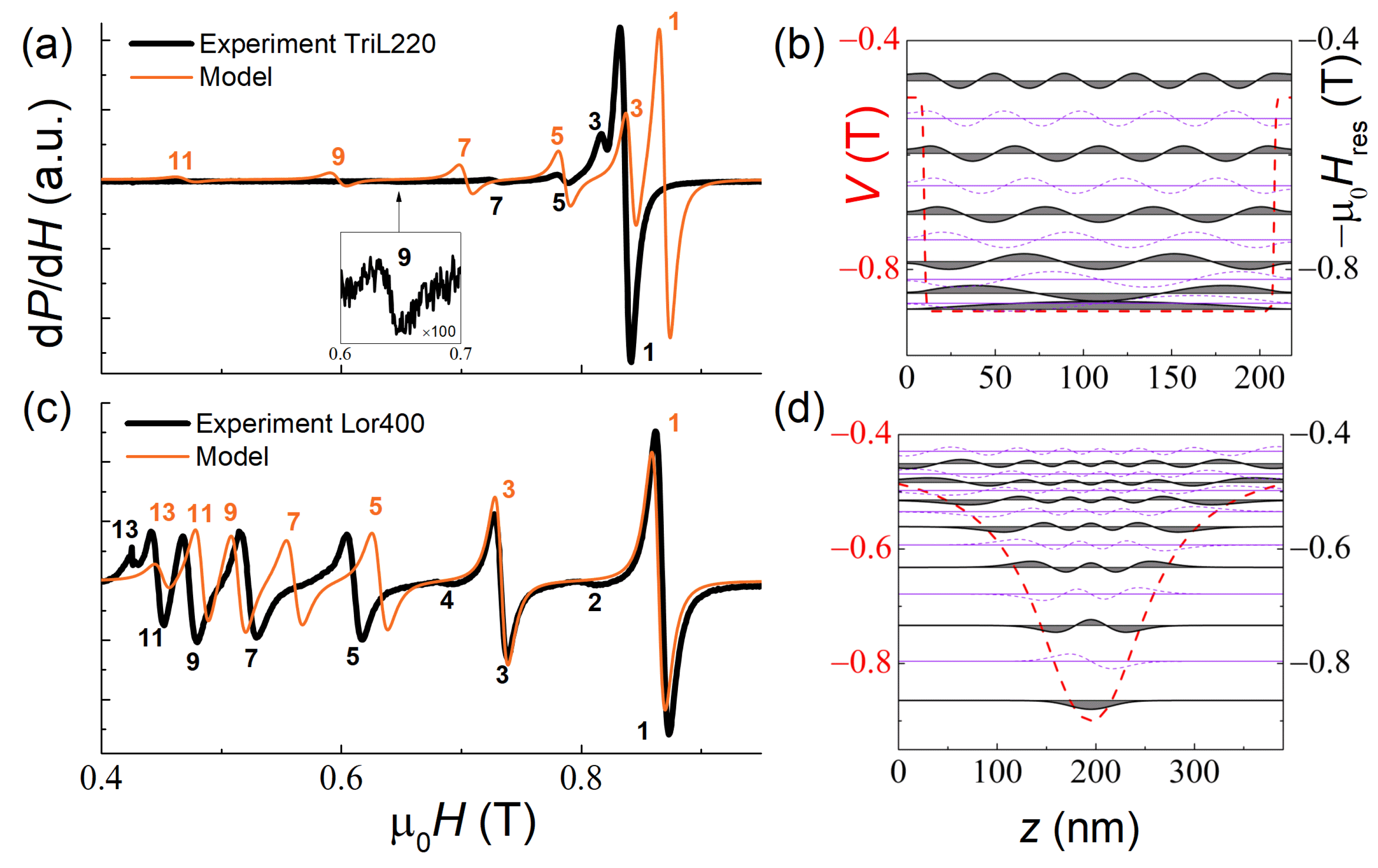
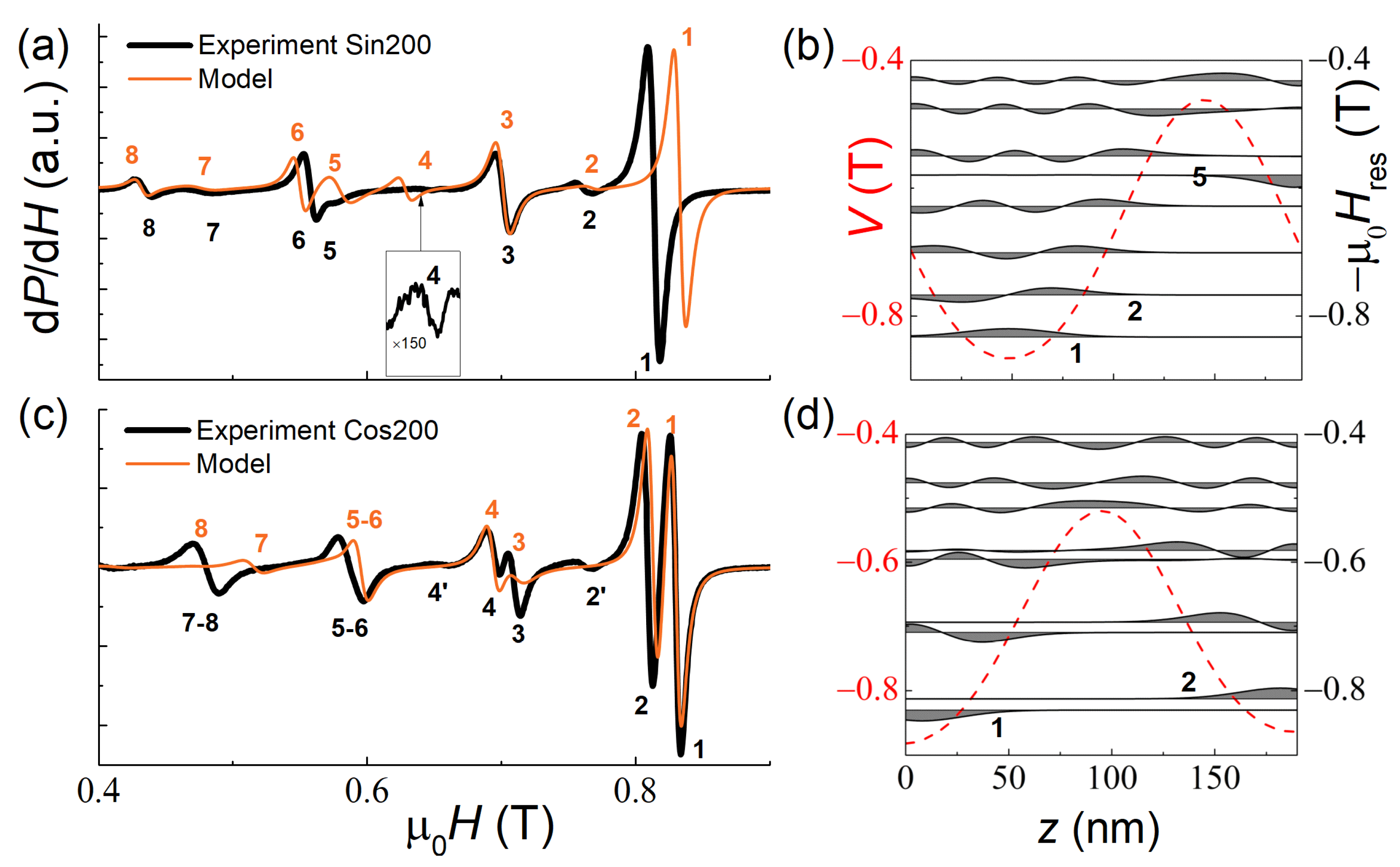
3.4. SSW in the Trilayer Structure and Films with Non-Linear Magnetization Profiles
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nikitov, S.A.; Safin, A.R.; Kalyabin, D.V.; Sadovnikov, A.V.; Beginin, E.N.; Logunov, M.V.; Morozova, M.A.; Odintsov, S.A.; Osokin, S.A.; Sharaevskaya, A.Y.; et al. Dielectric Magnonics—From Gigahertz to Terahertz. Uspekhi Fiz. Nauk 2020, 190, 945–974. [Google Scholar] [CrossRef]
- Mahmoud, A.; Ciubotaru, F.; Vanderveken, F.; Chumak, A.V.; Hamdioui, S.; Adelmann, C.; Cotofana, S. Introduction to Spin Wave Computing. J. Appl. Phys. 2020, 128, 161101. [Google Scholar] [CrossRef]
- Barman, A.; Gubbiotti, G.; Ladak, S.; Adeyeye, A.O.; Krawczyk, M.; Grafe, J.; Adelmann, C.; Cotofana, S.; Naeemi, A.; Vasyuchka, V.I.; et al. The 2021 Magnonics Roadmap. J. Phys. Condens. Matter 2021, 33, 413001. [Google Scholar] [CrossRef] [PubMed]
- Chumak, A.V.; Kabos, P.; Wu, M.; Abert, C.; Adelmann, C.; Adeyeye, A.O.; Akerman, J.; Aliev, F.G.; Anane, A.; Awad, A.; et al. Advances in Magnetics Roadmap on Spin-Wave Computing. IEEE Trans. Magn. 2022, 58, 0800172. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, W.; Tyberkevych, V.; Kwok, W.K.; Hoffmann, A.; Novosad, V. Hybrid Magnonics: Physics, Circuits, and Applications for Coherent Information Processing. J. Appl. Phys. 2020, 128, 130902. [Google Scholar] [CrossRef]
- Yu, H.; Xiao, J.; Schultheiss, H. Magnetic Texture Based Magnonics. Phys. Rep. 2021, 905, 1–59. [Google Scholar] [CrossRef]
- Dobrovolskiy, O.V.; Bunyaev, S.A.; Vovk, N.R.; Navas, D.; Gruszecki, P.; Krawczyk, M.; Sachser, R.; Huth, M.; Chumak, A.V.; Guslienko, K.Y.; et al. Spin-Wave Spectroscopy of Individual Ferromagnetic Nanodisks. Nanoscale 2020, 12, 21207–21217. [Google Scholar] [CrossRef] [PubMed]
- Dąbrowski, M.; Hicken, R.J.; Frisk, A.; Newman, D.G.; Klewe, C.; N’Diaye, A.T.; Shafer, P.; van der Laan, G.; Hesjedal, T.; Bowden, G.J. Canted Standing Spin-Wave Modes of Permalloy Thin Films Observed by Ferromagnetic Resonance. New J. Phys. 2021, 23, 023017. [Google Scholar] [CrossRef]
- Banerjee, C.; Chaurasiya, A.K.; Saha, S.; Sinha, J.; Barman, A. Tunable Spin Wave Properties in [Co/Ni80Fe20]r Multilayers with the Number of Bilayer Repetition. J. Phys. D. Appl. Phys. 2015, 48, 395001. [Google Scholar] [CrossRef]
- Dreyer, R.; Schäffer, A.F.; Bauer, H.G.; Liebing, N.; Berakdar, J.; Woltersdorf, G. Imaging and Phase-Locking of Non-Linear Spin Waves. Nat. Commun. 2022, 13, 4939. [Google Scholar] [CrossRef]
- Sarker, M.S.; Yamahara, H.; Yao, L.; Tang, S.; Liao, Z.; Seki, M.; Tabata, H. Sensitivity Enhancement in Magnetic Sensor Using CoFeB/Y3Fe5O12 Resonator. Sci. Rep. 2022, 12, 11105. [Google Scholar] [CrossRef] [PubMed]
- Krawczyk, M.; Grundler, D. Review and Prospects of Magnonic Crystals and Devices with Reprogrammable Band Structure. J. Phys. Condens. Matter 2014, 26, 123202. [Google Scholar] [CrossRef] [PubMed]
- Zakeri, K. Magnonic Crystals: Towards Terahertz Frequencies. J. Phys. Condens. Matter 2020, 32, 363001. [Google Scholar] [CrossRef] [PubMed]
- Gallardo, R.A.; Alvarado-Seguel, P.; Schneider, T.; Gonzalez-Fuentes, C.; Roldán-Molina, A.; Lenz, K.; Lindner, J.; Landeros, P. Spin-Wave Non-Reciprocity in Magnetization-Graded Ferromagnetic Films. New J. Phys. 2019, 21, 033026. [Google Scholar] [CrossRef]
- Ignatchenko, V.A.; Tsikalov, D.S. Spin-Wave Resonance in Gradient Ferromagnets with Concave and Convex Variations of Magnetic Parameters. J. Appl. Phys. 2020, 127, 123903. [Google Scholar] [CrossRef]
- Ignatchenko, V.A.; Tsikalov, D.S. Spin-Wave Oscillations in Gradient Ferromagnets: Exactly Solvable Models. J. Magn. Magn. Mater. 2020, 510, 166643. [Google Scholar] [CrossRef]
- Gallardo, R.A.; Alvarado-Seguel, P.; Brevis, F.; Roldán-Molina, A.; Lenz, K.; Lindner, J.; Landeros, P. Spin-Wave Channeling in Magnetization-Graded Nanostrips. Nanomaterials 2022, 12, 2785. [Google Scholar] [CrossRef]
- Fallarino, L.; Kirby, B.J.; Fullerton, E.E. Graded Magnetic Materials. J. Phys. D. Appl. Phys. 2021, 54, 303002. [Google Scholar] [CrossRef]
- Golovchanskiy, I.A.; Yanilkin, I.V.; Gumarov, A.I.; Gabbasov, B.F.; Abramov, N.N.; Yusupov, R.V.; Khaibullin, R.I.; Tagirov, L.R. Exchange Spin Waves in Thin Films with Gradient Composition. Phys. Rev. Mater. 2022, 6, 064406. [Google Scholar] [CrossRef]
- Esmaeili, A.; Yanilkin, I.V.; Gumarov, A.I.; Vakhitov, I.R.; Gabbasov, B.F.; Kiiamov, A.G.; Rogov, A.M.; Osin, Y.N.; Denisov, A.E.; Yusupov, R.V.; et al. Epitaxial Growth of Pd1−xFex Films on MgO Single-Crystal Substrate. Thin Solid Films 2019, 669, 338–344. [Google Scholar] [CrossRef]
- Esmaeili, A.; Vakhitov, I.R.; Yanilkin, I.V.; Gumarov, A.I.; Khaliulin, B.M.; Gabbasov, B.F.; Aliyev, M.N.; Yusupov, R.V.; Tagirov, L.R. FMR Studies of Ultra-Thin Epitaxial Pd0.92Fe0.08 Film. Appl. Magn. Reson. 2018, 49, 175–183. [Google Scholar] [CrossRef]
- Esmaeili, A.; Yanilkin, I.V.; Gumarov, A.I.; Vakhitov, I.R.; Gabbasov, B.F.; Yusupov, R.V.; Tatarsky, D.A.; Tagirov, L.R. Epitaxial Thin-Film Pd1−xFex Alloy: A Tunable Ferromagnet for Superconducting Spintronics. Sci. China Mater. 2020, 64, 1246–1255. [Google Scholar] [CrossRef]
- Kuz’min, M.D. Landau-Type Parametrization of the Equation of State of a Ferromagnet. Phys. Rev. B Condens. Matter Mater. Phys. 2008, 77, 184431. [Google Scholar] [CrossRef]
- Rappoport, T.G.; Redliński, P.; Liu, X.; Zaránd, G.; Furdyna, J.K.; Jankó, B. Anomalous Behavior of Spin-Wave Resonances in Ga1−xMnxAs Thin Films. Phys. Rev. B Condens. Matter Mater. Phys. 2004, 69, 125213. [Google Scholar] [CrossRef]
- Bihler, C.; Schoch, W.; Limmer, W.; Goennenwein, S.T.B.; Brandt, M.S. Spin-Wave Resonances and Surface Spin Pinning in Ga1−xMnxAs Thin Films. Phys. Rev. B Condens. Matter Mater. Phys. 2009, 79, 045205. [Google Scholar] [CrossRef]
- Almeida, N.; Mills, D. Eddy Currents and Spin Excitations in Conducting Ferromagnetic Films. Phys. Rev. B 1996, 53, 12232. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, L.; Wigen, P.E.; Ounadjela, K. Angular Dependence of Ferromagnetic Resonance in Exchange-Coupled Co/Ru/Co Trilayer Structures. Phys. Rev. B 1994, 50, 6094. [Google Scholar] [CrossRef]
- Heinrich, B. Ferromagnetic Resonance in Ultrathin Film Structures. In Ultrathin Magnetic Structures II; Heinrich, B., Bland, J.A.C., Eds.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 195–296. [Google Scholar] [CrossRef]
- Lindner, J.; Baberschke, K. Ferromagnetic Resonance in Coupled Ultrathin Films. J. Phys. Condens. Matter 2003, 15, S465. [Google Scholar] [CrossRef]
- Alayo, W.; Pelegrini, F.; Baggio-Saitovitch, E. Ferromagnetic Resonance Study of Sputtered NiFe/V/NiFe Heterostructures. J. Magn. Magn. Mater. 2015, 377, 104–110. [Google Scholar] [CrossRef][Green Version]
- Stenning, G.B.G.; Shelford, L.R.; Cavill, S.A.; Hoffmann, F.; Haertinger, M.; Hesjedal, T.; Woltersdorf, G.; Bowden, G.J.; Gregory, S.A.; Back, C.H.; et al. Magnetization Dynamics in an Exchange-Coupled NiFe/CoFe Bilayer Studied by x-Ray Detected Ferromagnetic Resonance. New J. Phys. 2015, 17, 013019. [Google Scholar] [CrossRef][Green Version]
- Castillo Alvarado, F.L.; Rutkowski, J.H.; Urbaniak-Kucharczyk, A.; Wojtczak, L. The Role of Interface Anisotropy in Spin Wave Resonance Spectra of Magnetic Multilayers Exchange Coupled through Nonmagnetic f.c.c. Spacer. Thin Solid Films 1998, 324, 225–229. [Google Scholar] [CrossRef]
- Puszkarski, H. Ferromagnetic-Bilayer Spin-Wave Resonance: Reassignment of Interface-Affected Lines. Phys. Rev. B 1992, 46, 8926. [Google Scholar] [CrossRef] [PubMed]
- Krawczyk, M.; Puszkarski, H.; Lévy, J.C.S.; Mercier, D. Spin-Wave Mode Profiles versus Surface/Interface Conditions in Ferromagnetic/Ni Layered Composites. J. Phys. Condens. Matter 2003, 15, 2449. [Google Scholar] [CrossRef]
- Belmeguenai, M.; Martin, T.; Woltersdorf, G.; Maier, M.; Bayreuther, G. Frequency- and Time-Domain Investigation of the Dynamic Properties of Interlayer-Exchange-Coupled Ni81 Fe19 Ru Ni81 Fe19 Thin Films. Phys. Rev. B Condens. Matter Mater. Phys. 2007, 76, 104414. [Google Scholar] [CrossRef]
- Zyuzin, A.M.; Bakulin, M.A.; Bezborodov, S.V.; Radaikin, V.V.; Sabaev, S.N. The Effect of the Frequency of an Alternating Magnetic Field on the Dispersion Characteristics of the Spin-Wave Resonance Spectra in Multilayer Films. Tech. Phys. Lett. 2015, 41, 832–835. [Google Scholar] [CrossRef]
- Ben Youssef, J.; Castel, V.; Vukadinovic, N.; Labrune, M. Spin-Wave Resonances in Exchange-Coupled Permalloy/Garnet Bilayers. J. Appl. Phys. 2010, 108, 063909. [Google Scholar] [CrossRef]
- Zyuzin, A.M.; Bakulin, M.A.; Radaikin, V.V.; Sabaev, S.N.; Yantsen, N.V. Spin-Wave Resonance Spectra for Two-Layer Films with Strongly Different Uniform Resonance Fields in the Layers. Tech. Phys. 2009, 54, 723–726. [Google Scholar] [CrossRef]
- Krawczyk, M.; Puszkarski, H.; Lévy, J.C.; Mamica, S.; Mercier, D. Theoretical Study of Spin Wave Resonance Filling Fraction Effect in Composite Ferromagnetic [A|B|A] Trilayer. J. Magn. Magn. Mater. 2002, 246, 93–100. [Google Scholar] [CrossRef]

| Profile Type | Label | Thickness, nm | c1 | c2 |
|---|---|---|---|---|
| Linear | Lin50 | 53 | 3 a | 9 b |
| Lin120 | 116 | 2.4 a | 9 b | |
| Lin200 | 202 | 2 a | 9.6 b | |
| Lin400 | 397 | 2 a | 10 b | |
| Bilayer | BiL20 | 10/10 | 3.9 | 7.8 |
| BiL40 | 20/20 | 4.1 | 8.1 | |
| BiL60 | 30/30 | 3.7 | 7.9 | |
| BiL200 | 100/100 | 4 | 8 | |
| Trilayer | TriL220 | 10/200/10 | 2 c | 9.8 |
| Lorentzian | Lor400 | 390/100 d | 2 a | 11 b |
| Sine | Sin200 | 193 e | 2 a | 10 b |
| Cosine | Cos200 | 190 e | 2 a | 10 b |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yanilkin, I.; Gumarov, A.; Golovchanskiy, I.; Gabbasov, B.; Yusupov, R.; Tagirov, L. Engineering the Exchange Spin Waves in Graded Thin Ferromagnetic Films. Nanomaterials 2022, 12, 4361. https://doi.org/10.3390/nano12244361
Yanilkin I, Gumarov A, Golovchanskiy I, Gabbasov B, Yusupov R, Tagirov L. Engineering the Exchange Spin Waves in Graded Thin Ferromagnetic Films. Nanomaterials. 2022; 12(24):4361. https://doi.org/10.3390/nano12244361
Chicago/Turabian StyleYanilkin, Igor, Amir Gumarov, Igor Golovchanskiy, Bulat Gabbasov, Roman Yusupov, and Lenar Tagirov. 2022. "Engineering the Exchange Spin Waves in Graded Thin Ferromagnetic Films" Nanomaterials 12, no. 24: 4361. https://doi.org/10.3390/nano12244361
APA StyleYanilkin, I., Gumarov, A., Golovchanskiy, I., Gabbasov, B., Yusupov, R., & Tagirov, L. (2022). Engineering the Exchange Spin Waves in Graded Thin Ferromagnetic Films. Nanomaterials, 12(24), 4361. https://doi.org/10.3390/nano12244361







