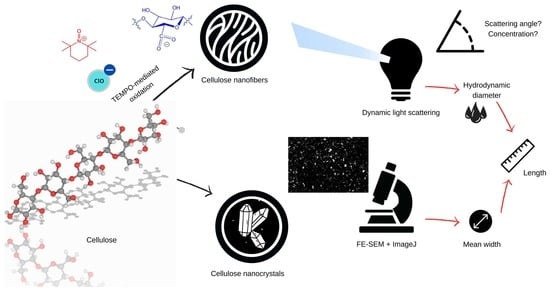
Dynamic Light Scattering Plus Scanning Electron Microscopy: Usefulness and Limitations of a Simplified Estimation of Nanocellulose Dimensions
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Production of CNFs
2.3. Production of CNCs
2.4. Other Characterization Techniques
2.5. Dynamic Light Scattering
2.6. Estimation of Particle Dimensions
3. Results and Discussion
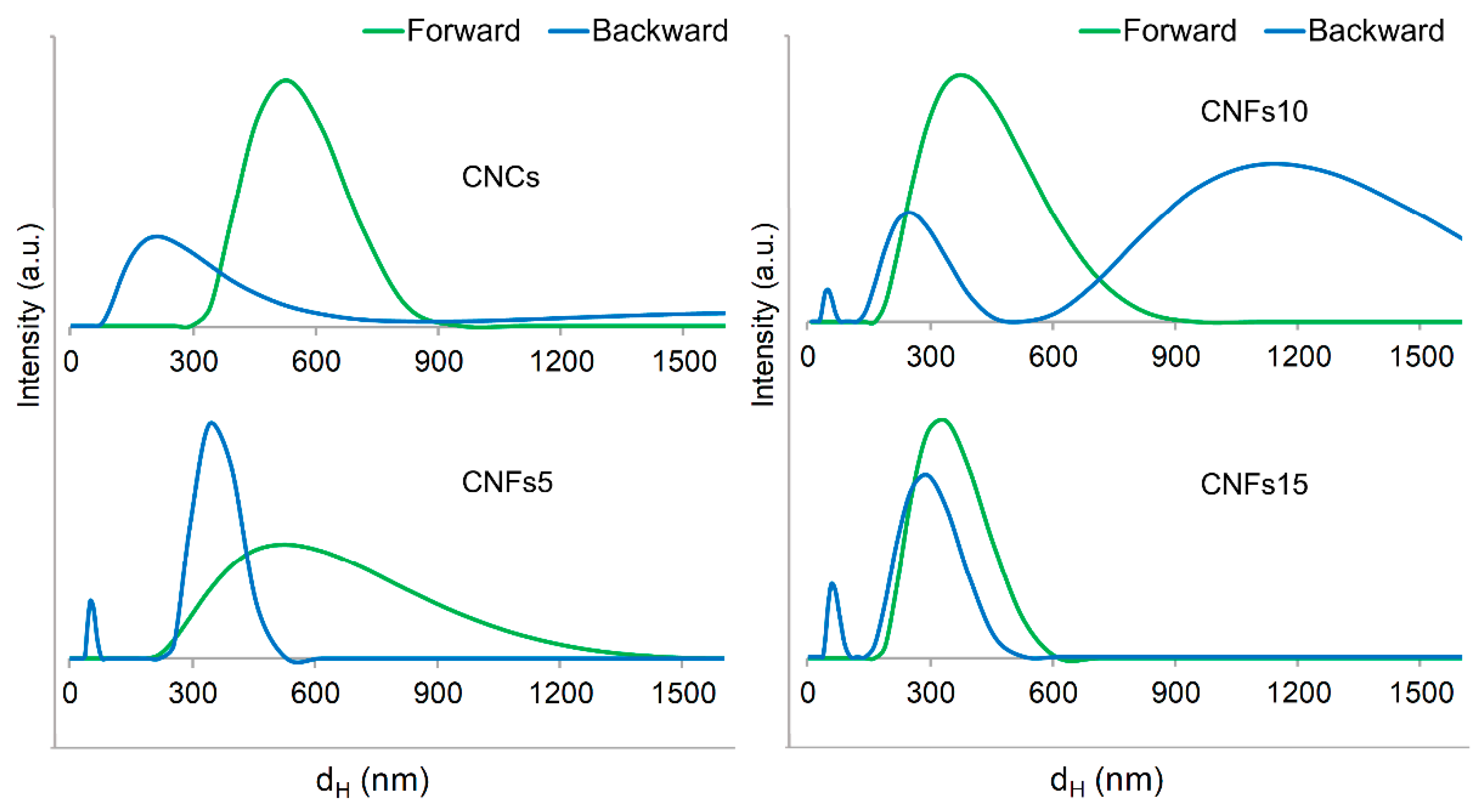
3.1. Definition of Proper Testing Conditions
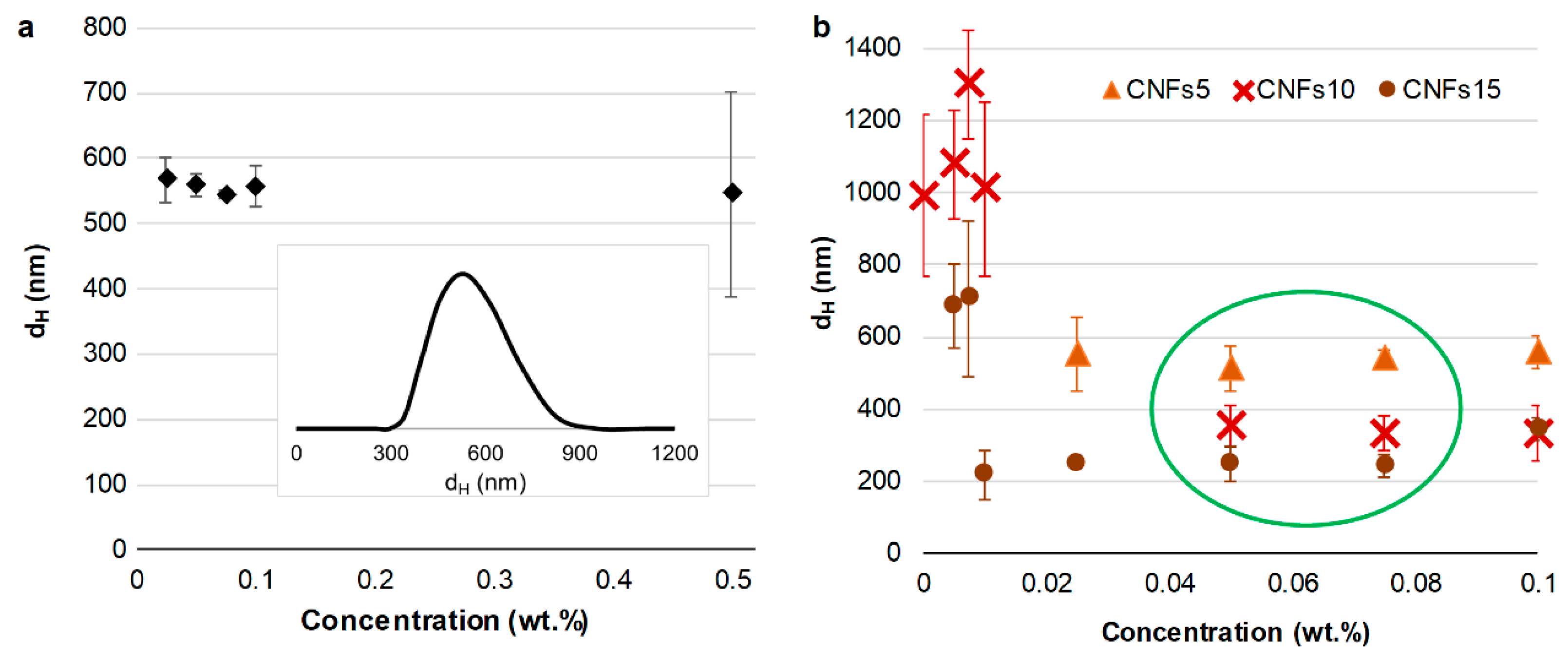
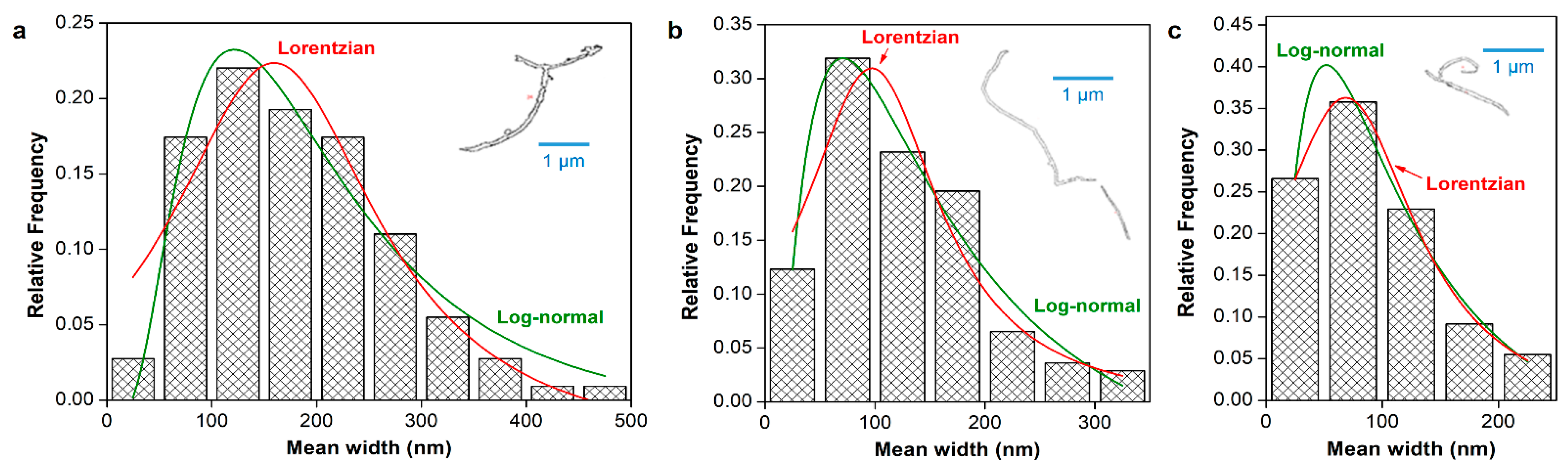
3.2. Dimensions of CNCs
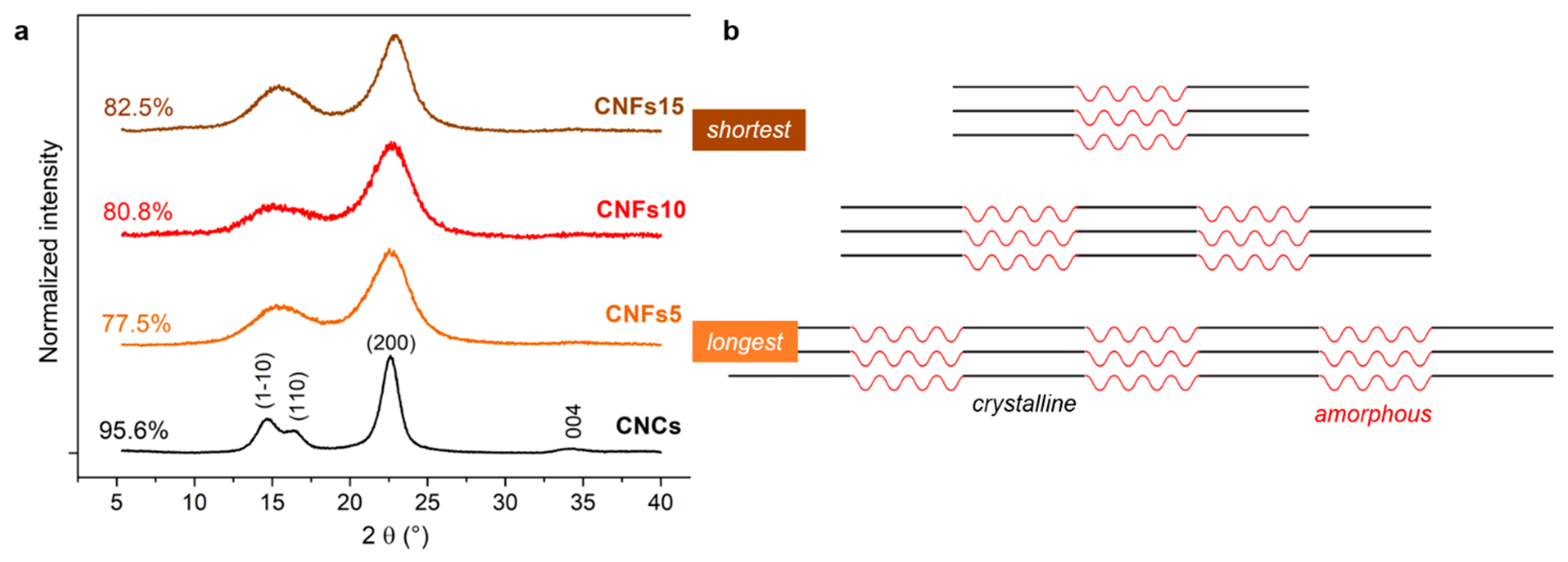
3.3. Dimensions of CNFs with Different Oxidation Degrees
3.4. Relating Key Properties of Nanocellulose to Its Dimensions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fraschini, C.; Chauve, G.; Le Berre, J.-F.; Ellis, S.; Méthot, M.; O’Connor, B.; Bouchard, J. Critical Discussion of Light Scattering and Microscopy Techniques for CNC Particle Sizing. Nord. Pulp Pap. Res. J. 2014, 29, 31–40. [Google Scholar] [CrossRef]
- Gamelas, J.A.F.; Pedrosa, J.; Lourenço, A.F.; Mutjé, P.; González, I.; Chinga-Carrasco, G.; Singh, G.; Ferreira, P.J.T. On the Morphology of Cellulose Nanofibrils Obtained by TEMPO-Mediated Oxidation and Mechanical Treatment. Micron 2015, 72, 28–33. [Google Scholar] [CrossRef]
- Sanchez-Salvador, J.L.; Balea, A.; Negro, C.; Monte, M.C.; Blanco, A. Gel Point as Measurement of Dispersion Degree of Nano-Cellulose Suspensions and Its Application in Papermaking. Nanomaterials 2022, 12, 790. [Google Scholar] [CrossRef]
- Aguado, R.; Tarrés, Q.; Pèlach, M.À.; Mutjé, P.; de la Fuente, E.; Sanchez-Salvador, J.L.; Negro, C.; Delgado-Aguilar, M. Micro- and Nanofibrillated Cellulose from Annual Plant-Sourced Fibers: Comparison between Enzymatic Hydrolysis and Mechanical Refining. Nanomaterials 2022, 12, 1612. [Google Scholar] [CrossRef] [PubMed]
- Hotaling, N.A.; Bharti, K.; Kriel, H.; Simon, C.G. DiameterJ: A Validated Open Source Nanofiber Diameter Measurement Tool. Biomaterials 2015, 61, 327–338. [Google Scholar] [CrossRef]
- Sanchez-Salvador, J.L.; Campano, C.; Balea, A.; Tarrés, Q.; Delgado-Aguilar, M.; Mutjé, P.; Blanco, A.; Negro, C. Critical Comparison of the Properties of Cellulose Nanofibers Produced from Softwood and Hardwood through Enzymatic, Chemical and Mechanical Processes. Int. J. Biol. Macromol. 2022, 205, 220–230. [Google Scholar] [CrossRef]
- Campano, C.; Balea, A.; Blanco, Á.; Negro, C. A Reproducible Method to Characterize the Bulk Morphology of Cellulose Nanocrystals and Nanofibers by Transmission Electron Microscopy. Cellulose 2020, 27, 4871–4887. [Google Scholar] [CrossRef]
- Radakisnin, R.; Abdul Majid, M.S.; Jamir, M.R.; Jawaid, M.; Sultan, M.T.; Mat Tahir, M.F. Structural, Morphological and Thermal Properties of Cellulose Nanofibers from Napier Fiber (Pennisetum purpureum). Materials 2020, 13, 4125. [Google Scholar] [CrossRef] [PubMed]
- Aguado, R.; Lourenço, A.F.; Ferreira, P.J.; Moral, A.; Tijero, A. Cationic Cellulosic Derivatives as Flocculants in Papermaking. Cellulose 2017, 24, 3015–3027. [Google Scholar] [CrossRef]
- Zakharov, P.; Scheffold, F. Advances in Dynamic Light Scattering Techniques BT—Light Scattering Reviews 4: Single Light Scattering and Radiative Transfer; Kokhanovsky, A.A., Ed.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2009; pp. 433–467. ISBN 978-3-540-74276-0. [Google Scholar]
- Fotie, G.; Gazzotti, S.; Ortenzi, M.A.; Piergiovanni, L. Implementation of High Gas Barrier Laminated Films Based on Cellulose Nanocrystals for Food Flexible Packaging. Appl. Sci. 2020, 10, 3201. [Google Scholar] [CrossRef]
- Gallardo-Sánchez, M.A.; Diaz-Vidal, T.; Navarro-Hermosillo, A.B.; Figueroa-Ochoa, E.B.; Ramirez Casillas, R.; Anzaldo Hernández, J.; Rosales-Rivera, L.C.; Soltero Martínez, J.F.; García Enríquez, S.; Macías-Balleza, E.R. Optimization of the Obtaining of Cellulose Nanocrystals from Agave Tequilana Weber Var. Azul Bagasse by Acid Hydrolysis. Nanomaterials 2021, 11, 520. [Google Scholar] [CrossRef]
- Metzger, C.; Drexel, R.; Meier, F.; Briesen, H. Effect of Ultrasonication on the Size Distribution and Stability of Cellulose Nanocrystals in Suspension: An Asymmetrical Flow Field-Flow Fractionation Study. Cellulose 2021, 28, 10221–10238. [Google Scholar] [CrossRef]
- Bao, C.; Chen, X.; Liu, C.; Liao, Y.; Huang, Y.; Hao, L.; Yan, H.; Lin, Q. Extraction of Cellulose Nanocrystals from Microcrystalline Cellulose for the Stabilization of Cetyltrimethylammonium Bromide-Enhanced Pickering Emulsions. Colloids Surfaces A Physicochem. Eng. Asp. 2021, 608, 125442. [Google Scholar] [CrossRef]
- Delepierre, G.; Eyley, S.; Thielemans, W.; Weder, C.; Cranston, E.D.; Zoppe, J.O. Patience Is a Virtue: Self-Assembly and Physico-Chemical Properties of Cellulose Nanocrystal Allomorphs. Nanoscale 2020, 12, 17480–17493. [Google Scholar] [CrossRef]
- Khlebtsov, B.N.; Khlebtsov, N.G. On the Measurement of Gold Nanoparticle Sizes by the Dynamic Light Scattering Method. Colloid J. 2011, 73, 118–127. [Google Scholar] [CrossRef]
- Boluk, Y.; Danumah, C. Analysis of Cellulose Nanocrystal Rod Lengths by Dynamic Light Scattering and Electron Microscopy. J. Nanopart. Res. 2013, 16, 2174. [Google Scholar] [CrossRef]
- Kohl, K. Comparison of Dynamic Light Scattering and Rheometrical Methods to Determine the Gel Point of a Radically Polymerized Hydrogel under Mechanical Shear. Micromachines 2020, 11, 462. [Google Scholar] [CrossRef]
- Leong, S.S.; Ng, W.M.; Lim, J.; Yeap, S.P. Dynamic Light Scattering: Effective Sizing Technique for Characterization of Magnetic Nanoparticles. In Handbook of Materials Characterization; Sharma, S.K., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 77–111. ISBN 978-3-319-92955-2. [Google Scholar]
- Aguado, R.; Murtinho, D.; Valente, A.J.M. Association of Antioxidant Monophenolic Compounds with β-Cyclodextrin-Functionalized Cellulose and Starch Substrates. Carbohydr. Polym. 2021, 267, 118189. [Google Scholar] [CrossRef]
- Haddad, G.; Fontanini, A.; Bellali, S.; Takakura, T.; Ominami, Y.; Hisada, A.; Hadjadj, L.; Rolain, J.M.; Raoult, D.; Bou Khalil, J.Y. Rapid Detection of Imipenem Resistance in Gram-Negative Bacteria Using Tabletop Scanning Electron Microscopy: A Preliminary Evaluation. Front. Microbiol. 2021, 12, 658322. [Google Scholar] [CrossRef] [PubMed]
- Serra-Parareda, F.; Tarrés, Q.; Sanchez-Salvador, J.L.; Campano, C.; Pèlach, M.À.; Mutjé, P.; Negro, C.; Delgado-Aguilar, M. Tuning Morphology and Structure of Non-Woody Nanocellulose: Ranging between Nanofibers and Nanocrystals. Ind. Crops Prod. 2021, 171, 113877. [Google Scholar] [CrossRef]
- Tarrés, Q.; Aguado, R.; Pèlach, M.À.; Mutjé, P.; Delgado-Aguilar, M. Electrospray Deposition of Cellulose Nanofibers on Paper: Overcoming the Limitations of Conventional Coating. Nanomaterials 2022, 12, 79. [Google Scholar] [CrossRef] [PubMed]
- Noguchi, Y.; Homma, I.; Matsubara, Y. Complete Nanofibrillation of Cellulose Prepared by Phosphorylation. Cellulose 2017, 24, 1295–1305. [Google Scholar] [CrossRef]
- Tarrés, Q.; Boufi, S.; Mutjé, P.; Delgado-Aguilar, M. Enzymatically Hydrolyzed and TEMPO-Oxidized Cellulose Nanofibers for the Production of Nanopapers: Morphological, Optical, Thermal and Mechanical Properties. Cellulose 2017, 24, 3943–3954. [Google Scholar] [CrossRef]
- Serra-Parareda, F.; Aguado, R.; Tarrés, Q.; Mutjé, P.; Delgado-Aguilar, M. Potentiometric Back Titration as a Robust and Simple Method for Specific Surface Area Estimation of Lignocellulosic Fibers. Cellulose 2021, 28, 10815–10825. [Google Scholar] [CrossRef]
- Filipova, I.; Serra, F.; Tarrés, Q.; Mutjé, P.; Delgado-Aguilar, M. Oxidative Treatments for Cellulose Nanofibers Production: A Comparative Study between TEMPO-Mediated and Ammonium Persulfate Oxidation. Cellulose 2020, 27, 10671–10688. [Google Scholar] [CrossRef]
- Eckelt, J.; Knopf, A.; Röder, T.; Weber, H.K.; Sixta, H.; Wolf, B.A. Viscosity-Molecular Weight Relationship for Cellulose Solutions in Either NMMO Monohydrate or Cuen. J. Appl. Polym. Sci. 2011, 119, 670–676. [Google Scholar] [CrossRef]
- Segal, L.; Creely, J.J.; Martin, A.E.; Conrad, C.M. An Empirical Method for Estimating the Degree of Crystallinity of Native Cellulose Using the X-Ray Diffractometer. Text. Res. J. 1959, 29, 786–794. [Google Scholar] [CrossRef]
- Velásquez-Cock, J.; Gañán, P.; Posada, P.; Castro, C.; Serpa, A.; Gómez H., C.; Putaux, J.-L.; Zuluaga, R. Influence of Combined Mechanical Treatments on the Morphology and Structure of Cellulose Nanofibrils: Thermal and Mechanical Properties of the Resulting Films. Ind. Crops Prod. 2016, 85, 1–10. [Google Scholar] [CrossRef]
- Taheri, A.; Mohammadi, M. The Use of Cellulose Nanocrystals for Potential Application in Topical Delivery of Hydroquinone. Chem. Biol. Drug Des. 2015, 86, 102–106. [Google Scholar] [CrossRef]
- Verma, C.; Chhajed, M.; Gupta, P.; Roy, S.; Maji, P.K. Isolation of Cellulose Nanocrystals from Different Waste Bio-Mass Collating Their Liquid Crystal Ordering with Morphological Exploration. Int. J. Biol. Macromol. 2021, 175, 242–253. [Google Scholar] [CrossRef]
- Vallejos, M.E.; Felissia, F.E.; Area, M.C.; Ehman, N.V.; Tarrés, Q.; Mutjé, P. Nanofibrillated Cellulose (CNF) from Eucalyptus Sawdust as a Dry Strength Agent of Unrefined Eucalyptus Handsheets. Carbohydr. Polym. 2016, 139, 99–105. [Google Scholar] [CrossRef]
- Sanchez-Salvador, J.L.; Campano, C.; Lopez-Exposito, P.; Tarrés, Q.; Mutjé, P.; Delgado-Aguilar, M.; Monte, M.C.; Blanco, A. Enhanced Morphological Characterization of Cellulose Nano/Microfibers through Image Skeleton Analysis. Nanomaterials 2021, 11, 2077. [Google Scholar] [CrossRef]
- Ang, S.; Haritos, V.; Batchelor, W. Cellulose Nanofibers from Recycled and Virgin Wood Pulp: A Comparative Study of Fiber Development. Carbohydr. Polym. 2020, 234, 115900. [Google Scholar] [CrossRef]
- Saito, T.; Kimura, S.; Nishiyama, Y.; Isogai, A. Cellulose Nanofibers Prepared by TEMPO-Mediated Oxidation of Native Cellulose. Biomacromolecules 2007, 8, 2485–2491. [Google Scholar] [CrossRef] [PubMed]
- Baati, R.; Magnin, A.; Boufi, S. High Solid Content Production of Nanofibrillar Cellulose via Continuous Extrusion. ACS Sustain. Chem. Eng. 2017, 5, 2350–2359. [Google Scholar] [CrossRef]
- Ioelovich, M. Study of Cellulose Interaction with Concentrated Solutions of Sulfuric Acid. ISRN Chem. Eng. 2012, 2012, 428974. [Google Scholar] [CrossRef]
- Spier, V.C.; Sierakowski, M.R.; Reed, W.F.; de Freitas, R.A. Polysaccharide Depolymerization from TEMPO-Catalysis: Effect of TEMPO Concentration. Carbohydr. Polym. 2017, 170, 140–147. [Google Scholar] [CrossRef]
- Shinoda, R.; Saito, T.; Okita, Y.; Isogai, A. Relationship between Length and Degree of Polymerization of TEMPO-Oxidized Cellulose Nanofibrils. Biomacromolecules 2012, 13, 842–849. [Google Scholar] [CrossRef]
- Ensor, D.S.; Pilat, M.J. The Effect of Particle Size Distribution on Light Transmittance Measurement. Am. Ind. Hyg. Assoc. J. 1971, 32, 287–292. [Google Scholar] [CrossRef]

| Dimension | FE-SEM | DLS | Calculated | ||
|---|---|---|---|---|---|
| Average | Mode | Average | Mode | ||
| Diameter (nm) | 237 | 125–150 | 544 ± 6 | 459–571 | -- |
| Length (μm) | 1.29 | 1.80–2.00 | -- | 1.91 | |
| Sample | dm (nm) | dH (nm) | Calculated Length (μm) | ||
|---|---|---|---|---|---|
| Average | Mode | Average | Mode | ||
| CNFs5 | 178 | 100–150 | 543 ± 20 | 459–571 | 3.37 |
| CNFs10 | 121 | 50–100 | 332 ± 49 | 295–342 | 1.67 |
| CNFs15 | 92 | 50–100 | 250 ± 5 | 220–255 | 1.23 |
| Sample | DP | WRV (g/g) | CD (meq/g) | Transmittance (%) |
|---|---|---|---|---|
| CNCs | -- | -- | 0.07 | 71.8 |
| CNFs5 | 260 | 13.3 | 1.36 | 89.8 |
| CNFs10 | 135 | 11.8 | 1.70 | 94.0 |
| CNFs15 | 117 | 13.5 | 1.99 | 99.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarrés, Q.; Aguado, R.; Zoppe, J.O.; Mutjé, P.; Fiol, N.; Delgado-Aguilar, M. Dynamic Light Scattering Plus Scanning Electron Microscopy: Usefulness and Limitations of a Simplified Estimation of Nanocellulose Dimensions. Nanomaterials 2022, 12, 4288. https://doi.org/10.3390/nano12234288
Tarrés Q, Aguado R, Zoppe JO, Mutjé P, Fiol N, Delgado-Aguilar M. Dynamic Light Scattering Plus Scanning Electron Microscopy: Usefulness and Limitations of a Simplified Estimation of Nanocellulose Dimensions. Nanomaterials. 2022; 12(23):4288. https://doi.org/10.3390/nano12234288
Chicago/Turabian StyleTarrés, Quim, Roberto Aguado, Justin O. Zoppe, Pere Mutjé, Núria Fiol, and Marc Delgado-Aguilar. 2022. "Dynamic Light Scattering Plus Scanning Electron Microscopy: Usefulness and Limitations of a Simplified Estimation of Nanocellulose Dimensions" Nanomaterials 12, no. 23: 4288. https://doi.org/10.3390/nano12234288
APA StyleTarrés, Q., Aguado, R., Zoppe, J. O., Mutjé, P., Fiol, N., & Delgado-Aguilar, M. (2022). Dynamic Light Scattering Plus Scanning Electron Microscopy: Usefulness and Limitations of a Simplified Estimation of Nanocellulose Dimensions. Nanomaterials, 12(23), 4288. https://doi.org/10.3390/nano12234288