Abstract
We investigate the origin of ferroelectricity in the BiFeO3–LaFeO3 system in rhombohedral R3c and tetragonal P4mm symmetries by ab initio density functional theory calculations and compare their electronic features with paraelectric orthorhombic Pnma symmetry. We show that a coherent accommodation of stereo-active lone pair electrons of Bi is the detrimental factor of ferroelectricity. A Bloch function arising from an indirect Bi_6p–Fe_3d hybridization mediated through O_2p is the primary origin of spontaneous polarization (Ps) in the rhombohedral system. In the orthorhombic system, a similar Bloch function was found, whereas a staggered accommodation of stereo-active lone pair electrons of Bi exclusively results in paraelectricity. A giant Ps reported in the tetragonal system originates from an orbital hybridization of Bi_6p and O_2p, where Fe-3d plays a minor role. The Ps in the rhombohedral system decreases with increasing La content, while that in the tetragonal system displays a discontinuous drop at a certain La content. We discuss the electronic factors affecting the Ps evolutions with La content.
1. Introduction
Perovskite ferroelectrics have attracted much attention because of their fascinating properties, such as electromechanical response and switchable spontaneous polarization (Ps) by external stimuli. Lead titanate (PbTiO3) has tetragonal P4mm symmetry and features a high Curie temperature (TC) of 495 °C and a robust Ps [1]. Ferroelectric tetragonal PbTiO3 forms a solid solution with antiferroelectric rhombohedral PbZrO3 [2,3]. Their dielectric and piezoelectric properties are maximal at around the morphotropic phase boundary (MPB) [4], and the properties around the MPB have been widely utilized for sensors, ultrasonic motors, and medical transducers [5,6,7]. Single crystals of Pb(Mg, Nb)O3–PbTiO3 and Pb(Zn, Nb)O3–PbTiO3 exhibit extraordinary high electromechanical coupling factors because a bridging phase in monoclinic symmetry [4,8,9,10] is capable of a rotation of Ps under electric fields [8,11,12,13,14].
Ferroelectric BiFeO3 has been intensively studied from the viewpoints not only of multiferroic nature [15,16,17,18] but also of a Pb-free piezoelectric material [19,20,21,22]. In BiFeO3 [18,23], Ps coexists with an incommensurate spin structure, which can be approximated as an antiferromagnetic spin configuration [15,17]. A large Ps of 80–100 μC/cm2 along with a high TC of 830 °C [24,25] is present along [111]c in rhombohedral R3c symmetry [24,25] (the subscript ‘c’ indicates pseudo-cubic), while strained tetragonal films display a giant Ps of over 130 μC/cm2 [26].
A formation of composition-driven phase boundaries, such as MPBs, is expected in the systems of BiFeO3–REFeO3 [27,28,29,30,31,32,33,34,35] (RE: rare-earth elements) and BiFeO3–BaTiO3 [20,21,36,37]. The simplest solid solution is the BiFeO3–LaFeO3 system with a composition of Bi1−xLaxFeO3, the detail of which has been comprehensively summarized in the review paper [27]. Karimi et al. [28] reported that a phase boundary between the ferroelectric R3c and the paraelectric orthorhombic Pnma phases exists at x ~ 0.23 at room temperature. Rusakov et al. reported that single-phase materials with R3c symmetry can be prepared after annealing for composition 0 ≤ x ≤ 0.1, and the Pnma phase is stable at 0.50 ≤ x ≤ 1; these results were verified by synchrotron radiation X-ray diffraction, electron diffraction, and high-resolution transmission electron microscopy [38]. They also found that an incommensurate phase in orthorhombic Imma symmetry is formed at 0.19 ≤ x ≤ 0.30. Karpinsky et al. [29] proposed a temperature-composition phase diagram, in which the ferroelectric R3c (x < 0.15) and the paraelectric Pnma (x > 0.4) phases are mediated through a bridging anti-polar phase in orthorhombic Pbam symmetry.
One possible reason for the wide variety of experimental reports on the phase diagrams is incomplete solubility of La on the A site [39]. Moreover, the abovementioned phases are energetically competing with each other and some of them are likely to be energetically degenerate [31]. Therefore, ab initio studies based on density functional theory (DFT) are expected to provide clues for uncovering the ground-state crystal structure and the phase stability.
Lee et al. investigated the effect of the La doping on the variation of the off-center distortion and the orbital mixing in BiFeO3 by experiments in conjunction with DFT calculations [30]. They reported that both an Fe–O bond anisotropy and off-center cation displacements are suppressed by the La doping. As a result, the degree of Fe 3d–4p orbital mixing decreases in the solid solution samples. An impact of the La content on the polarization and the electronic band structure was also reported by You et al. [40]. They reported that the La doping induces a chemically driven rotational instability. It modifies the local crystal field along with the electronic structure, which gives rise to a direct-to-indirect transition of the bandgap and provides an enhancement in ferroelectric photovoltaic effect. In contrast, Tan et al. reported that the La doping has little influence on Ps in tetragonal BiFeO3 [34]. In spite of extensive research by DFT studies [30,31,32,33,34,35], the Ps’s evolution with the La content and its electronic origin still remain unclear.
The purpose of this study is to elucidate the origin of ferroelectricity in rhombohedral R3c, tetragonal P4mm in the BiFeO3-LaFeO3 system (Bi1−xLaxFeO3). The electronic feature and structural distortion in the paraelectric orthorhombic Pnma symmetry are also investigated because Bi1−xLaxFeO3 with x ≥ 0.5 is of the orthorhombic phase [29]. We show DFT energy evolutions with x but focus on the relation between the orbital hybridizations and the ferroelectric (paraelectric) distortions. We show that the Bloch function arising from a Bi_6p-Fe_3d hybridization mediated through O_2p is the primary origin of Ps in the rhombohedral system. In the orthorhombic system, a similar Bloch function and the resultant structural distortion are constructed, whereas a staggered accommodation of stereo-active lone pair electrons of Bi never allow the presence of Ps. We discuss a large Ps and its dependence on x in the tetragonal system.
2. DFT Calculations
Density functional theory (DFT) calculations were conducted using the generalized gradient approximation [41] with a plane-wave basis set. We used the projector-augmented wave method [42] as implemented in the Vienna ab initio simulation package (VASP) [43]. We employed the Perdew–Burke–Ernzerhof gradient-corrected exchange-correlation functional revised for solids (PBEsol) [44], a plane-wave cut-off energy of 520 eV, an electronic iterations convergence of 1 × 10−6 eV, and a criterion for ionic relaxations of 1 meV/nm. The Γ-centered k-point mesh was set to 3 × 3 × 3 for the structural optimizations and 5 × 5 × 5 for density of states (DOS) and band structure calculations.
Within the simplified generalized gradient approximation (GGA) + U approach [45], we added on-site Coulomb interaction parameters of U–J of 6 eV to Fe-3d throughout the calculations. The on-site Coulomb interaction parameters of U–J for Fe-3d has been employed in the range of 2–6 eV for BiFeO3 [34,45,46,47]. The bandgap value is enlarged when U–J is increased, while the essential feature, such as Ps, and the valence-band electronic structure remain unchanged. One main reason why we adopted U–J = 6 eV is as follows: the bandgap becomes narrow for a specific Bi–La arrangement on the A site and eventually vanishes when the arrangement of Bi and La is an ordered configuration along the polar c axis, as will be described later. In order to maintain the bandgap above ca. 2 eV, we set U–J to 6 eV for Fe-3d throughout the calculations.
Considering the spin configuration in BiFeO3 can be approximated as the G-type antiferromagnet [46], we set the spin arrangement in which the adjacent Fe ions have an antiparallel spin configuration as much as possible irrespective of the La content (x) on the A site.
We employed three symmetries shown in Figure 1 and compared their total energies (see Figure 2): ferroelectric rhombohedral R3c, ferroelectric tetragonal P4mm, and nonpolar orthorhombic Pnma. The antiparallel spin configuration of adjacent Fe ions enforces a change in space group from R3c to R3 (or P3) for the rhombohedral cells, from Pnma to P21/m for the orthorhombic ones, while the tetragonal P4mm remains unchanged, the details of which are summarized in Tables S1–S3. Although the orthorhombic cells were optimized in monoclinic P21/m symmetry, we restricted the monoclinic angle of β to 90.0 degree, and then the crystal system is regarded as orthorhombic.
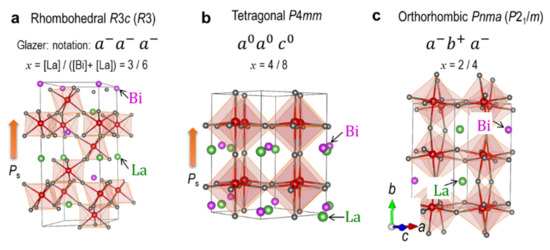
Figure 1.
Optimized crystal structures in (a) rhombohedral, (b) tetragonal, and (c) orthorhombic symmetries of the Bi1−xLaxFeO3 cells with x = 1/2. The tetragonal cells with x = 0, ½, and 1 do not have octahedral tilt, while those with x = 1/8, 2/8, 3/8, 5/8, and 7/8 have their distinct tilt modes. We adopt a rock-salt structure in an arrangement of Bi and La on the A site as much as possible, the details of which are displayed in Figures S1 and S2. The symmetry in parenthesis denotes the space group taking account of the antiferromagnetic spin configuration.
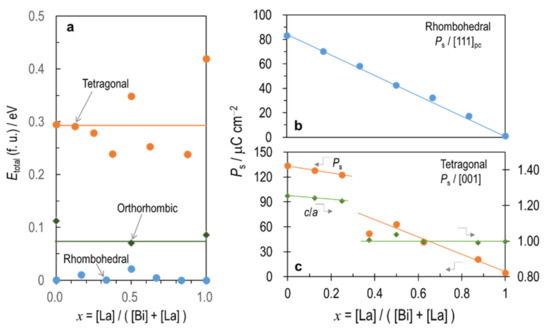
Figure 2.
Phase stability and Ps: (a) total energy (Etotal) of the ABO3 formula unit (f. u.); (b) Ps in the rhombohedral system; and (c) Ps and c/a in the tetragonal system as a function of La content (x). For comparing Etotal in different symmetries, we set the energies obtained by fitting the DFT energies of the rhombohedral cells by a quadratic function to zero.
Because our calculations were performed in the anti-ferromagnetic spin configuration, the total DOS is identical both in the majority and minority spin bands. In a similar manner, the band structure in the majority spin band is the same with that in the minority spin band. We display the DOS in the majority spin band in the right panel and that in the minority spin band in the left one, e.g., see Figure 3c. For simplicity, we show the band structure only in the majority spin band. As for wavefunctions (partial charge densities), we visualize the majority spin component at an iso-surface level of 1 × 10−4, e.g., see Figure 4. The Fermi energy is set to zero throughout our manuscript.
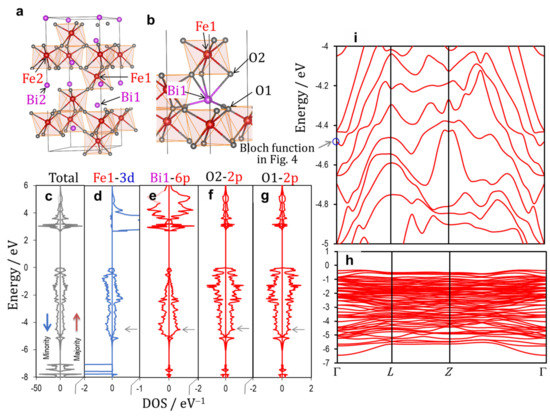
Figure 3.
Crystal structures (a,b), electronic density of states (DOS) (c–g), and band structures (of the majority spin band) in the valence band (h,i) of the rhombohedral BiFeO3 (x = 0). The wavefunction of the band shown in blue circle in (i) is displayed in Figure 4. The up (red) and down (blue) arrows in (c) denote the majority and minority spin bands, respectively. The horizontal arrows (gray) in (c–g) correspond to the energy level of the blue circle in (i).
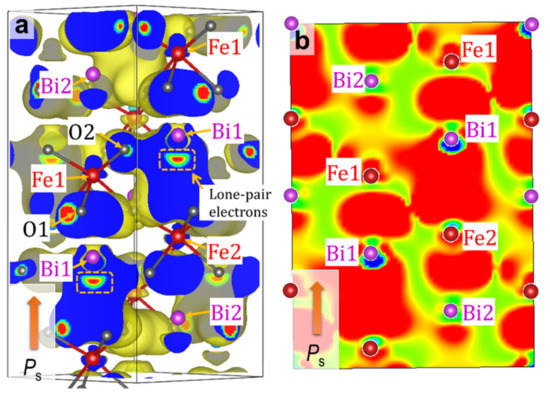
Figure 4.
Wavefunction (partial charge density) of the ↑ band shown in the blue circle in (i) of the rhombohedral BiFeO3 (x = 0): (a) 3D plot and (b) 2D visualization on the lattice plane including Bi1 and Fe1. This wavefunction arising from an indirect Bi1_6p–Fe1_3d hybridization mediated through O_2p is termed ‘Bloch function’. The roles of O1 and O2 in this band are almost identical, and therefore, we do not distinguish them.
For building a BiFeO3–LaFeO3 solid solution cell, there exists several choices of the arrangement of Bi and La. We adopted the rock-salt arrangement of Bi and La, especially along the polar c axis, as much as possible, as can be seen in Figures S1 and S2. This is because the electronic structure in the rhombohedral cell with a layered Bi and La ordering along the polar c axis has a non-realistic metallic feature (Figure S10), which is not consistent with the experimental fact of an insulating nature of BiFeO3–LaFeO3 solid solutions [47,48]. We therefore avoid such a Bi–La ordering along the specific crystallographic axis and adopt the rock-salt-like orderings of Bi and La. The details of the structure parameters are listed in Tables S4–S10 for the rhombohedral cells, Tables S11–S18 for the tetragonal cells, and Tables S19–S21 for the orthorhombic cells.
From the structure parameters of the optimized cell (Tables S4–S18), we obtained the atomic displacements (∆z) from the corresponding positions in the hypothetical non-polar paraelectric lattice. We also calculated the Born effective charges (Z*) [49] by density-functional perturbation theory. We estimated spontaneous polarization (Ps) using the following equation
where denotes the site multiplicity of the constituent atom i and its dipole moment. The summation in Equation (1) is taken over the cell with cell volume (V).
3. Results and Discussion
3.1. Ground-State Structures
Figure 2a shows the total energy (Etotal) per the ABO3 formula unit as a function of the La content (x) expressed by x = [La]/([Bi] + [La]). For comparing Etotal in different symmetries, x should be the same. Indeed, x has a discrete value depending on the total number of the A-site atoms, i.e., six in the rhombohedral cells, eight in the tetragonal ones, and four in the orthorhombic ones (Tables S1–S3). We, therefore, set the energies obtained by fitting the DFT energies of the rhombohedral cells by a quadratic function to zero of Etotal. The Etotal of the rhombohedral cells are lower than those of the tetragonal and orthorhombic cells irrespective of x. These results are different from those reported in the literature [31,50,51]. The orthorhombic cells are slightly higher in Etotal by ~0.1 eV while the tetragonal cells have a higher Etotal by ~0.3 eV. In reality, the tetragonal BiFeO3 is stabilized under a compressive strain in epitaxial films [26].
Figure 2b shows the Ps of the rhombohedral cells as a function of x. The Ps of the rhombohedral BiFeO3 is 83.2 μC/cm2, which is in good agreement with the previous DFT calculations [26,31,52] and experiments [53]. With increasing x, the rhombohedral Ps exhibits a monotonic decrease, which is consistent with other calculations [31]. The tetragonal BiFeO3 (Figure 2c) possesses a giant Ps of 133.4 μC/cm2, which is close to the values obtained for epitaxially strained films and from DFT calculations [26]. Zhang et al. [26] have reported that this large Ps is associated with a high tetragonality c/a of 1.24 and also with a coherent displacement of Fe (∆Fe’) by 0.033 nm with respect to the Bi sublattice. These values accord with our calculations of c/a = 1.25 and ∆Fe’ = 0.032. The Ps and c/a decrease with increasing x followed by discontinuous drops at 2/8 < x < 3/8. At x = 3/8, the c/a is almost in unity whereas the apparent Ps of 52.0 μC/cm2 exists. With a further increase in x, the Ps again shows a monotonic decrease while the c/a remains constant (ca. ~1.0).
3.2. Electronic Structures
3.2.1. Ferroelectric Rhombohedral System
Figure 3 shows (a,b) the crystal structures of the rhombohedral BiFeO3 (x = 0) along with (c–g) the total and partial DOS results and (h,i) the electronic band structures in the valence band. The wavefunction of the band shown in the blue circle in i is depicted in Figure 4. The off-center displacements of Fe and Bi are stabilized by the following two orbital hybridizations, respectively: Fe_3d–O_2p (Figure 5a) and Bi_6p–O_2p (Figure 5b). Because Fe atoms have either a positive (↑) or a negative (↓) magnetic moment, the majority spin (↑) and minority spin (↓) bands have to be taken into account in a distinct manner. Here, we consider the orbital interaction in the ↑ band that leads to DOS components in the valence band in the range of −7 to 0 eV (in the right panel in Figure 3c–g). Although O1 and O2 have a slightly different magnetic moment, the DOS characters are almost identical both in the ↑ and ↓ bands. When the magnetic moments are ignored, O1 and O2 have the same site symmetry, and therefore, we do not distinguish O1 and O2. Due to the same reason, we regard Bi1 and Bi2 as identical Bi atoms.
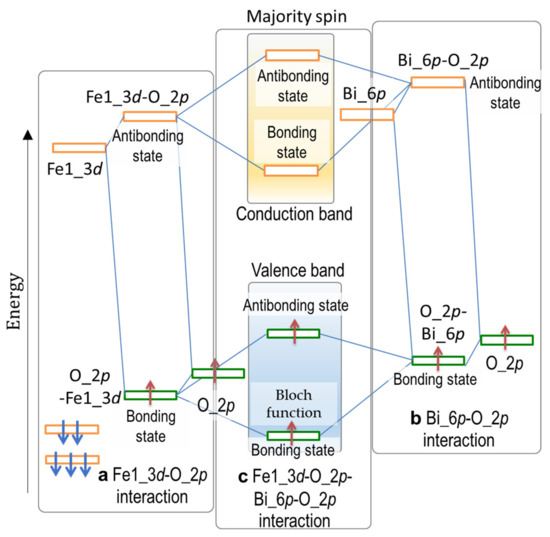
Figure 5.
Orbital interactions delivering the Bloch function of the majoring spin (↑) band shown in Figure 4 of the rhombohedral BiFeO3 (x = 0): (a) Fe1_3d–O_2p mixing leading to a bonding state in the valence band and an antibonding state in the conduction band; (b) Bi_6p–O_2p mixing resulting in a low-lying bonding state and a high-lying antibonding state; and (c) hybridization between Fe1_3d–O_2p and Bi_6p–O_2p leading to the Bloch function at a deep level in the valence band.
The simple ionic model considering the electron configuration of 6s2 6p0 for Bi3+ leads to zero DOS of Bi_6p in the valence band, because the states of the isolated Bi_6p are unoccupied. The Bi_6p–O_2p interaction (Figure 5b) results in a low-lying bonding state and a high-lying antibonding state. The low-lying states are occupied by electrons and thereby the Bi_6p states have apparent DOS components in the valence band (Figure 3e).
Next, we consider the Fe_3d–O_2p interaction leading to the DOS component in the ↑ band. The Fe1 atom with a negative magnetic moment has the electron configuration of 3d with ↓5↑0. These five ↓ electrons of Fe1 are present at deep levels in the ↓ band [54]. We focus our attention on the interaction between the empty Fe1_3d (↑) and the occupied O_2p states (Figure 5a). The hybridization of these orbitals delivers an occupied bonding state and an empty antibonding state. Therefore, Fe1 has not only the major DOS in the band but also the minor DOS in the ↑ band, as displayed in Figure 3d.
The bands in the range of −7 to −5 eV (Figure 3h) are derived primarily from the bonding states of Fe2_3d (↑)–O_2p. The Bi_6p–O_2p interaction yields a low-lying bonding state at around −4.5 eV at the Γ point (marked with a blue circle in Figure 3i), whose wavefunction is visualized in Figure 4. The distinct Fe1_3d–O_2p and Bi_6p–O_2p interactions are seen in the respective local regions of Fe1O6 octahedra and BiO polyhedrons. We note that the interaction between the bonding states of Fe1_3d–O_2p and Bi_6p–O_2p (Figure 5c) forms a coherent wavefunction that is spread throughout the crystal (Figure 4). Namely, the interaction between the Fe1_3d–O_2p- and the Bi_6p–O_2p-derived bonding states yields the low-lying bonding state, termed Bloch function, arising from the –Fe1–O–Bi–O– network (Figure 4). It results also in the high-lying antibonding state in the valence band, as shown in Figure 5c. We conclude that the Bloch function stemming from the indirect Bi_6p–Fe_3d hybridization mediated through O_2p is the primary origin of Ps in the rhombohedral system.
Figure S3 shows (a) the crystal structure of the rhombohedral cell (x = 2/6) along with (b–f) the total and partial DOS results and (g,h) the electronic band structures in the valence band. The wavefunction of the band shown in the blue circle in h is depicted in i. The orbital interactions displayed in Figure 4 are seen also in this cell. The Bloch function arising from the Fe_3d–O_2p–Bi_6p hybridization appears at −4.5 eV (at the Γ point), while its connection along the c axis is relatively weak compared with that in the BiFeO3 cell. The similar electronic feature was found for the rhombohedral cell (x = 4/6) in Figure S4. It is interesting to note that the Bloch function is formed through the Bi–O–Fe bond avoiding La.
3.2.2. Ferroelectric Tetragonal System
The large Ps of the tetragonal BiFeO3 is derived from the cooperative off-center displacements of Bi and Fe along the polar c axis with respect to the oxygen sublattice (Figure S5 for the BiFeO3 cell). This off-center feature is maintained in the tetragonal cell with x = 2/8. Figure S6 shows (a) the crystal structure of the tetragonal cell (x = 2/8) along with (b–f) the total and partial DOS results and (g, h) the electronic band structures in the valence band. The wavefunction of the band shown in the blue circle in h is depicted in i. The Bloch function where a Bi_6p–O2_p interaction plays a central role (Figure S6i) is present at ca. −4.2 eV at the Γ point and spreads also along the c axis through the Bi_6pz orbital. Note that the Fe-3d state indeed does not participate in the Bloch function, which is in contrast to the rhombohedral system (Figure 4, Figures S3 and S4). Additionally, in the BiFeO3 cell (Figure S5), the similar Bloch function with a small contribution of Fe-3d appears.
Figure 6 shows (a) the crystal structure of the tetragonal cell (x = 3/8) along with (b–f) the total and partial DOS results and (g,h) the electronic band structures in the valence band. The wavefunction of the band shown in the blue circle in h is depicted in (i). The Bi_6p–O2_p hybridization results in a bonding state at ca. −4.6 eV at the Γ point. The Bloch function has a robust connection in the a–a plane whereas that is markedly weakened along the polar c axis. The discontinuous drops in Ps and c/a at 2/8 < x < 3/8 stems from the in-plane feature of the Bloch function formed by the Bi_6p–O2_p hybridization.
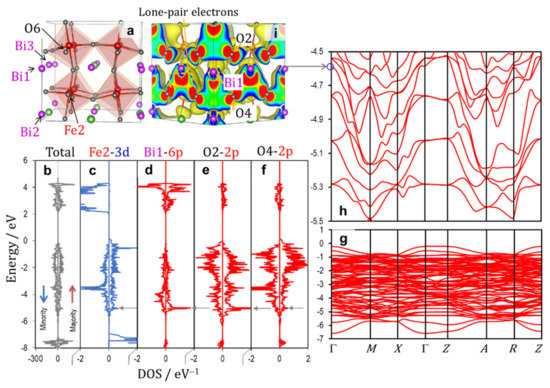
Figure 6.
Crystal structure (a), electronic density of states (DOS) (b–f), band structures (of the majority spin band) in the valence band (g,h), and i wavefunction of the band shown in the blue circle of the tetragonal cell (x = 3/8). The up (red) and down (blue) arrows in (b) denote the majority and minority spin bands, respectively. The horizontal arrows (gray) in (c–g) correspond to the energy level of the blue circle in (h).
3.2.3. Paraelectric Orthorhombic System
We think that the variations of Ps and c/a can be qualitatively understood from a decrease in the number of the Bi pillar along the c axis. Figure S7 shows the arrangement of Bi and La in the tetragonal cells at (a) x = 2/8 and (b) x = 3/8. The tetragonal BiFeO3 (x = 0) has a large Ps, which is ascribed to the full set of the Bi pillars. The substitution of La on the A site decreases the number of the Bi pillar and two Bi pillars are maintained until x ≤ 2/8. These Bi pillars contribute to the formation of the Bloch function spreading along the c axis through the Bi_6pz orbital. With increasing x above 3/8, the number of the pillar becomes only one, and thereby the Bloch function has an in-plane feature, which is accompanied by a marked decrease in Ps.
Figure 7 shows (a) the crystal structure of the orthorhombic cell (x = 1/2) along with (b–e) the total and partial DOS results and (f,g) the electronic band structures in the valence band. The wavefunction of the band shown in the blue circle (g) is depicted in (h). The magnetic moment of Fe1 is negative, and then the orbital interaction shown in Figure 6a is expected for Fe1 and the adjacent oxygen atoms. The Fe1_3d states have a marked DOS component in the ↑ band, which stems from the orbital hybridization of Fe1_3d (↑)–O3_2p. An apparent DOS of Bi1_6p arising from the mixing with O3_2p appears in the valence band. The wavefunction of the band at the Γ point (Figure 7h) clearly shows that the Bloch function originating from a coherent interaction between the bonding states of Fe1_3d (↑)–O3_2p and Bi1_6p–O3_2p spreads throughout the crystal. Moreover, this Bloch function is present at −5.4 eV, which is lower by 0.9 eV than that of the rhombohedral cell (x = 2/6) (Figure 3).
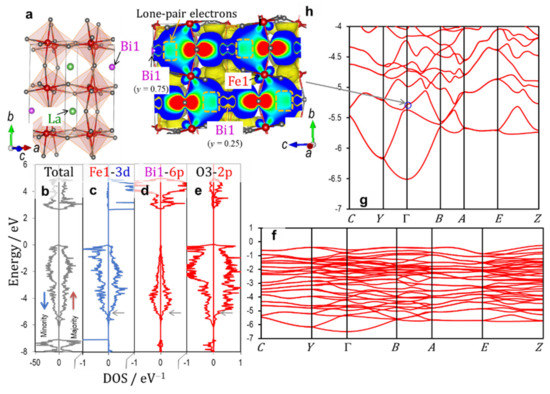
Figure 7.
Crystal structure (a), electronic density of states (DOS) (b–e), band structures (of the majority spin band) in the valence band (f,g), and (h) wavefunction of the band shown in the blue circle of the orthorhombic cell (x = 1/2). The up (red) and down (blue) arrows in (c) denote the majority and minority spin bands, respectively. The horizontal arrows (gray) in (c–e) correspond to the energy level of the blue circle in (g).
3.3. Factors Affecting Ferroelectricity
As described above, the Bloch function arising from the indirect Bi_6p–Fe_3d hybridization via O_2p is the origin of Ps in the rhombohedral system. The hybridized orbital is accompanied by the formation of the covalent bonds not only in the direction of Ps but also in the opposite direction of Ps, e.g., see Figure 4. The Bloch function is closely related to the bond lengths of Bi–Fe (see Tables S1–S3); this is the first (structural) factor leading to a robust Ps.
In the rhombohedral system (Figure S9a), the first shortest Bi–Fe bond is parallel to Ps, while the second shortest Bi–Fe bond is almost normal to Ps. For the tetragonal system (Figure S9b), the first and second shortest Bi–Fe bonds are aligned along pseudo-cubic <111> direction. In the rhombohedral cells at x ≤ 4/6, the first shortest Bi–Fe length is ~0.31 nm, and the second shortest one is ~0.33 nm. In the tetragonal cells, the first shortest Bi–Fe length is ~0.33 nm, which is comparable to that in the rhombohedral one. We note that the second shortest length is as long as ~0.37 nm even at x = 0 (BiFeO3). This long Bi–Fe length does not allow the Fe_3d orbital to participate in the Bi_6p–O_2p hybridization, and thereby, the Bloch function is indeed formed by the Bi_6p–O_2p interaction in the tetragonal system, as shown in Figure 6.
In the paraelectric orthorhombic cells at x ≤ 1/2, the first and second shortest Bi–Fe lengths are ~ 0.32 nm and ~ 0.33 nm, respectively, which are comparable to those in the rhombohedral cells. Actually, the Bloch function resulting from the Fe_3d–O_2p–Bi_6p mixture is extended throughout the crystal at x = 1/2 (see Figure 7). The most significant difference between the ferroelectric and paraelectric cells appears in an accommodation mode of stereo-active lone pair electrons of Bi [26,55,56] (derived from the mixture of Bi_6s–6p), which is the second factor that dominates the presence or absence of Ps. For the ferroelectrics in the rhombohedral (Figure 4a) and tetragonal systems (Figure 6i), the lone pair electrons of Bi are directed coherently along the c axis, which is the detrimental factor of ferroelectricity. The alignment of the lone pair electrons contributes to an enhancement of off-center displacements of cations, as in ferroelectric PbTiO3 [57]. For the orthorhombic cell (Figure 7h), the lone pair electrons of Bi1 (y = 0.75) are directed opposite to those of Bi1 (y = 0.25) along the c axis (which is the symmetry constraint). This staggered accommodation of the lone pair electrons of Bi exclusively provides paraelectricity.
The Bi–Fe bond lengths and the resultant Bloch functions can be qualitatively understood by the tilt and rotation of FeO6 octahedra expressed by the Glazer notation [58]. The ferroelectric rhombohedral cells have an out-of-phase octahedral tilt expressed by , which are accompanied by the short Bi–Fe bonds along with relatively large unit-cell densities of 8.595 g cm−3 at x = 0 and 7.779 g cm−3 at x = 0.5. In contrast, the ferroelectric tetragonal cells do not have any tilt or rotation of FeO6 octahedra at x = 0 and 0.5, leading to the long (second shortest) Bi–Fe lengths and low densities of 8.027 g cm−3 at x = 0 and 7.669 g cm−3 at x = 0.5. The paraelectric orthorhombic cells have a tilt system of , resulting in the short Bi–Fe lengths and high densities of 8.836 g cm−3 at x = 0 and 7.807 g cm−3 at x = 0.5.
4. Conclusions
We have investigated the origin of ferroelectricity of Bi1−xLaxFeO3 in rhombohedral R3c and tetragonal P4mm symmetries by DFT calculations. In the rhombohedral system, a Bloch function arising from an indirect Bi_6p–Fe_3d hybridization via O_2p is the primary origin of Ps. In contrast, the Ps of the tetragonal phase stems from a Bloch function arising from a Bi_6p–O_2p mixing with a weak contribution of Fe-3d. The detrimental factor of the presence/absence of Ps is an accommodation of stereo-active lone pair electrons of Bi. The paraelectric orthorhombic Pnma phase has a staggered accommodation of lone pair electrons of Bi, while the ferroelectric R3c and P4mm systems exhibit a coherent alignment of lone pair electrons of Bi. The rhombohedral system shows a monotonic decrease in Ps with increasing x, which is directly associated with a weakening of the Fe_3d–O_2p–Bi_6p hybridization. In contrast, the tetragonal system displays a discontinuous drop of Ps at ca. x = 0.3, which is ascribed to a transition from a 3D extension to an in-plane feature of the Bi_6p–O_2p mixed orbital.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/nano12234163/s1, Figure S1: Bi and La arrangement on the A site in the rhombohedral system with Bi1−xLaxFeO3; Figure S2: Bi and La arrangement on the A site in the tetragonal system with Bi1−xLaxFeO3; Figure S3: Crystal structures (a), electronic density of states (DOS) (b–f), and band structures (of the majority spin band) in the valence band (g,h) of the rhombohedral cell with x = 2/6. The wavefunction of the band shown in the blue circle in h is displayed in i; Figure S4: Crystal structures (a), electronic density of states (DOS) (b–f), and band structures (of the majority spin band) in the valence band (g,h) of the rhombohedral cell with x = 4/6. The wavefunction of the band shown in the blue circle in h is displayed in i; Figure S5: Crystal structures (a), electronic density of states (DOS) (b–f), and band structures (of the majority spin band) in the valence band (g,h) of the tetragonal BiFeO3 cell with x = 0. The wavefunction of the band shown in the blue circle in h is displayed in j; Figure S6: Crystal structures (a), electronic density of states (DOS) (b–f), and band structures (of the majority spin band) in the valence band (g,h) of the tetragonal cell with x = 2/8. The wavefunction of the band shown in the blue circle in (h) is displayed in i; Figure S7: Bi and La arrangement along with Bi pillars along the polar c axis of the tetragonal cells with a x = 2/8 and b 3/8; Figure S8: Bi and La arrangement along with Bi pillars along the polar c axis of the rhombohedral cells at a x = 2/6 and b 4/6; Figure S9: Bi–Fe bond lengths of BiFeO3 in a rhombohedral and (b) tetragonal symmetries; Figure S10: Crystal structures in the (a) hexagonal and (b) primitive settings, electronic density of states (DOS) (c–f) and band structure (of the majority spin band) in the valence band (g) of the rhombohedral (x = 1/2) with an ordered Bi–La arrangement along the polar c axis. Table S1: Empirical formula, space group, numbers of Bi and La, and bond lengths of Bi–Fe in the unit cells of the rhombohedral cells; Table S2: Empirical formula, space group, numbers of Bi and La, and bond lengths of Bi–Fe in the unit cells of the tetragonal cells; Table S3: Empirical formula, space group, numbers of Bi and La, and bond lengths of Bi–Fe in the unit cells of the orthorhombic cells; Table S4: Structural parameters of the rhombohedral BiFeO3 cell (space group R3) with an antiferromagnetic spin configuration; Table S5: Structural parameters of the rhombohedral (Bi5La)Fe6O18 cell (space group P3) with an antiferromagnetic spin configuration; Table S6: Structural parameters of the rhombohedral (Bi2La)Fe3O9 cell (space group P3) with an antiferromagnetic spin configuration; Table S7: Structural parameters of the rhombohedral (BiLa)Fe2O6 cell (space group R3) with an antiferromagnetic spin configurations; Table S8: Structural parameters of the rhombohedral (BiLa2)Fe3O9 cell (space group P3) with an antiferromagnetic spin configuration; Table S9: Structural parameters of the rhombohedral (BiLa5)Fe6O18 cell (space group P3) with an antiferromagnetic spin configuration; Table S10: Structural parameters of the rhombohedral LaFeO3 cell (space group R3) with an antiferromagnetic spin configuration; Table S11: Structural parameters of the tetragonal BiFeO3 cell (space group P4mm) with an antiferromagnetic spin configuration; Table S12: Structural parameters of the tetragonal (Bi7La)Fe8O24 cell (space group P4mm) with an antiferromagnetic spin configuration; Table S13: Structural parameters of the tetragonal (Bi3La)Fe4O12 cell (space group P4mm) with an antiferromagnetic spin configuration; Table S14: Structural parameters of the tetragonal (Bi5La3)Fe8O24 cell (space group P4mm) with an antiferromagnetic spin configuration; Table S15: Structural parameters of the tetragonal (BiLa)Fe2O6 cell (space group P4mm) with an antiferromagnetic spin configuration; Table S16: Structural parameters of the tetragonal (Bi3La5)Fe8O24 cell (space group P4mm) with an antiferromagnetic spin configuration; Table S17: Structural parameters of the tetragonal (BiLa7)Fe8O24 cell (space group P4mm) with an antiferromagnetic spin configuration; Table S18: Structural parameters of the tetragonal LaFeO3 cell (space group P4mm) with an antiferromagnetic spin configuration; Table S19: Structural parameters of the orthorhombic BiFeO3 cell (space group P21/m) with an antiferromagnetic spin configuration; Table S20: Structural parameters of the orthorhombic (BiLa)Fe2O6 cell (space group P21/m) with an antiferromagnetic spin configuration; Table S21: Structural parameters of the orthorhombic LaFeO3 cell (space group P21/m) with an antiferromagnetic spin configuration.
Author Contributions
Y.N. and H.M. conceived and initiated the project. Y.N. carried out theoretical calculations and wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by JSPS through Grant-in-Aid for JSPS Fellows (26-4693). This research is partly supported by JSPS KAKENHI Grant Numbers 26249094 and 17H06239.
Data Availability Statement
The data that support the findings of this study are available upon reasonable request from the corresponding author.
Acknowledgments
We thank H. Maki for the preliminary work of thin-film deposition and experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bhide, V.G.; Deshmukh, K.G.; Hegde, M.S. Ferroelectric Properties of PbTiO3. Physica 1962, 28, 871–876. [Google Scholar] [CrossRef]
- Sawaguchi, E. Ferroelectricity versus Antiferroelectricity in the Solid Solutions of PbZrO3 and PbTiO3. J. Phys. Soc. Japan 1953, 8, 615–629. [Google Scholar] [CrossRef]
- Jaffe, B.; Roth, R.S.; Marzullo, S. Piezoelectric Properties of Lead Zirconate-Lead Titanate Solid-Solution Ceramics. J. Appl. Phys. 1954, 25, 809. [Google Scholar] [CrossRef]
- Noheda, B.; Gonzalo, J.; Cross, L.; Guo, R.; Park, S. Tetragonal-to-Monoclinic Phase Transition in a Ferroelectric Perovskite: The Structure of PbZr0.52Ti0.48O3. Phys. Rev. B 2000, 61, 8687–8695. [Google Scholar] [CrossRef]
- Kweon, S.-H.; Tani, K.; Kanda, K.; Nahm, S.; Kanno, I. Piezoelectric PZT Thin-Film Transformers with a Ring–Dot Structure. Jpn. J. Appl. Phys. 2020, 59, SPPD09. [Google Scholar] [CrossRef]
- Genenko, Y.A.; Glaum, J.; Hoffmann, M.J.; Albe, K. Mechanisms of Aging and Fatigue in Ferroelectrics. Mater. Sci. Eng. B Solid-State Mater. Adv. Technol. 2015, 192, 52–82. [Google Scholar] [CrossRef]
- Yamashita, T.; Takeshita, T.; Oouchi, A.; Kobayashi, T. Ultra-Thin PZT/Si Chip Integrated on Paper Substrates. Jpn. J. Appl. Phys. 2021, 60, SFFB12. [Google Scholar] [CrossRef]
- Fu, H.; Cohen, R.E. Polarization Rotation Mechanism for Ultrahigh Electromechanical Response in Single-Crystal Piezoelectrics. Nature 2000, 403, 281–283. [Google Scholar] [CrossRef]
- Damjanovic, D. A Morphotropic Phase Boundary System Based on Polarization Rotation and Polarization Extension. Appl. Phys. Lett. 2010, 97, 2010–2013. [Google Scholar] [CrossRef]
- Kutnjak, Z.; Petzelt, J.; Blinc, R. The Giant Electromechanical Response in Ferroelectric Relaxors as a Critical Phenomenon. Nature 2006, 441, 956–959. [Google Scholar] [CrossRef]
- Heitmann, A.A.; Rossetti, G.A. Thermodynamics of Ferroelectric Solid Solutions with Morphotropic Phase Boundaries. J. Am. Ceram. Soc. 2014, 97, 1661–1685. [Google Scholar] [CrossRef]
- Park, S.-E.; Shrout, T.R. Ultrahigh Strain and Piezoelectric Behavior in Relaxor Based Ferroelectric Single Crystals. J. Appl. Phys. 1997, 82, 1804. [Google Scholar] [CrossRef]
- Sun, E.; Cao, W. Relaxor-Based Ferroelectric Single Crystals: Growth, Domain Engineering, Characterization and Applications. Prog. Mater. Sci. 2014, 65, 124–210. [Google Scholar] [CrossRef]
- Luo, C.; Karaki, T.; Sun, Y.; Yamashita, Y.J.; Xu, J. Effect of Field Cooling AC Poling on Electrical and Physical Properties for Pb(Mg 1/3 Nb 2/3 )O3 -PbTiO3 -Based Single Crystals Manufactured by a Continuous-Feeding Bridgman Process. Jpn. J. Appl. Phys. 2020, 59, SPPD07. [Google Scholar] [CrossRef]
- Ederer, C.; Spaldin, N.A. Weak Ferromagnetism and Magnetoelectric Coupling in Bismuth Ferrite. Phys. Rev. B 2005, 71, 060401. [Google Scholar] [CrossRef]
- Yang, S.C.; Kumar, A.; Petkov, V.; Priya, S. Room-Temperature Magnetoelectric Coupling in Single-Phase BaTiO3-BiFeO3 System. J. Appl. Phys. 2013, 113, 144101. [Google Scholar] [CrossRef]
- Ramesh, R.; Spaldin, N.A. Multiferroics: Progress and Prospects in Thin Films. Nat. Mater. 2007, 6, 21–29. [Google Scholar] [CrossRef]
- Fiebig, M. Revival of the Magnetoelectric Effect. J. Phys. D. Appl. Phys. 2005, 38, R123. [Google Scholar] [CrossRef]
- Noguchi, Y.; Matsuo, H.; Kitanaka, Y.; Miyayama, M. Ferroelectrics with a Controlled Oxygen-Vacancy Distribution by Design. Sci. Rep. 2019, 9, 4225. [Google Scholar] [CrossRef]
- Kim, S.; Khanal, G.P.; Nam, H.W.; Fujii, I.; Ueno, S.; Moriyoshi, C.; Kuroiwa, Y.; Wada, S. Structural and Electrical Characteristics of Potential Candidate Lead-Free BiFeO3-BaTiO3 Piezoelectric Ceramics. J. Appl. Phys. 2017, 122, 164105. [Google Scholar] [CrossRef]
- Noguchi, Y.; Matsuo, H. Polarization and Dielectric Properties of BiFeO3-BaTiO3 Superlattice-Structured Ferroelectric Films. Nanomaterials 2021, 11, 1857. [Google Scholar] [CrossRef] [PubMed]
- Matsuo, H.; Noguchi, Y.; Miyayama, M.; Kiguchi, T.; Konno, T.J. Enhanced Photovoltaic Effects in Ferroelectric Solid Solution Thin Films with Nanodomains. Appl. Phys. Lett. 2020, 116, 132901. [Google Scholar] [CrossRef]
- Wang, J.; Neaton, J.B.; Zheng, H.; Nagarajan, V.; Ogale, S.B.; Liu, B.; Viehland, D.; Vaithyanathan, V.; Schlom, D.G.; Waghmare, U.V.; et al. Epitaxial BiFeO3 Multiferroic Thin Film Heterostructures. Science 2003, 299, 1719–1722. [Google Scholar] [CrossRef]
- Michel, C.; Moreau, J.M.; Achenbach, G.D.; Gerson, R.; James, W.J. The Atomic Structure of BiFeO3. Solid State Commun. 1969, 7, 701–704. [Google Scholar] [CrossRef]
- Kubel, F.; Schmid, H. Structure of a Ferroelectric and Ferroelastic Monodomain Crystal of the Perovskite BiFeO3. Acta Crystallogr. Sect. B Struct. Sci. 1990, 46, 698–702. [Google Scholar] [CrossRef]
- Zhang, J.X.; He, Q.; Trassin, M.; Luo, W.; Yi, D.; Rossell, M.D.; Yu, P.; You, L.; Wang, C.H.; Kuo, C.Y.; et al. Microscopic Origin of the Giant Ferroelectric Polarization in Tetragonal-like BiFeO3. Phys. Rev. Lett. 2011, 107, 147602. [Google Scholar] [CrossRef]
- Arnold, D. Composition-Driven Structural Phase Transitions in Rare-Earth-Doped Bifeo3 Ceramics: A Review. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 62–82. [Google Scholar] [CrossRef]
- Karimi, S.; Reaney, I.M.; Han, Y.; Pokorny, J.; Sterianou, I. Crystal Chemistry and Domain Structure of Rare-Earth Doped BiFeO3 Ceramics. J. Mater. Sci. 2009, 44, 5102–5112. [Google Scholar] [CrossRef]
- Karpinsky, D.V.; Troyanchuk, I.O.; Tovar, M.; Sikolenko, V.; Efimov, V.; Kholkin, A.L. Evolution of Crystal Structure and Ferroic Properties of La-Doped BiFeO3 Ceramics near the Rhombohedral-Orthorhombic Phase Boundary. J. Alloys Compd. 2013, 555, 101–107. [Google Scholar] [CrossRef]
- Lee, J.-H.; Choi, H.J.; Lee, D.; Kim, M.G.; Bark, C.W.; Ryu, S.; Oak, M.-A.; Jang, H.M. Variations of ferroelectric off-centering distortion and 3 d− 4 p orbital mixing in La-doped BiFeO3 multiferroics. Phys. Rev. B 2010, 82, 045113. [Google Scholar] [CrossRef]
- González-Vázquez, O.E.; Wojdeł, J.C.; Diéguez, O.; Íñiguez, J. First-principles investigation of the structural phases and enhanced response properties of the BiFeO3-LaFeO3 multiferroic solid solution. Phys. Rev. B 2012, 85, 064119. [Google Scholar] [CrossRef]
- Mazumdar, D.; Knut, R.; Thöle, F.; Gorgoi, M.; Faleev, S.; Mryasov, O.N.; Shelke, V.; Ederer, C.; Spaldin, N.A.; Gupta, A.; et al. The Valence Band Electronic Structure of Rhombohedral-like and Tetragonal-like BiFeO3 Thin Films from Hard X-Ray Photoelectron Spectroscopy and First-Principles Theory. J. Electron Spectros. Relat. Phenom. 2016, 208, 63–66. [Google Scholar] [CrossRef]
- Chang, W.S.; Tu, C.-S.; Chen, P.-Y.; Chen, C.-S.; Lin, C.-Y.; Feng, K.-C.; Hsieh, Y.L.; Huang, Y.H. Effects of Fe3d–O2p and Bi 6sp–O2p Orbital Hybridizations in Nd Doped BiFeO3 Ceramics. J. Alloys Compd. 2017, 710, 670–679. [Google Scholar] [CrossRef]
- Tan, Q.; Wang, Q.; Liu, Y. Magnetic Properties and Spontaneous Polarization of La-, Mn- and N-Doped Tetragonal BiFeO3: A First-Principles Study. Materials 2018, 11, 985. [Google Scholar] [CrossRef]
- Mumtaz, F.; Nasir, S.; Jaffari, G.H.; Shah, S.I. Chemical Pressure Exerted by Rare Earth Substitution in BiFeO3: Effect on Crystal Symmetry, Band Structure and Magnetism. J. Alloys Compd. 2021, 876, 160178. [Google Scholar] [CrossRef]
- Kiyanagi, R.; Yamazaki, T.; Sakamoto, Y.; Kimura, H.; Noda, Y.; Ohyama, K.; Torii, S.; Yonemura, M.; Zhang, J.; Kamiyama, T. Structural and Magnetic Phase Determination of (1-x)BiFeO3–xBaTiO3 Solid Solution. J. Phys. Soc. Jpn. 2012, 81, 024603. [Google Scholar] [CrossRef]
- Leontsev, S.O.; Eitel, R.E. Dielectric and Piezoelectric Properties in Mn-Modified (1−x)BiFeO3-xBaTiO3 Ceramics. J. Am. Ceram. Soc. 2009, 92, 2957–2961. [Google Scholar] [CrossRef]
- Rusakov, D.A.; Abakumov, A.M.; Yamaura, K.; Belik, A.A.; Van Tendeloo, G.; Takayama-Muromachi, E. Structural Evolution of the BiFeO3−LaFeO3 System. Chem. Mater. 2011, 23, 285–292. [Google Scholar] [CrossRef]
- Troyanchuk, I.O.; Bushinsky, M.V.; Karpinsky, D.V.; Mantytskaya, O.S.; Fedotova, V.V.; Prochnenko, O.I. Structural Transformations and Magnetic Properties of Bi1-xLnxFeO3 (Ln = La, Nd, Eu) Multiferroics. Phys. Status Solidi 2009, 246, 1901–1907. [Google Scholar] [CrossRef]
- You, L.; Zheng, F.; Fang, L.; Zhou, Y.; Tan, L.Z.; Zhang, Z.; Ma, G.; Schmidt, D.; Rusydi, A.; Wang, L.; et al. Enhancing Ferroelectric Photovoltaic Effect by Polar Order Engineering. Sci. Adv. 2018, 4, eaat3438. [Google Scholar] [CrossRef]
- Langreth, D.C.; Perdew, J.P. Theory of Nonuniform Electronic Systems. I. Analysis of the Gradient Approximation and a Generalization That Works. Phys. Rev. B 1980, 21, 5469–5493. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal–Amorphous-Semiconductor Transition in Germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band Theory and Mott Insulators: Hubbard U Instead of Stoner I. Phys. Rev. B 1991, 44, 943–954. [Google Scholar] [CrossRef]
- Neaton, J.B.; Ederer, C.; Waghmare, U.V.; Spaldin, N.A.; Rabe, K.M. First-Principles Study of Spontaneous Polarization in Multiferroic BiFeO3. Phys. Rev. B 2005, 71, 014113. [Google Scholar] [CrossRef]
- Singh, S.K.; Ishiwara, H. Doping Effect of Rare-Earth Ions on Electrical Properties of BiFeO3 Thin Films Fabricated by Chemical Solution Deposition. Jpn. J. Appl. Phys. 2006, 45, 3194–3197. [Google Scholar] [CrossRef]
- Jangid, S.; Barbar, S.K.; Bala, I.; Roy, M. Structural, Thermal, Electrical and Magnetic Properties of Pure and 50% La Doped BiFeO3 Ceramics. Phys. B Condens. Matter 2012, 407, 3694–3699. [Google Scholar] [CrossRef]
- Gonze, X.; Lee, C. Dynamical Matrices, Born Effective Charges, Dielectric Permittivity Tensors, and Interatomic Force Constants from Density-Functional Perturbation Theory. Phys. Rev. B 1997, 55, 10355–10368. [Google Scholar] [CrossRef]
- Antonov, V.; Georgieva, I.; Trendafilova, N.; Kovacheva, D.; Krezhov, K. First Principles Study of Structure and Properties of La- and Mn-Modified BiFeO3. Solid State Sci. 2012, 14, 782–788. [Google Scholar] [CrossRef]
- Lee, J.-H.; Oak, M.-A.; Choi, H.J.; Son, J.Y.; Jang, H.M. Rhombohedral–Orthorhombic Morphotropic Phase Boundary in BiFeO3-Based Multiferroics: First-Principles Prediction. J. Mater. Chem. 2012, 22, 1667–1672. [Google Scholar] [CrossRef]
- Matsuo, H.; Kitanaka, Y.; Inoue, R.; Noguchi, Y.; Miyayama, M. Heavy Mn-Doping Effect on Spontaneous Polarization in Ferroelectric BiFeO3 Thin Films. Jpn. J. Appl. Phys. 2015, 54, 10NA03. [Google Scholar] [CrossRef]
- Yoneda, Y.; Kitanaka, Y.; Noguchi, Y.; Miyayama, M. Electronic and Local Structures of Mn-Doped BiFeO3 Crystals. Phys. Rev. B 2012, 86, 184112. [Google Scholar] [CrossRef]
- Matsuo, H.; Noguchi, Y.; Miyayama, M. Gap-State Engineering of Visible-Light-Active Ferroelectrics for Photovoltaic Applications. Nat. Commun. 2017, 8, 207. [Google Scholar] [CrossRef]
- Noguchi, Y.; Matsuo, H. Ferroelectric Polarization of Tetragonal BiFeO3—An Approach from DFT Calculations for BiFeO3–BaTiO3 Superlattices. Jpn. J. Appl. Phys. 2022, 61, SN1002. [Google Scholar] [CrossRef]
- Ravindran, P.; Vidya, R.; Kjekshus, A.; Fjellvåg, H.; Eriksson, O. Theoretical Investigation of Magnetoelectric Behavior in BiFe O3. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 74, 224412. [Google Scholar] [CrossRef]
- Cohen, R.E. Origin of Ferroelectricity in Perovskite Oxides. Nature 1992, 358, 136–138. [Google Scholar] [CrossRef]
- Glazer, A.M. The Classification of Tilted Octahedra in Perovskites. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1972, 28, 3384–3392. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).