Abstract
The use of hybrid nanoparticles to increase heat transfer is a favorable area of research, and therefore, numerous scientists, researchers, and scholars have expressed their appreciation for and interest in this field. Determining the dynamic role of nanofluids in the cooling of microscopic electronic gadgets, such as microchips and related devices, is also one of the fundamental tasks. With such interesting and useful applications of hybrid nanofluids in mind, the main objective is to deal with the analysis of the unsteady flow towards a shrinking sheet in a water-based hybrid ferrite nanoparticle in porous media, with heat sink/source effects. Moreover, the impact of these parameters on heat and mass transfers is also reported. Numerical results are obtained using MATLAB software. Non-unique solutions are determined for a certain shrinking strength, in addition to the unsteadiness parameter. The mass transfer and friction factor increase for the first solution due to the hybrid nanoparticles, but the heat transfer rate shows the opposite effect.
1. Introduction
Heat transfer through heat exchangers in multi-phase flow applications is among the most important processes in industry. Despite the built-in and well-developed models that have been applied since the 1970s, much attention has been focused on the experimental works, due to the needs and strong desires from industry. In recent years, considerable efforts have been expended toward improving the phenomenon of heat transport, one of which is to improve the thermal conductivity. Earlier researchers, such as Choi and Eastman [1], conducted a study of nanofluids and their capabilities regarding heat transmission. Saidur et al. [2] presented the new properties of fluids that enable the achievement of incredible advances in a variety of applications in industry, including hybrid motors, domestic refrigerators, microelectronics, and coolers. Motsumi and Makinde [3] investigated the radiative flow over a moving porous plate using nanofluid. Sheikholeslami [4] investigated the heat transmission of a nanofluid from a cylinder using a steady suction and explained the escalating function of the Nusselt number in conjunction with the percentage of nanoparticles. The heat transmission in a nanofluid passed over a porous shrinkable/stretchable sheet with the magnetic field was analyzed by Naramgari and Sulochana [5], which indicated that the drag force and heat transport phenomenon is bounded by the magnetic field. Other research regarding nanofluids can be found in recent articles [6,7,8,9,10].
Recently, researchers have paid particular attention to hybrid nanofluids, and many reports have suggested that hybrid nanofluids may improve the heat transfer rate and reduce production costs compared to the use of ordinary nanofluids, benefits that can lead to efficient outputs [11]. Hybrid nanofluids are formed by mixing two or more types of nanometer-sized particles in the base fluids. The preparation of hybrid nanofluids, as well as the discussion on their thermal properties, was conducted by Sundar et al. [12]. Devi and Devi [13] examined the heat transfer enrichment induced by stretchable sheets of dispersed water-based alumina and copper hybrid nanoparticles. Yousefi et al. [14] explored the copper-titania nanoparticles flowing towards a stagnation region of a wavy cylinder. Waini et al. [15] investigated the time-varying flow and heat transfer over shrinkable/stretchable surfaces in hybrid nanofluids. They found non-unique solutions for a particular range of the moving parameter. Sreedevi et al. [16] examined the radiative consequences of time-dependent flow on a stretched sheet induced by a hybrid nanofluid with slip effects. Recently, some researchers [17,18,19,20,21] debated the significance of hybrid nanofluids from different aspects. Valuable references on hybrid nanofluids can be also found in the book by Merkin et al. [22].
The various potential and actual thermal engineering applications of porous media flow in areas such as packed bed reactors, thermal insulation systems, heat storage beds, geothermal engineering, petroleum recovery, groundwater pollution, and ceramic processing frequently motivate interest in such studies. Several investigations have been conducted on the flow with the problems of mass and heat transfer in homogeneous saturated porous media. Abel et al. [23] examined the viscoelastic fluid flow, with heat transport rate, past a non-isothermal stretchable surface subjected to the impacts of the porous medium. Ahmad and Pop [24] studied the mixed convective flow from a smooth plate in a porous medium. Pal and Mondal [25] investigated the Dufour and Soret diffusion effects on a radiative flow induced by a stretchable surface with a chemical reaction in porous media. They scrutinized that the heat uplifts due to the Dufour, as well as the radiation, effect. The impact of suction on a micropolar fluid flow through a stretchable sheet was studied by Rosali et al. [26], and they reported double solutions. Vyas and Srivastava [27] examined the flow over a shrinkable sheet in a porous media with radiative heat transfer and reported double solutions for certain values of suction. The forced convection flow in Darcy–Brinkman porous media was inspected by Pantokratoras [28]. Kumar and Sood [29] examined the magnetic effect on the Darcy—Brinkman—Forchheimer flow over a shrinkable sheet in a porous medium with mixed convection. Hussanan et al. [30] reported an analytic solution for the time-varying magnetohydrodynamic flow of a Casson liquid via a vertical oscillating infinite plate-saturated porous media. Hassan et al. [31] scrutinized the flow of convective and heat transport rate comprising porous media, with water-based nanofluid, past a wavy surface by considering copper oxide nanoparticles. The entropy impact on the buoyancy or mixed convective nanofluid flow induced by micropolar fluid towards a vertical plate comprising a non-Darcy medium was inspected by Zaib et al. [32]. Recently, Khan et al. [33] considered the buoyancy effects on micropolar fluid comprising porous media through a vertical plate containing hybrid nanoparticles and reported double solutions.
The study of mass and heat transmission using hybrid nanofluid has been disclosed to be reasonably important in different engineering processes, such as heating development, biomedical processes, polymer extrusion, and many more. Thus, the present work intends to study the unsteady flow over a stretchable/shrinkable sheet in a saturated porous medium containing ferrite hybrid nanoparticles. Tiwari and Das [34] models are utilized to propose the hybrid nanofluid model. By using a numerical approach, the computed dual solutions of the transformed equations are provided. The behavior of the flow, combined with the characteristics of mass and heat transfers, are inspected for plentiful parameters, which are depicted in graphical and tabular forms.
2. Description and Framework of the Mathematical Model
Consider the time-dependent flow past a shrinking continuously sheet in the presence of a hybrid nanofluid, as shown in Figure 1, where are the Cartesian coordinates, with —axis measured along the surface of the sheet, and the —axis normal to it, the flow being . The stretching velocity is assumed as , where is the time, while and are constants, while the velocity of the mass flux is . Two types of nanoparticles are studied, namely cobalt ferrite (CoFe2O4) and manganese-zinc ferrite (Mn-ZnFe2O4), which are dispersed in the water-based fluid. For the hybrid nanofluid, it is assumed that the size of the nanoparticles is uniform, and the effect of the agglomeration of the nanoparticles is neglected because the nanofluids are synthesized as a stable mixture of the base fluid and the nanoparticles. The governing equations of the conservation of mass, momentum, energy, and concentration by using the usual boundary layer approximations are written as [15,35]:
subject to:
where , represent the velocity components, the temperature, the concentration, the heat sink or source coefficient, and the essential permeability of the porous media. Besides, signifies the stretchable/shrinkable parameter, with indicates the stationary sheet, while and indicate the shrinking and stretching sheet, respectively.
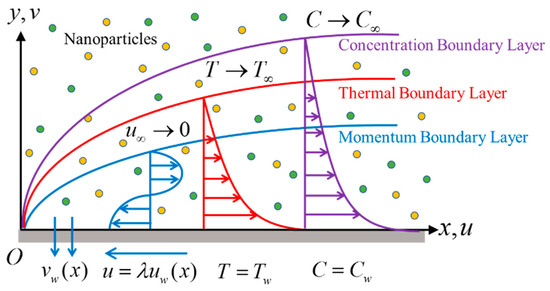
Figure 1.
Physical flow configuration.
Table 1 gives the thermophysical properties of the water, Mn-ZnFe2O4, and CoFe2O4 nanomaterials [36,37]. Meanwhile, the correlations of the hybrid nanofluid are given in Equation (6) as follow [38,39,40]:
where is the heat capacity, signifies the thermal conductivity, represents the fluid density, and μ is the dynamic viscosity. Note that the symbols and denote the volume fraction of nanoparticles CoFe2O4, and Mn-ZnFe2O4, respectively, where . We also note that in Equation (6), the effective thermal conductivity does not consider the interfacial thermal resistance between the nanoparticles and the host fluid (see Ref. [41]).

Table 1.
The thermophysical properties.
The following similarity variables are employed in order to obtain the similarity solutions:
where is a positive constant and is the stream function, which is defined as
which satisfies Equation (1). By setting , the mass flux velocity becomes:
with the fluid kinematic viscosity . The mass flux parameter is denoted by , while signifies the impermeable surface. Moreover, and are for blowing and suction, respectively.
Substitute (7) and (8) into Equations (2)–(4), and the similarity ODEs are acquired as follows:
subject to BCs:
where is the porous medium parameter, is the Schmidt number, is the Prandtl number, is the heat sink or source parameter, and is the unsteady parameter, defined as:
The parameter shows the expansion/contraction strength. For a positive value of , the stretching/shrinking surface becomes smaller with time, e.g., contracting, while for a negative value of the stretching/shrinking surface becomes larger with time, e.g., expanding (see Fang et al. [42]).
The physical quantities of practical interests are:
with representing the shear stress coefficient, the local Nusselt number, and the local Sherwood number. Using (7) and (15), one obtains:
where signifies the local Reynolds number.
3. Time Stability Analysis
The time stability of the dual solutions is evaluated [43,44] by considering the following variables:
where
and is dimensionless time.
Then, by using Equations (17) and (18), one obtains:
subject to BCs:
Then, consider the perturbation function [43]:
where , , and are arbitrary functions and are relatively small compared to , , and , and denotes the eigenvalue. By setting , then , , and . Moreover, after linearization, the eigenvalue problems become
subject to:
Here, to obtain from Equations (24)–(26), in Equation (27) is substituted by , as suggested by Harris et al. [45].
4. Analysis of Results and Discussion
Equations (10)–(13) were numerically solved by utilizing the bvp4c package available in MATLAB software. The detailed description of this method is given in [46]. The solver bvp4c is based on a finite difference method that employs the three-stage Lobatto IIIa formula, with fourth-order accuracy. To achieve the accuracy of the numerical values, the selection of the initial guess and the boundary layer thickness must be precise. Suitable finite values of , namely for the first solution, is within 6–10, while that of the second solution is in the range 20–50. The velocity, temperature, and concentration profile generated by the guess value must satisfy the far field boundary conditions (13) asymptotically. Determining an initial guess for the first solution is not difficult because the solution will converge rapidly, even using poor guesses. However, it is rather difficult to determine a sufficiently good guess for the second solution of Equations (10)–(13). In this case, we use the technique called continuation (Shampine et al. [46]).
Comparison is done for the physical quantity of Kameswaran et al. [47] for different values of when , and , as shown in Table 2. A favorable agreement is found for all parameters considered. Table 3 presents the values of the related quantities, i.e., the mass transfer rate , the heat transport rate , and the friction factor for several values of the involved constraints when (shrinking sheet), , and . The consequence of increasing is to augment the quantities of and , but declines the quantities of . Meanwhile, all these quantities enhance with the increase in and . Greater values of lower the heat transfer rate , but the values of and are not influenced due to the fact that this parameter appears only in the energy equation. The value of decreases when the deceleration flow is stronger; however, the values of and enlarge.

Table 2.
Values of for different values of when , and .

Table 3.
Values of the physical quantities for several choices of constraints when (shrinking sheet), , and .
Figure 2, Figure 3 and Figure 4 present the outcomes of , , and for different choices of for the viscous pure fluid and the CoFe2O4-Mn-ZnFe2O4/water hybrid nanofluid . Note that the magnitude of and are higher, whereas is lower for a hybrid nanofluid. Physically, the fluid velocity reduces by adding nanoparticles into the fluid, which produces a higher velocity gradient. Moreover, this pertains to the concentration profile that leads to the increase in the mass transfer. The energy is dissipating in the form of heat, thus raising the fluid temperature. Due to this matter, the gradient of temperature decreases and thus lowers the heat transmission rate. The bifurcation, or critical values, climb with superior values of with and that contribute to delay the separations of the boundary layer. In contrast, the rates of and lessen for the steady-state flow and become higher when stronger deceleration flow is considered . However, the opposite behavior is seen for . From these figures, it can be concluded that the deceleration flow is one of the factors in managing the mass and heat transfer of a hybrid nanofluid. Additionally, Figure 5, Figure 6 and Figure 7 are provided to show the effect of the unsteadiness parameter on the velocity, temperature, and concentration profiles. Meanwhile, Figure 8 represents the streamlines for the first solution.
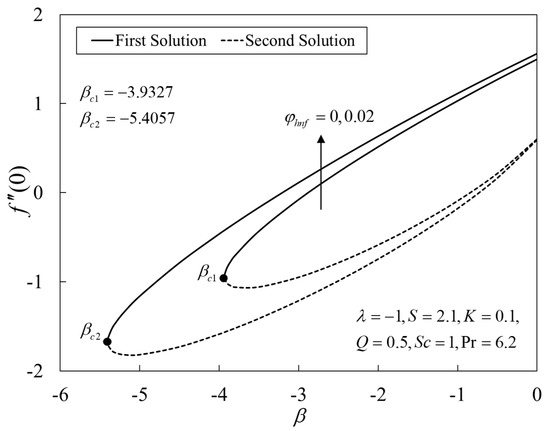
Figure 2.
Plot of against β.
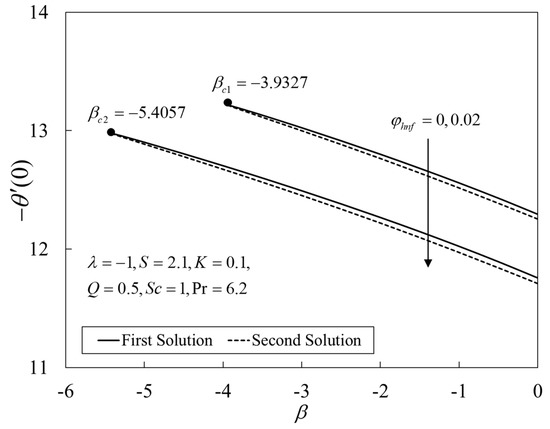
Figure 3.
Plot of against .
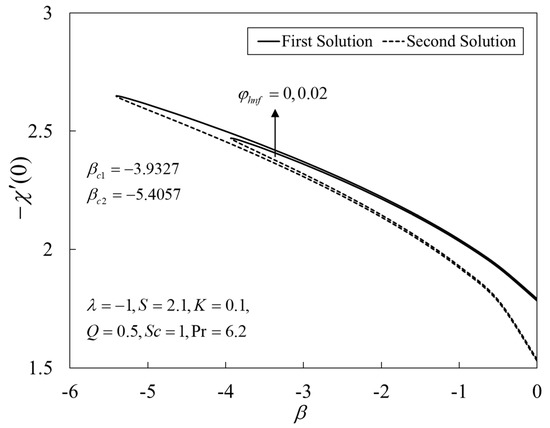
Figure 4.
Plot of against .
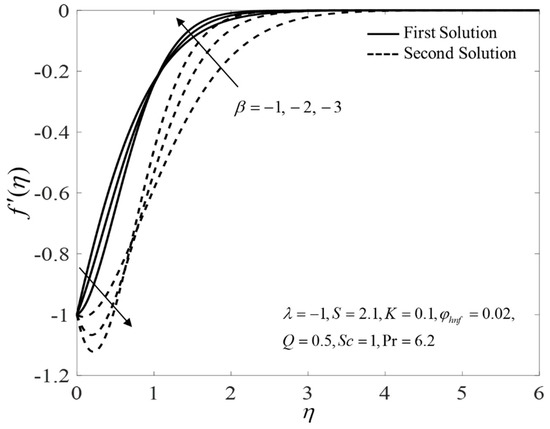
Figure 5.
Plot of for several values of .
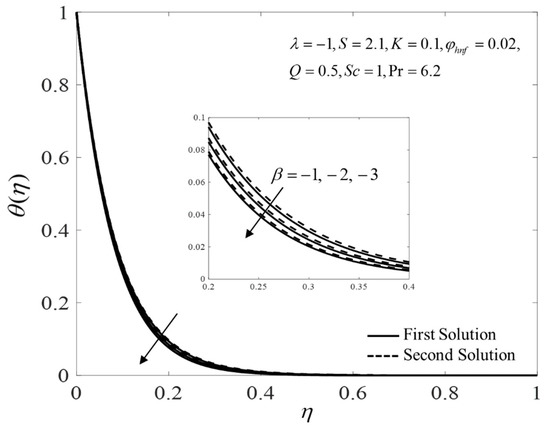
Figure 6.
Plot of for several values of .
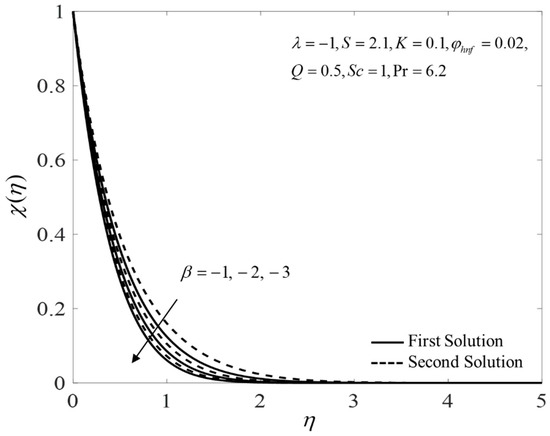
Figure 7.
Plot of for several values of .
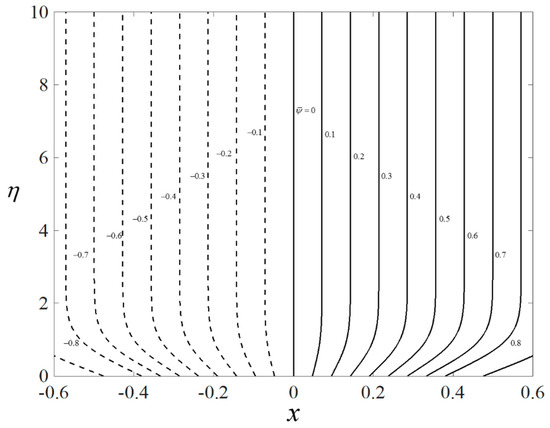
Figure 8.
Plot of streamlines.
Further, Figure 9, Figure 10 and Figure 11 show the deviations of , , and versus for several choices of . The upshot of is to boost the values of the physical amounts, such as the gradients. From the physical explanation, the porous medium amplifies the flow resistance, thus reducing the thickness of the momentum boundary layer by increasing its velocity on the shrinking sheet. Similar behaviors are seen for the temperature and the concentration profiles. This leads to the rise in the heat and mass transfers. Besides, the solutions terminate later for larger , where the critical values are given by , , and .
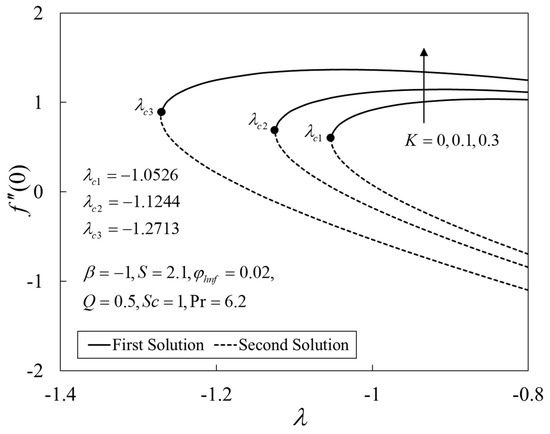
Figure 9.
Plot of against λ.
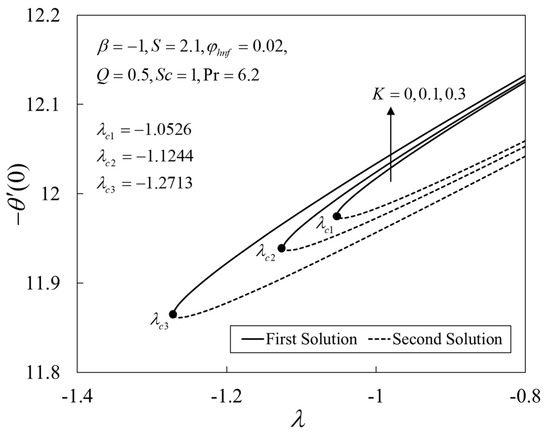
Figure 10.
Plot of against .
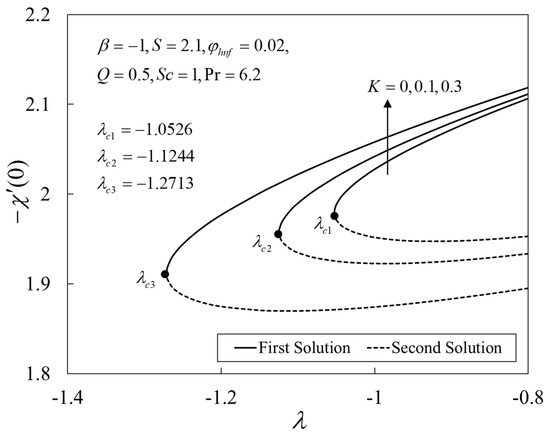
Figure 11.
Plot of against .
The behaviors of the smallest eigenvalues against are displayed in Figure 12, where the first solutions represent positive eigenvalues, while the negative counterparts represent the second solution. Based on Equation (23), the first solution is stable, but the second solution is unstable as time evolves, .
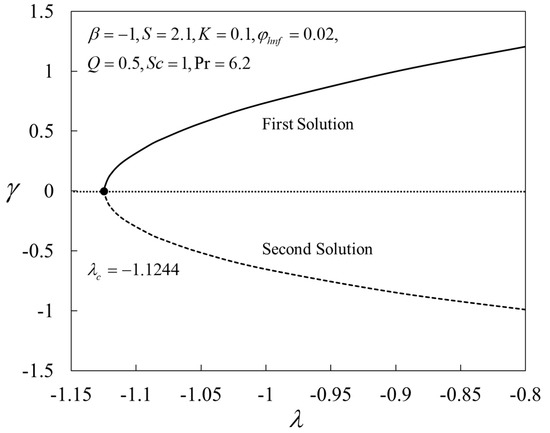
Figure 12.
Plot of against .
This study offers valuable insight into fundamental transport phenomena, such as the transmission of momentum, heat, and mass. Thus, it provides valuable information on the gradients of essential factors to control the boundary layer flow pattern. The results would allow scientists and engineers to become familiar with the flow behavior of nanofluid and the way to predict the properties of this fluid for the possibility of using it in various engineering and industrial processes, such as blood flows, lubrication processes using grease and heavy oils, glass blowing, electronic chips, food stuff, slurries, etc.
5. Conclusions
The current study examined the time-varying flow over a shrinkable sheet with mixed ferrite nanoparticles, where the significant effects of porous media and the heat sinks/sources were taken into consideration. Numerical results for the similar equations were computed using MATLAB software. The key findings are summarized as:
- The mass transfer rate and the friction factor accelerate for the first branch solution, but decelerate for the second branch solution for high values of nanoparticle volume fraction , while the heat transfer rate abruptly diminished in both branch solutions.
- The heat and mass transfer rates, as well as the friction factor, enrich for the first solution for larger values of , while the opposite is seen for the second solution.
- The magnitude of the critical values augments with larger values of and , which ultimately causes the separations in the boundary layer to diminish.
- The first branch solution shows an inertial decay of disturbance, which is thus physically reliable as time passes, whereas the second branch solution shows the opposite response.
Author Contributions
Conceptualization, I.P., I.W. and U.K.; methodology, I.W. and U.K.; software, I.W. and U.K.; validation, A.I., A.Z., N.A., U.K. and I.W.; formal analysis, I.W., A.I., N.A., A.Z., I.P. and U.K.; investigation, I.W., N.A., U.K. and A.I.; resources, I.W.; data curation, I.W. and U.K.; writing—original draft preparation, I.W., A.I., A.Z. and U.K.; writing—review and editing, A.I., I.W., N.A. and I.P.; visualization, I.W. and U.K.; supervision, A.I.; project administration, A.I.; funding acquisition, A.I. All authors have read and agreed to the published version of the manuscript.
Funding
Funding for this project was provided by the Universiti Kebangsaan Malaysia (Project Code: DIP-2020-001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This research was supported by the Universiti Teknikal Malaysia Melaka (Grant No.: JURNAL/2019/FTKMP/Q00042) and Universiti Kebangsaan Malaysia (Project Code: DIP-2020-001). The work of I. Pop was supported by the grant PN-III-P4-PCE-2021-0993, UEFISCDI, Romania. The authors wish to express their thanks to the very competent reviewers for their useful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| constant | |
| C | concentration |
| ambient concentration | |
| surface concentration | |
| skin friction coefficient | |
| specific heat at constant pressure (J kg−1 K−1) | |
| mass diffusivity coefficient | |
| dimensionless stream function | |
| arbitrary functions | |
| permeability of the porous media | |
| porous medium parameter | |
| thermal conductivity of the fluid (W m−1 K−1) | |
| local Nusselt number | |
| Prandtl number | |
| heat sink or source coefficient | |
| heat sink or source parameter | |
| local Reynolds number | |
| mass flux velocity parameter | |
| Schmidt number | |
| local Sherwood number | |
| time (s) | |
| fluid temperature (K) | |
| ambient temperature (K) | |
| surface temperature (K) | |
| velocity component in the x- and y- directions (m s−1) | |
| velocity of the surface (m s−1) | |
| velocity of the mass flux (m s−1) | |
| Cartesian coordinates (m) | |
| Greek symbols | |
| constant | |
| unsteady parameter | |
| dimensionless time variable | |
| eigenvalue | |
| similarity variable | |
| dimensionless temperature | |
| stretching/shrinking parameter | |
| dynamic viscosity (kg m−1 s−1) | |
| kinematic viscosity of the fluid (m2 s−1) | |
| density of the fluid (kg m−3) | |
| nanoparticle volume fractions for CoFe2O4 (cobalt ferrite) | |
| nanoparticle volume fractions for MnZnFe2O4 (manganese-zinc ferrite) | |
| hybrid nanoparticle volume fractions | |
| dimensionless concentration | |
| stream function | |
| Subscripts | |
| base fluid | |
| hybrid nanofluid | |
| solid component for CoFe2O4, (cobalt ferrite) | |
| solid component for MnZnFe2O4 (manganese-zinc ferrite) | |
| Superscript | |
| differentiation with respect to | |
References
- Choi, S.U.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the 1995 International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995. [Google Scholar]
- Saidur, R.; Leong, K.Y.; Mohammed, H.A. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2019, 15, 1646–1668. [Google Scholar] [CrossRef]
- Motsumi, T.G.; Makinde, O.D. Effects of thermal radiation and viscous dissipation on boundary layer flow of nanofluids over a permeable moving flat plate. Phys. Scr. 2012, 86, 045003. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Effect of uniform suction on nanofluid flow and heat transfer over a cylinder. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 1623–1633. [Google Scholar] [CrossRef]
- Naramgari, S.; Sulochana, C. MHD flow over a permeable stretching/shrinking sheet of a nanofluid with suction/injection. Alex. Eng. J. 2016, 55, 819–827. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Effects of thermal radiation, viscous and Joule heating on electrical MHD nanofluid with double stratification. Chin. J. Phys. 2017, 55, 630–651. [Google Scholar] [CrossRef]
- Maleki, H.; Safaei, M.R.; Alrashed, A.A.; Kasaeian, A. Flow and heat transfer in non-Newtonian nanofluids over porous surfaces. J. Therm. Anal. Calorim. 2019, 135, 1656–1666. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Dufour and Soret effects on Al2O3-water nanofluid flow over a moving thin needle: Tiwari and Das model. Int. J. Num. Meth. Heat Fluid Flow 2020, 31, 766–782. [Google Scholar] [CrossRef]
- Shuaib, M.; Ali, A.; Khan, M.A.; Ali, A. Numerical investigation of an unsteady nanofluid flow with magnetic and suction effects to the moving upper plate. Adv. Mech. Eng. 2020, 12, 1687814020903588. [Google Scholar] [CrossRef]
- Ramzan, M.; Khan, N.S.; Kumam, P.; Khan, R. A numerical study of chemical reaction in a nanofluid flow due to rotating disk in the presence of magnetic field. Sci. Rep. 2021, 11, 19399. [Google Scholar] [CrossRef]
- Ghadikolaei, S.S.; Yassari, M.; Sadeghi, H.; Hosseinzadeh, K.; Ganji, D.D. Investigation on thermophysical properties of TiO2–Cu/H2O hybrid nanofluid transport dependent on shape factor in MHD stagnation point flow. Powder Technol. 2017, 322, 428–438. [Google Scholar] [CrossRef]
- Sundar, L.S.; Sharma, K.V.; Singh, M.K.; Sousa, A.C.M. Hybrid nanofluids preparation, thermal properties, heat transfer and friction factor—A review. Renew. Sustain. Energy Rev. 2017, 68, 185–198. [Google Scholar] [CrossRef]
- Devi, S.S.U.; Devi, S.P.A. Heat transfer enhancement of Cu-Al2O3/water hybrid nanofluid flow over a stretching sheet. J. Nigerian Mathem. Soc. 2017, 36, 419–433. [Google Scholar]
- Yousefi, R.M.; Dinarvand, S.; Yazdi, M.E.; Pop, I. Stagnation-point flow of an aqueous titania-copper hybrid nanofluid toward a wavy cylinder. Int. J. Numer. Method Heat Fluid Flow 2018, 28, 1716–1735. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Sreedevi, P.; Reddy, P.S.; Chamkha, A. Heat and mass transfer analysis of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation. SN Appl. Sci. 2020, 2, 1222. [Google Scholar] [CrossRef]
- Khan, U.; Ishak, A.; Zaib, A. Hybrid nanofluid flow containing single-wall and multi-wall CNTs induced by a slender stretchable sheet. Chin. J. Phys. 2021, 74, 350–364. [Google Scholar] [CrossRef]
- Wakif, A.; Chamkha, A.; Thumma, T.; Animasaun, I.L.; Sehaqui, R. Thermal radiation and surface roughness effects on the thermo-magneto-hydrodynamic stability of alumina–copper oxide hybrid nanofluids utilizing the generalized Buongiorno’s nanofluid model. J. Therm. Anal. Calorim. 2021, 143, 1201–1220. [Google Scholar] [CrossRef]
- Jyothi, A.M.; Naveen Kumar, R.; Punith Gowda, R.J.; Veeranna, Y.; Prasannakumara, B.C. Impact of activation energy and gyrotactic microorganisms on flow of Casson hybrid nanofluid over a rotating moving disk. Heat Transf. 2021, 50, 5380–5399. [Google Scholar] [CrossRef]
- Elnaqeeb, T.; Animasaun, I.L.; Shah, N.A. Ternary-hybrid nanofluids: Significance of suction and dual-stretching on three-dimensional flow of water conveying nanoparticles with various shapes and densities. Z. Naturforsch. A 2021, 76, 231–243. [Google Scholar] [CrossRef]
- Mabood, F.; Yusuf, T.A.; Khan, W.A. Cu–Al2O3–H2O hybrid nanofluid flow with melting heat transfer, irreversibility analysis and nonlinear thermal radiation. J. Therm. Anal. Calorim. 2021, 143, 973–984. [Google Scholar] [CrossRef]
- Merkin, J.H.; Pop, I.; Lok, Y.Y.; Grosan, T. Similarity Solutions for the Boundary Layer Flow and Heat Transfer of Viscous Fluids, Nanofluids, Porous Media, and Micropolar Fluids; Elsevier: Oxford, UK, 2021. [Google Scholar]
- Abel, M.S.; Khan, S.K.; Prasad, K.V. Study of visco-elastic fluid flow and heat transfer over a stretching sheet with variable viscosity. Int. J. Non-Linear Mech. 2002, 37, 81–88. [Google Scholar] [CrossRef]
- Ahmad, S.; Pop, I. Mixed convection boundary layer flow from a vertical flat plate embedded in a porous medium filled with nanofluids. Int. Commun. Heat Mass Transf. 2010, 37, 987–991. [Google Scholar] [CrossRef]
- Pal, D.; Mondal, H. Influence of chemical reaction and thermal radiation on mixed convection heat and mass transfer over a stretching sheet in Darcian porous medium with Soret and Dufour effects. Energy Convers. Manag. 2012, 62, 102–108. [Google Scholar] [CrossRef]
- Rosali, H.; Ishak, A.; Pop, I. Micropolar fluid flow towards a stretching/shrinking sheet in a porous medium with suction. Int. Commun. Heat Mass Transf. 2012, 39, 826–829. [Google Scholar] [CrossRef]
- Vyas, P.; Srivastava, N. Radiative boundary layer in porous medium due to exponentially shrinking permeable sheet. Int. Sch. Res. Not. 2012, 2012, 214362. [Google Scholar] [CrossRef]
- Pantokratoras, A. Forced convection in a Darcy–Brinkman porous medium with a convective thermal boundary condition. J. Porous Media 2015, 18, 873–878. [Google Scholar] [CrossRef]
- Kumar, R.; Sood, S. Effect of quadratic density variation on mixed convection stagnation point heat transfer and MHD fluid flow in porous medium towards a permeable shrinking sheet. J. Porous Media 2016, 19, 1083–1097. [Google Scholar] [CrossRef]
- Hussanan, A.; Salleh, M.Z.; Khan, I.; Tahar, R.M. Heat transfer in magnetohydrodynamic flow of a casson fluid with porous medium and Newtonian heating. J. Nanofluids 2017, 6, 784–793. [Google Scholar] [CrossRef]
- Hassan, M.; Marin, M.; Alsharif, A.; Ellahi, R. Convective heat transfer flow of nanofluid in a porous medium over wavy surface. Phys. Lett. A 2018, 382, 2749–2753. [Google Scholar] [CrossRef]
- Zaib, A.; Haq, R.U.; Sheikholeslami, M.; Chamkha, A.J.; Rashidi, M.M. Impact of non-Darcy medium on mixed convective flow towards a plate containing micropolar water-based TiO2 nanomaterial with entropy generation. J. Porous Media 2020, 23, 11–26. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Bakar, S.A.; Roy, N.C.; Ishak, A. Buoyancy effect on the stagnation point flow of a hybrid nanofluid toward a vertical plate in a saturated porous medium. Case Stud. Therm. Eng. 2021, 27, 101342. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Kameswaran, P.K.; Makukula, Z.G.; Sibanda, P.; Motsa, S.S.; Murthy, P.V.S.N. A new algorithm for internal heat generation in nanofluid flow due to a stretching sheet in a porous medium. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 1020–1043. [Google Scholar] [CrossRef]
- Haq, R.U.; Noor, N.F.M.; Khan, Z.H. Numerical simulation of water based magnetite nanoparticles between two parallel disks. Adv. Powder Technol. 2016, 27, 1568–1575. [Google Scholar] [CrossRef]
- Ahmed, N.; Tassaddiq, A.; Alabdan, R.; Adnan; Khan, U.; Noor, S.; Mohyud-Din, S.T.; Khan, I. Applications of nanofluids for the thermal enhancement in radiative and dissipative flow over a wedge. Appl. Sci. 2019, 9, 1976. [Google Scholar] [CrossRef]
- Takabi, B.; Salehi, S. Augmentation of the heat transfer performance of a sinusoidal corrugated enclosure by employing hybrid nanofluid. Adv. Mech. Eng. 2014, 6, 147059. [Google Scholar] [CrossRef]
- Hussain, S.; Ahmed, S.E.; Akbar, T. Entropy generation analysis in MHD mixed convection of hybrid nanofluid in an open cavity with a horizontal channel containing an adiabatic obstacle. Int. J. Heat Mass Transf. 2017, 114, 1054–1066. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Radiative and magnetohydrodynamic micropolar hybrid nanofluid flow over a shrinking sheet with Joule heating and viscous dissipation effects. Neural Comput. Appl. 2022, 34, 3783–3794. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, X.; Hao, Q. A mini review on thermally conductive polymers and polymer-based composites. Compos. Commun. 2021, 24, 100617. [Google Scholar] [CrossRef]
- Fang, T.; Zhang, J.; Zhong, Y. Note on unsteady viscous flow on the outside of an expanding or contracting cylinder. Commun. Nonlinear Sci. Numer. Simulat. 2012, 12, 3124–3128. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Shampine, L.F.; Gladwell, I.; Thompson, S. Solving ODEs with MATLAB; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Kameswaran, P.K.; Shaw, S.; Sibanda, P.; Murthy, P.V.S.N. Homogeneous-heterogeneous reactions in a nanofluid flow due to a porous stretching sheet. Int. J. Heat Mass Transf. 2013, 57, 465–472. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).