Optical Ultracompact Directional Antennas Based on a Dimer Nanorod Structure
Abstract
:1. Introduction
2. Materials and Methods
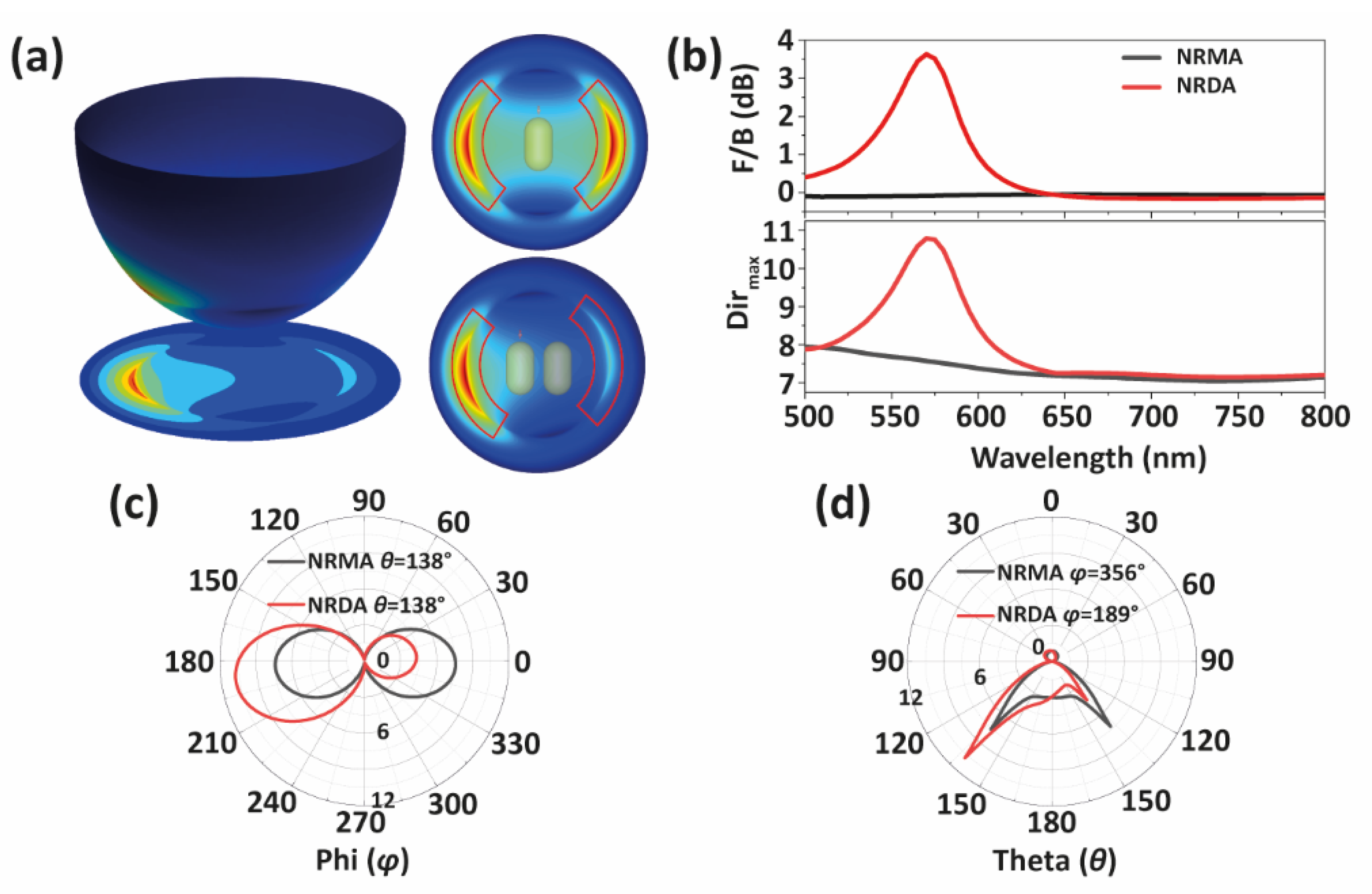
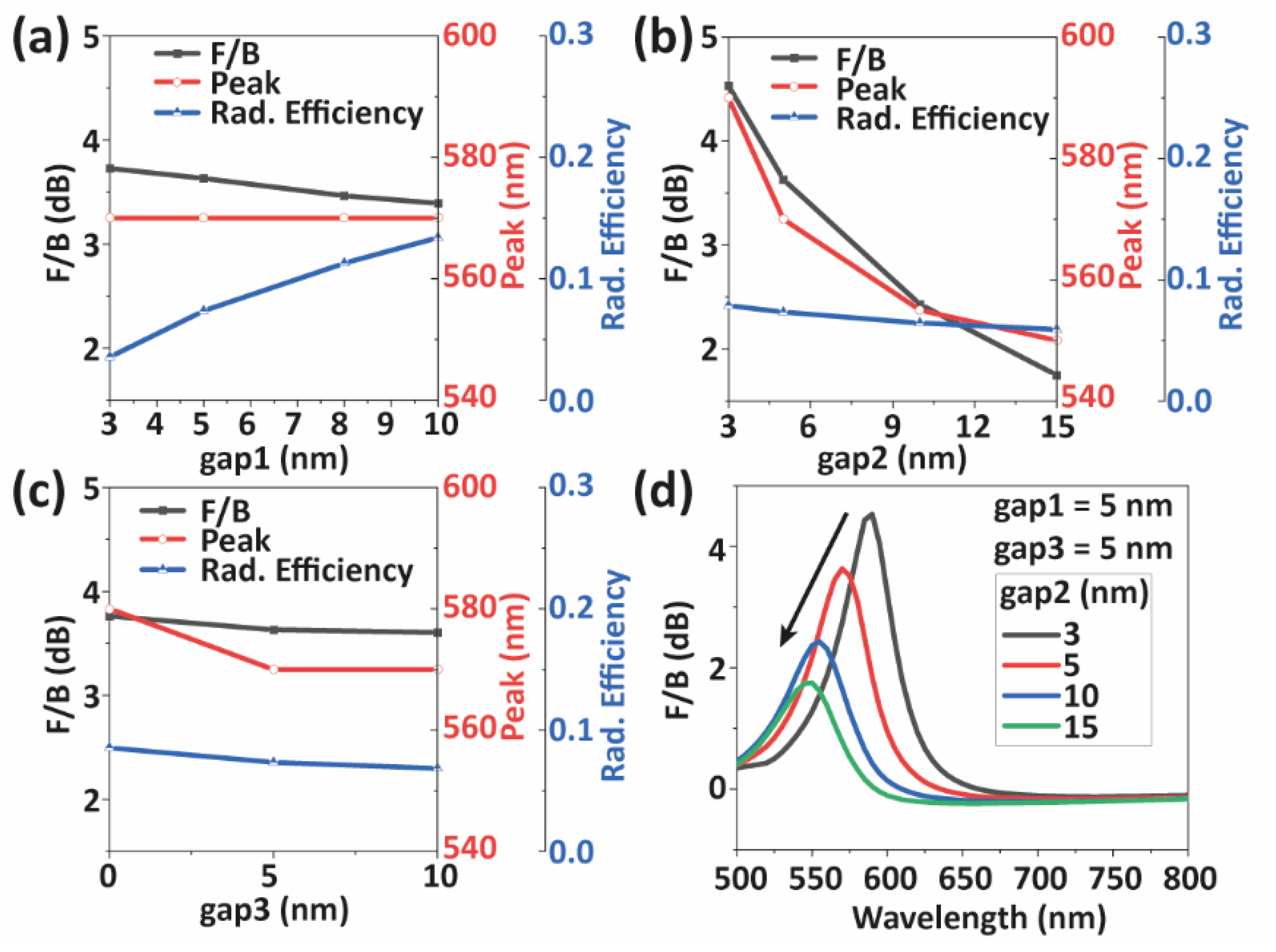
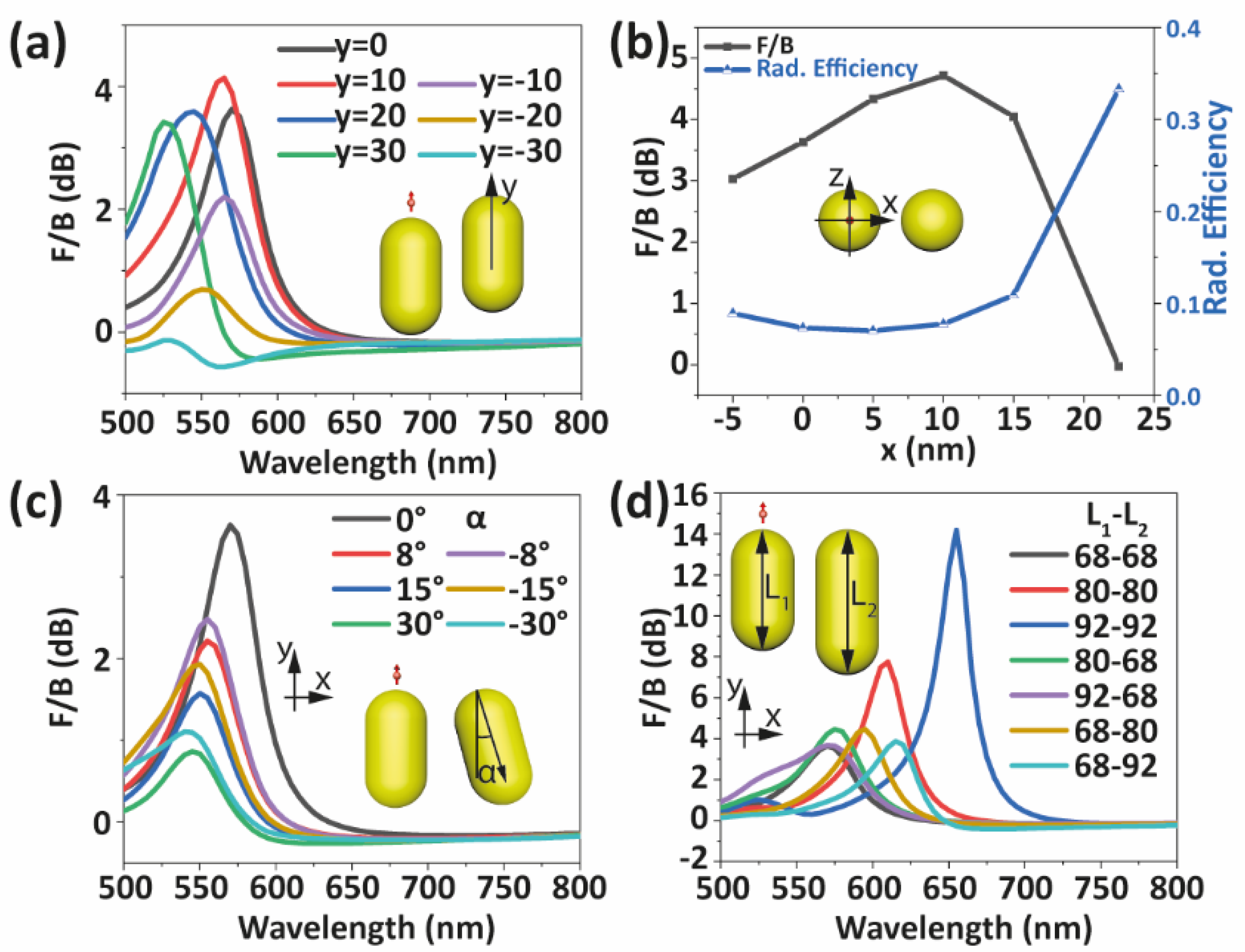
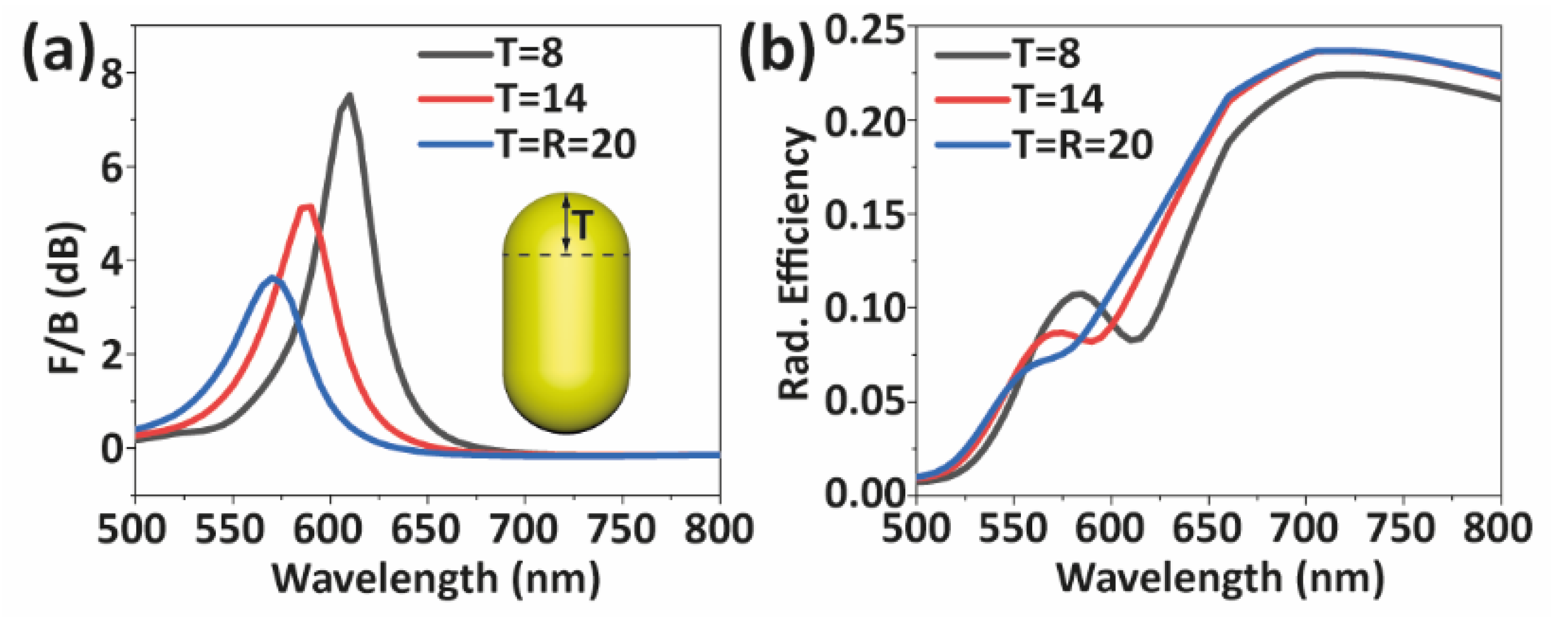
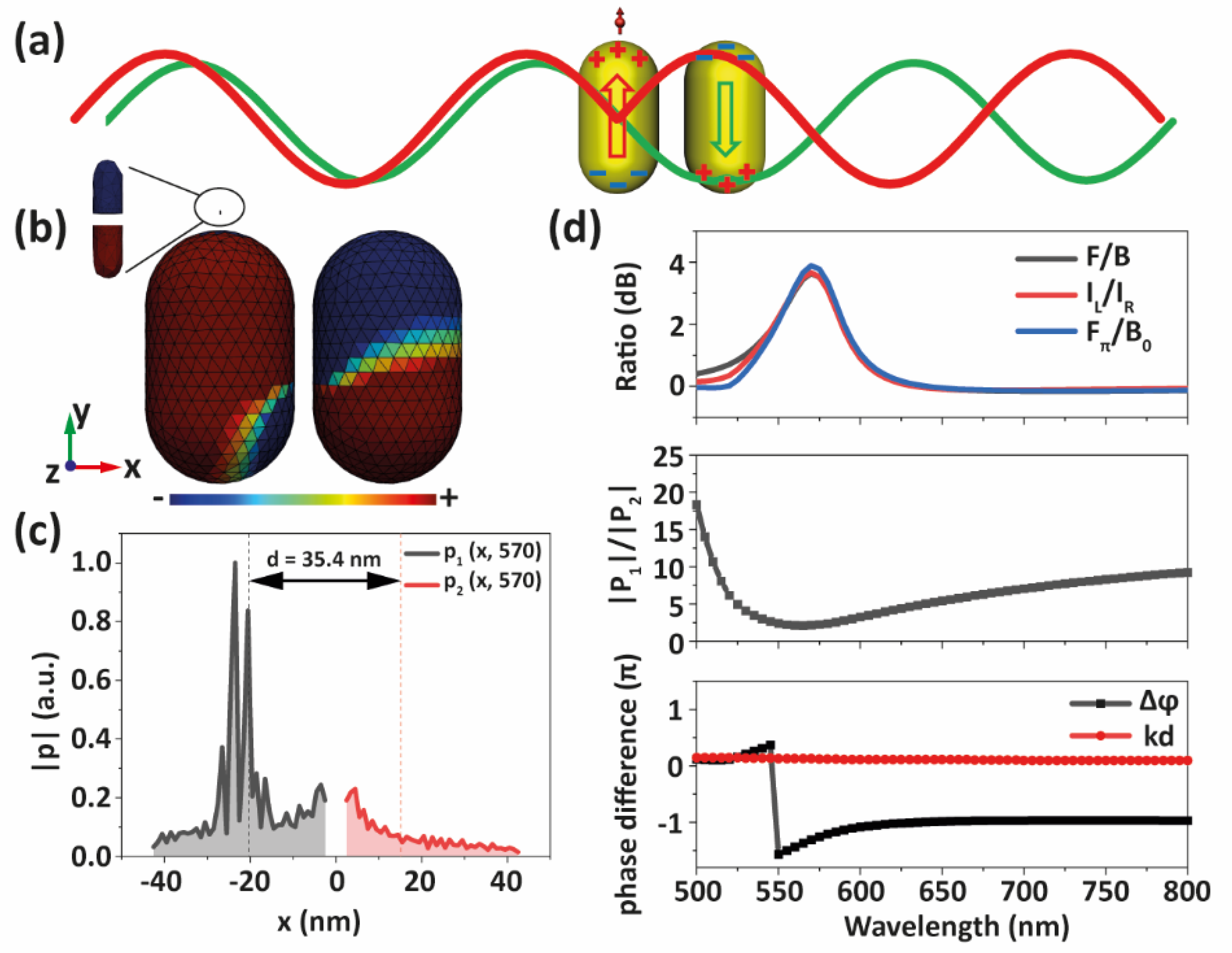
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koenderink, A.F. Single-Photon Nanoantennas. ACS Photonics 2017, 4, 710–722. [Google Scholar] [CrossRef]
- Kullock, R.; Ochs, M.; Grimm, P.; Emmerling, M.; Hecht, B. Electrically-driven Yagi-Uda antennas for light. Nat. Commun. 2020, 11, 115. [Google Scholar] [CrossRef]
- Filter, R.; Slowik, K.; Straubel, J.; Lederer, F.; Rockstuhl, C. Nanoantennas for ultrabright single photon sources. Opt. Lett. 2014, 39, 1246–1249. [Google Scholar] [CrossRef]
- Singh, A.; de Roque, P.M.; Calbris, G.; Hugall, J.T.; van Hulst, N.F. Nanoscale Mapping and Control of Antenna-Coupling Strength for Bright Single Photon Sources. Nano Lett. 2018, 18, 2538–2544. [Google Scholar] [CrossRef]
- Lee, K.G.; Chen, X.W.; Eghlidi, H.; Kukura, P.; Lettow, R.; Renn, A.; Sandoghdar, V.; Götzinger, S. A planar dielectric antenna for directional single-photon emission and near-unity collection efficiency. Nat. Photonics 2011, 5, 166–169. [Google Scholar] [CrossRef]
- Novotny, L.; van Hulst, N. Antennas for light. Nat. Photonics 2011, 5, 83–90. [Google Scholar] [CrossRef]
- Sakat, E.; Wojszvzyk, L.; Greffet, J.-J.; Hugonin, J.-P.; Sauvan, C. Enhancing Light Absorption in a Nanovolume with a Nanoantenna: Theory and Figure of Merit. ACS Photonics 2020, 7, 1523–1528. [Google Scholar] [CrossRef]
- Andersen, S.K.H.; Kumar, S.; Bozhevolnyi, S.I. Ultrabright Linearly Polarized Photon Generation from a Nitrogen Vacancy Center in a Nanocube Dimer Antenna. Nano Lett. 2017, 17, 3889–3895. [Google Scholar] [CrossRef]
- Baiyasi, R.; Goldwyn, H.J.; McCarthy, L.A.; West, C.A.; Jebeli, S.A.H.; Masiello, D.J.; Link, S.; Landes, C.F. Coupled-Dipole Modeling and Experimental Characterization of Geometry-Dependent Trochoidal Dichroism in Nanorod Trimers. ACS Photonics 2021, 8, 1159–1168. [Google Scholar] [CrossRef]
- Chen, W.; Roelli, P.; Hu, H.; Verlekar, S.; Amirtharaj, S.P.; Barreda, A.I.; Kippenberg, T.J.; Kovylina, M.; Verhagen, E.; Martinez, A.; et al. Continuous-wave frequency upconversion with a molecular optomechanical nanocavity. Science 2021, 374, 1264–1267. [Google Scholar] [CrossRef]
- Xomalis, A.; Zheng, X.; Chikkaraddy, R.; Koczor-Benda, Z.; Miele, E.; Rosta, E.; Vandenbosch, G.A.E.; Martinez, A.; Baumberg, J.J. Detecting mid-infrared light by molecular frequency upconversion in dual-wavelength nanoantennas. Science 2021, 374, 1268–1271. [Google Scholar] [CrossRef]
- Saemisch, L.; Liebel, M.; van Hulst, N.F. Control of Vibronic Transition Rates by Resonant Single-Molecule-Nanoantenna Coupling. Nano Lett. 2020, 20, 4537–4542. [Google Scholar] [CrossRef]
- Tanaka, Y.Y.; Kimura, T.; Shimura, T. Unidirectional emission of phase-controlled second harmonic generation from a plasmonic nanoantenna. Nanophotonics 2021, 10, 4601–4609. [Google Scholar] [CrossRef]
- Curto, A.G.; Volpe, G.; Taminiau, T.H.; Kreuzer, M.P.; Quidant, R.; van Hulst, N.F. Unidirectional Emission of a Quantum Dot Coupled to a Nanoantenna. Science 2010, 329, 930–933. [Google Scholar] [CrossRef]
- Kosako, T.; Kadoya, Y.; Hofmann, H.F. Directional control of light by a nano-optical Yagi–Uda antenna. Nat. Photonics 2010, 4, 312–315. [Google Scholar] [CrossRef]
- See, K.M.; Lin, F.C.; Chen, T.Y.; Huang, Y.X.; Huang, C.H.; Yesilyurt, A.T.M.; Huang, J.S. Photoluminescence-Driven Broadband Transmitting Directional Optical Nanoantennas. Nano Lett. 2018, 18, 6002–6008. [Google Scholar] [CrossRef]
- Abedi, S.; Pakizeh, T. Packed Yagi-Uda nano-antennas using a unidirectional feed at visible wavelengths. Opt. Lett. 2017, 42, 4788–4791. [Google Scholar] [CrossRef]
- Shegai, T.; Johansson, P.; Langhammer, C.; Kall, M. Directional scattering and hydrogen sensing by bimetallic Pd-Au nanoantennas. Nano Lett. 2012, 12, 2464–2469. [Google Scholar] [CrossRef]
- Shegai, T.; Chen, S.; Miljkovic, V.D.; Zengin, G.; Johansson, P.; Kall, M. A bimetallic nanoantenna for directional colour routing. Nat. Commun. 2011, 2, 481. [Google Scholar] [CrossRef]
- Vercruysse, D.; Sonnefraud, Y.; Verellen, N.; Fuchs, F.B.; Di Martino, G.; Lagae, L.; Moshchalkov, V.V.; Maier, S.A.; Van Dorpe, P. Unidirectional Side Scattering of Light by a Single-Element Nanoantenna. Nano Lett. 2013, 13, 3843–3849. [Google Scholar] [CrossRef]
- Vercruysse, D.; Zheng, X.; Sonnefraud, Y.; Verellen, N.; Di Martino, G.; Lagae, L.; Vandenbosch, G.A.; Moshchalkov, V.V.; Maier, S.A.; Van Dorpe, P. Directional fluorescence emission by individual V-antennas explained by mode expansion. ACS Nano 2014, 8, 8232–8241. [Google Scholar] [CrossRef]
- Lu, G.; Wang, Y.; Chou, R.Y.; Shen, H.; He, Y.; Cheng, Y.; Gong, Q. Directional side scattering of light by a single plasmonic trimer. Laser Photonics Rev. 2015, 9, 530–537. [Google Scholar] [CrossRef]
- Lai, Y.H.; Cui, X.M.; Li, N.N.; Shao, L.; Zhang, W.; Wang, J.F.; Lin, H.Q. Asymmetric Light Scattering on Heterodimers Made of Au Nanorods Vertically Standing on Au Nanodisks. Adv. Opt. Mater. 2021, 9, 2001595. [Google Scholar] [CrossRef]
- Pezeshki, H.; Wright, A.J.; Larkins, E.C. Ultra-compact and ultra-broadband hybrid plasmonic-photonic vertical coupler with high coupling efficiency, directivity, and polarisation extinction ratio. IET Optoelectron. 2021, 16, 124–132. [Google Scholar] [CrossRef]
- Taminiau, T.H.; Stefani, F.D.; van Hulst, N.F. Enhanced directional excitation and emission of single emitters by a nano-optical Yagi-Uda antenna. Opt. Express 2008, 16, 10858–10866. [Google Scholar] [CrossRef]
- Kasani, S.; Curtin, K.; Wu, N. A review of 2D and 3D plasmonic nanostructure array patterns: Fabrication, light management and sensing applications. Nanophotonics 2019, 8, 2065–2089. [Google Scholar] [CrossRef]
- Pakizeh, T.; Käll, M. Unidirectional Ultracompact Optical Nanoantennas. Nano Lett. 2009, 9, 2343–2349. [Google Scholar] [CrossRef]
- Liu, M.; Lee, T.-W.; Gray, S.K.; Guyot-Sionnest, P.; Pelton, M. Excitation of Dark Plasmons in Metal Nanoparticles by a Localized Emitter. Phys. Rev. Lett. 2009, 102, 107401. [Google Scholar] [CrossRef]
- Shen, H.; Lu, G.; He, Y.; Cheng, Y.; Gong, Q. Unidirectional enhanced spontaneous emission with metallo-dielectric optical antenna. Opt. Commun. 2017, 395, 133–138. [Google Scholar] [CrossRef]
- Shen, H.; Chou, R.Y.; Hui, Y.Y.; He, Y.; Cheng, Y.; Chang, H.-C.; Tong, L.; Gong, Q.; Lu, G. Directional fluorescence emission from a compact plasmonic-diamond hybrid nanostructure. Laser Photonics Rev. 2016, 10, 647–655. [Google Scholar] [CrossRef]
- Bonod, N.; Devilez, A.; Rolly, B.; Bidault, S.; Stout, B. Ultracompact and unidirectional metallic antennas. Phys. Rev. B 2010, 82, 115429. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, J.; Deng, Z.L.; Hu, D.; Qin, F.; Li, X. Unidirectional Enhanced Dipolar Emission with an Individual Dielectric Nanoantenna. Nanomaterials 2019, 9, 629. [Google Scholar] [CrossRef] [PubMed]
- Barreda, A.I.; Saiz, J.M.; González, F.; Moreno, F.; Albella, P. Recent advances in high refractive index dielectric nanoantennas: Basics and applications. AIP Adv. 2019, 9, 040701. [Google Scholar] [CrossRef]
- Bidault, S.; Mivelle, M.; Bonod, N. Dielectric nanoantennas to manipulate solid-state light emission. J. Appl. Phys. 2019, 126, 094104. [Google Scholar] [CrossRef]
- Alaee, R.; Albooyeh, M.; Tretyakov, S.; Rockstuhl, C. Phase-change material-based nanoantennas with tunable radiation patterns. Opt. Lett. 2016, 41, 4099–4102. [Google Scholar] [CrossRef]
- Yao, K.; Liu, Y. Controlling Electric and Magnetic Resonances for Ultracompact Nanoantennas with Tunable Directionality. ACS Photonics 2016, 3, 953–963. [Google Scholar] [CrossRef]
- Kerker, M.; Wang, D.S.; Giles, C.L. Electromagnetic scattering by magnetic spheres. J. Opt. Soc. Am. 1983, 73, 765–767. [Google Scholar] [CrossRef]
- Zhu, F.; Sanz-Paz, M.; Fernández-Domínguez, A.I.; Zhuo, X.; Liz-Marzán, L.M.; Stefani, F.D.; Pilo-Pais, M.; Acuna, G.P. DNA-Templated Ultracompact Optical Antennas for Unidirectional Single-Molecule Emission. Nano Lett. 2022, 22, 6402–6408. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Huang, Y.; Ringe, E.; Hou, M.; Ma, L.; Zhang, Z. Near-field mapping of three-dimensional surface charge poles for hybridized plasmon modes. AIP Adv. 2015, 5, 107221. [Google Scholar] [CrossRef]
- Lieb, M.A.; Zavislan, J.M.; Novotny, L. Single-molecule orientations determined by direct emission pattern imaging. J. Opt. Soc. Am. B 2004, 21, 1210–1215. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory: Analysis and Design, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 145–155. [Google Scholar]
- Bharadwaj, P.; Deutsch, B.; Novotny, L. Optical Antennas. Adv. Opt. Photonics 2009, 1, 438–483. [Google Scholar] [CrossRef]
- Prodan, E.; Radloff, C.; Halas, N.J.; Nordlander, P. A hybridization model for the plasmon response of complex nanostructures. Science 2003, 302, 419–422. [Google Scholar] [CrossRef] [PubMed]
- Jain, P.K.; Eustis, S.; El-Sayed, M.A. Plasmon Coupling in Nanorod Assemblies: Optical Absorption, Discrete Dipole Approximation Simulation, and Exciton-Coupling Model. J. Phys. Chem. B 2006, 110, 18243–18253. [Google Scholar] [CrossRef] [PubMed]
- Basyooni, M.A.; Ahmed, A.M.; Shaban, M. Plasmonic hybridization between two metallic nanorods. Optik 2018, 172, 1069–1078. [Google Scholar] [CrossRef]
- Li, J.N.; Liu, T.Z.; Zheng, H.R.; Gao, F.; Dong, J.; Zhang, Z.L.; Zhang, Z.Y. Plasmon resonances and strong electric field enhancements in side-by-side tangent nanospheroid homodimers. Opt. Express 2013, 21, 17176–17185. [Google Scholar] [CrossRef]
- Flauraud, V.; Bernasconi, G.D.; Butet, J.; Alexander, D.T.L.; Martin, O.J.F.; Brugger, J. Mode Coupling in Plasmonic Heterodimers Probed with Electron Energy Loss Spectroscopy. ACS Nano 2017, 11, 3485–3495. [Google Scholar] [CrossRef]
- Lukosz, W.; Kunz, R.E. Light emission by magnetic and electric dipoles close to a plane interface. I. Total radiated power. J. Opt. Soc. Am. 1977, 67, 1607–1615. [Google Scholar] [CrossRef]
- Lukosz, W.; Kunz, R.E. Light emission by magnetic and electric dipoles close to a plane dielectric interface. II. Radiation patterns of perpendicular oriented dipoles. J. Opt. Soc. Am. 1977, 67, 1615–1619. [Google Scholar] [CrossRef]
- Lukosz, W. Light emission by magnetic and electric dipoles close to a plane dielectric interface. III. Radiation patterns of dipoles with arbitrary orientation. J. Opt. Soc. Am. 1979, 69, 1495–1503. [Google Scholar] [CrossRef]
- Hellen, E.H.; Axelrod, D. Fluorescence Emission at Dielectric and Metal-Film Interfaces. J. Opt. Soc. Am. B 1987, 4, 337–350. [Google Scholar] [CrossRef]
- Hubner, K.; Joshi, H.; Aksimentiev, A.; Stefani, F.D.; Tinnefeld, P.; Acuna, G.P. Determining the In-Plane Orientation and Binding Mode of Single Fluorescent Dyes in DNA Origami Structures. ACS Nano 2021, 15, 5109–5117. [Google Scholar] [CrossRef] [PubMed]
- Mathur, D.; Kim, Y.C.; Díaz, S.A.; Cunningham, P.D.; Rolczynski, B.S.; Ancona, M.G.; Medintz, I.L.; Melinger, J.S. Can a DNA Origami Structure Constrain the Position and Orientation of an Attached Dye Molecule? J. Phys. Chem. C 2020, 125, 1509–1522. [Google Scholar] [CrossRef]
- Adamczyk, A.K.; Huijben, T.A.; Sison, M.; di Luca, A.; Chiarelli, G.; Vanni, S.; Brasselet, S.; Mortensen, K.; Stefani, F.D.; Pilo-Pais, M.; et al. DNA self-assembly of single molecules with deterministic position and orientation. arXiv 2022, arXiv:2207.06472. [Google Scholar] [CrossRef]
- Kern, A.M.; Martin, O.J. Excitation and reemission of molecules near realistic plasmonic nanostructures. Nano Lett. 2011, 11, 482–487. [Google Scholar] [CrossRef]
- Rothemund, P.W. Folding DNA to create nanoscale shapes and patterns. Nature 2006, 440, 297–302. [Google Scholar] [CrossRef]
- Kuzyk, A.; Jungmann, R.; Acuna, G.P.; Liu, N. DNA Origami Route for Nanophotonics. ACS Photonics 2018, 5, 1151–1163. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, F.; Sanz-Paz, M.; Fernández-Domínguez, A.I.; Pilo-Pais, M.; Acuna, G.P. Optical Ultracompact Directional Antennas Based on a Dimer Nanorod Structure. Nanomaterials 2022, 12, 2841. https://doi.org/10.3390/nano12162841
Zhu F, Sanz-Paz M, Fernández-Domínguez AI, Pilo-Pais M, Acuna GP. Optical Ultracompact Directional Antennas Based on a Dimer Nanorod Structure. Nanomaterials. 2022; 12(16):2841. https://doi.org/10.3390/nano12162841
Chicago/Turabian StyleZhu, Fangjia, María Sanz-Paz, Antonio I. Fernández-Domínguez, Mauricio Pilo-Pais, and Guillermo P. Acuna. 2022. "Optical Ultracompact Directional Antennas Based on a Dimer Nanorod Structure" Nanomaterials 12, no. 16: 2841. https://doi.org/10.3390/nano12162841
APA StyleZhu, F., Sanz-Paz, M., Fernández-Domínguez, A. I., Pilo-Pais, M., & Acuna, G. P. (2022). Optical Ultracompact Directional Antennas Based on a Dimer Nanorod Structure. Nanomaterials, 12(16), 2841. https://doi.org/10.3390/nano12162841





