Hyperelastic Microcantilever AFM: Efficient Detection Mechanism Based on Principal Parametric Resonance
Abstract
:1. Introduction
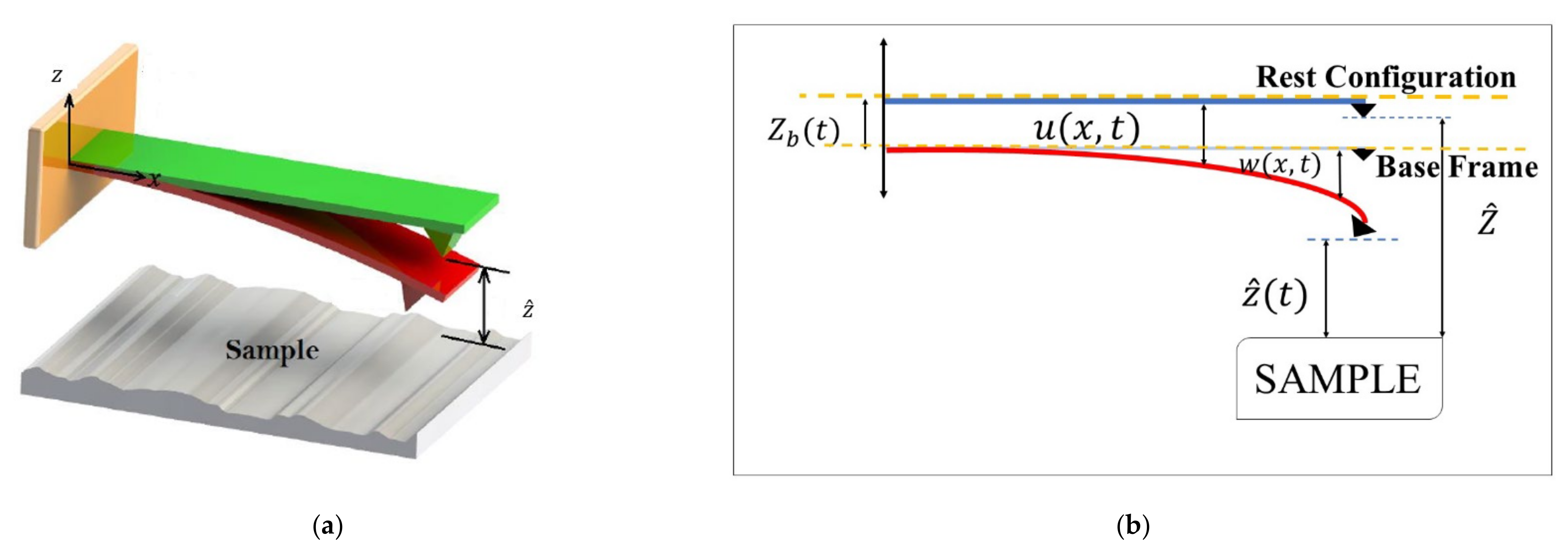
2. Mathematical Modeling
2.1. Beam Theory with Finite Rotation and Deformation
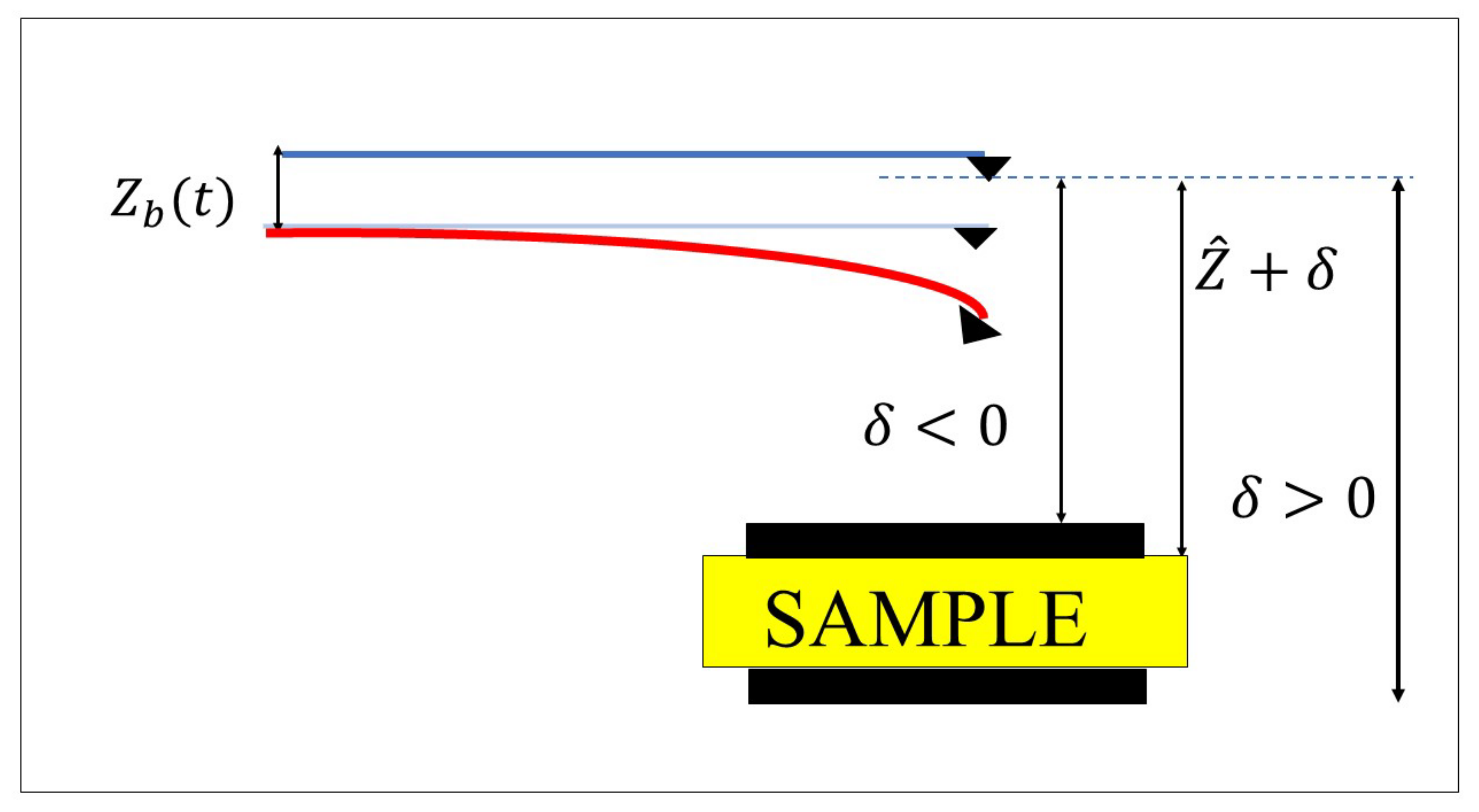
2.2. Tip–Sample Interaction
2.3. Kinetic Energy
2.4. Surrounding Damping Force
2.5. Hamilton’s Principle and Equation of Motion
2.6. Nondimensionalization
3. Discretization of the Governing Motion’s Equation
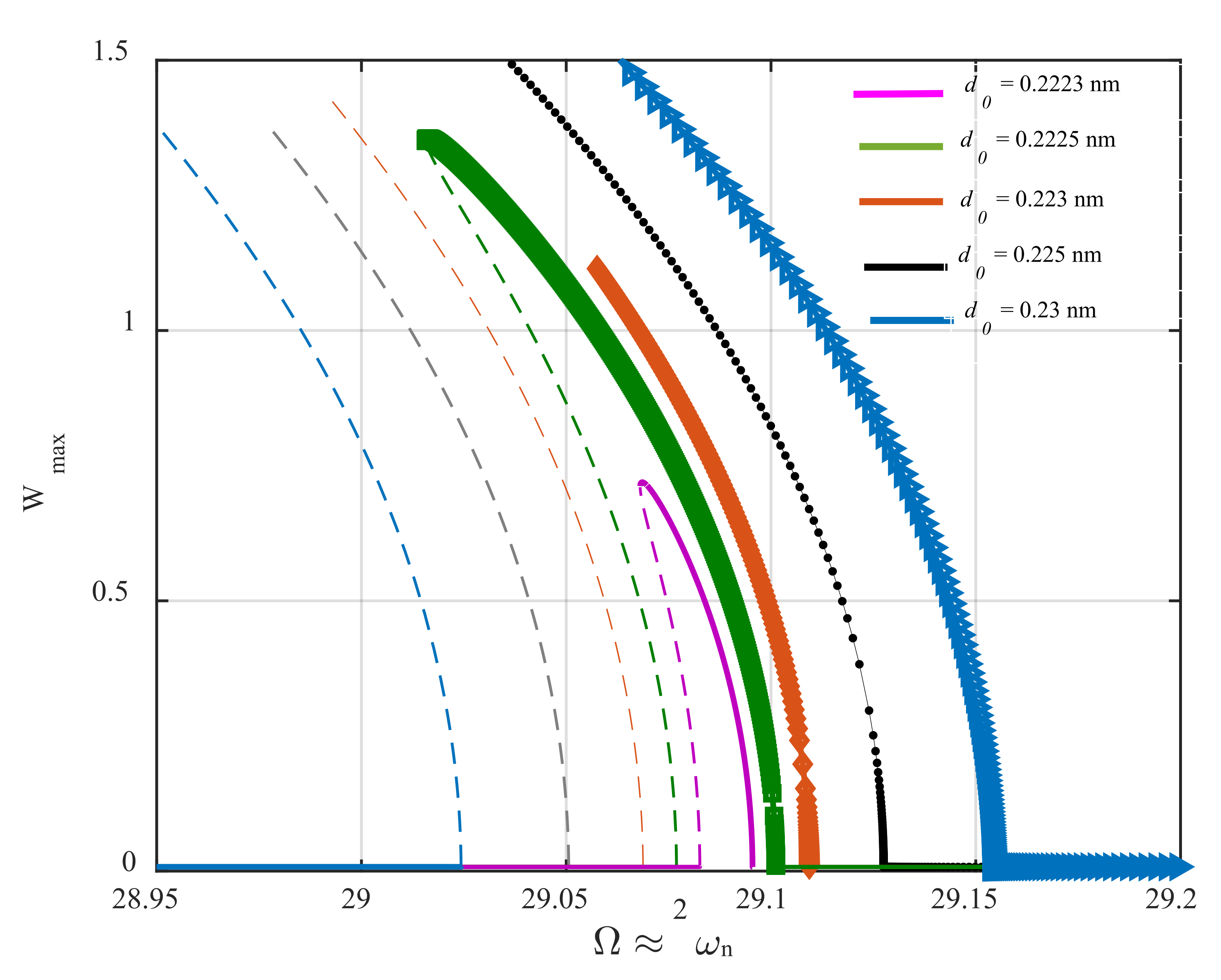
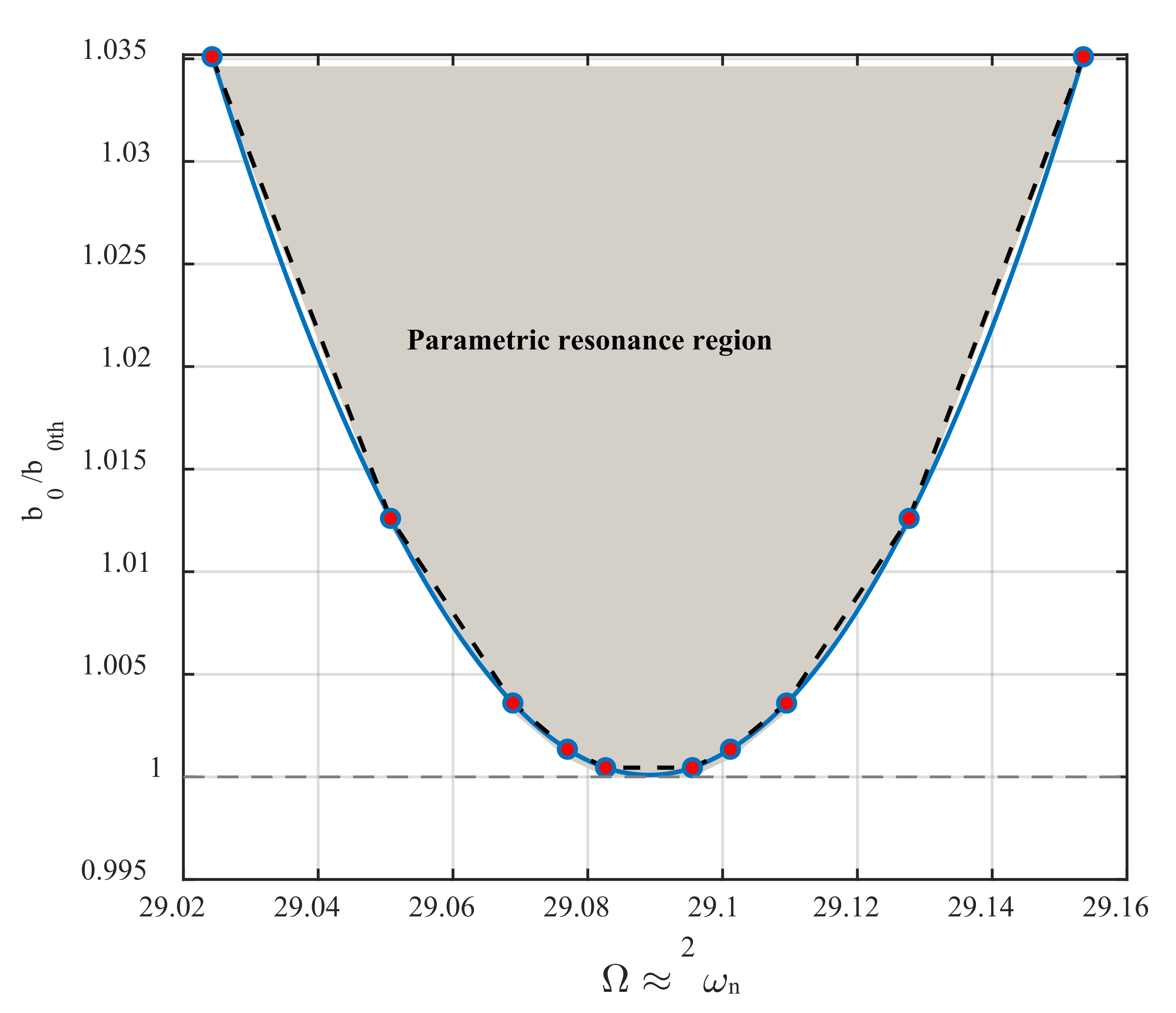
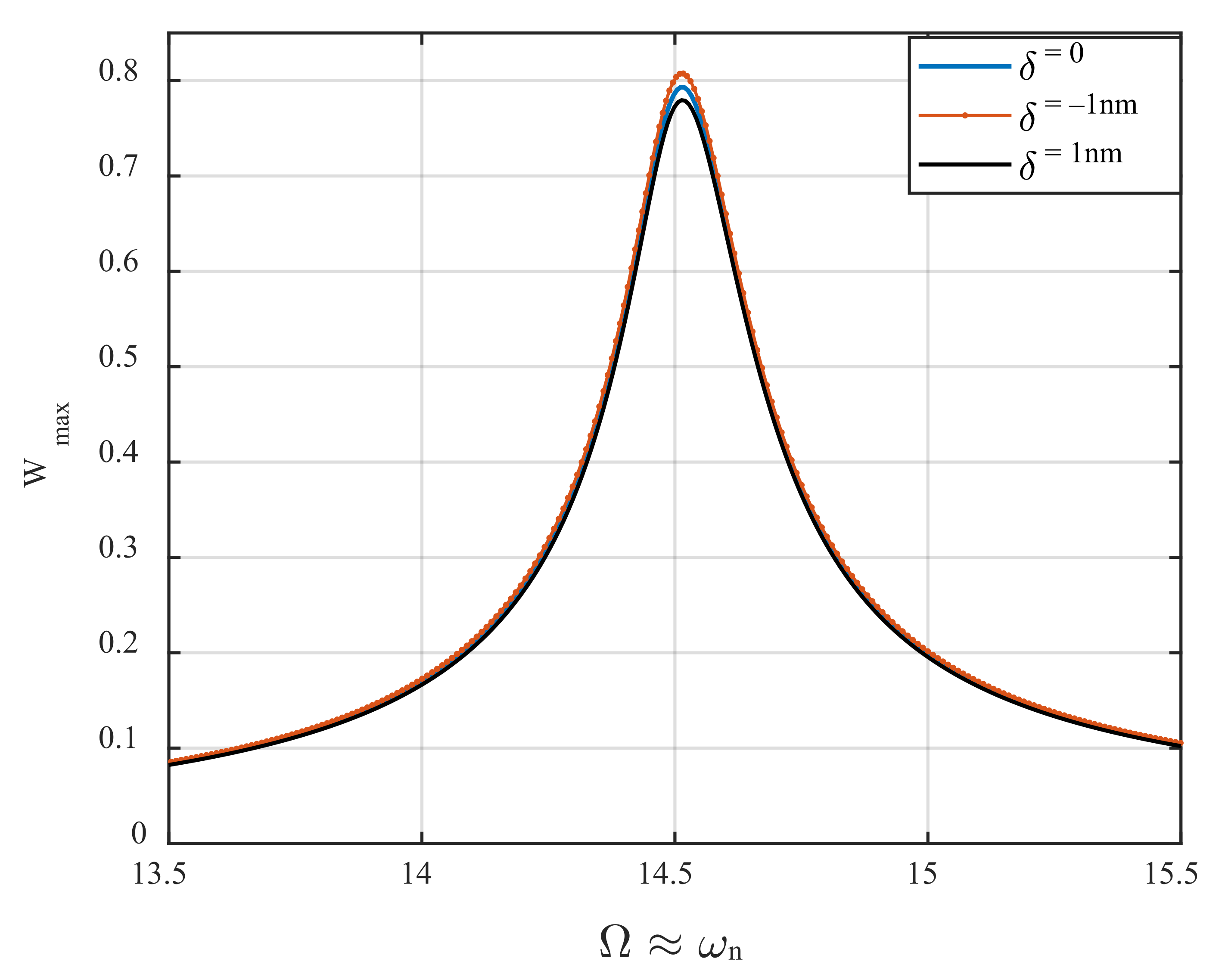
4. Result and Discussion
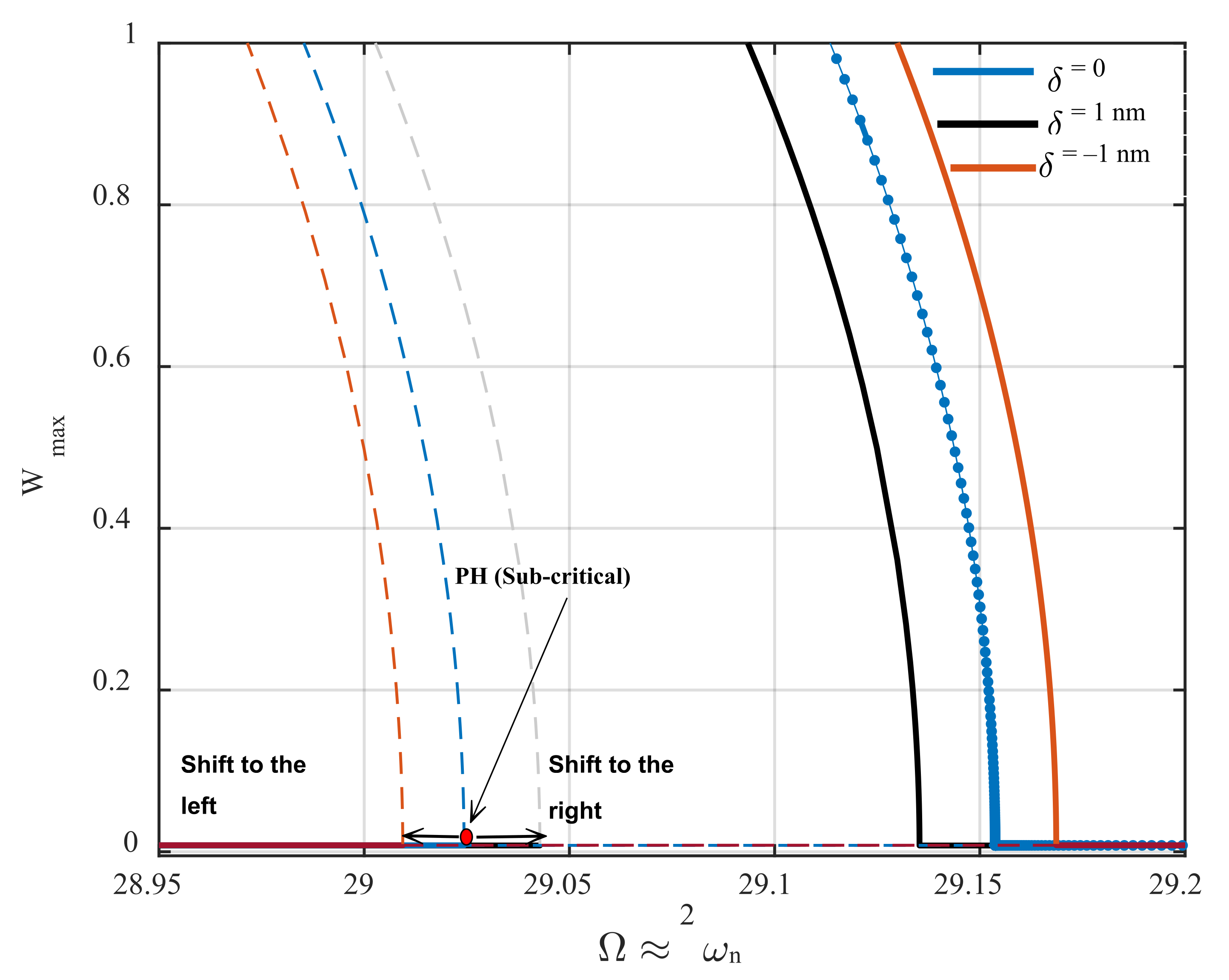
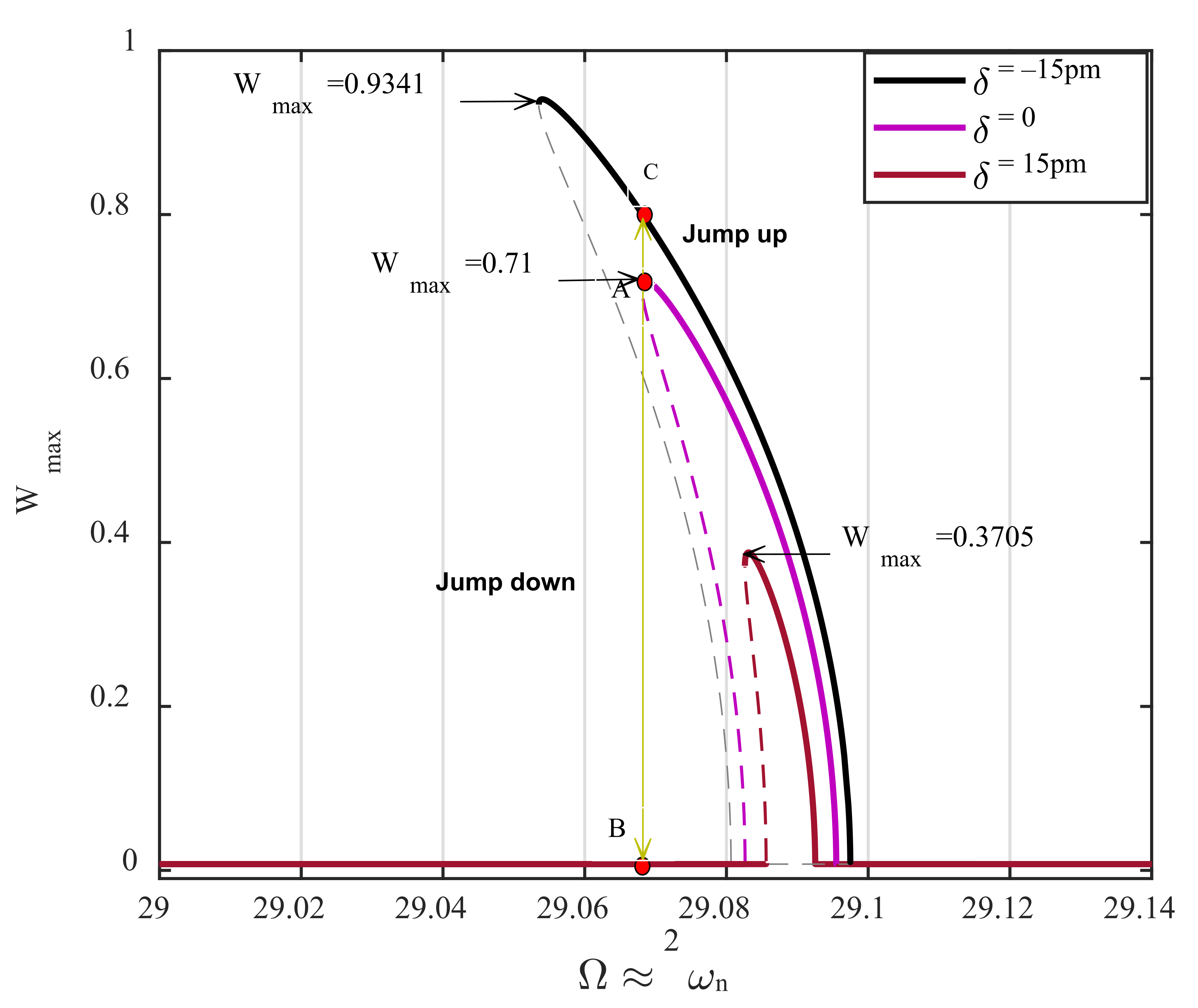
Profile Height Detection Mechanism
5. Conclusions
- The hyperelastic microcantilever of the AFM device undergoes softening behavior near its principal parametric resonance.
- The frequency–displacement curve governing the resonator’s dynamics comprises stable trivial, unstable trivial, stable nontrivial, and unstable nontrivial branches.
- The resonance of the AFM exhibits both super- and sub-critical Hopf bifurcations for the considerable value of , and cyclic-fold bifurcation, for a small value of .
- Increasing the incompressibility condition (higher values of the Poisson’s ratio) results in stronger softening nonlinearity, and the resonance bandwidth becomes wider.
- Surface profile depression and rise in the height of a surface profile can be detected by inspecting the bifurcation points’ position.
- According to the sensitivity analysis presented in Equation (35), the proposed AFM can detect surface depression in the order of a picometer, providing ultrahigh sensitivity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kuo, C.-F.J.; Huy, V.Q.; Chiu, C.-H.; Chiu, S.-F. Dynamic modeling and control of an atomic force microscope probe measurement system. J. Vib. Control 2011, 18, 101–116. [Google Scholar] [CrossRef]
- Sajjadi, M.; Chahari, M.; Pishkenari, H.N.; Vossoughi, G. Designing nonlinear observer for topography estimation in trolling mode atomic force microscopy. J. Vib. Control 2021, 10775463211038140. [Google Scholar] [CrossRef]
- Jalili, N.; Laxminarayana, K. A review of atomic force microscopy imaging systems: Application to molecular metrology and biological sciences. Mechatronics 2004, 14, 907–945. [Google Scholar] [CrossRef]
- Alunda, B.O.; Lee, Y.J. Review: Cantilever-Based Sensors for High Speed Atomic Force Microscopy. Sensors 2020, 20, 4784. [Google Scholar] [CrossRef]
- Sugimoto, Y.; Pou, P.; Abe, M.; Jelínek, P.; Perez, R.; Morita, S.; Custance, O. Chemical identification of individual surface atoms by atomic force microscopy. Nature 2007, 446, 64–67. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Payton, O.D.; Picco, L.; Scott, T.B. High-speed atomic force microscopy for materials science. Int. Mater. Rev. 2016, 61, 473–494. [Google Scholar] [CrossRef] [Green Version]
- Alessandrini, A.; Facci, P. AFM: A versatile tool in biophysics. Meas. Sci. Technol. 2005, 16, R65–R92. [Google Scholar] [CrossRef]
- Zypman, F.R. Charge-Regulated Interactions: The Case of a Nanoparticle and a Sphere of Arbitrary Dielectric Constants. Langmuir 2022, 38, 3561–3567. [Google Scholar] [CrossRef] [PubMed]
- Russillo, A.F.; Failla, G.; Amendola, A.; Luciano, R. On the Free Vibrations of Non-Classically Damped Locally Resonant Metamaterial Plates. Nanomaterials 2022, 12, 541. [Google Scholar] [CrossRef] [PubMed]
- Mahmure, A.; Tornabene, F.; Dimitri, R.; Kuruoglu, N. Free Vibration of Thin-Walled Composite Shell Structures Reinforced with Uniform and Linear Carbon Nanotubes: Effect of the Elastic Foundation and Nonlinearity. Nanomaterials 2021, 11, 2090. [Google Scholar] [CrossRef] [PubMed]
- Selim, M.M.; Musa, A. Nonlinear Vibration of a Pre-Stressed Water-Filled Single-Walled Carbon Nanotube Using Shell Model. Nanomaterials 2020, 10, 974. [Google Scholar] [CrossRef]
- Civalek, Ö.; Akbaş, Ş.D.; Akgöz, B.; Dastjerdi, S. Forced Vibration Analysis of Composite Beams Reinforced by Carbon Nanotubes. Nanomaterials 2021, 11, 571. [Google Scholar] [CrossRef] [PubMed]
- Yagasaki, K. Bifurcations and chaos in vibrating microcantilevers of tapping mode atomic force microscopy. Int. J. Non-Linear Mech. 2007, 42, 658–672. [Google Scholar] [CrossRef]
- Bahrami, A.; Nayfeh, A.H. On the dynamics of tapping mode atomic force microscope probes. Nonlinear Dyn. 2012, 70, 1605–1617. [Google Scholar] [CrossRef]
- Kahrobaiyan, M.; Ahmadian, M.; Haghighi, P. Sensitivity and resonant frequency of an AFM with sidewall and top-surface probes for both flexural and torsional modes. Int. J. Mech. Sci. 2010, 52, 1357–1365. [Google Scholar] [CrossRef]
- Arafat, H.N.; Nayfeh, A.H.; Abdel-Rahman, E.M. Modal interactions in contact-mode atomic force microscopes. Nonlinear Dyn. 2008, 54, 151–166. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Abbasi, M. A vibration analysis of a cracked micro-cantilever in an atomic force microscope by using transfer matrix method. Ultramicroscopy 2018, 196, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Mahmoudi, M.S.; Ebrahimian, A.; Bahrami, A. Higher modes and higher harmonics in the non-contact atomic force microscopy. Int. J. Non-Linear Mech. 2019, 110, 33–43. [Google Scholar] [CrossRef]
- Saeidi, H.; Zajkani, A.; Ghadiri, M. Nonlinear micromechanically analysis of forced vibration of the rectangular-shaped atomic force microscopes incorporating contact model and thermal influences. Mech. Based Des. Struct. Mach. 2020, 50, 609–629. [Google Scholar] [CrossRef]
- Ahmadi, M.; Ansari, R.; Darvizeh, M. Free and forced vibrations of atomic force microscope piezoelectric cantilevers considering tip-sample nonlinear interactions. Thin-Walled Struct. 2019, 145, 106382. [Google Scholar] [CrossRef]
- Kouchaksaraei, M.G.; Bahrami, A. High-resolution compositional mapping of surfaces in non-contact atomic force microscopy by a new multi-frequency excitation. Ultramicroscopy 2021, 227, 113317. [Google Scholar] [CrossRef] [PubMed]
- Alibakhshi, A.; Heidari, H. Nonlinear dynamic responses of electrically actuated dielectric elastomer-based microbeam resonators. J. Intell. Mater. Syst. Struct. 2021, 33, 558–571. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Imam, A.; Haghighi, S.E. Effect of the second invariant of the Cauchy–Green deformation tensor on the local dynamics of dielectric elastomers. Int. J. Non-Linear Mech. 2021, 137, 103807. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Chen, W.; Destrade, M. Nonlinear Vibration and Stability of a Dielectric Elastomer Balloon Based on a Strain-Stiffening Model. J. Elast. 2022, 1–16. [Google Scholar] [CrossRef]
- Zeng, C.; Gao, X. Stability of an anisotropic dielectric elastomer plate. Int. J. Non-Linear Mech. 2020, 124, 103510. [Google Scholar] [CrossRef]
- He, L.; Lou, J.; Kitipornchai, S.; Yang, J.; Du, J. Peeling mechanics of hyperelastic beams: Bending effect. Int. J. Solids Struct. 2019, 167, 184–191. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Tarantino, A.M. Finite bending of hyperelastic beams with transverse isotropy generated by longitudinal porosity. Eur. J. Mech.-A/Solids 2020, 85, 104131. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Dastjerdi, S.; Malikan, M.; Eremeyev, V.A. Nonlinear Free and Forced Vibrations of a Hyperelastic Micro/Nanobeam Considering Strain Stiffening Effect. Nanomaterials 2021, 11, 3066. [Google Scholar] [CrossRef] [PubMed]
- Alibakhshi, A.; Dastjerdi, S.; Fantuzzi, N.; Rahmanian, S. Nonlinear free and forced vibrations of a fiber-reinforced dielectric elastomer-based microbeam. Int. J. Non-Linear Mech. 2022, 144, 104092. [Google Scholar] [CrossRef]
- Amabili, M.; Balasubramanian, P.; Breslavsky, I.D.; Ferrari, G.; Garziera, R.; Riabova, K. Experimental and numerical study on vibrations and static deflection of a thin hyperelastic plate. J. Sound Vib. 2016, 385, 81–92. [Google Scholar] [CrossRef]
- Du, P.; Dai, H.-H.; Wang, J.; Wang, Q. Analytical study on growth-induced bending deformations of multi-layered hyperelastic plates. Int. J. Non-Linear Mech. 2019, 119, 103370. [Google Scholar] [CrossRef]
- Amabili, M.; Breslavsky, I.; Reddy, J. Nonlinear higher-order shell theory for incompressible biological hyperelastic materials. Comput. Methods Appl. Mech. Eng. 2018, 346, 841–861. [Google Scholar] [CrossRef]
- Mihai, L.A.; Alamoudi, M. Likely oscillatory motions of stochastic hyperelastic spherical shells and tubes. Int. J. Non-Linear Mech. 2021, 130, 103671. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Dastjerdi, S.; Malikan, M.; Eremeyev, V.A. Nonlinear free and forced vibrations of a dielectric elastomer-based microcantilever for atomic force microscopy. Contin. Mech. Thermodyn. 2022, 1–18. [Google Scholar] [CrossRef]
- Schmidt, R.; Reddy, J.N. A Refined Small Strain and Moderate Rotation Theory of Elastic Anisotropic Shells. J. Appl. Mech. 1988, 55, 611–617. [Google Scholar] [CrossRef]
- Şimşek, M.; Reddy, J. Bending and vibration of functionally graded microbeams using a new higher order beam theory and the modified couple stress theory. Int. J. Eng. Sci. 2013, 64, 37–53. [Google Scholar] [CrossRef]
- Srinivasa, A.; Reddy, J. A model for a constrained, finitely deforming, elastic solid with rotation gradient dependent strain energy, and its specialization to von Kármán plates and beams. J. Mech. Phys. Solids 2012, 61, 873–885. [Google Scholar] [CrossRef]
- Reddy, J.; Srinivasa, A. Non-linear theories of beams and plates accounting for moderate rotations and material length scales. Int. J. Non-Linear Mech. 2014, 66, 43–53. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Dastjerdi, S.; Akgöz, B.; Civalek, Ö. Parametric vibration of a dielectric elastomer microbeam resonator based on a hyperelastic cosserat continuum model. Compos. Struct. 2022, 287, 115386. [Google Scholar] [CrossRef]
- Mindlin, R. Influence of Couple-Stresses on Stress Concentrations; Columbia University: New York, NY, USA, 1962. [Google Scholar]
- Choi, J.-H.; Kim, H.; Kim, J.-Y.; Lim, K.-H.; Lee, B.-C.; Sim, G.-D. Micro-cantilever bending tests for understanding size effect in gradient elasticity. Mater. Des. 2022, 214, 110398. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Akgöz, B.; Civalek, Ö. On the effect of viscoelasticity on behavior of gyroscopes. Int. J. Eng. Sci. 2020, 149, 103236. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Amabili, M. Nonlinear behaviour of electrically actuated MEMS resonators. Int. J. Eng. Sci. 2013, 71, 137–155. [Google Scholar] [CrossRef]
- Malikan, M.; Krasheninnikov, M.; Eremeyev, V.A. Torsional stability capacity of a nano-composite shell based on a nonlocal strain gradient shell model under a three-dimensional magnetic field. Int. J. Eng. Sci. 2020, 148, 103210. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Amabili, M. Nonlinear dynamics of a geometrically imperfect microbeam based on the modified couple stress theory. Int. J. Eng. Sci. 2013, 68, 11–23. [Google Scholar] [CrossRef]
- Aranda-Ruiz, J.; Fernández-Sáez, J. On the use of variable-separation method for the analysis of vibration problems with time-dependent boundary conditions. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 2912–2924. [Google Scholar] [CrossRef] [Green Version]
- Rahmanian, S.; Hosseini-Hashemi, S.; Rezaei, M. Out-of-plane motion detection in encapsulated electrostatic MEMS gyroscopes: Principal parametric resonance. Int. J. Mech. Sci. 2020, 190, 106022. [Google Scholar] [CrossRef]
- Gent, A.N. A New Constitutive Relation for Rubber. Rubber Chem. Technol. 1996, 69, 59–61. [Google Scholar] [CrossRef]
- Anssari-Benam, A.; Bucchi, A. A generalised neo-Hookean strain energy function for application to the finite deformation of elastomers. Int. J. Non-Linear Mech. 2020, 128, 103626. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Heidari, H. Nonlinear dynamics of dielectric elastomer balloons based on the Gent-Gent hyperelastic model. Eur. J. Mech.-A/Solids 2020, 82, 103986. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Modulus of elasticity, | 3 GPa |
| Length, | 225 m |
| Cross-section area, | |
| The second moment of area, | |
| Hamaker constant, | J |
| Tip radius, | 10 nm |
| Initial tip–sample distance, | 60 nm |
| Poisson’s ratio | 0.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alibakhshi, A.; Rahmanian, S.; Dastjerdi, S.; Malikan, M.; Karami, B.; Akgöz, B.; Civalek, Ö. Hyperelastic Microcantilever AFM: Efficient Detection Mechanism Based on Principal Parametric Resonance. Nanomaterials 2022, 12, 2598. https://doi.org/10.3390/nano12152598
Alibakhshi A, Rahmanian S, Dastjerdi S, Malikan M, Karami B, Akgöz B, Civalek Ö. Hyperelastic Microcantilever AFM: Efficient Detection Mechanism Based on Principal Parametric Resonance. Nanomaterials. 2022; 12(15):2598. https://doi.org/10.3390/nano12152598
Chicago/Turabian StyleAlibakhshi, Amin, Sasan Rahmanian, Shahriar Dastjerdi, Mohammad Malikan, Behrouz Karami, Bekir Akgöz, and Ömer Civalek. 2022. "Hyperelastic Microcantilever AFM: Efficient Detection Mechanism Based on Principal Parametric Resonance" Nanomaterials 12, no. 15: 2598. https://doi.org/10.3390/nano12152598
APA StyleAlibakhshi, A., Rahmanian, S., Dastjerdi, S., Malikan, M., Karami, B., Akgöz, B., & Civalek, Ö. (2022). Hyperelastic Microcantilever AFM: Efficient Detection Mechanism Based on Principal Parametric Resonance. Nanomaterials, 12(15), 2598. https://doi.org/10.3390/nano12152598






