Enhanced Spin Thermopower in Phosphorene Nanoribbons via Edge-State Modifications
Abstract
:1. Introduction
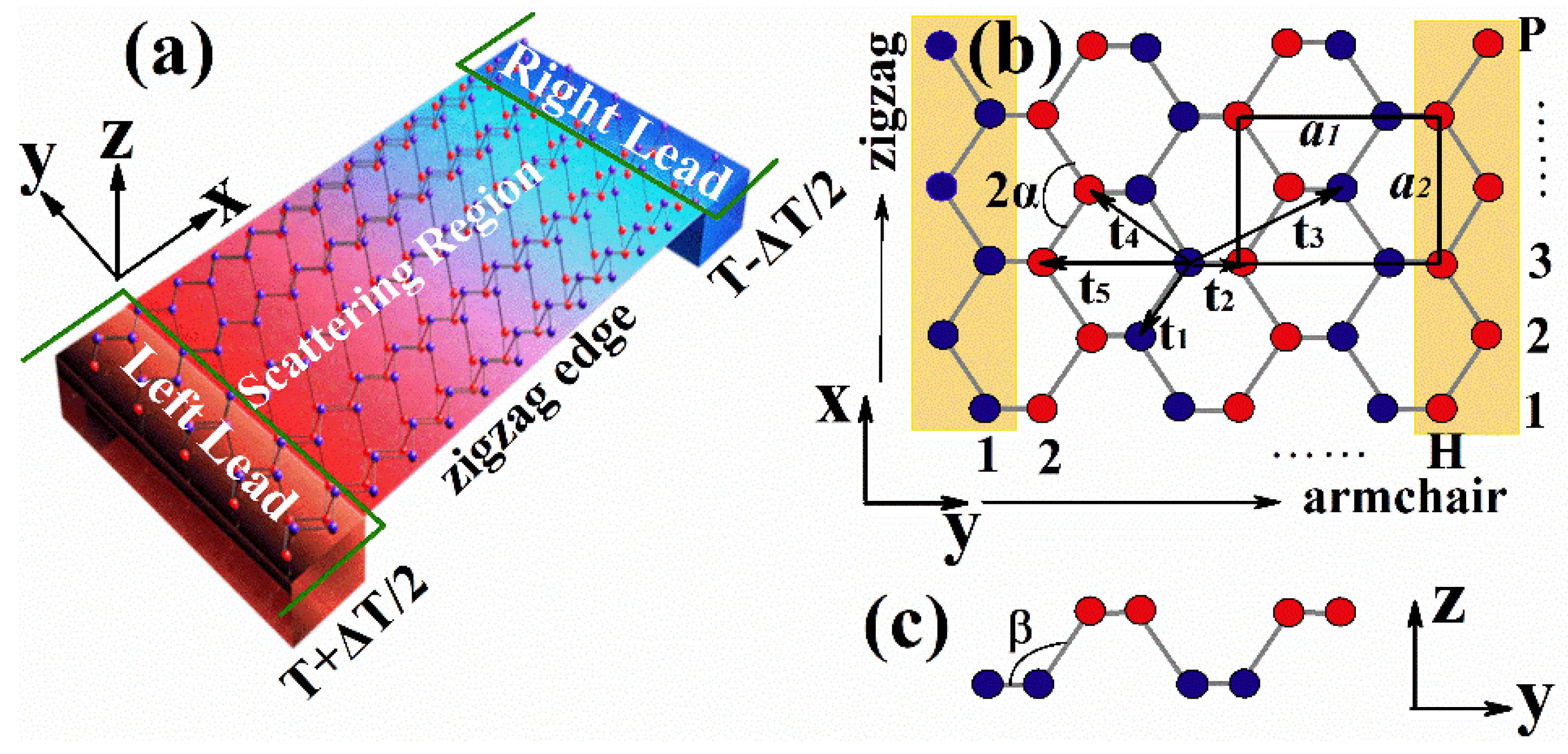
2. Model and Methods
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.E.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neto, A.C.; Guinea, F.; Peres, N.M.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef] [Green Version]
- Manzeli, S.; Ovchinnikov, D.; Pasquier, D.; Yazyev, O.V.; Kis, A. 2D transition metal dichalcogenides. Nat. Rev. Mater. 2017, 2, 17033. [Google Scholar] [CrossRef]
- Radisavljevic, B.; Radenovic, A.; Brivio, J.; Giacometti, V.; Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 2011, 6, 147. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Lin, Y.M.; Bol, A.A.; Jenkins, K.A.; Xia, F.; Farmer, D.B.; Zhu, Y.; Avouris, P. High-frequency, scaled graphene transistors on diamond-like carbon. Nature 2011, 472, 74. [Google Scholar] [CrossRef] [PubMed]
- Yoon, Y.; Ganapathi, K.; Salahuddin, S. How good can monolayer MoS2 transistors be? Nano Lett. 2011, 11, 3768. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Lei, Z.; Huang, B.; Wei, A.; Tao, L.; Yang, Y.; Zheng, Z.; Feng, X.; Li, J.; Zhao, Y. Non-Layered Te/In2S3 Tunneling Heterojunctions with Ultrahigh Photoresponsivity and Fast Photoresponse. Small 2022, 18, 2200445. [Google Scholar] [CrossRef] [PubMed]
- Batmunkh, M.; Bat-Erdene, M.; Shapter, J.G. Phosphorene and phosphorene-based materials-prospects for future applications. Adv. Mater. 2016, 28, 8586. [Google Scholar] [CrossRef]
- Qiu, D.Y.; da Jornada, F.H.; Louie, S.G. Environmental screening effects in 2D materials: Renormalization of the bandgap, electronic structure, and optical spectra of few-layer black phosphorus. Nano Lett. 2017, 17, 4706. [Google Scholar] [CrossRef]
- Reich, E.S. Phosphorene excites materials scientists. Nature 2014, 506, 19. [Google Scholar] [CrossRef]
- Koenig, S.P.; Doganov, R.A.; Schmidt, H.; Castro Neto, A.H.; Özyilmaz, B. Electric field effect in ultrathin black phosphorus. Appl. Phys. Lett. 2014, 104, 103106. [Google Scholar] [CrossRef] [Green Version]
- Xia, F.; Wang, H.; Jia, Y. Rediscovering black phosphorus as an anisotropic layered material for optoelectronics and electronics. Nat. Commun. 2014, 5, 4458. [Google Scholar] [CrossRef] [Green Version]
- Sarma, S.D.; Adam, S.; Hwang, E.H.; Rossi, E. Electronic transport in two-dimensional graphene. Rev. Mod. Phys. 2011, 83, 407. [Google Scholar] [CrossRef] [Green Version]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [Green Version]
- Tongay, S.; Zhou, J.; Ataca, C.; Lo, K.; Matthews, T.S.; Li, J.; Grossman, J.C.; Wu, J. Thermally driven crossover from indirect toward direct bandgap in 2D semiconductors: MoSe2 versus MoS2. Nano Lett. 2012, 12, 5576. [Google Scholar] [CrossRef] [PubMed]
- Rodin, A.S.; Carvalho, A.; Neto, A.C. Strain-Induced gap modification in black phosphorus. Phys. Rev. Lett. 2014, 112, 176801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Das, S.; Zhang, W.; Demarteau, M.; Hoffmann, A.; Dubey, M.; Roelofs, A. Tunable transport gap in phosphorene. Nano Lett. 2014, 14, 5733–5739. [Google Scholar] [CrossRef]
- Akhtar, M.; Anderson, G.; Zhao, R.; Alruqi, A.; Mroczkowska, J.E.; Sumanasekera, G.; Jasinski, J.B. Recent advances in synthesis, properties, and applications of phosphorene. npj 2D Mater. Appl. 2017, 1, 5. [Google Scholar] [CrossRef]
- Qiao, J.; Kong, X.; Hu, Z.X.; Yang, F.; Ji, W. High-mobility transport anisotropy and linear dichroism in few-layer black phosphorus. Nat. Commun. 2014, 5, 4475. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Yu, Y.; Ye, G.J.; Ge, Q.; Ou, X.; Wu, H.; Feng, D.; Chen, X.H.; Zhang, Y. Black phosphorus field-effect transistors. Nat. Nanotechnol. 2014, 9, 372–377. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Neal, A.T.; Zhu, Z.; Luo, Z.; Xu, X.; Tománek, D.; Ye, P.D. Phosphorene: An unexplored 2D semiconductor with a high hole mobility. Acs Nano 2014, 8, 4033–4041. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Junior, P.E.F.; Kurpas, M.; Gmitra, M.; Fabian, J. k · p theory for phosphorene: Effective g-factors, Landau levels, and excitons. Phys. Rev. B 2019, 100, 115203. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.Y.; Zhang, R.; Sun, J.P.; Zou, Y.L.; Zhang, D.; Lou, W.K.; Cheng, F.; Zhou, G.H.; Zhai, F.; Chang, K. Landau levels and magneto-transport property of monolayer phosphorene. Sci. Rep. 2015, 5, 12295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, X.; Lou, W.K.; Zhai, F.; Chang, K. Anomalous magneto-optical response of black phosphorus thin films. Phys. Rev. B 2015, 92, 165405. [Google Scholar] [CrossRef]
- Quereda, J.; San-Jose, P.; Parente, V.; Vaquero-Garzon, L.; Molina-Mendoza, A.J.; Agraït, N.; Rubio-Bollinger, G.; Guinea, F.; Roldán, R.; Castellanos-Gomez, A. Strong modulation of optical properties in black phosphorus through strain-engineered rippling. Nano Lett. 2016, 16, 2931. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lv, H.Y.; Lu, W.J.; Shao, D.F.; Sun, Y.P. Enhanced thermoelectric performance of phosphorene by strain-induced band convergence. Phys. Rev. B 2014, 90, 085433. [Google Scholar] [CrossRef] [Green Version]
- Castellanos-Gomez, A.; Vicarelli, L.; Prada, E.; Island, J.O.; Narasimha-Acharya, K.L.; Blanter, S.I.; Groenendijk, D.J.; Buscema, M.; Steele, G.A.; Alvarez, J.V.; et al. Isolation and characterization of few-layer black phosphorus. 2D Mater. 2014, 1, 025001. [Google Scholar] [CrossRef]
- Carvalho, A.; Wang, M.; Zhu, X.; Rodin, A.S.; Su, H.; Castro Neto, A.H. Phosphorene: From theory to applications. Nat. Rev. Mater. 2016, 1, 16061. [Google Scholar] [CrossRef]
- Guo, H.; Lu, N.; Dai, J.; Wu, X.; Zeng, X.C. Phosphorene nanoribbons, phosphorus nanotubes, and van der Waals Multilayers. J. Phys. Chem. C 2014, 118, 14051–14059. [Google Scholar] [CrossRef] [Green Version]
- Han, X.; Stewart, H.M.; Shevlin, S.A.; Catlow, C.R.A.; Guo, Z.X. Strain and orientation modulated bandgaps and effective masses of phosphorene nanoribbons. Nano Lett. 2014, 14, 4607. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, A.; Rodin, A.S.; Neto, A.C. Phosphorene nanoribbons. Europhys. Lett. 2014, 108, 47005. [Google Scholar] [CrossRef] [Green Version]
- Ezawa, M. Highly anisotropic physics in phosphorene. J. Phys. Conf. Ser. 2015, 603, 012006. [Google Scholar] [CrossRef]
- Ezawa, M. Topological origin of quasi-flat edge band in phosphorene. New J. Phys. 2014, 16, 115004. [Google Scholar] [CrossRef]
- Sisakht, E.T.; Zare, M.H.; Fazileh, F. Scaling laws of band gaps of phosphorene nanoribbons: A tight-binding calculation. Phys. Rev.B 2015, 91, 085409. [Google Scholar] [CrossRef] [Green Version]
- Watts, M.C.; Picco, L.; Russell-Pavier, F.S.; Cullen, P.L.; Miller, T.S.; Bartuś, S.P.; Payton, O.D.; Skipper, N.T.; Tileli, V.; Howard, C.A. Production of phosphorene nanoribbons. Nature 2019, 568, 216. [Google Scholar] [CrossRef]
- Macdonald, T.J.; Clancy, A.J.; Xu, W.; Jiang, Z.; Lin, C.T.; Mohan, L.; Du, T.; Tune, D.D.; Lanzetta, L.; Min, G.; et al. Phosphorene nanoribbon-augmented optoelectronics for enhanced hole extraction. J. Am. Chem. Soc. 2021, 143, 21549–21559. [Google Scholar] [CrossRef] [PubMed]
- Bauer, G.; Saitoh, E.; van Wees, B. Spin caloritronics. Nat. Mater. 2012, 11, 391–399. [Google Scholar] [CrossRef] [Green Version]
- Uchida, K.; Takahashi, S.; Harii, K.; Ieda, J.; Koshibae, W.; Ando, K.; Maekawa, S.; Saitoh, E. Observation of the spin Seebeck effect. Nature 2008, 455, 778–781. [Google Scholar] [CrossRef]
- Wu, S.M.; Zhang, W.; Amit, K.C.; Borisov, P.; Pearson, J.E.; Jiang, J.S.; Lederman, D.; Hoffmann, A.; Bhattacharya, A. Antiferromagnetic Spin Seebeck Effect. Phys. Rev. Lett. 2016, 116, 097204. [Google Scholar] [CrossRef]
- Wu, S.M.; Pearson, J.E.; Bhattacharya, A. Paramagnetic Spin Seebeck Effect. Phys. Rev. Lett. 2015, 114, 186602. [Google Scholar] [CrossRef] [Green Version]
- Inglot, M.; Dugaev, V.K.; Barnaś, J. Thermoelectric and thermospin transport in a ballistic junction of graphene. Phys. Rev. B 2015, 92, 085418. [Google Scholar] [CrossRef] [Green Version]
- Rameshti, B.Z.; Moghaddam, A.G. Spin-dependent Seebeck effect and spin caloritronics in magnetic graphene. Phys. Rev. B 2015, 91, 155407. [Google Scholar] [CrossRef] [Green Version]
- Farghadan, R.; Ildarabadi, F. Gate-voltage induced giant spin Seebeck effect in phosphorene nanoribbons. Phys. Rev. B 2020, 102, 035430. [Google Scholar] [CrossRef]
- Lee, S.; Song, J.P.; Kang, S.H.; Kwon, Y.K. Oxidation-enhanced thermoelectric efficiency in a two-dimensional phosphorene oxide. Sci. Rep. 2021, 11, 18525. [Google Scholar] [CrossRef] [PubMed]
- Flores, E.; Ares, J.R.; Castellanos-Gomez, A.; Barawi, M.; Ferrer, I.J.; Sánchez, C. Thermoelectric power of bulk black-phosphorus. Appl. Phys. Lett. 2015, 106, 022102. [Google Scholar] [CrossRef]
- Ma, R.; Geng, H.; Deng, W.Y.; Chen, M.N.; Sheng, L.; Xing, D.Y. Effect of the edge states on the conductance and thermopower in zigzag phosphorene nanoribbons. Phys. Rev. B 2016, 94, 125410. [Google Scholar] [CrossRef] [Green Version]
- Mani, A.; Benjamin, C. Strained-graphene-based highly efficient quantum heat engine operating at maximum power. Phys. Rev. E 2017, 96, 032118. [Google Scholar] [CrossRef] [Green Version]
- Ildarabadi, F.; Farghadan, R. Spin-thermoelectric transport in nonuniform strained zigzag graphene nanoribbons. Phys. Rev.B 2021, 103, 115424. [Google Scholar] [CrossRef]
- Saiz-Bretín, M.; Malyshev, A.V.; Orellana, P.A.; Domínguez-Adame, F. Enhancing thermoelectric properties of graphene quantum rings. Phys. Rev. B 2015, 91, 085431. [Google Scholar] [CrossRef]
- Wierzbicki, M.; Swirkowicz, R.; Barnaś, J. Giant spin thermoelectric efficiency in ferromagnetic graphene nanoribbons with antidots. Phys. Rev. B 2013, 88, 235434. [Google Scholar] [CrossRef]
- Gunst, T.; Markussen, T.; Jauho, A.-P.; Brandbyge, M. Thermoelectric properties of finite graphene antidot lattices. Phys. Rev. B 2011, 84, 155449. [Google Scholar] [CrossRef] [Green Version]
- Terada, T.; Uematsu, Y.; Ishibe, T.; Naruse, N.; Sato, K.; Nguyen, T.Q.; Kobayashi, E.; Nakano, H.; Nakamura, Y. Giant Enhancement of Seebeck Coefficient by Deformation of Silicene Buckled Structure in Calcium-Intercalated Layered Silicene Film. Adv. Mater. Interfaces 2022, 9, 2101752. [Google Scholar] [CrossRef]
- Kurpas, M.; Gmitra, M.; Fabian, J. Spin properties of black phosphorus and phosphorene, and their prospects for spincalorics. J. Phys. D Appl. Phys. 2018, 51, 174001. [Google Scholar] [CrossRef]
- Chen, H.; Li, B.; Yang, J. Proximity Effect Induced Spin Injection in Phosphorene on Magnetic Insulator. ACS Appl. Mater. Interfaces 2017, 9, 38999–39010. [Google Scholar] [CrossRef]
- Rudenko, A.N.; Katsnelson, M.I. Quasiparticle band structure and tight-binding model for single- and bilayer black phosphorus. Phys. Rev. B 2014, 89, 201408. [Google Scholar] [CrossRef] [Green Version]
- Groth, C.W.; Wimmer, M.; Akhmerov, A.R.; Waintal, X. Kwant: A software package for quantum transport. New J. Phys. 2014, 16, 063065. [Google Scholar] [CrossRef]
- Hao, L.; Lee, T.K. Thermopower of gapped bilayer graphene. Phys. Rev. B 2010, 81, 165445. [Google Scholar] [CrossRef] [Green Version]
- Páez, C.J.; Bahamon, D.A.; Pereira, A.L.; Schulz, P.A. Zigzag phosphorene nanoribbons: One-dimensional resonant channels in two-dimensional atomic crystals. Beilstein J. Nanotechnol. 2016, 7, 1983–1990. [Google Scholar] [CrossRef] [Green Version]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, J.; Zhang, Q. Enhanced Spin Thermopower in Phosphorene Nanoribbons via Edge-State Modifications. Nanomaterials 2022, 12, 2350. https://doi.org/10.3390/nano12142350
Ou J, Zhang Q. Enhanced Spin Thermopower in Phosphorene Nanoribbons via Edge-State Modifications. Nanomaterials. 2022; 12(14):2350. https://doi.org/10.3390/nano12142350
Chicago/Turabian StyleOu, Junheng, and Qingtian Zhang. 2022. "Enhanced Spin Thermopower in Phosphorene Nanoribbons via Edge-State Modifications" Nanomaterials 12, no. 14: 2350. https://doi.org/10.3390/nano12142350
APA StyleOu, J., & Zhang, Q. (2022). Enhanced Spin Thermopower in Phosphorene Nanoribbons via Edge-State Modifications. Nanomaterials, 12(14), 2350. https://doi.org/10.3390/nano12142350





