The Design of Aluminum-Matrix Composites Reinforced with AlCoCrFeNi High-Entropy Alloy Nanoparticles by First-Principles Studies on the Properties of Interfaces
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussion
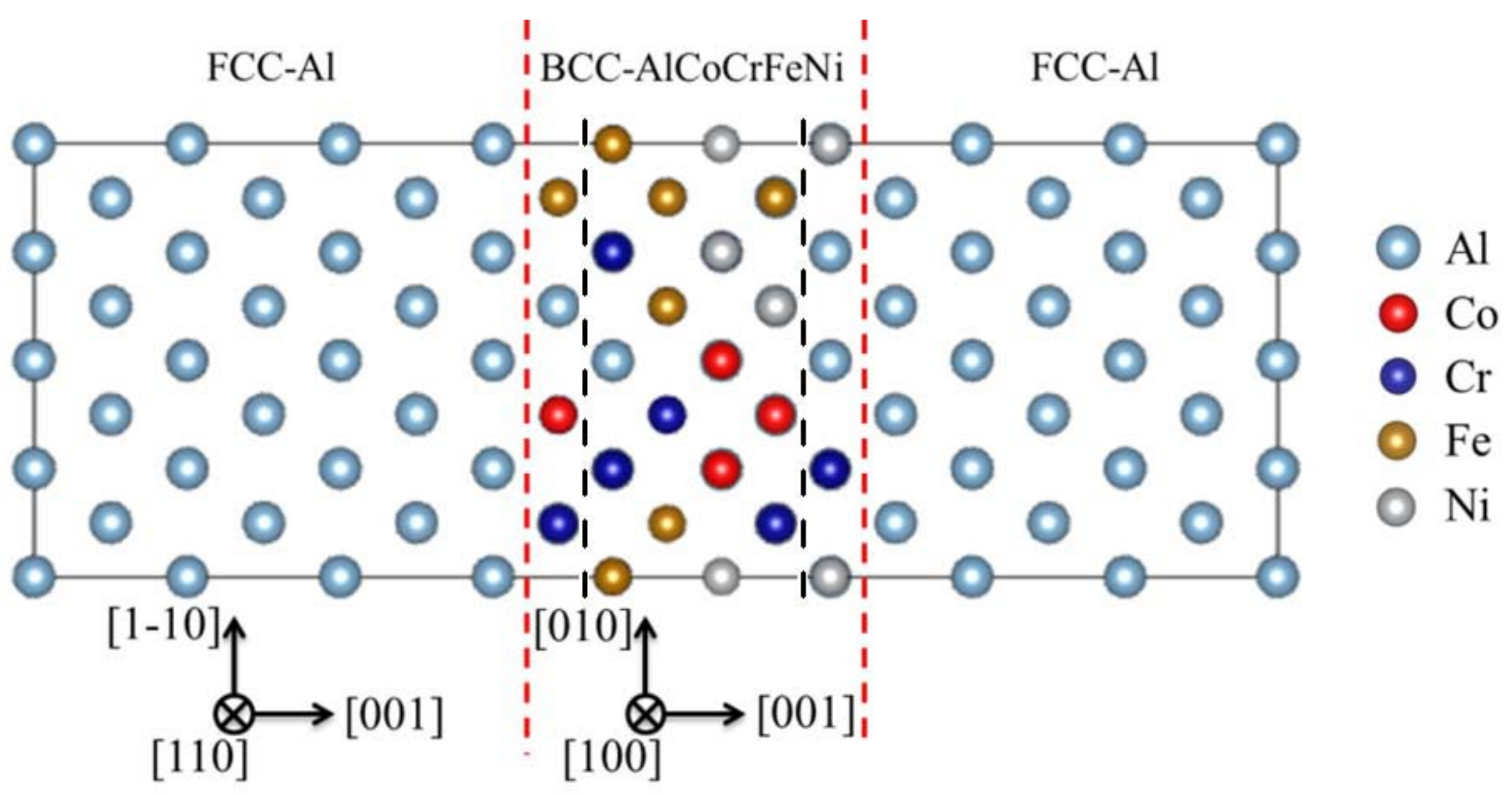
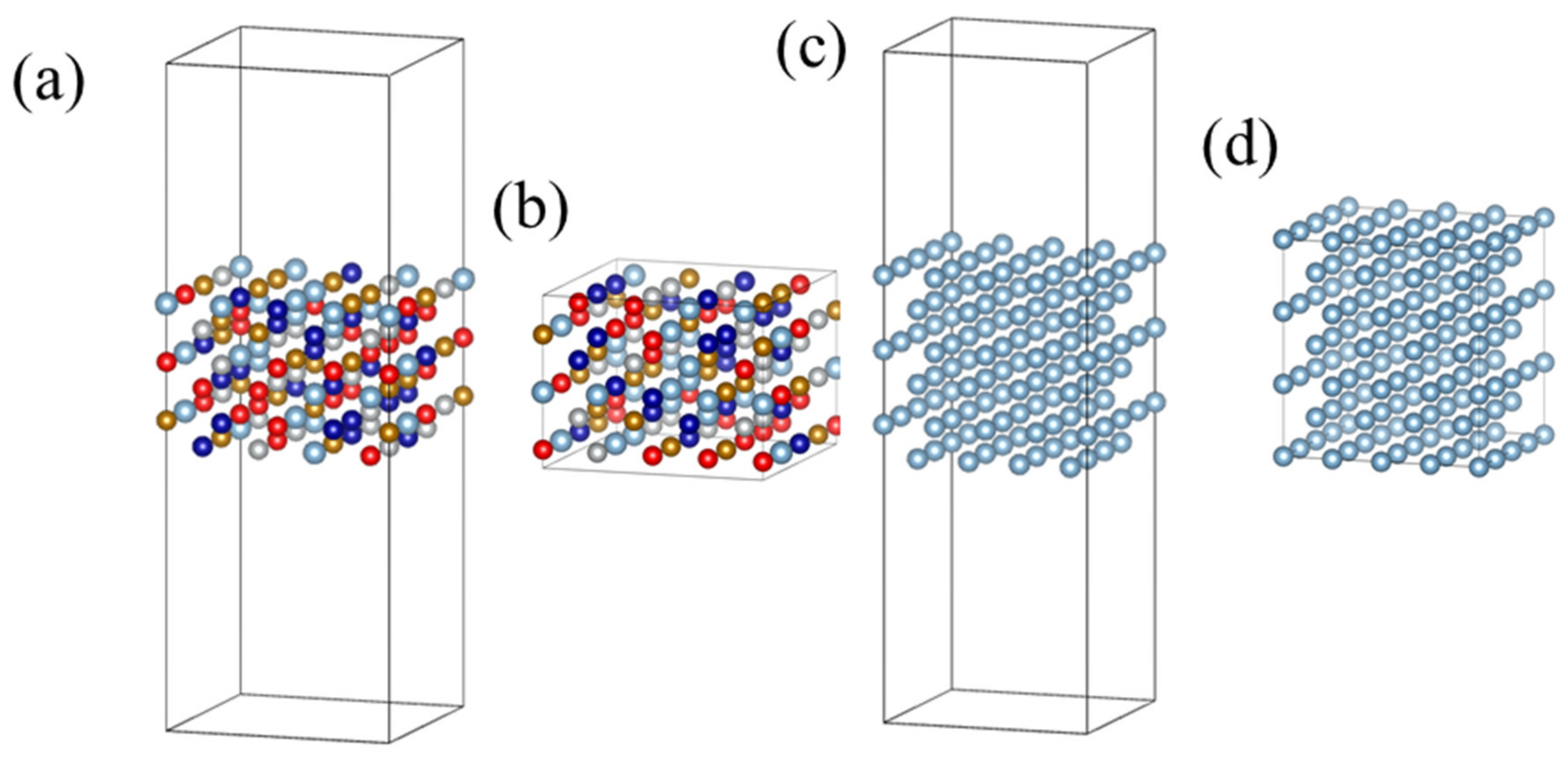
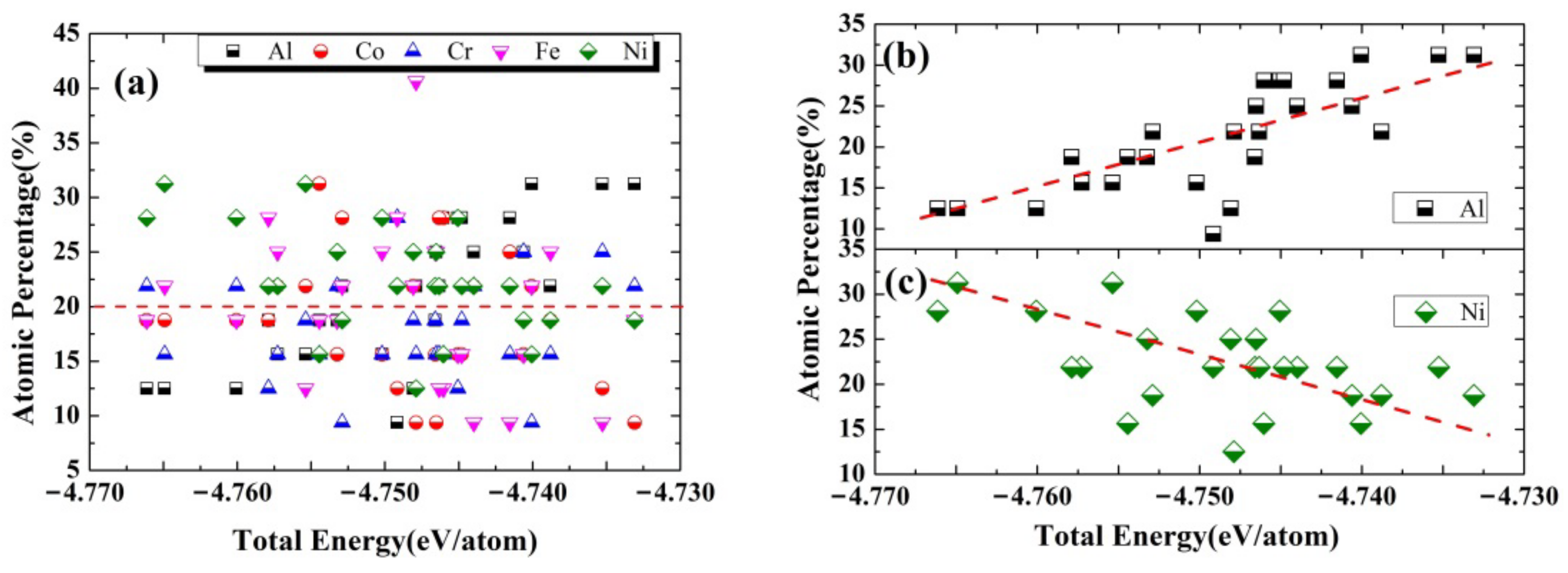
3.1. The Stability of HEA-Reinforced AMCs
3.2. Electronic Properties
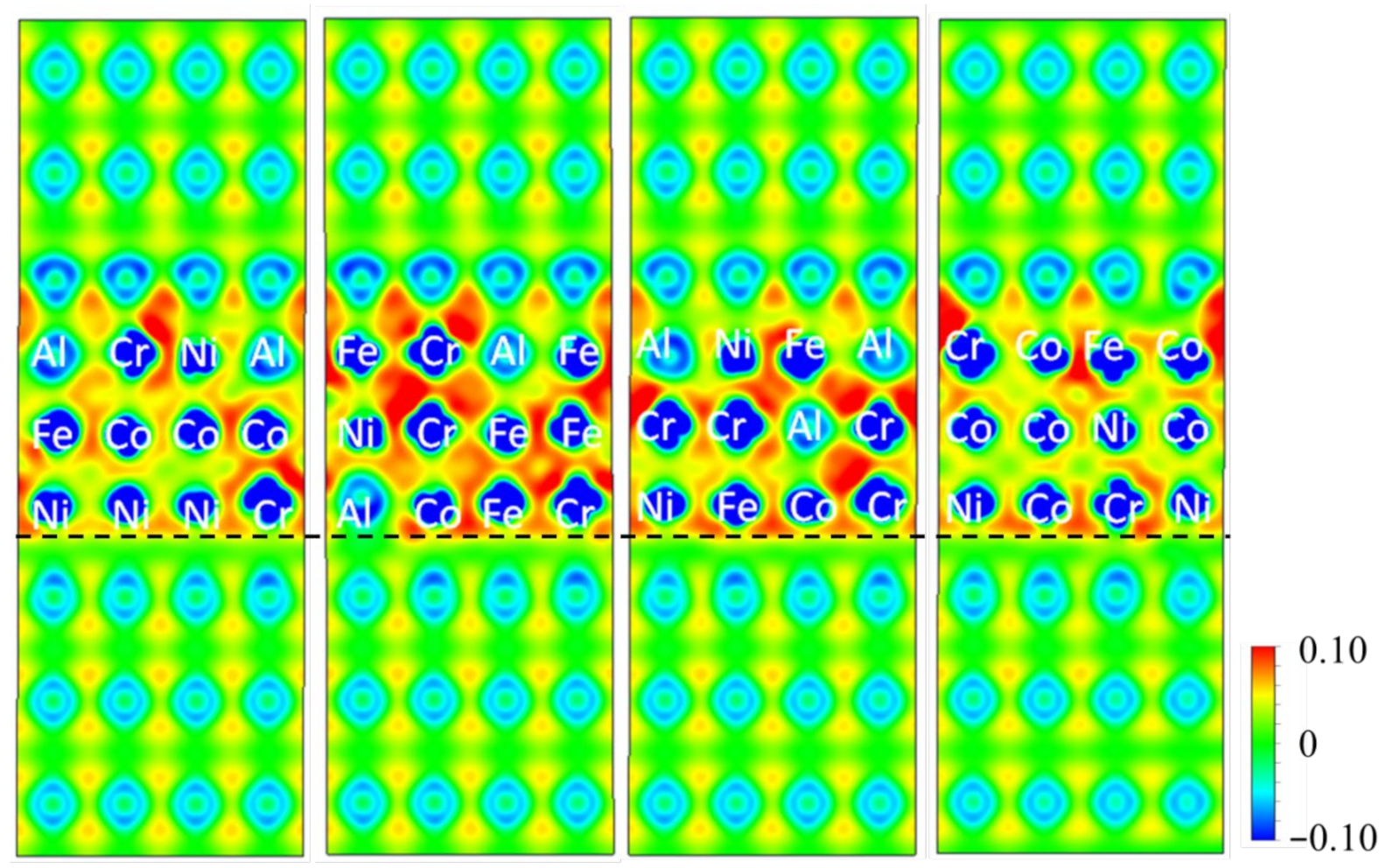
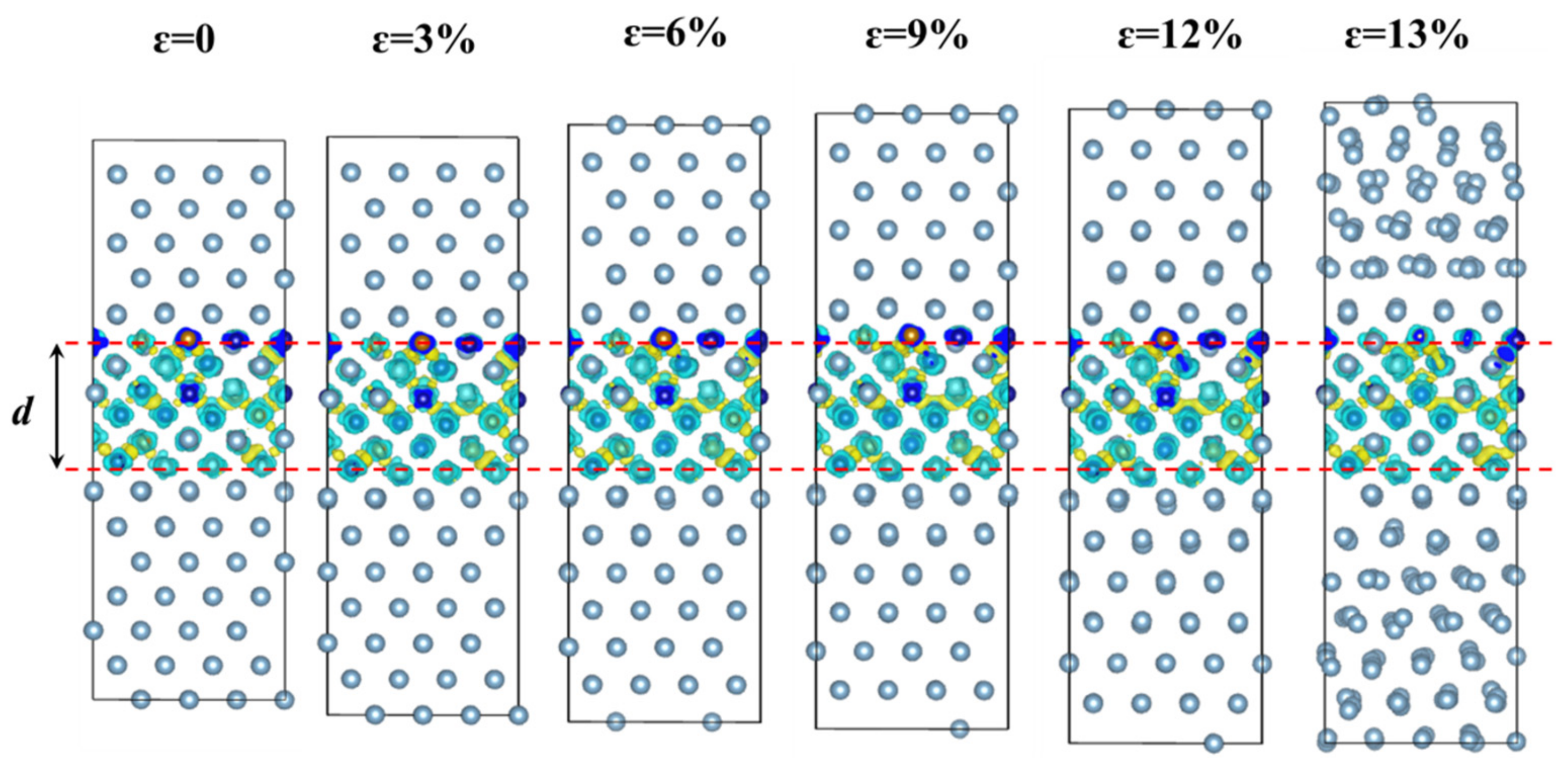
3.2.1. Differential Charge Density
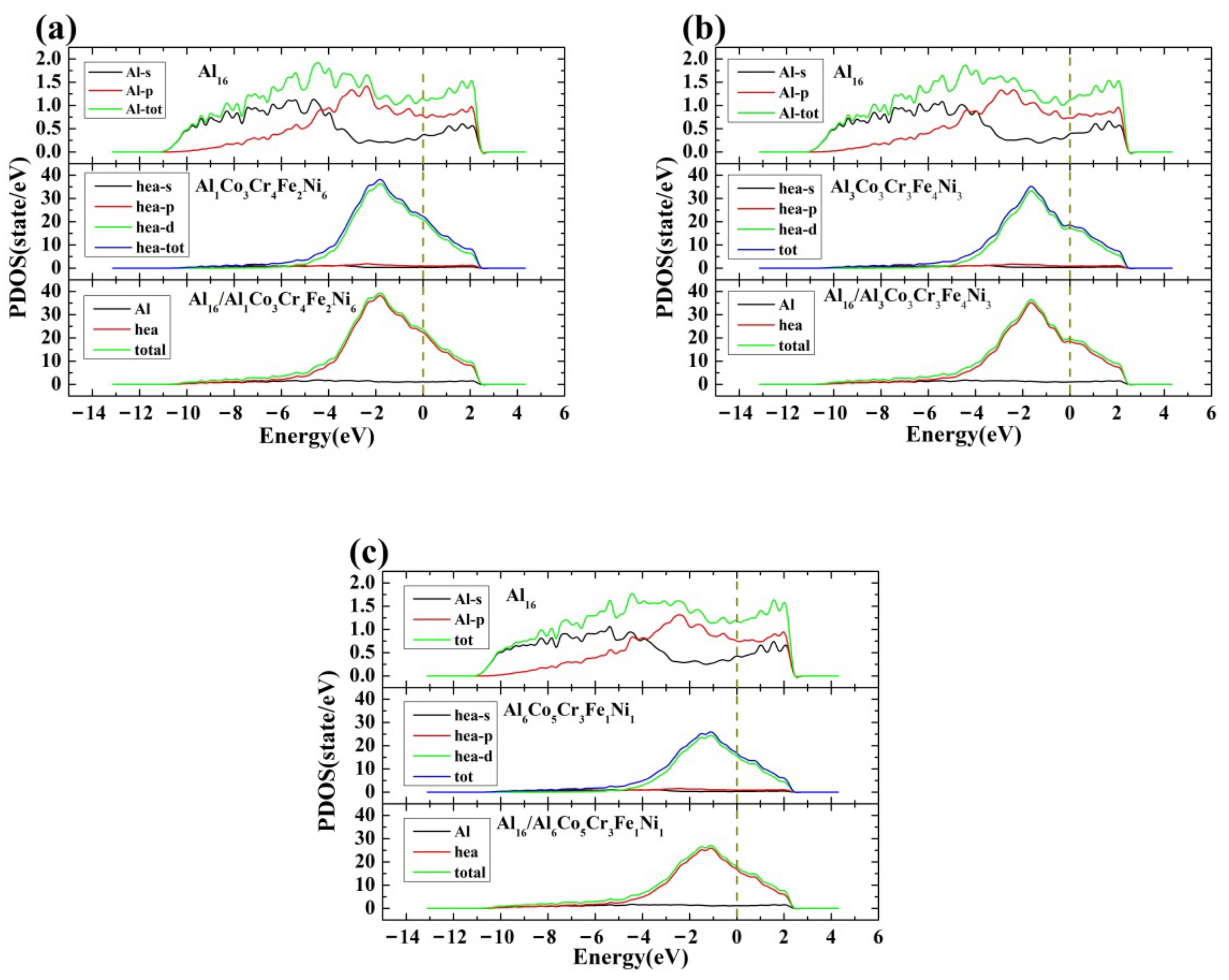
3.2.2. Density of States
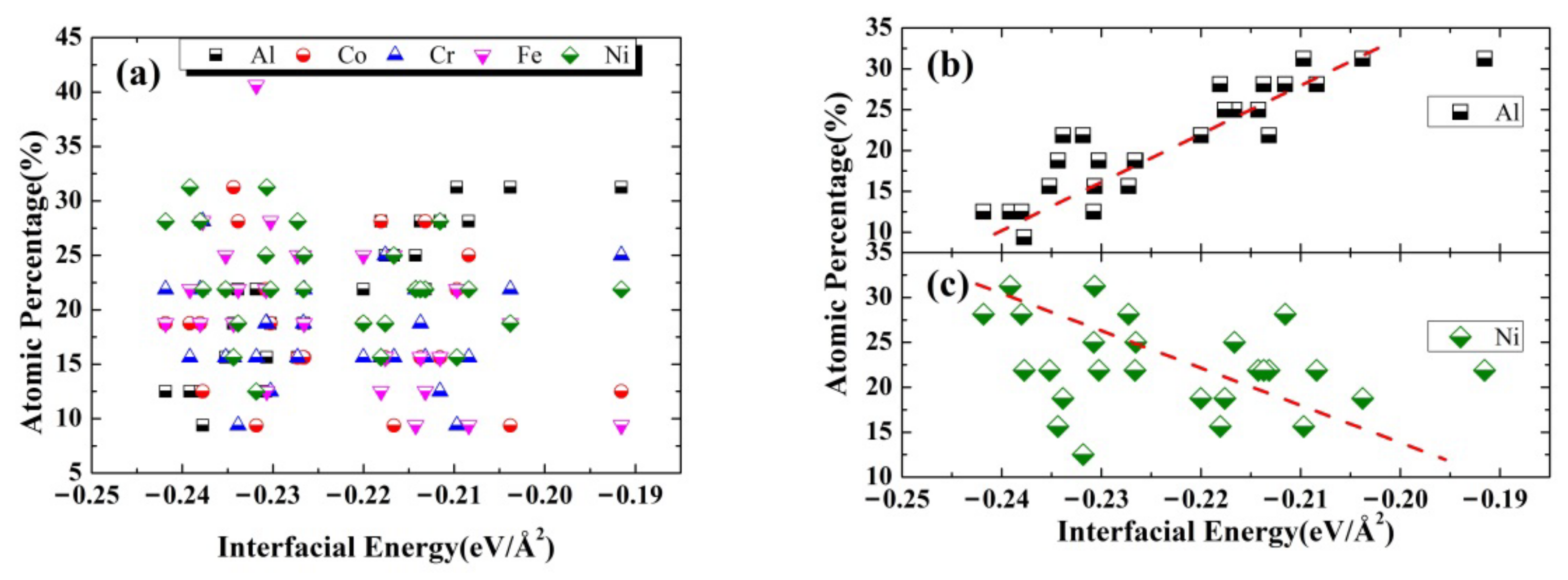
3.3. The Interfacial Energy
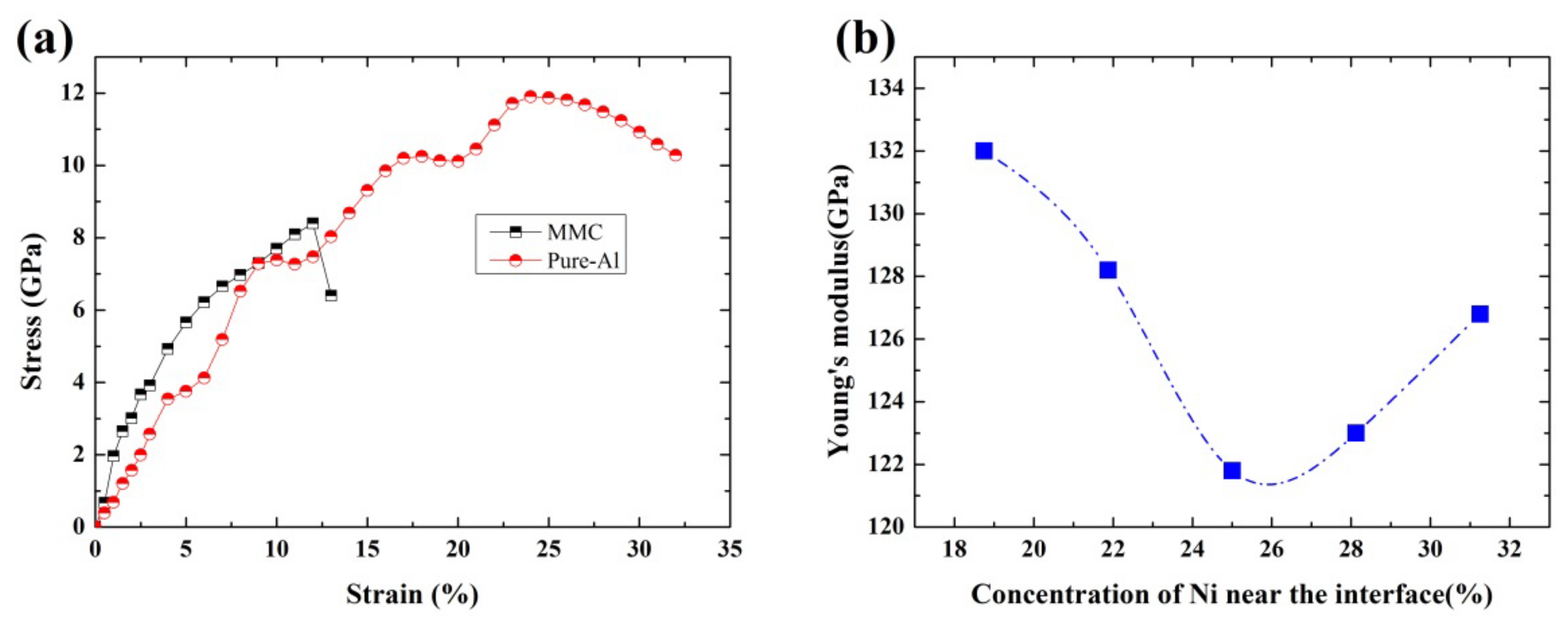
3.4. Mechanical Properties
3.5. Discussion and Remarks on the Designs of HEA-Reinforced AMCs
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Selvakumar, S.; Dinaharan, I.; Palanivel, R.; Babu, B.G. Characterization of molybdenum particles reinforced Al6082 aluminum matrix composites with improved ductility produced using friction stir processing. Mater. Charact. 2017, 125, 13–22. [Google Scholar] [CrossRef]
- Ferraris, M.; Gili, F.; Lizarralde, X.; Igartua, A.; Mendoza, G.; Blugan, G.; Gorjan, L.; Casalegno, V. SiC particle reinforced Al matrix composites brazed on aluminum body for lightweight wear resistant brakes. Ceram. Int. 2022, 48, 10941–10951. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, H.M.; Cui, Z.S.; Chen, Z.; Chen, D. Compressive response and microstructural evolution of in-situ TiB2 particle-reinforced 7075 aluminum matrix composite. Trans. Nonferrous Met. Soc. China 2021, 31, 1235–1248. [Google Scholar] [CrossRef]
- Guan, H.D.; Li, C.J.; Gao, P.; Prashanth, K.G.; Tan, J.; Eckert, J.; Tao, J.M.; Yi, J.H. Aluminum matrix composites reinforced with metallic glass particles with core-shell structure. Mater. Sci. Eng. A 2020, 771, 138630. [Google Scholar] [CrossRef]
- Hong, S.J.; Kim, H.M.; Huh, D.; Suryanarayana, C.; Chun, B.S. Effect of clustering on the mechanical properties of SiC particulate-reinforced aluminum alloy 2024 metal matrix composites. Mater. Sci. Eng. A 2003, 347, 198–204. [Google Scholar] [CrossRef]
- Moses, J.J.; Dinaharan, I.; Sekhar, S.J. Prediction of influence of process parameters on tensile strength of AA6061/TiC aluminum matrix composites produced using stir casting. Trans. Nonferrous Met. Soc. China 2016, 26, 1498–1511. [Google Scholar] [CrossRef]
- He, B.; Li, H.; Ma, X.; Li, J.; Fan, S. Plane Machining by Inner-Jet Electrochemical Milling of TiB2/7050 Aluminum Matrix Composite. Appl. Sci. 2021, 11, 8087. [Google Scholar] [CrossRef]
- Zhao, Y.T.; Zhang, S.L.; Chen, G. Aluminum matrix composites reinforced by in situ Al2O3 and Al3Zr particles fabricated via magnetochemistry reaction. Trans. Nonferrous Met. Soc. China 2010, 20, 2129–2133. [Google Scholar] [CrossRef]
- Liu, X.; Dong, H.; Lv, X.; Bai, C. The wettability and interfacial characterization between γ-TiAl alloy and ceramic reinforcements. Compos. Interfaces 2018, 25, 713–723. [Google Scholar] [CrossRef]
- Voigt, C.; Ditscherlein, L.; Werzner, E.; Zienert, T.; Nowak, R.; Peuker, U.; Sobczak, N.; Aneziris, C.G. Wettability of AlSi7Mg alloy on alumina, spinel, mullite and rutile and its influence on the aluminum melt filtration efficiency. Mater. Des. 2018, 150, 75–85. [Google Scholar] [CrossRef]
- Balakrishnan, M.; Dinaharan, I.; Kalaiselvan, K.; Palanivel, R. Friction stir processing of Al3Ni intermetallic particulate reinforced cast aluminum matrix composites: Microstructure and tensile properties. J. Mater. Res. Technol. 2020, 9, 4356–4367. [Google Scholar] [CrossRef]
- Zheng, R.; Yang, H.; Liu, T.; Ameyama, K.; Ma, C. Microstructure and mechanical properties of aluminum alloy matrix composites reinforced with Fe-based metallic glass particles. Mater. Des. 2014, 53, 512–518. [Google Scholar] [CrossRef]
- Heim, F.M.; Zhang, Y.; Li, X. Uniting Strength and Toughness of Al Matrix Composites with Coordinated Al3Ni and Al3Ti Reinforcements. Adv. Eng. Mater. 2018, 20, 1700605. [Google Scholar] [CrossRef]
- Qiu, X.W. Microstructure and properties of AlCrFeNiCoCu high entropy alloy prepared by powder metallurgy. J. Alloys Compd. 2013, 555, 246–249. [Google Scholar] [CrossRef]
- Shao, L.; Zhang, T.; Li, L.; Zhao, Y.; Huang, J.; Liaw, P.K.; Zhang, Y. A Low-Cost Lightweight Entropic Alloy with High Strength. J. Mater. Eng. Perform. 2018, 27, 6648–6656. [Google Scholar] [CrossRef]
- Wu, M.; Li, Z.; Gault, B.; Munroe, P.; Baker, I. The effects of carbon on the phase stability and mechanical properties of heat-treated FeNiMnCrAl high entropy alloys. Mater. Sci. Eng. A 2019, 748, 59–73. [Google Scholar] [CrossRef]
- Varvenne, C.; Curtin, W.A. Strengthening of high entropy alloys by dilute solute additions: CoCrFeNiAlx and CoCrFeNiMnAlx alloys. Scr. Mater. 2017, 138, 92–95. [Google Scholar] [CrossRef] [Green Version]
- Antillon, E.; Woodward, C.; Rao, S.I.; Akdim, B.; Parthasarathy, T.A. Chemical short range order strengthening in a model FCC high entropy alloy. Acta Mater. 2020, 190, 29–42. [Google Scholar] [CrossRef]
- Guo, S.; Liu, C.T. Phase stability in high entropy alloys: Formation of solid-solution phase or amorphous phase. Prog. Nat. Sci. Mater. Int. 2011, 21, 433–446. [Google Scholar] [CrossRef] [Green Version]
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Karthik, G.M.; Panikar, S.; Ram, G.D.J.; Kottada, R.S. Additive manufacturing of an aluminum matrix composite reinforced with nanocrystalline high-entropy alloy particles. Mater. Sci. Eng. A 2017, 679, 193–203. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, J.; Li, Z.; Wang, X.; Fan, X.; Liu, J. Formation of transition layer and its effect on mechanical properties of AlCoCrFeNi high-entropy alloy/Al composites. J. Alloys Compd. 2019, 780, 558–564. [Google Scholar] [CrossRef]
- Chen, W.; Li, Z.; Lu, T.; He, T.; Li, R.; Li, B.; Wan, B.; Fu, Z.; Scudino, S. Effect of ball milling on microstructure and mechanical properties of 6061Al matrix composites reinforced with high-entropy alloy particles. Mater. Sci. Eng. A 2019, 762, 138116. [Google Scholar] [CrossRef]
- Yang, X.; Zhai, X.; Dong, P.; Yan, Z.; Cheng, B.; Zhang, H.; Wang, W. Interface characteristics of high-entropy alloy/Al-Mg composites by underwater friction stir processing. Mater. Lett. 2020, 275, 128200. [Google Scholar] [CrossRef]
- Yuan, Z.; Tian, W.; Li, F.; Fu, Q.; Wang, X.; Qian, W.; An, W. Effect of heat treatment on the interface of high-entropy alloy particles reinforced aluminum matrix composites. J. Alloys Compd. 2020, 822, 153658. [Google Scholar] [CrossRef]
- Zhang, T.; Feng, K.; Li, Z.; Kokawa, H. Effects of rare earth elements on the microstructure and wear properties of TiB2 reinforced aluminum matrix composite coatings: Experiments and first principles calculations. Appl. Surf. Sci. 2020, 530, 147051. [Google Scholar] [CrossRef]
- Wang, Z.J.; Liu, S.; Qiu, Z.X.; Sun, H.Y.; Liu, W.C. First-principles calculations on the interface of the Al/TiC aluminum matrix composites. Appl. Surf. Sci. 2020, 505, 144502. [Google Scholar] [CrossRef]
- Liu, P.; Xie, J.; Wang, A.; Ma, D.; Mao, Z. First-principles prediction of enhancing graphene/Al interface bonding strength by graphene doping strategy. Appl. Surf. Sci. 2020, 517, 146040. [Google Scholar] [CrossRef]
- Mohanty, S.; Maity, T.N.; Mukhopadhyay, S.; Sarkar, S.; Gurao, N.P.; Bhowmick, S.; Biswas, K. Powder metallurgical processing of equiatomic AlCoCrFeNi high entropy alloy: Microstructure and mechanical properties. Mater. Sci. Eng. A 2017, 679, 299–313. [Google Scholar] [CrossRef]
- Jacobs, M.H.G.; Schmid-Fetzer, R. Thermodynamic properties and equation of state of fcc aluminum and bcc iron, derived from a lattice vibrational method. Phys. Chem. Miner. 2010, 37, 721–739. [Google Scholar] [CrossRef]
- Van, W.A. Multicomponent multisublattice alloys, nonconfigurational entropy and other additions to the Alloy Theoretic Automated Toolkit. Calphad 2009, 33, 266–278. [Google Scholar]
- Kresse, G.; Furthmüller, J. Software VASP, Vienna (1999). Phys. Rev. B 1996, 54, 169. [Google Scholar]
- Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Hafner, J. Materials simulations using VASP—a quantum perspective to materials science. Comput. Phys. Commun. 2007, 177, 6–13. [Google Scholar] [CrossRef]
- Evarestov, R.A.; Smirnov, V.P. Modification of the Monkhorst-Pack special points meshes in the Brillouin zone for density functional theory and Hartree-Fock calculations. Phys. Rev. B 2004, 70, 233101. [Google Scholar] [CrossRef]
- Zheng, G. Molecular dynamics and first-principles studies on the deformation mechanisms of nanostructured cobalt. J. Alloys Compd. 2010, 504, S467–S471. [Google Scholar] [CrossRef]
- Allred, A.L. Electronegativity values from thermochemical data. J. Inorg. Nucl. Chem. 1961, 17, 215–221. [Google Scholar] [CrossRef]
- Liu, Y.; Wen, J.C.; Zhang, X.Y.; Huang, Y.C. A comparative study on heterogeneous nucleation and mechanical properties of the fcc-Al/L12-Al3M (M = Sc, Ti, V, Y, Zr, Nb) interface from first-principles calculations. Phys. Chem. Chem. Phys. 2021, 23, 4718–4727. [Google Scholar] [CrossRef]
- Doležal, T.D.; Samin, A.J. Adsorption of Oxygen to High Entropy Alloy Surfaces for up to 2 ML Coverage Using Density Functional Theory and Monte Carlo Calculations. Langmuir 2022, 38, 3158–3169. [Google Scholar] [CrossRef]
- Gupta, S.S.; van Huis, M.A.; Dijkstra, M.; Sluiter, M.H.F. Depth dependence of vacancy formation energy at (100), (110), and (111) Al surfaces: A first-principles study. Phys. Rev. B 2016, 93, 085432. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Li, Y.; Wang, F.; Meng, X.; Wan, L.; Dong, Z.; Huang, Y. Friction stir processing of high-entropy alloy reinforced aluminum matrix composites for mechanical properties enhancement. Mater. Sci. Eng. A 2020, 792, 139755. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zheng, G. The Design of Aluminum-Matrix Composites Reinforced with AlCoCrFeNi High-Entropy Alloy Nanoparticles by First-Principles Studies on the Properties of Interfaces. Nanomaterials 2022, 12, 2157. https://doi.org/10.3390/nano12132157
Liu Y, Zheng G. The Design of Aluminum-Matrix Composites Reinforced with AlCoCrFeNi High-Entropy Alloy Nanoparticles by First-Principles Studies on the Properties of Interfaces. Nanomaterials. 2022; 12(13):2157. https://doi.org/10.3390/nano12132157
Chicago/Turabian StyleLiu, Yu, and Guangping Zheng. 2022. "The Design of Aluminum-Matrix Composites Reinforced with AlCoCrFeNi High-Entropy Alloy Nanoparticles by First-Principles Studies on the Properties of Interfaces" Nanomaterials 12, no. 13: 2157. https://doi.org/10.3390/nano12132157
APA StyleLiu, Y., & Zheng, G. (2022). The Design of Aluminum-Matrix Composites Reinforced with AlCoCrFeNi High-Entropy Alloy Nanoparticles by First-Principles Studies on the Properties of Interfaces. Nanomaterials, 12(13), 2157. https://doi.org/10.3390/nano12132157




