Investigation on Plastic Flow Behaviors of FCC Polycrystalline Aluminum under Pre-Cyclic Tension-Compression Loading: Experiments and Crystal Plasticity Modeling
Abstract
:1. Introduction
2. Material and Experimental Procedure
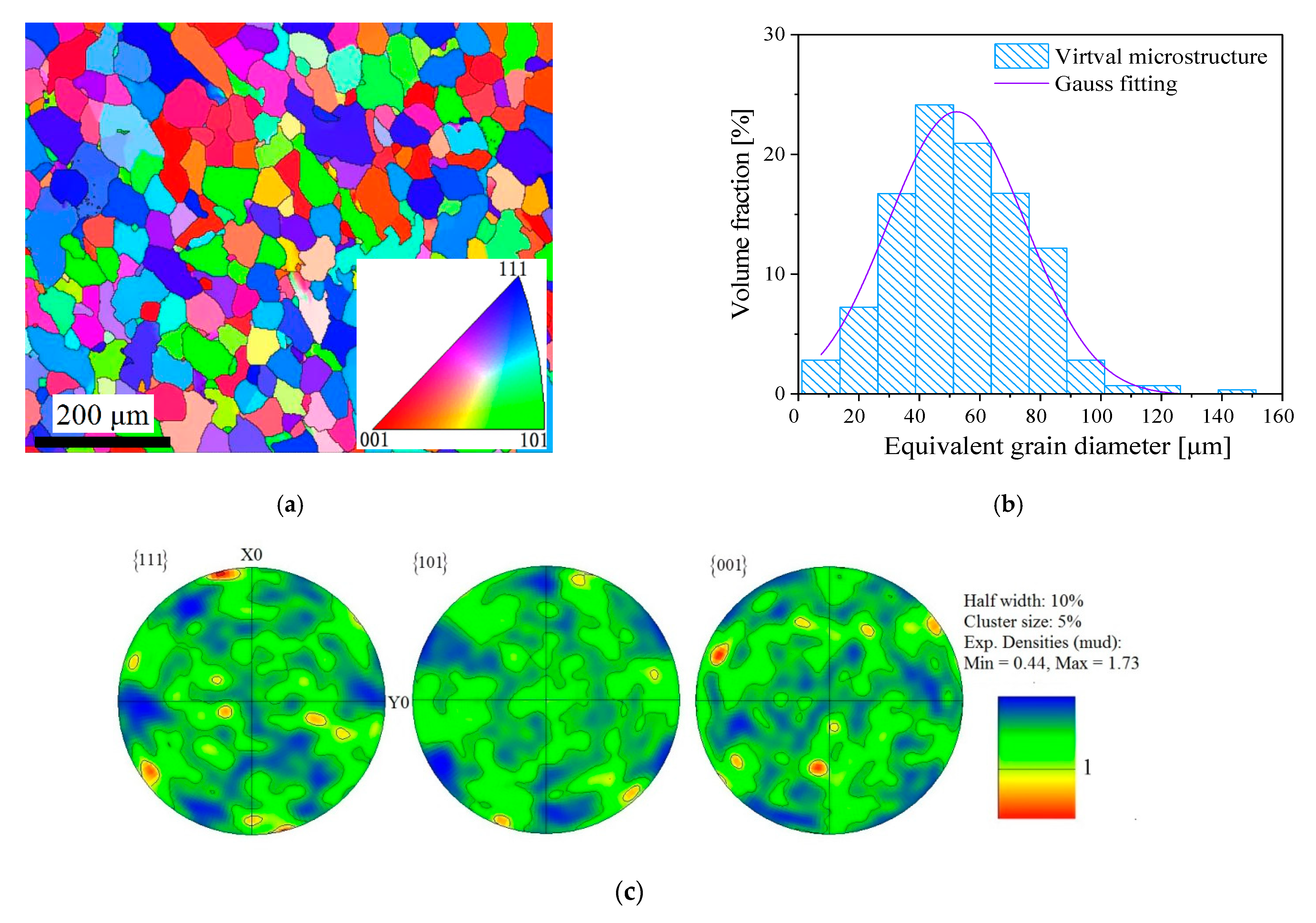
2.1. Experimrntal Material and Specimen
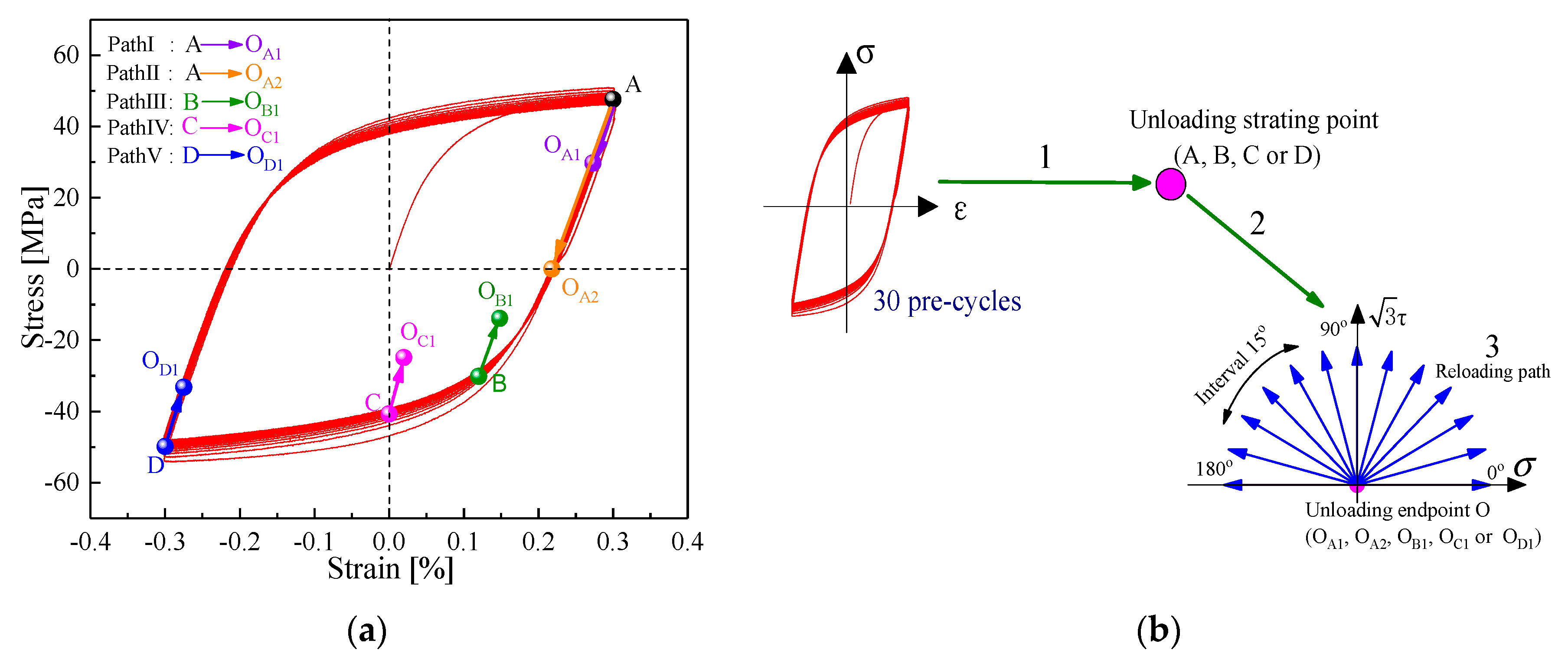
2.2. Experiment Produce
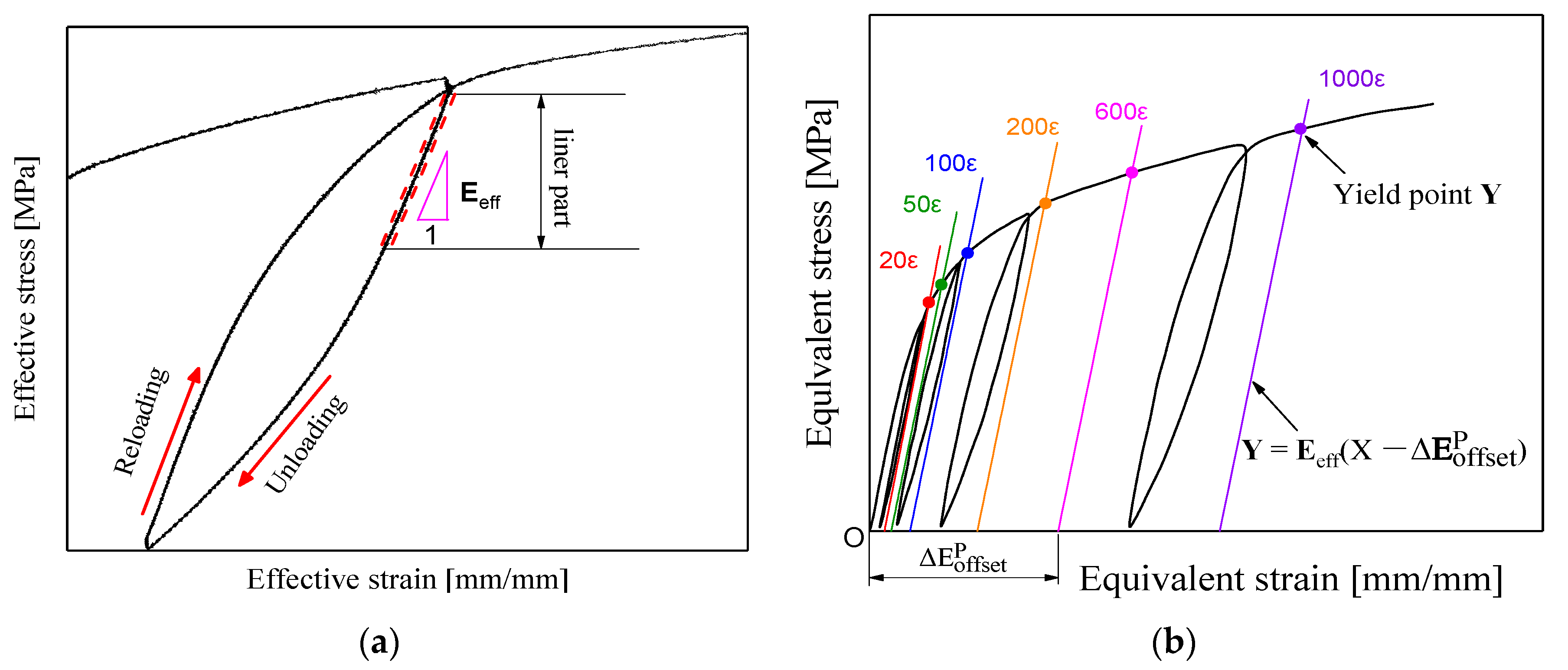
2.3. Determining the Orthogonal Direction and Plastic Strain Incremental Direction of Yield Point
3. Constitutive Relationships and Coupling Methodology
3.1. Flow Rule and Strain Hardening Modeling
3.2. Hardening Rules
3.3. Back Stress Evolution
4. Modeling
4.1. Finite Element Models
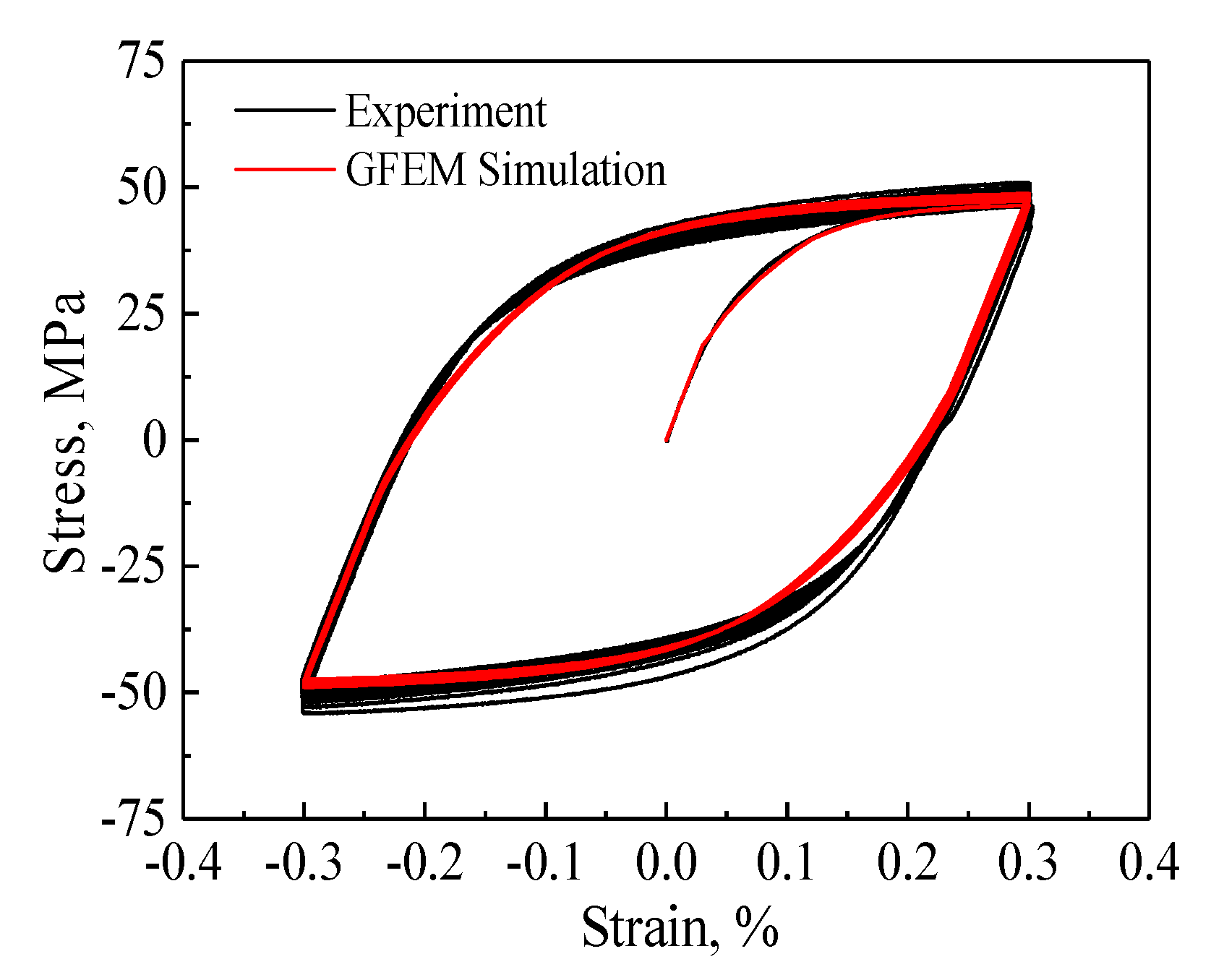
4.2. Parameter Calibration of Crystalline Plasticity Models
4.3. Effects of Loading Direction on Anisotropic Hardening Characteristics
5. Results and Discussion
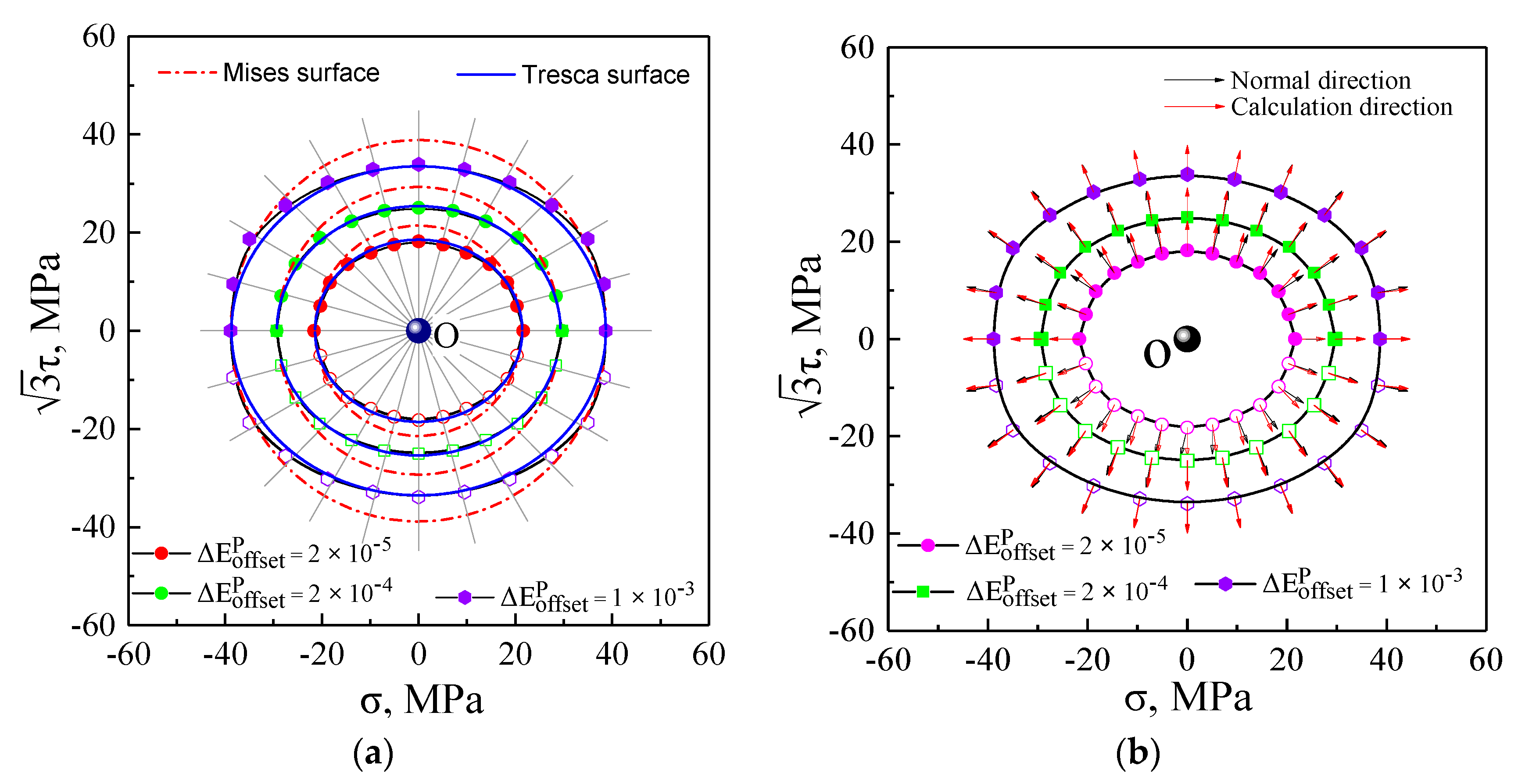
5.1. Initial Yield Surfaces and Plastic Flow Directions
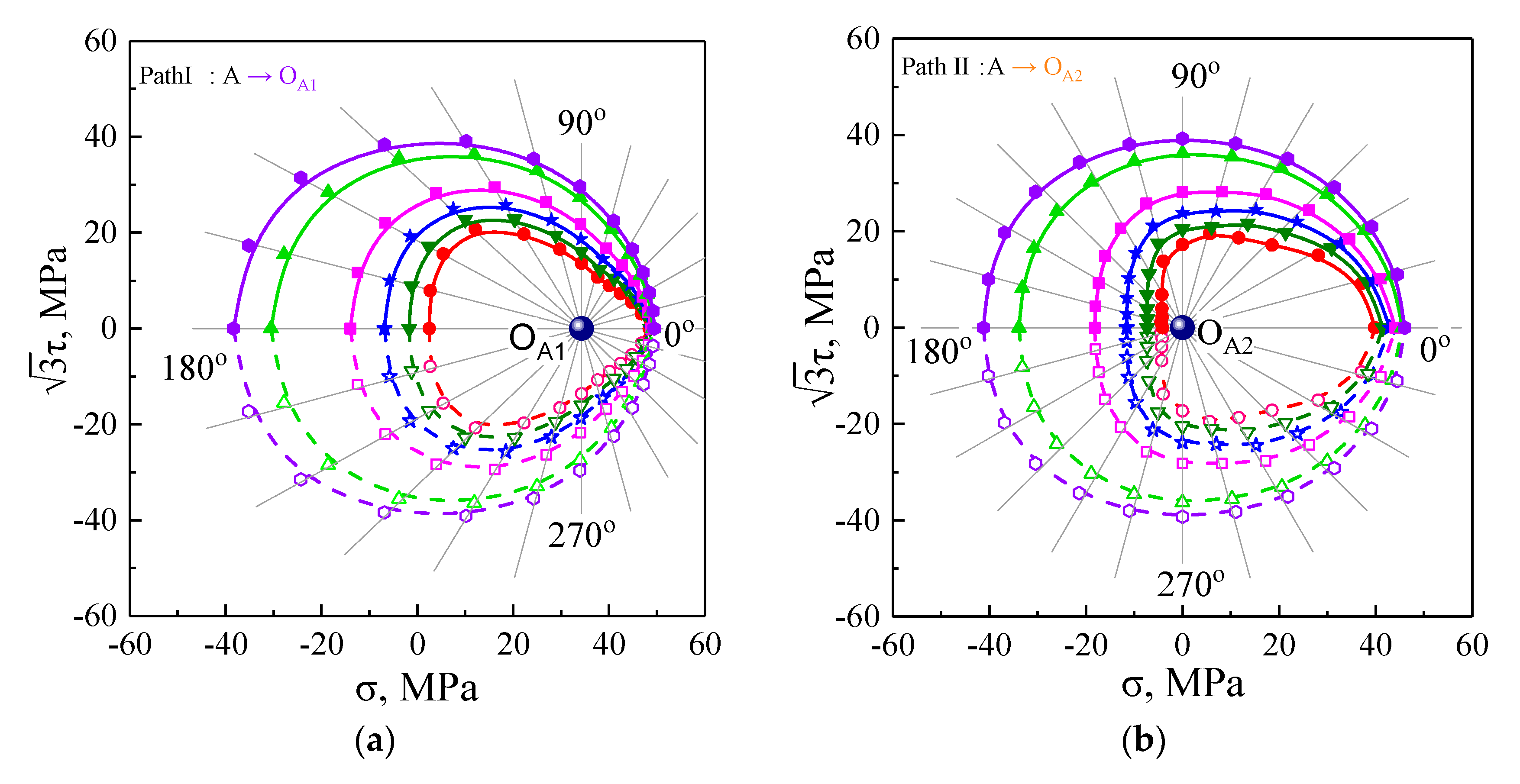
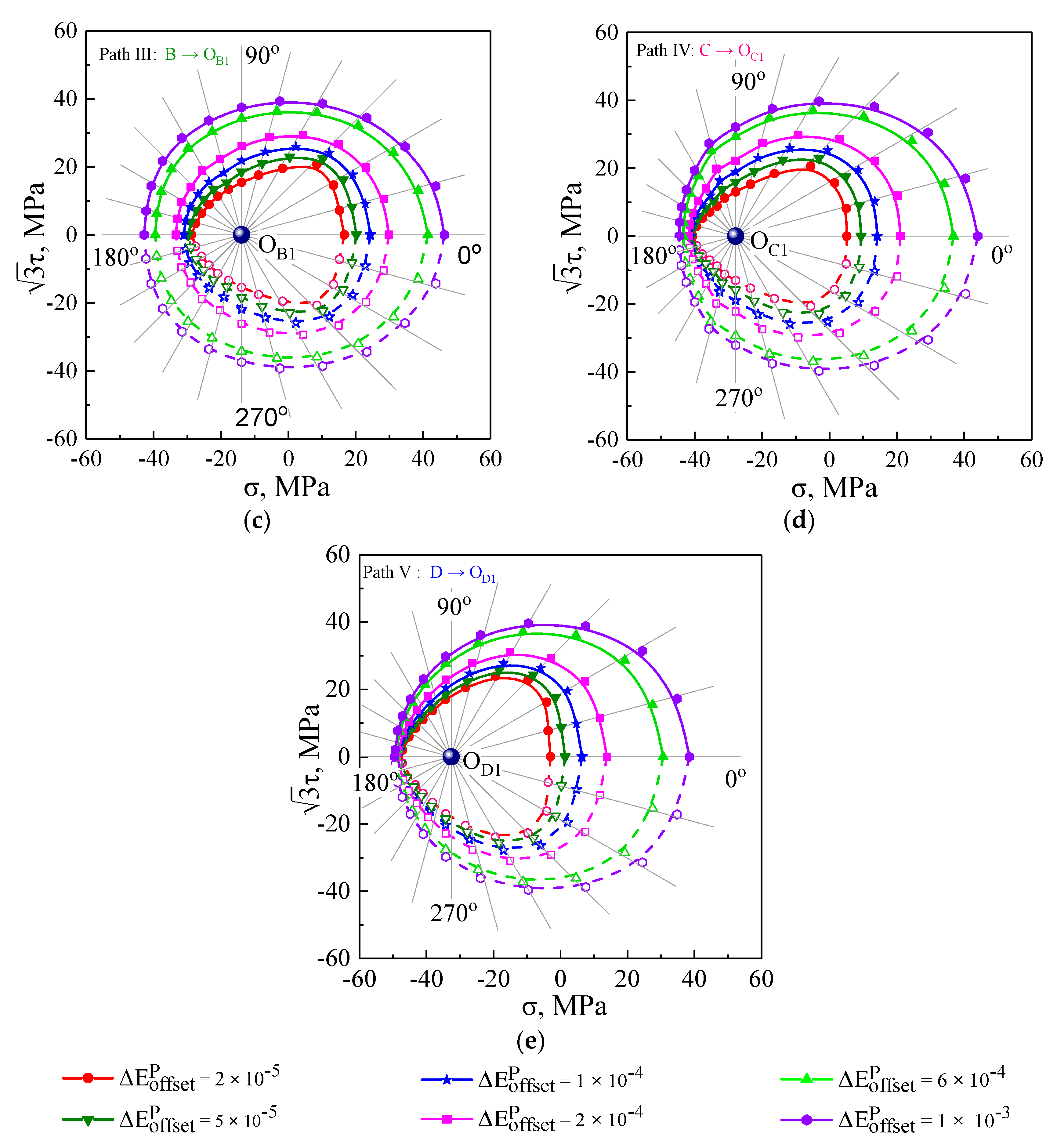
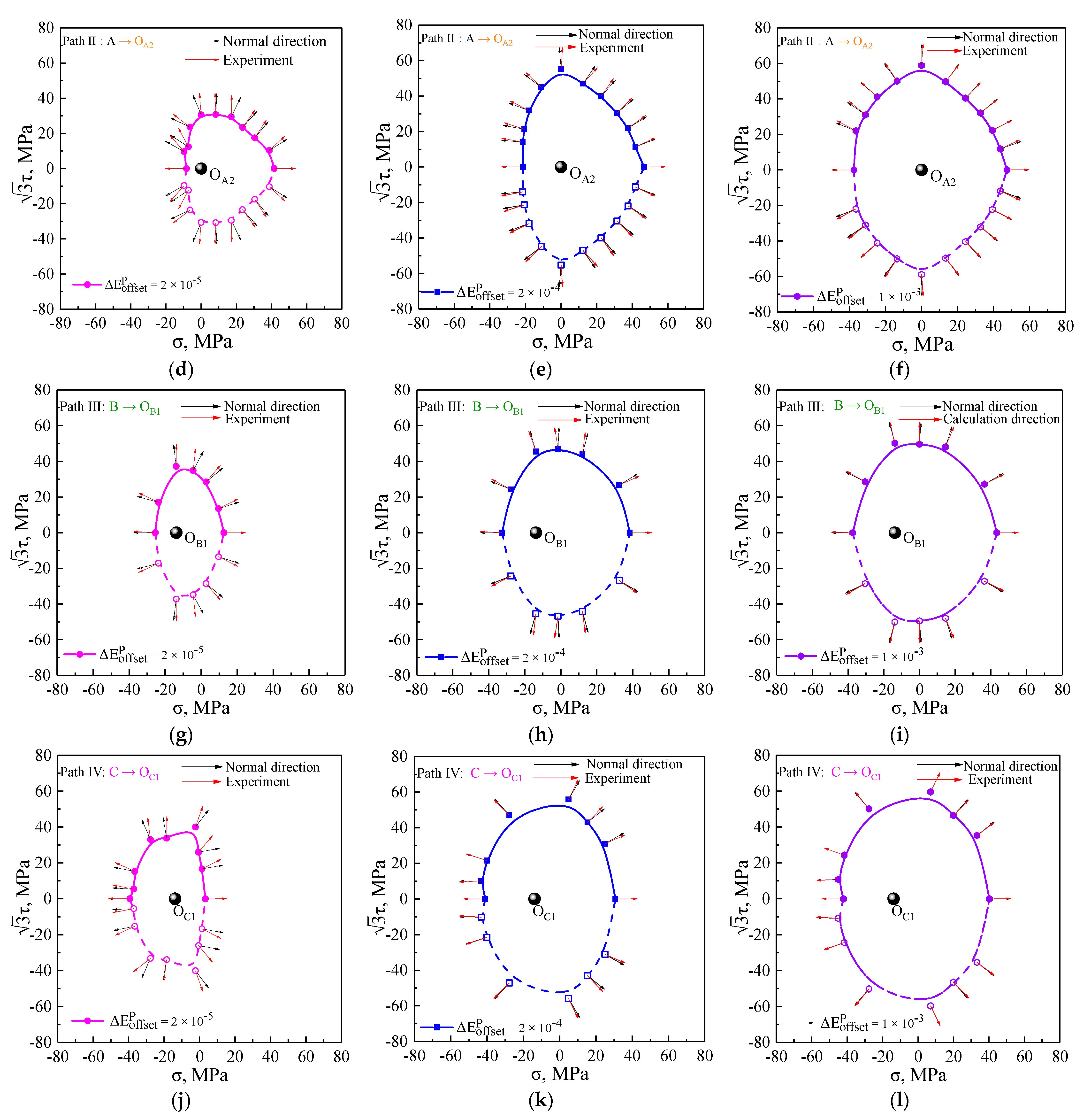
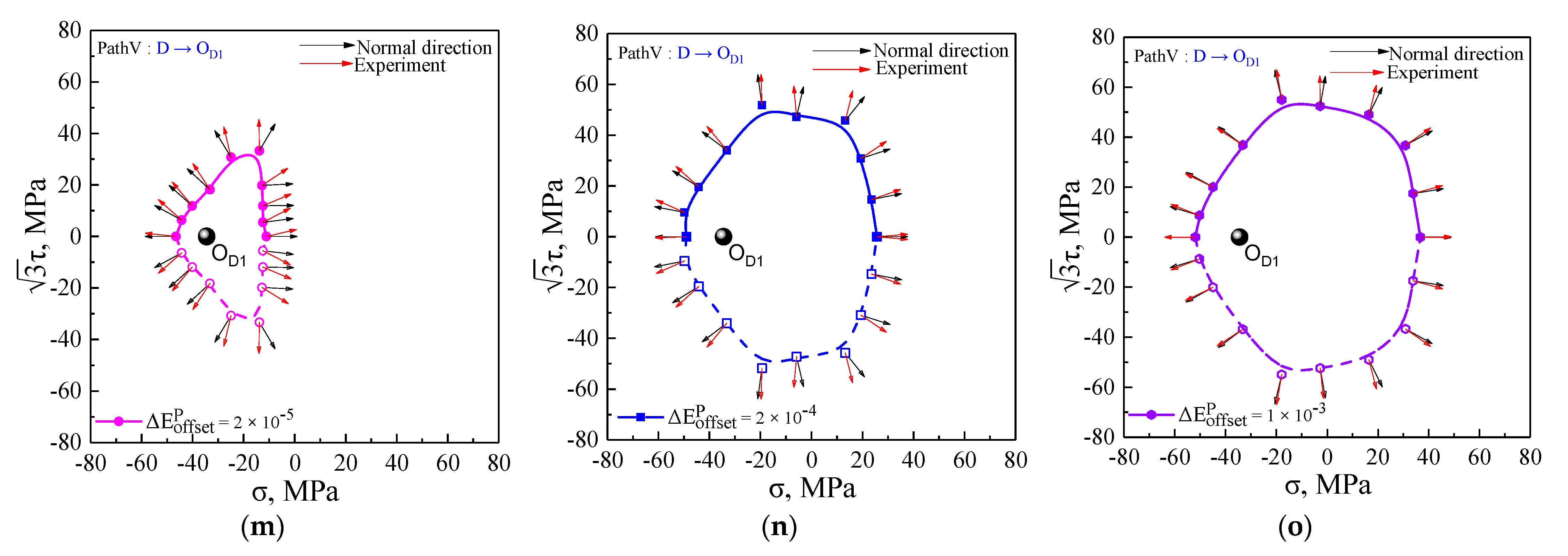
5.2. Subsequent Yield Surfaces under Five Unloading Cases
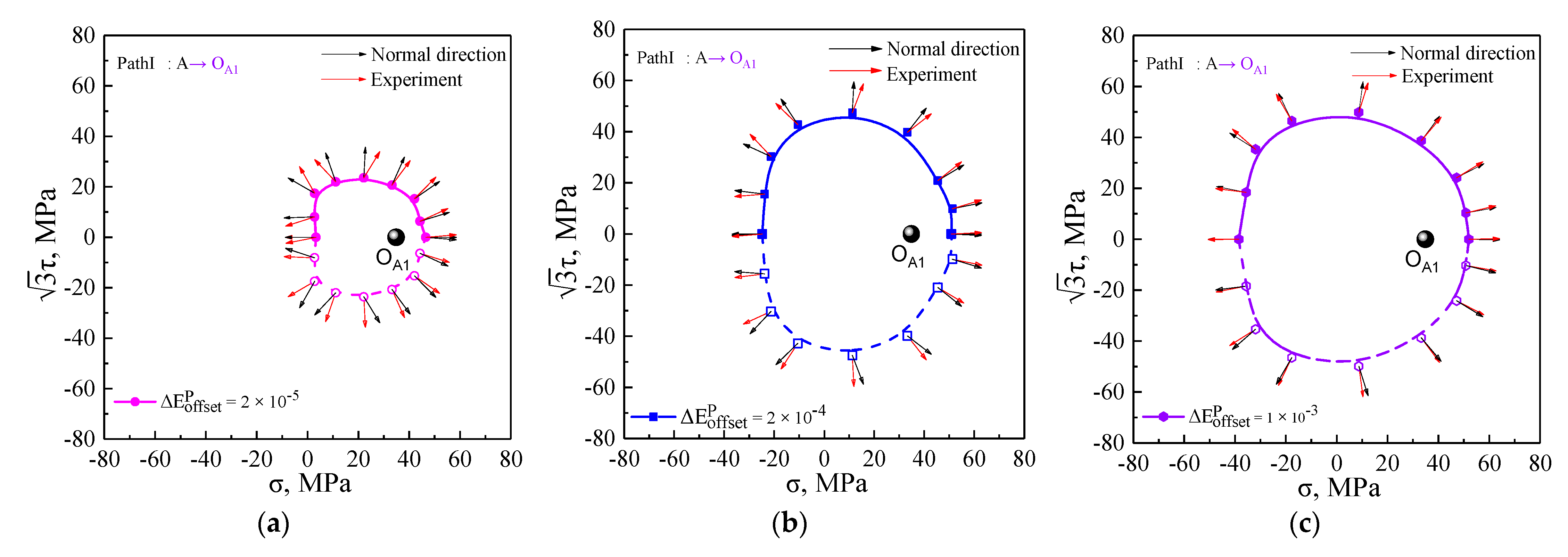
5.3. The Plastic Flow Direction of Subsequent Yield Surfaces
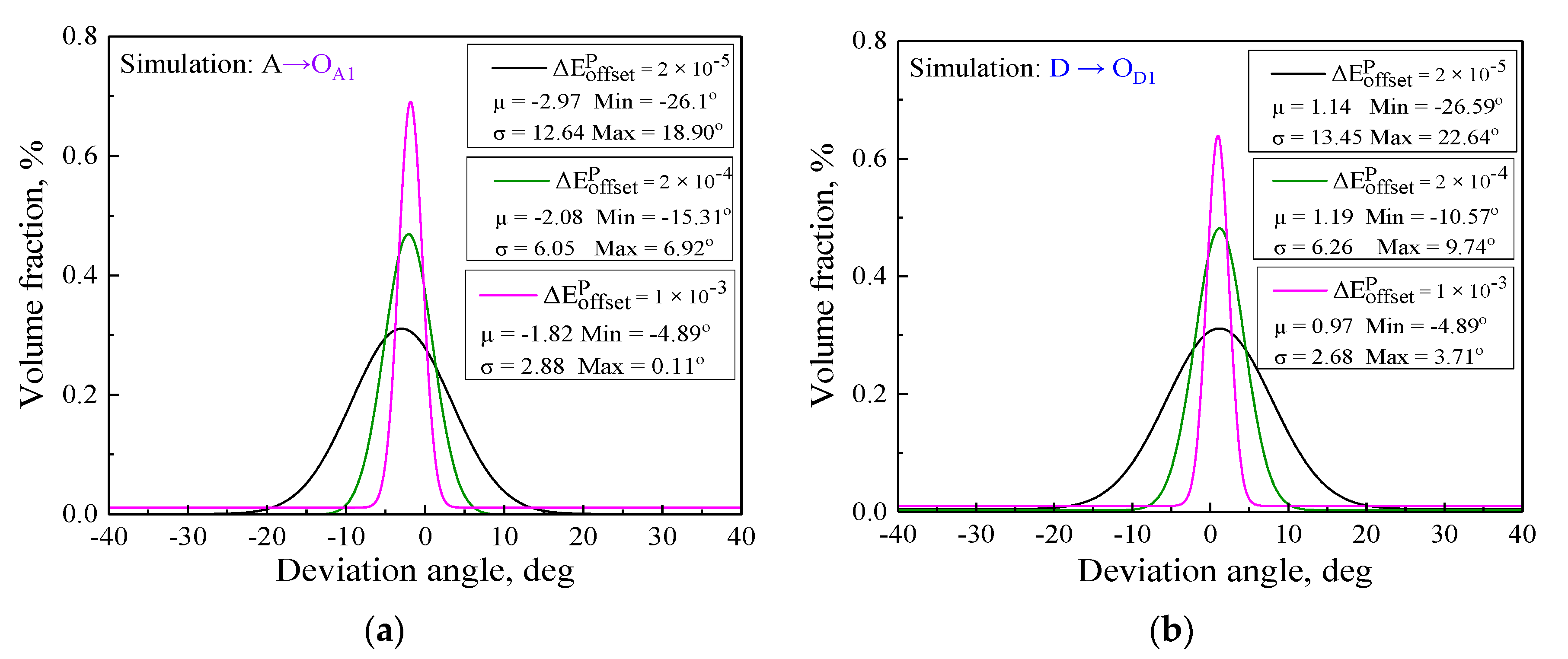
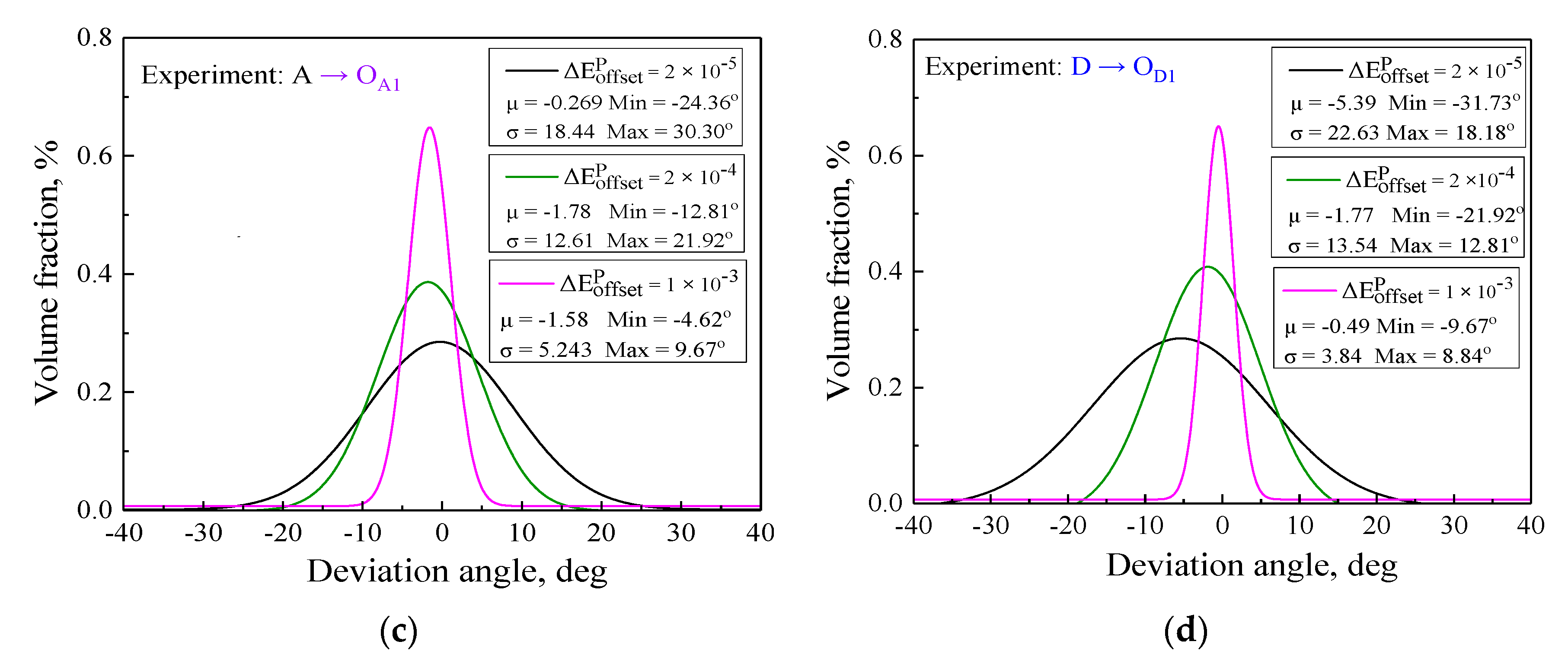
5.4. Statistical Analysis for Plastic Flow Direction of Subsequent Yield Surfaces
6. Conclusions
- The crystal plasticity theory introducing a back-stress in conjunction with the GFEM provided the accurate simulated results with respect to the remarkable sharp corner and the non-associated flow direction of the subsequent yield surfaces as experimental observations under all explored cyclic pre-loading paths.
- For the arbitrarily specified offset strain definition, the initial yield surfaces of the ploycrystal aluminum exhibited approximate isotropic evolution and obeyed the Tresca yield criterion, noting that the performance was different from the Von Mises criterion predicted by the common software, in the stress plane, and the plastic flow directions approximatively obeyed the normal flow rule.
- The evolution and plastic flow directions of the subsequent yield surfaces strongly depended on the offset strain levels. The subsequent yield surfaces defined with the smaller offset strain exhibited more severe distortion and larger deviation angles from the normal direction in comparison with those results using the larger offset strain. However, with the larger offset strain, the subsequent yield surfaces were similar to the convex ellipse, and the plastic flow directions approximatively obeyed the normal flow rule.
- The dependency of plastic flow on the anisotropic evolution of subsequent yield surfaces found that the normality rule of plasticity followed the smooth yield locus; conversely, the significant non-associated flow was attributed to the distorted yield locus. Furthermore, it is necessary to study the subsequent yield surfaces in depth and the plastic flow behaviors under multi-axial proportional and non-proportional cyclic loading conditions with different cycles in our future work.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Safaei, M.; Zang, S.-L.; Lee, M.-G.; Waele, W.D. Evaluation of anisotropic constitutive models: Mixed anisotropic hardening and non-associated flow rule approach. Int. J. Mech. Sci. 2013, 73, 53–68. [Google Scholar] [CrossRef]
- Liao, K.C. Yield and Damage Criteria for Sheet Metal Forming Simulations. Ph.D. Thesis, The University of Michigan, Ann Arbor, MI, USA, 1997. [Google Scholar]
- Barlat, F.; Richmond, O. Prediction of tricomponent plane stress yield surfaces and associated flow and failure behavior of strongly textured f.c.c. polycrystalline sheets. Mater. Sci. Eng. 1987, 95, 15–29. [Google Scholar] [CrossRef]
- Barlat, F. Crystallographic texture, anisotropic yield surfaces and forming limits of sheet metals. Mater. Sci. Eng. 1987, 91, 55–72. [Google Scholar] [CrossRef]
- Lademo, O.G.; Hopperstad, O.S.; Langseth, M. An evaluation of yield criteria and flow rules for aluminium alloys. Int. J. Plast. 1999, 15, 191–208. [Google Scholar] [CrossRef]
- Estrada, N.; Taboada, A. Yield surfaces and plastic potentials of cemented granular materials from discrete element simulations. Comput. Geotech. 2013, 49, 62–69. [Google Scholar] [CrossRef]
- Zhang, K.S.; Shi, Y.K.; Xu, L.B. Anisotropy of yielding/hardening and microinhomogeneity of deforming/rotating for a polycrystalline metal under cyclic tension-compression. Acta Metall. Sin. 2011, 47, 1292–1300. [Google Scholar]
- Beradai, C.; Berveiller, M.; Lipinski, P. Plasticity of metallic polycrystals under complex loading paths. Int. J. Plast. 1987, 3, 143–162. [Google Scholar] [CrossRef]
- Khan, A.S.; Kazmi, R.; Pandey, A.; Stoughton, T. Evolution of subsequent yield surfaces and elastic constants with finite plastic deformation. Part-I: A very low work hardening aluminum alloy (Al 6061-T6511). Int. J. Plast. 2009, 25, 1611–1625. [Google Scholar] [CrossRef]
- Khan, A.S.; Pandey, A.; Stoughton, T. Evolution of subsequent yield surfaces and elastic constants with finite plastic deformation. Part III: Yield surface in tension–tension stress space (Al 6061–T 6511 and annealed 1100 Al). Int. J. Plast. 2010, 26, 1432–1441. [Google Scholar] [CrossRef]
- Hu, G.J.; Zhang, K.S.; Huang, S.H.; Ju, J.-W. Yield surfaces and plastic flow of 45 steel under tension-torsion loading paths. Acta Mech. Solida. Sin. 2012, 25, 360. [Google Scholar] [CrossRef]
- Chen, J.Y. Subsequent Yield Behavior of HRB400 Steel under Tension-Torsion Combined Loading and Anisotropic Yield Surface Model. Ph.D. Thesis, Guangxi University, Nanning, China, 2019. [Google Scholar]
- Mollica, F.; Srinivasa, A.R. A general framework for generating convex yield surfaces for anisotropic metals. Acta Mech. 2002, 154, 61–84. [Google Scholar] [CrossRef]
- Lee, E.H.; Stoughton, T.B.; Yoon, J.W. A yield criterion through coupling of quadratic and non-quadratic functions for anisotropic hardening with non-associated flow rule. Int. J. Plast. 2017, 99, 120–143. [Google Scholar] [CrossRef]
- Hou, Y.; Min, J.Y.; Stoughton, T.B.; Lin, J.P.; Carsley, J.E.; Carlson, B.E. A non-quadratic pressure-sensitive constitutive model under non-associated flow rule with anisotropic hardening: Modeling and validation. Int. J. Plast. 2020, 135, 102808. [Google Scholar] [CrossRef]
- Adzima, F.; Balan, T.; Manach, P.Y.; Bonnet, N.; Tabourot, L. Crystal plasticity and phenomenological approaches for the simulation of deformation behavior in thin copper alloy sheets. Int. J. Plast. 2017, 94, 171–191. [Google Scholar] [CrossRef]
- Liu, W.; Chen, B.K.; Pang, Y.; Najafzadeh, A. A 3D phenomenological yield function with both in and out-of-plane mechanical anisotropy using full-field crystal plasticity spectral method for modelling sheet metal forming of strong textured aluminum alloy. Int. J. Solids Struct. 2020, 193, 117–133. [Google Scholar] [CrossRef]
- Han, F.; Diehl, M.; Roters, F.; Raabe, D. Using spectral-based representative volume element crystal plasticity simulations to predict yield surface evolution during large scale forming simulations. J. Mater. Process. Technol. 2020, 277, 116449. [Google Scholar] [CrossRef]
- Barlat, F.; Lian, K. Plastic behavior and stretchability of sheet metals. Part I: A yield function for orthotropic sheets under plane stress conditions. Int. J. Plast. 1989, 5, 51–66. [Google Scholar] [CrossRef]
- Lee, E.-H.; Choi, H.; Stoughton, T.B.; Yoon, J.W. Combined anisotropic and distortion hardening to describe directional response with Bauschinger effect. Int. J. Plast. 2019, 122, 73–78. [Google Scholar] [CrossRef]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. Roy. Soc. Lon. 1948, 193, 281–297. [Google Scholar]
- Hosford, W.F. A Generalized Isotropic Yield Criterion. J. Appl. Mech. 1972, 39, 607–609. [Google Scholar] [CrossRef]
- Lin, S.B.; Ding, J.L. A modified form of Hill’s orientation dash dependent yield criterion for orthotropic sheet metals. J. Mech. Phys. Solids 1996, 44, 1739–1764. [Google Scholar] [CrossRef]
- Valanis, K.C.; Peters, J.F. An endochronic plasticity theory with shear-volumetric coupling. Int. J. Numer. Anal. Met. 1991, 15, 77–102. [Google Scholar] [CrossRef]
- Valanis, K.C. Fundamental consequences of a new intrinsic time measure plasticity as a limit of the endochronic theory. Arch. Mech. 1980, 32, 171. [Google Scholar]
- Valanis, K.C. A theory of viscoplasticity without yield surface, Part II. Application to mechanical behavior of metals. Arch. Mech. 1971, 23, 535–551. [Google Scholar]
- Valanis, K.C.; Fan, J. A numerical algorithm for endochronic plasticity and comparison with experiment. Comput. Struct. 1984, 19, 717–724. [Google Scholar] [CrossRef] [Green Version]
- Khoei, A.R.; Bakhshiani, A. A hypoelasto-plastic finite strain simulation of powder compaction processes with density-dependent endochronic model. Int. J. Solids Struct. 2004, 41, 6081–6110. [Google Scholar] [CrossRef]
- Yeh, W.C.; Lin, H.Y. An endochronic model of yield surface accounting for deformation induced anisotropy. Int. J. Plast. 2006, 22, 16–38. [Google Scholar] [CrossRef]
- Stoughton, T.B.; Yoon, J.W. Anisotropic hardening and non-associated flow in proportional loading of sheet metals. Int. J. Plast. 2009, 25, 1777–1817. [Google Scholar] [CrossRef]
- Schurig, M.; Bertram, A.; Petryk, H. Micromechanical analysis of the development of a yield vertex in polycrystal plasticity. Acta Mech. 2007, 194, 141–158. [Google Scholar] [CrossRef]
- Saai, A.; Dumoulin, S.; Hopperstad, O.S.; Lademo, O.-G. Simulation of yield surfaces for aluminium sheets with rolling and recrystallization textures. Comput. Mater. Sci. 2013, 67, 424–433. [Google Scholar] [CrossRef]
- Canova, G.R.; Kocks, U.F.; Tomé, C.N.; Jonas, J.J. The yield surface of textured polycrystals. J. Mech. Phys. Solids 1985, 33, 371–397. [Google Scholar] [CrossRef]
- Inal, K.; Mishra, R.K.; Cazacu, O. Forming simulation of aluminum sheets using an anisotropic yield function coupled with crystal plasticity theory. Int. J. Solids Struct. 2010, 47, 2223–2233. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, I.; Terada, K. A method of predicting macroscopic yield strength of polycrystalline metals subjected to plastic forming by micro-macro de-coupling scheme. Int. J. Mech. Sci. 2010, 52, 343–355. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Nakamachi, E.; Xie, C.L.; Harimoto, M. Drawability assessment of BCC steel sheet by using elastic/crystalline viscoplastic finite element analyses. Int. J. Mech. Sci. 2001, 43, 631–652. [Google Scholar] [CrossRef]
- Zhao, Z.; Roters, F.; Mao, W.; Raabe, D. Introduction of a texture component crystal plasticity finite element method for anisotropy simulations. Adv. Eng. Mater. 2001, 3, 984–990. [Google Scholar] [CrossRef]
- Xie, C.L.; Nakamachi, E. Investigations of the formability of BCC steel sheets by using crystalline plasticity finite element analysis. Mater. Des. 2002, 23, 59–68. [Google Scholar] [CrossRef]
- Hill, R.; Rice, J.R. Constitutive analysis of elastic-plastic crystals at arbitrary strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Asaro, R.J.; Rice, J.R. Strain localization in ductile single crystals. J. Mech. Phys. Solids 1977, 25, 309–338. [Google Scholar] [CrossRef] [Green Version]
- Needleman, A.; Asaro, R.J.; Lemonds, J.; Peirce, D. Finite element analysis of crystalline solids. Comput. Methods Appl. Mech. Eng. 1985, 52, 689–708. [Google Scholar] [CrossRef]
- Rice, J.R. Inelastic constitutive relations for solids: An internal-variable theory and its application to metal plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. Lond. A 1976, 348, 101–127. [Google Scholar]
- Hill, R. Generalized constitutive relations for incremental deformation of metal crystals by multislip. J. Mech. Phys. Solids 1966, 14, 95–102. [Google Scholar] [CrossRef]
- Chang, Y.W.; Asaro, R.J. An experimental study of shear localization in aluminum-copper single crystals. Acta Metall. 1981, 29, 241–257. [Google Scholar] [CrossRef]
- Walker, K.P. Research and Development Program for Non-linear Structural Modeling with Advanced Time-temperature Dependent Constitutive Relationships; Report PWA-5700-50; NASA CR-1655331981. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19820008207.pdf (accessed on 1 July 2021).
- Chaboche, J.L. On some modifications of kinematic hardening to improve the description of ratcheting effects. Int. J. Plast. 1991, 7, 661–678. [Google Scholar] [CrossRef]
- Zhang, K.-S.; Shi, Y.-K.; Ju, J.W. Grain-level statistical plasticity analysis on strain cycle fatigue of a FCC metal. Mech. Mater. 2013, 64, 76–90. [Google Scholar] [CrossRef]
- Lu, D.M.; Zhang, K.S.; Hu, G.J.; Lan, Y.T.; Chang, Y.J. Investigation of Yield Surfaces Evolution for Polycrystalline Aluminum After Pre-Cyclic Loading by Experiment and Crystal Plasticity Simulation. Materials 2020, 13, 3069. [Google Scholar] [CrossRef] [PubMed]






| Chemical Composition | Mechanical Properties | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Al/% | Cu/% | Mg/% | Si/% | Mn/% | Zn/% | E/GPa | G/GPa | |||
| 99.89 | 0.02 | 0.03 | 0.03 | 0.02 | 0.01 | 57 | 25 | 20 | 81 | 24% |
| /GPa | /GPa | /GPa | /MPa | /MPa | /MPa | /GPa | /GPa | /s−1 | /s−1 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 75.64 | 36.86 | 25.4 | 8.42 | 9.2 | 65 | 22.5 | 2.5 | 0.1 | 1.0 | 0 | 0.001 | 200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, D.; Zhang, K.; Hu, G. Investigation on Plastic Flow Behaviors of FCC Polycrystalline Aluminum under Pre-Cyclic Tension-Compression Loading: Experiments and Crystal Plasticity Modeling. Nanomaterials 2021, 11, 2397. https://doi.org/10.3390/nano11092397
Lu D, Zhang K, Hu G. Investigation on Plastic Flow Behaviors of FCC Polycrystalline Aluminum under Pre-Cyclic Tension-Compression Loading: Experiments and Crystal Plasticity Modeling. Nanomaterials. 2021; 11(9):2397. https://doi.org/10.3390/nano11092397
Chicago/Turabian StyleLu, Damin, Keshi Zhang, and Guijuan Hu. 2021. "Investigation on Plastic Flow Behaviors of FCC Polycrystalline Aluminum under Pre-Cyclic Tension-Compression Loading: Experiments and Crystal Plasticity Modeling" Nanomaterials 11, no. 9: 2397. https://doi.org/10.3390/nano11092397
APA StyleLu, D., Zhang, K., & Hu, G. (2021). Investigation on Plastic Flow Behaviors of FCC Polycrystalline Aluminum under Pre-Cyclic Tension-Compression Loading: Experiments and Crystal Plasticity Modeling. Nanomaterials, 11(9), 2397. https://doi.org/10.3390/nano11092397






