Scalable Graphene Defect Prediction Using Transferable Learning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Molecular Dynamics Simulation of Defect-Containing Graphene
2.2. Machine Learning
3. Results and Discussion
3.1. One-Defect Scenarios
3.2. Multiple-Defect Scenarios
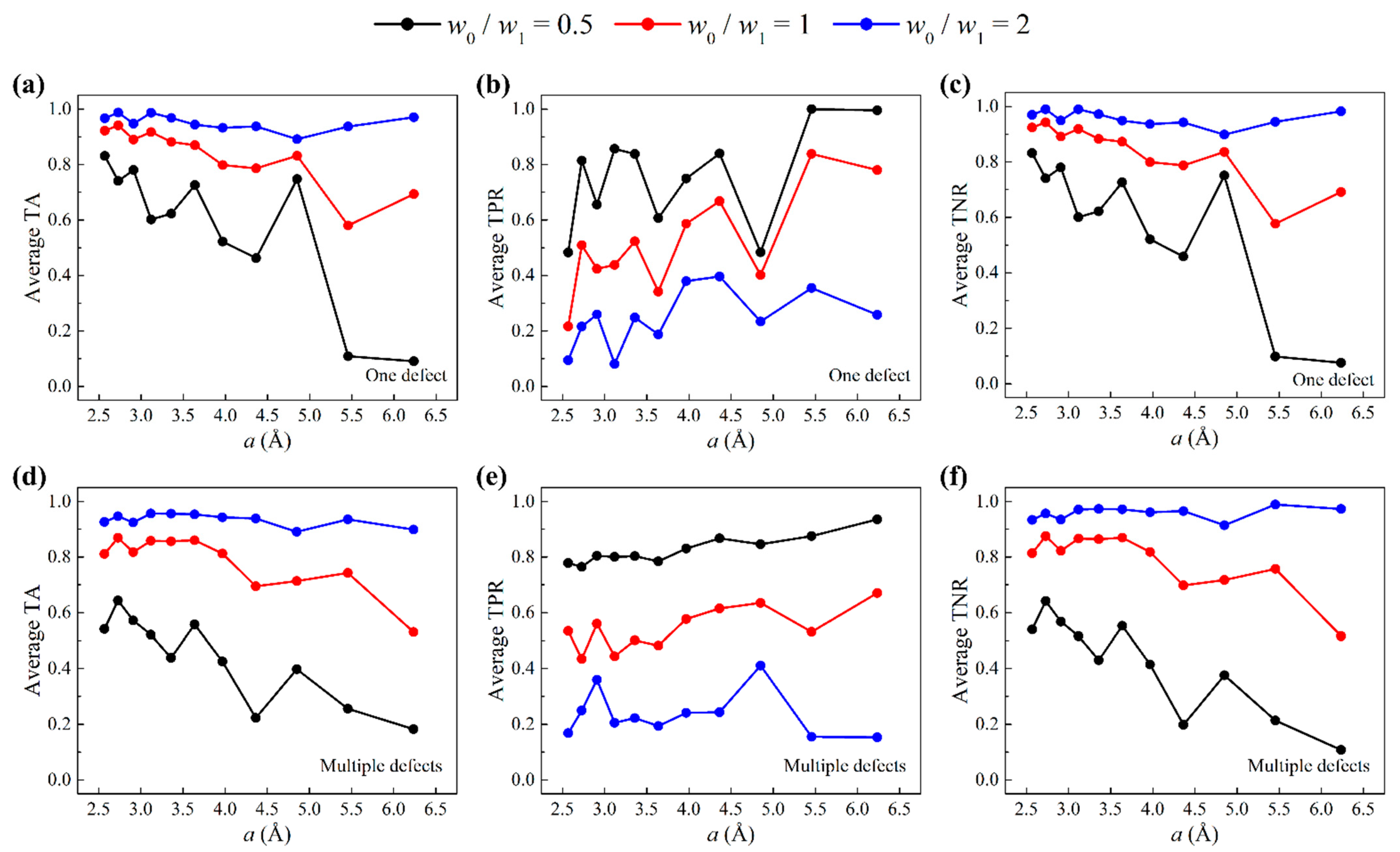
3.3. Weighted Cost Function
3.4. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, S.J.; Choi, K.; Lee, B.; Kim, Y.; Hong, B.H. Materials for Flexible, Stretchable Electronics: Graphene and 2D Materials. Annu. Rev. Mater. Sci. 2015, 45, 63–84. [Google Scholar] [CrossRef]
- Jang, H.; Park, Y.J.; Chen, X.; Das, T.; Kim, M.-S.; Ahn, J.-H. Graphene-Based Flexible and Stretchable Electronics. Adv. Mater. 2016, 28, 4184–4202. [Google Scholar] [CrossRef]
- Chen, C.-T.; Chrzan, D.C.; Gu, G.X. Nano-topology optimization for materials design with atom-by-atom control. Nat. Commun. 2020, 11, 1–9. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, Z.; Huang, Y.; Ma, Y.; Wang, C.; Chen, M.; Chen, Y. Supercapacitor Devices Based on Graphene Materials. J. Phys. Chem. C 2009, 113, 13103–13107. [Google Scholar] [CrossRef]
- Liu, C.; Yu, Z.; Neff, D.; Zhamu, A.; Jang, B.Z. Graphene-Based Supercapacitor with an Ultrahigh Energy Density. Nano Lett. 2010, 10, 4863–4868. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.-T.; Martin-Martinez, F.J.; Ling, S.; Qin, Z.; Buehler, M.J. Nacre-inspired design of graphene oxide–polydopamine nanocomposites for enhanced mechanical properties and multi-functionalities. Nano Futures 2017, 1, 011003. [Google Scholar] [CrossRef] [Green Version]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Balandin, A.A. Thermal properties of graphene and nanostructured carbon materials. Nat. Mater. 2011, 10, 569–581. [Google Scholar] [CrossRef] [Green Version]
- Zheng, B.; Gu, G.X. Tuning graphene mechanical anisotropy via defect engineering. Carbon 2019, 155, 697–705. [Google Scholar] [CrossRef]
- Zhang, P.; Ma, L.; Fan, F.; Zeng, Z.; Peng, C.; Loya, P.E.; Liu, Z.; Gong, Y.; Zhang, J.; Zhang, X.; et al. Fracture toughness of graphene. Nat. Commun. 2014, 5, 3782. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Stehr, J.; Buyanova, I.; Chen, W. Defects in Advanced Electronic Materials and Novel Low Dimensional Structures; Woodhead Publishing: Duxford, UK, 2018; ISBN 978-008-102-053-1. [Google Scholar]
- Lim, D.-H.; Negreira, A.S.; Wilcox, J. DFT Studies on the Interaction of Defective Graphene-Supported Fe and Al Nanoparticles. J. Phys. Chem. C 2011, 115, 8961–8970. [Google Scholar] [CrossRef]
- Zheng, B.; Gu, G.X. Recovery from mechanical degradation of graphene by defect enlargement. Nanotechnology 2019, 31, 085707. [Google Scholar] [CrossRef]
- Kotakoski, J.; Krasheninnikov, A.V.; Kaiser, U.; Meyer, J.C. From Point Defects in Graphene to Two-Dimensional Amorphous Carbon. Phys. Rev. Lett. 2011, 106, 105505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mortazavi, B.; Ahzi, S. Thermal conductivity and tensile response of defective graphene: A molecular dynamics study. Carbon 2013, 63, 460–470. [Google Scholar] [CrossRef]
- Zheng, B.; Gu, G.X. Stress Field Characteristics and Collective Mechanical Properties of Defective Graphene. J. Phys. Chem. C 2020, 124, 7421–7431. [Google Scholar] [CrossRef]
- He, L.; Guo, S.; Lei, J.; Sha, Z.; Liu, Z. The effect of Stone–Thrower–Wales defects on mechanical properties of graphene sheets—A molecular dynamics study. Carbon 2014, 75, 124–132. [Google Scholar] [CrossRef]
- Chen, C.-T.; Gu, G.X. Generative Deep Neural Networks for Inverse Materials Design Using Backpropagation and Active Learning. Adv. Sci. 2020, 7, 1902607. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, J.; Marques, M.R.G.; Botti, S.; Marques, M.A.L. Recent advances and applications of machine learning in solid-state materials science. NPJ Comput. Mater. 2019, 5, 83. [Google Scholar] [CrossRef]
- Chen, C.-T.; Gu, G.X. Learning hidden elasticity with deep neural networks. Proc. Natl. Acad. Sci. USA 2021, 118, e2102721118. [Google Scholar] [CrossRef]
- Kim, Y.; Yang, C.; Kim, Y.; Gu, G.X.; Ryu, S. Designing an adhesive pillar shape with deep learning-based optimization. ACS Appl. Mater. Interfaces 2020, 12, 24458–24465. [Google Scholar] [CrossRef]
- Raccuglia, P.; Elbert, K.C.; Adler, P.D.F.; Falk, C.; Wenny, M.B.; Mollo, A.; Zeller, M.; Friedler, S.A.; Schrier, J.; Norquist, A.J. Machine-learning-assisted materials discovery using failed experiments. Nature 2016, 533, 73–76. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Kim, Y.; Ryu, S.; Gu, G.X. Prediction of composite microstructure stress-strain curves using convolutional neural networks. Mater. Des. 2020, 189, 108509. [Google Scholar] [CrossRef]
- Zhang, Z.; Gu, G.X. Finite element based deep learning model for deformation behavior of digital materials. Adv. Theory Simul. 2020, 3, 2000031. [Google Scholar] [CrossRef]
- Hanakata, P.Z.; Cubuk, E.D.; Campbell, D.K.; Park, H.S. Accelerated search and design of stretchable graphene kirigami using machine learning. Phys. Rev. Lett. 2018, 121, 255304. [Google Scholar] [CrossRef] [Green Version]
- Zheng, B.; Gu, G.X. Machine Learning-Based Detection of Graphene Defects with Atomic Precision. Nano-Micro Lett. 2020, 12, 181. [Google Scholar] [CrossRef]
- Gupta, K.K.; Mukhopadhyay, T.; Roy, A.; Roy, L.; Dey, S. Sparse machine learning assisted deep computational insights on the mechanical properties of graphene with intrinsic defects and doping. J. Phys. Chem. Solids 2021, 155, 110111. [Google Scholar] [CrossRef]
- Zheng, B.; Gu, G.X. Prediction of Graphene Oxide Functionalization Using Gradient Boosting: Implications for Material Chemical Composition Identification. ACS Appl. Nano Mater. 2021, 4, 3167–3174. [Google Scholar] [CrossRef]
- Demirpolat, A.B.; Das, M. Prediction of Viscosity Values of Nanofluids at Different pH Values by Alternating Decision Tree and Multilayer Perceptron Methods. Appl. Sci. 2019, 9, 1288. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef] [Green Version]
- Kag, D.; Luhadiya, N.; Patil, N.D.; Kundalwal, S.I. Strain and defect engineering of graphene for hydrogen storage via atomistic modelling. Int. J. Hydrog. Energy 2021, 46, 22599–22610. [Google Scholar] [CrossRef]
- Li, M.; Deng, T.; Zheng, B.; Zhang, Y.; Liao, Y.; Zhou, H. Effect of Defects on the Mechanical and Thermal Properties of Graphene. Nanomaterials 2019, 9, 347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, J.; Ragab, T.; Basaran, C. Influence of vacancy defects on the damage mechanics of graphene nanoribbons. Int. J. Damage Mech. 2017, 26, 29–49. [Google Scholar] [CrossRef]
- Bunch, J.S.; van der Zande, A.M.; Verbridge, S.S.; Frank, I.W.; Tanenbaum, D.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Electromechanical Resonators from Graphene Sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn Res. 2011, 12, 2825–2830. [Google Scholar]
- Lehtinen, O.; Tsai, I.L.; Jalil, R.; Nair, R.R.; Keinonen, J.; Kaiser, U.; Grigorieva, I.V. Non-invasive transmission electron microscopy of vacancy defects in graphene produced by ion irradiation. Nanoscale 2014, 6, 6569–6576. [Google Scholar] [CrossRef] [Green Version]
- Zhong, J.-H.; Zhang, J.; Jin, X.; Liu, J.-Y.; Li, Q.; Li, M.-H.; Cai, W.; Wu, D.-Y.; Zhan, D.; Ren, B. Quantitative Correlation between Defect Density and Heterogeneous Electron Transfer Rate of Single Layer Graphene. J. Am. Chem. Soc. 2014, 136, 16609–16617. [Google Scholar] [CrossRef]
- Robertson, A.W.; Montanari, B.; He, K.; Allen, C.S.; Wu, Y.A.; Harrison, N.M.; Kirkland, A.I.; Warner, J.H. Structural Reconstruction of the Graphene Monovacancy. ACS Nano 2013, 7, 4495–4502. [Google Scholar] [CrossRef]
- Banhart, F.; Kotakoski, J.; Krasheninnikov, A.V. Structural Defects in Graphene. ACS Nano 2011, 5, 26–41. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Sanchez, D.; van der Zande, A.M.; Paulo, A.S.; Lassagne, B.; McEuen, P.L.; Bachtold, A. Imaging Mechanical Vibrations in Suspended Graphene Sheets. Nano Lett. 2008, 8, 1399–1403. [Google Scholar] [CrossRef] [PubMed] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, B.; Zheng, Z.; Gu, G.X. Scalable Graphene Defect Prediction Using Transferable Learning. Nanomaterials 2021, 11, 2341. https://doi.org/10.3390/nano11092341
Zheng B, Zheng Z, Gu GX. Scalable Graphene Defect Prediction Using Transferable Learning. Nanomaterials. 2021; 11(9):2341. https://doi.org/10.3390/nano11092341
Chicago/Turabian StyleZheng, Bowen, Zeyu Zheng, and Grace X. Gu. 2021. "Scalable Graphene Defect Prediction Using Transferable Learning" Nanomaterials 11, no. 9: 2341. https://doi.org/10.3390/nano11092341
APA StyleZheng, B., Zheng, Z., & Gu, G. X. (2021). Scalable Graphene Defect Prediction Using Transferable Learning. Nanomaterials, 11(9), 2341. https://doi.org/10.3390/nano11092341





