Efficient Structural Relaxation of Polycrystalline Graphene Models
Abstract
1. Introduction
2. Materials and Methods
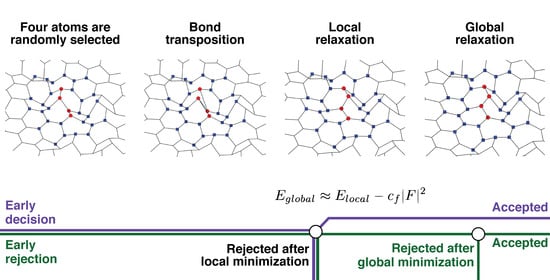
2.1. Early Rejection
2.2. Early Decision
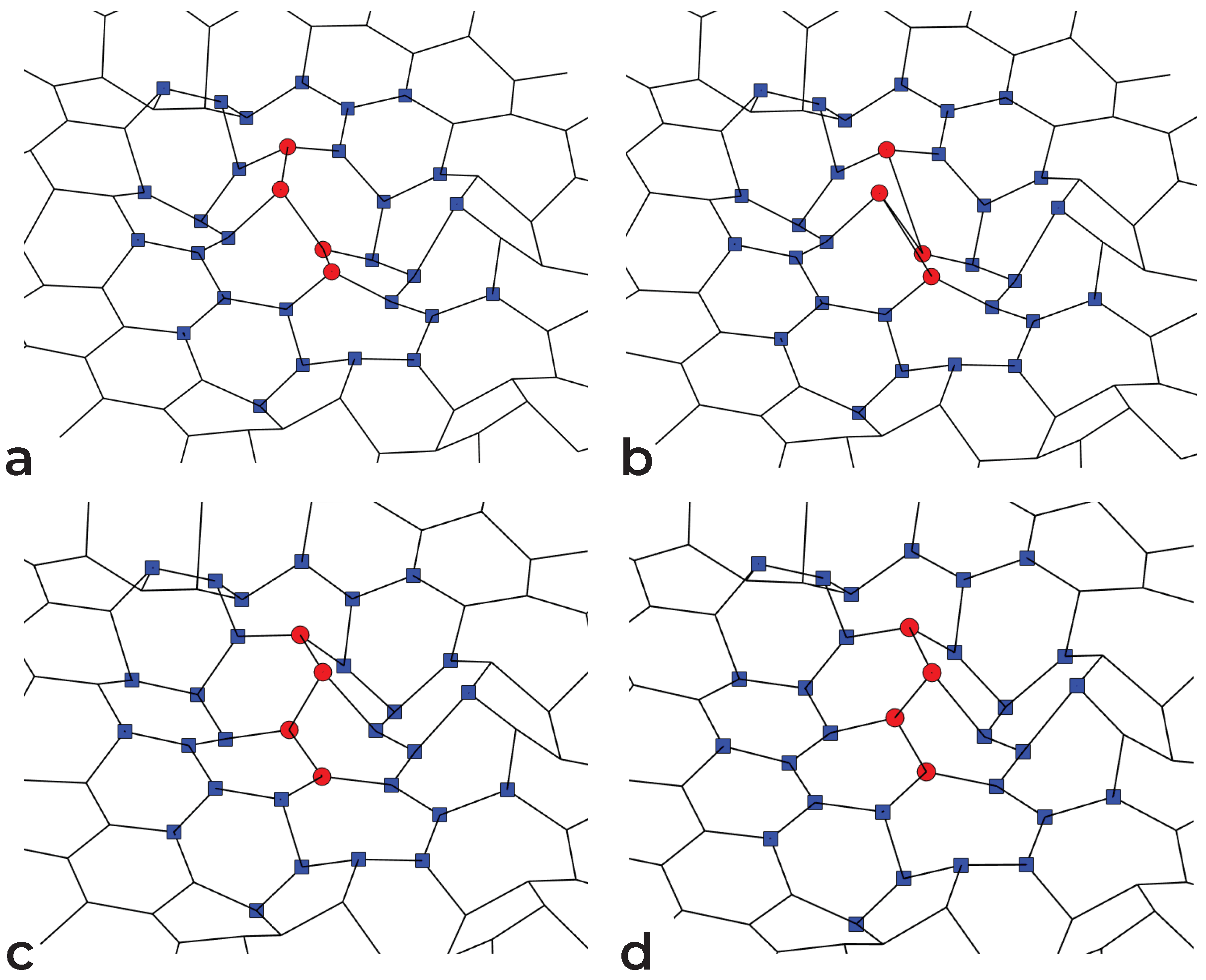
2.3. Manipulation Tool
3. Results
3.1. Early Rejection
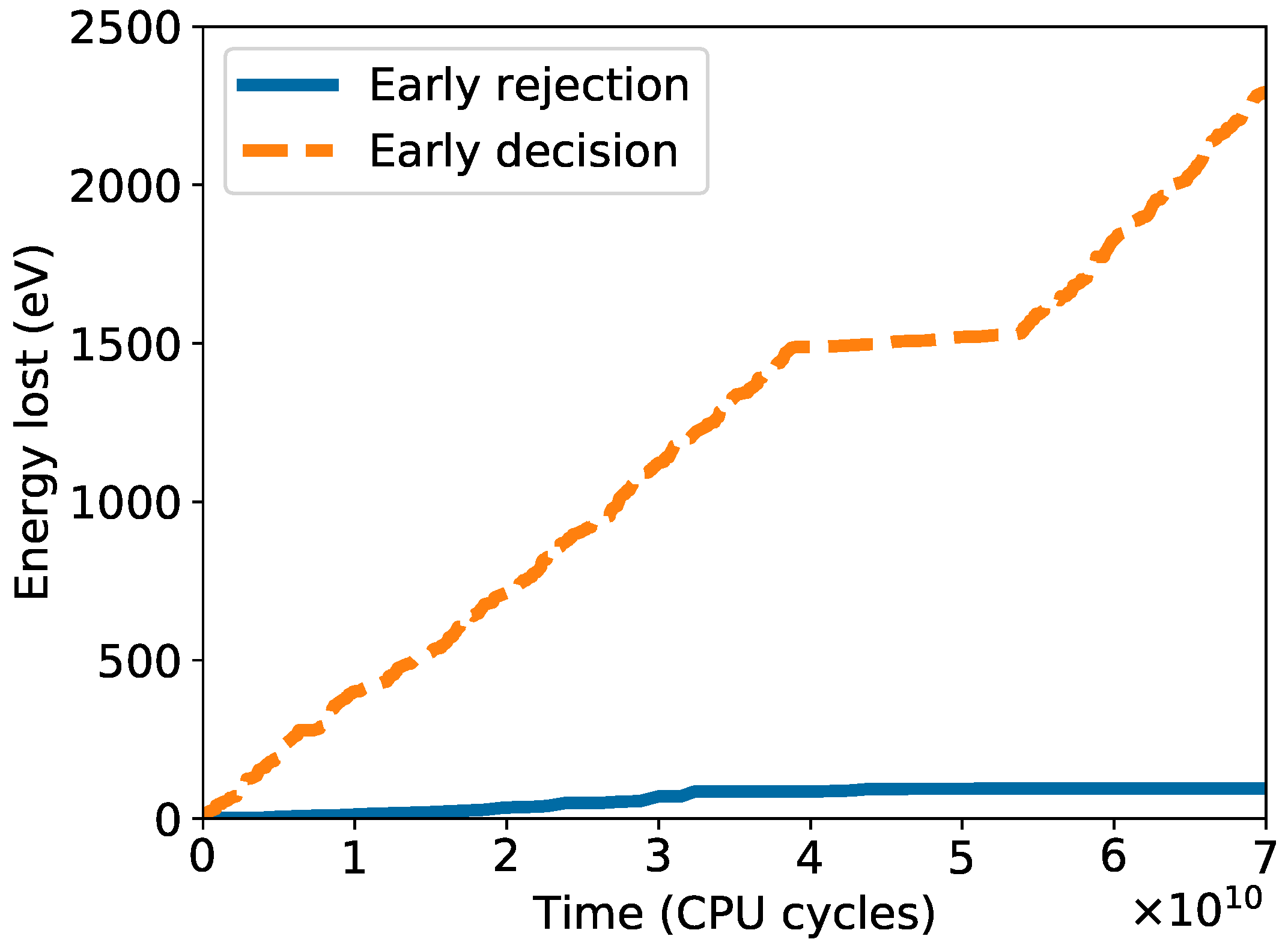
3.2. Early Decision
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: Status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed]
- Nair, R.R.; Wu, H.A.; Jayaram, P.N.; Grigorieva, I.V.; Geim, A.K. Unimpeded Permeation of Water through Helium-Leak-Tight Graphene-Based Membranes. Science 2012, 335, 442–444. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.D.; Niklaus, F.; Paussa, A.; Vaziri, S.; Fischer, A.C.; Sterner, M.; Forsberg, F.; Delin, A.; Esseni, D.; Palestri, P.; et al. Electromechanical piezoresistive sensing in suspended graphene membranes. Nano Lett. 2013, 13, 3237–3242. [Google Scholar] [CrossRef]
- Dolleman, R.J.; Davidovikj, D.; Cartamil-Bueno, S.J.; Van Der Zant, H.S.; Steeneken, P.G. Graphene Squeeze-Film Pressure Sensors. Nano Lett. 2016, 16, 568–571. [Google Scholar] [CrossRef]
- Cartamil-Bueno, S.J.; Steeneken, P.G.; Centeno, A.; Zurutuza, A.; van der Zant, H.S.J.; Houri, S. Colorimetry Technique for Scalable Characterization of Suspended Graphene. Nano Lett. 2016, 16, 6792–6796. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Milowska, K.Z.; Woińska, M.; Wierzbowska, M. Contrasting elastic properties of heavily B-and N-doped graphene with random impurity distributions including aggregates. J. Phys. Chem. C 2013, 117, 20229–20235. [Google Scholar] [CrossRef][Green Version]
- Yazyev, O.V.; Chen, Y.P. Polycrystalline graphene and other two-dimensional materials. Nat. Nanotechnol. 2014, 9, 755–767. [Google Scholar] [CrossRef]
- Rasool, H.I.; Ophus, C.; Zhang, Z.; Crommie, M.F.; Yakobson, B.I.; Zettl, A. Conserved Atomic Bonding Sequences and Strain Organization of Graphene Grain Boundaries. Nano Lett. 2014, 14, 7057–7063. [Google Scholar] [CrossRef]
- Tison, Y.; Lagoute, J.; Repain, V.; Chacon, C.; Girard, Y.; Joucken, F.; Sporken, R.; Gargiulo, F.; Yazyev, O.V.; Rousset, S. Grain Boundaries in Graphene on SiC (0001) Substrate. Nano Lett. 2014, 14, 6382–6386. [Google Scholar] [CrossRef]
- Araujo, P.T.; Terrones, M.; Dresselhaus, M.S. Defects and impurities in graphene-like materials. Mater. Today 2012, 15, 98–109. [Google Scholar] [CrossRef]
- Du, X.; Skachko, I.; Barker, A.; Andrei, E.Y. Approaching ballistic transport in suspended graphene. Nat. Nanotechnol. 2008, 3, 491–495. [Google Scholar] [CrossRef]
- Bolotin, K.I.; Sikes, K.J.; Jiang, Z.; Klima, M.; Fudenberg, G.; Hone, J.; Kim, P.; Stormer, H.L. Ultrahigh electron mobility in suspended graphene. Solid State Commun. 2008, 146, 351–355. [Google Scholar] [CrossRef]
- Lu, J.; Bao, Y.; Su, C.L.; Loh, K.P. Properties of Strained Structures and Topological Defects in Graphene. ACS Nano 2013, 7, 8350–8357. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Qing, M.; Wang, Y.; Chen, S. Defects in Graphene: Generation, Healing, and Their Effects on the Properties of Graphene: A Review. J. Mater. Sci. Technol. 2015, 31, 599–606. [Google Scholar] [CrossRef]
- Güryel, S.; Hajgató, B.; Dauphin, Y.; Blairon, J.M.; Edouard Miltner, H.; De Proft, F.; Geerlings, P.; Van Lier, G. Effect of structural defects and chemical functionalisation on the intrinsic mechanical properties of graphene. Phys. Chem. Chem. Phys. 2013, 15, 659–665. [Google Scholar] [CrossRef]
- D’Ambrosio, F.; Juričić, V.; Barkema, G.T. Discontinuous evolution of the structure of stretching polycrystalline graphene. Phys. Rev. B 2019, 100, 161402. [Google Scholar] [CrossRef]
- Banhart, F.; Kotakoski, J.; Krasheninnikov, A.V. Structural Defects in Graphene. ACS Nano 2011, 5, 26–41. [Google Scholar] [CrossRef]
- Hashimoto, A.; Suenaga, K.; Gloter, A.; Urita, K.; Iijima, S. Direct evidence for atomic defects in graphene layers. Nature 2004, 430, 870–873. [Google Scholar] [CrossRef]
- Meyer, J.C.; Kisielowski, C.; Erni, R.; Rossell, M.D.; Crommie, M.F.; Zettl, A. Direct Imaging of Lattice Atoms and Topological Defects in Graphene Membranes. Nano Lett. 2008, 8, 3582–3586. [Google Scholar] [CrossRef] [PubMed]
- Kotakoski, J.; Krasheninnikov, A.V.; Kaiser, U.; Meyer, J.C. From Point Defects in Graphene to Two-Dimensional Amorphous Carbon. Phys. Rev. Lett. 2011, 106, 105505. [Google Scholar] [CrossRef]
- Vicarelli, L.; Heerema, S.J.; Dekker, C.; Zandbergen, H.W. Controlling Defects in Graphene for Optimizing the Electrical Properties of Graphene Nanodevices. ACS Nano 2015, 9, 3428–3435. [Google Scholar] [CrossRef]
- Jain, S.K.; Barkema, G.T.; Mousseau, N.; Fang, C.M.; van Huis, M.A. Strong Long-Range Relaxations of Structural Defects in Graphene Simulated Using a New Semiempirical Potential. J. Phys. Chem. C 2015, 119, 9646–9655. [Google Scholar] [CrossRef]
- Zachariasen, W.H. The Atomic Arrangement in Glass. J. Am. Chem. Soc. 1932, 54, 3841–3851. [Google Scholar] [CrossRef]
- Wooten, F.; Winer, K.; Weaire, D. Computer Generation of Structural Models of Amorphous Si and Ge. Phys. Rev. Lett. 1985, 54, 1392–1395. [Google Scholar] [CrossRef]
- Wooten, F.; Weaire, D. Modeling Tetrahedrally Bonded Random Networks by Computer. In Solid State Physics—Advances in Research and Applications; Academic Press: Cambridge, MA, USA, 1987; Volume 40, pp. 1–42. [Google Scholar]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les parallélloèdres primitifs. J. für Die Reine und Angewandte Mathematik 1908, 1908, 198–287. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Bitzek, E.; Koskinen, P.; Gähler, F.; Moseler, M.; Gumbsch, P. Structural Relaxation Made Simple. Phys. Rev. Lett. 2006, 97, 170201. [Google Scholar] [CrossRef]
- Barkema, G.T.; Mousseau, N. High-quality continuous random networks. Phys. Rev. B 2000, 62, 4985–4990. [Google Scholar] [CrossRef]
- Matsumoto, M.; Baba, A.; Ohmine, I. Topological building blocks of hydrogen bond network in water. J. Chem. Phys. 2007, 127, 134504. [Google Scholar] [CrossRef]
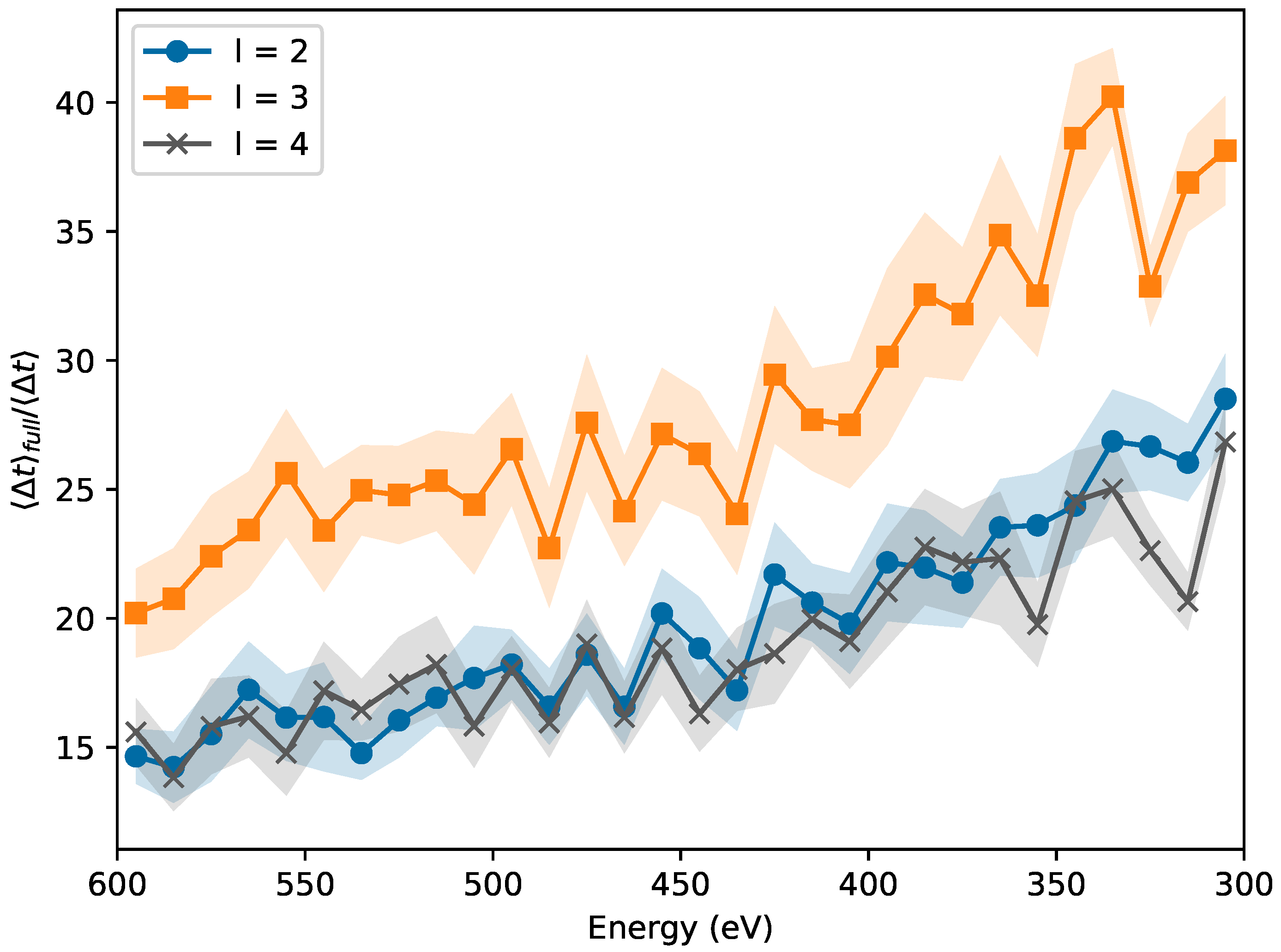


| l | [s u] | |
|---|---|---|
| 1 | 13 | |
| 2 | 28 | |
| 3 | 53 | |
| 4 | 90 |
| Atoms | Full Relaxation | Early Rejection | ||
|---|---|---|---|---|
| Size | # | % | # | % |
| 5 | 56 | 3.50 | 60 | 3.75 |
| 6 | 1489 | 93.06 | 1480 | 92.50 |
| 7 | 54 | 3.38 | 60 | 3.75 |
| 8 | 1 | <0.01 | 0 | 0.00 |
| Atoms | 10,024 | 20,000 | ||
|---|---|---|---|---|
| Size | # | % | # | % |
| 5 | 231 | 4.6 | 487 | 4.87 |
| 6 | 4554 | 90.86 | 9043 | 90.43 |
| 7 | 223 | 4.45 | 453 | 4.53 |
| 8 | 4 | 0.08 | 17 | 0.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Ambrosio, F.; Barkema, J.; Barkema, G.T. Efficient Structural Relaxation of Polycrystalline Graphene Models. Nanomaterials 2021, 11, 1242. https://doi.org/10.3390/nano11051242
D’Ambrosio F, Barkema J, Barkema GT. Efficient Structural Relaxation of Polycrystalline Graphene Models. Nanomaterials. 2021; 11(5):1242. https://doi.org/10.3390/nano11051242
Chicago/Turabian StyleD’Ambrosio, Federico, Joris Barkema, and Gerard T. Barkema. 2021. "Efficient Structural Relaxation of Polycrystalline Graphene Models" Nanomaterials 11, no. 5: 1242. https://doi.org/10.3390/nano11051242
APA StyleD’Ambrosio, F., Barkema, J., & Barkema, G. T. (2021). Efficient Structural Relaxation of Polycrystalline Graphene Models. Nanomaterials, 11(5), 1242. https://doi.org/10.3390/nano11051242