Nonlinear Free and Forced Vibrations of a Hyperelastic Micro/Nanobeam Considering Strain Stiffening Effect
Abstract
:1. Introduction
2. Governing Equations
3. Solution Method
3.1. Forced Vibration Solution
3.2. Free Vibration Solution
4. Result and Discussion
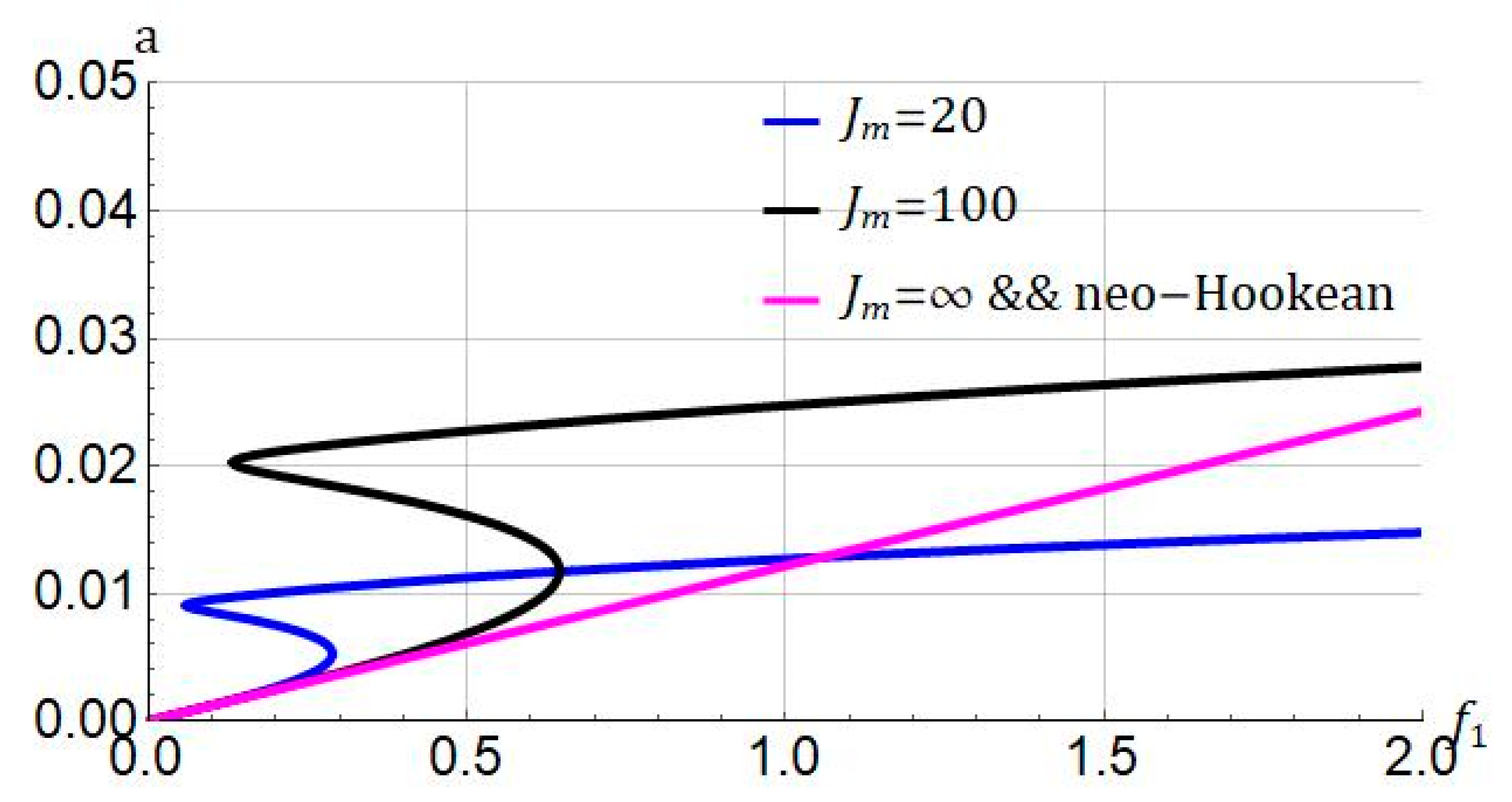
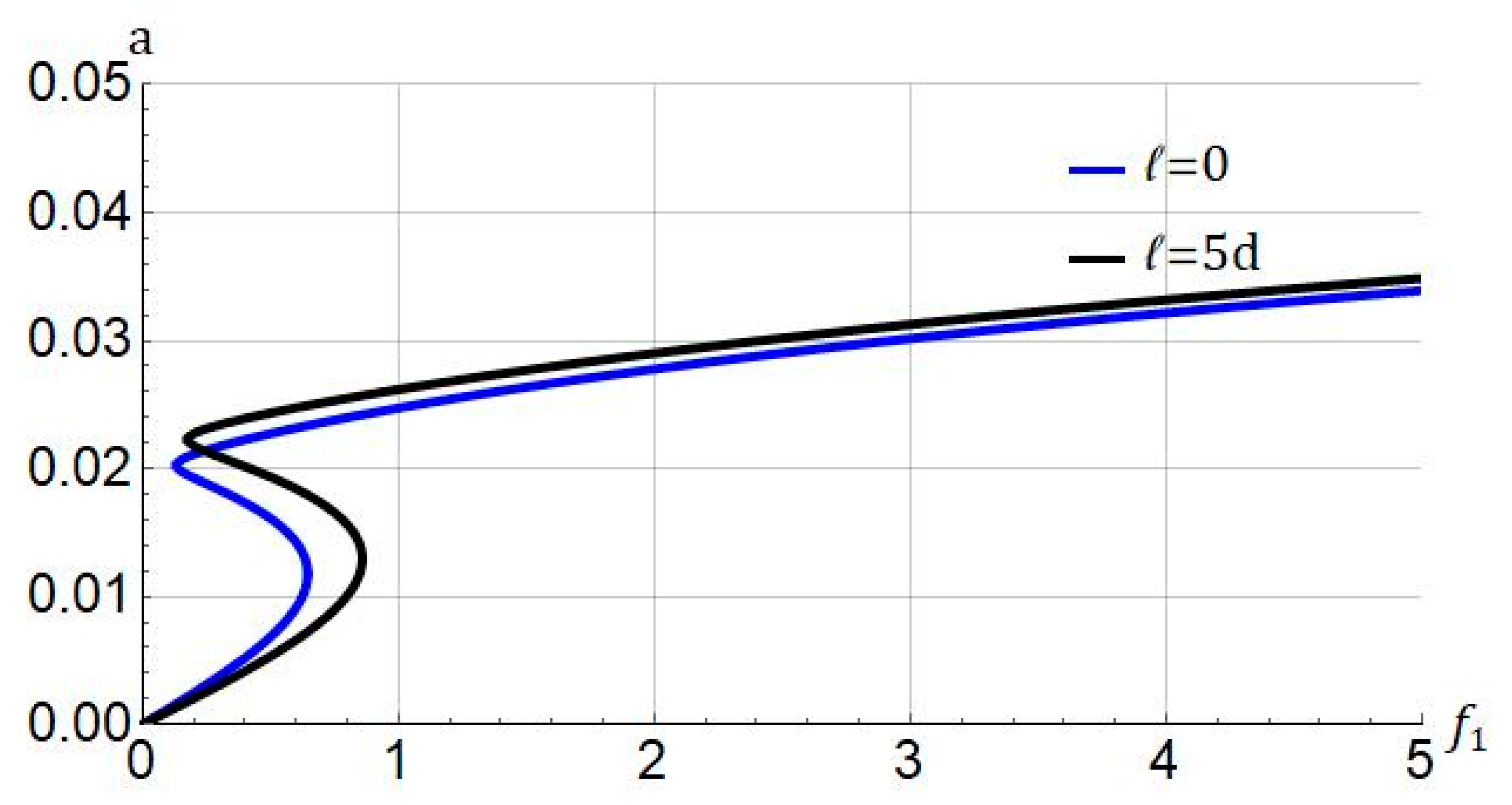
4.1. Frequency Response
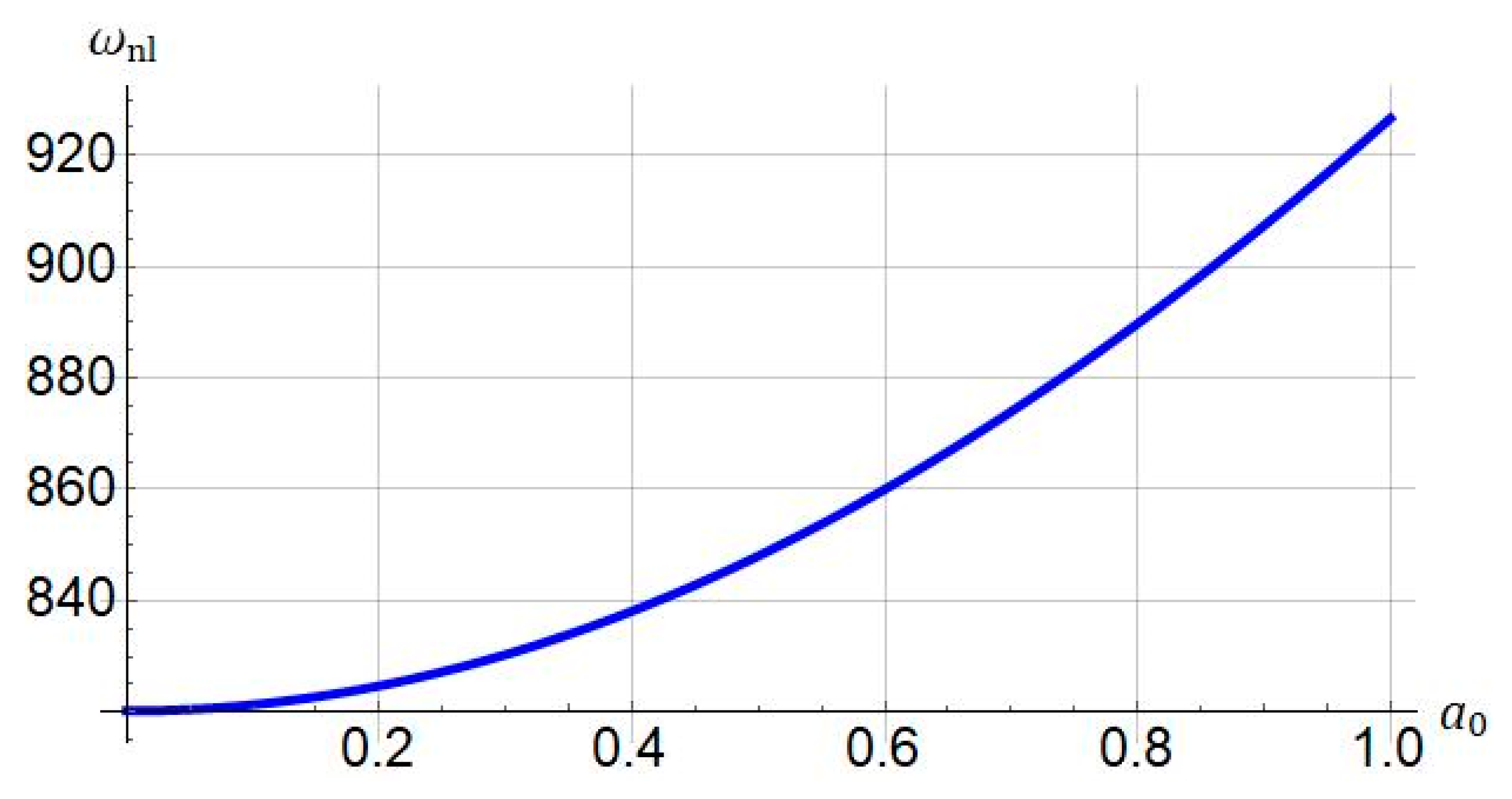
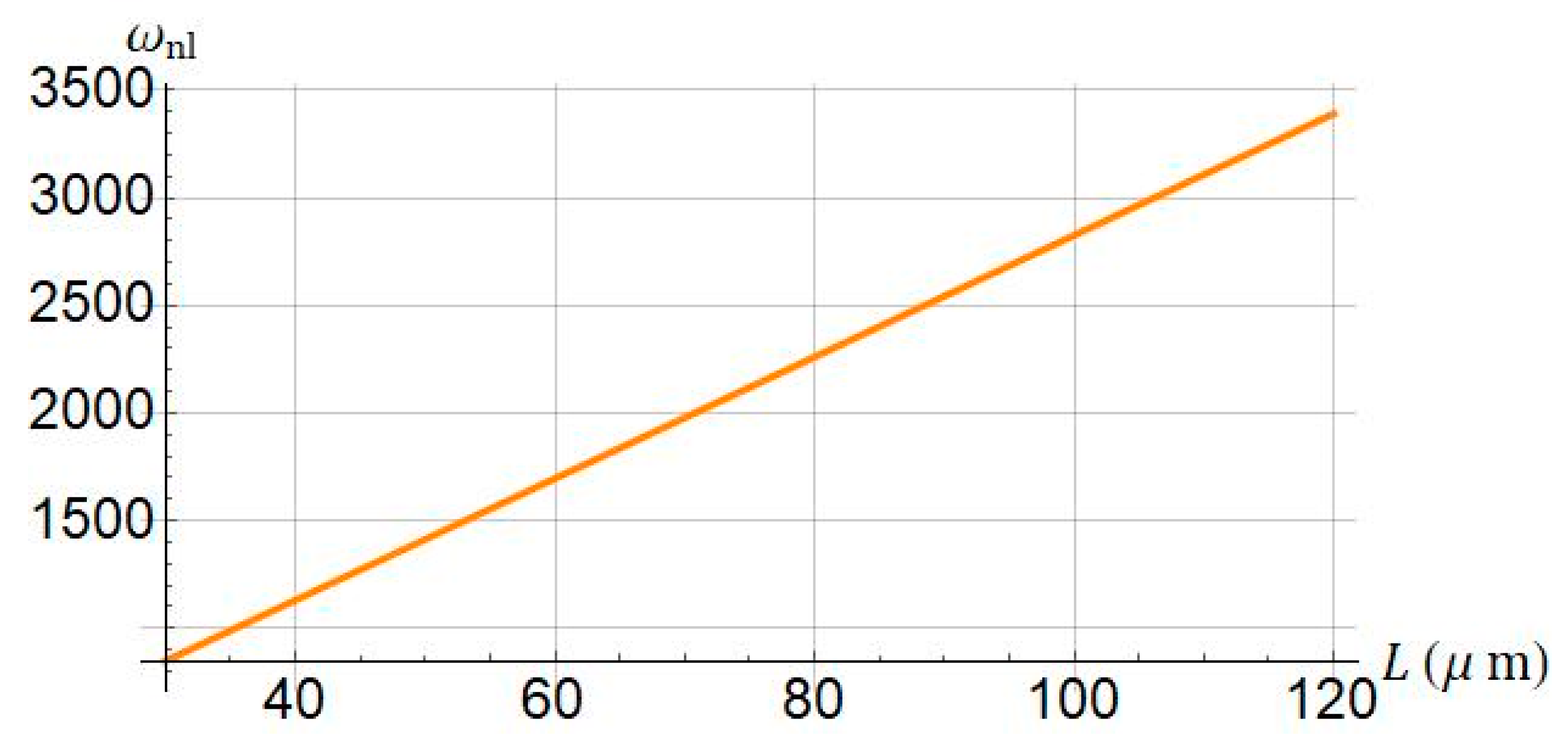
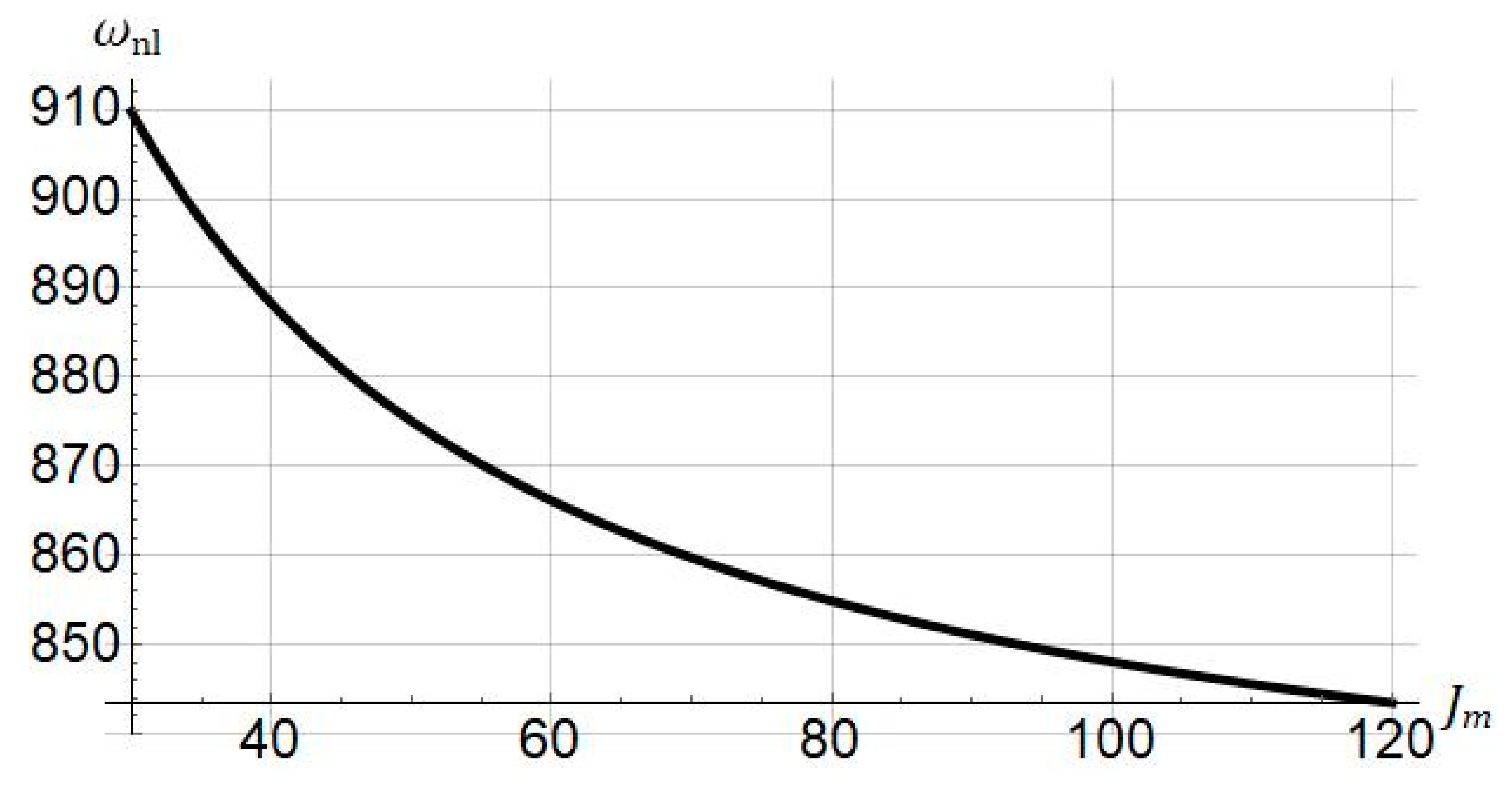
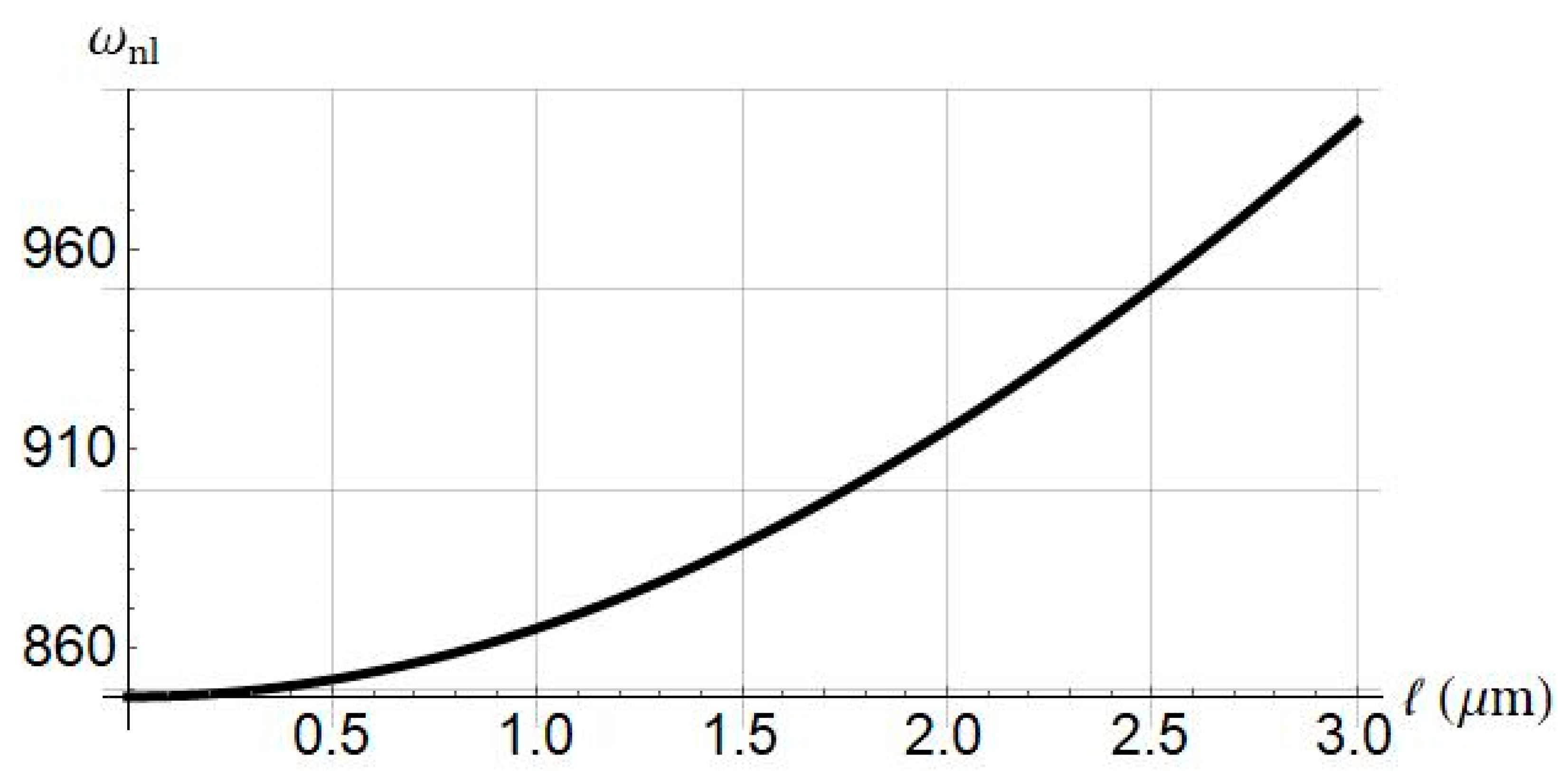
4.2. Nonlinear Frequency
5. Discussion on the Strain-Stiffening
6. Conclusions
- Increasing the strain-stiffening effect leads to increasing hardening nonlinearity.
- For the neo-Hookean model with , the nonlinearity vanishes, and the response is transformed into a linear type.
- As the stiffening parameter is increased, the nonlinear natural frequency decreases.
- The length of the micro/nanobeam, the damping, and size effects were identified as influential parameters in the system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Avey, M.; Tornabene, F.; Dimitri, R.; Kuruoglu, N. Free vibration of thin-walled composite shell structures reinforced with uniform and linear carbon nanotubes: Effect of the elastic foundation and nonlinearity. Nanomaterials 2021, 11, 2090. [Google Scholar] [CrossRef]
- Yi, X.; Li, B.; Wang, Z. Vibration analysis of fluid conveying carbon nanotubes based on nonlocal timoshenko beam theory by spectral element method. Nanomaterials 2019, 9, 1780. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Xie, K.; Fu, T.; Shi, C. Bending and elastic vibration of a novel functionally graded polymer nanocomposite beam reinforced by graphene nanoplatelets. Nanomaterials 2019, 9, 1690. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.F.; Wang, Y.Q. Thermo-electro-mechanical vibrations of porous functionally graded piezoelectric nanoshells. Nanomaterials 2019, 9, 301. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhang, F. Vibration and buckling of shear deformable functionally graded nanoporous metal foam nanoshells. Nanomaterials 2019, 9, 271. [Google Scholar] [CrossRef] [Green Version]
- Dastjerdi, S.; Akgöz, B.; Civalek, Ö. On the effect of viscoelasticity on behavior of gyroscopes. Int. J. Eng. Sci. 2020, 149, 103236. [Google Scholar] [CrossRef]
- Liu, D. Free vibration of functionally graded graphene platelets reinforced magnetic nanocomposite beams resting on elastic foundation. Nanomaterials 2020, 10, 2193. [Google Scholar] [CrossRef] [PubMed]
- Selim, M.M.; Musa, A. Nonlinear vibration of a pre-stressed water-filled single-walled carbon nanotube using shell model. Nanomaterials 2020, 10, 974. [Google Scholar] [CrossRef]
- Kiani, K.; Żur, K.K. Dynamic behavior of magnetically affected rod-like nanostructures with multiple defects via nonlocal-integral/differential-based models. Nanomaterials 2020, 10, 2306. [Google Scholar] [CrossRef] [PubMed]
- Civalek, Ö.; Akbaş, Ş.D.; Akgöz, B.; Dastjerdi, S. Forced vibration analysis of composite beams reinforced by carbon nanotubes. Nanomaterials 2021, 11, 571. [Google Scholar] [CrossRef] [PubMed]
- Hackett, R.M. Hyperelasticity Primer. In Hyperelasticity Primer; Springer: Cham, Switzerland, 2015; pp. 1–170. [Google Scholar] [CrossRef]
- Amabili, M. Nonlinear Mechanics of Shells and Plates in Composite, Soft and Biological Materials; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Chaves, E.W.V. Notes on Continuum Mechanics, 1st ed.; Oñate, E., Ed.; Lecture Notes on Numerical Methods in Engineering and Sciences; Springer: Amsterdam, The Netherlands, 2013; p. 673. Available online: https://www.springer.com/gp/book/9789400759855 (accessed on 21 October 2021).
- Maloisel, G.; Knoop, E.; Schumacher, C.; Bacher, M. Automated Routing of Muscle Fibers for Soft Robots. IEEE Trans. Robot. 2021, 37, 996–1008. [Google Scholar] [CrossRef]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G.A. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 2006, 3, 15–35. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A.; Ogden, R.W. Constitutive modelling of arteries. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 1551–1597. [Google Scholar] [CrossRef]
- Moseley, P.; Florez, J.M.; Sonar, H.A.; Agarwal, G.; Curtin, W.; Paik, J. Modeling, Design, and Development of Soft Pneumatic Actuators with Finite Element Method. Adv. Eng. Mater. 2016, 18, 978–988. [Google Scholar] [CrossRef]
- Zhang, C.; Wei, W.; Sun, H.; Zhu, Q. Study on the properties of different dielectric elastomers applying to actuators. Sensors Actuators A Phys. 2021, 329, 112806. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, M.Y. Multi-Axis Soft Sensors Based on Dielectric Elastomer. Soft Robot. 2016, 3, 3–12. [Google Scholar] [CrossRef]
- Chen, D.; Pei, Q. Electronic Muscles and Skins: A Review of Soft Sensors and Actuators. Chem. Rev. 2017, 117, 11239–11268. [Google Scholar] [CrossRef]
- Dong, L.; Grissom, M.D.; Prasad, M.G.; Fisher, F.T. Application of mechanical stretch to tune the resonance frequency of hyperelastic membrane-based energy harvesters. Sens. Actuators A Phys. 2016, 252, 165–173. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Yang, S. Enhancing the Electromechanical Coupling in Soft Energy Harvesters by Using Graded Dielectric Elastomers. Micromachines 2021, 12, 1187. [Google Scholar] [CrossRef]
- Heidari, H.; Alibakhshi, A.; Azarboni, H.R. Chaotic Motion of a Parametrically Excited Dielectric Elastomer. Int. J. Appl. Mech. 2020, 12, 2050033. [Google Scholar] [CrossRef]
- Breslavsky, I.D.; Amabili, M.; Legrand, M. Nonlinear vibrations of thin hyperelastic plates. J. Sound Vib. 2014, 333, 4668–4681. [Google Scholar] [CrossRef] [Green Version]
- Alibakhshi, A.; Heidari, H. Analytical approximation solutions of a dielectric elastomer balloon using the multiple scales method. Eur. J. Mech. A/Solids 2019, 74, 485–496. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Heidari, H. Nonlinear resonance analysis of dielectric elastomer actuators under thermal and isothermal conditions. Int. J. Appl. Mech. 2020, 12, 2050100. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Heidari, H. Nonlinear dynamic responses of electrically actuated dielectric elastomer-based microbeam resonators. J. Intell. Mater. Syst. Struct. 2021. [Google Scholar] [CrossRef]
- Du, P.; Dai, H.H.; Wang, J.; Wang, Q. Analytical study on growth-induced bending deformations of multi-layered hyperelastic plates. Int. J. Non-Linear Mech. 2020, 119, 103370. [Google Scholar] [CrossRef]
- Tripathi, A.; Bajaj, A.K. Topology optimization and internal resonances in transverse vibrations of hyperelastic plates. Int. J. Solids Struct. 2016, 81, 311–328. [Google Scholar] [CrossRef]
- Amabili, M.; Breslavsky, I.D.; Reddy, J.N. Nonlinear higher-order shell theory for incompressible biological hyperelastic materials. Comput. Methods Appl. Mech. Eng. 2019, 346, 841–861. [Google Scholar] [CrossRef]
- Breslavsky, I.D.; Amabili, M.; Legrand, M. Static and Dynamic Behavior of Circular Cylindrical Shell Made of Hyperelastic Arterial Material. J. Appl. Mech. Trans. ASME 2016, 83, 051002. [Google Scholar] [CrossRef] [Green Version]
- Soares, R.M.; Amaral, P.F.T.; Silva, F.M.A.; Gonçalves, P.B. Nonlinear breathing motions and instabilities of a pressure-loaded spherical hyperelastic membrane. Nonlinear Dyn. 2020, 99, 351–372. [Google Scholar] [CrossRef]
- Vedeneev, V. Nonlinear steady states of hyperelastic membrane tubes conveying a viscous non-Newtonian fluid. J. Fluids Struct. 2020, 98, 103113. [Google Scholar] [CrossRef]
- Soares, R.M.; Gonçalves, P.B. Nonlinear vibrations of a rectangular hyperelastic membrane resting on a nonlinear elastic foundation. Meccanica 2018, 53, 937–955. [Google Scholar] [CrossRef]
- Soares, R.M.; Gonalves, P.B. Nonlinear vibrations and instabilities of a stretched hyperelastic annular membrane. Int. J. Solids Struct. 2012, 49, 514–526. [Google Scholar] [CrossRef] [Green Version]
- Lubbers, L.A.; van Hecke, M.; Coulais, C. A nonlinear beam model to describe the postbuckling of wide neo-Hookean beams. J. Mech. Phys. Solids 2017, 106, 191–206. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Ding, H.; Chen, L.Q. Nonlinear vibration of axially accelerating hyperelastic beams. Int. J. Non-Linear Mech. 2018, 99, 302–310. [Google Scholar] [CrossRef]
- He, L.; Lou, J.; Dong, Y.; Kitipornchai, S.; Yang, J. Variational modeling of plane-strain hyperelastic thin beams with thickness-stretching effect. Acta Mech. 2018, 229, 4845–4861. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, J. An improved dynamic model for a silicone material beam with large deformation. Acta Mech. Sin. Xuebao 2018, 34, 744–753. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, H.; Chen, L.Q. Vibration of axially moving hyperelastic beam with finite deformation. Appl. Math. Model. 2019, 71, 269–285. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, W. Nonlinear transverse vibration of a hyperelastic beam under harmonic axial loading in the subcritical buckling regime. Appl. Math. Model. 2021, 94, 597–618. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Tarantino, A.M. Bending of hyperelastic beams made of transversely isotropic material in finite elasticity. Appl. Math. Model. 2021, 100, 55–76. [Google Scholar] [CrossRef]
- Dadgar-Rad, F.; Sahraee, S. Large deformation analysis of fully incompressible hyperelastic curved beams. Appl. Math. Model. 2021, 93, 89–100. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Tarantino, A.M. Finite anticlastic bending of hyperelastic laminated beams with a rubberlike core. Mech. Adv. Mater. Struct. 2021. [Google Scholar] [CrossRef]
- Lanzoni, L.; Tarantino, A.M. Nonuniform bending theory of hyperelastic beams in finite elasticity. Int. J. Non-Linear Mech. 2021, 135, 103765. [Google Scholar] [CrossRef]
- Dadgar-Rad, F.; Firouzi, N. Large deformation analysis of two-dimensional visco-hyperelastic beams and frames. Arch. Appl. Mech. 2021, 91, 4279–4301. [Google Scholar] [CrossRef]
- Reddy, J.N.; Srinivasa, A.R. Non-linear theories of beams and plates accounting for moderate rotations and material length scales. Int. J. Non-Linear Mech. 2014, 66, 43–53. [Google Scholar] [CrossRef]
- Srinivasa, A.R.; Reddy, J.N. A model for a constrained, finitely deforming, elastic solid with rotation gradient dependent strain energy, and its specialization to von Kármán plates and beams. J. Mech. Phys. Solids 2013, 61, 873–885. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Imam, A.; Haghighi, S.E. Effect of the second invariant of the Cauchy–Green deformation tensor on the local dynamics of dielectric elastomers. Int. J. Non-Linear Mech. 2021, 137, 103807. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Heidari, H. Nonlinear dynamics of dielectric elastomer balloons based on the Gent-Gent hyperelastic model. Eur. J. Mech. A/Solids 2020, 82, 103986. [Google Scholar] [CrossRef]
- Mangan, R.; Destrade, M. Gent models for the inflation of spherical balloons. Int. J. Non-Linear Mech. 2015, 68, 52–58. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Liu, Y.; Luo, X.; Li, B.; Leng, J. Electromechanical instability and snap-through instability of dielectric elastomers undergoing polarization saturation. Mech. Mater. 2012, 55, 60–72. [Google Scholar] [CrossRef]
- Gent, A.N. A new constitutive relation for rubber. Rubber Chem. Technol. 1996, 69, 59–61. [Google Scholar] [CrossRef]
- Breslavsky, I.D.; Amabili, M.; Legrand, M. Physically and geometrically non-linear vibrations of thin rectangular plates. Int. J. Non-Linear Mech. 2014, 58, 30–40. [Google Scholar] [CrossRef] [Green Version]
- Ghayesh, M.H.; Farokhi, H.; Amabili, M. Nonlinear dynamics of a microscale beam based on the modified couple stress theory. Compos. Part. B Eng. 2013, 50, 318–324. [Google Scholar] [CrossRef]
- Azarboni, H.R.; Rahimzadeh, M.; Heidari, H.; Keshavarzpour, H.; Edalatpanah, S.A. Chaotic dynamics and primary resonance analysis of a curved carbon nanotube considering influence of thermal and magnetic fields. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 294. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Wiley-VCH: Weinheim, Germany, 1995. [Google Scholar] [CrossRef]
- Choulaie, M.; Bagheri, A.; Khademifar, A. Nonlinear Vibration and Stability Analysis of Beam on the Variable Viscoelastic Foundation. J. Comput. Appl. Mech. 2017, 48, 99–110. [Google Scholar] [CrossRef]
- Raayai-Ardakani, S.; Cohen, T. Capturing strain stiffening using Volume Controlled Cavity Expansion. Extrem. Mech. Lett. 2019, 31, 100536. [Google Scholar] [CrossRef] [Green Version]
- Horgan, C.O.; Saccomandi, G. A molecular-statistical basis for the Gent constitutive model of rubber elasticity. J. Elast. 2002, 68, 167–176. [Google Scholar] [CrossRef]
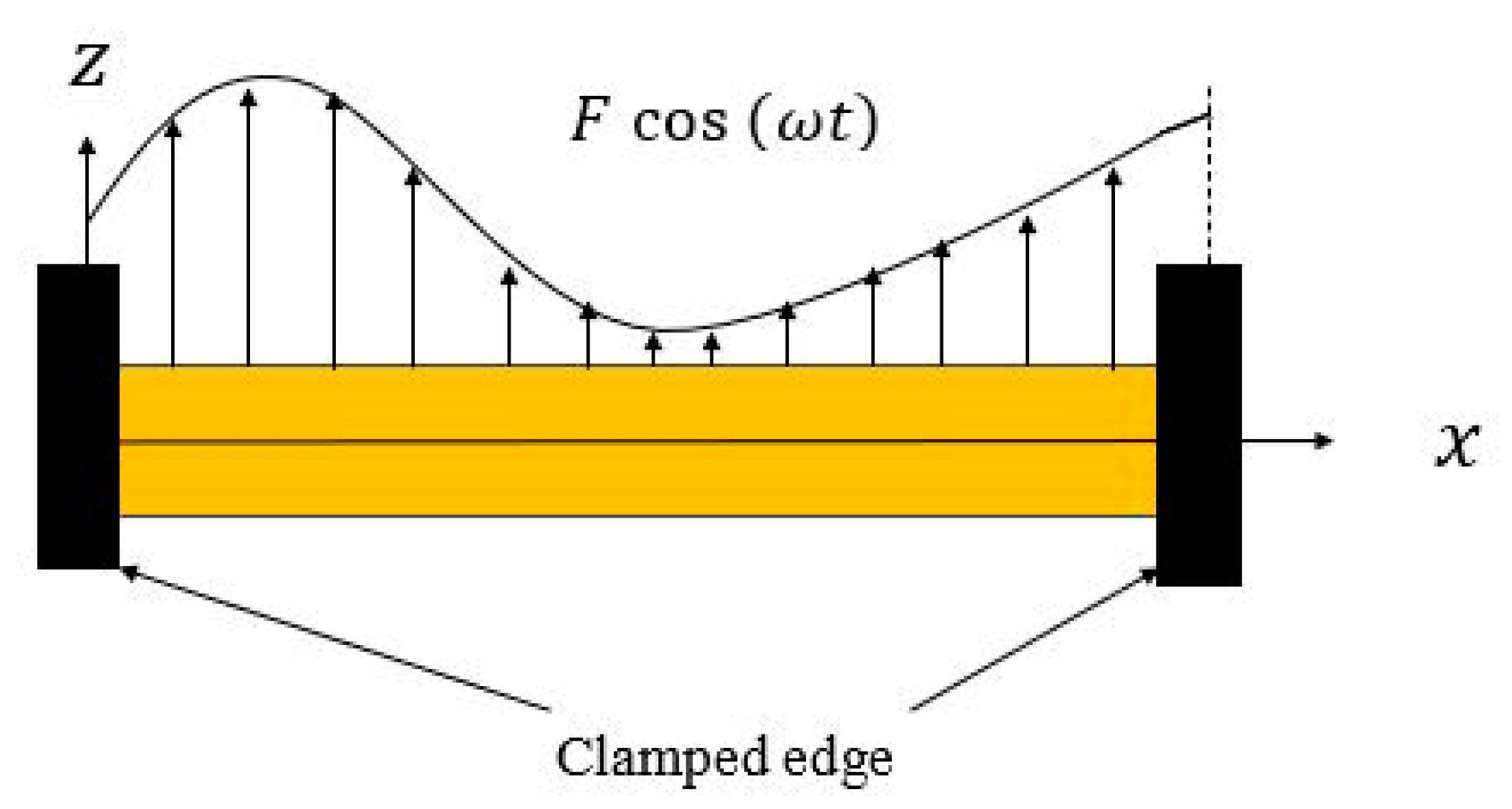

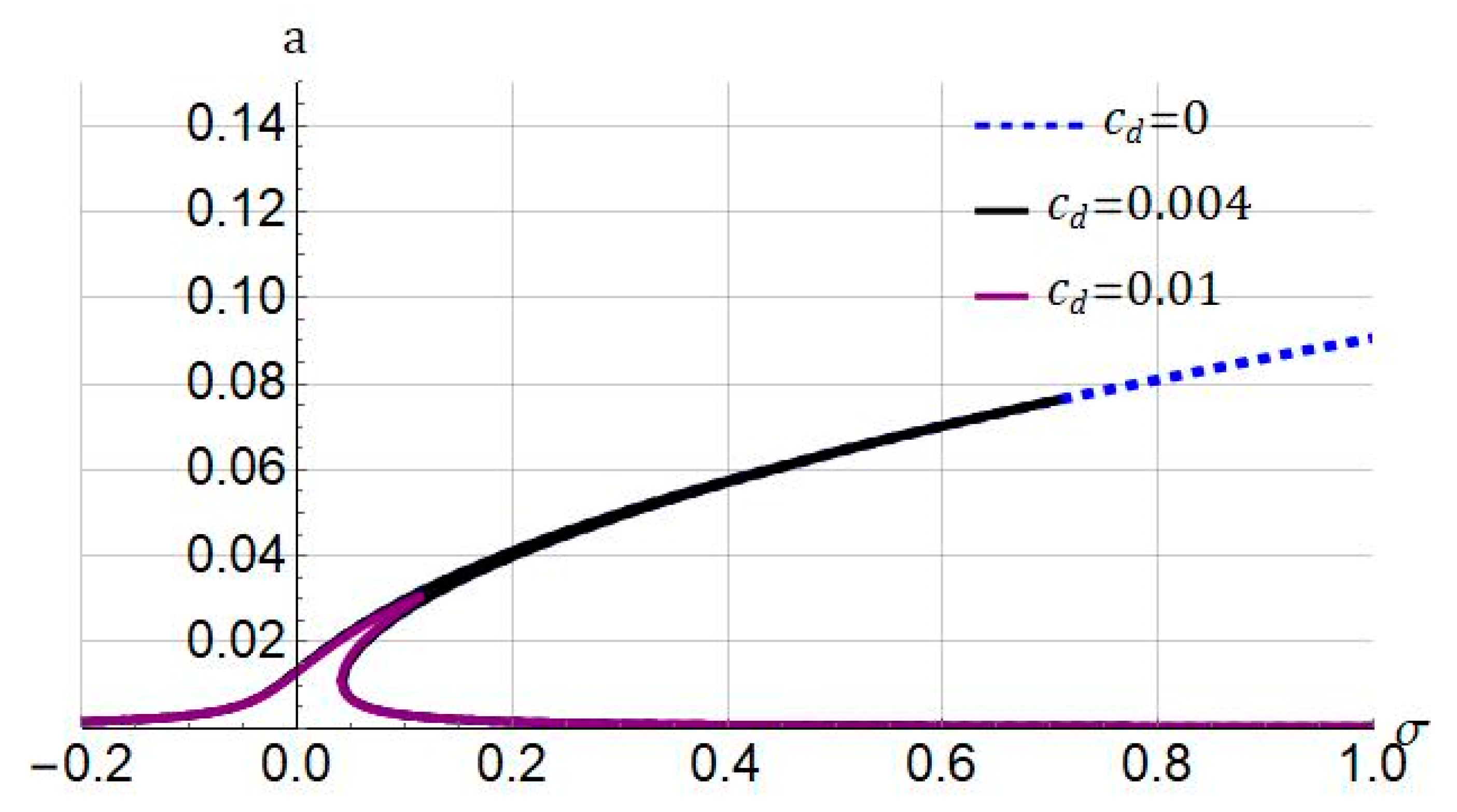
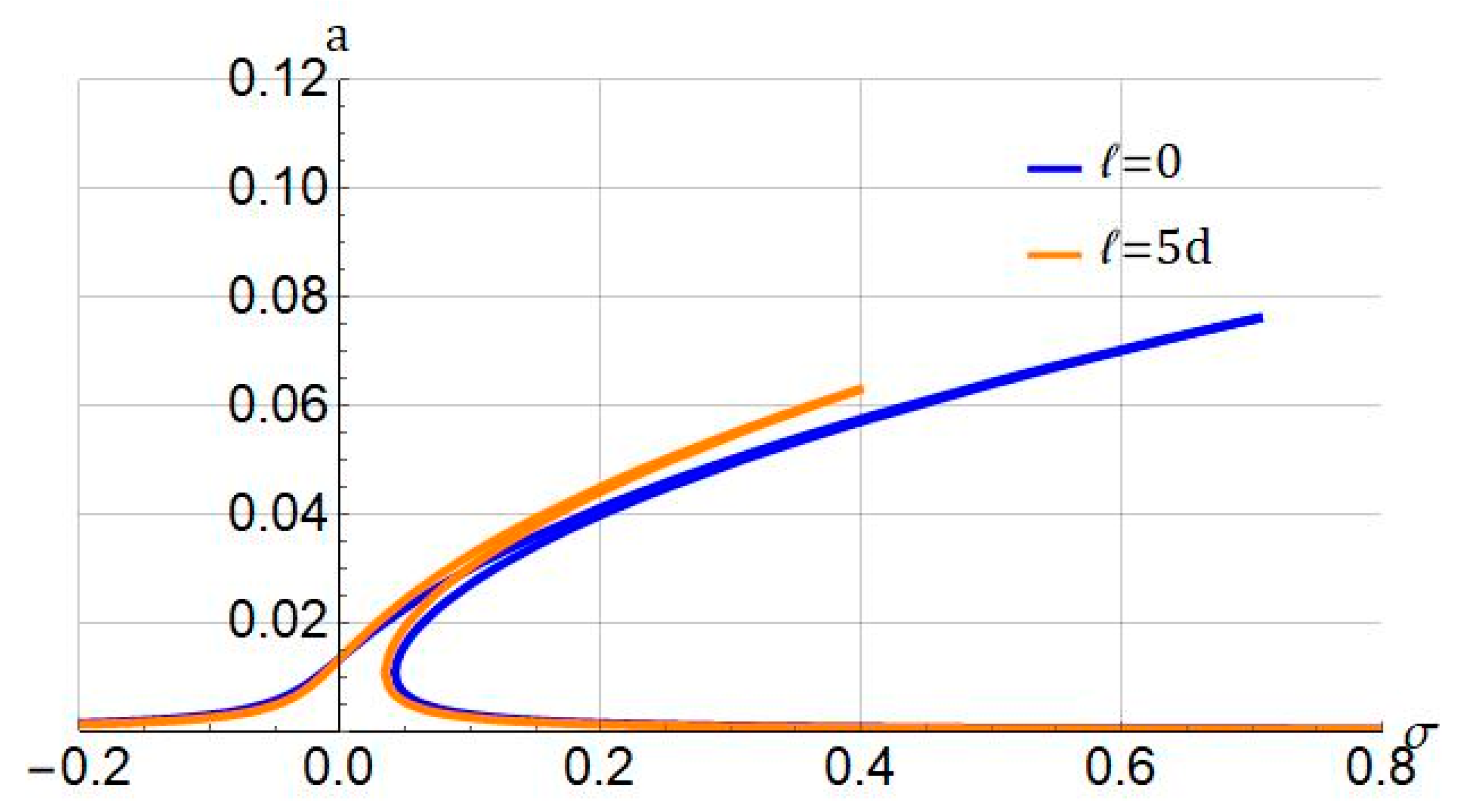

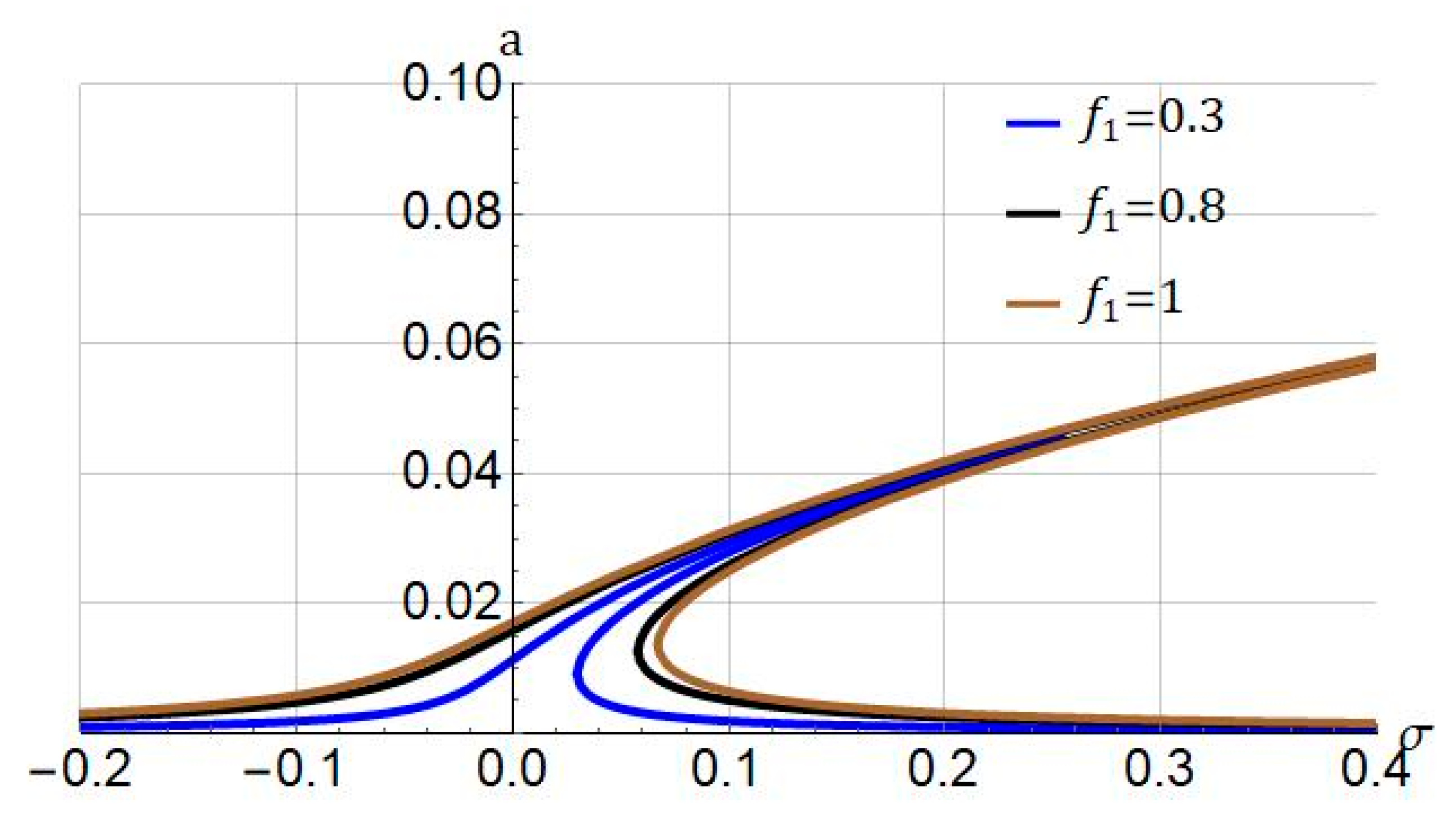
| Parameters | Value |
|---|---|
| Length | |
| Width | |
| Height | |
| Young’s modulus | |
| Shear modulus |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alibakhshi, A.; Dastjerdi, S.; Malikan, M.; Eremeyev, V.A. Nonlinear Free and Forced Vibrations of a Hyperelastic Micro/Nanobeam Considering Strain Stiffening Effect. Nanomaterials 2021, 11, 3066. https://doi.org/10.3390/nano11113066
Alibakhshi A, Dastjerdi S, Malikan M, Eremeyev VA. Nonlinear Free and Forced Vibrations of a Hyperelastic Micro/Nanobeam Considering Strain Stiffening Effect. Nanomaterials. 2021; 11(11):3066. https://doi.org/10.3390/nano11113066
Chicago/Turabian StyleAlibakhshi, Amin, Shahriar Dastjerdi, Mohammad Malikan, and Victor A. Eremeyev. 2021. "Nonlinear Free and Forced Vibrations of a Hyperelastic Micro/Nanobeam Considering Strain Stiffening Effect" Nanomaterials 11, no. 11: 3066. https://doi.org/10.3390/nano11113066
APA StyleAlibakhshi, A., Dastjerdi, S., Malikan, M., & Eremeyev, V. A. (2021). Nonlinear Free and Forced Vibrations of a Hyperelastic Micro/Nanobeam Considering Strain Stiffening Effect. Nanomaterials, 11(11), 3066. https://doi.org/10.3390/nano11113066







