On the Shape-Selected, Ligand-Free Preparation of Hybrid Perovskite (CH3NH3PbBr3) Microcrystals and Their Suitability as Model-System for Single-Crystal Studies of Optoelectronic Properties
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
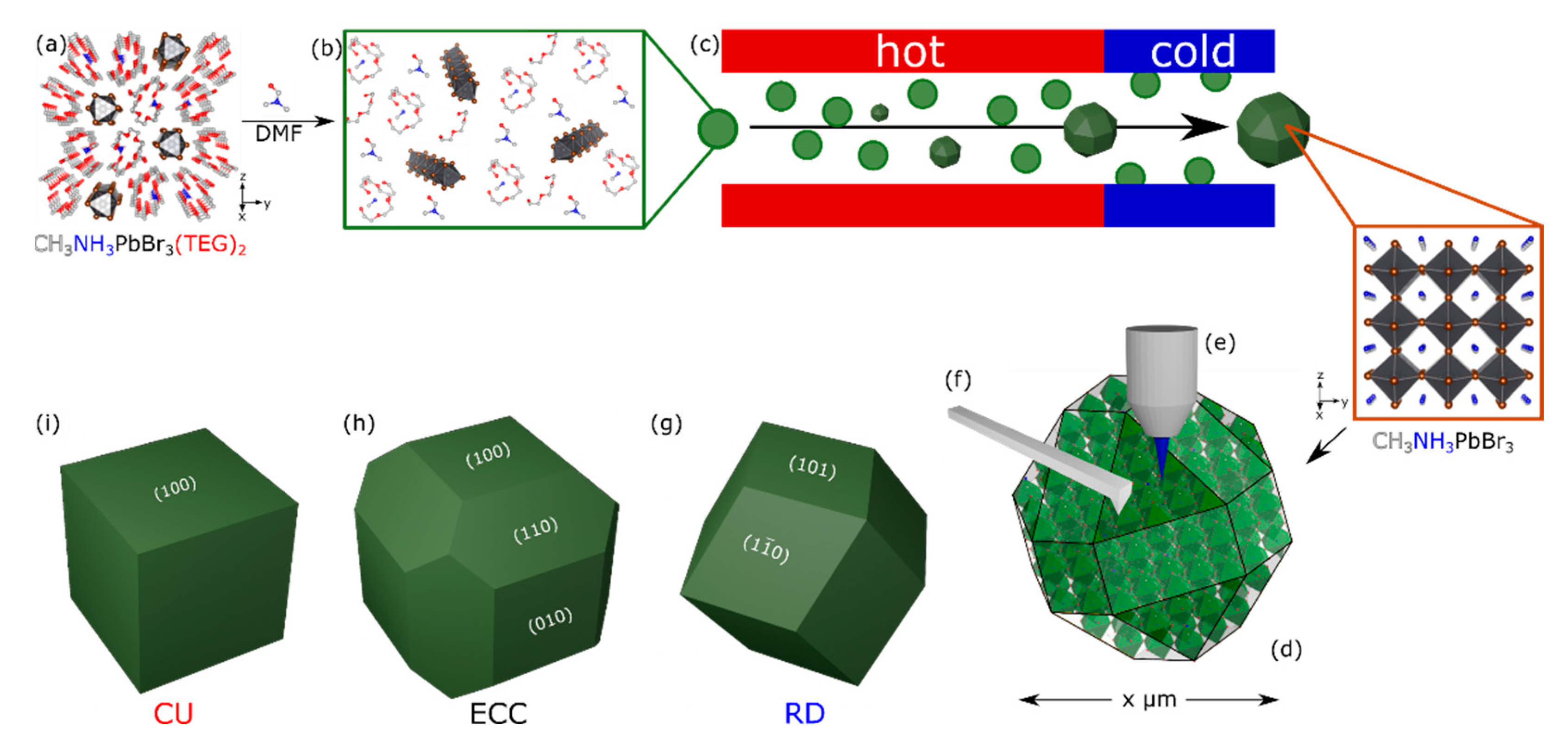
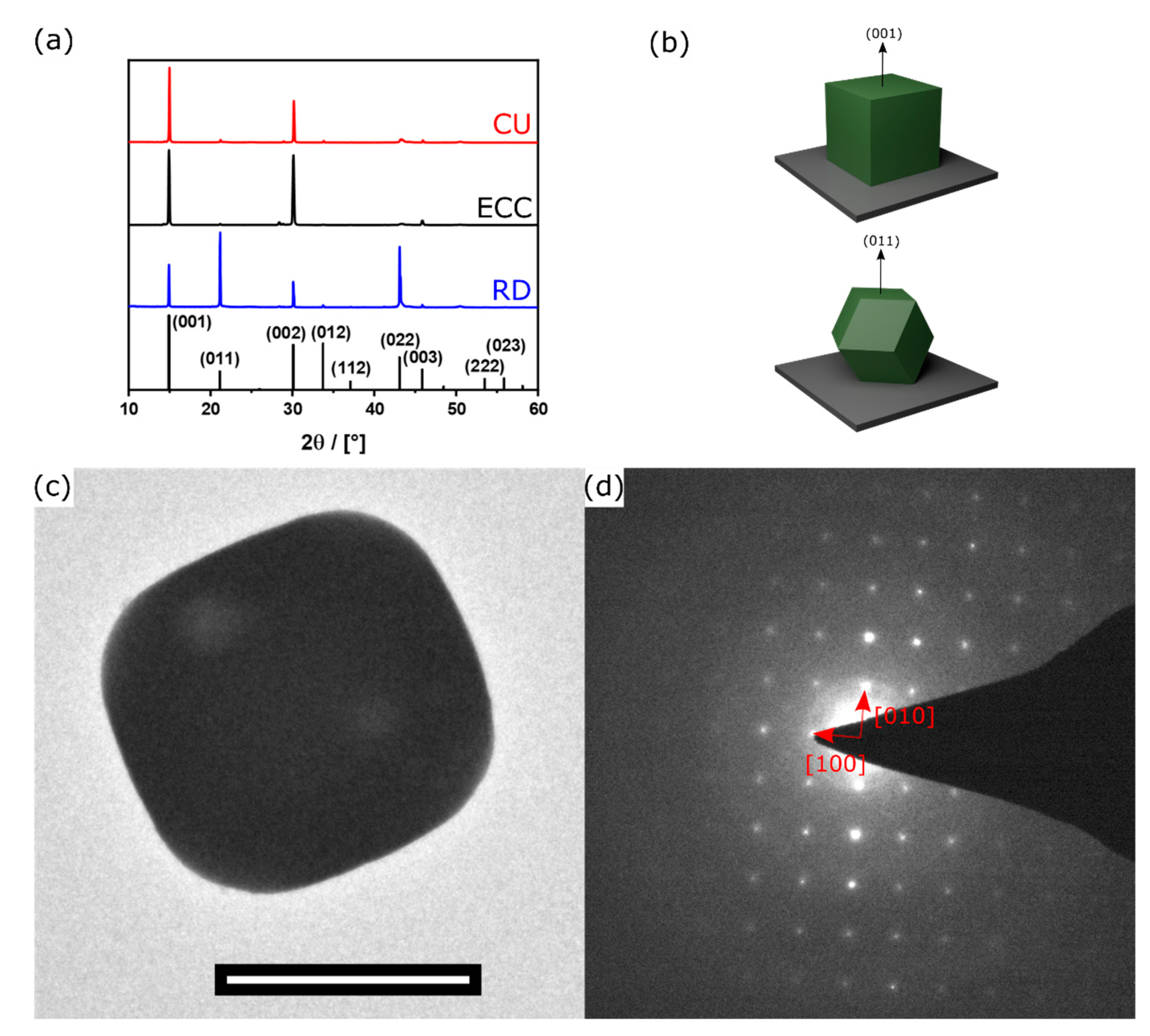
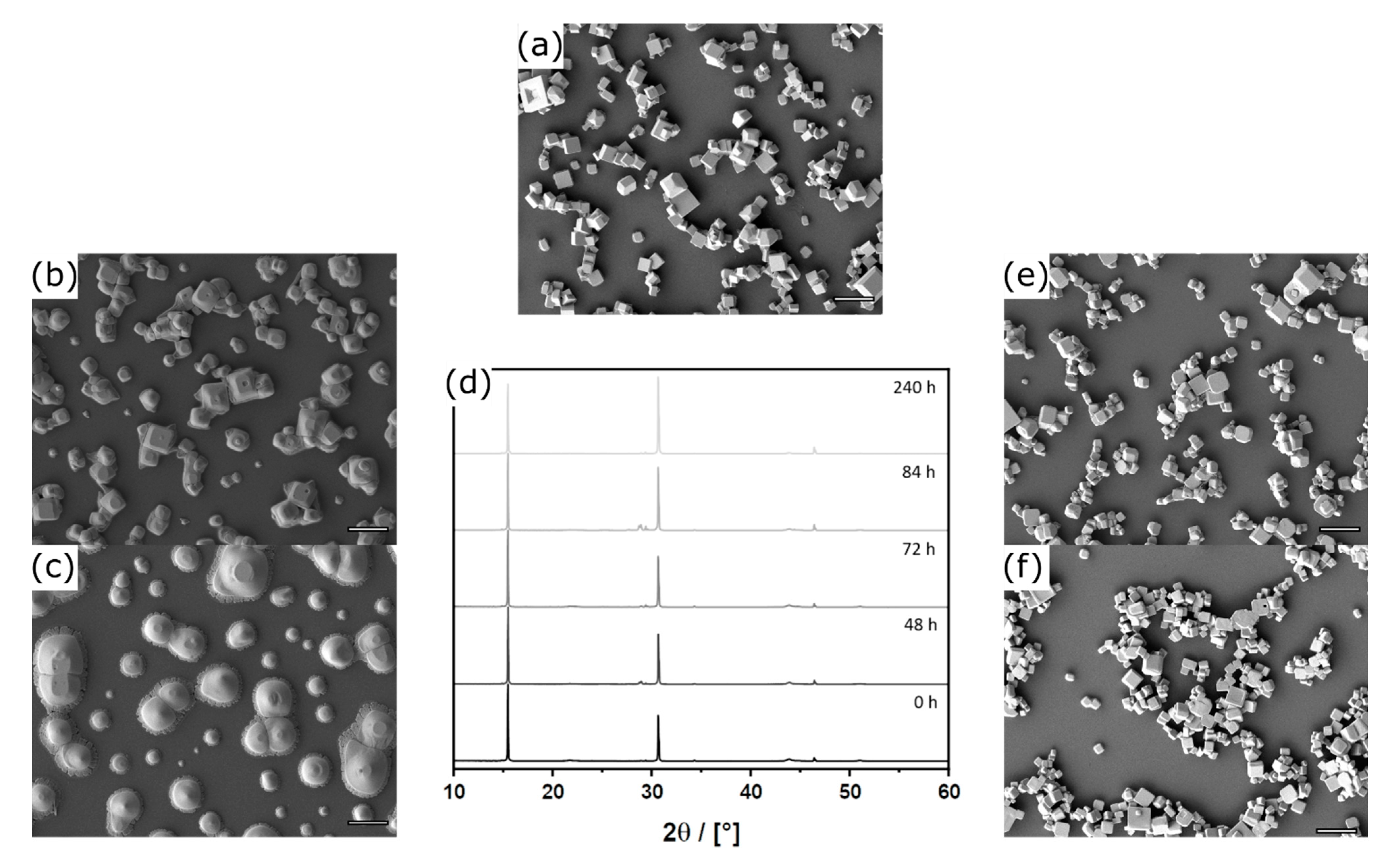
3.1. Aerosol Synthesis of Shape-Controlled Perovskite Microcrystals
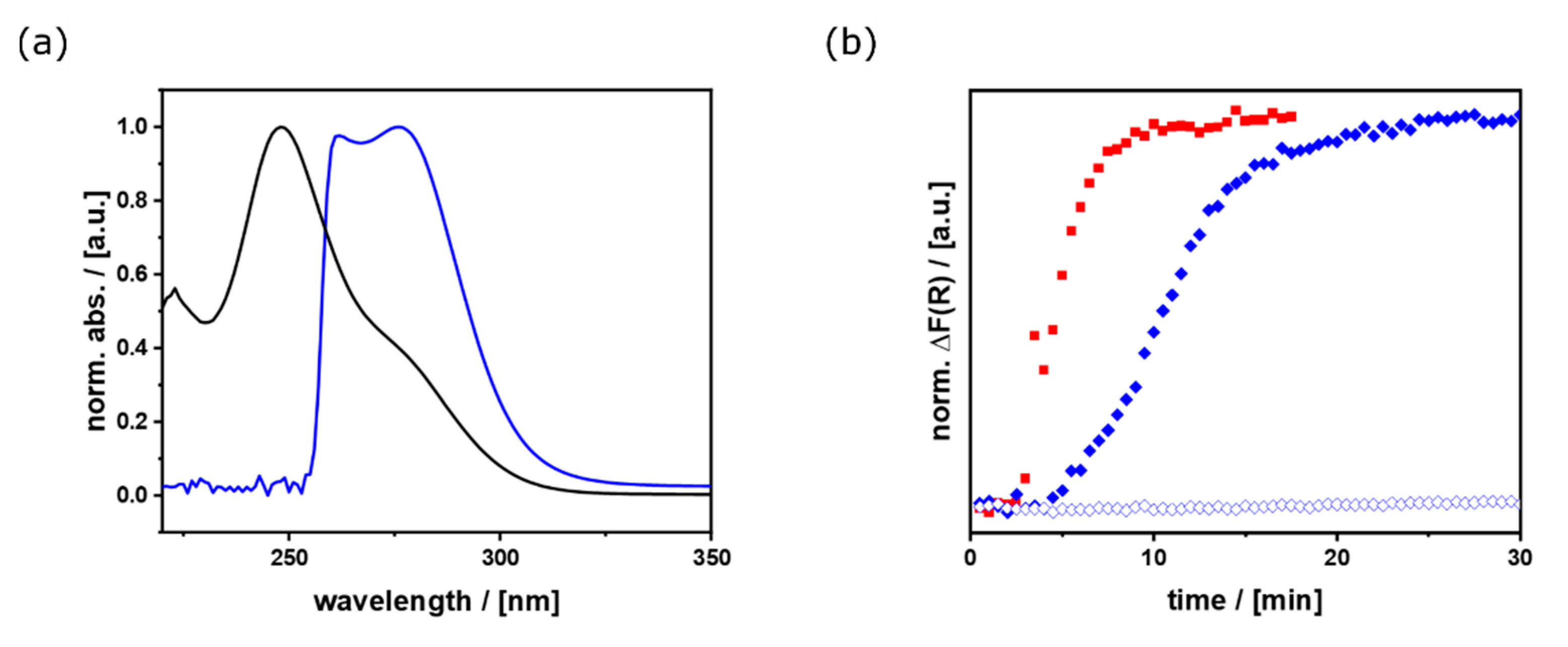
3.2. Ensemble Measurements of Optoelectronic Properties
3.3. Ab-Initio Calculations and Theoretical Considerations
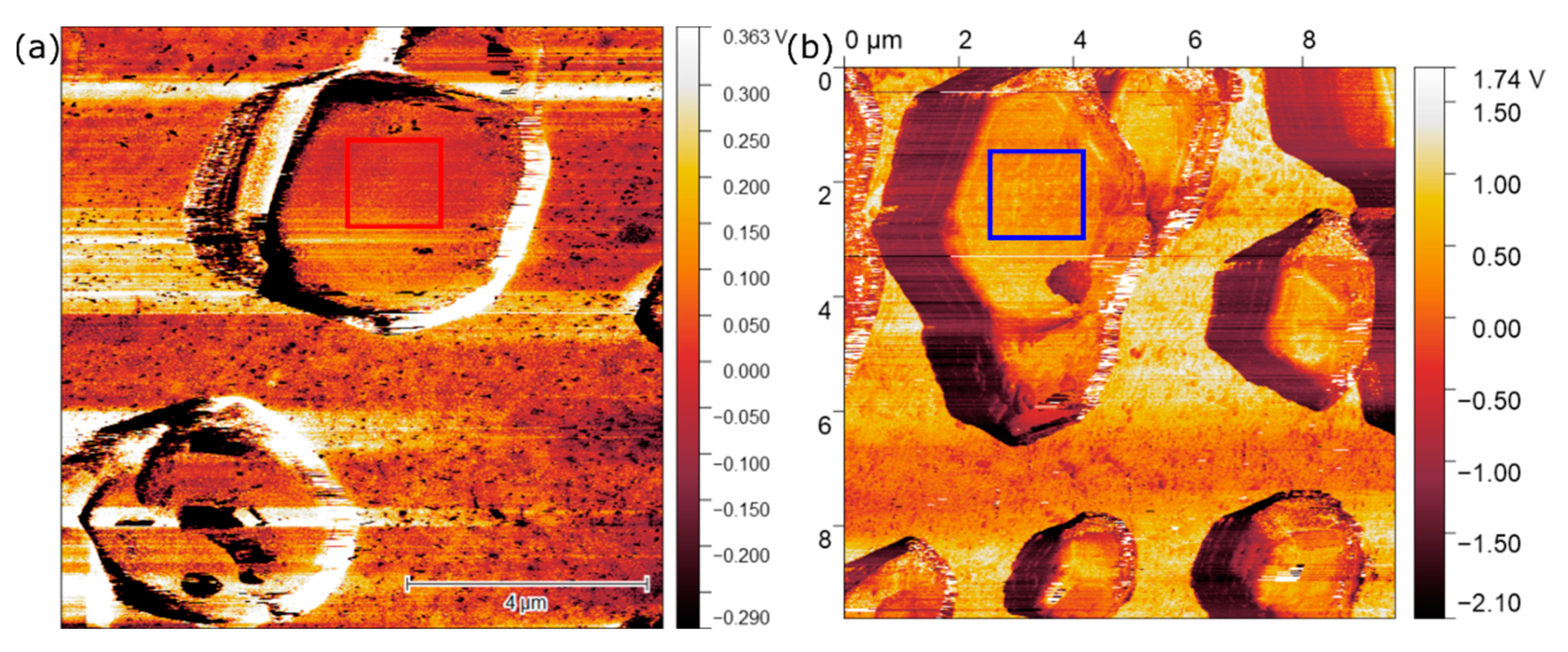
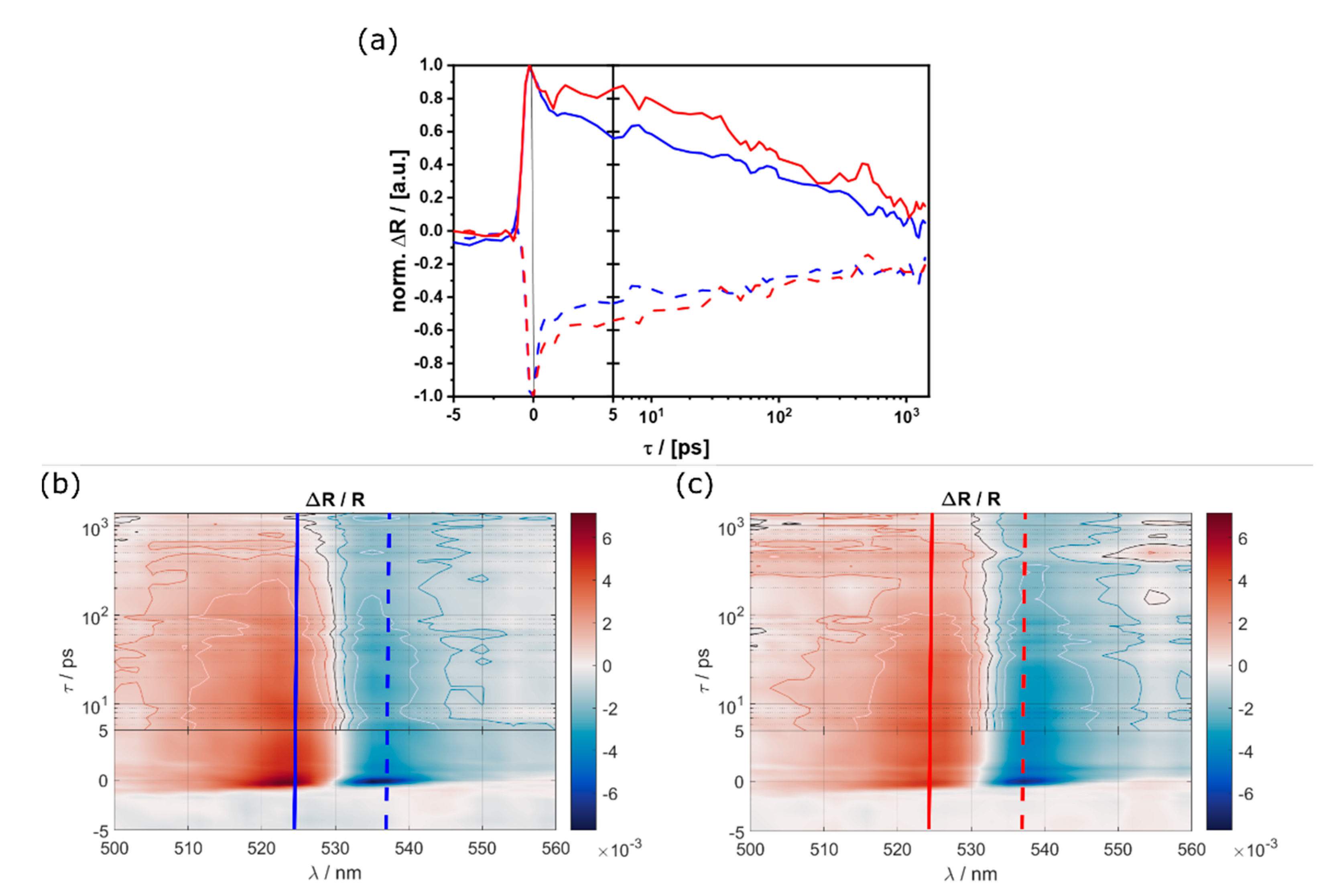
3.4. Single-Particle Measurements
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, J.; Saunders, B.R. Third-generation solar cells: A review and comparison of polymer: Fullerene, hybrid polymer and perovskite solar cells. RSC Adv. 2014, 4, 43286–43314. [Google Scholar] [CrossRef]
- Wright, M.; Uddin, A. Organic-inorganic hybrid solar cells: A comparative review. Sol. Energy Mater. Sol. Cells 2012, 107, 87–111. [Google Scholar] [CrossRef]
- Lee, T.D.; Ebong, A.U. A review of thin film solar cell technologies and challenges. Renew. Sustain. Energy Rev. 2017, 70, 1286–1297. [Google Scholar] [CrossRef]
- Kazim, S.; Nazeeruddin, M.K.; Graetzel, M.; Ahmad, S. Perovskite as Light Harvester: A Game Changer in Photovoltaics. Angew. Chem.-Int. Ed. 2014, 53, 2812–2824. [Google Scholar] [CrossRef]
- Stranks, S.D.; Snaith, H.J. Metal-halide perovskites for photovoltaic and light-emitting devices. Nat. Nanotechnol. 2015, 10, 391–402. [Google Scholar] [CrossRef]
- Jung, H.S.; Park, N.-G. Perovskite Solar Cells: From Materials to Devices. Small 2015, 11, 10–25. [Google Scholar] [CrossRef]
- Gao, P.; Graetzel, M.; Nazeeruddin, M.K. Organohalide lead perovskites for photovoltaic applications. Energy Environ. Sci. 2014, 7, 2448–2463. [Google Scholar] [CrossRef]
- Weber, D. CH3NH3PbX3, ein Pb(II)-System mit kubischer Perowskitstruktur/CH3NH3PbX3, a Pb(II)-System with Cubic Perovskite Structure. Z. Nat. B 1978, 33, 1443–1445. [Google Scholar] [CrossRef]
- Mitzi, D.B. Synthesis, Structure, and Properties of Organic-Inorganic Perovskites and Related Materials. In Progress in Inorganic Chemistry; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1999; pp. 1–121. ISBN 978-0-470-16649-9. [Google Scholar]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory, Best Research-Cell Efficiencies Chart. Available online: https://onlinelibrary.wiley.com/doi/full/10.1002/solr.202100506 (accessed on 27 September 2021).
- Haruyama, J.; Sodeyama, K.; Han, L.; Tateyama, Y. Surface Properties of CH3NH3PbI3 for Perovskite Solar Cells. Acc. Chem. Res. 2016, 49, 554–561. [Google Scholar] [CrossRef]
- Haruyama, J.; Sodeyama, K.; Han, L.; Tateyama, Y. Termination Dependence of Tetragonal CH3NH3PbI3 Surfaces for Perovskite Solar Cells. J. Phys. Chem. Lett. 2014, 5, 2903–2909. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Sumpter, B.G.; Huang, J.; Zhang, H.; Liu, P.; Yang, H.; Zhao, H. Density Functional Studies of Stoichiometric Surfaces of Orthorhombic Hybrid Perovskite CH3NH3PbI3. J. Phys. Chem. C 2015, 119, 1136–1145. [Google Scholar] [CrossRef]
- She, L.; Liu, M.; Zhong, D. Atomic Structures of CH3NH3PbI3 (001) Surfaces. ACS Nano 2016, 10, 1126–1131. [Google Scholar] [CrossRef]
- Wenger, B.; Nayak, P.K.; Wen, X.; Kesava, S.V.; Noel, N.K.; Snaith, H.J. Consolidation of the optoelectronic properties of CH3NH3PbBr3 perovskite single crystals. Nat. Commun. 2017, 8, 590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ball, J.M.; Petrozza, A. Defects in perovskite-halides and their effects in solar cells. Nat. Energy 2016, 1, 16149. [Google Scholar] [CrossRef]
- Yin, W.-J.; Shi, T.; Yan, Y. Unusual defect physics in CH3NH3PbI3 perovskite solar cell absorber. Appl. Phys. Lett. 2014, 104, 063903. [Google Scholar] [CrossRef]
- Wang, F.; Bai, S.; Tress, W.; Hagfeldt, A.; Gao, F. Defects engineering for high-performance perovskite solar cells. NPJ Flex. Electron. 2018, 2, 22. [Google Scholar] [CrossRef] [Green Version]
- de Quilettes, D.W.; Koch, S.; Burke, S.; Paranji, R.K.; Shropshire, A.J.; Ziffer, M.E.; Ginger, D.S. Photoluminescence Lifetimes Exceeding 8 μs and Quantum Yields Exceeding 30% in Hybrid Perovskite Thin Films by Ligand Passivation. ACS Energy Lett. 2016, 1, 438–444. [Google Scholar] [CrossRef]
- Saliba, M.; Matsui, T.; Domanski, K.; Seo, J.-Y.; Ummadisingu, A.; Zakeeruddin, S.M.; Correa-Baena, J.-P.; Tress, W.R.; Abate, A.; Hagfeldt, A.; et al. Incorporation of rubidium cations into perovskite solar cells improves photovoltaic performance. Science 2016, 354, 206–209. [Google Scholar] [CrossRef] [PubMed]
- Abdi-Jalebi, M.; Andaji-Garmaroudi, Z.; Cacovich, S.; Stavrakas, C.; Philippe, B.; Richter, J.M.; Alsari, M.; Booker, E.P.; Hutter, E.M.; Pearson, A.J.; et al. Maximizing and stabilizing luminescence from halide perovskites with potassium passivation. Nature 2018, 555, 497. [Google Scholar] [CrossRef] [PubMed]
- Ono, L.K.; Qi, Y. Surface and Interface Aspects of Organometal Halide Perovskite Materials and Solar Cells. J. Phys. Chem. Lett. 2016, 7, 4764–4794. [Google Scholar] [CrossRef]
- Tennyson, E.M.; Gong, C.; Leite, M.S. Imaging Energy Harvesting and Storage Systems at the Nanoscale. ACS Energy Lett. 2017, 2, 2761–2777. [Google Scholar] [CrossRef]
- Axt, A.; Hermes, I.M.; Bergmann, V.W.; Tausendpfund, N.; Weber, S.A.L. Know your full potential: Quantitative Kelvin probe force microscopy on nanoscale electrical devices. Beilstein J. Nanotechnol. 2018, 9, 1809–1819. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.C.; Jeon, N.J.; Noh, J.H.; Yang, W.S.; Seo, J.; Yun, J.S.; Ho-Baillie, A.; Huang, S.; Green, M.A.; Seidel, J.; et al. Beneficial Effects of PbI2 Incorporated in Organo-Lead Halide Perovskite Solar Cells. Adv. Energy Mater. 2015, 6, 1502104. [Google Scholar] [CrossRef]
- Jiang, C.-S.; Yang, M.; Zhou, Y.; To, B.; Nanayakkara, S.U.; Luther, J.M.; Zhou, W.; Berry, J.J.; van de Lagemaat, J.; Padture, N.P.; et al. Carrier separation and transport in perovskite solar cells studied by nanometre-scale profiling of electrical potential. Nat. Commun. 2015, 6, 8397. [Google Scholar] [CrossRef] [PubMed]
- Bergmann, V.W.; Weber, S.A.L.; Ramos, F.J.; Nazeeruddin, M.K.; Gratzel, M.; Li, D.; Domanski, A.L.; Lieberwirth, I.; Ahmad, S.; Berger, R. Real-space observation of unbalanced charge distribution inside a perovskite-sensitized solar cell. Nat. Commun. 2014, 5, 9. [Google Scholar] [CrossRef]
- Bergmann, V.W.; Guo, Y.; Tanaka, H.; Hermes, I.M.; Li, D.; Klasen, A.; Bretschneider, S.A.; Nakamura, E.; Berger, R.; Weber, S.A.L. Local Time-Dependent Charging in a Perovskite Solar Cell. ACS Appl. Mater. Interfaces 2016, 8, 19402–19409. [Google Scholar] [CrossRef] [PubMed]
- Cai, M.; Ishida, N.; Li, X.; Yang, X.; Noda, T.; Wu, Y.; Xie, F.; Naito, H.; Fujita, D.; Han, L. Control of Electrical Potential Distribution for High-Performance Perovskite Solar Cells. Joule 2018, 2, 296–306. [Google Scholar] [CrossRef] [Green Version]
- Leblebici, S.Y.; Leppert, L.; Li, Y.; Reyes-Lillo, S.E.; Wickenburg, S.; Wong, E.; Lee, J.; Melli, M.; Ziegler, D.; Angell, D.K.; et al. Facet-dependent photovoltaic efficiency variations in single grains of hybrid halide perovskite. Nat. Energy 2016, 1, 7. [Google Scholar] [CrossRef]
- Li, J.-J.; Ma, J.-Y.; Ge, Q.-Q.; Hu, J.-S.; Wang, D.; Wan, L.-J. Microscopic Investigation of Grain Boundaries in Organolead Halide Perovskite Solar Cells. ACS Appl. Mater. Interfaces 2015, 7, 28518–28523. [Google Scholar] [CrossRef] [PubMed]
- Kutes, Y.; Zhou, Y.; Bosse, J.L.; Steffes, J.; Padture, N.P.; Huey, B.D. Mapping the Photoresponse of CH3NH3PbI3 Hybrid Perovskite Thin Films at the Nanoscale. Nano Lett. 2016, 16, 3434–3441. [Google Scholar] [CrossRef] [PubMed]
- deQuilettes, D.W.; Jariwala, S.; Burke, S.; Ziffer, M.E.; Wang, J.T.-W.; Snaith, H.J.; Ginger, D.S. Tracking Photoexcited Carriers in Hybrid Perovskite Semiconductors: Trap-Dominated Spatial Heterogeneity and Diffusion. ACS Nano 2017, 11, 11488–11496. [Google Scholar] [CrossRef]
- Yin, J.; Cortecchia, D.; Krishna, A.; Chen, S.; Mathews, N.; Grimsdale, A.C.; Soci, C. Interfacial Charge Transfer Anisotropy in Polycrystalline Lead Iodide Perovskite Films. J. Phys. Chem. Lett. 2015, 6, 1396–1402. [Google Scholar] [CrossRef]
- Saidaminov, M.I.; Abdelhady, A.L.; Murali, B.; Alarousu, E.; Burlakov, V.M.; Peng, W.; Dursun, I.; Wang, L.; He, Y.; Maculan, G.; et al. High-quality bulk hybrid perovskite single crystals within minutes by inverse temperature crystallization. Nat. Commun. 2015, 6, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Shi, D.; Adinolfi, V.; Comin, R.; Yuan, M.; Alarousu, E.; Buin, A.; Chen, Y.; Hoogland, S.; Rothenberger, A.; Katsiev, K.; et al. Low trap-state density and long carrier diffusion in organolead trihalide perovskite single crystals. Science 2015, 347, 519–522. [Google Scholar] [CrossRef] [Green Version]
- Murali, B.; Yengel, E.; Yang, C.; Peng, W.; Alarousu, E.; Bakr, O.M.; Mohammed, O.F. The Surface of Hybrid Perovskite Crystals: A Boon or Bane. ACS Energy Lett. 2017, 2, 846–856. [Google Scholar] [CrossRef]
- Murali, B.; Kolli, H.K.; Yin, J.; Ketavath, R.; Bakr, O.M.; Mohammed, O.F. Single Crystals: The Next Big Wave of Perovskite Optoelectronics. ACS Mater. Lett. 2020, 2, 184–214. [Google Scholar] [CrossRef]
- Wu, B.; Nguyen, H.T.; Ku, Z.; Han, G.; Giovanni, D.; Mathews, N.; Fan, H.J.; Sum, T.C. Discerning the Surface and Bulk Recombination Kinetics of Organic–Inorganic Halide Perovskite Single Crystals. Adv. Energy Mater. 2016, 6, 1600551. [Google Scholar] [CrossRef]
- Kriso, C.; Stein, M.; Haeger, T.; Pourdavoud, N.; Gerhard, M.; Rahimi-Iman, A.; Riedl, T.; Koch, M. Nonlinear refraction in CH3NH3PbBr3 single crystals. Opt. Lett. 2020, 45, 2431–2434. [Google Scholar] [CrossRef] [Green Version]
- Gao, L.; Zeng, K.; Guo, J.; Ge, C.; Du, J.; Zhao, Y.; Chen, C.; Deng, H.; He, Y.; Song, H.; et al. Passivated Single-Crystalline CH3NH3PbI3 Nanowire Photodetector with High Detectivity and Polarization Sensitivity. Nano Lett. 2016, 16, 7446–7454. [Google Scholar] [CrossRef]
- Kollek, T.; Polarz, S. Facet-controlled preparation of hybrid perovskite microcrystals in the gas phase and the remarkable effect on optoelectronic properties. Crystengcomm 2017, 19, 4615–4621. [Google Scholar] [CrossRef]
- Polarz, S. Shape Matters: Anisotropy of the Morphology of Inorganic Colloidal Particles—Synthesis and Function. Adv. Funct. Mater. 2011, 21, 3214–3230. [Google Scholar] [CrossRef]
- Lai, J.; Niu, W.; Luque, R.; Xu, G. Solvothermal synthesis of metal nanocrystals and their applications. Nano Today 2015, 10, 240–267. [Google Scholar] [CrossRef]
- Owens, J.; Brus, L. Chemical Synthesis and Luminescence Applications of Colloidal Semiconductor Quantum Dots. J. Am. Chem. Soc. 2017, 139, 10939–10943. [Google Scholar] [CrossRef]
- Yang, D.; Li, X.; Zeng, H. Surface Chemistry of All Inorganic Halide Perovskite Nanocrystals: Passivation Mechanism and Stability. Adv. Mater. Interfaces 2018, 5, 1701662. [Google Scholar] [CrossRef] [Green Version]
- Kollek, T.; Wurmbrand, D.; Birkhold, S.T.; Zimmermann, E.; Kalb, J.; Schmidt-Mende, L.; Polarz, S. Thiophene-Functionalized Hybrid Perovskite Microrods and their Application in Photodetector Devices for Investigating Charge Transport Through Interfaces in Particle-Based Materials. ACS Appl. Mater. Interfaces 2017, 9, 1077–1085. [Google Scholar] [CrossRef] [PubMed]
- Birkhold, S.T.; Zimmermann, E.; Kollek, T.; Wurmbrand, D.; Polarz, S.; Schmidt-Mende, L. Impact of Crystal Surface on Photoexcited States in Organic-Inorganic Perovskites. Adv. Funct. Mater. 2017, 27, 1604995. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Huang, F.; Mi, Q. Preferential Facet Growth of Methylammonium Lead Halide Single Crystals Promoted by Halide Coordination. Chem. Lett. 2016, 45, 1030–1032. [Google Scholar] [CrossRef] [Green Version]
- Stranks, S.D.; Eperon, G.E.; Grancini, G.; Menelaou, C.; Alcocer, M.J.P.; Leijtens, T.; Herz, L.M.; Petrozza, A.; Snaith, H.J. Electron-Hole Diffusion Lengths Exceeding 1 Micrometer in an Organometal Trihalide Perovskite Absorber. Science 2013, 342, 341–344. [Google Scholar] [CrossRef] [Green Version]
- Hansen, W.N.; Hansen, G.J. Standard reference surfaces for work function measurements in air. Surf. Sci. 2001, 481, 172–184. [Google Scholar] [CrossRef]
- Kollek, T.; Gruber, D.; Gehring, J.; Zimmermann, E.; Schmidt-Mende, L.; Polarz, S. Porous and Shape-Anisotropic Single Crystals of the Semiconductor Perovskite CH3NH3PbI3 from a Single-Source Precursor. Angew. Chem.-Int. Ed. 2015, 54, 1341–1346. [Google Scholar] [CrossRef]
- Kollek, T.; Fischer, C.; Goettker-Schnetmann, I.; Polarz, S. Microwave Induced Crystallization of the Hybrid Perovskite CH3NH3PbI3 from a Supramolecular Single-Source Precursor. Chem. Mater. 2016, 28, 4134–4138. [Google Scholar] [CrossRef]
- Fillafer, N.; Seewald, T.; Schmidt-Mende, L.; Polarz, S. Interfacial charge transfer processes in 2D and 3D semiconducting hybrid perovskites: Azobenzene as photoswitchable ligand. Beilstein J. Nanotechnol. 2020, 11, 466–479. [Google Scholar] [CrossRef]
- Stamplecoskie, K.G.; Manser, J.S.; Kamat, P.V. Dual nature of the excited state in organic–inorganic lead halide perovskites. Energy Environ. Sci. 2014, 8, 208–215. [Google Scholar] [CrossRef]
- Yoon, S.J.; Stamplecoskie, K.G.; Kamat, P.V. How Lead Halide Complex Chemistry Dictates the Composition of Mixed Halide Perovskites. J. Phys. Chem. Lett. 2016, 7, 1368–1373. [Google Scholar] [CrossRef]
- Geiser, L.; Cherkaoui, S.; Veuthey, J.-L. Potential of formamide and N-methylformamide in nonaqueous capillary electrophoresis coupled to electrospray ionization mass spectrometry: Application to the analysis of β-blockers. J. Chromatogr. A 2002, 979, 389–398. [Google Scholar] [CrossRef]
- Le, Q.V.; Shin, J.W.; Jung, J.-H.; Park, J.; Ozturk, A.; Kim, S.Y. Control of the Crystal Growth Shape in CH3NH3PbBr3 Perovskite Materials. J. Nanosci. Nanotechnol. 2017, 17, 8169–8174. [Google Scholar] [CrossRef]
- Dong, L.; Shi, H.; Cheng, K.; Wang, Q.; Weng, W.; Han, W. Shape-controlled growth of SrTiO3 polyhedral submicro/nanocrystals. Nano Res. 2014, 7, 1311–1318. [Google Scholar] [CrossRef]
- Knop, O.; Wasylishen, R.E.; White, M.A.; Cameron, T.S.; Oort, M.J.M.V. Alkylammonium lead halides. Part 2. CH3NH3 PbX3 (X = Cl, Br, I) perovskites: Cuboctahedral halide cages with isotropic cation reorientation. Can. J. Chem. 1990, 68, 412–422. [Google Scholar] [CrossRef] [Green Version]
- Jaffe, A.; Lin, Y.; Beavers, C.M.; Voss, J.; Mao, W.L.; Karunadasa, H.I. High-Pressure Single-Crystal Structures of 3D Lead-Halide Hybrid Perovskites and Pressure Effects on their Electronic and Optical Properties. ACS Cent. Sci. 2016, 2, 201–209. [Google Scholar] [CrossRef]
- Noh, J.H.; Im, S.H.; Heo, J.H.; Mandal, T.N.; Seok, S.I. Chemical Management for Colorful, Efficient, and Stable Inorganic–Organic Hybrid Nanostructured Solar Cells. Nano Lett. 2013, 13, 1764–1769. [Google Scholar] [CrossRef] [PubMed]
- Christians, J.A.; Miranda Herrera, P.A.; Kamat, P.V. Transformation of the Excited State and Photovoltaic Efficiency of CH3NH3PbI3 Perovskite upon Controlled Exposure to Humidified Air. J. Am. Chem. Soc. 2015, 137, 1530–1538. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, A.; Roy, M.; Pathoor, N.; Aslam, M.; Chowdhury, A. Influence of Atmospheric Constituents on Spectral Instability and Defect-Mediated Carrier Recombination in Hybrid Perovskite Nanoplatelets. J. Phys. Chem. C 2021, 125, 17133–17143. [Google Scholar] [CrossRef]
- Zhang, Z.-Y.; Wang, H.-Y.; Zhang, Y.-X.; Li, K.-J.; Zhan, X.-P.; Gao, B.-R.; Chen, Q.-D.; Sun, H.-B. Size-dependent one-photon- and two-photon-pumped amplified spontaneous emission from organometal halide CH3NH3PbBr3 perovskite cubic microcrystals. Phys. Chem. Chem. Phys. 2017, 19, 2217–2224. [Google Scholar] [CrossRef]
- Tian, Y.; Scheblykin, I.G. Artifacts in Absorption Measurements of Organometal Halide Perovskite Materials: What Are the Real Spectra? J. Phys. Chem. Lett. 2015, 6, 3466–3470. [Google Scholar] [CrossRef] [Green Version]
- Schötz, K.; Askar, A.M.; Peng, W.; Seeberger, D.; Gujar, T.P.; Thelakkat, M.; Köhler, A.; Huettner, S.; Bakr, O.M.; Shankar, K.; et al. Double peak emission in lead halide perovskites by self-absorption. J. Mater. Chem. C 2020, 8, 2289–2300. [Google Scholar] [CrossRef]
- Reuter, K. Ab Initio Thermodynamics and First-Principles Microkinetics for Surface Catalysis. Catal. Lett. 2016, 146, 541–563. [Google Scholar] [CrossRef]
- Onoda-Yamamuro, N.; Matsuo, T.; Suga, H. Calorimetric and IR spectroscopic studies of phase transitions in methylammonium trihalogenoplumbates (II). J. Phys. Chem. Solids 1990, 51, 1383–1395. [Google Scholar] [CrossRef]
- van Lenthe, E.; Ehlers, A.; Baerends, E.-J. Geometry optimizations in the zero order regular approximation for relativistic effects. J. Chem. Phys. 1999, 110, 8943–8953. [Google Scholar] [CrossRef] [Green Version]
- Lupis, C.H.P. Chemical Thermodynamics of Materials; Elsevier Science Publishing Co., Inc.: New York, NY, USA, 1983; ISBN 978-0-444-00713-1. [Google Scholar]
- Huang, X.; Paudel, T.R.; Dowben, P.A.; Dong, S.; Tsymbal, E.Y. Electronic structure and stability of the CH3NH3PbBr3 (001) surface. Phys. Rev. B 2016, 94, 195309. [Google Scholar] [CrossRef] [Green Version]
- Philipsen, P.H.T.; te Velde, G.; Baerends, E.J.; Berger, J.A.; de Boeij, P.L.; Franchini, M.; Groeneveld, J.A.; Kadantsev, E.S.; Klooster, R.; Kootstra, F.; et al. Band; SCM, Theoretical Chemistry; Vrije Universiteit: Amsterdam, The Netherlands.
- te Velde, G.; Baerends, E.J. Precise density-functional method for periodic structures. Phys. Rev. B 1991, 44, 7888–7903. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef] [Green Version]
- Oschinski, H.; Kesuma, I.; Gebensleben, T.; Becker, J.A. Structures and Thermodynamics of MgO/SiO Interfaces. J. Phys. Chem. C 2020, 124, 1923–1931. [Google Scholar] [CrossRef]
- Zhang, W.; Pathak, S.; Sakai, N.; Stergiopoulos, T.; Nayak, P.K.; Noel, N.K.; Haghighirad, A.A.; Burlakov, V.M.; deQuilettes, D.W.; Sadhanala, A.; et al. Enhanced optoelectronic quality of perovskite thin films with hypophosphorous acid for planar heterojunction solar cells. Nat. Commun. 2015, 6, 10030. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, H.; Fu, Y.; Meng, F.; Wu, X.; Gong, Z.; Ding, Q.; Gustafsson, M.V.; Trinh, M.T.; Jin, S.; Zhu, X.-Y. Lead halide perovskite nanowire lasers with low lasing thresholds and high quality factors. Nat. Mater. 2015, 14, 636–642. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Dong, H.; Jiang, M.; Zheng, W.; Sun, L.; Zhao, B.; Tang, B.; Pan, A.; Zhang, L. Single-mode lasing and 3D confinement from perovskite micro-cubic cavity. J. Mater. Chem. C 2018, 6, 11740–11748. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, L.; Liu, J.; Tang, A.; Hu, J.-S.; Yao, J.; Zhao, Y.S. Controlling the Cavity Structures of Two-Photon-Pumped Perovskite Microlasers. Adv. Mater. 2016, 28, 4040–4046. [Google Scholar] [CrossRef] [PubMed]
- Tiguntseva, E.; Koshelev, K.; Furasova, A.; Tonkaev, P.; Mikhailovskii, V.; Ushakova, E.V.; Baranov, D.G.; Shegai, T.; Zakhidov, A.A.; Kivshar, Y.; et al. Room-Temperature Lasing from Mie-Resonant Nonplasmonic Nanoparticles. ACS Nano 2020, 14, 8149–8156. [Google Scholar] [CrossRef] [PubMed]


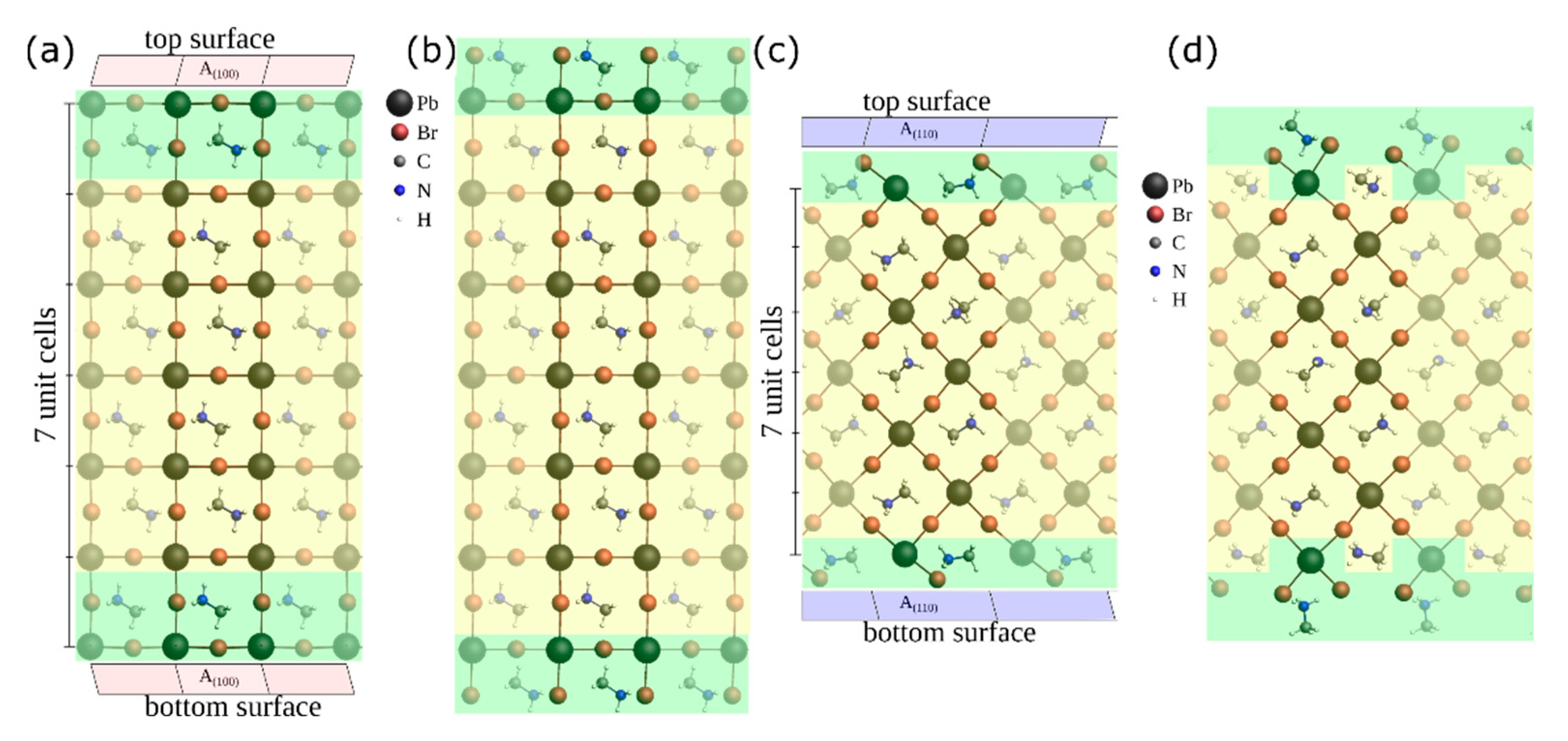
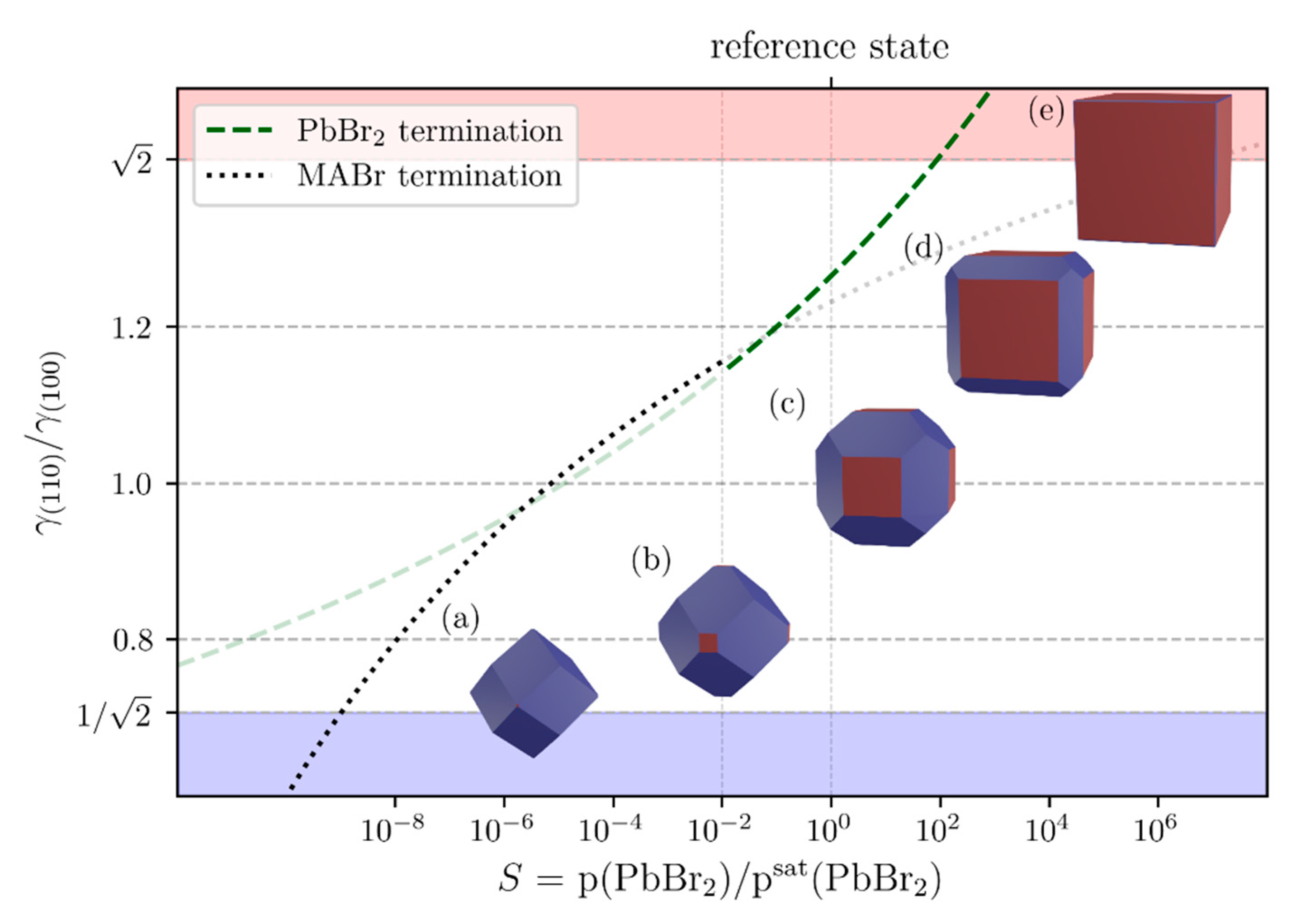

| Termination | Surface Tension/(J/m²) | |
|---|---|---|
| (100)-surface | ||
| (a) PbBr2 | 1 | 0.416 |
| (b) MABr | −1 | 0.498 |
| (110)-surface | ||
| (c) mixed | 0 | 0.526 |
| (d) 2 × MABr | −2 | 0.614 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahnmüller, U.J.; Kuper, H.; Seewald, T.; Yalҫinkaya, Y.; Becker, J.A.; Schmidt-Mende, L.; Weber, S.A.L.; Polarz, S. On the Shape-Selected, Ligand-Free Preparation of Hybrid Perovskite (CH3NH3PbBr3) Microcrystals and Their Suitability as Model-System for Single-Crystal Studies of Optoelectronic Properties. Nanomaterials 2021, 11, 3057. https://doi.org/10.3390/nano11113057
Bahnmüller UJ, Kuper H, Seewald T, Yalҫinkaya Y, Becker JA, Schmidt-Mende L, Weber SAL, Polarz S. On the Shape-Selected, Ligand-Free Preparation of Hybrid Perovskite (CH3NH3PbBr3) Microcrystals and Their Suitability as Model-System for Single-Crystal Studies of Optoelectronic Properties. Nanomaterials. 2021; 11(11):3057. https://doi.org/10.3390/nano11113057
Chicago/Turabian StyleBahnmüller, Ulrich Johannes, Henning Kuper, Tobias Seewald, Yenal Yalҫinkaya, Jörg August Becker, Lukas Schmidt-Mende, Stefan A. L. Weber, and Sebastian Polarz. 2021. "On the Shape-Selected, Ligand-Free Preparation of Hybrid Perovskite (CH3NH3PbBr3) Microcrystals and Their Suitability as Model-System for Single-Crystal Studies of Optoelectronic Properties" Nanomaterials 11, no. 11: 3057. https://doi.org/10.3390/nano11113057
APA StyleBahnmüller, U. J., Kuper, H., Seewald, T., Yalҫinkaya, Y., Becker, J. A., Schmidt-Mende, L., Weber, S. A. L., & Polarz, S. (2021). On the Shape-Selected, Ligand-Free Preparation of Hybrid Perovskite (CH3NH3PbBr3) Microcrystals and Their Suitability as Model-System for Single-Crystal Studies of Optoelectronic Properties. Nanomaterials, 11(11), 3057. https://doi.org/10.3390/nano11113057







