Critical Temperatures for Vibrations and Buckling of Magneto-Electro-Elastic Nonlocal Strain Gradient Plates
Abstract
1. Introduction
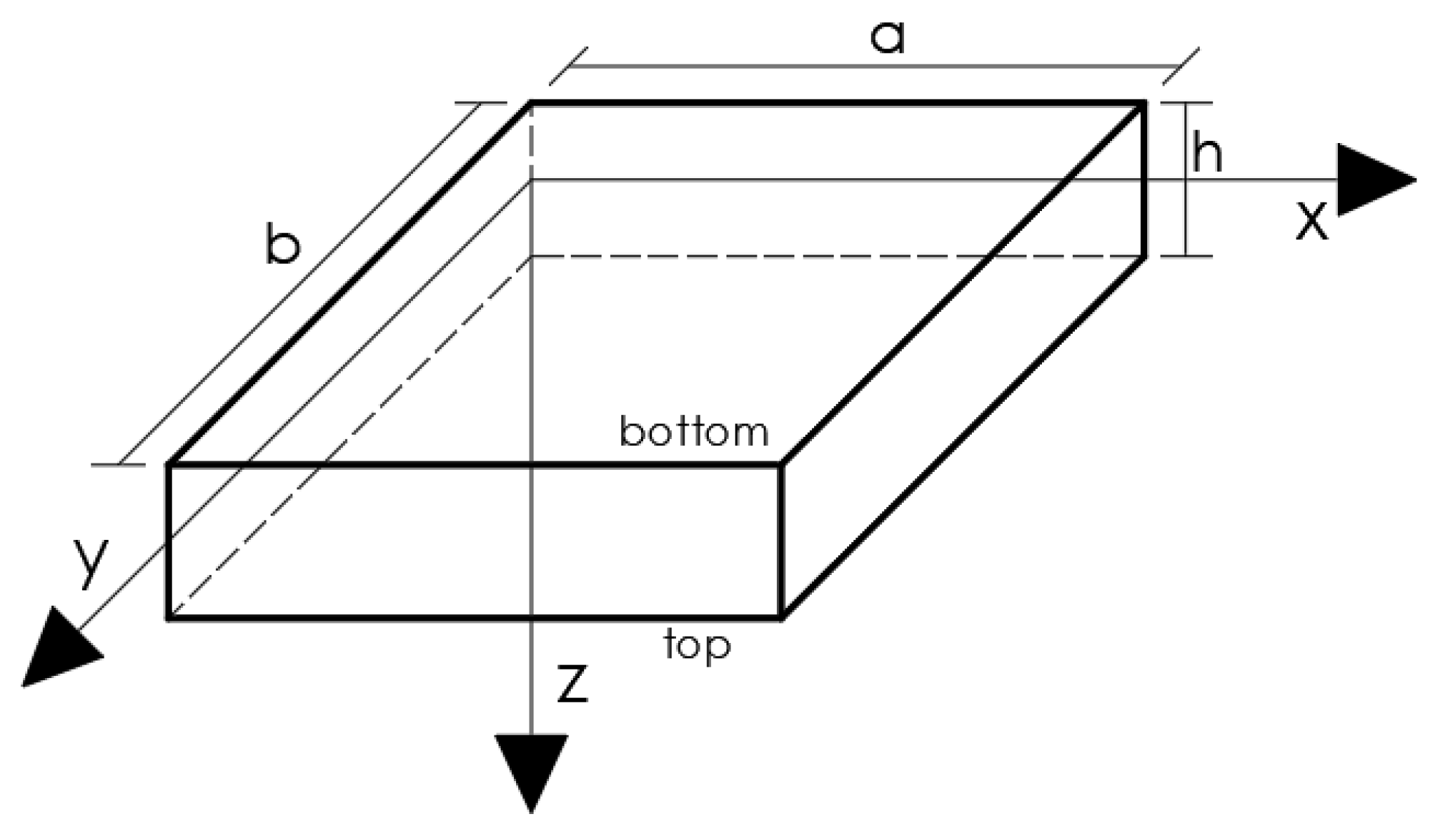
2. Theoretical Background
3. Electric and Magnetic Potentials
4. Equations of Motion
5. Navier Solution
5.1. Buckling Analysis
5.2. Thermal Free Vibration
6. Numerical Results
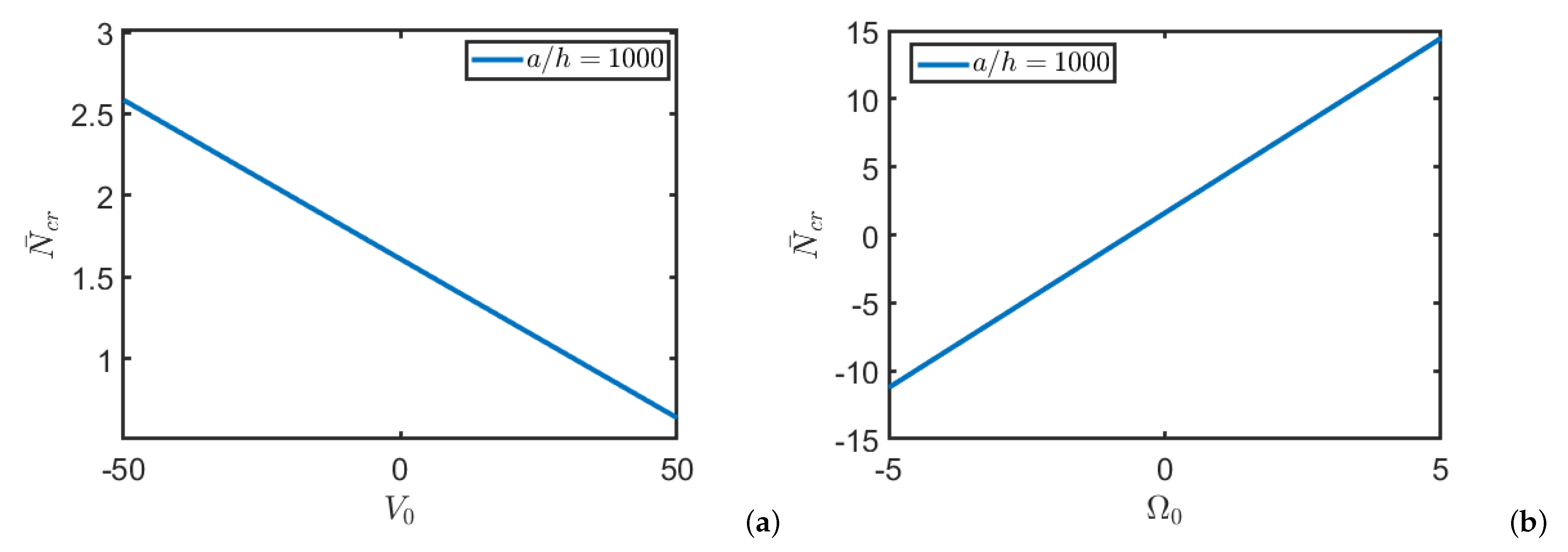
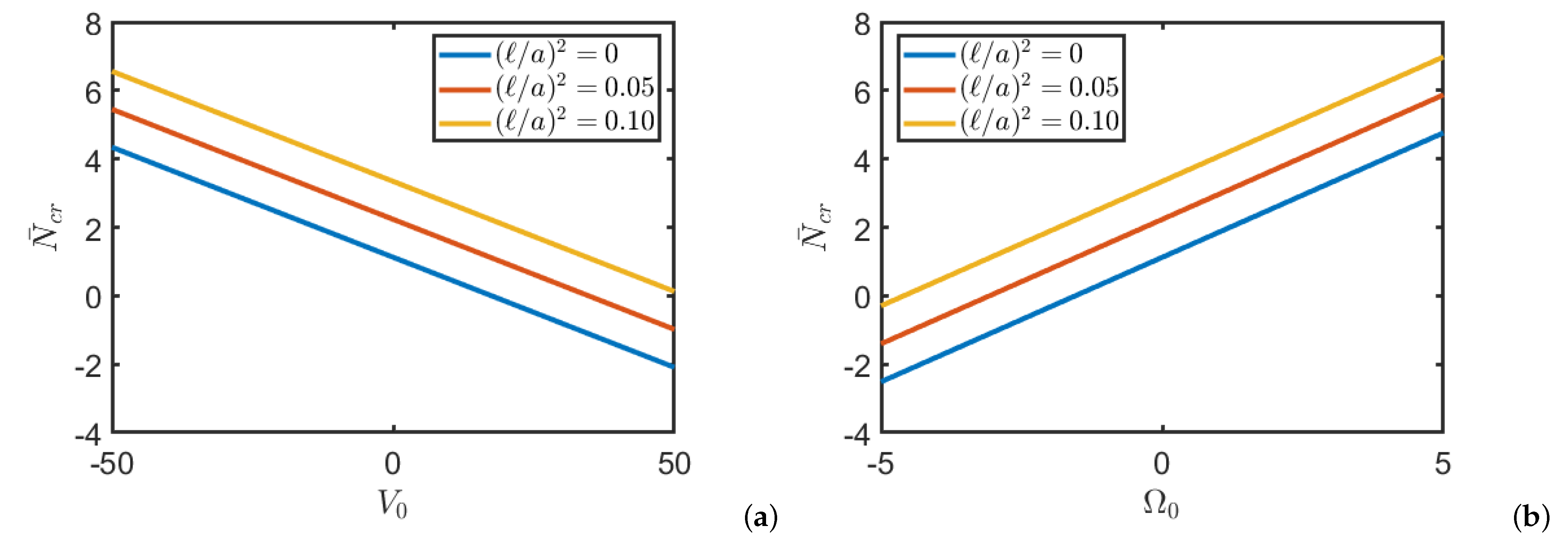
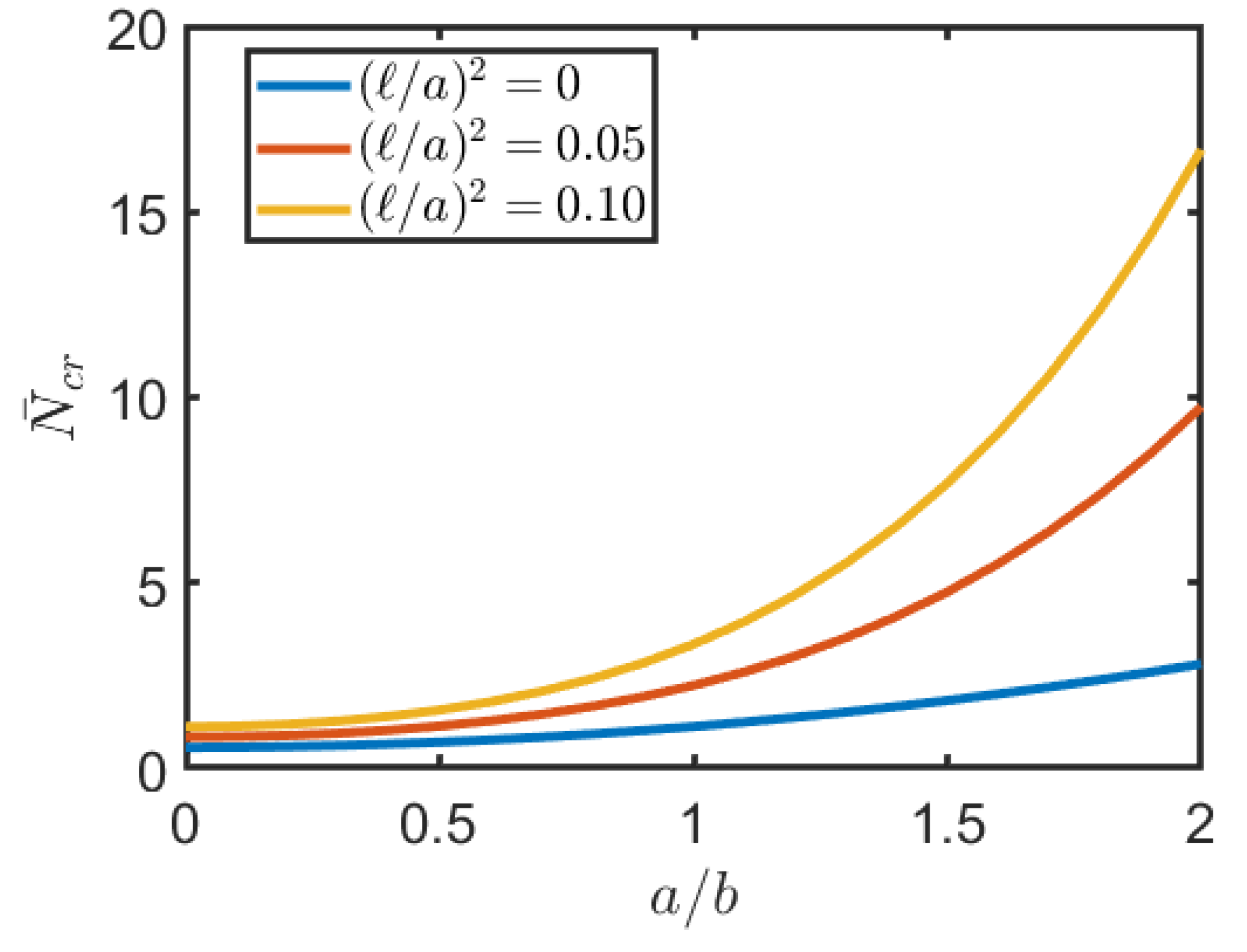
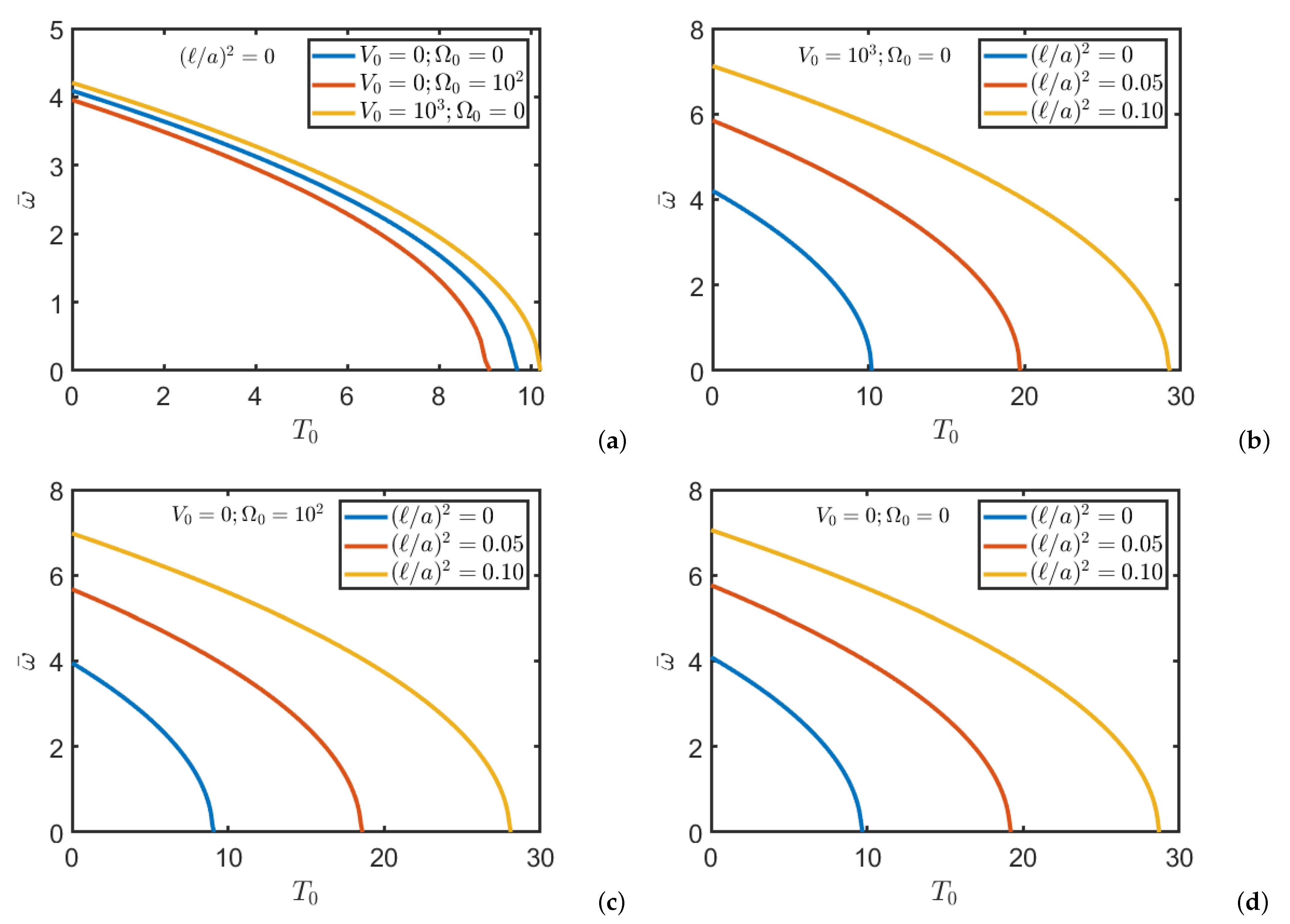
6.1. Buckling
6.2. Thermal Free Vibration
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Saji, V.S.; Choe, H.C.; Yeung, K.W. Nanotechnology in biomedical applications: A review. Int. J. Nano-Biomater. 2010, 3, 119–139. [Google Scholar] [CrossRef]
- Berman, D.; Krim, J. Surface science, MEMS and NEMS: Progress and opportunities for surface science research performed on, or by, microdevices. Prog. Surf. Sci. 2013, 88, 171–211. [Google Scholar] [CrossRef]
- Bhushan, B. Nanotribology and nanomechanics of MEMS/NEMS and BioMEMS/BioNEMS materials and devices. Microelectron. Eng. 2007, 84, 387–412. [Google Scholar] [CrossRef]
- Ekinci, K.L.; Roukes, M.L. Nanoelectromechanical systems. Rev. Sci. Instruments 2005, 76, 061101. [Google Scholar] [CrossRef]
- Barretta, R.; Fabbrocino, F.; Luciano, R.; de Sciarra, F.M.; Ruta, G. Buckling loads of nano-beams in stress-driven nonlocal elasticity. Mech. Adv. Mater. Struct. 2020, 27, 869–875. [Google Scholar] [CrossRef]
- Bonanni, A.; del Valle, M. Use of nanomaterials for impedimetric DNA sensors: A review. Anal. Chim. Acta 2010, 678, 7–17. [Google Scholar] [CrossRef]
- Wu, W. Inorganic nanomaterials for printed electronics: A review. Nanoscale 2017, 9, 7342–7372. [Google Scholar] [CrossRef]
- Gohardani, O.; Elola, M.C.; Elizetxea, C. Potential and prospective implementation of carbon nanotubes on next generation aircraft and space vehicles: A review of current and expected applications in aerospace sciences. Prog. Aerosp. Sci. 2014, 70, 42–68. [Google Scholar] [CrossRef]
- Singh, T. A review of nanomaterials in civil engineering works. Inter. J. Struct. Civ. Eng. Res. 2014, 3, 31–35. [Google Scholar]
- Amabili, M. Nonlinear Mechanics of Shells and Plates in Composite, Soft and Biological Materials; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Lakes, R. Experimental microelasticity of two porous solids. Int. J. Solids Struct. 1986, 22, 55–63. [Google Scholar] [CrossRef]
- Stölken, J.; Evans, A. A microbend test method for measuring the plasticity length scale. Acta Mater. 1998, 46, 5109–5115. [Google Scholar] [CrossRef]
- Mancusi, G.; Fabbrocino, F.; Feo, L.; Fraternali, F. Size effect and dynamic properties of 2D lattice materials. Compos. Part B Eng. 2017, 112, 235–242. [Google Scholar] [CrossRef]
- Fabbrocino, F.; Carpentieri, G. Three-dimensional modeling of the wave dynamics of tensegrity lattices. Compos. Struct. 2017, 173, 9–16. [Google Scholar] [CrossRef]
- Eringen, A.; Edelen, D. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Trovalusci, P. Molecular Approaches for Multifield Continua: Origins and Current Developments. In Multiscale Modeling of Complex Materials; Sadowski, T., Trovalusci, P., Eds.; Springer: Vienna, Austria, 2014; pp. 211–278. [Google Scholar]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Aifantis, E. Update on a class of gradient theories. Mech. Mater. 2003, 35, 259–280. [Google Scholar] [CrossRef]
- Meenen, J.; Altenbach, H.; Eremeyev, V.; Naumenko, K. A Variationally Consistent Derivation of Microcontinuum Theories. Adv. Struct. Mater. 2011, 15. [Google Scholar]
- Mindlin, R.; Eshel, N. On first strain-gradient theories in linear elasticity. Int. J. Solids Struct. 1968, 4, 109–124. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Rabczuk, T. Static analysis of functionally graded anisotropic nanoplates using nonlocal strain gradient theory. Compos. Struct. 2019, 227, 111249. [Google Scholar] [CrossRef]
- Eremeyev, V.; Altenbach, H. On the Direct Approach in the Theory of Second Gradient Plates. In Shell and Membrane Theories in Mechanics and Biology; Altenbach, H., Mikhasev, G.I., Eds.; Springer: Cham, Switzerland, 2015; Volume 45, pp. 147–154. [Google Scholar]
- Bacciocchi, M.; Fantuzzi, N.; Ferreira, A. Conforming and nonconforming laminated finite element Kirchhoff nanoplates in bending using strain gradient theory. Comput. Struct. 2020, 239, 106322. [Google Scholar] [CrossRef]
- Barretta, R.; Feo, L.; Luciano, R.; Marotti de Sciarra, F.; Penna, R. Functionally graded Timoshenko nanobeams: A novel nonlocal gradient formulation. Compos. Part B Eng. 2016, 100, 208–219. [Google Scholar] [CrossRef]
- Sahmani, S.; Aghdam, M.M.; Rabczuk, T. Nonlinear bending of functionally graded porous micro/nano-beams reinforced with graphene platelets based upon nonlocal strain gradient theory. Compos. Struct. 2018, 186, 68–78. [Google Scholar] [CrossRef]
- Jamalpoor, A.; Hosseini, M. Biaxial buckling analysis of double-orthotropic microplate-systems including in-plane magnetic field based on strain gradient theory. Compos. Part B Eng. 2015, 75, 53–64. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Faghidian, S.; Luciano, R.; Marotti de Sciarra, F. Free vibrations of elastic beams by modified nonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 133, 99–108. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.; Lam, D.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Mühlhaus, H.; Oka, F. Dispersion and wave propagation in discrete and continuous models for granular materials. Int. J. Solids Struct. 1996, 33, 2841–2858. [Google Scholar] [CrossRef]
- Leonetti, L.; Greco, F.; Trovalusci, P.; Luciano, R.; Masiani, R. A multiscale damage analysis of periodic composites using a couple-stress/Cauchy multidomain model: Application to masonry structures. Compos. Part B Eng. 2018, 141, 50–59. [Google Scholar] [CrossRef]
- Farajpour, A.; Howard, C.Q.; Robertson, W.S. On size-dependent mechanics of nanoplates. Int. J. Eng. Sci. 2020, 156, 103368. [Google Scholar] [CrossRef]
- Barretta, R.; Faghidian, S.A.; Marotti de Sciarra, F. Stress-driven nonlocal integral elasticity for axisymmetric nano-plates. Int. J. Eng. Sci. 2019, 136, 38–52. [Google Scholar] [CrossRef]
- Trovalusci, P.; Bellis, M.D.; Ostoja-Starzewski, M. A Statistically-Based Homogenization Approach for Particle Random Composites as Micropolar Continua. Adv. Struct. Mater. 2016, 42. [Google Scholar]
- Reccia, E.; De Bellis, M.L.; Trovalusci, P.; Masiani, R. Sensitivity to material contrast in homogenization of random particle composites as micropolar continua. Compos. Part B Eng. 2018, 136, 39–45. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Leonetti, L.; Trovalusci, P.; Tornabene, F. Some Novel Numerical Applications of Cosserat Continua. Int. J. Comput. Methods 2018, 15, 1850054. [Google Scholar] [CrossRef]
- Rega, G.; Saetta, E.; Settimi, V. Modeling and nonlinear dynamics of thermomechanically coupled composite plates. Int. J. Mech. Sci. 2020, 187, 106106. [Google Scholar] [CrossRef]
- Kim, J.Y. Micromechanical analysis of effective properties of magneto-electro-thermo-elastic multilayer composites. Int. J. Eng. Sci. 2011, 49, 1001–1018. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R. Size-Dependent Buckling and Postbuckling Analyses of First-Order Shear Deformable Magneto-Electro-Thermo Elastic Nanoplates Based on the Nonlocal Elasticity Theory. Int. J. Struct. Stab. Dyn. 2017, 17, 1750014. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R. Nonlocal free vibration in the pre- and post-buckled states of magneto-electro-thermo elastic rectangular nanoplates with various edge conditions. Smart Mater. Struct. 2016, 25, 095033. [Google Scholar] [CrossRef]
- Lei, Z.; Liew, K.; Yu, J. Buckling analysis of functionally graded carbon nanotube-reinforced composite plates using the element-free kp-Ritz method. Compos. Struct. 2013, 98, 160–168. [Google Scholar] [CrossRef]
- Mota, A.F.; Loja, M.A.R.; Barbosa, J.I.; Rodrigues, J.A. Porous Functionally Graded Plates: An Assessment of the Influence of Shear Correction Factor on Static Behavior. Math. Comput. Appl. 2020, 25, 25. [Google Scholar] [CrossRef]
- Zhong, Z.; Yu, T. Vibration of a simply supported functionally graded piezoelectric rectangular plate. Smart Mater. Struct. 2006, 15, 1404–1412. [Google Scholar] [CrossRef]
- Tomczyk, B.; Szczerba, P. Combined asymptotic-tolerance modelling of dynamic problems for functionally graded shells. Compos. Struct. 2018, 183, 176–184, In honor of Prof. Y. Narita. [Google Scholar] [CrossRef]
- Tomczyk, B.; Szczerba, P. A new asymptotic-tolerance model of dynamic and stability problems for longitudinally graded cylindrical shells. Compos. Struct. 2018, 202, 473–481, Special issue dedicated to Ian Marshall. [Google Scholar] [CrossRef]
- Kondaiah, P.; Shankar, K.; Ganesan, N. Pyroelectric and pyromagnetic effects on multiphase magneto–electro–elastic cylindrical shells for axisymmetric temperature. Smart Mater. Struct. 2012, 22, 025007. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. On the Dynamics of a Visco–Piezo–Flexoelectric Nanobeam. Symmetry 2020, 12, 643. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. On Nonlinear Bending Study of a Piezo-Flexomagnetic Nanobeam Based on an Analytical-Numerical Solution. Nanomaterials 2020, 10, 1762. [Google Scholar] [CrossRef] [PubMed]
- Bacciocchi, M.; Tarantino, A. Natural Frequency Analysis of Functionally Graded Orthotropic Cross-Ply Plates Based on the Finite Element Method. Math. Comput. Appl. 2019, 24, 52. [Google Scholar] [CrossRef]
- Uzun, B.; Civalek, O. Nonlocal FEM Formulation for Vibration Analysis of Nanowires on Elastic Matrix with Different Materials. Math. Comput. Appl. 2019, 24, 38. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Reza Barati, M. Magnetic field effects on buckling behavior of smart size-dependent graded nanoscale beams. Eur. Phys. J. Plus 2016, 131, 238. [Google Scholar] [CrossRef]
- Xu, X.J.; Deng, Z.C.; Zhang, K.; Meng, J.M. Surface effects on the bending, buckling and free vibration analysis of magneto-electro-elastic beams. Acta Mech. 2016, 227, 1557–1573. [Google Scholar] [CrossRef]
- Heyliger, P.; Ramirez, G. Free Vibration of Laminated Circular Piezoelectric Plates and Discs. J. Sound Vib. 2000, 229, 935–956. [Google Scholar] [CrossRef]
- Mohammadimehr, M.; Rostami, R. Bending, buckling, and forced vibration analyses of nonlocal nanocomposite microplate using TSDT considering MEE properties dependent to various volume fractions of CoFe2O4-BaTiO3. J. Theor. Appl. Mech. 2017, 55, 853. [Google Scholar] [CrossRef][Green Version]
- Farahmand, H.; Naseralavi, S.S.; Iranmanesh, A.; Mohammadi, M. Navier Solution for Buckling Analysis of Size-Dependent Functionally Graded Micro-Plates. Lat. Am. J. Solids Struct. 2016, 13, 3161–3173. [Google Scholar] [CrossRef][Green Version]
- Altenbach, H.; Eremeyev, V.A. On the shell theory on the nanoscale with surface stresses. Int. J. Eng. Sci. 2011, 49, 1294–1301. [Google Scholar] [CrossRef]
- Ghobadi, A.; Golestanian, H.; Beni, Y.T.; Kamil Żur, K. On the size-dependent nonlinear thermo-electro-mechanical free vibration analysis of functionally graded flexoelectric nano-plate. Commun. Nonlinear Sci. Numer. Simul. 2020, 105585. [Google Scholar] [CrossRef]
- Simões Moita, J.M.; Mota Soares, C.M.; Mota Soares, C.A. Analyses of magneto-electro-elastic plates using a higher order finite element model. Compos. Struct. 2009, 91, 421–426. [Google Scholar] [CrossRef]
- Jędrysiak, J. Free vibrations of thin periodic plates interacting with an elastic periodic foundation. Int. J. Mech. Sci. 2003, 45, 1411–1428. [Google Scholar] [CrossRef]
- Zhou, X.; Yu, D.; Shao, X.; Wang, S.; Zhang, S. Simplified-super-element-method for analyzing free flexural vibration characteristics of periodically stiffened-thin-plate filled with viscoelastic damping material. Thin-Walled Struct. 2015, 94, 234–252. [Google Scholar] [CrossRef]
- Wirowski, A.; Michalak, B.; Gajdzicki, M. Dynamic Modelling of Annular Plates of Functionally Graded Structure Resting on Elastic Heterogeneous Foundation with Two Modules. J. Mech. 2015, 31, 493–504. [Google Scholar] [CrossRef]
- Michalak, B. 2D tolerance and asymptotic models in elastodynamics of a thin-walled structure with dense system of ribs. Arch. Civ. Mech. Eng. 2015, 15, 449–455. [Google Scholar] [CrossRef]
- Tomczyk, B.; Szczerba, P. Tolerance and asymptotic modelling of dynamic problems for thin microstructured transversally graded shells. Compos. Struct. 2017, 162, 365–373. [Google Scholar] [CrossRef]
- Xiang, H.J.; Shi, Z.F. Analysis of flexural vibration band gaps in periodic beams using differential quadrature method. Comput. Struct. 2009, 87, 1559–1566. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, X.; Wang, W.; Wang, L.; Peng, F.; Li, B. On natural frequencies of non-uniform beams modulated by finite periodic cells. Phys. Lett. A 2016, 380, 3278–3283. [Google Scholar] [CrossRef]
- Jędrysiak, J. Tolerance Modelling of Vibrations and Stability for Periodic Slender Visco-Elastic Beams on a Foundation with Damping. Revisiting. Materials 2020, 13, 3939. [Google Scholar] [CrossRef] [PubMed]
- Jędrysiak, J. Tolerance modelling of free vibration frequencies of thin functionally graded plates with one-directional microstructure. Compos. Struct. 2017, 161, 453–468. [Google Scholar] [CrossRef]
- Marczak, J.; Jędrysiak, J. Some remarks on modelling of vibrations of periodic sandwich structures with inert core. Compos. Struct. 2018, 202, 752–758, Special issue dedicated to Ian Marshall. [Google Scholar] [CrossRef]
- Wu, Z.J.; Li, F.M.; Wang, Y.Z. Vibration band gap properties of periodic Mindlin plate structure using the spectral element method. Meccanica 2014, 49, 725–737. [Google Scholar] [CrossRef]
- Cheng, Z.; Xu, Y.; Zhang, L. Analysis of flexural wave bandgaps in periodic plate structures using differential quadrature element method. Int. J. Mech. Sci. 2015, 100, 112–125. [Google Scholar] [CrossRef]
- Zhou, X.; Yu, D.; Shao, X.; Wang, S.; Tian, Y. Band gap characteristics of periodically stiffened-thin-plate based on center-finite-difference-method. Thin-Walled Struct. 2014, 82, 115–123. [Google Scholar] [CrossRef]
- Yu, D.; Wen, J.; Shen, H.; Xiao, Y.; Wen, X. Propagation of flexural wave in periodic beam on elastic foundations. Phys. Lett. A 2012, 376, 626–630. [Google Scholar] [CrossRef]
- Chen, T. Investigations on flexural wave propagation of a periodic beam using multi-reflection method. Arch. Appl. Mech. 2013, 83, 315–329. [Google Scholar] [CrossRef]
- Wang, Q. On buckling of column structures with a pair of piezoelectric layers. Eng. Struct. 2002, 24, 199–205. [Google Scholar] [CrossRef]
- Li, Y. Buckling analysis of magnetoelectroelastic plate resting on Pasternak elastic foundation. Mech. Res. Commun. 2014, 56, 104–114. [Google Scholar] [CrossRef]
- Park, W.T.; Han, S.C. Buckling analysis of nano-scale magneto-electro-elastic plates using the nonlocal elasticity theory. Adv. Mech. Eng. 2018, 10, 1687814018793335. [Google Scholar] [CrossRef]
- Ramirez, F.; Heyliger, P.R.; Pan, E. Discrete Layer Solution to Free Vibrations of Functionally Graded Magneto-Electro-Elastic Plates. Mech. Adv. Mater. Struct. 2006, 13, 249–266. [Google Scholar] [CrossRef]
| BaTiO | CoFeO | ||
|---|---|---|---|
| [GPa] | 166 | 286 | |
| 166 | 286 | ||
| 162 | 269.5 | ||
| 78 | 170.5 | ||
| 78 | 170.5 | ||
| 77 | 173 | ||
| 43 | 45.3 | ||
| 43 | 45.3 | ||
| 44.5 | 56.5 | ||
| [C/m] | −4.4 | 0 | |
| −4.4 | 0 | ||
| 18.6 | 0 | ||
| [N/A·m] | 0 | 580.3 | |
| 0 | 580.3 | ||
| 0 | 699.7 | ||
| [C/N·m] | 11.2 | 0.08 | |
| 11.2 | 0.08 | ||
| 12.6 | 0.093 | ||
| [s/m] | 0 | 0 | |
| [N·s/C] | 5 | −590 | |
| 5 | −590 | ||
| 10 | 157 | ||
| [ C/mK] | 0 | 0 | |
| −11.4 | 0 | ||
| [ Wb/mK] | 0 | 0 | |
| 0 | −36.2 | ||
| [K] | 15.8 | 10 | |
| [kg/m] | 5300 | 5800 |
| [V] | ||||||
|---|---|---|---|---|---|---|
| [A] | −5 | −2.5 | 0 | 2.5 | 5 | |
| 0.00 | 1 | 2.1733 | 2.0124 | 1.8516 | 1.6907 | 1.5299 |
| 0 | 1.4456 | 1.2848 | 1.1239 | 0.9631 | 0.8022 | |
| −1 | 0.7180 | 0.5572 | 0.3963 | 0.2355 | 0.0746 | |
| 0.05 | 1 | 3.2825 | 3.1217 | 2.9608 | 2.8000 | 2.6391 |
| 0 | 2.5549 | 2.3940 | 2.2332 | 2.0723 | 1.9115 | |
| −1 | 1.8273 | 1.6664 | 1.5056 | 1.3447 | 1.1838 | |
| 0.10 | 1 | 4.3918 | 4.2309 | 4.0701 | 3.9092 | 3.7484 |
| 0 | 3.6642 | 3.5033 | 3.3424 | 3.1816 | 3.0207 | |
| −1 | 2.9365 | 2.7757 | 2.6148 | 2.4540 | 2.2931 | |
| Ref. [76] | Present | |
|---|---|---|
| 1 | 9.525 | 10.0244 |
| 2 | 28.762 | 32.5716 |
| 3 | 50.966 | 66.2842 |
| 4 | 131.186 | 104.0065 |
| 5 | 139.106 | 129.6477 |
| Mode | Ref. [57] | |||
|---|---|---|---|---|
| B | F | B/F/B | F/B/F | |
| 1 | 12,863.98 | 15,185.24 | 13,024.78 | 15,043.32 |
| 2 | 25,106.78 | 28,177.03 | 25,401.26 | 27,880.80 |
| Present | ||||
| 1 | 15,044.28 | 17,253.16 | 15,281.37 | 17,159.99 |
| 2 | 34,945.88 | 39,415.58 | 28,264.36 | 39,871.43 |
| Present | ||||
| 1 | 21,065.74 | 24,351.13 | 20,932.93 | 24,069.44 |
| 2 | 63,337.77 | 73,727.92 | 62,619.25 | 72,511.91 |
| Present | ||||
| 1 | 25,723.93 | 29,805.02 | 25,499.40 | 29,410.18 |
| 2 | 82,655.46 | 96,547.86 | 81,654.82 | 94,727.82 |
| 0 | 0.05 | 0.10 | |
| 1 | 4.0913 | 5.7671 | 7.0554 |
| 2 | 10.2270 | 19.0434 | 24.9141 |
| 3 | 20.4499 | 49.8179 | 67.4200 |
| 4 | 34.7550 | 106.4926 | 146.5385 |
| 5 | 53.1353 | 197.6005 | 274.3517 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tocci Monaco, G.; Fantuzzi, N.; Fabbrocino, F.; Luciano, R. Critical Temperatures for Vibrations and Buckling of Magneto-Electro-Elastic Nonlocal Strain Gradient Plates. Nanomaterials 2021, 11, 87. https://doi.org/10.3390/nano11010087
Tocci Monaco G, Fantuzzi N, Fabbrocino F, Luciano R. Critical Temperatures for Vibrations and Buckling of Magneto-Electro-Elastic Nonlocal Strain Gradient Plates. Nanomaterials. 2021; 11(1):87. https://doi.org/10.3390/nano11010087
Chicago/Turabian StyleTocci Monaco, Giovanni, Nicholas Fantuzzi, Francesco Fabbrocino, and Raimondo Luciano. 2021. "Critical Temperatures for Vibrations and Buckling of Magneto-Electro-Elastic Nonlocal Strain Gradient Plates" Nanomaterials 11, no. 1: 87. https://doi.org/10.3390/nano11010087
APA StyleTocci Monaco, G., Fantuzzi, N., Fabbrocino, F., & Luciano, R. (2021). Critical Temperatures for Vibrations and Buckling of Magneto-Electro-Elastic Nonlocal Strain Gradient Plates. Nanomaterials, 11(1), 87. https://doi.org/10.3390/nano11010087







