Tuning the Magnetic Moment of Small Late 3d-Transition-Metal Oxide Clusters by Selectively Mixing the Transition-Metal Constituents
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
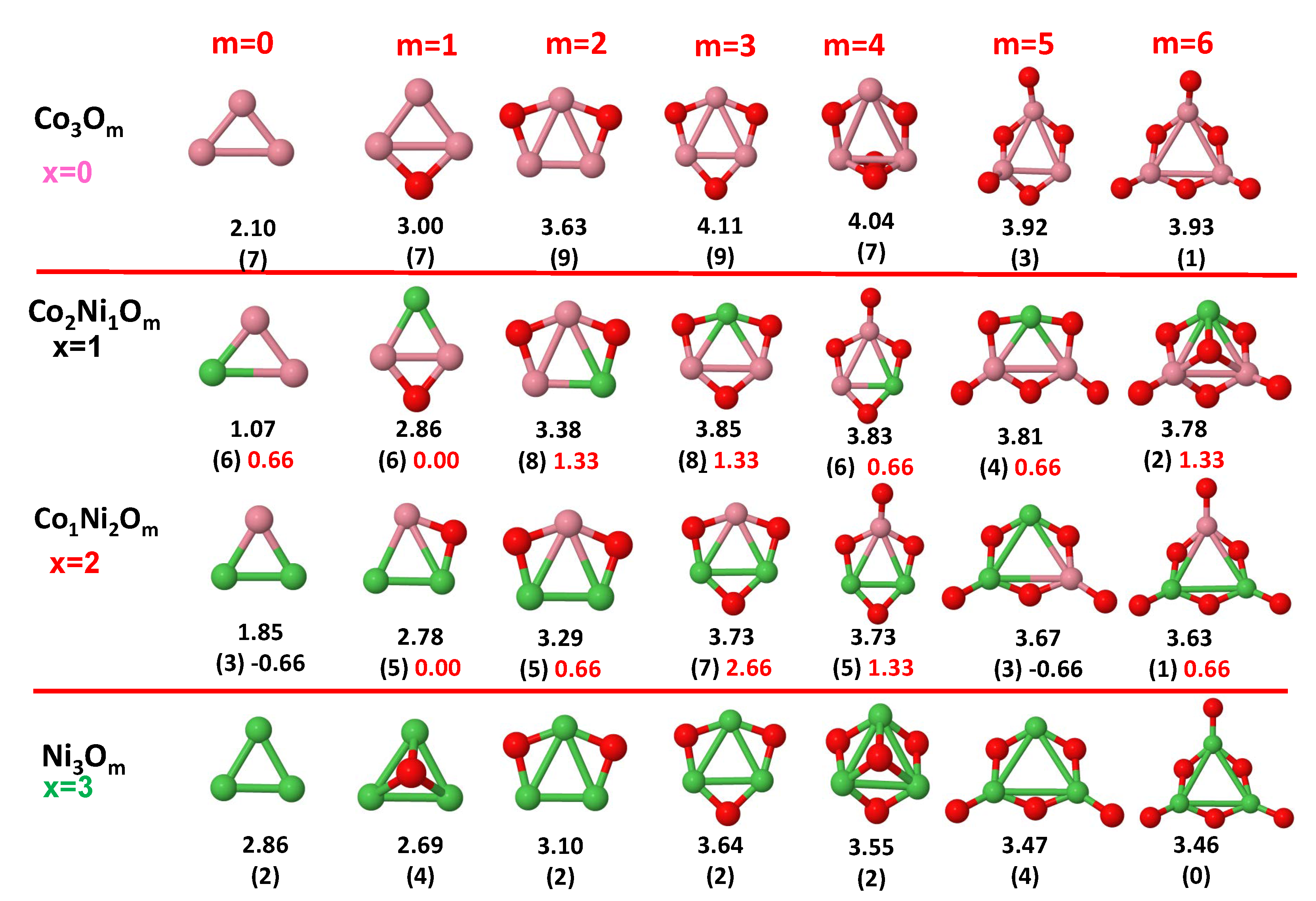
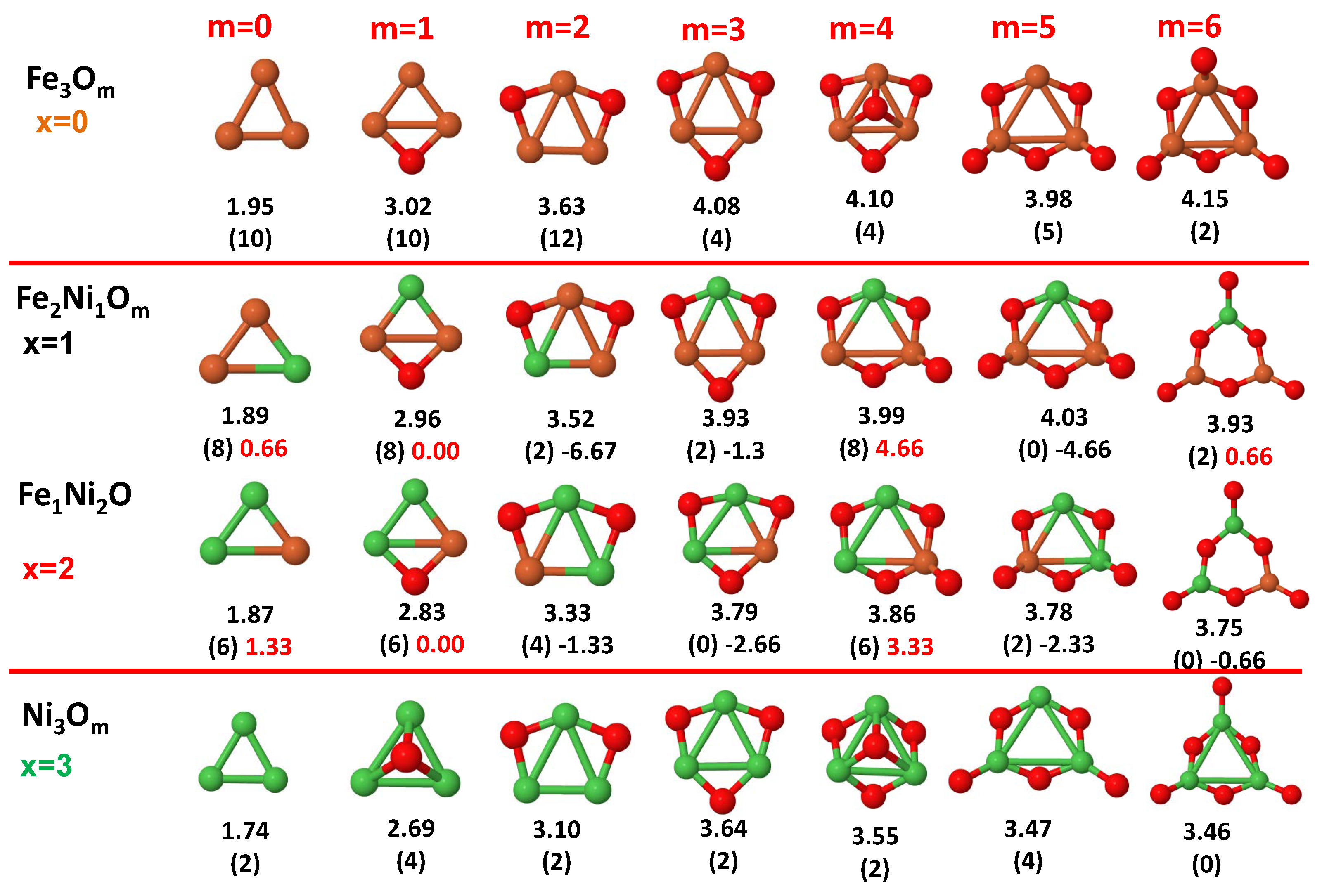
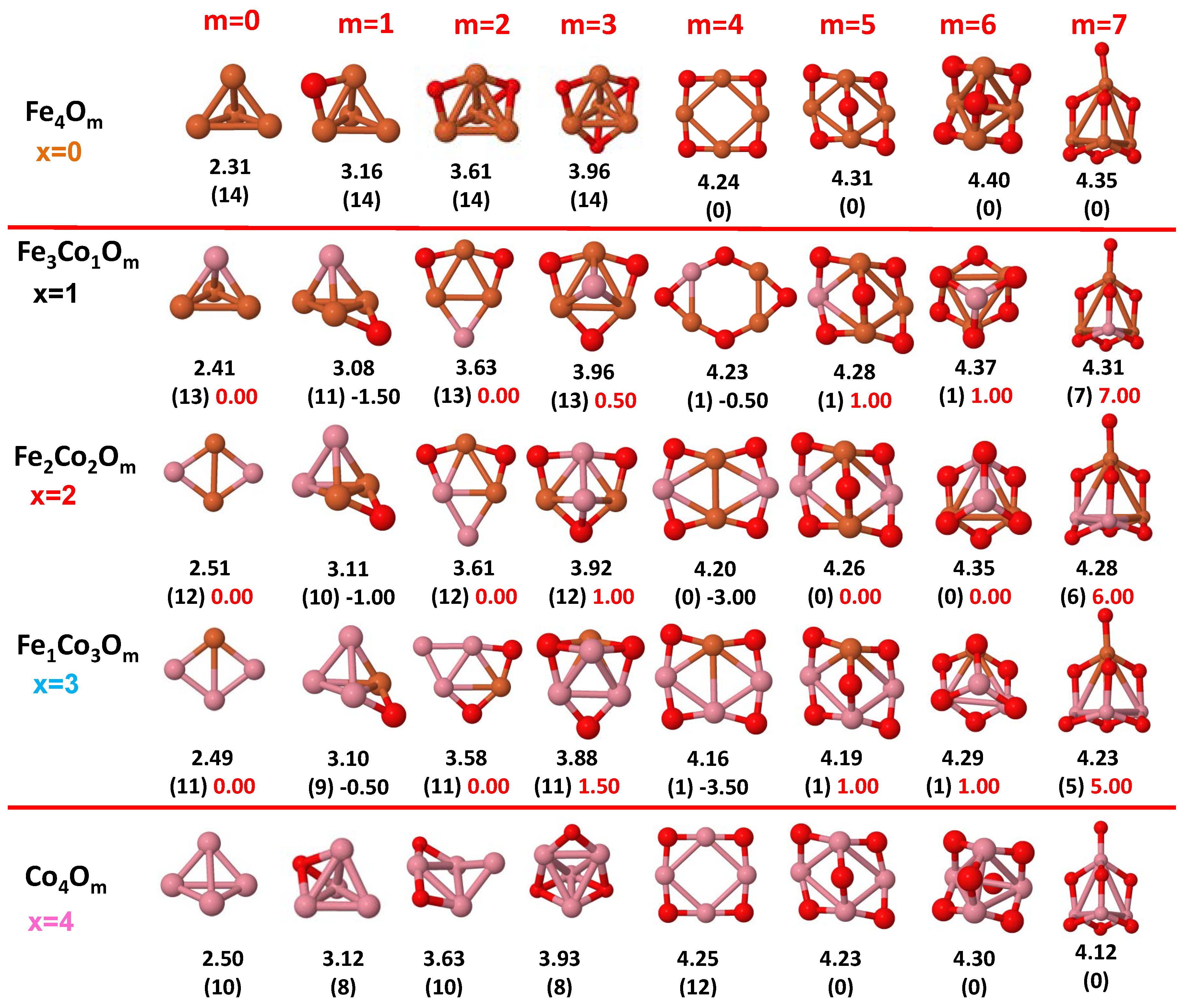
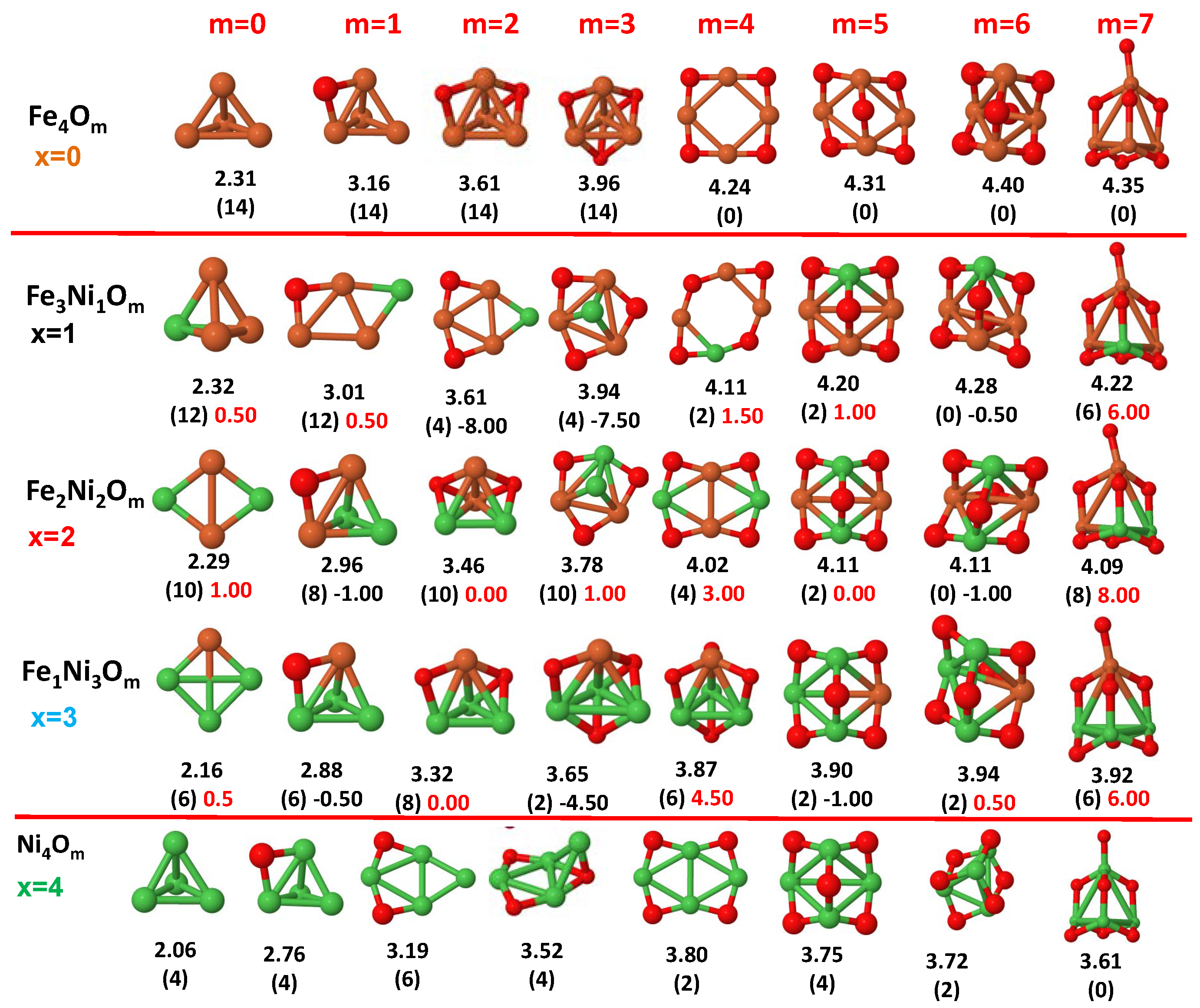
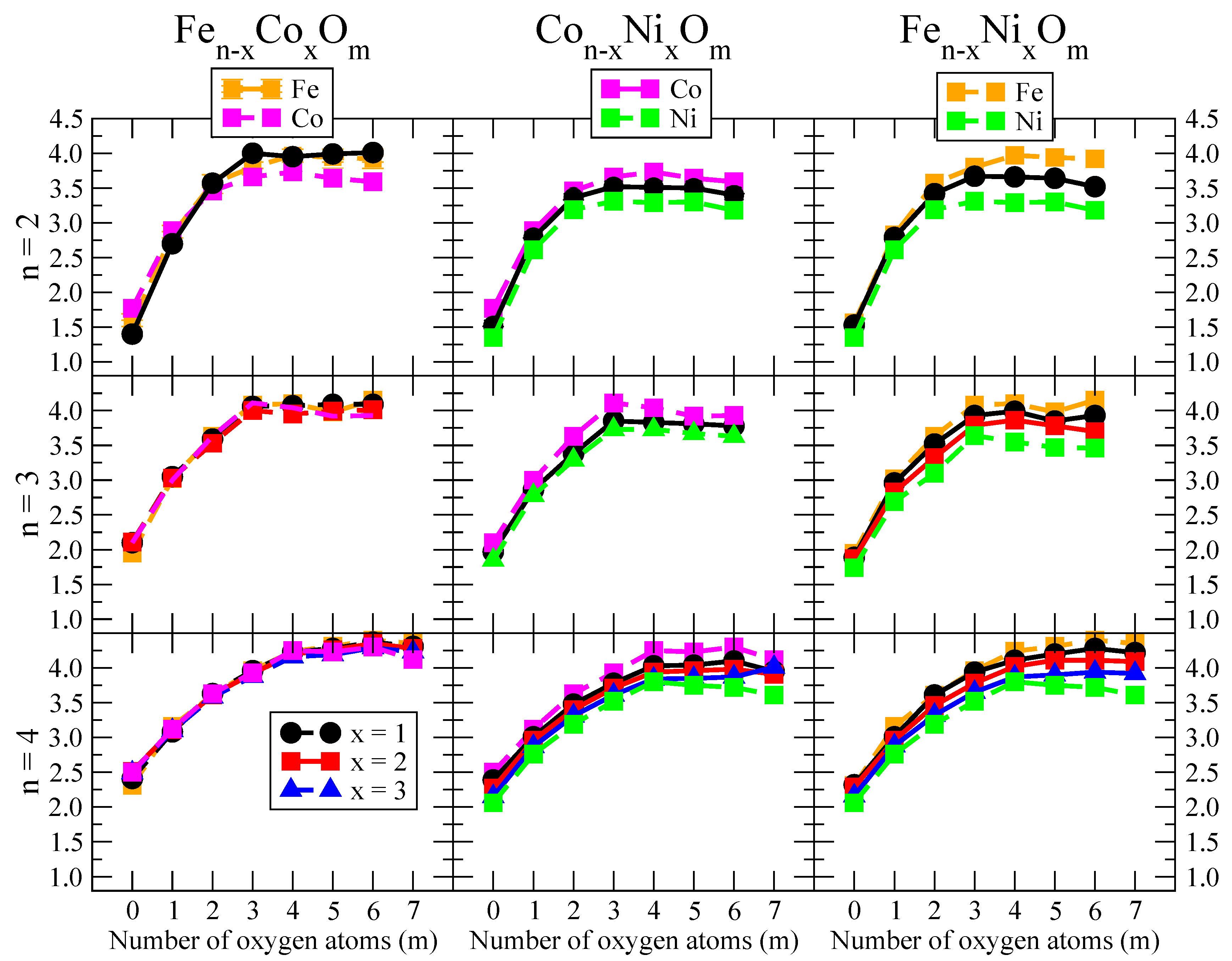
3.1. Structural Properties and Stability
- (i)
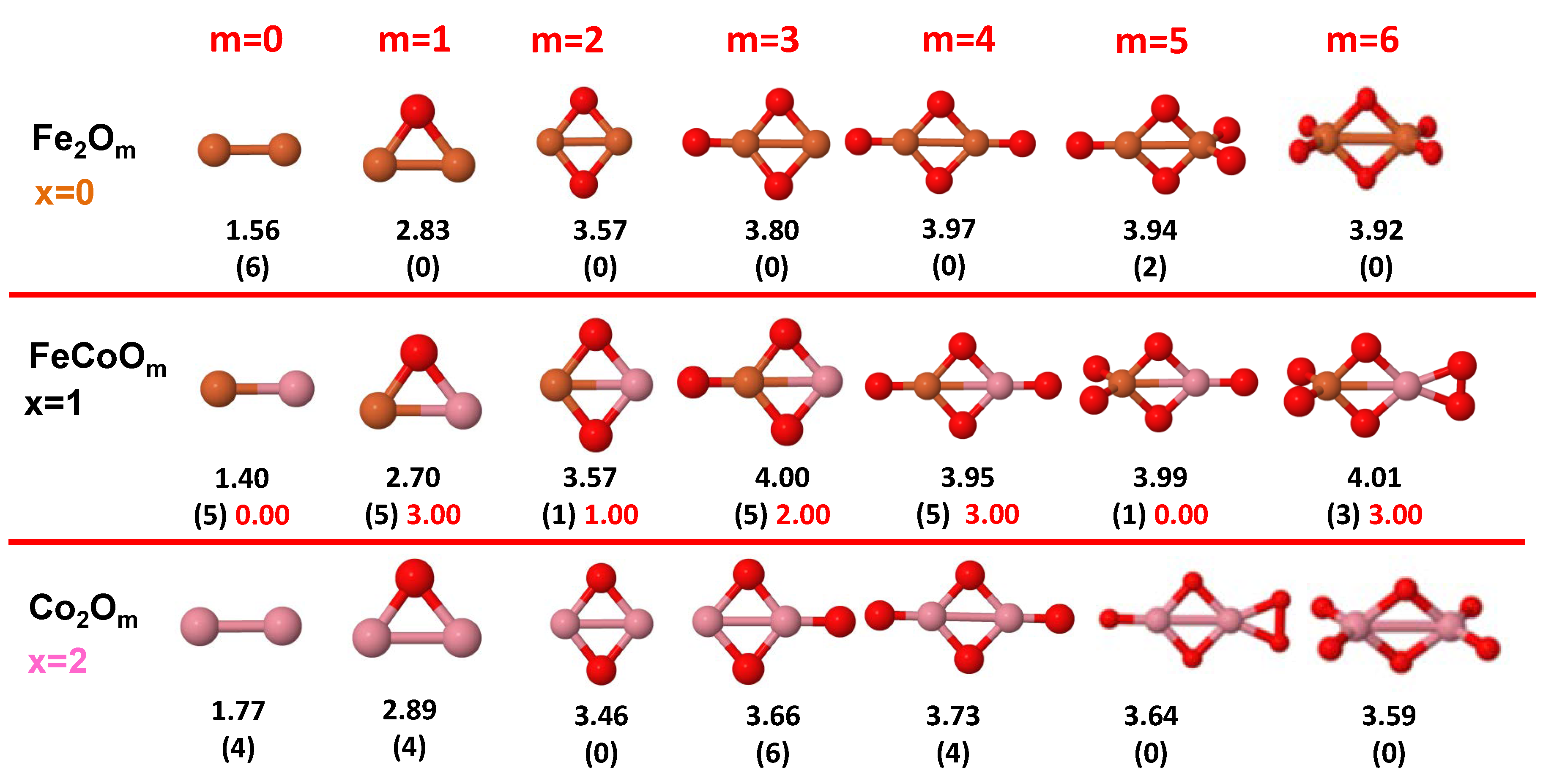
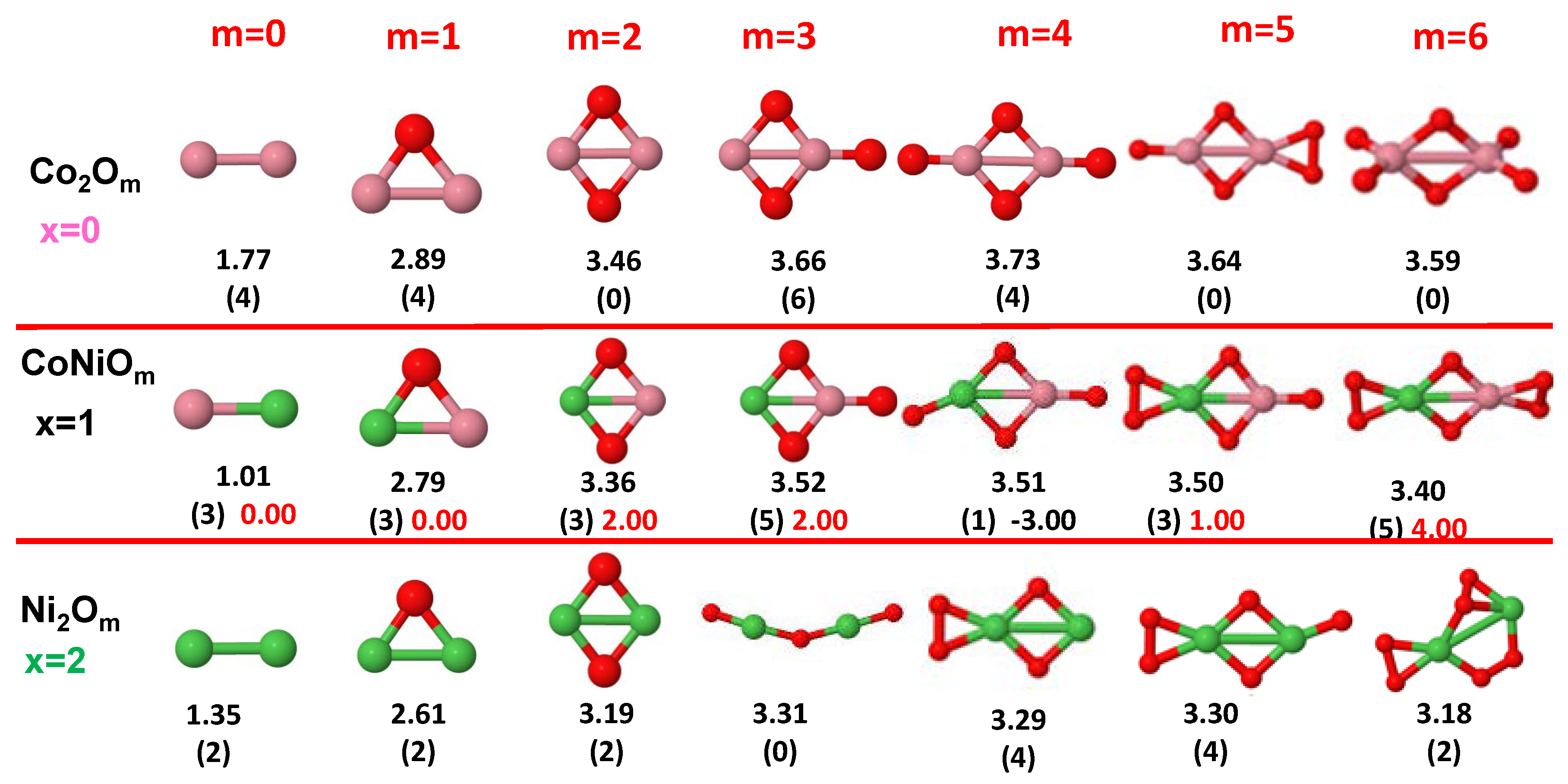
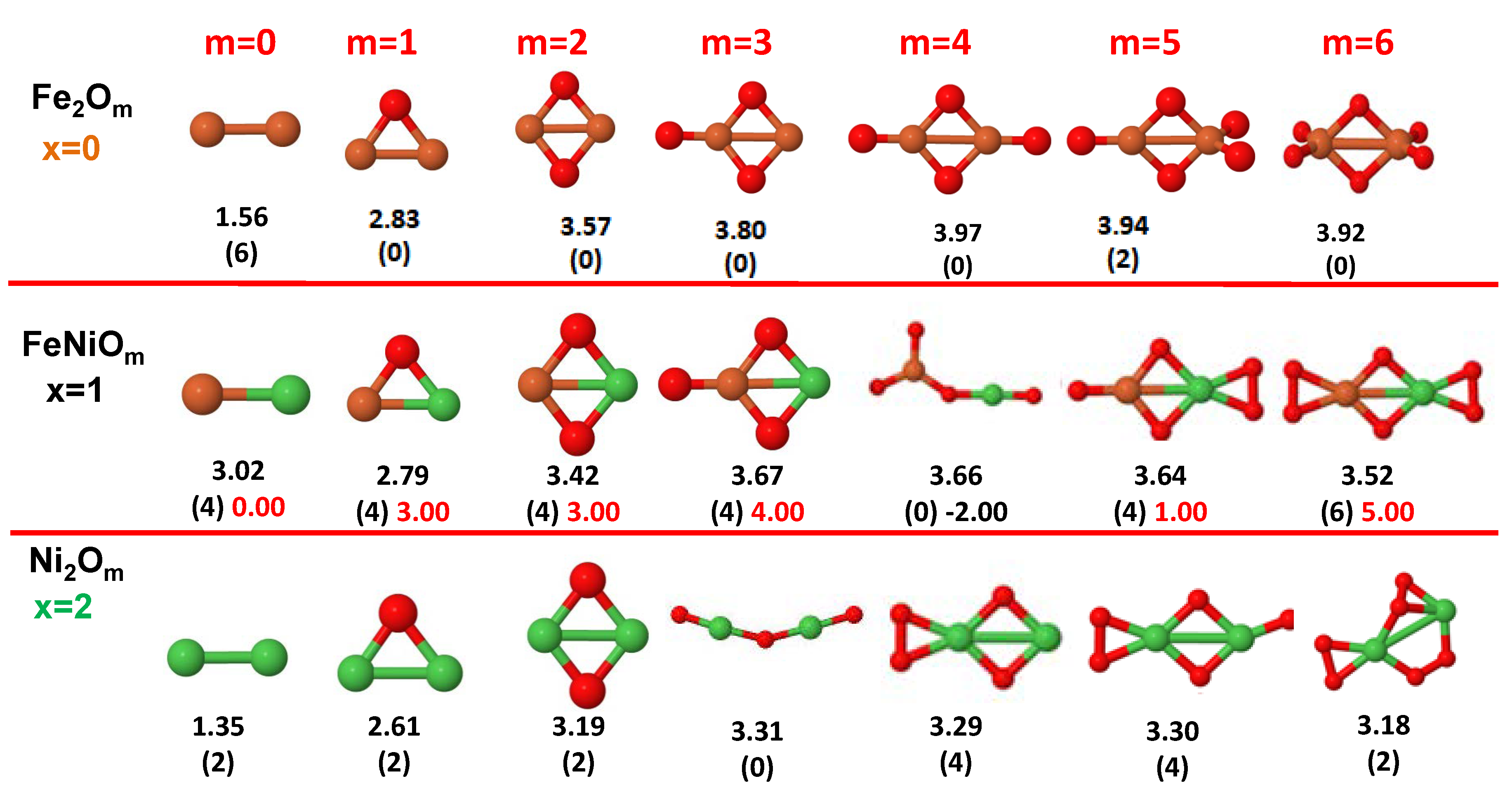
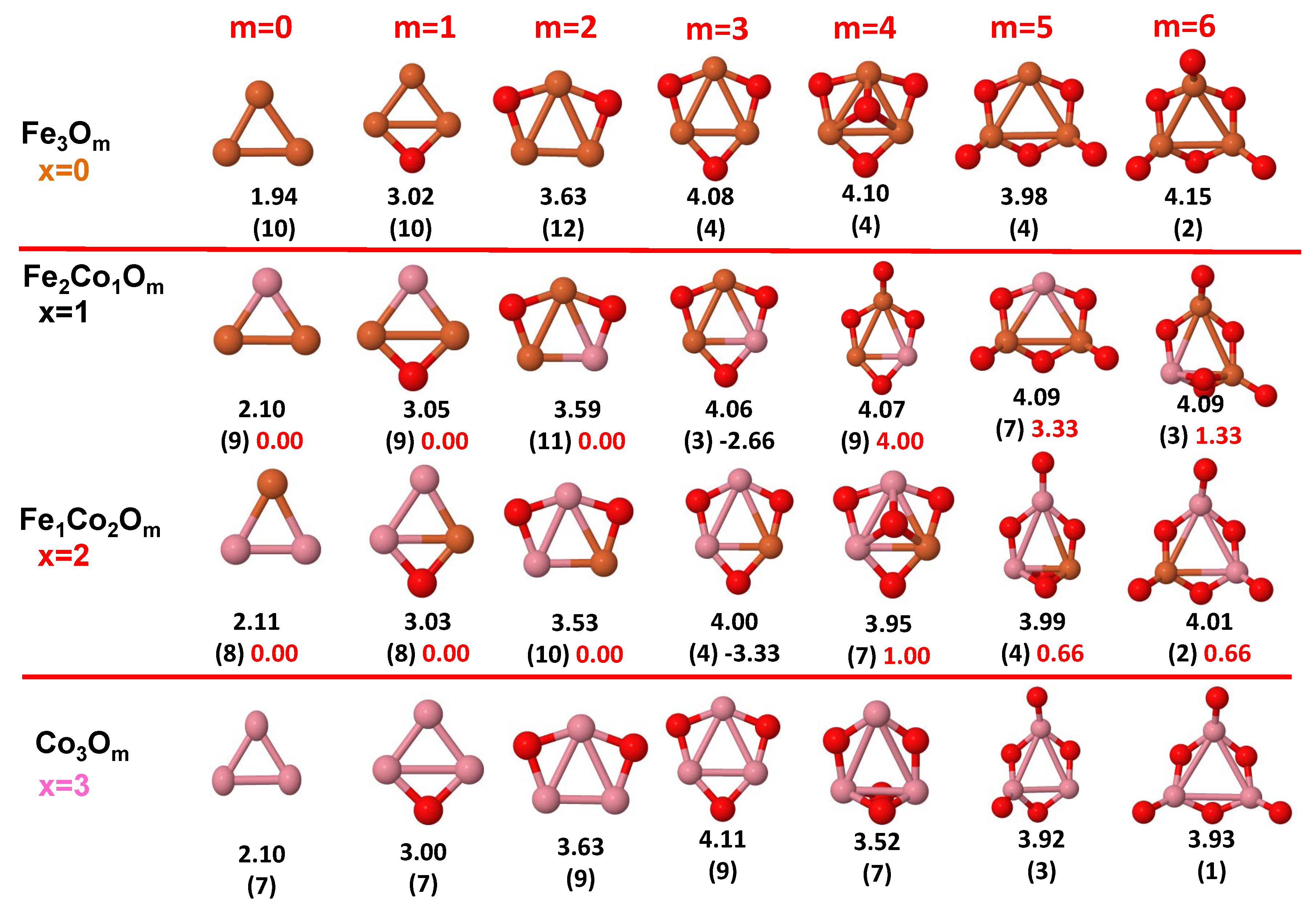
- The oxygen atoms tend to occupy bridge sites between the TM atoms ( for and for ), and when bridge sites are saturated, O atoms tend to occupy top sites ( for , for and for ).
- (ii)
- The oxygen binds preferentially with Fe atoms. When the oxygen rate increases, the next preferential coordination is Co and finally Ni.
- (iii)
- The net electronic charge in the O atoms, resulting from the charge transfer from the metal atoms, favors an uniform distribution of the O atoms in the cluster.
- (iv)
- At oxidation rates where the number of O atoms equals the number of metal atoms, ring-like structures are formed for all sizes considered in this work. In this atomic configuration all metal–metal bonds are mediated by oxygen. This trend was already discussed in our previous works for the pure Fe, Co and Ni oxidized clusters [39,40,41], and it has been also discussed by other groups for other systems [33,51] in this small size range. We now demonstrate that these ring-like structures are preserved in the TM oxidized nanoalloys, except for FeNiO, for which a tetrahedral structure is obtained, as stated above.
- (v)
- We considered up to m = 6 or 7 oxygen atoms which is enough to analyze the transition from atomic to molecular adsorption in the case of the TM dimers (not yet in the trimers and tetramers). When the oxygen concentration is high enough, oxygen starts to be adsorbed molecularly, preserving short O–O inter-atomic distances. The critical oxygen concentration for this to occur lowers while going from Fe to Co and Ni, as it can be clearly seen in the structures of the oxidized dimers in Figure 1, Figure 2 and Figure 3: while in FeO no molecular adsorption takes place for , in CoO occurs earlier (for ) and in NiO it starts even earlier (for ). Concerning mixed oxidized clusters, in FeCoO no molecular adsorption takes place for m = 6 while in CoNiO and FeNiO it already occurs for m = 5. The molecular adsorption is a manifestation of oxygen saturation of the system and its emergence at different oxygen concentrations for the different TM compositions is connected with the relative strength of the respective metal–oxygen bonds. The stronger the metal–oxygen binding is, the more oxygen is bound in an atomic form. In Table 1 we give, as a reference, the binding energies of Fe–O, Co–O and Ni–O, along with those of the different TM dimers. The metal–oxygen binding lowers for TM oxides while going from Fe to Co and Ni, as electronic charge transfer decreases and bond distance slightly increases.
- (vi)
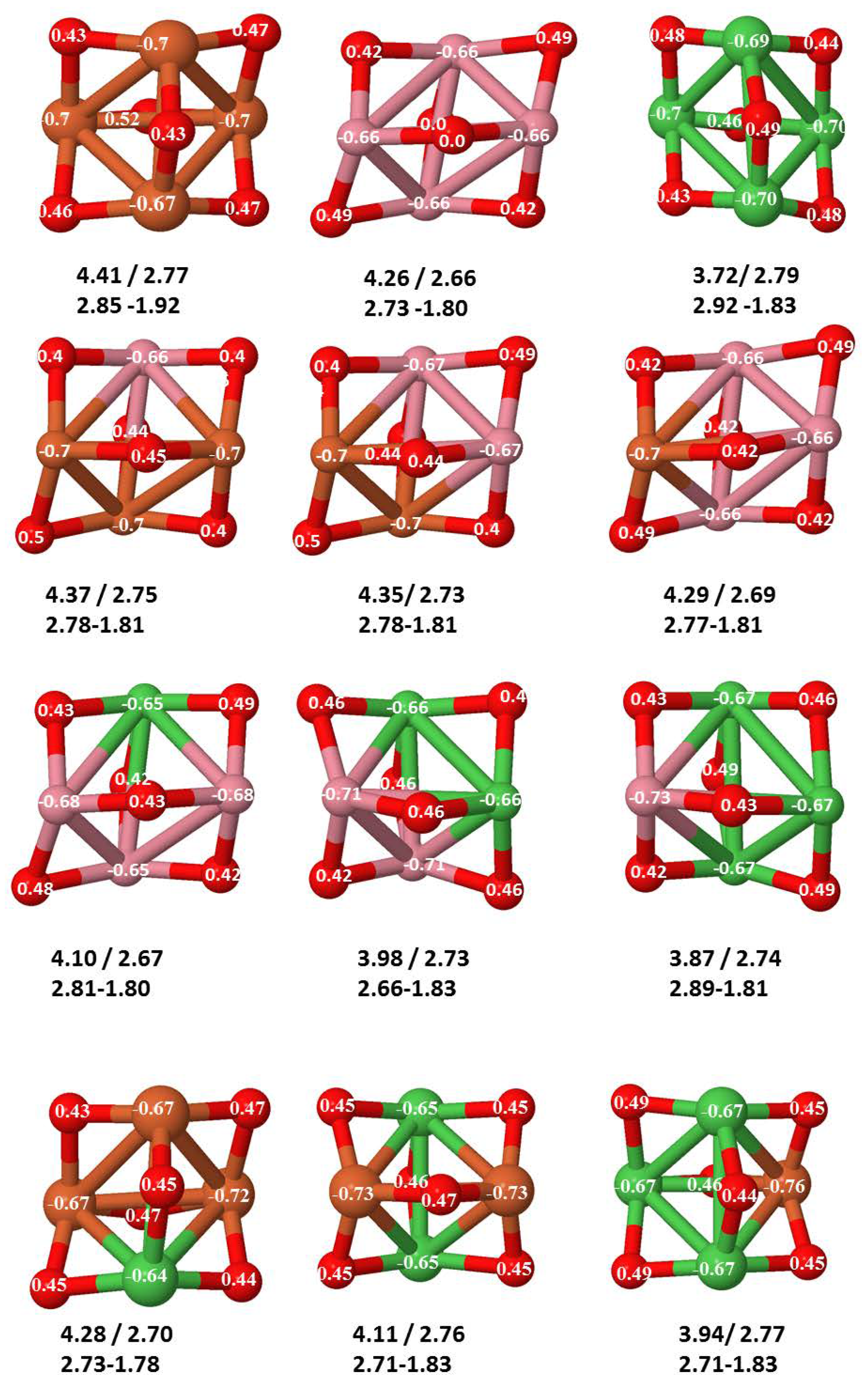
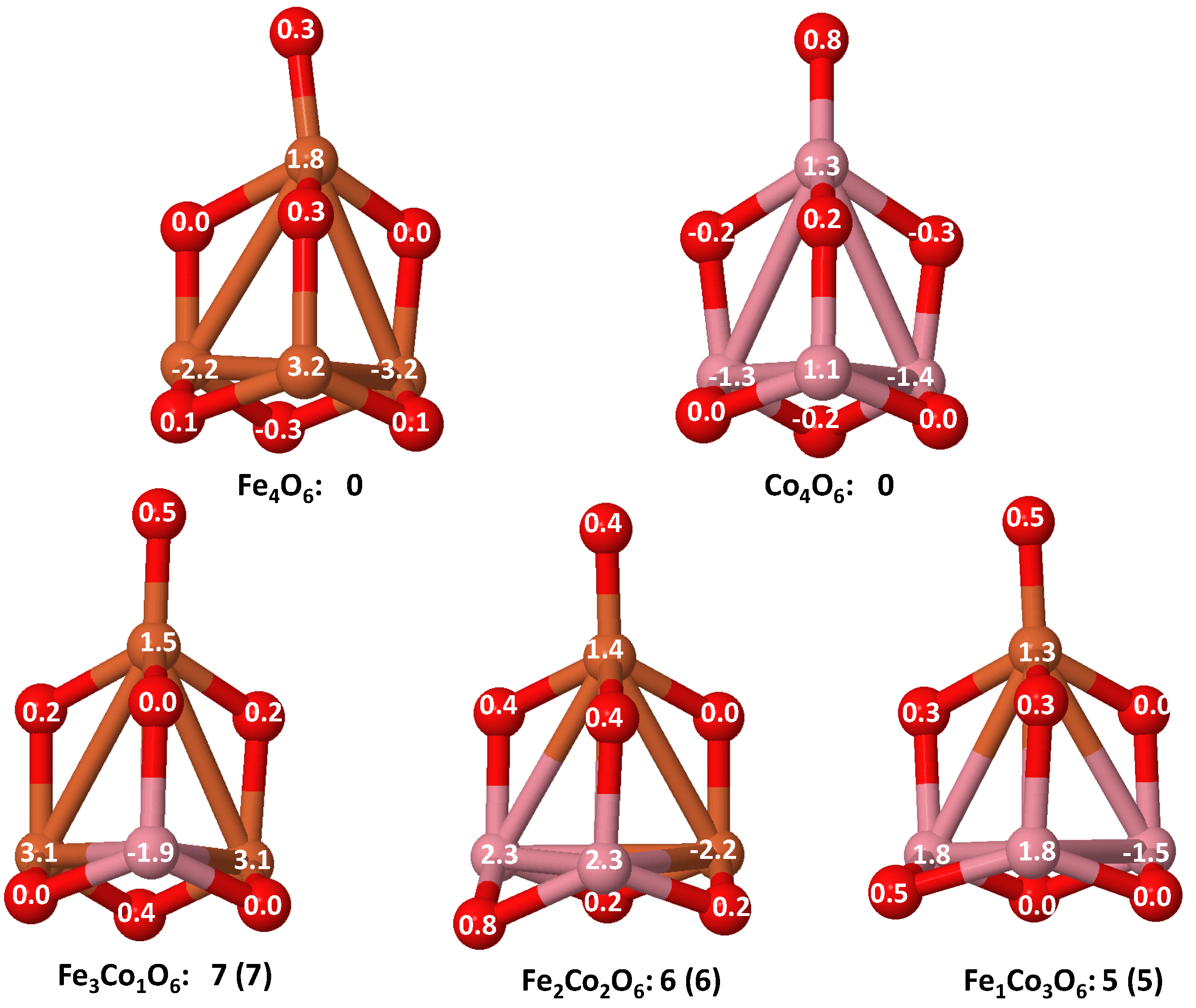
- The metal–metal binding also lowers while going from Fe to Ni (see Table 1). However, the Co dimer has the highest binding (and the lowest bond distance). General structural trends are also consistent with the binding energy per atom plotted in Figure 10 for the oxides. Consequently, for TM oxide dimers, and in connection with the discussion of the oxygen saturation, we note a shift to lower m in the maximum of binding energy while going from Fe to Co and Ni which means that adsorption of more oxygen atoms beyond this critical value of m does not increase the binding, because the metal–metal bonding weakens as m increases. The weakening of the metal–metal bonding is manifested in the less compact metal skeleton (lower average metal–metal inter-atomic distance) that results as m increases.The upper panel of Figure S1 shows the increase on the average metal–metal distance for the CoNiO ( nanoalloys. This distance increases until the triangular structure has all the oxygen atoms on the bridge positions (), the increase being higher when both bridge and top positions are occupied by oxygen (), where an open triangular subcluster is found. The average Co–Co and Ni–Co distances are also shown. Both increase also as the oxygen rate increases, with the Co atoms remaining somewhat further apart from each other than the Ni atoms, for a given oxidation rate. The lower panel of Figure S1 displays the average distance between the TM atoms and the O atoms located on bridge sites, which slightly decreases as the amount of oxygen decreases, mainly due to the reduction of the average Co–O distance. As the triangular subcluster opens up, the TM atoms are nearest to the bridge O atoms.Moreover, the results for the binding energies indicate that the higher the concentration of Fe in the TM oxide clusters, the higher their absolute stability, which may be important for practical purposes. On the other hand, the higher the Ni content, the lower the exothermic character of oxidation, or in other words, the less prone to oxidation the nanoparticle will be, which may also be important for practical purposes.
- (vii)
- The relative differences of electronegativities between the TM atoms, although small, also support this trend. Electronegativity increases while going from Fe to Ni so that the tendency towards electron donation to O should be stronger in Fe atoms. Electronic charge transfers also corroborate this fact. Figure 11 illustrates an example of the correlation between the binding energies and the electronic charge transfer from the TM atoms to the O ones for all pure oxides and oxidized nanoalloys for a given oxidation rate, ABO (A, B = Fe, Co, Ni, and ). Moreover, the binding energy per atom and the average electronic charge transfer are plotted in Figure S2 for FeCoO, CoNiO, and FeNiO as a function of x. The binding energy decreases for pure TM oxides from FeO to CoO and from CoO to NiO, and it also decreases for any type of oxidized mixture, as the concentration (x) of the B constituent increases. For Fe–Co nanoalloys, the decrease of binding energy is the lowest among all mixtures, the highest being for Fe–Ni nanoalloys. Regarding the electronic charge transfer, Ni atoms are less prone to donate electrons to O due to their higher electronegativity. This is illustrated in the local electronic charges on the atoms of the respective structures shown in the Figure 11. In addition, as the concentration of Ni increases both in Co–Ni and Fe–Ni mixtures, each of theTM atoms (Fe, Co, Ni) increases its electronic donation, and consequently, the total transferred electronic charge becomes higher (see Figure S2); and this fact is reflected in a weakening of the bonding between the TMs, and therefore, in a decrease of the binding energy. However, in the case of FeCo mixtures, the binding energies do not vary significantly as the concentration of Co(x) increases, because the electronic transfer remains almost constant. Since the electronic transfer of Fe is higher than that of Co, and there is a lesser concentration of the former, the total electronic charge transfer from the TM atoms to oxygen decreases slightly instead of increasing as in the rest of the mixtures. Consequently, the binding energies in Fe–Co mixtures are more similar. That is, the oxides scarcely loose stability upon the substitution of Fe by Co. This fact, together with the magnetism that these mixtures present, makes them remarkable. In Figure 11, both average TM–TM and TM–O distances are also provided. The former are almost constant for both Fe–Co and Fe–Ni mixtures, and in the case of Co–Ni mixtures for , the TM subcluster is somewhat more compact. The TM–O distances have little variation.
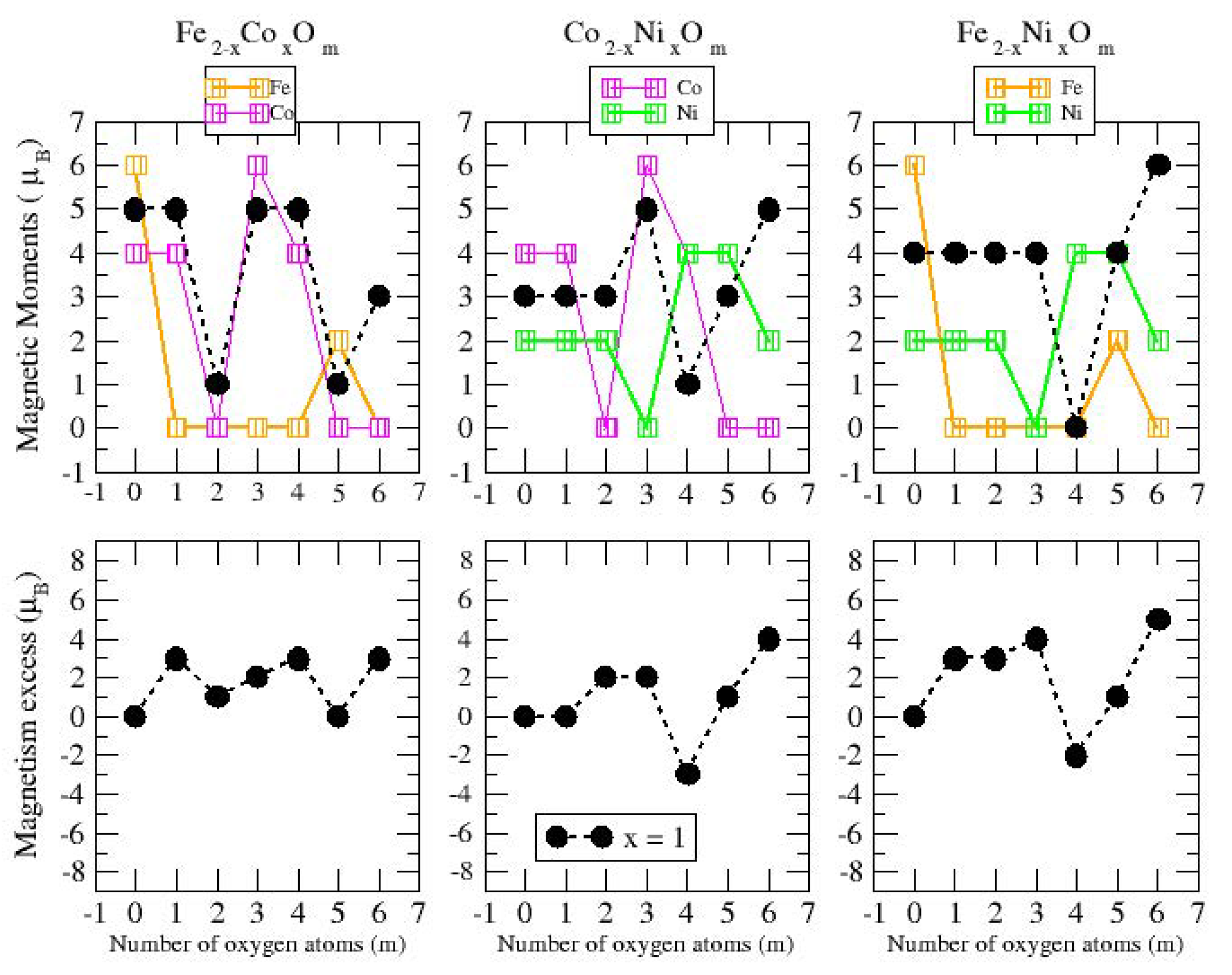
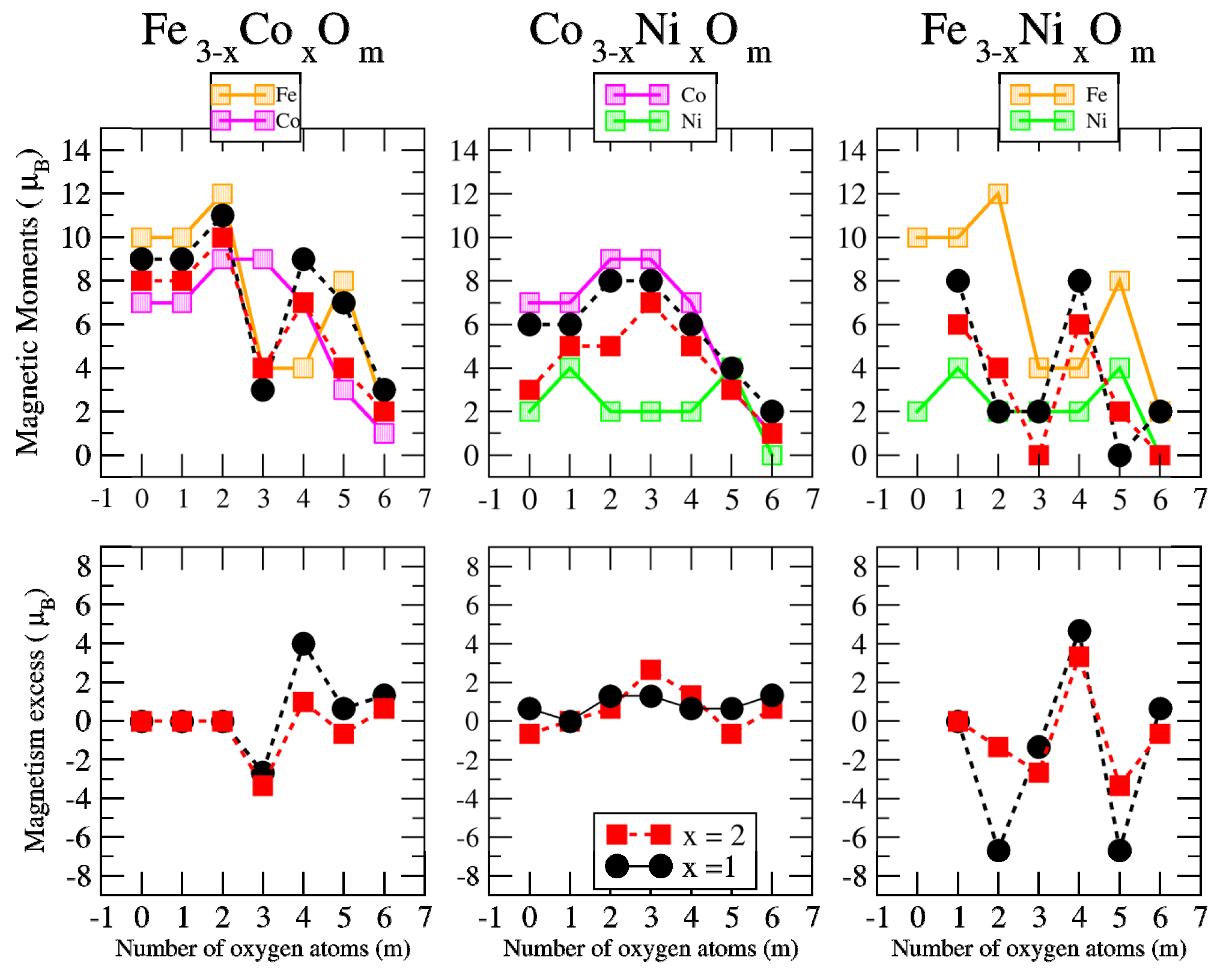
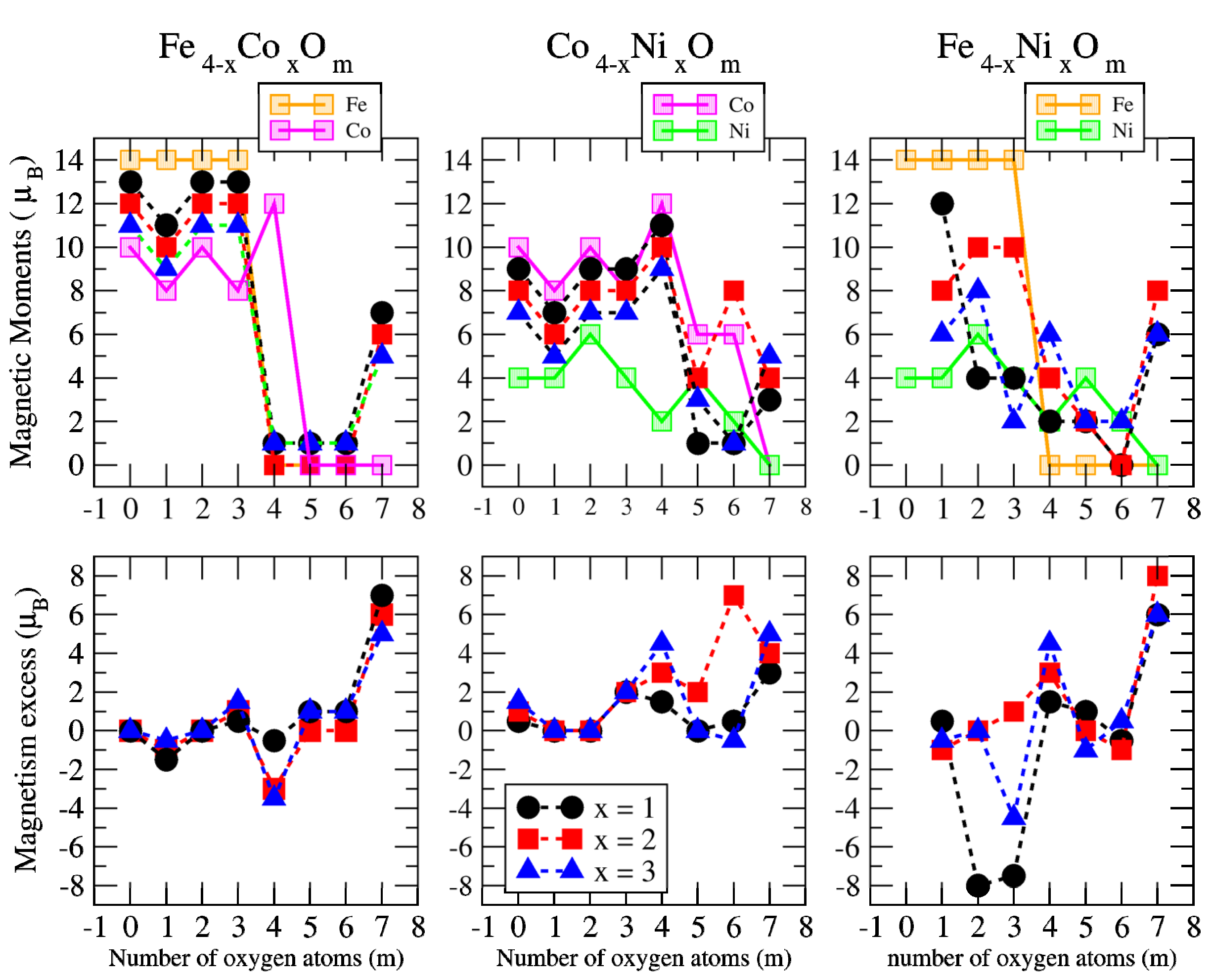
3.2. Magnetic Properties
3.2.1. A-B Non-Oxidized Nanoalloys; A, B = Fe, Co, Ni
3.2.2. Fe–Co Oxided Nanoalloys
3.2.3. Fe–Ni Oxided Nanoalloys
3.2.4. Co–Ni Oxided Nanoalloys
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lungu, I.I.; Rǎdulescu, M.; Mogoşanu, G.D.; Grumezescu, A.M. pH sensitive core-shell magnetic nanoparticles for targeted drug delivery in cancer therapy. Rom. J. Morphol. Embryol. 2016, 57, 23–32. [Google Scholar] [PubMed]
- Jadhav, S.; Gaikwad, S.; Nimse, M.; Rajbhoj, A. Copper oxide nanoparticles: Synthesis, characterization and their antibacterial activity. J. Clust. Sci. 2011, 22, 121–129. [Google Scholar] [CrossRef]
- Qiang, Y.; Antony, J.; Sharma, A.; Nutting, J.; Sikes, D.; Meyer, D. Iron/iron oxide core-shell nanoclusters for biomedical applications. J. Nanopart. Res. 2006, 8, 489–496. [Google Scholar] [CrossRef]
- Nie, S.; Xing, Y.; Kim, G.J.; Simons, J.W. Nanotechnology applications in cancer. Annu. Rev. Biomed. Eng. 2007, 9, 257–288. [Google Scholar] [CrossRef]
- Gupta, A.S. Nanotechnology applications in diagnosis and treatment of metastasis. Nanomedicine 2014, 9, 1517–1529. [Google Scholar] [CrossRef]
- Azam, A.; Ahmed, A.S.; Oves, M.; Khan, M.S.; Habib, S.S.; Memic, A. Antimicrobial activity of metal oxide nanoparticles against Gram-positive and Gram-negative bacteria: A comparative study. Int. J. Nanomed. 2012, 7, 6003–6009. [Google Scholar] [CrossRef]
- Laurent, S.; Forge, D.; Port, M.; Roch, A.; Robic, C.; Elst, L.V.; Muller, R.N. Magnetic iron oxide nanoparticles: Synthesis, stabilization, vectorization, physicochemical characterizations, and biological applications. Chem. Rev. 2008, 108, 2064–2110. [Google Scholar] [CrossRef]
- Jones, N.; Ray, B.; Ranjit, K.T.; Manna, A.C. Antibacterial activity of ZnO nanoparticle suspensions on a broad spectrum of microorganisms. FEMS Microbiol. Lett. 2008, 279, 71–76. [Google Scholar] [CrossRef]
- Pankhurst, Q.A.; Connolly, J.; Jones, S.K.; Dobson, J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R167. [Google Scholar] [CrossRef]
- Wang, H.; Cui, L.-F.; Yang, Y.; Casalongue, H.S.; Robinson, J.T.; Liang, Y.; Cui, Y.; Da, H. Mn3O4 Graphene hybrid as a high-capacity anode material for lithium ion batteries. J. Am. Chem. Soc. 2010, 132, 13978–13980. [Google Scholar] [CrossRef]
- Koo, B.; Xiong, H.; Slater, M.D.; Prakapenka, V.B.; Balasubramanian, M.; Podsiadlo, P.; Johnson, C.S.; Rajh, T.; Shevchenko, E.V. Hollow iron oxide nanoparticles for application in lithium ion batteries. Nano Lett. 2012, 12, 2429–2435. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.S.; Ren, W.; Wen, L.; Gao, L.; Zhao, J.; Chen, Z.; Zhou, G.; Li, F.; Cheng, H.M. Graphene anchored with Co3O4 nanoparticles as anode of lithium ion batteries with enhanced reversible capacity and cyclic performance. ACS Nano 2010, 4, 3187–3194. [Google Scholar] [CrossRef] [PubMed]
- Stoimenov, P.K.; Klinger, R.L.; Marchin, G.L.; Klabunde, K.J. Metal oxide nanoparticles as bactericidal agents. Langmuir 2002, 18, 6679–6686. [Google Scholar] [CrossRef]
- Tran, M.; Mir, A.; Mallik, D.; Sinha, A.; Nayar, S.; Webster, T.J. Bactericidal effect of iron oxide nanoparticles on Staphylococcus aureus. Int. J. Nanomed. 2010, 5, 277–283. [Google Scholar] [CrossRef]
- Sondi, I.; Salopek-Sondi, B. Silver nanoparticles as antimicrobial agent: A case study on E. coli as a model for Gram-negative bacteria. J. Colloid Interface Sci. 2004, 275, 177–182. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhao, X.; Niu, H.; Shi, Y.; Cai, Y.; Jiang, G. Superparamagnetic Fe3O4 nanoparticles as catalysts for the catalytic oxidation of phenolic and aniline compounds. J. Hazard. Mater. 2009, 167, 560–566. [Google Scholar] [CrossRef]
- Jiao, F.; Frei, H. Nanostructured cobalt oxide clusters in mesoporous silica as efficient oxygen evolving catalysts. Angew. Chem. 2009, 121, 1873–1876. [Google Scholar] [CrossRef]
- Teja, A.S.; Koh, P.-Y. Synthesis, properties, and applications of magnetic iron oxide nanoparticles. Prog. Cryst. Growth Charact. Mater. 2009, 55, 22–45. [Google Scholar] [CrossRef]
- Carnes, C.L.; Klabunde, K.J. The catalytic methanol synthesis over nanoparticle metal oxide catalysts. J. Mol. Catal. A Chem. 2003, 194, 227–236. [Google Scholar] [CrossRef]
- Lopez, N.; Norskov, J.K. Catalytic CO oxidation by a gold nanoparticle: A density functional study. J. Am. Chem. Soc. 2002, 124, 11262–11263. [Google Scholar] [CrossRef]
- Johnson, G.E.; Reilly, N.M.; Castleman, A.W., Jr. Effect of charge state and stoichiometry on the structure and reactivity of nickel oxide clusters with CO. Int. J. Mass Spectrom. 2009, 208, 93–100. [Google Scholar] [CrossRef]
- Wan, J.; Yuan, R.; Zhang, C.; Wu, N.; Yan, F.; Yu, S.; Chen, K. Potential application of metal dichalcogenides double-layered heterostructures as anode materials for Li-ion batteries. J. Phys. Chem. C 2016, 120, 23799–23806. [Google Scholar] [CrossRef]
- Casula, M.F.; Conca, E.; Bakaimi, I.; Sathya, A.; Materia, M.E.; Casu, A.; Falqui, A.; Sogne, E.; Pellegrino, T.; Kanaras, A.G. Manganese doped-iron oxide nanoparticle clusters and their potential as agents for magnetic resonance imaging and hyperthermia. Phys. Chem. Chem. Phys. 2016, 18, 16848–16855. [Google Scholar] [CrossRef] [PubMed]
- Szczerba, W.; Zukrowski, J.; Przybylski, M.; Sikora, M.; Safonova, O.; Shmeliov, A.; Nicolosi, V.; Schneider, M.; Granath, T.; Oppmann, M.; et al. Pushing up the magnetisation values for iron oxide nanoparticles via zinc doping: X-ray studies on the particle’s sub-nano structure of different synthesis routes. Phys. Chem. Chem. Phys. 2016, 18, 25221–25229. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Chen, Q.; Wang, J. Ab initio study of structure and magnetism of late transition metal oxide TMnOm (TM = Fe, Co, Ni, n = 1, 2, m = 1–6). J. Nanosci. Nanotechnol. 2012, 12, 6488–6493. [Google Scholar] [CrossRef]
- Erlebach, A.; Hunhn, C.; Jana, R.; Sierka, M. Structure and magnetic properties of (Fe2O3)n clusters (n = 1–5). Phys. Chem. Chem. Phys. 2014, 16, 26421–26426. [Google Scholar] [CrossRef]
- Reilly, N.M.; Reveles, J.U.; Johnson, G.E.; Khanna, S.N.; Castelman, A.W. Experimental and theoretical study of the structure and reactivity of Fe1−2 clusters with CO. J. Phys. Chem. A 2007, 111, 4158–4166. [Google Scholar] [CrossRef]
- Reilly, N.M.; Reveles, J.U.; Johnson, G.E.; del Campo, J.M.; Khanna, S.N.; Köster, A.M.; Castleman, A.W. Experimental and theoretical study of the structure and reactivity of FemOn+ (m = 1,2; n = 1–5) with CO. J. Phys. Chem. C 2007, 111, 19086–19097. [Google Scholar] [CrossRef]
- Ota, K.; Koyasu, K.; Ohshimo, K.; Misaizu, F. Structures of cobalt oxide cluster cations studied by ion mobility mass spectrometry. Chem. Phys. Lett. 2013, 588, 63–67. [Google Scholar] [CrossRef]
- Tung, N.T.; Tam, N.M.; Nguyen, M.T.; Lievens, P.; Janssens, E. Influence of Cr doping on the stability and structure of small cobalt oxide clusters. J. Chem. Phys. 2014, 141, 044311. [Google Scholar] [CrossRef]
- Johnson, G.E.; Reveles, J.U.; Reilly, N.M.; Tyo, E.C.; Khanna, S.N.; Castelman, A.W., Jr. Influence of stoichiometry and charge state on the structure and reactivity of cobalt oxide clusters with CO. J. Phys. Chem. A 2008, 112, 11330–11340. [Google Scholar] [CrossRef] [PubMed]
- Kumavat, S.; Deshpande, M. Alkali metal doped nickel oxide clusters: A density functional study. Comput. Theor. Chem. 2014, 1035, 19–27. [Google Scholar] [CrossRef]
- Yin, S.; Xue, W.; Ding, X.-L.; Wang, W.-G.; He, S.-G.; Ge, M.-F. Formation, distribution, and structures of oxygen-rich iron and cobalt oxide clusters. Int. J. Mass Spectrom. 2009, 281, 72–78. [Google Scholar] [CrossRef]
- Dible, C.J.; Akin, S.T.; Ard, S.; Fowler, C.P.; Duncan, M.A. Photodissociation of cobalt and nickel oxide cluster cations. J. Phys. Chem. A 2012, 116, 5398–5404. [Google Scholar] [CrossRef] [PubMed]
- Kirilyuk, A.; Fielicke, A.; Demyk, K.; von Helden, G.; Meijer, G.; Rasing, T.H. Ferrimagnetic cagelike Fe4O6 cluster: Structure determination from infrared dissociation spectroscopy. Phys. Rev. B 2010, 82, 020405(R). [Google Scholar] [CrossRef]
- Li, S.; Zhai, H.-J.; Wang, L.-S.; Dixon, D.A. Structural and electronic properties of reduced transition metal oxide clusters, M4O10 and M4O10− (M = Cr, W), from photoelectron spectroscopy and quantum chemical calculations. J. Phys. Chem. A 2012, 116, 5256–5271. [Google Scholar] [CrossRef]
- Wang, H.-Q.; Li, H.-F. Probing the structural and electronic properties of small vanadium dioxide clusters by density functional theory and comparison with experimental photoelectron spectroscopy. J. Chem. Phys. 2012, 137, 164304. [Google Scholar] [CrossRef]
- Ohshimo, K.; Komukai, T.; Moriyama, R.; Misaizu, F. Isomer separation of iron oxide cluster cations by ion mobility mass spectrometry. J. Phys. Chem. A 2014, 118, 3899–3905. [Google Scholar] [CrossRef]
- Aguilera-del-Toro, R.H.; Aguilera-Granja, F.; Vega, A.; Balbás, L.C. Structure, fragmentation patterns, and magnetic properties of small cobalt oxide clusters. Phys. Chem. Chem. Phys. 2014, 16, 21732–21741. [Google Scholar] [CrossRef]
- Aguilera-del-Toro, R.H.; Aguilera-Granja, F.; Balbás, L.C. Structure, fragmentation patterns, and magnetic properties of small nickel oxide clusters. Phys. Chem. Chem. Phys. 2017, 19, 3366–3383. [Google Scholar] [CrossRef]
- Aguilera-del-Toro, R.H.; Aguilera-Granja, F.; Torres, M.B.; Vega, A. Relation between structural patterns and magnetism in small iron oxide clusters; reentrance of magnetic moment at hich oxidation rates. to be published.
- Torres, M.B.; Aguado, A.; Aguilera-Granja, F.; Vega, A.; Balbás, L.C. Structural, vibrational, and magnetic properties of FeCoOn0/+ (n = 1–6) bimetallic oxide clusters. Phys. Chem. C 2015, 119, 11200–11209. [Google Scholar]
- Borzorth, R.M. Ferromagnetism; Wiley-IEEE Press: Piscataway, NJ, USA, 1993; ISBN 978-0-780-31032-2. [Google Scholar]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef] [PubMed]
- Kleinman, L.; Bylander, D.M. Efficacious form for model pseudopotentials. Phys. Rev. Lett. 1982, 48, 1425–1428. [Google Scholar] [CrossRef]
- Louie, S.G.; Froyen, S.; Cohen, M.L. Nonlinear ionic pseudopotentials in spin-density-functional calculations. Phys. Rev. B 1982, 26, 1738–1742. [Google Scholar] [CrossRef]
- Pauling, L. The Nature of the Chemical Bond; Cornell University Press: Ithaca, NY, USA, 1960. [Google Scholar]
- Aguilera-del-Toro, R.H.; Aguilera-Granja, F.; Balbás, L.C.; Vega, A. Synthesis and characterization of indium oxide nanoparticles. Theor. Chem. Acc. 2018, 137, 54. [Google Scholar] [CrossRef]
- Ohshimo, K.; Azuma, A.; Komukai, T.; Moriyama, R.; Misaizu, F. Structures and CO-adsorption reactivities of nickel oxide cluster cations studied by ion mobility mass spectrometry. J. Phys. Chem. C 2015, 119, 11014–11021. [Google Scholar] [CrossRef]
- Fritsch, D.; Koepernik, K.; Richter, M.; Eschrig, H. Transition metal dimers as potential molecular magnets: A challenge to computational chemistry. J. Comput. Chem. 2007, 29, 2210–2219. [Google Scholar] [CrossRef]
- Bloński, P.; Hafner, J. Magnetic anisotropy of transition-metal dimers: Density functional calculations. Phys. Rev. B 2009, 79, 224418. [Google Scholar] [CrossRef]
- Bloński, P.; Hafner, J. Magneto-structural properties and magnetic anisotropy of small transition-metal clusters: A first-principles study. J. Phys. Condens. Matter 2011, 23, 136001. [Google Scholar] [CrossRef] [PubMed]
- Fortunelli, A.; Velasco, A.M. Structural and electronic properties of Pt/Fe nanoclusters from EHT calculations. J. Mol. Struct. Theochem 1999, 487, 251–266. [Google Scholar] [CrossRef]
- Aguado, A.; López, J.M. Identifying structural and energetic trends in isovalent core-shell nanoalloys as a function of composition and size mismatch. J. Chem. Phys. 2011, 135, 134305. [Google Scholar] [CrossRef] [PubMed]

| FeO | CoO | NiO | Fe | Co | Ni | |
|---|---|---|---|---|---|---|
| E (eV) | 2.75 | 2.63 | 2.29 | 1.56 | 1.77 | 1.35 |
| d (Å) | 1.67 | 1.70 | 1.70 | 2.04 | 2.01 | 2.17 |
| q (e) | 0.46 | 0.45 | 0.43 | – | – | – |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilera-del-Toro, R.H.; Torres, M.B.; Aguilera-Granja, F.; Vega, A. Tuning the Magnetic Moment of Small Late 3d-Transition-Metal Oxide Clusters by Selectively Mixing the Transition-Metal Constituents. Nanomaterials 2020, 10, 1814. https://doi.org/10.3390/nano10091814
Aguilera-del-Toro RH, Torres MB, Aguilera-Granja F, Vega A. Tuning the Magnetic Moment of Small Late 3d-Transition-Metal Oxide Clusters by Selectively Mixing the Transition-Metal Constituents. Nanomaterials. 2020; 10(9):1814. https://doi.org/10.3390/nano10091814
Chicago/Turabian StyleAguilera-del-Toro, Rodrigo H., María B. Torres, Faustino Aguilera-Granja, and Andrés Vega. 2020. "Tuning the Magnetic Moment of Small Late 3d-Transition-Metal Oxide Clusters by Selectively Mixing the Transition-Metal Constituents" Nanomaterials 10, no. 9: 1814. https://doi.org/10.3390/nano10091814
APA StyleAguilera-del-Toro, R. H., Torres, M. B., Aguilera-Granja, F., & Vega, A. (2020). Tuning the Magnetic Moment of Small Late 3d-Transition-Metal Oxide Clusters by Selectively Mixing the Transition-Metal Constituents. Nanomaterials, 10(9), 1814. https://doi.org/10.3390/nano10091814





