Graphene Oxide: Study of Pore Size Distribution and Surface Chemistry Using Immersion Calorimetry
Abstract
1. Introduction
Basic Fundamentals of PSD, NLDFT, and QSDFT (Pore Size Distribution, Non-Local Density Functional Theory and Quenched Solid Density Functional Theory)
2. Materials and Methods
2.1. Materials and Reagents
2.2. Characteristics of the Samples Used in this Work
2.3. N2 Adsorption Isotherms at −196 °C
2.4. Determination of Functional Groups Using Boehm Titrations
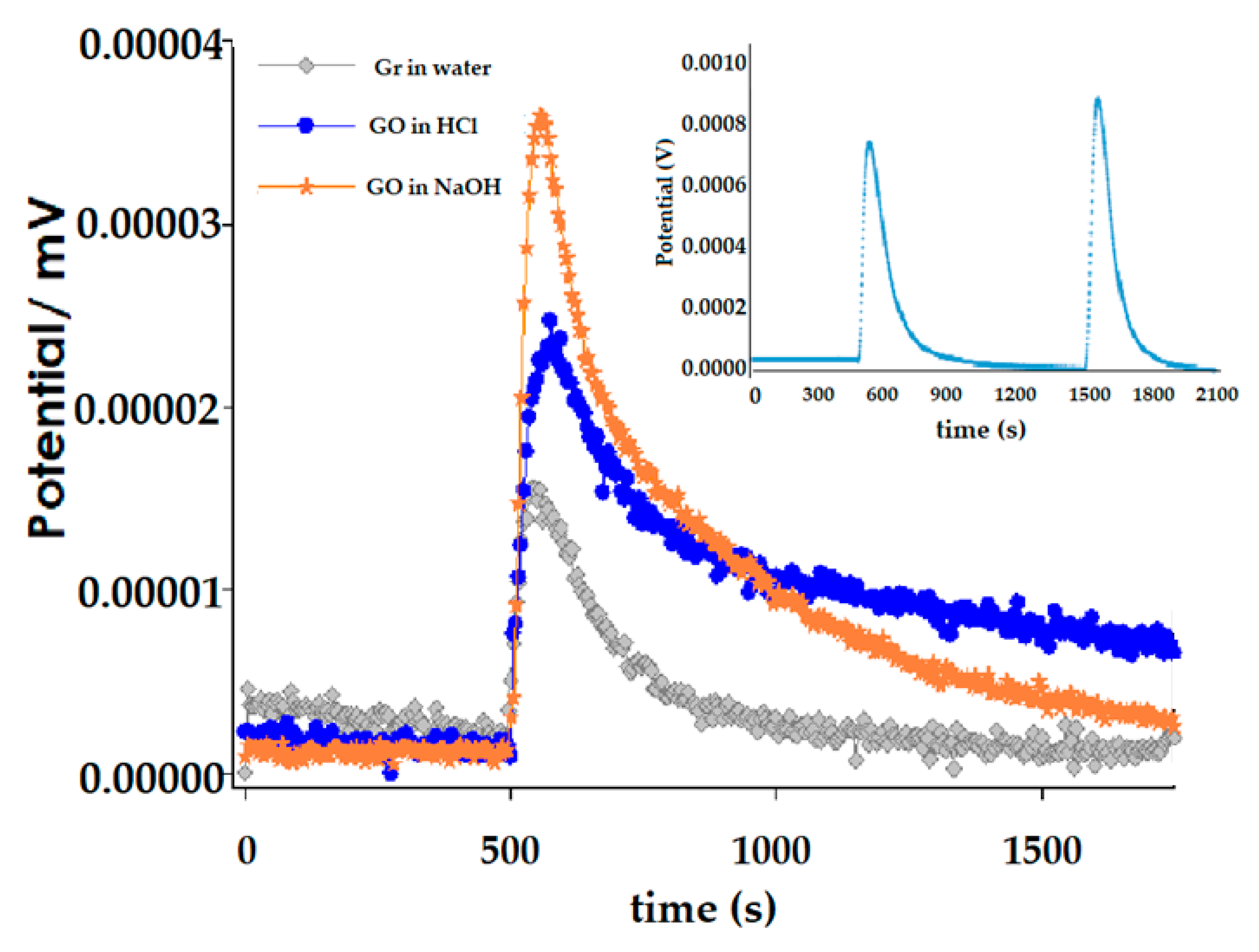
2.5. Immersion Enthalpy Studies
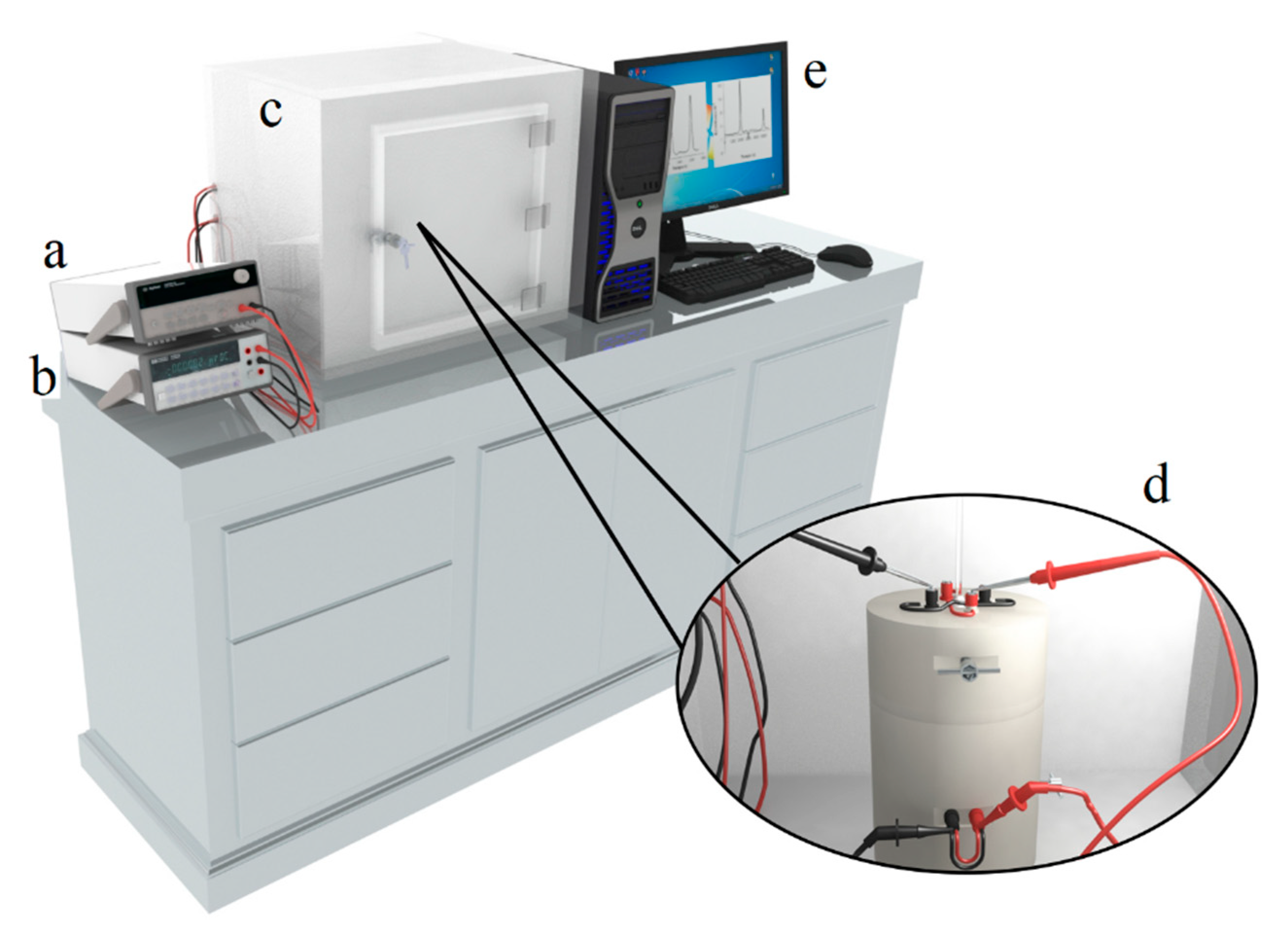
2.5.1. Description of Immersion Calorimeter
2.5.2. Immersion Calorimetry Experimental
3. Results and Discussion
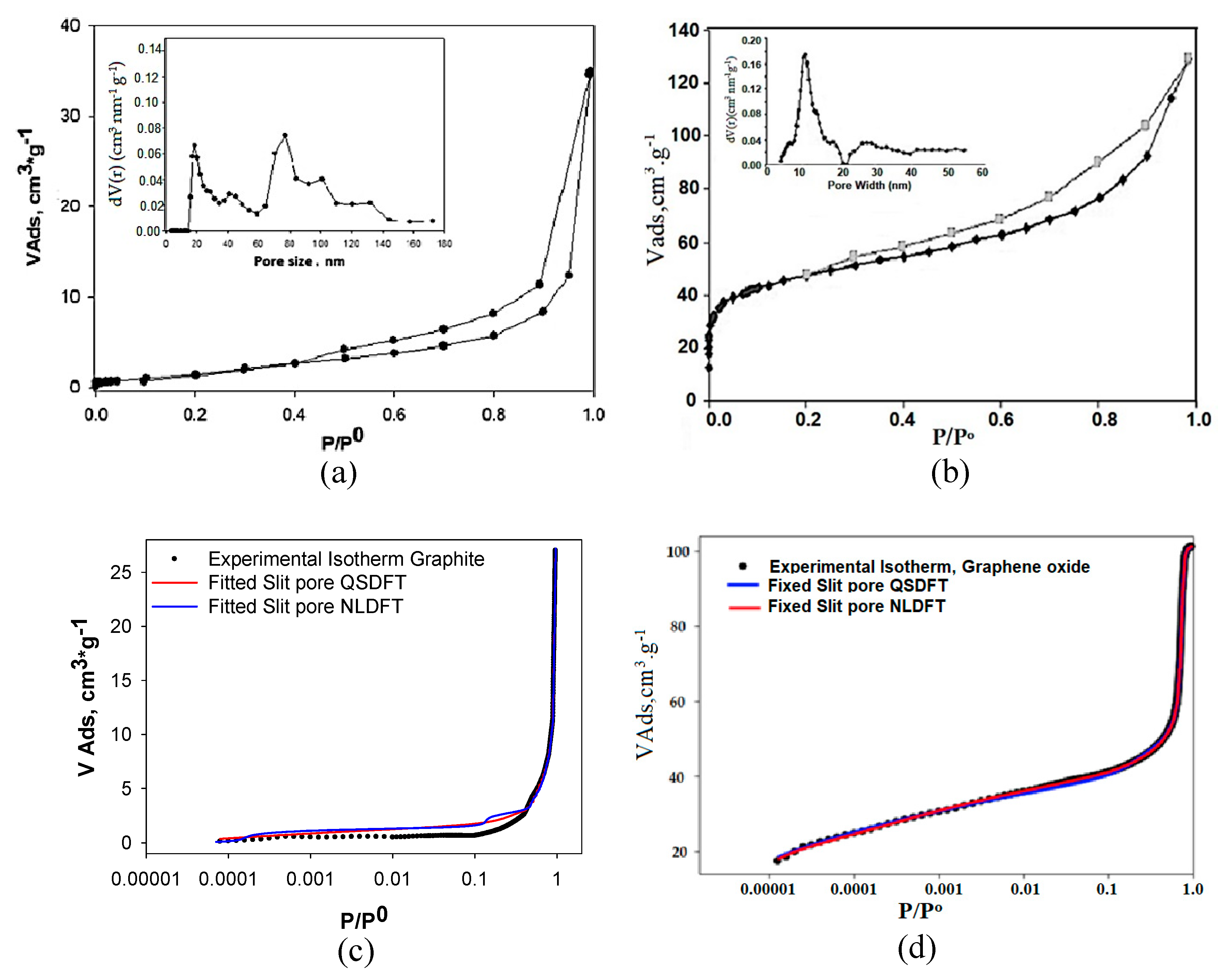
3.1. Analysis of N2 Adsorption Isotherms at −196 °C
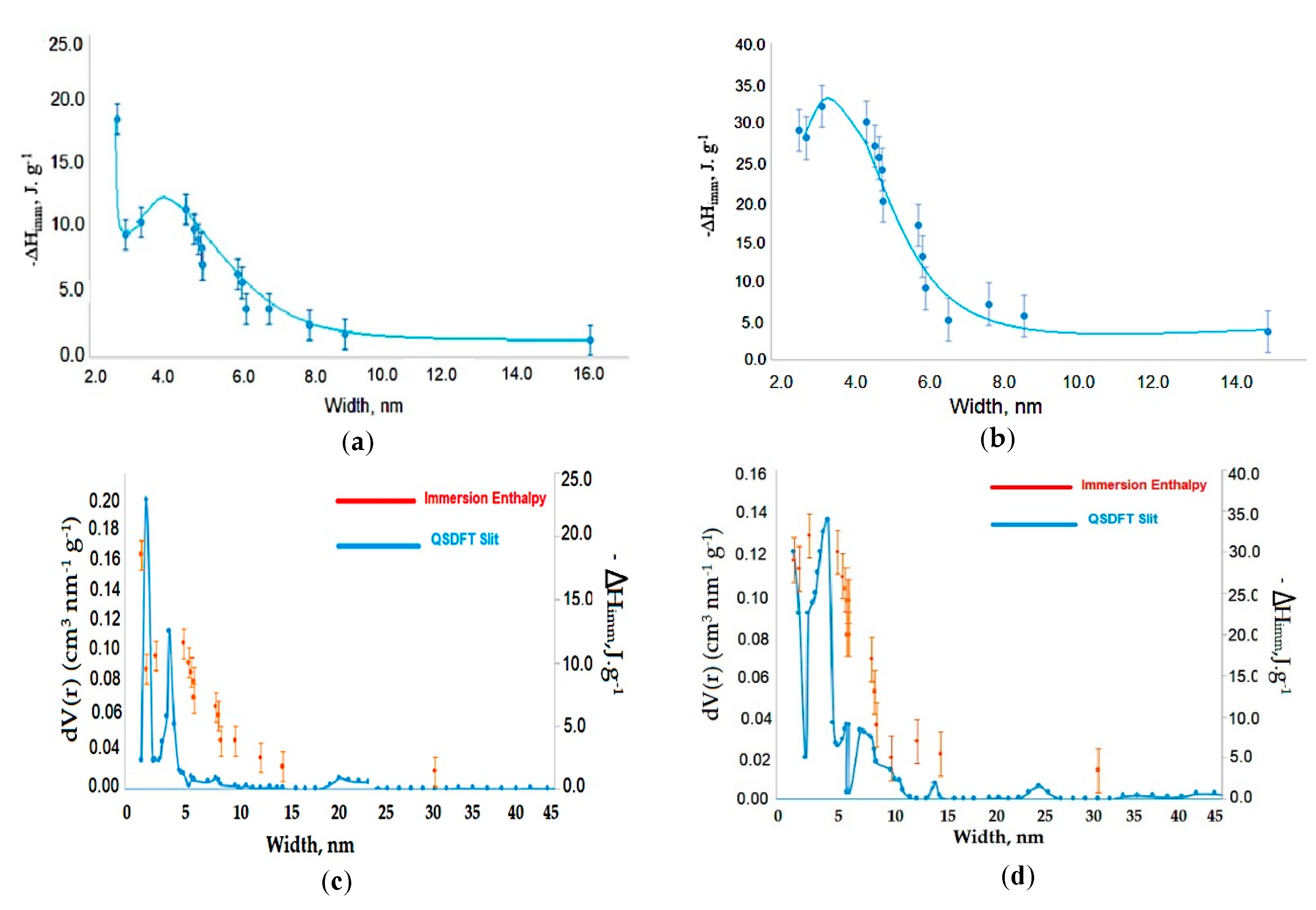
3.2. Analysis of the Results of the Chemical Groups: Boehm Titrations and Immersion Calorimetry
3.3. Immersion Calorimetry Results Analysis Using Different Probes Molecules
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dreyer, D.R.; Park, S.; Bielawski, C.W.; Ruoff, R.S. The chemistry of graphene oxide. Chem. Soc. Rev. 2010, 39, 228–240. [Google Scholar] [CrossRef] [PubMed]
- De Jesus, K.A.; Freire, E.; Guimarães, M.J.O.C. Grafeno: Aplicações e tendências tecnológicas. Dep. Process. Orgânicos 2012, 737, 14–19. [Google Scholar]
- Lavín, M.P.; Valverde, J.L.; Sanchez, M.L.; Romero, A. Optimization of the synthesis procedures of graphene and graphite oxide. Recent Adv. Graphene Res. 2016, 12, 113–133. [Google Scholar]
- Zardin, G.J.A.; Oliveira, M.M. Nanoestructura de carbono (nanotubos, grafeno): Quo vadis? Química Nova 2013, 36, 1533–1539. [Google Scholar]
- Shen, J.; Hu, Y.; Shi, M.; Lu, X.; Qin, C.; Li, C.; Ye, M. Fast and Facile Preparation of Graphene Oxide and Reduced Graphene Oxide Nanoplatelets. Chem. Mater. 2009, 21, 3514–3520. [Google Scholar] [CrossRef]
- Pei, S.; Cheng, H.-M. The reduction of graphene oxide. Carbon 2012, 50, 3210–3228. [Google Scholar] [CrossRef]
- Bissessur, R.; Scully, S.F. Intercalation of solid polymer electrolytes into graphite oxide. Solid State Ion. 2007, 178, 877–882. [Google Scholar] [CrossRef]
- Liu, P.G.; Gong, K.C.; Xiao, P.; Xiao, M. Preparation and characterization of poly(vinyl acetate)—intercalated graphite oxide nanocomposite. J. Mater. Chem. 2000, 10, 933–935. [Google Scholar] [CrossRef]
- Wang, G.C.; Yang, Z.Y.; Li, X.W.; Li, C.Z. Synthesis of poly(aniline-co-o-anisidine)—intercalated graphite oxide composite by delamination/reassembling method. Carbon 2005, 43, 2564–2570. [Google Scholar] [CrossRef]
- Bissessur, R.; Liu, P.K.Y.; Scully, S.F. Intercalation of polypyrrole into graphite oxide. Synth. Met. 2006, 156, 1023–1027. [Google Scholar] [CrossRef]
- Liu, Z.H.; Wang, Z.M.; Yang, X.J.; Ooi, K.T. Intercalation of organic ammonium ions into layered graphite oxide. Langmuir 2002, 18, 4926–4932. [Google Scholar] [CrossRef]
- Herrera-Alonso, M.; Abdala, A.A.; McAllister, M.J.; Aksay, I.A.; Prud’homme, R.K. Intercalation and stitching of graphite oxide with diaminoalkanes. Langmuir 2007, 23, 10644–10649. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.K.; Liang, S.; Zou, L.F.; Huang, L.W.; Park, C.; Zhu, L.S.; Fang, J.Y.; Fu, Q.; Wang, H. Intercalating oleylamines in graphite oxide. Langmuir 2012, 28, 2904–2908. [Google Scholar] [CrossRef] [PubMed]
- You, S.J.; Yu, J.C.; Sundqvist, B.; Belyaeva, L.A.; Avramenko, N.V.; Korobov, M.V.; Talyzin, A.V. Selective intercalation of graphite oxide by methanol in water/methanol mixtures. J. Phys. Chem. C 2013, 117, 1963–1968. [Google Scholar] [CrossRef]
- Zhang, Q.O.; He, Y.Q.; Chen, X.G.; Hu, D.H.; Li, L.J.; Yin, T.; Ji, L.L. Structure and photocatalytic properties of tio2-graphene oxide intercalated composite. Chin. Sci. Bull. 2011, 56, 331–339. [Google Scholar] [CrossRef]
- Mi, B.X. Graphene oxide membranes for ionic and molecular sieving. Science 2014, 343, 740–742. [Google Scholar] [CrossRef]
- Joshi, R.K.; Carbone, P.; Wang, F.C.; Kravets, V.G.; Su, Y.; Grigorieva, I.V.; Wu, H.A.; Geim, A.K.; Nair, R.R. Precise and ultrafast molecular sieving through graphene oxide membranes. Science 2014, 343, 752–754. [Google Scholar] [CrossRef]
- Kim, H.W.; Yoon, H.W.; Yoon, S.M.; Yoo, B.M.; Ahn, B.K.; Cho, Y.H.; Shin, H.J.; Yang, H.; Paik, U.; Kwon, S.; et al. Selective gas transport through few-layered graphene and graphene oxide membranes. Science 2013, 342, 91–95. [Google Scholar] [CrossRef]
- Li, H.; Song, Z.N.; Zhang, X.J.; Huang, Y.; Li, S.G.; Mao, Y.T.; Ploehn, H.J.; Bao, Y.; Yu, M. Molecular-sieving graphene oxide membranes for selective hydrogen separation. Science 2013, 342, 95–98. [Google Scholar] [CrossRef]
- Nair, R.R.; Wu, H.A.; Jayaram, P.N.; Grigorieva, I.V.; Geim, A.K. Unimpeded permeation of water through helium-leak-tight graphene-based membranes. Science 2012, 335, 442–444. [Google Scholar] [CrossRef]
- Kim, D.; Kim, D.W.; Lim, H.K.; Jeon, J.; Kim, H.; Jung, H.-T.; Lee, H. Intercalation of gas molecules in graphene oxide interlayer: The role of water. J. Phys. Chem. C 2014, 118, 11142–11148. [Google Scholar] [CrossRef]
- Madani, S.H.; Hu, C.; Silvestre-Albero, A.; Biggs, M.J.; Rodríguez-Reinoso, F.; Pendleton, P. Pore size distributions derived from adsorption isotherms, immersion calorimetry, and isosteric heats: A comparative study. Carbon 2016, 96, 1106–1113. [Google Scholar] [CrossRef]
- Madani, S.H.; Badalyan, A.; Biggs, M.J.; Pendleton, P. Uncertainty in pore size distribution derived from adsorption isotherms: I. classical methods. Microporous Mesoporous Mater. 2015, 214, 210–216. [Google Scholar] [CrossRef]
- Moon, H.S.; Lee, J.H.; Kwon, S.; Kim, I.T.; Lee, S.G. Mechanisms of Na adsorption on graphene and graphene oxide: Density functional theory approach. Carbon Lett. 2015, 16, 116–120. [Google Scholar] [CrossRef]
- Kenvin, J.; Jagiello, J.; Mitchell, S.; Pérez-Ramírez, J. Unified method for the total pore volume and pore size distribution of hierarchical zeolites from argon adsorption and mercury intrusion. Langmuir 2015, 31, 1242–1247. [Google Scholar] [CrossRef]
- Badalyan, A.; Pendleton, P. Analysis of uncertainties in manometric gas-adsorption measurements. I: Propagation of uncertainties in BET analyses. Langmuir 2003, 19, 7919–7928. [Google Scholar] [CrossRef]
- Kupgan, G.; Liyana-Arachchi, T.P.; Colina, C.M. NLDFT pore size distribution in amorphous microporous materials. Langmuir 2017, 33, 11138–11145. [Google Scholar] [CrossRef]
- Kaneko, K. Determination of pore size and pore size distribution. 1. Adsorbents and Catalysts. J. Membr. Sci. 1994, 96, 59–89. [Google Scholar] [CrossRef]
- Hill, A.J.; Pas, S.J.; Hill, M.R.; Freeman, B.D. Characterising the pore size distribution in nanoporous materials. Polym. Prepr. 2008, 42, 511–512. [Google Scholar]
- Seaton, N.A.; Walton, J.P.R.B.; Quirke, N.A. New analysis method for the determination of the pore size distribution of porous carbons from nitrogen adsorption measurements. Carbon 1989, 27, 853–861. [Google Scholar] [CrossRef]
- Lastoskie, C.; Gubbins, K.E.; Quirke, N. Pore size distribution analysis of microporous carbons: A density functional theory approach. J. Phys. Chem. 1993, 97, 4786–4796. [Google Scholar] [CrossRef]
- Olivier, J.P.; Conklin, W.B.; Szombathely, M.V. Determination of pore size distribution from density functional theory: A comparison of nitrogen and argon results. Stud. Surf. Sci. Catal. 1994, 87, 81–89. [Google Scholar]
- Barrett, E.P.; Joyner, L.G.; Halenda, P.P. The determination of pore volume and area distributions in porous substances. I. Computations from nitrogen isotherms. J. Am. Chem. Soc. 1951, 73, 373–380. [Google Scholar] [CrossRef]
- Kruk, M.; Jaroniec, M.; Sayari, A. Application of large pore MCM-41 molecular sieve to improve pore size analysis using nitrogen adsorption measurements. Langmuir 1997, 13, 6267–6273. [Google Scholar] [CrossRef]
- Kruk, M.; Jaroniec, M. Accurate method for calculating mesopore size distributions from argon adsorption data at 87 K developed using model MCM-41 materials. Chem. Mater. 2000, 12, 222–230. [Google Scholar] [CrossRef]
- Broekhoff, J.C.P.; de Boer, J.H. Studies on pore systems in catalysts IX. Calculation of pore distribution from the adsorption branch of nitrogen sorption isotherm in the case of open cylindrical pores A. Fundamental equation. J. Catal. 1967, 9, 8–14. [Google Scholar] [CrossRef]
- Broekhoff, J.C.P.; de Boer, J.H. Pore systems in catalysts. X. Calculations of pore distributions from the adsorption branch of nitrogen sorption isotherms in the case of open cylindrical pores. 2. Applications. J. Catal. 1968, 9, 15–27. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Lu, G.Q.; Zhao, X.S. Thickness and stability of adsorbed film in cylindrical mesopores. J. Phys. Chem. B 1998, 102, 7371–7376. [Google Scholar] [CrossRef]
- Bhatia, S.K.; Sonwane, C.G. Capillary coexistence and criticality in mesopores: Modification of the Kelvin theory. Langmuir 1998, 14, 1521–1524. [Google Scholar] [CrossRef]
- Qiao, S.Z.; Bhatia, S.K.; Zhao, X.S. Prediction of multiplayer adsorption and capillary condensation phenomena in cylindrical mesopores. Micropor Mesopor Mater. 2003, 65, 287–298. [Google Scholar] [CrossRef]
- Ustinov, E.A.; Do, D.D.; Jaroniec, M. Equilibrium adsorption in cylindrical mesopores: A modified Broekhoff and de Boer theory versus density functional theory. J. Phys. Chem. B 2005, 109, 1947–1958. [Google Scholar] [CrossRef] [PubMed]
- Horvath, G.; Kawazoe, K. Method for the calculation of effective pore size distribution in molecular sieve. J. Chem. Eng. Jpn. 1983, 16, 470–475. [Google Scholar] [CrossRef]
- Lastoskie, C.; Gubbins, K.E.; Quirke, N. Pore size heterogeneity and the carbon slit pore: A density functional theory model. Langmuir 1993, 9, 2693–2702. [Google Scholar] [CrossRef]
- Ravikovitch, P.I.; Neimark, A.V. Calculations of pore size distributions in nanoporous materials from adsorption and desorption isotherms. Stud. Surf. Sci. Catal. 2000, 129, 597–606. [Google Scholar]
- Jaroniec, M.; Kruk, M.; Olivier, J.P. Standard nitrogen adsorption data for characterization of nanoporous silicas. Langmuir 1999, 15, 5410–5413. [Google Scholar] [CrossRef]
- Ravikovitch, P.; Vishnyakov, A.; Russo, R.; Neimark, A. Unified approach to pore size characterization of microporous carbonaceous materials from N2, Ar and CO2 adsorption isotherms. Langmuir 2000, 16, 2311–2320. [Google Scholar] [CrossRef]
- Lawson, C.L.; Hanson, R.J. Solving Least Squares Problems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1974; Volume 15. [Google Scholar]
- Ravikovitch, P.I. Characterization of Nanoporous Materials by Gas Adsorption and Density Functional Theory. Ph.D. Thesis, Yale University, New Haven, NH, USA, 1998. [Google Scholar]
- Jagiello, J. Stable numerical solution of the adsorption integral equation using splines. Langmuir 1994, 10, 2778–2785. [Google Scholar] [CrossRef]
- Jagiello, J.; Thommes, M. Comparison of DFT characterization methods based on n2, ar, co2, and h2 adsorption applied to carbons with various pore size distributions. Carbon 2004, 42, 1227–1232. [Google Scholar] [CrossRef]
- Dombrowski, R.J.; Hyduke, D.R.; Lastoskie, C.M. Pore size analysis of activated carbons from argon and nitrogen porosimetry using density functional theory. Langmuir 2000, 16, 5041–5050. [Google Scholar] [CrossRef]
- Toso, J.P.; Oliveira, J.C.A.; Soares Maia, D.A.; Cornette, V.; Lopéz, R.H.; Azevedo, D.C.S.; Zgrablich, G. Effect of the pore geometry in the characterization of the pore size distribution of activated carbons. Adsorption 2013, 19, 601–609. [Google Scholar] [CrossRef]
- Toso, J.P.; Cornette, V.; Yelpo, V.A.; de Oliveira, J.C.A.; Azevedo, D.C.S.; Lopéz, R.H. Why the pore geometry model could affect the uniqueness of the PSD in ac characterization. Adsorption 2016, 22, 215–222. [Google Scholar] [CrossRef]
- Olivier, J.P. Improving the models used for calculating the size distribution of micropore volume of activated carbons from adsorption data. Carbon 1998, 36, 1469–1472. [Google Scholar] [CrossRef]
- Lueking, A.; Kim, H.-Y.; Jagiello, J.; Bancroft, K.; Johnson, J.K.; Cole, M. Tests of pore-size distributions deduced from inversion of simulated and real adsorption data. J. Low Temp. Phys. 2009, 157, 410–428. [Google Scholar] [CrossRef]
- Jagiello, J.; Olivier, J.P. A Simple two-dimensional NLDFT model of gas adsorption in finite carbon pores. application to pore structure analysis. J. Phys. Chem. C 2009, 113, 19382–19385. [Google Scholar] [CrossRef]
- Jagiello, J.; Olivier, J.P. 2D-NLDFT adsorption models for carbon slit-shaped pores with surface energetical heterogeneity and geometrical corrugation. Carbon 2013, 55, 70–80. [Google Scholar] [CrossRef]
- Neimark, A.V.; Lin, Y.; Ravikovitch, P.I.; Thommes, M. Quenched solid density functional theory and pore size analysis of micro-mesoporous carbons. Carbon 2009, 47, 1617–1628. [Google Scholar] [CrossRef]
- Ustinov, E.A.; Do, D.D. Application of Density Functional Theory to Analysis of energetic Heterogeneity and Pore Size Distribution of Activated Carbons. Langmuir 2004, 20, 3791–3797. [Google Scholar] [CrossRef]
- Maddox, M.W.; Olivier, J.P.; Gubbins, K.E. Characterization of MCM-41 using molecular simulation: Heterogeneity effects. Langmuir 1997, 13, 1737–1745. [Google Scholar] [CrossRef]
- Coasne, B.; Hung, F.R.; Pellenq, R.J.M.; Siperstein, F.R.; Gubbins, K.E. Adsorption of simple gases in MCM-41 materials: The role of surface roughness. Langmuir 2006, 22, 194–202. [Google Scholar] [CrossRef]
- Bandosz, T.J.; Biggs, M.J.; Gubbins, K.E.; Hattori, Y.; Iiyama, T.; Kaneko, K.; Pikunic, J.; Thomson, K.T. Molecular models of porous carbons. Chem. Phys. Carbon. 2003, 28, 41–228. [Google Scholar]
- Bakaev, V.A. Rumpled graphite basal plane as a model heterogeneous carbon surface. J. Chem. Phys. 1995, 102, 1398–1404. [Google Scholar] [CrossRef]
- Turner, A.R.; Quirke, N. A grand canonical Monte Carlo study of adsorption on graphitic surfaces with defects. Carbon 1998, 36, 1439–1446. [Google Scholar] [CrossRef]
- Do, D.D.; Do, H.D. Modeling of adsorption on nongraphitized carbon surface: GCMC simulation studies and comparison with experimental data. J. Phys. Chem. B 2006, 110, 17531–17538. [Google Scholar] [CrossRef]
- Ravikovitch, P.I.; Neimark, A.V. Density functional theory model of adsorption on amorphous and microporous silica materials. Langmuir 2006, 22, 11171–11179. [Google Scholar] [CrossRef]
- Pendleton, P.; Badalyan, A. Gas adsorption data uncertainty and propagation analyses. Adsorption 2005, 11, 61–66. [Google Scholar] [CrossRef]
- Lopez-Ramón, M.V.; Jagiello, J.; Bandosz, T.J.; Seaton, N.A. Determination of the pore size distribution and network connectivity in microporous solids by adsorption measurements and monte carlo simulation. Langmuir 1997, 13, 4435–4445. [Google Scholar] [CrossRef]
- Cai, Q.; Buts, A.; Seaton, N.A.; Biggs, M.J. A pore network model for diffusion in nanoporous carbons: Validation by molecular dynamics simulation. Chem. Eng. Sci. 2008, 63, 3319–3327. [Google Scholar] [CrossRef]
- Cai, Q.; Buts, A.; Biggs, M.J.; Seaton, N.A. Evaluation of methods for determining the pore size distribution and pore-network connectivity of porous carbons. Langmuir 2007, 23, 8430–8440. [Google Scholar] [CrossRef]
- Marsh, H.; Rodriguez-Reinoso, F. Activated Carbons, 1st ed.; Elsevier Science: North Shields, UK, 2006. [Google Scholar]
- Scaife, S.; Kluson, P.; Quirke, N. Characterization of porous materials by gas adsorption: Do different molecular probes give different pore structures. J. Phys. Chem. B 1999, 104, 313–318. [Google Scholar] [CrossRef]
- Sweatman, M.B.; Quirke, N. Characterization of porous materials by gas adsorption: Comparison of nitrogen at 77 K and carbon dioxide at 298 K for activated carbon. Langmuir 2001, 17, 5011–5020. [Google Scholar] [CrossRef]
- Ania, C.O.; Parra, J.B.; Rubiera, F.; Arenillas, A.; Pis, J.J. A comparison of characterization methods based on N2 and CO2 adsorption for the assessment of the pore size distribution of carbons. In Studies in Surface Science and Catalysis; Llewellyn, P.L., Rodríguez-Reinoso, F., Rouquerol, J., Seaton, N., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; Volume 160, pp. 319–326. [Google Scholar]
- Jagiello, J.; Bandosz, J.T.; Schwarz, J.A. Characterization of microporous carbons using adsorption at near ambient temperatures. Langmuir 1996, 12, 2837–2842. [Google Scholar] [CrossRef]
- Gauden, P.A.; Terzyk, A.P.; Rychlicki, G.; Kowalczyk, P.; . Cwiertnia, M.S.; Garbacz, J.K. Estimating the pore size distribution of activated carbons from adsorption data of different ad sorbates by various methods. J. Colloid. Interface Sci. 2004, 273, 39–63. [Google Scholar] [CrossRef] [PubMed]
- Sylwester, F.; Artur, P.T.; Piotr, A.G.; Peter, J.F.H.; Piotr, K. Can carbon surface oxidation shift the pore size distribution curve calculated from Ar, N2 and CO2 adsorption isotherms? simulation results for a realistic carbon model. J. Phys. Condens. Matter. 2009, 21, 315005. [Google Scholar]
- Kruk, M.; Jaroniec, M.; Choma, J. Critical discussion of simple adsorption methods used to evaluate the micropore size distribution. Adsorption 1997, 3, 209–219. [Google Scholar] [CrossRef]
- Kruk, M.; Jaroniec, M.; Choma, J. Comparative analysis of simple and advanced sorption methods for assessment of microporosity in activated carbons. Carbon 1998, 36, 1447–1458. [Google Scholar] [CrossRef]
- Valladares, D.L.; Rodríguez-Reinoso, F.; Zgrablich, G. Characterization of active carbons: The influence of the method in the determination of the pore size distribution. Carbon 1998, 36, 1491–1499. [Google Scholar] [CrossRef]
- Terzyk, A.P.; Furmaniak, S.; Harris, P.J.F.; Gauden, P.A.; Wloch, J.; Kowalczyk, P. How realistic is the pore size distribution calculated from adsorption isotherms if activated carbon is composed of fullerene-like fragments. Phys. Chem. Chem. Phys. 2007, 9, 5919–5927. [Google Scholar] [CrossRef]
- Davies, G.M.; Seaton, N.A. The effect of the choice of pore model on the characterization of the internal structure of microporous carbons using pore size distributions. Carbon 1998, 36, 1473–1490. [Google Scholar] [CrossRef]
- Wongkoblap, A.; Do, D.D. Characterization of cabot non-graphitized carbon blacks with a defective surface model: Adsorption of argon and nitrogen. Carbon 2007, 45, 1527–1534. [Google Scholar] [CrossRef]
- Biggs, M.J. Virtual porous carbons: What they are and what they can be used for. J. Mol. Simul. 2006, 32, 579–593. [Google Scholar] [CrossRef]
- Fonseca-Correa, R.A.; Giraldo, L.; Moreno-Piraján, J.C. Comparison of PSD of carbon aerogels obtained by QSDFT and immersion calorimetry at different resorcinol/catalyst ratio. Microporous Mesoporouse Mater. 2017, 248, 164–172. [Google Scholar] [CrossRef]
- Guerrero-Fajardo, C.A.; Giraldo, L.; Moreno-Piraján, J.C. Preparation and Characterization of Graphene Oxide for Pb(II) and Zn(II) Ions Adsorption from Aqueous Solution: Experimental, Thermodynamic and Kinetic Study. Nanomaterials 2020, 10, 1022. [Google Scholar] [CrossRef]
- Hummers, W.S.; Offeman, R.E. Preparation of graphite oxide. J. Am. Chem. Soc. 1958, 80, 1339. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Molecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Dubinin, M.M. Generalization of the theory of volume filling of micropores to nonhomogeneous microporous structures. Carbon 1985, 23, 373–380. [Google Scholar] [CrossRef]
- Carrott, P.J.M.; Ribeiro Carrott, M.M.L. Suhas Comparison of the Dubinin-Radushkevich and quenched solid density functional theory approaches for the characterisation of narrow microporosity in activated carbons obtained by chemical activation with KOH or NaOH of Kraft and hydrolytic lignins. Carbon 2010, 48, 4162–4169. [Google Scholar] [CrossRef]
- Stoeckli, F.; Guillot, A.; Slasli, A.M.; Hugi-Cleary, D. Microporosity in carbon blacks. Carbon 2002, 40, 211–215. [Google Scholar] [CrossRef]
- Stoeckli, F.; Slasli, A.; Hugi-Cleary, D.; Guillot, A. The characterization of microporosity in carbons with molecular sieve effects. Microporous Mesoporous Mater. 2002, 51, 197–202. [Google Scholar] [CrossRef]
- Stoeckli, H.F.; Rebstein, P.; Ballerini, L. On the assessment of microporosity in active carbons, a comparison of theoretical and experimental data. Carbon 1990, 28, 907–909. [Google Scholar] [CrossRef]
- Gregg, S.J.; Sing, K.S.W. Adsorption Surface Area and Porosity; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Seifi, A.; Bahramian, A.R.; Sharif, A. Correlation between structure and oxidation behavior of carbon aerogels. J. Energy Storage 2016, 7, 195–203. [Google Scholar] [CrossRef]
- Thommes, M.; Cychosz, K.A.; Neimark, A.V. Advanced Physical Adsorption Characterization of Nanoporous Carbons. In Novel Carbon Adsorbents; Tascón, D., Ed.; Elsevier: Amsterdam, The Netherlands, 2012; pp. 107–145. [Google Scholar]
- Boehm, H.P. Chemical identification of surface groups. In Advances in Catalysis; Eley, D.D., Herman, P., Weisz, P.B., Eds.; Academic Press: New York, NY, USA, 1966; Volume 16, pp. 179–274. [Google Scholar]
- Goertzen, S.L.; Thériault, K.D.; Oickle, A.M.; Tarasuk, A.C.; Andreas, H.A. Standardization of the Boehm titration. Part, I. CO2 expulsion and endpoint determination. Carbon 2010, 48, 1252–1261. [Google Scholar] [CrossRef]
- Giraldo, L.; Huertas, J.I.; Valencia, A.; Moreno-Piraján, J.C. Heat conduction microcalorimeter for the determination of the immersion heats of activated carbon into phenol aqueous solution. Instrum. Sci. Technol. 2003, 31, 385–397. [Google Scholar] [CrossRef]
- Moreno, J.C.; Giraldo, L.; Goméz, A. A batch-type heat conduction microcalorimeter for immersion heat determinations: Design, calibration and applications. Thermochim. Act. 1997, 290, 1–12. [Google Scholar] [CrossRef]
- Moreno-Piraján, J.C.; Giraldo, L. Determination of the Immersion Enthalpy of activated carbon by microcalorimetry of the heat conduction. Ins. Sci. Tech. 2000, 28, 171–178. [Google Scholar] [CrossRef]
- Gutmann, V. Solvent effects on the reactivities of organometallic compounds. Coord Chem Rev. 1976, 18, 225–255. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S.W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef]


| Solvent | CAS No. | Source | Initial a Purity | Purification Method | pKa |
|---|---|---|---|---|---|
| Benzene | 71-43-2 | Sigma Aldrich | ≥99.9% | HPLC | 43 |
| Dichloromethane | 75-09-2 | Sigma Aldrich | ≥99.9% | HPLC | - |
| Hexane | 110-54-3 | Sigma Aldrich | ≥97.0% | HPLC | 50 |
| Acetonitrile | 75-05-8 | Sigma Aldrich | ≥99.9% | HPLC | 25 |
| Triethylamine | 121-44-8 | Sigma Aldrich | ≥99.5% | GC | 10.8 |
| Water | 7732-18-5 | Sigma Aldrich | Water plus | supplier | 15.7 |
| Ethanol | 64-17-5 | Sigma Aldrich | 95% | supplier | 16 |
| Propanol | 71-31-8 | Sigma Aldrich | 99.7% | supplier | 16.1 |
| i-Propanol | 67-63-0 | Sigma Aldrich | 95.0% | supplier | 17.1 |
| Cyclohexane | 110-82-7 | Sigma Aldrich | 95.0% | supplier | 45 |
| Carbon Tetrachloride | 56-23-5 | Sigma Aldrich | 99.9% | supplier | - |
| t-Butanol | 75-65-0 | Sigma Aldrich | ≥99.5% | HPLC | 19.20 |
| p-Xylene | 106-42-3 | Sigma Aldrich | ≥99.0% | GC | 15 |
| 1,3,5-trimethylbenzene | 108-67-8 | Sigma Aldrich | 95.0% | supplier | 14 |
| Tri-2,4-xylyphosphate | 31570-04-4 | Sigma Aldrich | 98.0% | supplier | - |
| Samples | SBET [m2 g−1] | DR (P/Po < 0.1) | DFT (P/Po 10−7) | ||||
|---|---|---|---|---|---|---|---|
| Vmic [cm3 g−1] | Eo [kJ mol−1] | n | Pore Radius [Å] | Vp [cm3 g−1] | Half Pore Width [nm] | ||
| Graphite (Gr) | 5.2 | 0.010 | 7.250 | 3.4 | 7.4 | 0.04 | 7.80 |
| Graphene (GO) | 47.5 | 0.154 | 18.60 | 5.4 | 9.3 | 0.18 | 8.75 |
| NLDFT | QSDFT | |||||
|---|---|---|---|---|---|---|
| Sample | Fitting Error (slit pore) [%] | Fitting Error (cyl. pore) [%] | Fitting Error (cyl.-slit) [%] | Fitting Error (slit pore) [%] | Fitting Error (cyl. pore) [%] | Fitting Error (cyl.-silt) [%] |
| Graphite (Gr) | 5.296 | 6.819 | 6.819 | 4.364 | 7.510 | 7.910 |
| Graphene Ox. (GO) | 2.345 | 3.576 | 4.765 | 1.354 | 2.546 | 3.087 |
| Groups | Lactonic μmol g−1 | Carboxylic μmol g−1 | Phenolic μmol g−1 | Carbonyl μmol g−1 | Total Acidity μmol g−1 | Total Basicity μmol g−1 | Total Groups μmol g−1 | |
|---|---|---|---|---|---|---|---|---|
| Samples | ||||||||
| Gr | 0.000 * | 0.000 * | 0.000 * | 0.000 * | 0.000 * | 0.000 * | 0.000 * | |
| GO | 1.282 ± 0.003 | 0.626 ± 0.005 | 0.023 ± 0.0001 | 0.025 ± 0.004 | 3.564 ± 0.007 | 1.639 ± 0.006 | 5.203 ± 0.008 | |
| Solvent | Molecular Size (nm) | Gutmann Number (kcal/mol) | Structure | Dipole Moment | Dielectric Constant |
|---|---|---|---|---|---|
| Benzene | 0.585 | 0.1 |  | 0 | 2.28 |
| Dichloromethane | 0.334 | 1 |  | 1.58 | 9.1 |
| Hexane | 0.492 | 0 |  | 0 | 2.0 |
| Acetonitrile | 0.272 | 14.1 |  | 3.84 | 37 |
| Triethylamine | 0.770 | 61 |  | 1.60 | 2.42 |
| Water | 0.293 | 18 |  | 1.85 | 80.1 |
| Ethanol | 0.450 | 19.2 |  | 1.77 | 24.5 |
| Propanol | 0.490 | 19.8 |  | 1.68 | |
| i-Propanol | 0.472 | 21.1 |  | 1.56 | 17.9 |
| Cyclohexane | 0.482 | 0.0 |  | 0 | 2.02 |
| Carbon Tetrachloride | 0.595 | 0.0 |  | 0 | 2.24 |
| t-Butanol | 0.605 | 38.0 |  | 1.70 | 15.8 |
| p-Xylene | 0.665 | 5.0 |  | 0.02 | 2.27 |
| 1,3,5-trimethylbenzene | 0.862 | 10.0 |  | 0.10 | 2.40 |
| Tri-2,4-xylyphosphate | 1.50 | 25.0 | 1.5 | 25.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerrero-Fajardo, C.A.; Giraldo, L.; Moreno-Piraján, J.C. Graphene Oxide: Study of Pore Size Distribution and Surface Chemistry Using Immersion Calorimetry. Nanomaterials 2020, 10, 1492. https://doi.org/10.3390/nano10081492
Guerrero-Fajardo CA, Giraldo L, Moreno-Piraján JC. Graphene Oxide: Study of Pore Size Distribution and Surface Chemistry Using Immersion Calorimetry. Nanomaterials. 2020; 10(8):1492. https://doi.org/10.3390/nano10081492
Chicago/Turabian StyleGuerrero-Fajardo, Carlos A., Liliana Giraldo, and Juan Carlos Moreno-Piraján. 2020. "Graphene Oxide: Study of Pore Size Distribution and Surface Chemistry Using Immersion Calorimetry" Nanomaterials 10, no. 8: 1492. https://doi.org/10.3390/nano10081492
APA StyleGuerrero-Fajardo, C. A., Giraldo, L., & Moreno-Piraján, J. C. (2020). Graphene Oxide: Study of Pore Size Distribution and Surface Chemistry Using Immersion Calorimetry. Nanomaterials, 10(8), 1492. https://doi.org/10.3390/nano10081492






