Quantum Interference and Nonequilibrium Josephson Currents in Molecular Andreev Interferometers
Abstract
1. Introduction
2. Results
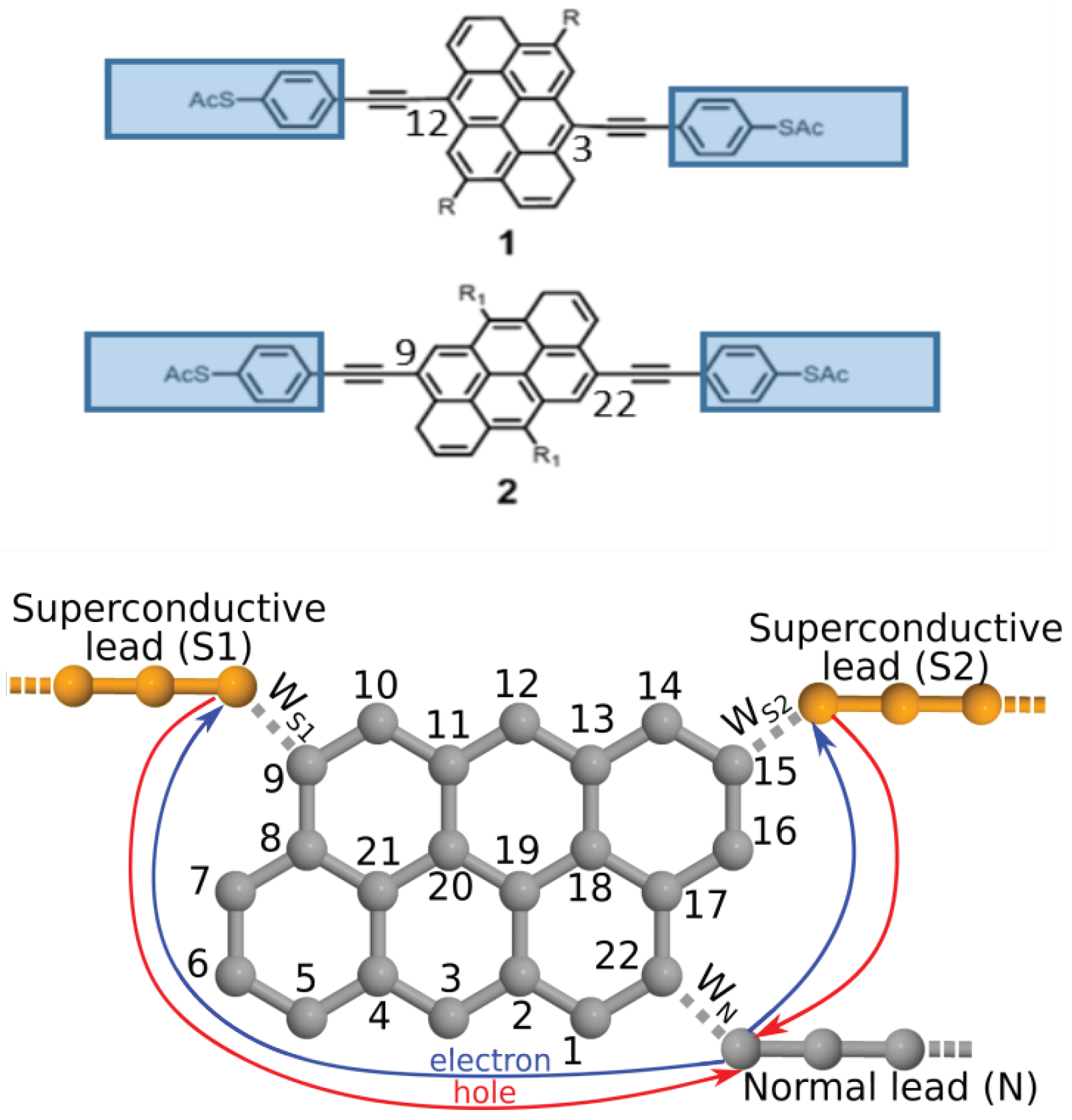
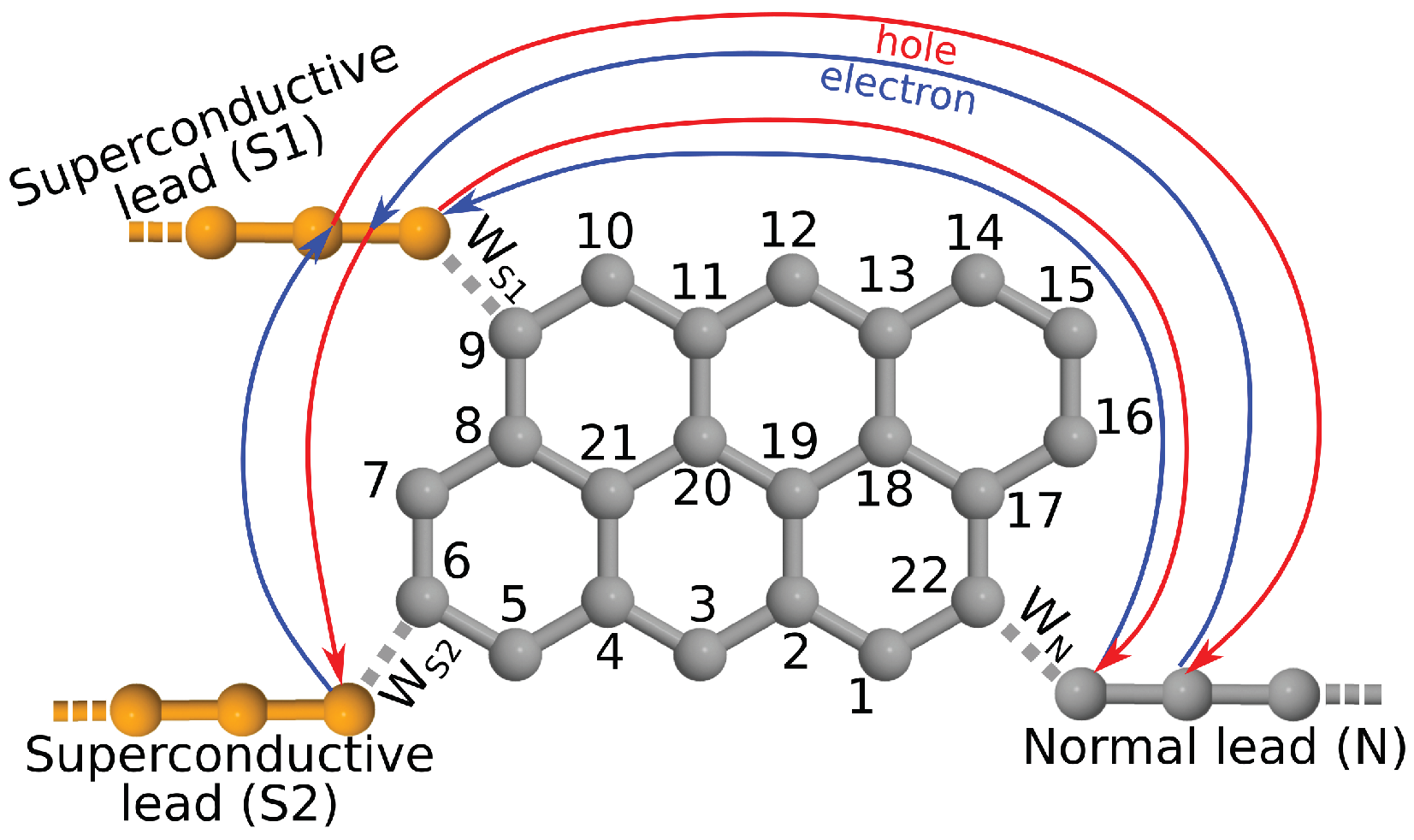
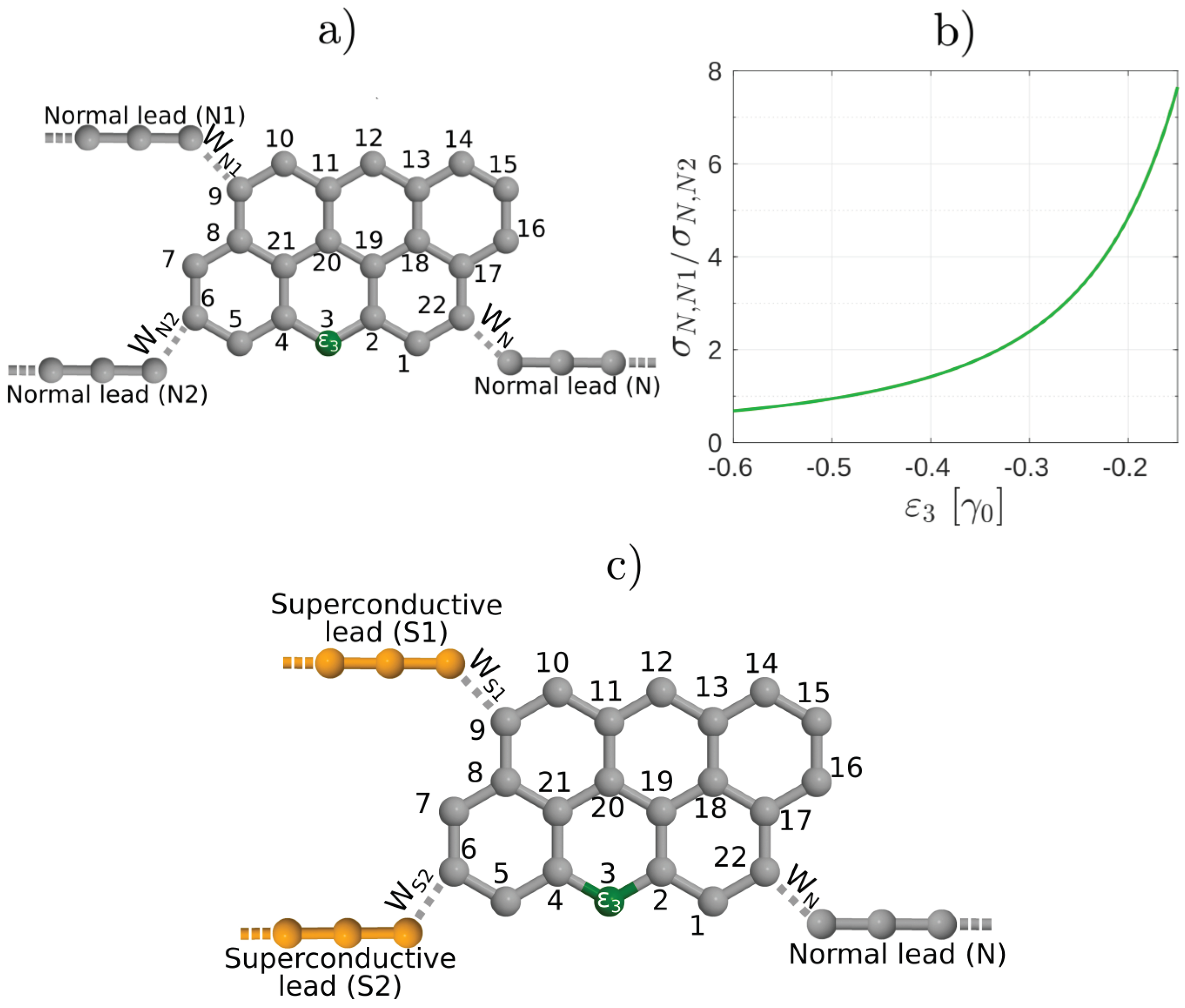
2.1. Theoretical Background: Equilibrium Molecular Andreev Interferometers
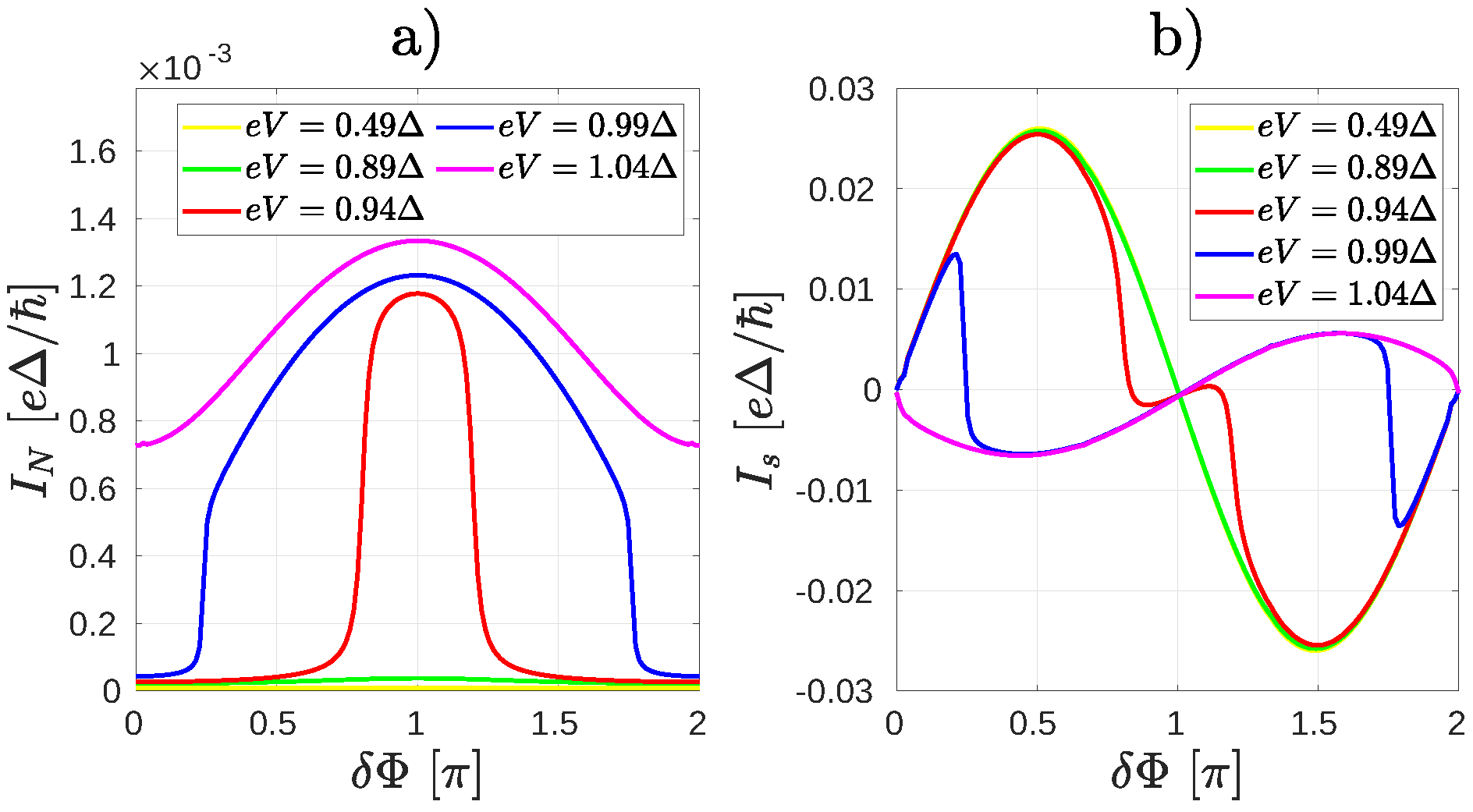
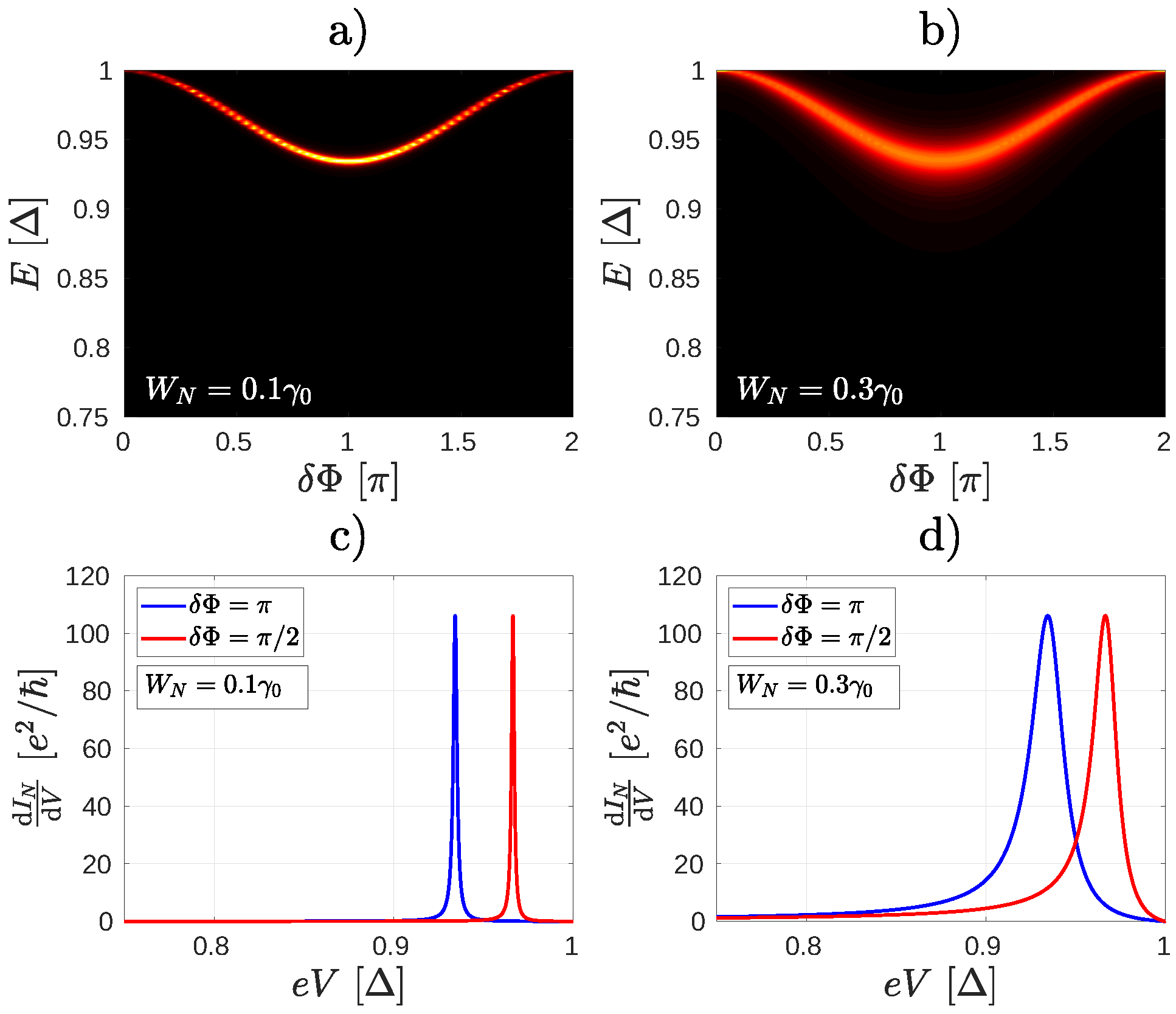
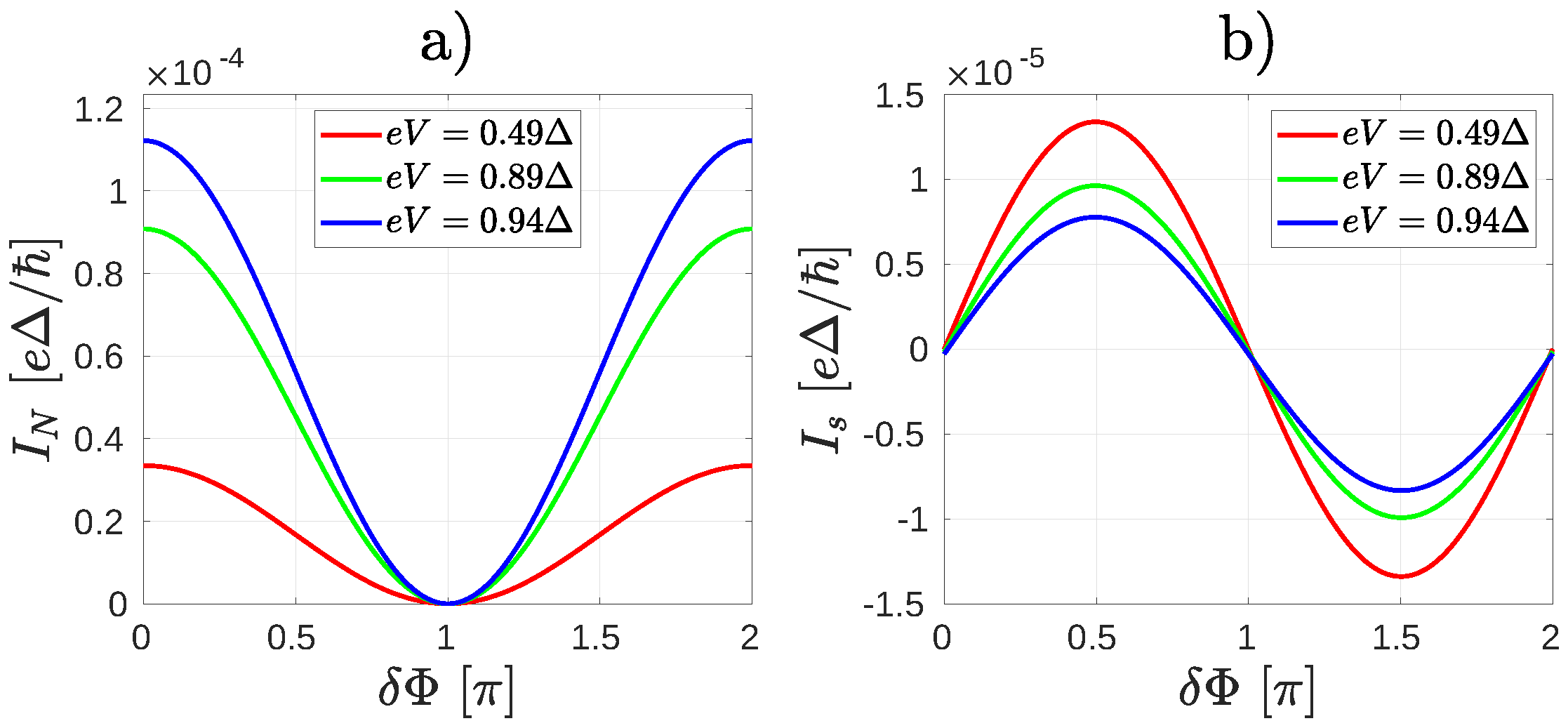
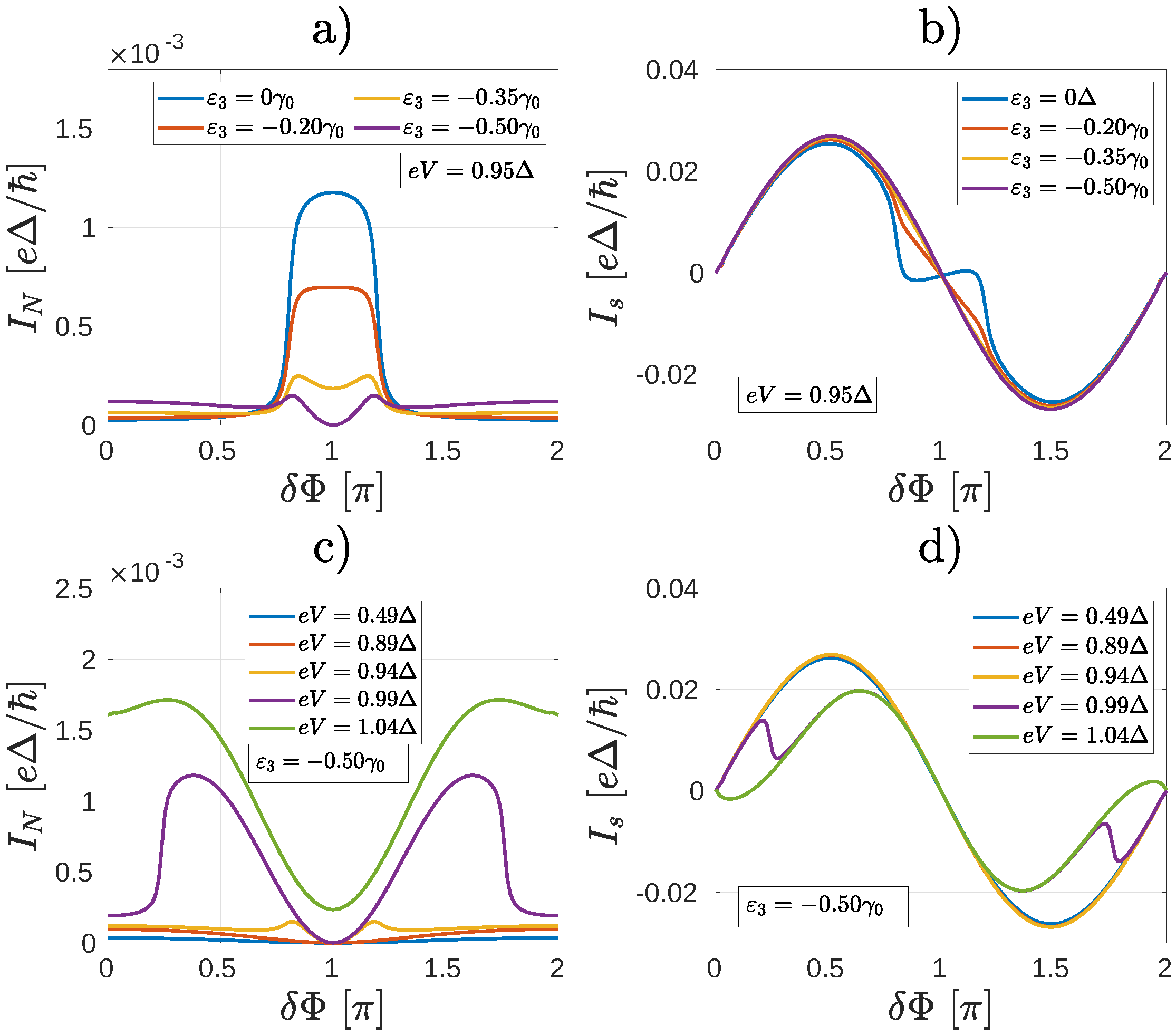
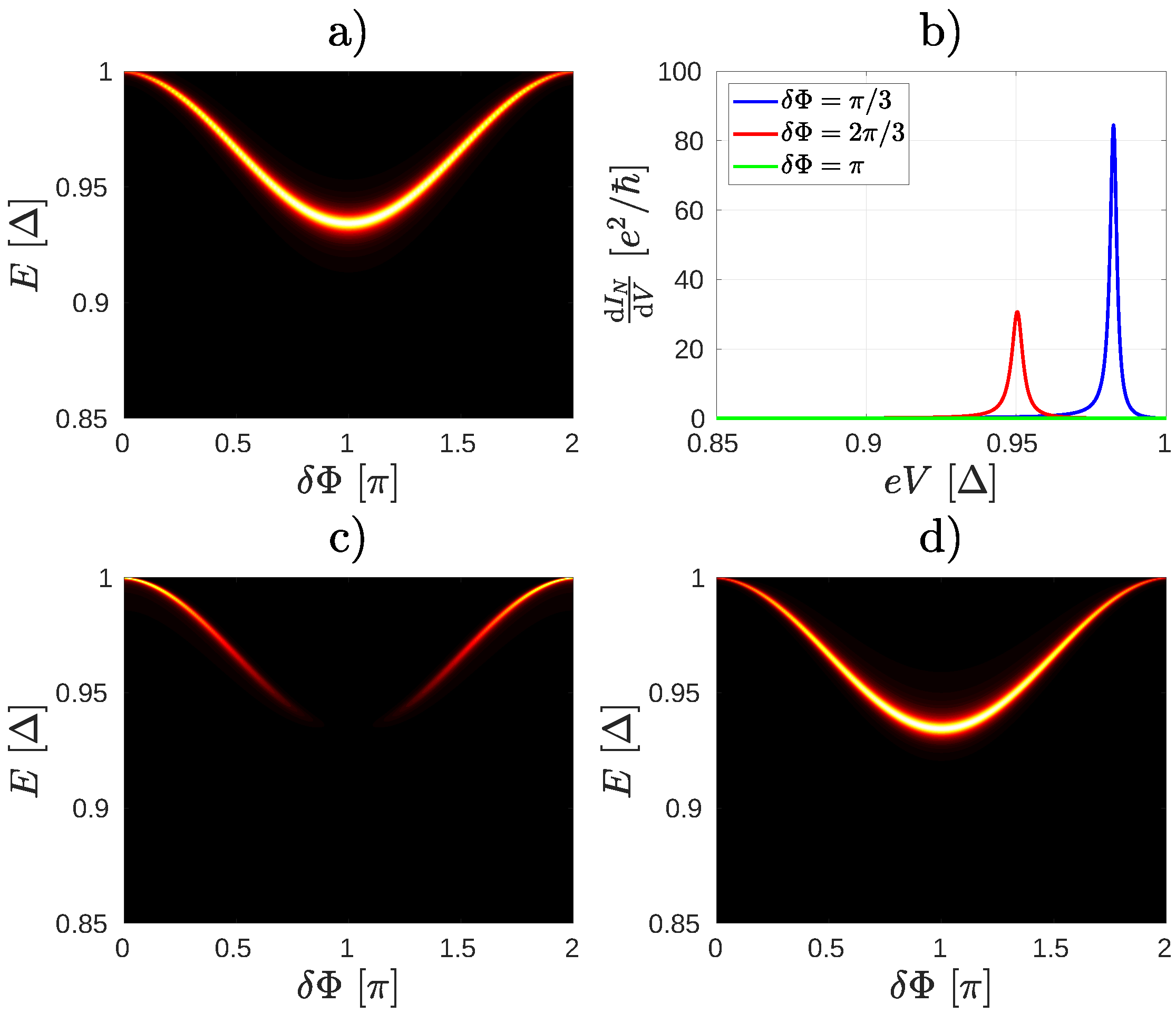
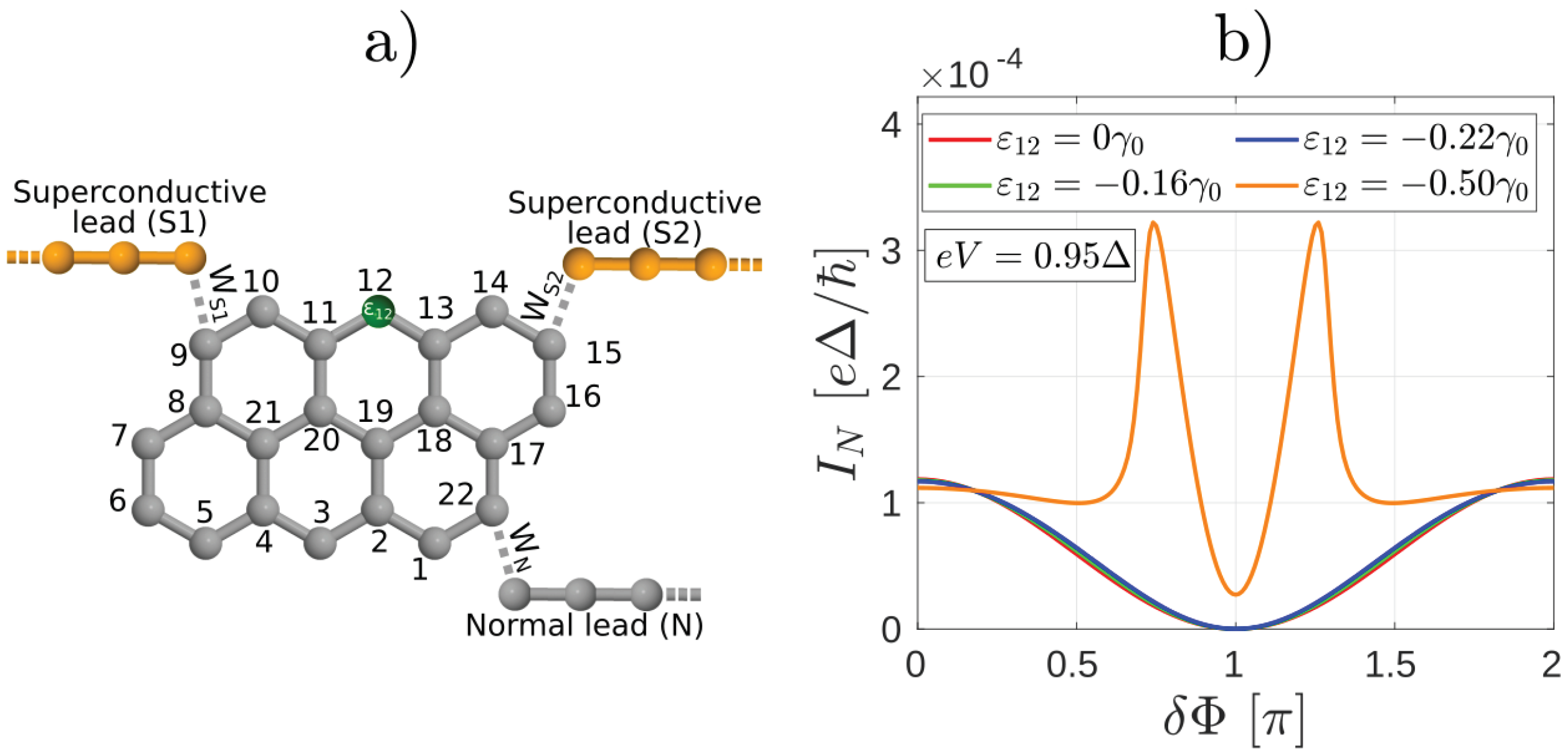
2.2. Non-Equilibrium Numerical Calculations
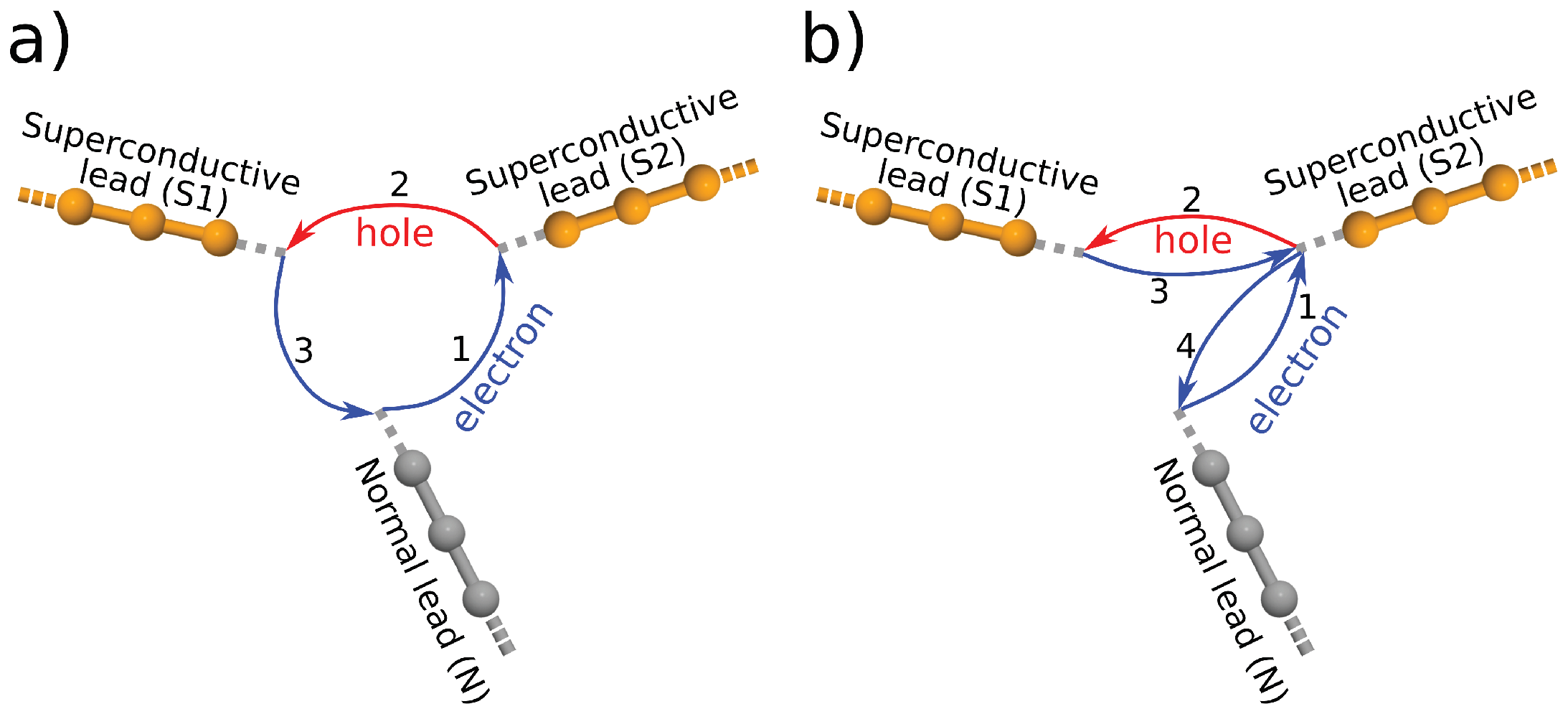
2.3. Non-Equilibrium Molecular Andreev Interferometers
3. Conclusions
Supplementary Materials
Supplementary File 1Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ABS | Andreev Bound States |
| CQI | Constructive Quantum interference |
| DQI | Destructive Quantum interference |
| LDOS | Local density of states |
| PAH | polyaromatic hydrocarbons |
| QI | Quantum interference |
| SQUID | Superconducting quantum interference device |
Appendix A. The Tight-Binding Model of the Molecular Junctions
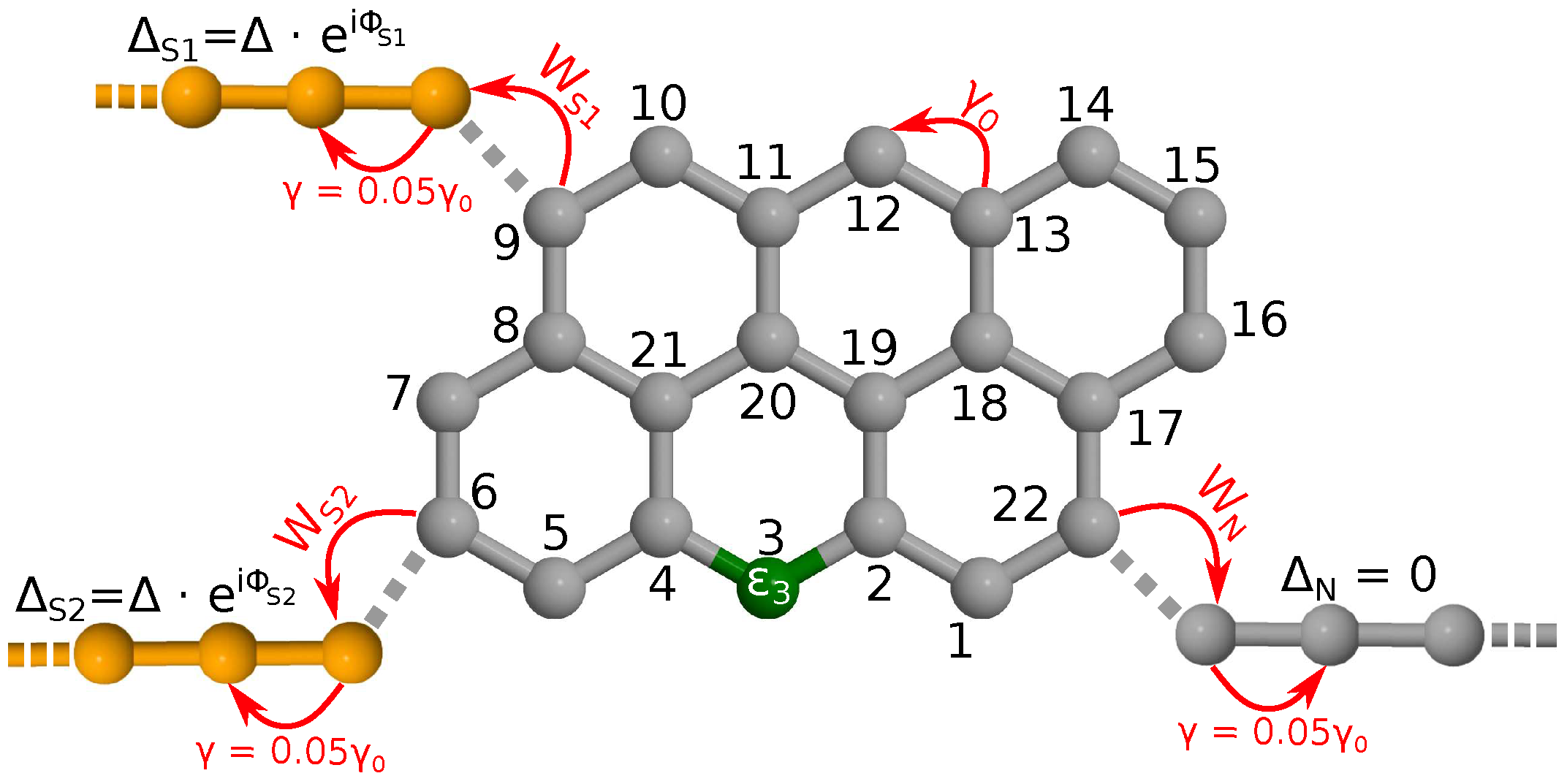
Appendix B. Theoretical Background to Calculate the Differential Conductance
Resonant Oscillation
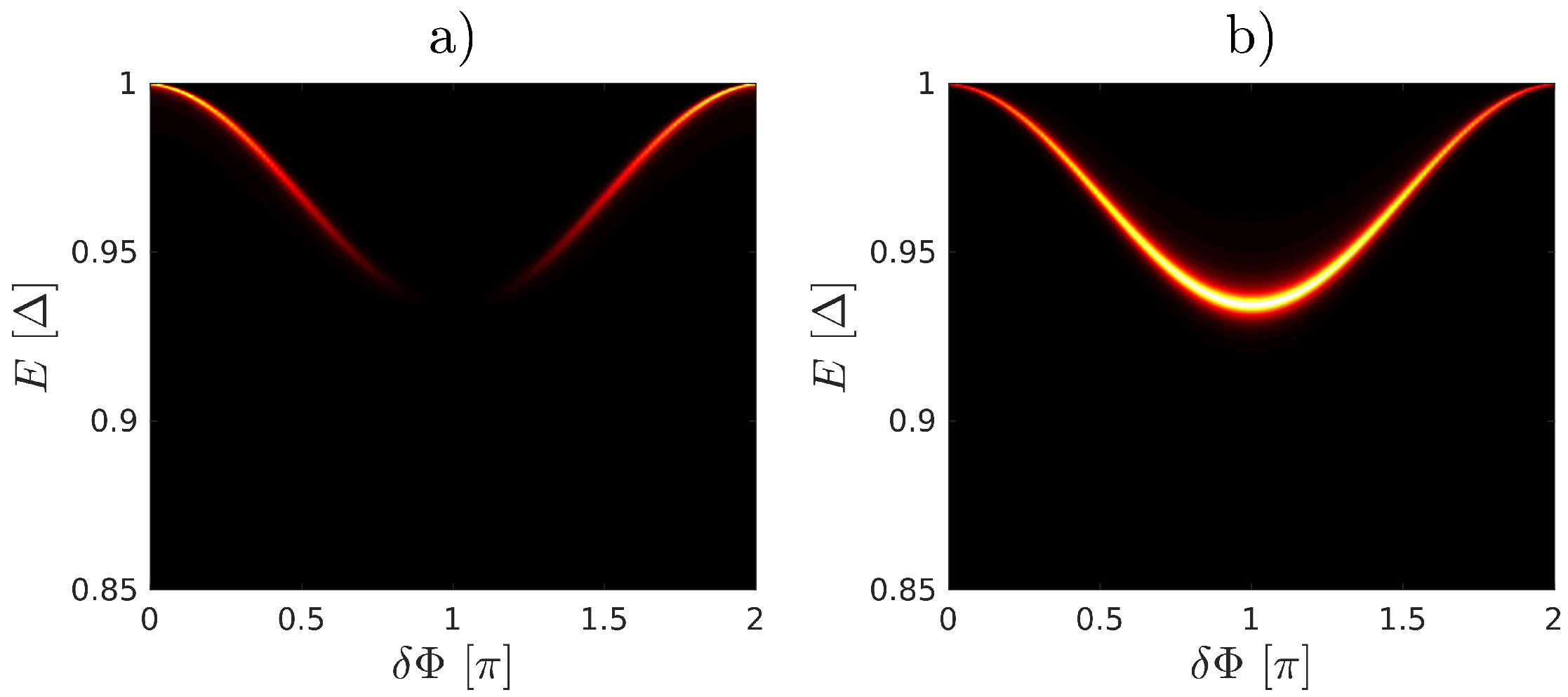
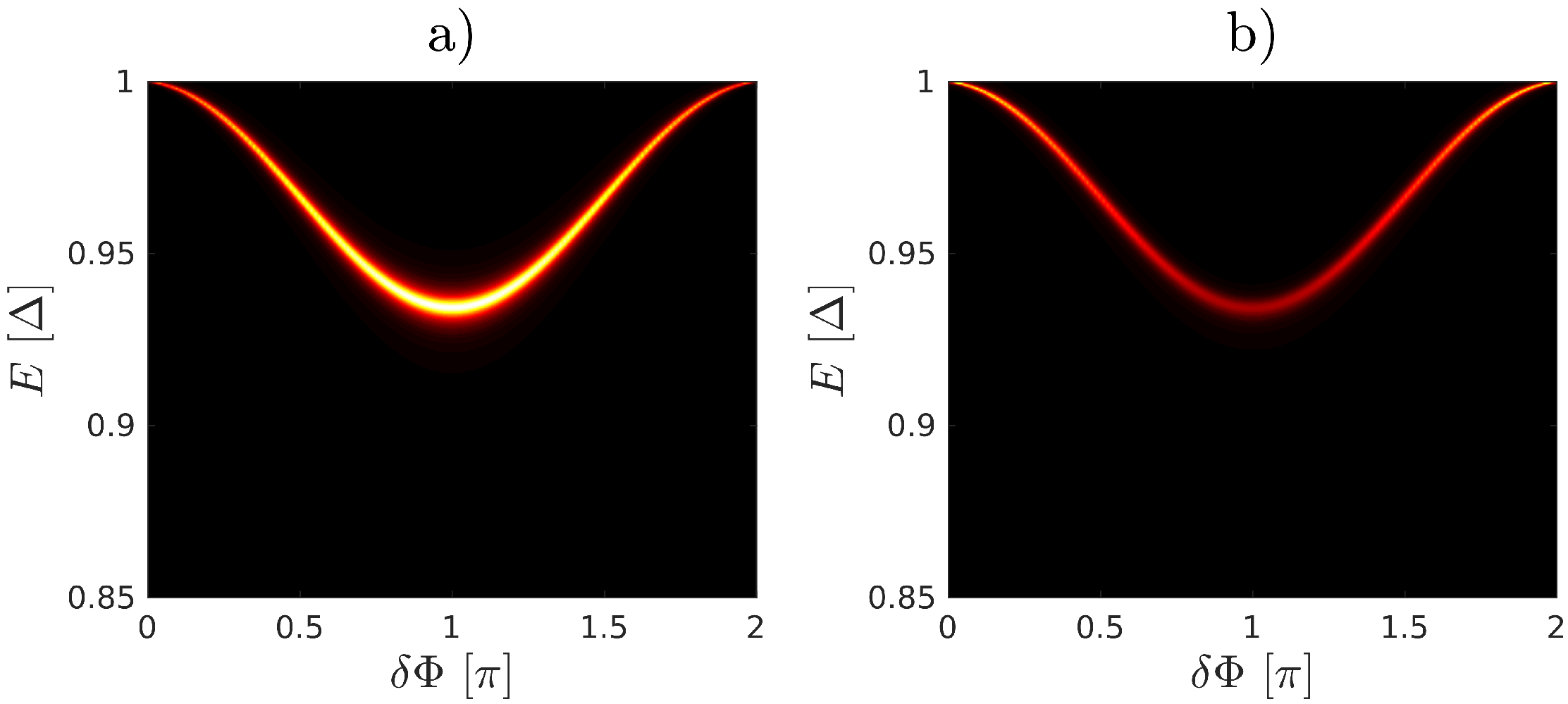
Appendix C. Density of States
Appendix D. Comparison of the Local Density of States on Two Molecular Sites
References
- Cuevas, J.C.; Scheer, E. Molecular Electronics, 2nd ed.; World Scientific: Singapore, 2017. [Google Scholar] [CrossRef]
- Ratner, M. A brief history of molecular electronics. Nat. Nanotechnol. 2013, 8, 378–381. [Google Scholar] [CrossRef] [PubMed]
- Tsutsui, M.; Taniguchi, M. Single Molecule Electronics and Devices. Sensors 2012, 12, 7259–7298. [Google Scholar] [CrossRef] [PubMed]
- Lörtscher, E. Wiring molecules into circuits. Nat. Nanotechnol. 2013, 8, 381–384. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Diaz-Fernandez, Y.A.; Gschneidtner, T.A.; Westerlund, F.; Lara-Avila, S.; Moth-Poulsen, K. Single-molecule electronics: From chemical design to functional devices. Chem. Soc. Rev. 2014, 43, 7378–7411. [Google Scholar] [CrossRef] [PubMed]
- Su, T.A.; Neupane, M.; Steigerwald, M.L.; Venkataraman, L.; Nuckolls, C. Chemical principles of single-molecule electronics. Nat. Rev. Mater. 2016, 1, 16002. [Google Scholar] [CrossRef]
- Xiang, D.; Wang, X.; Jia, C.; Lee, T.; Guo, X. Molecular-Scale Electronics: From Concept to Function. Chem. Rev. 2016, 116, 4318–4440. [Google Scholar] [CrossRef]
- Hybertsen, M.S.; Venkataraman, L. Structure-Property Relationships in Atomic-Scale Junctions: Histograms and Beyond. Accounts Chem. Res. 2016, 49, 452–460. [Google Scholar] [CrossRef]
- Gehring, P.; Thijssen, J.M.; van der Zant, H.S.J. Single-molecule quantum-transport phenomena in break junctions. Nat. Rev. Phys. 2019, 1, 381–396. [Google Scholar] [CrossRef]
- Liu, J.; Huang, X.; Wang, F.; Hong, W. Quantum Interference Effects in Charge Transport through Single-Molecule Junctions: Detection, Manipulation, and Application. Accounts Chem. Res. 2019, 52, 151–160. [Google Scholar] [CrossRef]
- Li, Y.; Yu, X.; Zhen, Y.; Dong, H.; Hu, W. Transmission mechanism and quantum interference in fused thienoacenes coupling to Au electrodes through the thiophene rings. Phys. Chem. Chem. Phys. 2019, 21, 16293–16301. [Google Scholar] [CrossRef]
- Sangtarash, S.; Huang, C.; Sadeghi, H.; Sorohhov, G.; Hauser, J.; Wandlowski, T.; Hong, W.; Decurtins, S.; Liu, S.X.; Lambert, C.J. Searching the Hearts of Graphene-like Molecules for Simplicity, Sensitivity, and Logic. J. Am. Chem. Soc. 2015, 137, 11425–11431. [Google Scholar] [CrossRef] [PubMed]
- Sangtarash, S.; Sadeghi, H.; Lambert, C.J. Exploring quantum interference in heteroatom-substituted graphene-like molecules. Nanoscale 2016, 8, 13199–13205. [Google Scholar] [CrossRef] [PubMed]
- Lambert, C.J. Quantum interference from superconducting islands in a mesoscopic solid. J. Phys. Condens. Matter 1993, 5, 707–716. [Google Scholar] [CrossRef]
- Hui, V.C.; Lambert, C.J. Andreev Scattering, Universal Conductance Fluctuations and Phase Periodic Transport. Europhys. Lett. (EPL) 1993, 23, 203–209. [Google Scholar] [CrossRef]
- Petrashov, V.T.; Chua, K.G.; Marshall, K.M.; Shaikhaidarov, R.S.; Nicholls, J.T. Andreev Probe of Persistent Current States in Superconducting Quantum Circuits. Phys. Rev. Lett. 2005, 95, 147001. [Google Scholar] [CrossRef]
- Amado, M.; Fornieri, A.; Biasiol, G.; Sorba, L.; Giazotto, F. A ballistic two-dimensional-electron-gas Andreev interferometer. Appl. Phys. Lett. 2014, 104, 242604. [Google Scholar] [CrossRef]
- Van Wees, B.J.; Lenssen, K.M.H.; Harmans, C.J.P.M. Transmission formalism for supercurrent flow in multiprobe superconductor-semiconductor-superconductor devices. Phys. Rev. B 1991, 44, 470–473. [Google Scholar] [CrossRef]
- Chang, L.F.; Bagwell, P.F. Control of Andreev-level occupation in a Josephson junction by a normal-metal probe. Phys. Rev. B 1997, 55, 12678–12690. [Google Scholar] [CrossRef]
- Baselmans, J.J.A.; Morpurgo, A.F.; van Wees, B.J.; Klapwijk, T.M. Reversing the direction of the supercurrent in a controllable Josephson junction. Nature 1999, 397, 43–45. [Google Scholar] [CrossRef]
- Baselmans, J.J.A.; Heikkilä, T.T.; van Wees, B.J.; Klapwijk, T.M. Direct Observation of the Transition from the Conventional Superconducting State to the π State in a Controllable Josephson Junction. Phys. Rev. Lett. 2002, 89, 207002. [Google Scholar] [CrossRef]
- Crosser, M.S.; Huang, J.; Pierre, F.; Virtanen, P.; Heikkilä, T.T.; Wilhelm, F.K.; Birge, N.O. Nonequilibrium transport in mesoscopic multi-terminal SNS Josephson junctions. Phys. Rev. B 2008, 77, 014528. [Google Scholar] [CrossRef]
- Geng, Y.; Sangtarash, S.; Huang, C.; Sadeghi, H.; Fu, Y.; Hong, W.; Wandlowski, T.; Decurtins, S.; Lambert, C.J.; Liu, S.X. Magic Ratios for Connectivity-Driven Electrical Conductance of Graphene-like Molecules. J. Am. Chem. Soc. 2015, 137, 4469–4476. [Google Scholar] [CrossRef] [PubMed]
- Winkelmann, C.B.; Roch, N.; Wernsdorfer, W.; Bouchiat, V.; Balestro, F. Superconductivity in a single-C60 transistor. Nat. Phys. 2009, 5, 876–879. [Google Scholar] [CrossRef]
- Bretheau, L.; Girit, Ç.Ö.; Pothier, H.; Esteve, D.; Urbina, C. Exciting Andreev pairs in a superconducting atomic contact. Nature 2013, 499, 312. [Google Scholar] [CrossRef]
- Weber, D.; Scheer, E. Superconducting properties of lithographic lead break junctions. Nanotechnology 2017, 29, 045703. [Google Scholar] [CrossRef]
- Island, J.O.; Gaudenzi, R.; de Bruijckere, J.; Burzurí, E.; Franco, C.; Mas-Torrent, M.; Rovira, C.; Veciana, J.; Klapwijk, T.M.; Aguado, R.; et al. Proximity-Induced Shiba States in a Molecular Junction. Phys. Rev. Lett. 2017, 118, 117001. [Google Scholar] [CrossRef]
- Kormányos, A.; Grace, I.; Lambert, C.J. Andreev reflection through Fano resonances in molecular wires. Phys. Rev. B 2009, 79, 075119. [Google Scholar] [CrossRef]
- Nappi, C.; Romeo, F.; Parlato, L.; Di Capua, F.; Aloisio, A.; Sarnelli, E. Quantum Interference in Single-Molecule Superconducting Field-Effect Transistors. J. Phys. Chem. C 2018, 122, 11498–11504. [Google Scholar] [CrossRef]
- Rakyta, P.; Alanazy, A.; Kormányos, A.; Tajkov, Z.; Kukucska, G.; Koltai, J.; Sangtarash, S.; Sadeghi, H.; Cserti, J.; Lambert, C.J. Magic Number Theory of Superconducting Proximity Effects and Wigner Delay Times in Graphene-Like Molecules. J. Phys. Chem. C 2019, 123, 6812–6822. [Google Scholar] [CrossRef]
- Lambert, C.J. Basic concepts of quantum interference and electron transport in single-molecule electronics. Chem. Soc. Rev. 2015, 44, 875–888. [Google Scholar] [CrossRef]
- Sadeghi, H.; Mol, J.A.; Lau, C.S.; Briggs, G.A.D.; Warner, J.; Lambert, C.J. Conductance enlargement in picoscale electroburnt graphene nanojunctions. Proc. Natl. Acad. Sci. USA 2015, 112, 2658–2663. [Google Scholar] [CrossRef] [PubMed]
- Sedghi, G.; García-Suárez, V.M.; Esdaile, L.J.; Anderson, H.L.; Lambert, C.J.; Martín, S.; Bethell, D.; Higgins, S.J.; Elliott, M.; Bennett, N.; et al. Long-range electron tunnelling in oligo-porphyrin molecular wires. Nat. Nanotechnol. 2011, 6, 517. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Huang, C.; Gulcur, M.; Batsanov, A.S.; Baghernejad, M.; Hong, W.; Bryce, M.R.; Wandlowski, T. Oligo(aryleneethynylene)s with Terminal Pyridyl Groups: Synthesis and Length Dependence of the Tunneling-to-Hopping Transition of Single-Molecule Conductances. Chem. Mater. 2013, 25, 4340–4347. [Google Scholar] [CrossRef]
- Papadopoulos, T.A.; Grace, I.M.; Lambert, C.J. Control of electron transport through Fano resonances in molecular wires. Phys. Rev. B 2006, 74, 193306. [Google Scholar] [CrossRef]
- Markussen, T.; Schiötz, J.; Thygesen, K.S. Electrochemical control of quantum interference in anthraquinone-based molecular switches. J. Chem. Phys. 2010, 132, 224104. [Google Scholar] [CrossRef]
- Vazquez, H.; Skouta, R.; Schneebeli, S.; Kamenetska, M.; Breslow, R.; Venkataraman, L.; Hybertsen, M.S. Probing the conductance superposition law in single-molecule circuits with parallel paths. Nat. Nanotechnol. 2012, 7, 663–667. [Google Scholar] [CrossRef]
- Ballmann, S.; Härtle, R.; Coto, P.B.; Elbing, M.; Mayor, M.; Bryce, M.R.; Thoss, M.; Weber, H.B. Experimental Evidence for Quantum Interference and Vibrationally Induced Decoherence in Single-Molecule Junctions. Phys. Rev. Lett. 2012, 109, 056801. [Google Scholar] [CrossRef]
- Aradhya, S.V.; Meisner, J.S.; Krikorian, M.; Ahn, S.; Parameswaran, R.; Steigerwald, M.L.; Nuckolls, C.; Venkataraman, L. Dissecting Contact Mechanics from Quantum Interference in Single-Molecule Junctions of Stilbene Derivatives. Nano Lett. 2012, 12, 1643–1647. [Google Scholar] [CrossRef]
- Arroyo, C.R.; Tarkuc, S.; Frisenda, R.; Seldenthuis, J.S.; Woerde, C.H.M.; Eelkema, R.; Grozema, F.C.; van der Zant, H.S.J. Signatures of Quantum Interference Effects on Charge Transport Through a Single Benzene Ring. Angew. Chem. Int. Ed. 2013, 52, 3152–3155. [Google Scholar] [CrossRef]
- Guedon, C.M.; Valkenier, H.; Markussen, T.; Thygesen, K.S.; Hummelen, J.C.; van der Molen, S.J. Observation of quantum interference in molecular charge transport. Nat. Nanotechnol. 2012, 7, 305–309. [Google Scholar] [CrossRef]
- Manrique, D.Z.; Huang, C.; Baghernejad, M.; Zhao, X.; Al-Owaedi, O.A.; Sadeghi, H.; Kaliginedi, V.; Hong, W.; Gulcur, M.; Wandlowski, T.; et al. A quantum circuit rule for interference effects in single-molecule electrical junctions. Nat. Commun. 2015, 6, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Famili, M.; Jia, C.; Liu, X.; Wang, P.; Grace, I.M.; Guo, J.; Liu, Y.; Feng, Z.; Wang, Y.; Zhao, Z.; et al. Self-Assembled Molecular-Electronic Films Controlled by Room Temperature Quantum Interference. Chem 2019, 5, 474–484. [Google Scholar] [CrossRef]
- Della Rocca, M.L.; Chauvin, M.; Huard, B.; Pothier, H.; Esteve, D.; Urbina, C. Measurement of the Current-Phase Relation of Superconducting Atomic Contacts. Phys. Rev. Lett. 2007, 99, 127005. [Google Scholar] [CrossRef] [PubMed]
- Nanda, G.; Aguilera-Servin, J.L.; Rakyta, P.; Kormányos, A.; Kleiner, R.; Koelle, D.; Watanabe, K.; Taniguchi, T.; Vandersypen, L.M.K.; Goswami, S. Current-Phase Relation of Ballistic Graphene Josephson Junctions. Nano Lett. 2017, 17, 3396–3401. [Google Scholar] [CrossRef] [PubMed]
- Andreev, A.F. The Thermal Conductivity of the Intermediate State in Superconductors. Zh. Eksp. Teor. Fiz. 1964, 46, 1823–1828. [Google Scholar]
- Bagwell, P.F. Suppression of the Josephson current through a narrow, mesoscopic, semiconductor channel by a single impurity. Phys. Rev. B 1992, 46, 12573–12586. [Google Scholar] [CrossRef] [PubMed]
- Cresti, A.; Farchioni, R.; Grosso, G.; Parravicini, G.P. Keldysh-Green function formalism for current profiles in mesoscopic systems. Phys. Rev. B 2003, 68, 075306. [Google Scholar] [CrossRef]
- Do, V.N. Non-equilibrium Green function method: Theory and application in simulation of nanometer electronic devices. Adv. Nat. Sci. Nanosci. Nanotechnol. 2014, 5, 033001. [Google Scholar] [CrossRef]
- Pala, M.G.; Governale, M.; König, J. Nonequilibrium Josephson and Andreev current through interacting quantum dots. New J. Phys. 2007, 9, 278. [Google Scholar] [CrossRef]
- Eötvös Quantum Utilities Software Package. Available online: http://eqt.elte.hu/EQuUs/html/ (accessed on 2 May 2020).
- Claughton, N.R.; Leadbeater, M.; Lambert, C.J. Theory of Andreev resonances in quantum dots. J. Phys. Condens. Matter 1995, 7, 8757–8784. [Google Scholar] [CrossRef]
- Russo, S.; Kroug, M.; Klapwijk, T.M.; Morpurgo, A.F. Experimental Observation of Bias-Dependent Nonlocal Andreev Reflection. Phys. Rev. Lett. 2005, 95, 027002. [Google Scholar] [CrossRef] [PubMed]
- Hofstetter, L.; Csonka, S.; Nygård, J.; Schönenberger, C. Cooper pair splitter realized in a two-quantum-dot Y-junction. Nature 2009, 461, 960–963. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, L.G.; Portier, F.; Roche, P.; Yeyati, A.L.; Kontos, T.; Strunk, C. Carbon Nanotubes as Cooper-Pair Beam Splitters. Phys. Rev. Lett. 2010, 104, 026801. [Google Scholar] [CrossRef] [PubMed]
- Hofstetter, L.; Csonka, S.; Baumgartner, A.; Fülöp, G.; d’Hollosy, S.; Nygård, J.; Schönenberger, C. Finite-Bias Cooper Pair Splitting. Phys. Rev. Lett. 2011, 107, 136801. [Google Scholar] [CrossRef]
- Cayssol, J. Crossed Andreev Reflection in a Graphene Bipolar Transistor. Phys. Rev. Lett. 2008, 100, 147001. [Google Scholar] [CrossRef]
- Chen, W.; Shen, R.; Sheng, L.; Wang, B.G.; Xing, D.Y. Resonant nonlocal Andreev reflection in a narrow quantum spin Hall system. Phys. Rev. B 2011, 84, 115420. [Google Scholar] [CrossRef]
- Schroer, A.; Silvestrov, P.G.; Recher, P. Valley-based Cooper pair splitting via topologically confined channels in bilayer graphene. Phys. Rev. B 2015, 92, 241404. [Google Scholar] [CrossRef]
- Bolech, C.J.; Giamarchi, T. Keldysh study of point-contact tunneling between superconductors. Phys. Rev. B 2005, 71, 024517. [Google Scholar] [CrossRef]
- Wu, S.T.; Yip, S. ac Josephson effect in asymmetric superconducting quantum point contacts. Phys. Rev. B 2004, 70, 104511. [Google Scholar] [CrossRef]
- Rungger, I.; Sanvito, S. Algorithm for the construction of self-energies for electronic transport calculations based on singularity elimination and singular value decomposition. Phys. Rev. B 2008, 78, 035407. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plaszkó, N.L.; Rakyta, P.; Cserti, J.; Kormányos, A.; Lambert, C.J. Quantum Interference and Nonequilibrium Josephson Currents in Molecular Andreev Interferometers. Nanomaterials 2020, 10, 1033. https://doi.org/10.3390/nano10061033
Plaszkó NL, Rakyta P, Cserti J, Kormányos A, Lambert CJ. Quantum Interference and Nonequilibrium Josephson Currents in Molecular Andreev Interferometers. Nanomaterials. 2020; 10(6):1033. https://doi.org/10.3390/nano10061033
Chicago/Turabian StylePlaszkó, Noel L., Peter Rakyta, József Cserti, Andor Kormányos, and Colin J. Lambert. 2020. "Quantum Interference and Nonequilibrium Josephson Currents in Molecular Andreev Interferometers" Nanomaterials 10, no. 6: 1033. https://doi.org/10.3390/nano10061033
APA StylePlaszkó, N. L., Rakyta, P., Cserti, J., Kormányos, A., & Lambert, C. J. (2020). Quantum Interference and Nonequilibrium Josephson Currents in Molecular Andreev Interferometers. Nanomaterials, 10(6), 1033. https://doi.org/10.3390/nano10061033




