3.1. Homogeneous Nanowire Networks
The resistance and Seebeck coefficient of homogeneous NW networks were measured for
10–320 K.
Table 1 provides the Seebeck coefficients of homogeneous NW networks made of several metals and alloys at RT. Both n-type and p-type thermoelectric NW networks with large absolute thermopower values were obtained. The results are consistent with reported bulk Seebeck coefficients [
23,
24,
25,
26]. Moreover, the value reported for the Co
Ni
NW network is also consistent with the ones reported for parallel arrays of NiCo NWs [
27,
28]. The resistivity of the homogeneous NW networks were estimated assuming that the Matthiesen’s rule holds for the different metallic NW networks. In that case, the resistivity at RT is given by
, where
is the resistivity of the FM that composes the NWs at RT due to thermally excited scatterings and
is the residual resistivity of the NWs due to impurities along with surface scattering within the NW network and internal grain-boundary scattering. For NW diameter not too small (
40 nm), the thermally induced scattering effects are independent on the sample dimensions, nanostructuration and defect concentration [
29]. Therefore,
can be taken as the ideal resistivity values at RT reported for bulk materials in the literature (from refs. [
30,
31,
32,
33]). Moreover, because the resistivity due to thermally excited scatterings tends to 0 at low temperatures, the resistivity at 10 K of the NW networks can be approximated to
. Finally, using the residual resistivity ratio
, the RT resistivity of the NWs can be estimated as
. The calculated resistivity are provided in
Table 1. Slightly larger resistivity compared to the bulk materials have been obtained, as expected for electrodeposited nanostructured materials. Indeed, electrodeposited materials display a relatively large amount of defects, leading to defect scattering into the NWs, while the NW transverse nanoscale dimensions lead to surface scattering effect. This engenders larger residual resistivity of the NW networks compared to bulk materials.
Table 1 also provides the power factors PF
together with the figure of merit
for the NW networks at RT. Due to the slightly larger electrical resistivity of the NW networks compared to bulk materials, slightly lower PF values have been found with respect to the bulk values. However, the PF values obtained are similar an even larger than to that of widely used thermoelectric material bismuth-telluride (in the range 1–6 mW/K
m) and at least one order of magnitude larger than the ones reported for flexible thermoelectric films based on optimized conducting polymers [
34,
35]. Large RT value of PF of about 11.0 mW/K
m have been obtained in interconnected Co NWs, which is almost as good as the bulk Co that display the largest PF value of about 15 mW/K
m [
36]. Moreover, regarding p-type materials, the RT PF estimated for the Fe and Ni
Cr
NW networks are close to the largest PF at RT of about 9 mW/K
m found for CePd
[
37,
38]. Therefore, electrodeposited magnetic NW networks are suitable for both n-type and p-type thermoelectric modules, in particular for active cooling applications as it has been recently shown that such application requires materials exhibiting large PF [
38,
39]. The efficiency of a material’s thermoelectric energy conversion is determined by its figure of merit
, with
the thermal conductivity. In a previous study, M. Ou et al [
40] have measured the thermal conductivity of a suspended Ni NW for
15–300 K. While the Lorenz ratio
departs from the Sommerfeld value (
V
/K
) at low temperatures,
L was found to be equal to
with a 5% margin of error above
50 K. Due to the very low thermal conductivity of polycarbonate (
0.2 W/Km at RT), the contribution of the polymer matrix to heat transport is much smaller than that of the metallic NW network. Indeed, assuming that the Wiedemann–Franz law holds for the NWs, estimations of the RT electronic thermal conductivities
provides values between 10 and 100 W/Km, hence at least two orders of magnitude above the thermal conductivity of the PC template. Moreover, in the limits of the Wiedemann–Franz law, the
value can be approximated by
. Using this approximation, the
values of the NWs networks at RT have been estimated and are reported in
Table 1. Although the figure of merit is more than one order of magnitude smaller than those of state-of-the-art thermoelectric materials (
1 in BiTe alloys), it is comparable to those of thermocouple alloys (
6 · 10
and
1.4 · 10
in constantan and chromel, respectively) and can be used in applications for devices with low energy requirements when the supply of heat essentially is free as with waste heat.
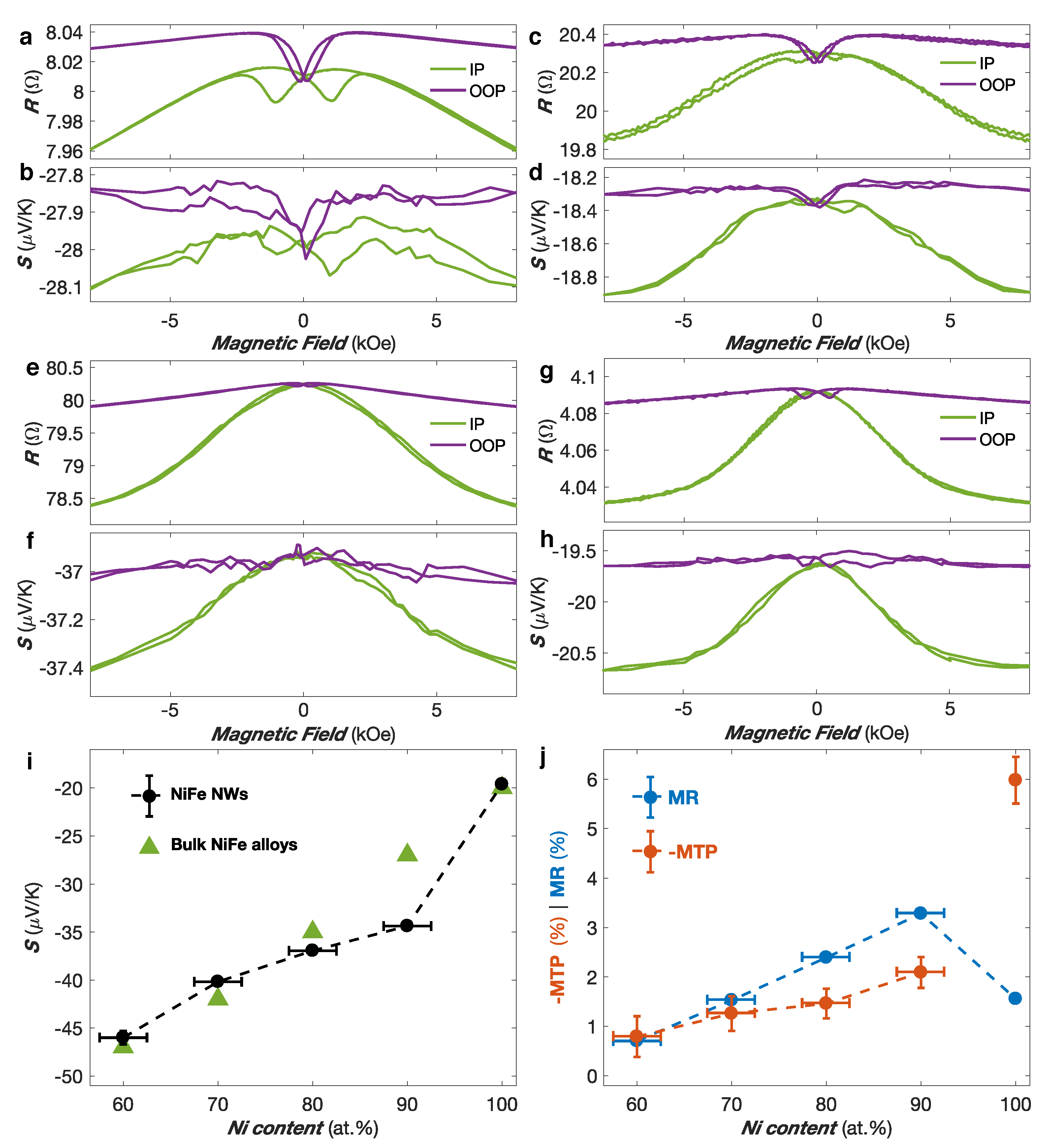
Besides, magneto-transport measurements have been conducted.
Figure 3a–h shows the variation of resistance and Seebeck coefficient with a magnetic field applied along the IP and OOP direction for the Co (a–b), Co
Ni
(c–d), Ni
Fe
(e–f) an Ni (g–h) NW networks. The MR curves show the anisotropic magnetoresistance (AMR) effect that leads to a decrease in resistivity as the angle between the magnetization and current directions is increased. Indeed, the current flow being restricted along the NW segments, the saturation magnetization in the IP direction makes an average angle of ±65
with the current. By comparison, when the magnetization is saturated in the OOP direction, the average angle between the magnetization and the current directions is much smaller (±25
), leading to a larger resistance at saturation when the field is applied in the OOP direction than when the field is applied in the IP direction. The lower resistance state expected for the perpendicular configuration between magnetization and current could not be achieved in such NW networks due to their geometry.
Figure 3a–h also shows that the absolute value of the thermopower increases with increasing angle between the magnetization and the current flow for the NW networks. At saturation, larger absolute thermopower is obtained in the IP direction compared to the OOP direction. This is in good agreement with previous studies performed on single NWs [
27]. Moreover, as shown in
Figure 3a–h for all NW networks, the MR and MTP effects exhibit similar behavior, indicating a direct relation between the two effects, as expected from Mott’s formula for the diffusion thermopower.
Table 1 provides the RT values of the MR and MTP ratio, defined as MR
and MTP
, respectively. Similar amplitudes have been obtained for the Co, Co
Ni
and NiFe alloys networks. The slightly larger MTP ratio amplitude compared to the MR ratio amplitude observed in Co
Ni
is also consistent with previous studies performed on NiCo alloy NWs [
27,
28]. In contrast,
Figure 3g,h reveals an enhancement of the MTP ratio up to three times larger than the corresponding MR ratio amplitude for the Ni NW network, in spite of similar field dependencies. Such definition of the MR ratios leads to an underestimation of the traditional AMR ratio defined as
, where
and
are the theoretical resistance states obtained for parallel and perpendicular orientations of the magnetization and current directions, respectively. However, the AMR ratio can be extracted from the resistance states measured at saturation in the OOP and IP directions
and
using the analytical model described in refs. [
17,
18,
19].
Figure 3i shows the Seebeck coefficients
S at RT of the NW networks made of Ni
Fe
alloys with 0.6
1. As seen, the thermopower increases continuously with increasing Fe content, reaching values between −20
V/K for pure Ni to about −45
V/K for Ni
Fe
. These results are in good agreement with the experimental data obtained on bulk NiFe alloys [
24,
41]. Therefore, NiFe alloys with fine-tune composition potentially yield significantly larger Seebeck coefficients than pure ferromagnetic metals like Co and thermocouple materials like constantan (Cu
Ni
:
−38
V/K). The measured value for Ni
Fe
NWs (
−37
V/K) is also very similar to the reported bulk values in the literature [
25,
26].
Figure 3j shows the magnitude of the MR and MTP ratios evaluated at RT for pure Ni and Ni
Fe
alloy NW networks as a function of the Ni content
x. It reveals a peak in the MR ratio for alloying compositions around 90% of Ni, in coherence with previous studies on bulk NiFe alloys [
42,
43]. Moreover, it highlights the very different behavior of the Ni NW network, compared to the NiFe alloys. For the Ni
Fe
alloy samples with 0.6
0.9, the magnitude of the MTP ratio is either comparable or smaller to the MR ratio. The smaller value of the MTP ratio with respect to the corresponding MR ratio for the Ni
Fe
NW network is in agreement with measurements performed on Ni
Fe
thin films [
44]. In contrast, the Ni NW network exhibits a MTP effect of −6% much larger than the MR ratio of ∼1.6%. This result is in good agreement with previous measurements performed on single Ni NWs and parallel arrays of Ni NWs, where MTP ratios were found up to 2.5–3 times larger than the corresponding MR ratios [
27,
28,
45] and may be related to the spin-dependent Seebeck coefficients,
and
, of opposite sign [
46]. It is interesting to note that for Ni thin films, the observed anisotropic MTP has approximately the same magnitude than the anisotropic MR (∼1.5%) [
44]. Further studies are needed to understand this unexpected enhanced MTP for Ni NWs.
The addition of transition metal impurities in ferromagnetic metals has been found to have a large influence on their spin-dependent electronic transport properties (see ref. [
47] for a review). It can be ascribed to a matching/mismatching of the d-electronic states between the host ferromagnetic metal and the transition metal impurities [
48]. Notably, diluted Cr impurities in Co, Fe and Ni generate stronger scattering in the majority-spin channel in a two-band model. This leads to a spin-asymmetry parameter
, which means that minority spin electrons dominate the electronic conduction, contrasting to that of pure ferromagnetic metals. In this context, NW networks made of dilute NiCr and CoCr alloys (Cr content ≤ 7 at.%) have been fabricated, and the influence of impurity concentration on the AMR effect and thermopower has been investigated [
20].
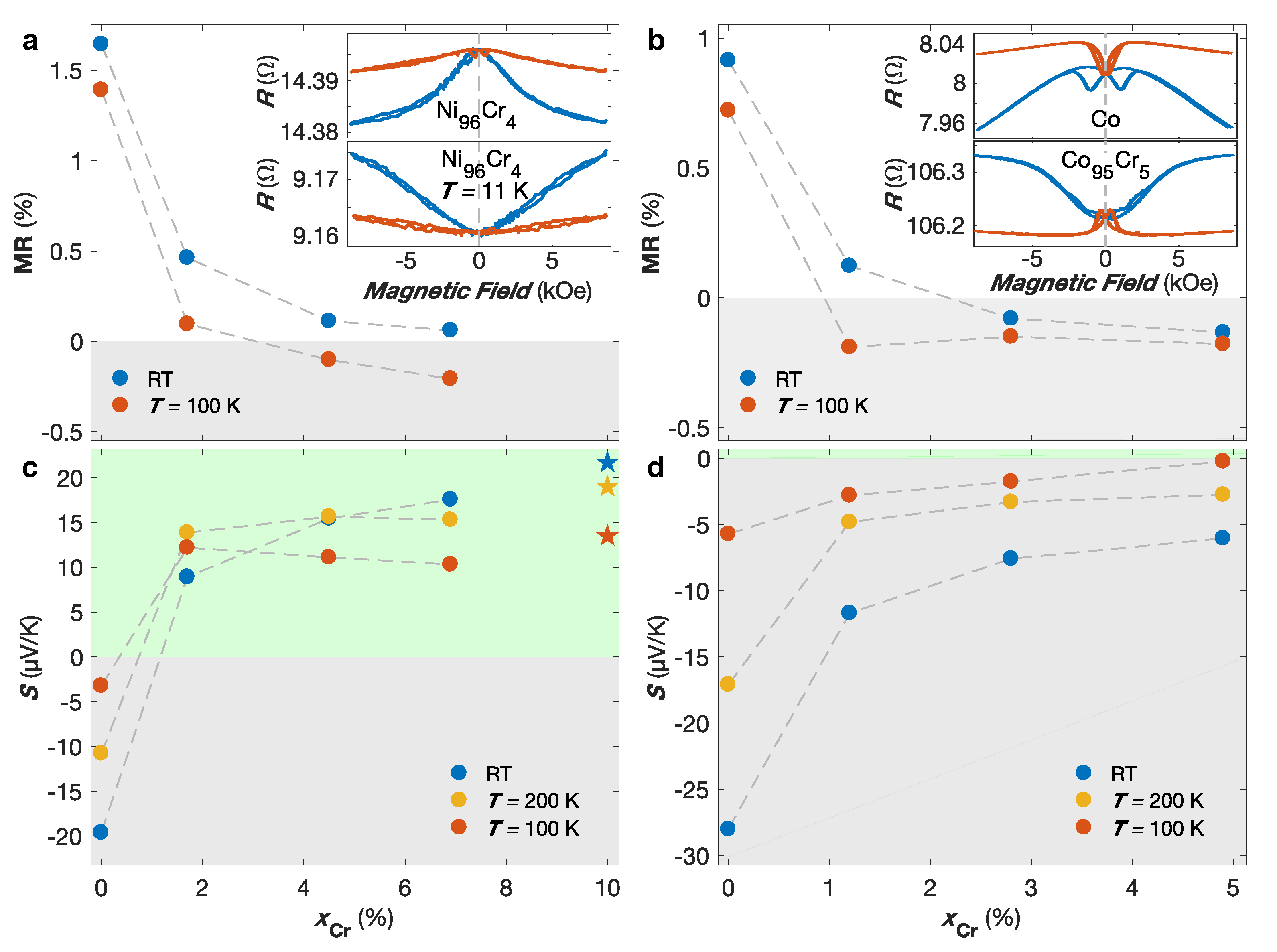
Figure 4a provides the MR ratio as a function of the Cr content for NiCr NW networks at RT and
100 K, where the MR ratio is defined as MR
, with
and
the resistance states reached at
10 kOe in the OOP and IP directions, respectively. Although this MR ratio underestimates the AMR effect, its sign correctly reflects the sign of the AMR effect. Indeed, when the magnetization is saturated along the OOP and IP directions, it makes respectively average angles of about 25
and 65
with the current flow that is strictly restricted along the NW segments. Therefore, the case
unambiguously indicates a positive AMR effect, as usually observed for ferromagnetic metals and alloys. As seen in
Figure 4a, positive AMR have been found at RT for all interconnected NiCr NW networks, with a decrease of the MR ratio with increasing Cr content. Conversely, negative AMR effect at
100 K has been observed for NiCr NW networks with Cr content >4%. This is illustrated in the inset of
Figure 4a that compares the MR curves measured at RT and
11 K for the Ni
Cr
sample. While the AMR is positive at RT, the Ni
Cr
NW network exhibits
at
11 K. Similar results have been observed on the NiCr NWs samples with Cr content > 4%. These observations are in agreement with previous negative AMR measurements reported at low temperatures in bulk NiCr dilute alloys [
49,
50,
51].
Figure 4b shows the MR curves for the dilute CoCr NW networks, where negative AMR have been observed at RT for Cr concentrations ≥3 at.% contrasting to pure Co NWs [
20]. Indeed, as seen in the inset of
Figure 4b, the RT MR curves measured for the Co and Co
Cr
samples show opposite behaviors (
and
for Co and Co
Cr
NW networks, respectively). Moreover, all CoCr NWs exhibit negative AMR with similar amplitude for all alloying composition down to ∼1 at.%. Even if the interpretation is still controversial [
52], Campbell, Fert and Jaoul have proposed a model based on a spin-orbit mechanism [
50,
53] predicting that the AMR ratio is proportional to
at low temperatures, where
is the spin asymmetry coefficient with
and
the residual resistivities of the spin down and spin up electrons. When
, negative AMR is thus expected. Moreover, in this simplified model,
is constant for a given impurity, independently of its concentration. When the temperature increases, the electron-phonon and electron-magnon scattering processes induces additional terms in the electrical resistivity. In consequence, as temperature rises, the AMR ratio of the dilute alloy should tend to that of the host pure ferromagnetic metal, converging more rapidly as the impurity concentration is lower [
53]. The predictions of Campbell, Fert and Jaoul [
50,
53] are mostly in qualitatively good agreement with the experimental results obtained for both interconnected NiCr and CoCr NW networks and the theoretic prediction of spin asymmetry coefficient
in these dilute alloys [
47,
54]. Notably, the negative MR ratios observed at low temperatures for CoCr NW networks are found to be independent of the Cr content, while the change of sign at RT is favored for the lowest Cr concentration (see
Figure 4b). However, the fact that the MR ratio remains negative for Cr content ≥3 at.% in CoCr NWs is unexpected because thermally activated scattering of conduction electrons should significantly weaken the effect. Similar unexpected negative AMR ratios at RT have already been observed in earlier studies performed on bulk CoIr alloys [
52]. One hypothetical justification for the RT negative MR ratio in the CoCr NW networks is that the residual resistivity due to impurity scatterings which is proportional to the Cr content becomes dominant compared to the thermally activated resistivity of the matrix at RT in CoCr alloys with Cr content ≥3%. Thus their influence over the AMR effect remain dominant at RT. This is illustrated by the residual ratio (R
/R
) below 2 (1.7 and 1.6 for 3 and 5 at.%Cr respectively) for the samples with RT negative AMR, up to 2 for the sample with positive RT AMR (5.4 and 2.7 for the Co and Co
Cr
samples, respectively).
Figure 4c,d show the Seebeck coefficient as a function of the Cr concentration in the absence of any external magnetic field for the interconnected NiCr and CoCr NW networks at RT,
200 K and
100 K. As seen in
Figure 4c, the thermopower of NiCr NWs abruptly changes sign, going from the pure Ni value (−20
V/K) to about +17.5
V/K for the Ni
Cr
NW network [
20]. Similar changes of sign in the Seebeck coefficient have been previously observed in bulk NiCr alloys with the electrical conduction dominated by minority spin electrons and have been related to drastic modifications in the density of states at the Fermi level by the addition of Cr impurities to the host ferromagnetic metals [
46,
47,
55].
Figure 4c also provides the recommended values for the thermocouple material Chromel P (Ni
Cr
), which are consistent with the Seebeck coefficients reported for the studied samples. In contrast, the sign of the Seebeck coefficient does not change for any value of Cr concentration for CoCr NW networks, as seen in
Figure 4d. The RT thermopower drops rapidly from −28
V/K for pure Co to much smaller negative values approaching −5
V/K for Co
Cr
NWs. Similar features are also observed at lower temperatures. These observations are consistent with experiments previously conducted on dilute Co-based alloys with
[
11]. The sudden drop of
S induced by the incorporation of few at. % of Cr in Co NWs can also be ascribed to significant changes in the density of states for the majority spin electrons. Please note that extremely small MTP effects (typically less than 1%) were found in all NiCr and CoCr samples.
3.2. Multilayered Nanowire Networks
We will now turn to the discussion to interconnected FM/Cu multilayered NW networks, which have been found to be good candidates for spin caloritronic devices with large spin-dependent thermoelectric transport properties as they combine large giant magnetoresistance (GMR) effect measured in the current-perpendicular-to-plane (CPP) configuration with large thermoelectric power factors [
13,
14,
22]. In addition, their macroscopic dimension leads to efficient energy conversion and opens the door to practical applications. In this context, interconnected FM/Cu multilayered NW networks, with FM = Co, Co
Ni
or Ni
Fe
and Ni, have been investigated. In CPP FM/Cu multilayers, the Seebeck coefficient along the axial direction (perpendicular direction to the layers) can be calculated from the corresponding transport properties using Kirchhoff’s rules [
56] as
Here
,
and
,
represent the thermopower and the thermal conductivity of the FM and Cu and
the thickness ratio of FM and Cu layers. If the Wiedemann–Franz law holds for the Cu and FM, Equation (
1) simply reduces to
with
and
being the corresponding electrical resistivities. According to Equation (
2), in the limits
, which is usually acceptable, and a thickness ratio
not too small,
is mainly determined by the large thermopower of the ferromagnetic metal. The same conclusion can be drawn when the FM layers are made of ferromagnetic alloys such as Co
Ni
and Ni
Fe
, because of highly contrasting thermal conductivity values between these alloys and Cu. By comparison, the Seebeck coefficient of a planar FM/Cu multilayer stack in the direction parallel to the layers (CIP) is given by
It shows that large thermopowers can be obtained only if the thickness ratio
is very large, although in CIP system with dominant interface scattering, the thermopower becomes less sensitive to the Cu bulk resistance, which leads to larger
S value [
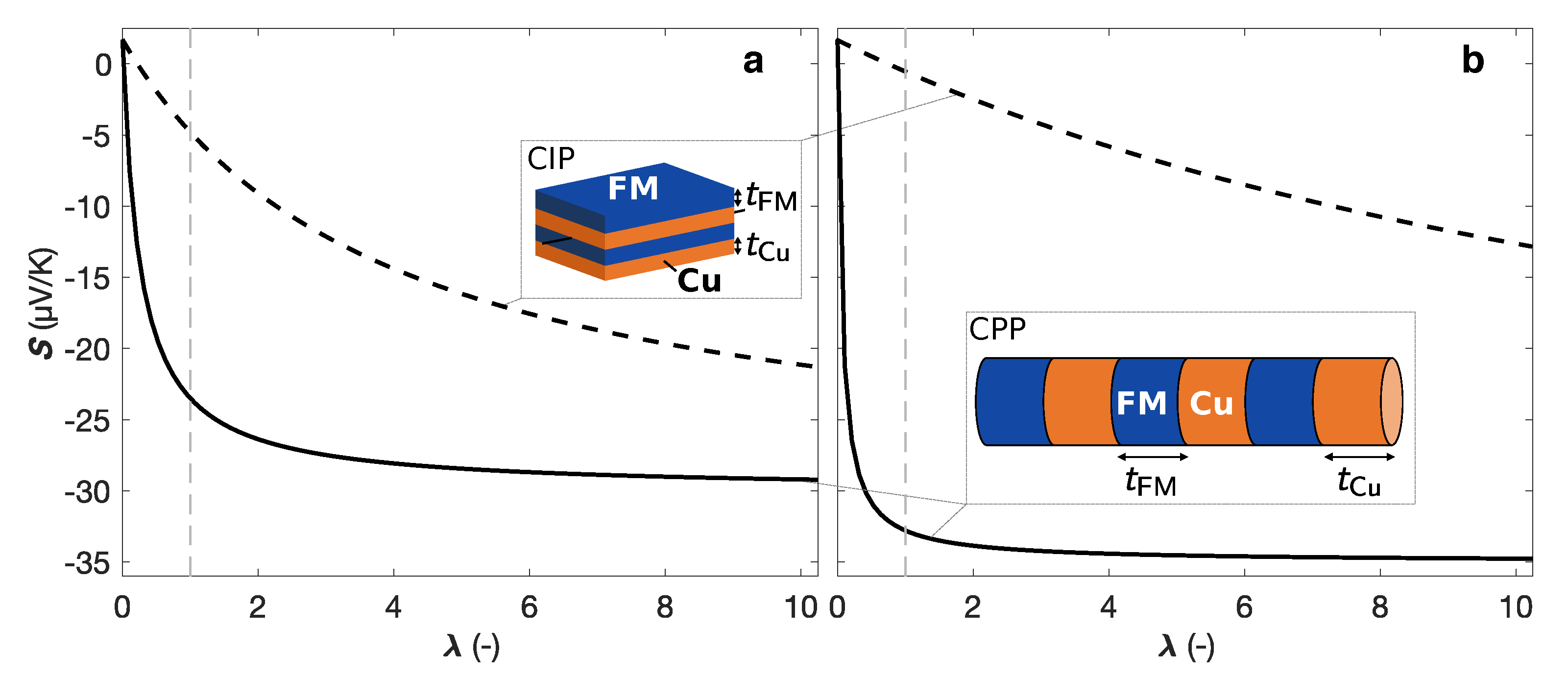
57]. This contrasting behavior between the Seebeck coefficient in the CIP and CPP configurations is illustrated in
Figure 5 for Co/Cu (a) and Ni
Fe
/Cu (b) multilayers, using Equations (
2) and (
3) and literature room-temperature resistivity and thermopower values for bulk Co, Ni
Fe
and Cu [
23,
25,
30,
41,
58]. Although the electrical resistivity and thermal conductivity values for multilayered nanowires may vary significantly compared with their respective bulk constituents, the same trends in the contrasting behavior between the two configurations remain. So, CPP FM/Cu multilayers are promising candidates for good thermoelectric materials.
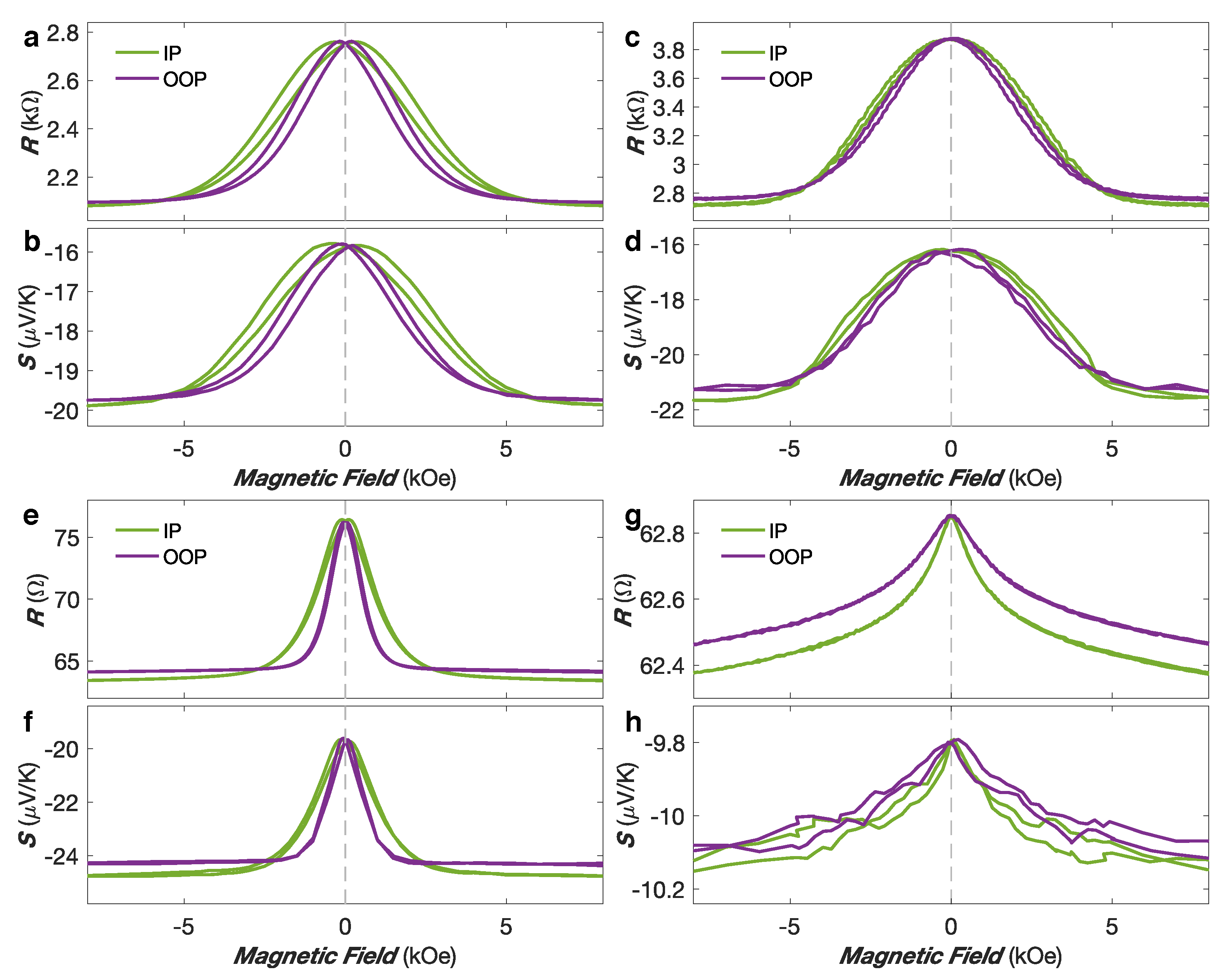
Figure 6 shows the resistance and thermopower variation with a magnetic field for the FM/Cu NW samples, with FM = Co (a–b), Co
Ni
(c–d), Ni
Fe
(e–f) and Ni (g–h). As shown in
Figure 6a,b, the resistance and thermopower of the Co/Cu NW sample show the same magnetic field dependencies and similar relative changes of ∼25% at
±8 kOe at RT. The value of
S in the saturated state of the Co/Cu NWs of about −20
V/K is only slightly lower than the one reported for homogeneous Co NW networks (∼−28
V/K), in good agreement with Equation (
2) and
Figure 5a. In addition, the sample is nearly magnetically isotropic, as observed from the magneto-transport curves obtained with the applied magnetic field along the OOP and IP directions. This behaviour corresponds to the one expected considering the crossed NW architecture and magneto-static arguments when using similar FM and NM layer thicknesses [
59]. Similar features have been observed on the Co
Ni
/Cu and Ni
Fe
/Cu NW networks. As seen in
Figure 6c,d, the resistance and thermopower of the Co
Ni
/Cu sample show the same magnetic field dependencies and relative changes of ∼30% at
±8 kOe at RT. Slightly higher Seebeck coefficients have been recorded in the Co
Ni
/Cu NW network, with a Seebeck coefficient in the saturated state in the IP direction of about −22
V/K. These values are in agreement with the results obtained from measurements carried out on single Co
Ni
and Co
Ni
/Cu NWs [
27,
60].
Figure 6e,f shows the RT resistance and thermopower of the Ni
Fe
/Cu NW network. Despite very similar magnetic field dependencies, the relative changes in Seebeck coefficient (∼26%) is found to be larger than the one of the resistance (∼17%) at
±8 kOe. As expected, the measured RT thermopower on the CPP-GMR Ni
Fe
/Cu sample in the saturated state (∼−25
V/K) is only slightly smaller than the value found in the homogeneous Ni
Fe
NW network (∼−35
V/K), in good agreement with Equation (
1) and
Figure 5b. In contrast, the RT Seebeck coefficients reported for Ni
Fe
/Cu multilayers in the CIP geometry (∼−10
V/K) are much smaller [
61]. A contrasting behavior has been observed in interconnected Ni/Cu NW networks.
Figure 6g,h shows the RT resistance and thermopower field dependencies with the applied magnetic field along the IP and OOP directions of the Ni/Cu NW network. Despite similar field dependencies, the amplitude of the magneto-thermopower effect (MTP ≈ −3.7%) is about four times larger than the corresponding magnetoresistance effect (MR ≈ 0.8%) at RT. This larger value of the MTP with respect to the MR ratio is consistent with our result obtained in homogeneous Ni NWs and previous studies on Ni/Cu multilayers [
62]. This significant boost of the MTP, compared to MR may indicate underlying contrasting
and
values. This is consistent with the values of
−43
V/K and
20
V/K reported by Cadeville and Roussell [
46].
Table 2 provides the Seebeck coefficient in the saturated states (
) for the different FM/Cu NW network together with the estimated electrical resistivity (
) and the thermoelectric power factor (
) at RT (see [
13,
14] for more details about the resistivity calculation). It shows that the CPP geometry of the device is suitable for spin caloritronic purposes since the RT thermopower and power factor of the FM/Cu NW networks in the saturated state are only slightly smaller than the value found in the pure corresponding ferromagnetic materials, as expected from conventional rules for a stacking arrangement in series (see Equation (
2)). The figure of merit of the FM/Cu NW networks was estimated by
at RT [
13,
14] and is reported in the saturated state in
Table 2. The values found are comparable to those of homogeneous NW networks. Furthermore, considering the energy conversion from heat to electric power, the
of the proposed device is much larger than that of a spin Seebeck power generator (
10
) based on a device using a two-step conversion process and the inverse spin Hall effect to convert spin current to charge current in non-magnetic materials [
63]. Finally,
Table 2 also provides the values at RT of the magnetoresistance ratio
, with
and
being respectively the high- and low-resistance states, and the absolute value of the magneto-thermopower
, with
and
the corresponding thermopowers in the high- and low-resistance states, respectively, for the FM/Cu NW networks.
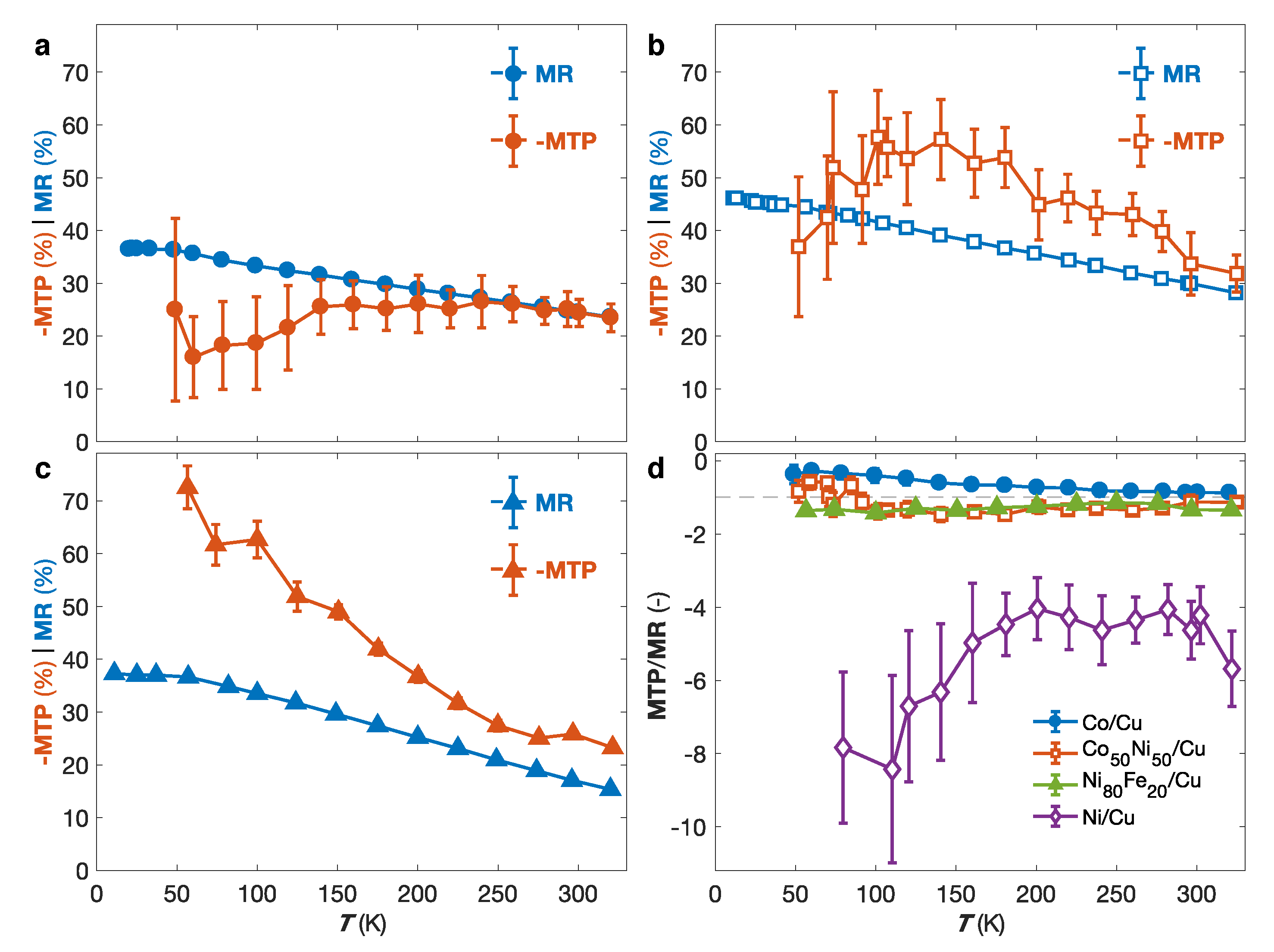
Figure 7a–c shows the temperature dependence of the MR and MTP ratios for the Co/Cu (a), Co
Ni
/Cu (b) and Ni
Fe
/Cu (c) NW networks. As seen, in all samples, the MR ratio shows a monotonic increase before reaching a plateau at low temperatures. This is expected because of the saturation of the resistivity at low temperatures and the vanishing of the spin mixing effect. Besides, for all three samples, the value of −MTP shows a similar increase with decreasing temperature as the MR ratio in the temperature range near RT. In contrast, in the low temperature range, the MTP exhibits very different behaviors depending on the material considered. For the Co/Cu sample, the MTP exhibits a less pronounced effect compared to the MR ratio, which is consistent with previous temperature dependency measurements of the MTP for Co/Cu multilayered NW networks [
64]. For the Co
Ni
/Cu sample, similar MR and −MTP values are observed over the whole investigated temperature range, while for the Ni
Fe
/Cu sample, the MTP exhibits a pronounced reinforcement compare to the MR in the low temperature range.
Figure 7d shows the ratio between the MR and MTP of the different FM/Cu NW networks, with FM = Co, Co
Ni
, Ni
Fe
and Ni, for temperatures in the range of 50 K to 320 K. While the ratios for Co/Cu, Co
Ni
/Cu and Ni
Fe
/Cu remain below −1.5, the MTP/MR values of the Ni/Cu sample are encompassed between −4 and −8 in the whole temperature range, revealing an enhanced MTP effect with respect to the corresponding MR effect in Ni/Cu multilayered NW networks. A MTP ratio of about −14% was obtained at
80 K for a corresponding MR slightly below 2% for the Ni/Cu NW network. Such larger value of the MTP with respect to the MR ratio is consistent with our results in Ni homogeneous NW networks, and previous studies in Ni/Cu multilayers [
62], and may be ascribed to Seebeck coefficients for spin up and spin down electrons of opposite sign. Furthermore, the magneto-power factor (
) can be expressed as
. This yields RT MPF ratio of 111%, 155%, 92% and 8% for the Co/Cu, Co
Ni
/Cu, Ni
Fe
/Cu and Ni/Cu NW networks, respectively.
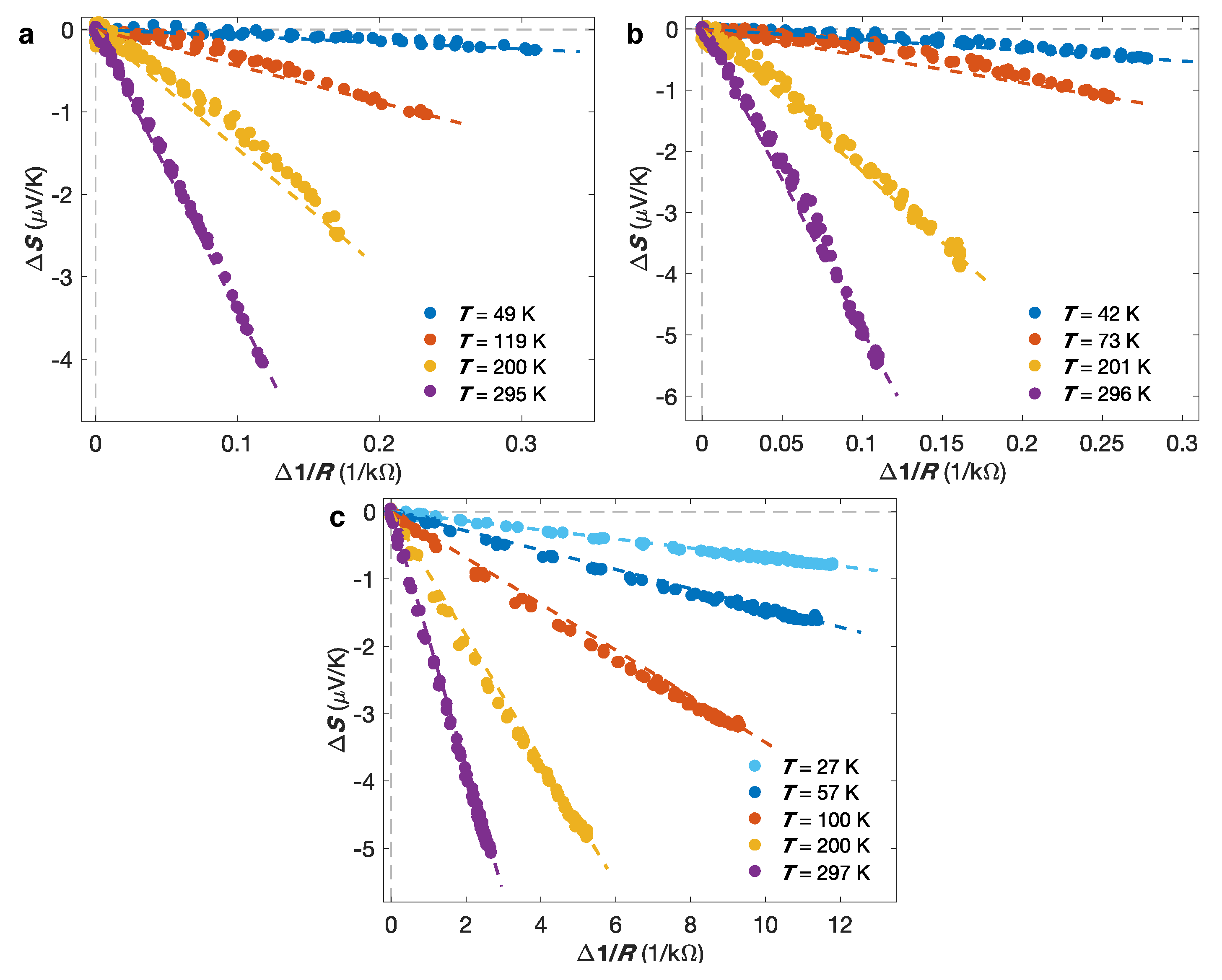
Figure 8a–c present evidences that the thermopower is dominated by electron diffusion over the whole temperature range investigated for the different multilayered NW networks considered. Defining the diffusion thermopower
by Mott’s formula with
the derivative of the electrical resistivity with respect to the energy evaluated at the Fermi level
, the diffusion thermopower for antiparallel (AP) and parallel (P) arrangement of the successive FM layer magnetization can be written as
and
. Then, the following expression describing an inverse relationship between the field-dependent thermopower
and electrical resistance
can be obtained [
21,
57,
65]:
where
and
. This expression corresponds to an equivalent form of the Gorter-Nordheim relation for diffusion thermopower in metals and alloys [
11], and has been observed at different temperatures in the FM/Cu NW network. This is illustrated by
Figure 8a–c, which display
with respect to
for the (a) Co/Cu, (b) Co
Ni
/Cu and (c) Ni
Fe
/Cu samples. The dashed lines correspond to the theoretical linear relation
. The data show relatively good accordance with the theoretical linear variation, despite some slight deviation, in particular in the intermediate temperature range.
In the limits of no-spin relaxation, most of the CPP-GMR data can be understood using a simple two-current series-resistor model, in which the resistance of layers and interfaces simply add and where ’up’ and ’down’ charge carriers are propagating independently in two spin channels with large spin asymmetries of the electron’s scattering [
66,
67]. Similarly, significantly different Seebeck coefficients for spin-up and spin-down electrons,
and
, are expected because the d-band is exchange-split in these ferromagnets, as suggested from previous studies performed on dilute magnetic alloys [
46,
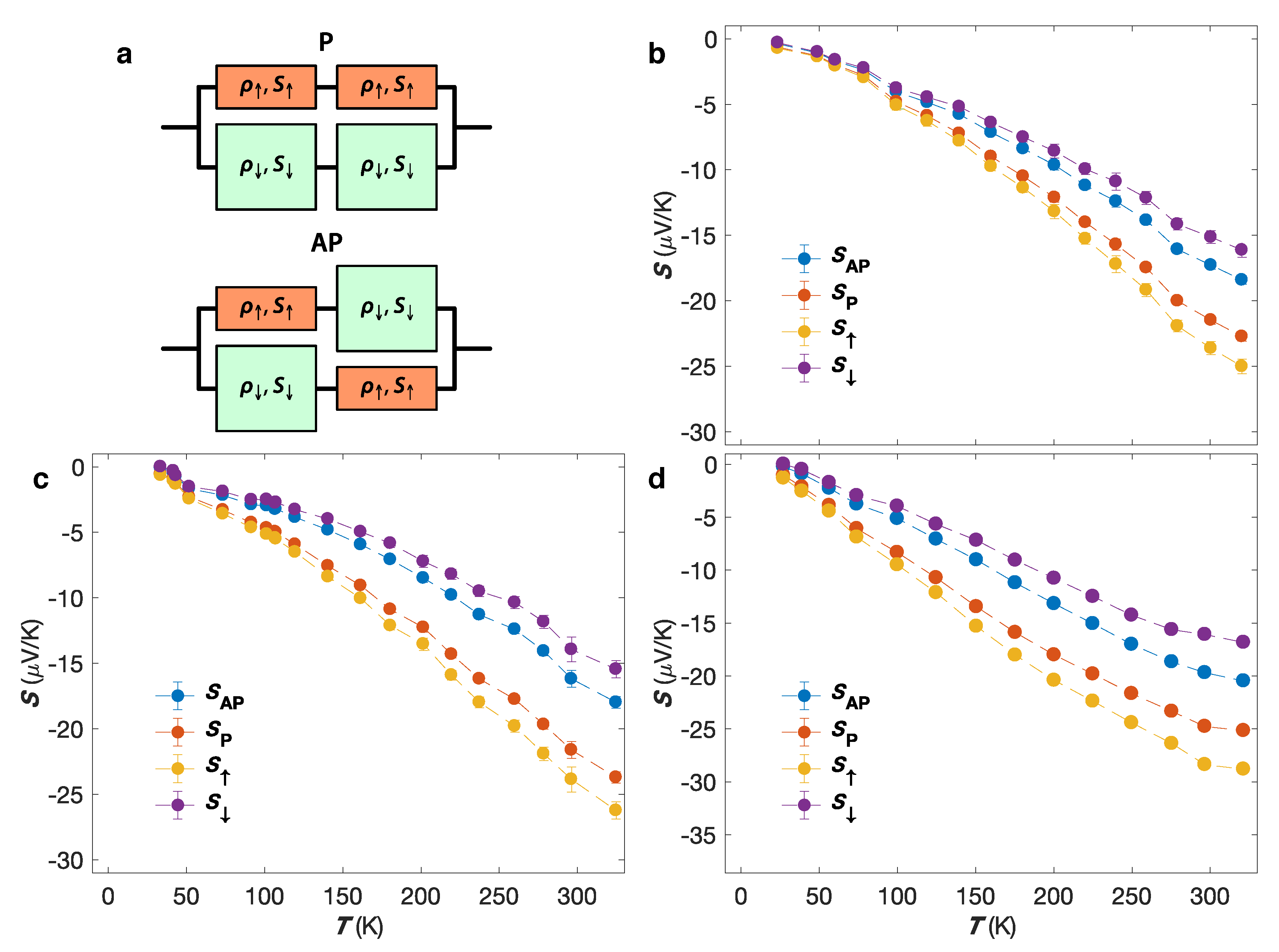
55]. Assuming that the layers of the magnetic multilayers are thin compared to the spin-diffusion lengths and according to the usual rule when the currents split to flow along two parallel paths (See
Figure 9a), the corresponding thermopowers
and
are simply given by [
57]
and
where separate resistivities
and
and Seebeck coefficients
and
are defined for majority and minority spin channels. From Equations (
5) and (
6), the following relations can be extracted:
and
where
denotes the spin asymmetry coefficient for resistivity. Combining Equations (
7) and (
8), the spin-dependent Seebeck coefficients,
and
can be expressed as follows [
13]:
From Equations (
9) and (
10), it can be easily deduced that
and
in the limits of an extremely large MR ratio (
).
The temperature dependencies of
,
,
and
are shown in
Figure 9b–d for the Co/Cu, Co
Ni
/Cu and Ni
Fe
/Cu multilayered NW networks. Below RT, the various Seebeck coefficients of all three samples decrease almost linearly with decreasing temperature, which is another indicative of the dominance of diffusion thermopower. The deviation from the linear regime in
Figure 9b–d can be ascribed to other possible contribution to the thermopower such as magnon-drag. The estimated values at RT of
and
are reported in
Table 3, using
in Equations (
9) and (
10). The values of
and
for Co/Cu NWs are similar to those previously reported in bulk Co (
V/K and
V/K) [
46]. In contrast, the value for
for Co/Cu, Co
Ni
/Cu and Ni
Fe
/Cu NWs shown in
Table 3, in the range of −8 to −12
V/K [
13,
14,
22], are much larger than the ones of −1.8
V/K and −3.8
V/K to −4.5
V/K extracted from measurements performed on Co/Cu/Co nanopillar spin valve and Ni
Fe
/Cu/Ni
Fe
nanopillar and lateral spin devices, respectively, using a 3D finite-element model [
6,
68]. The largest spin-dependent Seebeck coefficient is found in Ni
Fe
/Cu NWs, reaching −12.3
V/K [
22]. From the estimated values of
and
, the RT spin asymmetry for Seebeck coefficients
has been estimated, and are reported in
Table 3 for the interconnected Co/Cu, Co
Ni
/Cu and Ni
Fe
/Cu NWs, respectively. It is also found that the
value found for the crossed Co/Cu NW network is consistent with the values previously reported for parallel Co/Cu NWs [
64].
In the limit of MR
, the magnetothermopower can also be expressed as [
13]:
Considering first the case
1, this leads to
, which means that enhancement of the MTP ratio compared to the corresponding MR ratio is expected if
. The amplitudes of the MR and MTP effects for the Co/Cu, Co
Ni
/Cu and Ni
Fe
/Cu NW networks studied have been found comparable at RT, with
as seen in
Table 3. Similarities between the amplitudes of the MR and MTP at RT were already observed in arrays of parallel Co/Cu NWs [
64,
69,
69] and Co/Cu CIP multilayers [
57,
70]. However, the physical reason of this is unclear. In contrast to the other FM/Cu NW networks, the Ni/Cu system shows a much larger MTP ratio than its corresponding MR ratio, as seen in
Figure 7d. This significant boost of the MTP, compared to MR may indicate an underlying large
coefficient due to contrasting
and
values, while
is expected to be small in Ni. This is consistent with the values of
−43
V/K and
20
V/K reported by Cadeville and Roussell [
46], leading to
−3. Furthermore, from Equation (
11), infinitely large MTP effect is expected when the product
tends to
. While
,
can be reached if
and
exhibit opposite signs. Therefore, the fabrication of multilayered NWs with appropriate magnetic layer composition should make it possible to fine-tune the power factor of thermoelectric energy conversion with an external magnetic field. The limit case of an infinite MTP ratio underlies that the Seebeck coefficient obtained in the antiparallel state
reaches 0. Indeed, the Seebeck coefficients in the antiparallel and parallel states can be expressed as
and
For
−1, this yields
0 and
. As a consequence, for a practice device, Seebeck coefficients for spin up and spin down electrons of opposite sign and with largely asymmetrical amplitudes are required. This would lead to a system where at zero magnetic field, no thermoelectric current is generated, while under an applied external magnetic field, a large thermoelectric current is generated. It should be noted that the limit case
1 yields the opposite scenario where
and
. In that case, a thermoelectric current is generated in absence of magnetic fields, which vanishes under an applied external magnetic field. The case
1 also requires
and therefore Seebeck coefficients for spin up and spin down with opposite signs. Moreover, Equation (
7) indicates that the more different their amplitudes, the larger the
value, which is required for practical applications. In this context, the Ni/Cu system is expected to be a good potential candidate for the observation of highly enhanced MTP effect, since
and, according to Cadeville and Roussel [
46],
−3. Experimental challenge lies with making interconnected Ni/Cu NW networks with larger magneto-transport properties.
Interestingly, it can be shown that the diffusion thermopower of a ferromagnetic homogeneous NW network can be expressed as
Therefore, because
is expected for Co, the Seebeck coefficient obtained for homogeneous Co NW networks (−28
V/K, see
Table 1) is consistent with
. Moreover, the addition of a very small amount of Cr in Co is expected to induce
. As a consequence, the Seebeck coefficient of dilute CoCr alloys can be approximated by
, assuming that the very small amount of Cr does not significantly impact the Seebeck coefficient of spin down electron, which is also in good agreement with the value reported for
(−12
V/K). In contrast, because
is expected for Ni, Equation (
14) leads to
. The values of
−20
V/K is found in good agreement with the Seebeck coefficients for spin up and spin down electrons reported by Cadeville and Roussell (
V/K and
+20
V/K [
46]). Moreover, the addition of diluted Cr impurities in Ni is also expected to induce
. Therefore, the Seebeck coefficient of dilute NiCr alloys is expected to tend towards the value of
. The positive values obtained in dilute NiCr alloys is in good agreement with the positive value of
reported by Cadeville and Roussell [
46] as shown in
Figure 4c. This is another indication that Ni may exhibit a probable spin-dependent Seebeck coefficients of opposite sign.