First Proof-of-Principle of Inorganic Lead Halide Perovskites Deposition by Magnetron-Sputtering
Abstract
1. Introduction
2. Materials and Methods
3. Results
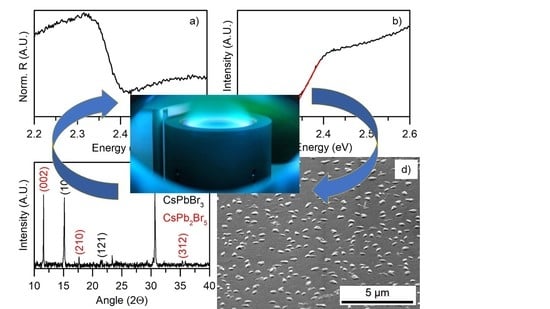
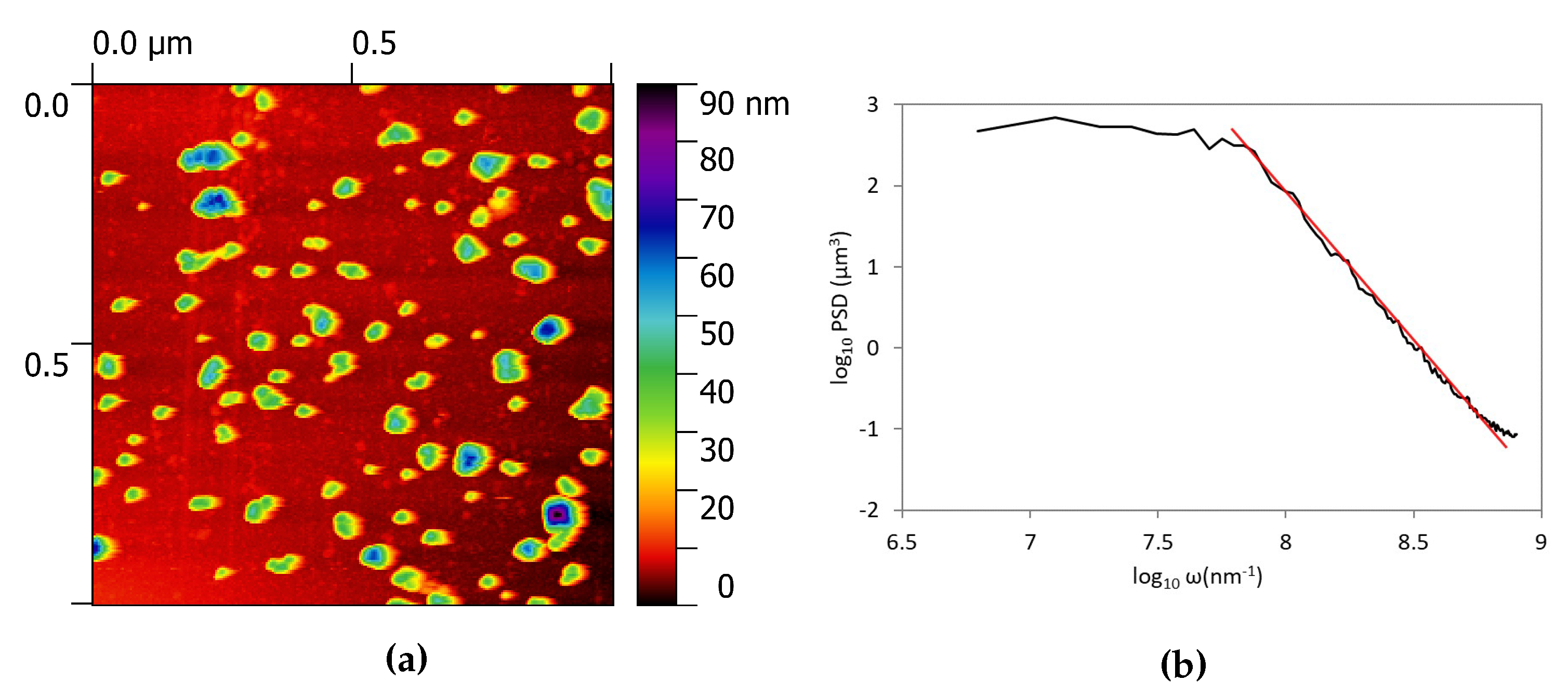
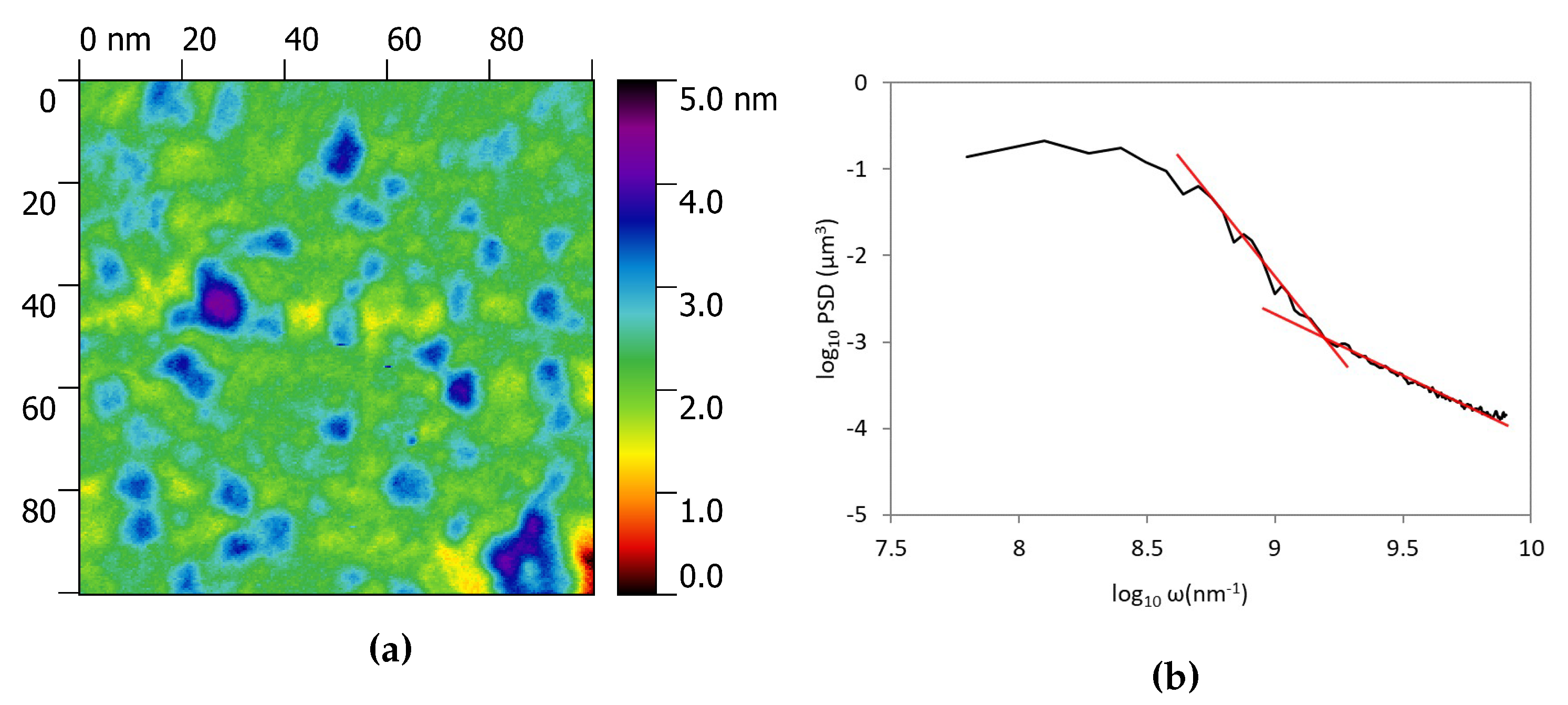
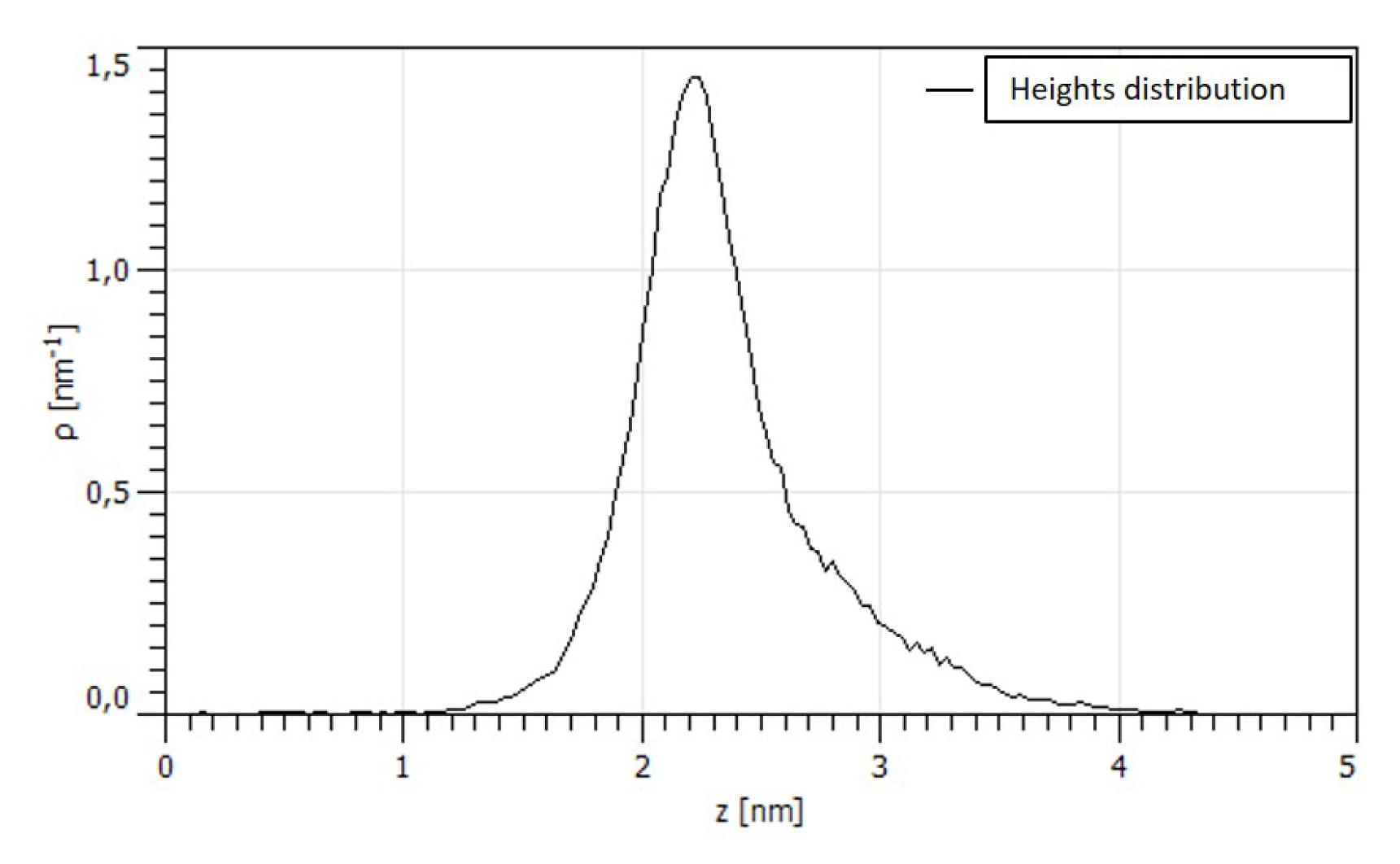
3.1. Morphological Characterization
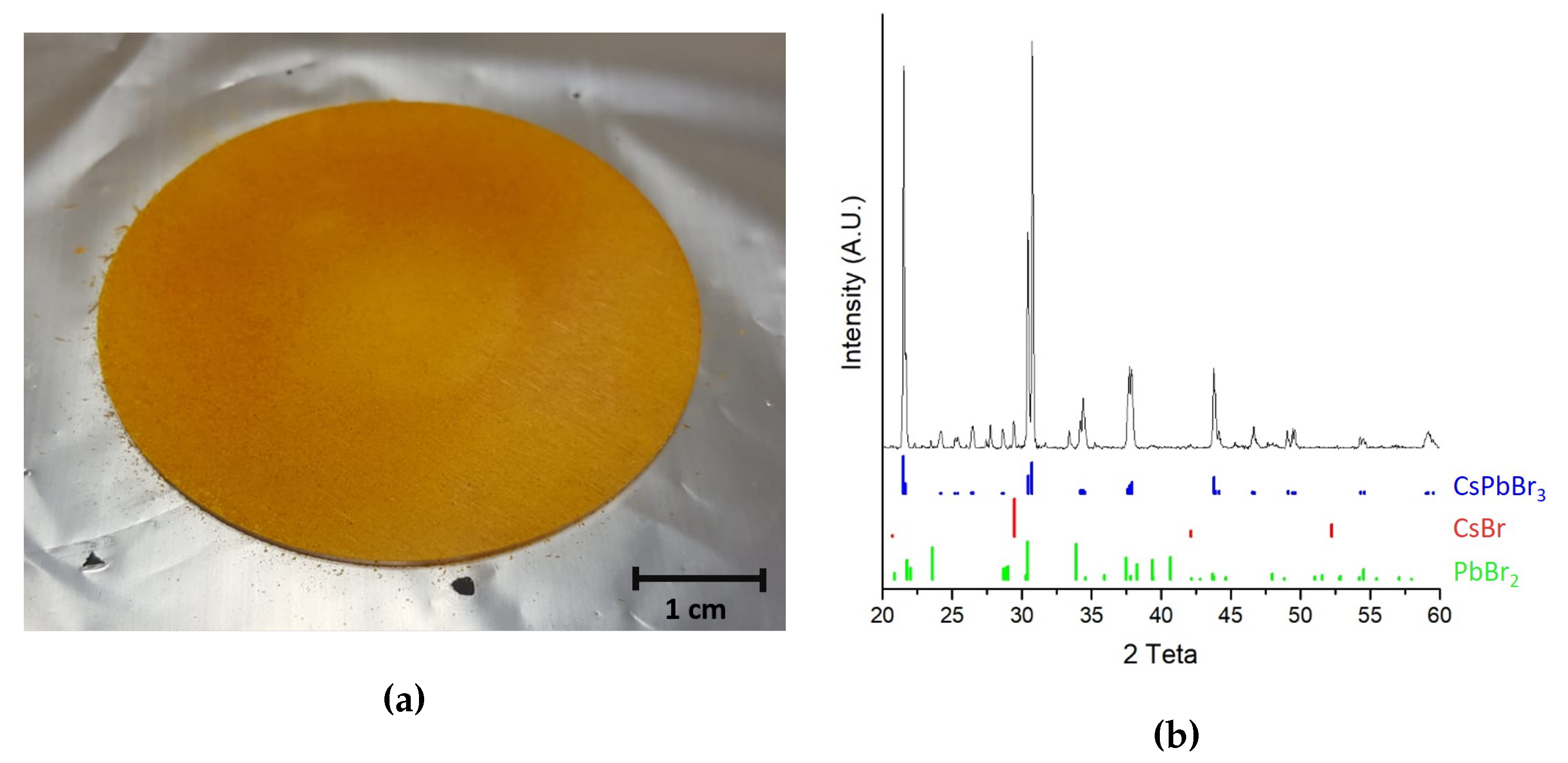
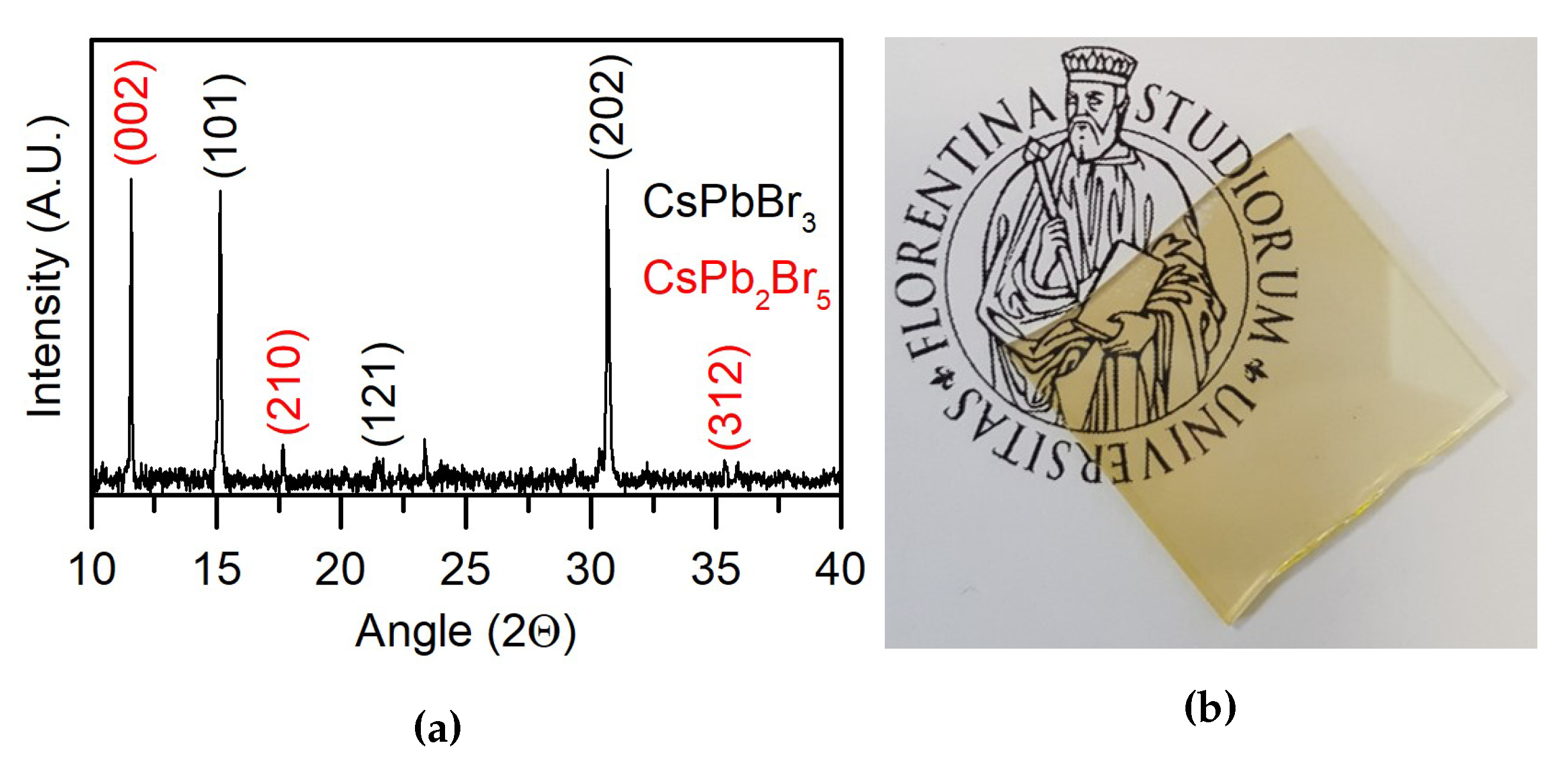
3.2. Chemical and Structural Characterization
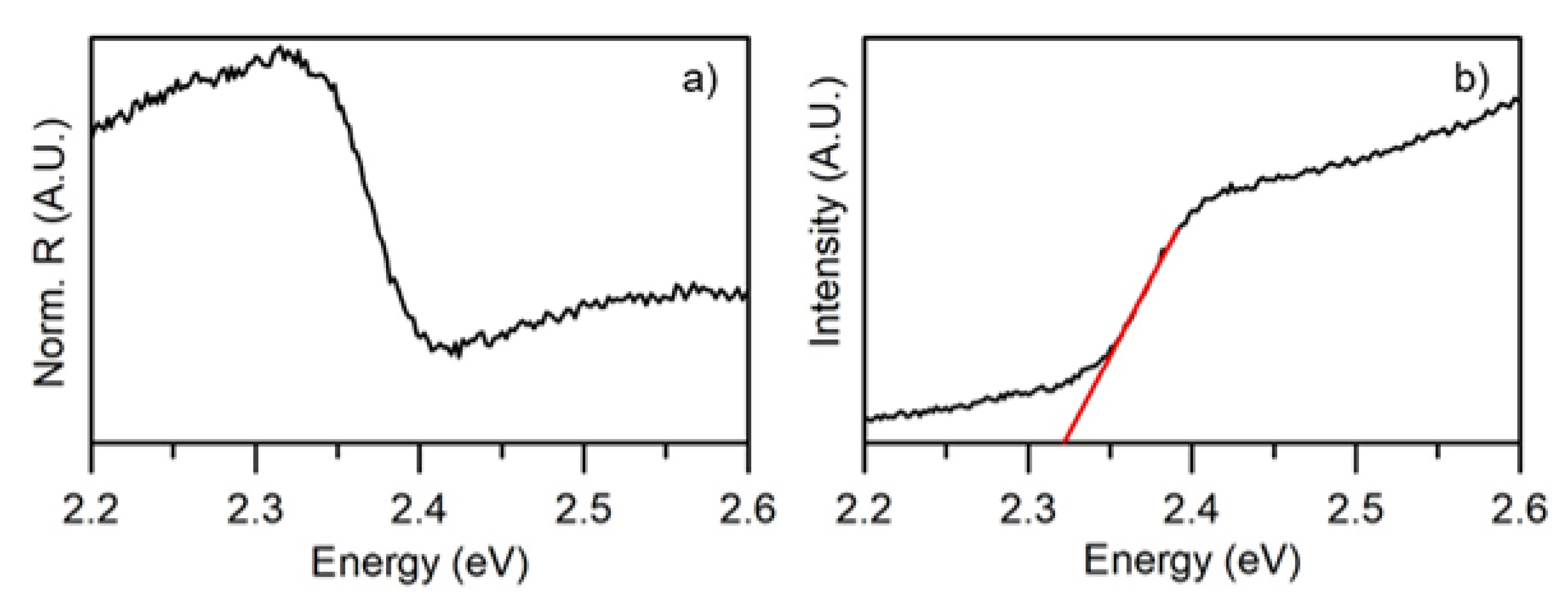
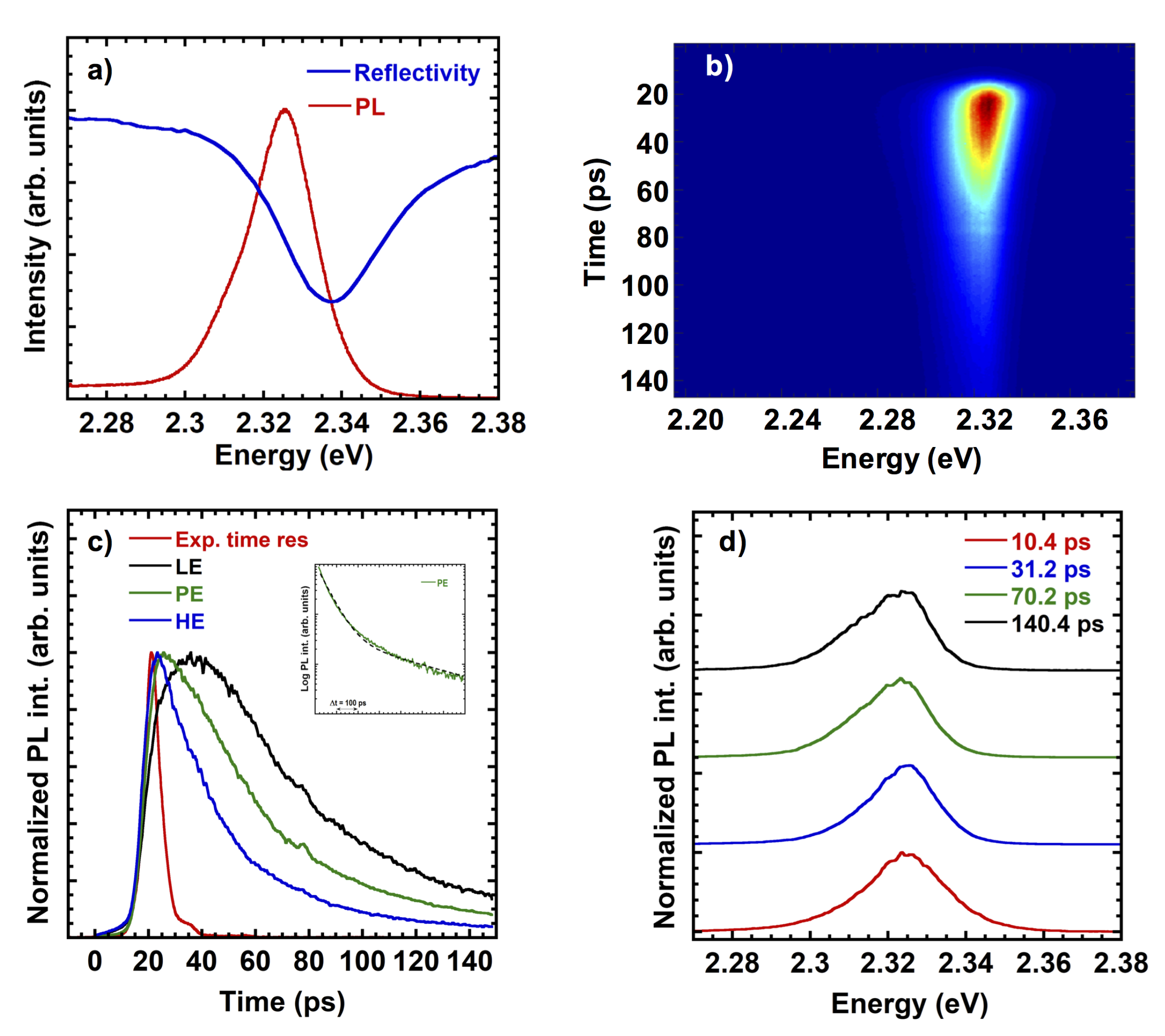
3.3. Optical Characterization
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BE | Binding energy |
| BSE | Backscattered |
| CTE | Thermal expansion coefficient |
| CW | Continuous wave |
| DRS | Direct reflectance spectroscopy |
| EDS | Energy dispersive spectroscopy |
| MA | Methyl ammonium |
| PSD | Power spectral density |
| RF | Radio frequency |
| XPS | X-ray photoelectron spectroscopy |
| XRD | X-ray diffraction |
References
- Vidyasagar, C.; Flores, B.M.M.; Pérez, V.M.J. Recent advances in synthesis and properties of hybrid halide perovskites for photovoltaics. Nano-Micro Lett. 2018, 10, 68. [Google Scholar] [CrossRef] [PubMed]
- Kanemitsu, Y.; Handa, T. Photophysics of metal halide perovskites: From materials to devices. Jpn. J. Appl. Phys. 2018, 57, 1–17. [Google Scholar] [CrossRef]
- Gholipour, S.; Saliba, M. From Exceptional Properties to Stability Challenges of Perovskite Solar Cells. Small 2018, 14, 1802385. [Google Scholar] [CrossRef] [PubMed]
- Mitzi, D.B. Synthesis, structure, and properties of organic-inorganic perovskites and related materials. In Progress in Inorganic Chemistry; Wiley: Hoboken, NJ, USA, 1999; pp. 1–121. [Google Scholar]
- Liang, K.; Mitzi, D.B.; Prikas, M.T. Synthesis and characterization of organic- inorganic perovskite thin films prepared using a versatile two-step dipping technique. Chem. Mater. 1998, 10, 403–411. [Google Scholar] [CrossRef]
- Park, N.G. Perovskite solar cells: An emerging photovoltaic technology. Mater. Today 2015, 18, 65–72. [Google Scholar] [CrossRef]
- Stoeckel, M.A.; Gobbi, M.; Bonacchi, S.; Liscio, F.; Ferlauto, L.; Orgiu, E.; Samorì, P. Reversible, fast, and wide-range oxygen sensor based on nanostructured organometal halide perovskite. Adv. Mater. 2017, 29, 1702469. [Google Scholar] [CrossRef]
- Xu, W.; Li, F.; Cai, Z.; Wang, Y.; Luo, F.; Chen, X. An ultrasensitive and reversible fluorescence sensor of humidity using perovskite CH3NH3PbBr3. J. Mater. Chem. C 2016, 4, 9651–9655. [Google Scholar] [CrossRef]
- Bruzzi, M.; Talamonti, C.; Calisi, N.; Caporali, S.; Vinattieri, A. First proof-of-principle of inorganic perovskites clinical radiotherapy dosimeters. APL Mater. 2019, 7, 051101. [Google Scholar] [CrossRef]
- Gabelloni, F.; Biccari, F.; Andreotti, G.; Balestri, D.; Checcucci, S.; Milanesi, A.; Calisi, N.; Caporali, S.; Vinattieri, A. Recombination dynamics in CsPbBr 3 nanocrystals: Role of surface states. Opt. Mater. Express 2017, 7, 4367–4373. [Google Scholar] [CrossRef]
- Shahbazi, M.; Wang, H. Progress in research on the stability of organometal perovskite solar cells. Sol. Energy 2016, 123, 74–87. [Google Scholar] [CrossRef]
- Calisi, N.; Caporali, S.; Milanesi, A.; Innocenti, M.; Salvietti, E.; Bardi, U. Composition-Dependent Degradation of Hybrid and Inorganic Lead Perovskites in Ambient Conditions. Top. Catal. 2018, 61, 1201–1208. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, S.; Li, L.; Chen, W. Research progress on large-area perovskite thin films and solar modules. J. Mater. 2017, 3, 231–244. [Google Scholar] [CrossRef]
- Lan, C.; Zhou, Z.; Wei, R.; Ho, J.C. Two-dimensional perovskite materials: From synthesis to energy-related applications. Mater. Today Energy 2019, 11, 61–82. [Google Scholar] [CrossRef]
- Orlovskaya, N.; Coratolo, A.; Johnson, C.; Gemmen, R. Structural characterization of lanthanum chromite perovskite coating deposited by magnetron sputtering on an iron-based chromium-containing alloy as a promising interconnect material for SOFCs. J. Am. Ceram. Soc. 2004, 87, 1981–1987. [Google Scholar] [CrossRef]
- Kim, T.C.; Lee, S.H.; Jung, H.K.; Kim, Y.E.; Choi, J.W.; Yang, D.; Kim, D.H. Effect of sputtering conditions on the structure and magnetic properties of self-assembled BiFeO3-CoFe2O4 nanocomposite thin films. J. Magn. Magn. Mater. 2019, 471, 116–123. [Google Scholar] [CrossRef]
- Rodová, M.; Brožek, J.; Knížek, K.; Nitsch, K. Phase transitions in ternary caesium lead bromide. J. Therm. Anal. Calorim. 2003, 71, 667–673. [Google Scholar] [CrossRef]
- Ramirez, C.; Yadavalli, S.K.; Garces, H.F.; Zhou, Y.; Padture, N.P. Thermo-mechanical behavior of organic-inorganic halide perovskites for solar cells. Scr. Mater. 2018, 150, 36–41. [Google Scholar] [CrossRef]
- Rolston, N.; Bush, K.A.; Printz, A.D.; Gold-Parker, A.; Ding, Y.; Toney, M.F.; McGehee, M.D.; Dauskardt, R.H. Engineering stress in perovskite solar cells to improve stability. Adv. Energy Mater. 2018, 8, 1802139. [Google Scholar] [CrossRef]
- Zhao, J.; Deng, Y.; Wei, H.; Zheng, X.; Yu, Z.; Shao, Y.; Shield, J.E.; Huang, J. Strained hybrid perovskite thin films and their impact on the intrinsic stability of perovskite solar cells. Sci. Adv. 2017, 3, eaao5616. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, M.; Liu, W.; Yue, X.; Cui, P.; Wei, D. CH3NH3PbI3 converted from reactive magnetron sputtered PbO for large area perovskite solar cells. Sol. Energy Mater. Sol. Cells 2017, 163, 250–254. [Google Scholar] [CrossRef]
- Bonomi, S.; Marongiu, D.; Sestu, N.; Saba, M.; Patrini, M.; Bongiovanni, G.; Malavasi, L. Novel Physical Vapor Deposition Approach to Hybrid Perovskites: Growth of MAPbI3 Thin Films by RF-Magnetron Sputtering. Sci. Rep. 2018, 8, 15388. [Google Scholar] [CrossRef] [PubMed]
- Jana, A.; Mittal, M.; Singla, A.; Sapra, S. Solvent-free, mechanochemical syntheses of bulk trihalide perovskites and their nanoparticles. Chem. Commun. 2017, 53, 3046–3049. [Google Scholar] [CrossRef] [PubMed]
- Shirley, D.A. High-resolution X-ray photoemission spectrum of the valence bands of gold. Phys. Rev. B 1972, 5, 4709. [Google Scholar] [CrossRef]
- Susi, T.; Pichler, T.; Ayala, P. X-ray photoelectron spectroscopy of graphitic carbon nanomaterials doped with heteroatoms. Beilstein J. Nanotechnol. 2015, 6, 177–192. [Google Scholar] [CrossRef]
- Giaccherini, A.; Colantoni, I.; D’acapito, F.; De Luca, A.; Capolupo, F.; Montegrossi, G.; Romanelli, M.; Innocenti, M.; Di Benedetto, F. Green synthesis of pyrite nanoparticles for energy conversion and storage: A spectroscopic investigation. Eur. J. Mineral. 2016, 28, 611–618. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. The statistical analysis of a random, moving surface. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 249, 321–387. [Google Scholar] [CrossRef]
- Nayak, P. Random process model of rough surfaces in plastic contact. Wear 1973, 26, 305–333. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Role of fractal geometry in roughness characterization and contact mechanics of surfaces. J. Tribol. 1990, 112, 205–216. [Google Scholar] [CrossRef]
- Barnsley, M.F.; Devaney, R.L.; Mandelbrot, B.B.; Peitgen, H.O.; Saupe, D.; Voss, R.F.; Fisher, Y.; McGuire, M. The Science of Fractal Images; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Wu, J.J. Characterization of fractal surfaces. Wear 2000, 239, 36–47. [Google Scholar] [CrossRef]
- Van Put, A.; Vertes, A.; Wegrzynek, D.; Treiger, B.; Van Grieken, R. Quantitative characterization of individual particle surfaces by fractal analysis of scanning electron microscope images. Fresenius’ J. Anal. Chem. 1994, 350, 440–447. [Google Scholar] [CrossRef]
- Mannelquist, A.; Almqvist, N.; Fredriksson, S. Influence of tip geometry on fractal analysis of atomic force microscopy images. Appl. Phys. A Mater. Sci. Process. 1998, 66, S891–S895. [Google Scholar] [CrossRef]
- Zahn, W.; Zösch, A. Characterization of thin-film surfaces by fractal geometry. Fresenius’ J. Anal. Chem. 1997, 358, 119–121. [Google Scholar] [CrossRef]
- Borri, C.; Paggi, M. Topology simulation and contact mechanics of bifractal rough surfaces. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 1345–1358. [Google Scholar] [CrossRef]
- Moulder, J.F.; Stickle, W.F.; Sobol, P.E.; Bomben, K.D. Handbook of X-ray Photoelectron Spectroscopy; Chastain, J., Ed.; Perkin-Elmer Corp.: Eden Prairie, MN, USA, 1992. [Google Scholar]
- Wang, Y.; Ren, Y.; Zhang, S.; Wu, J.; Song, J.; Li, X.; Xu, J.; Sow, C.H.; Zeng, H.; Sun, H. Switching excitonic recombination and carrier trapping in cesium lead halide perovskites by air. Commun. Phys. 2018, 1, 96. [Google Scholar] [CrossRef]
- Seth, S.; Ahmed, T.; De, A.; Samanta, A. Tackling the Defects, Stability, and Photoluminescence of CsPbX3 Perovskite Nanocrystals. ACS Energy Lett. 2019, 4, 1610–1618. [Google Scholar] [CrossRef]
- Boldish, S.I.; White, W.B. Optical band gaps of selected ternary sulfide minerals. Am. Mineral. 1998, 83, 865–871. [Google Scholar] [CrossRef]
- Tauc, J.; Grigorovici, R.; Vancu, A. Optical properties and electronic structure of amorphous germanium. Phys. Status Solidi b 1966, 15, 627–637. [Google Scholar] [CrossRef]
- Nolan, M.; O’Callaghan, S.; Fagas, G.; Greer, J.C.; Frauenheim, T. Silicon nanowire band gap modification. Nano Lett. 2007, 7, 34–38. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, T.; Zhao, X.; Zhu, Y. Controllable synthesis of Bi2MoO6 and effect of morphology and variation in local structure on photocatalytic activities. Appl. Catal. B Environ. 2010, 98, 138–146. [Google Scholar] [CrossRef]
- Pardeshi, S.; Patil, A. Effect of morphology and crystallite size on solar photocatalytic activity of zinc oxide synthesized by solution free mechanochemical method. J. Mol. Catal. A Chem. 2009, 308, 32–40. [Google Scholar] [CrossRef]
- Gabelloni, F.; Biccari, F.; Falsini, N.; Calisi, N.; Caporali, S.; Vinattieri, A. Long-living nonlinear behavior in CsPbBr3 carrier recombination dynamics. Nanophotonics 2019. [Google Scholar] [CrossRef]
- Diroll, B.T.; Zhou, H.; Schaller, R.D. Low-Temperature Absorption, Photoluminescence, and Lifetime of CsPbX3 (X = Cl, Br, I) Nanocrystals. Adv. Funct. Mater. 2018, 28, 1800945. [Google Scholar] [CrossRef]
- Becker, M.A.; Vaxenburg, R.; Nedelcu, G.; Sercel, P.C.; Shabaev, A.; Mehl, M.J.; Michopoulos, J.G.; Lambrakos, S.G.; Bernstein, N.; Lyons, J.L.; et al. Bright triplet excitons in caesium lead halide perovskites. Nature 2018, 553, 189. [Google Scholar] [CrossRef] [PubMed]

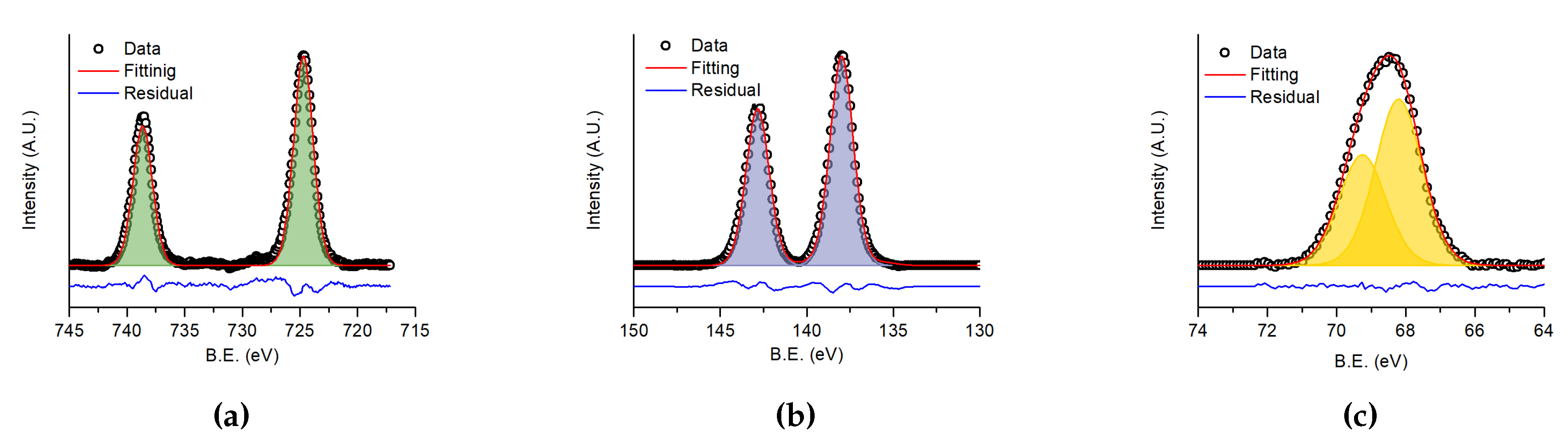
| Element | B.E. (eV) | Area | Measured Atomic Percentage | Expected Atomic Percentage |
|---|---|---|---|---|
| Cs | 724.7 | 3746 | 35 ± 3 | 20 |
| Pb | 138.0 | 10230 | 20 ± 2 | 20 |
| Br | 68.2 | 5661 | 45 ± 4 | 60 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borri, C.; Calisi, N.; Galvanetto, E.; Falsini, N.; Biccari, F.; Vinattieri, A.; Cucinotta, G.; Caporali, S. First Proof-of-Principle of Inorganic Lead Halide Perovskites Deposition by Magnetron-Sputtering. Nanomaterials 2020, 10, 60. https://doi.org/10.3390/nano10010060
Borri C, Calisi N, Galvanetto E, Falsini N, Biccari F, Vinattieri A, Cucinotta G, Caporali S. First Proof-of-Principle of Inorganic Lead Halide Perovskites Deposition by Magnetron-Sputtering. Nanomaterials. 2020; 10(1):60. https://doi.org/10.3390/nano10010060
Chicago/Turabian StyleBorri, Claudia, Nicola Calisi, Emanuele Galvanetto, Naomi Falsini, Francesco Biccari, Anna Vinattieri, Giuseppe Cucinotta, and Stefano Caporali. 2020. "First Proof-of-Principle of Inorganic Lead Halide Perovskites Deposition by Magnetron-Sputtering" Nanomaterials 10, no. 1: 60. https://doi.org/10.3390/nano10010060
APA StyleBorri, C., Calisi, N., Galvanetto, E., Falsini, N., Biccari, F., Vinattieri, A., Cucinotta, G., & Caporali, S. (2020). First Proof-of-Principle of Inorganic Lead Halide Perovskites Deposition by Magnetron-Sputtering. Nanomaterials, 10(1), 60. https://doi.org/10.3390/nano10010060