Simulation of Orbital Fractures Using Experimental and Mathematical Approaches: A Pilot Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Cadaveric Skulls
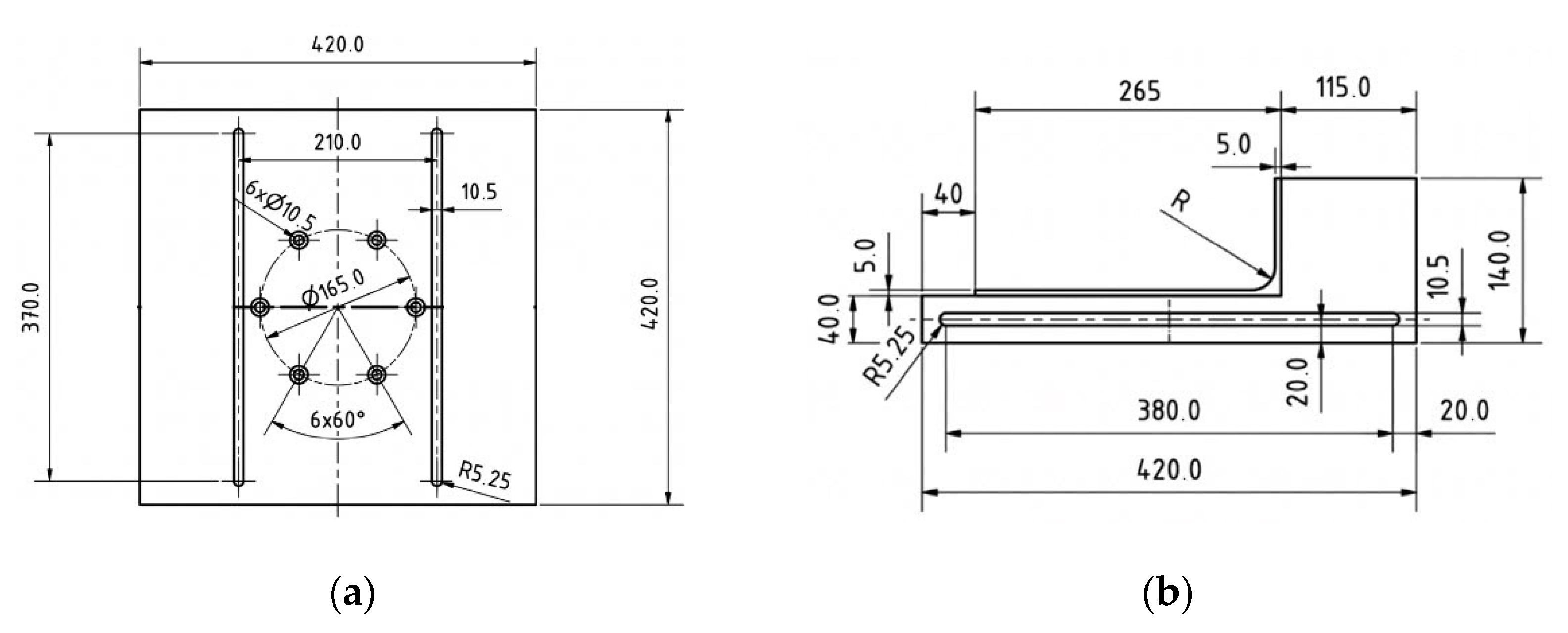
2.2. Compression Test of the Cadaveric Skulls
2.3. Experimental Modal Analysis
2.4. Numerical Model of Modal Analysis
3. Results and Discussion
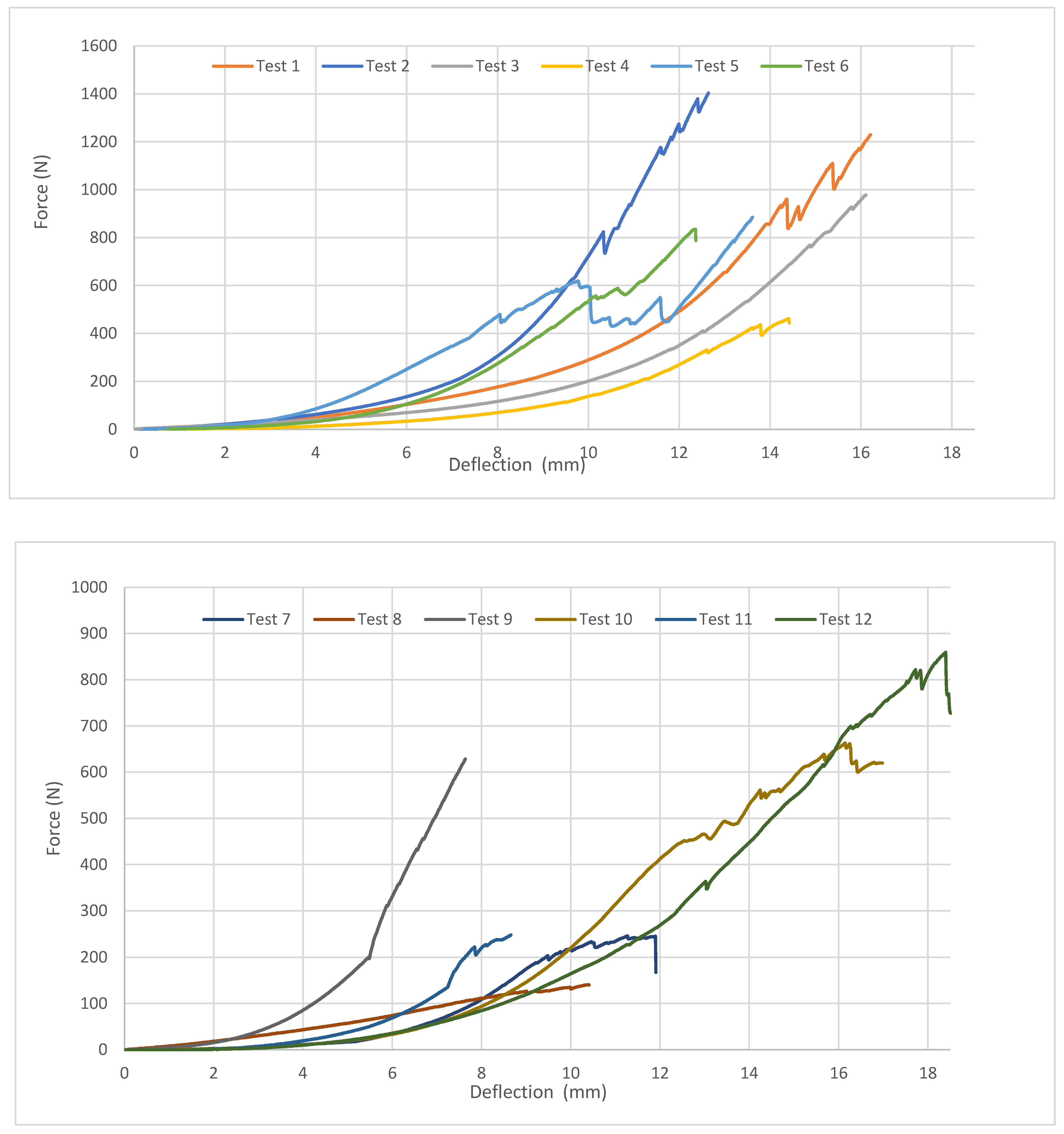
3.1. Static Compression Test Results for Cadaveric Crania
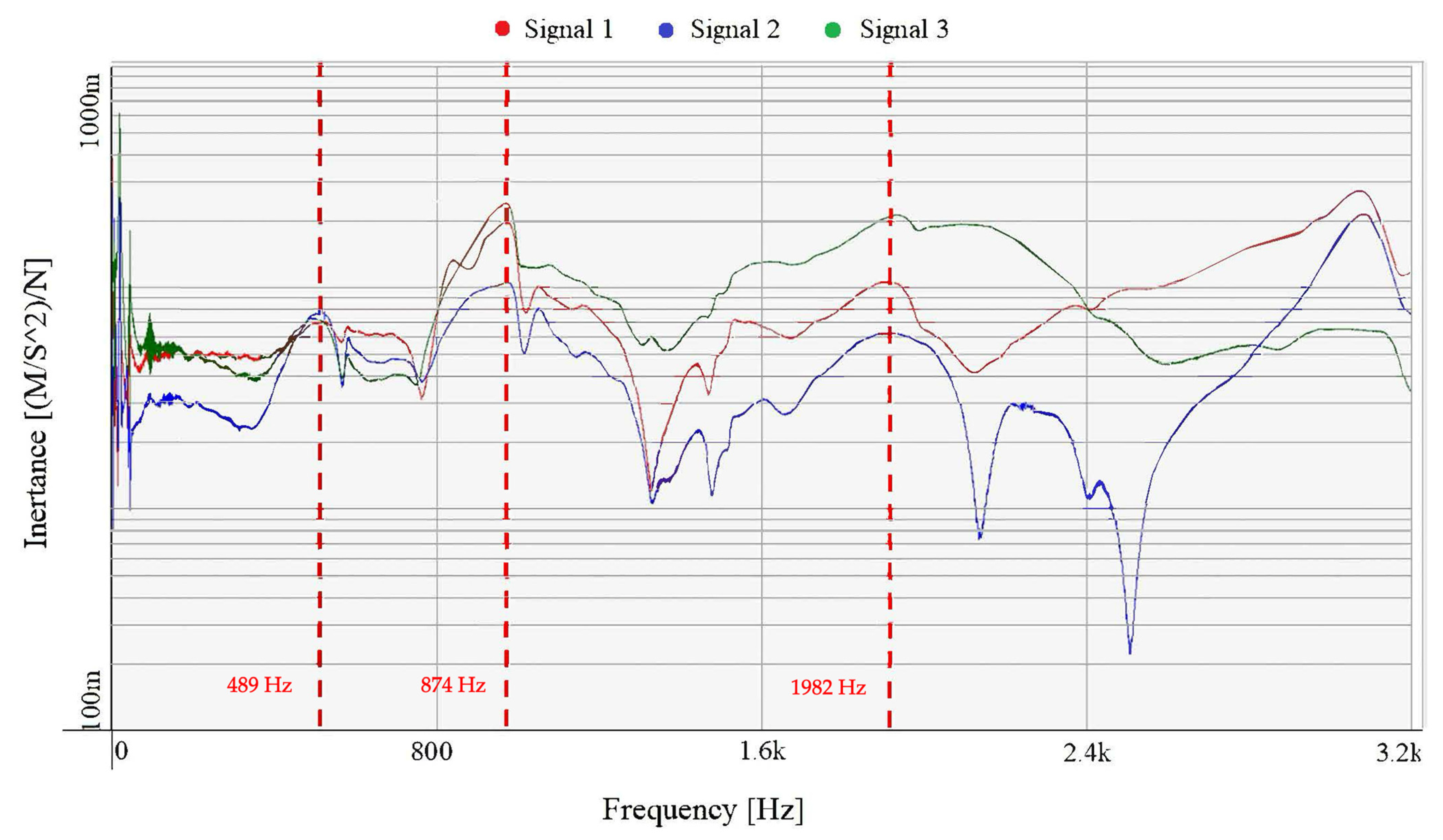
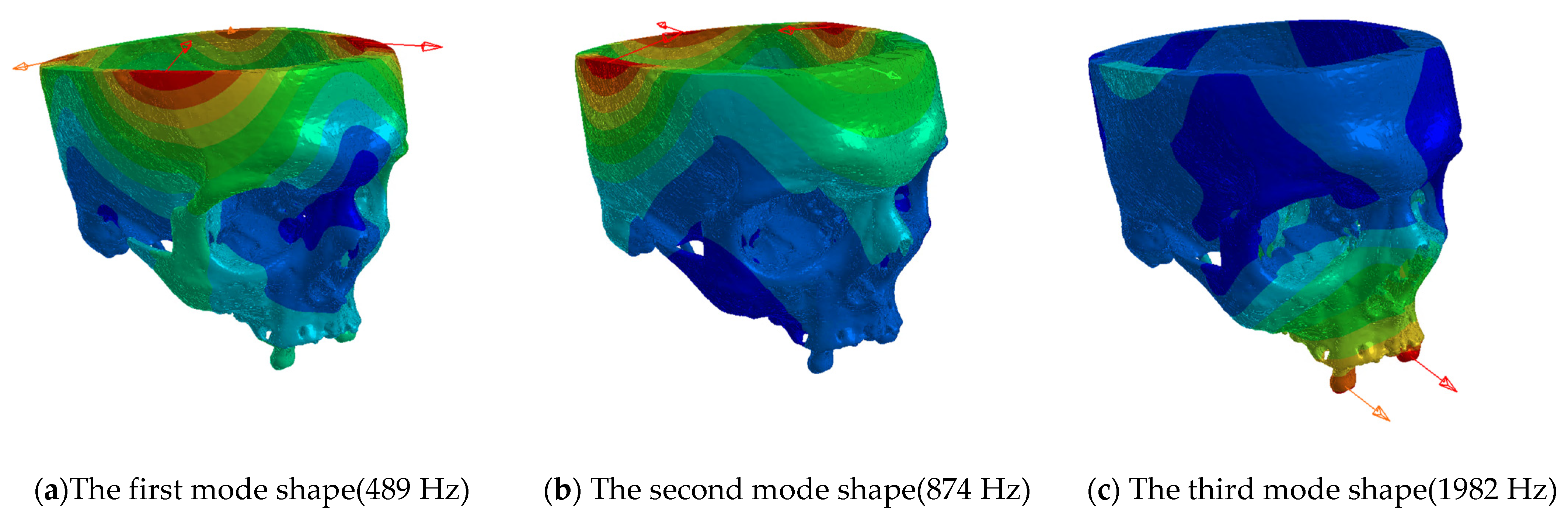
3.2. Dynamic Results of the Experimental Modal Analysis
3.3. Future Research
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Antonyshyn, O.; Gruss, J.S.; Kassel, E.E. Blow-In Fractures of the Orbit. Plast. Reconstr. Surg. 1989, 84, 10–20. [Google Scholar] [CrossRef] [PubMed]
- Hartstein, M.E.; Roper-Hall, G. Update on Orbital Floor Fractures: Indications and Timing for Repair. Facial Plast. Surg. 2000, 16, 95–106. [Google Scholar] [CrossRef] [PubMed]
- Kopecky, A.; Rokohl, A.C.; Nemcansky, J.; Koch, K.R.; Matousek, P.; Heindl, L.M. Retrobulbar Haematoma—A Complication that May Impair Vision. Klin. Monatsbl. Augenheilkd. 2021, 238, 609–615. [Google Scholar] [CrossRef]
- O’Hare, T.H. Blow-out fractures: A review. J. Emerg. Med. 1991, 9, 253–263. [Google Scholar] [CrossRef] [PubMed]
- Adeyemo, W.L.; Aribaba, O.T.; Ladehinde, A.L.; Ogunlewe, M.O. Mechanisms of orbital blowout fracture: A critical review of the literature. Niger. Postgrad. Med. J. 2008, 15, 251–254. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, F.; Kirkpatrick, N.A.; Lyne, J.; Urdang, M.; Waterhouse, N. Buckling and Hydraulic Mechanisms in Orbital Blowout Fractures: Fact or Fiction? J. Craniofacial Surg. 2006, 17, 438–441. [Google Scholar] [CrossRef] [PubMed]
- Gómez Roselló, E.; Quiles Granado, A.M.; Artajona Garcia, M.; Juanpere Martí, S.; Laguillo Sala, G.; Beltrán Mármol, B.; Pedraza Gutiérrez, S. Facial fractures: Classification and highlights for a useful report. Insights Imaging 2020, 11, 49. [Google Scholar] [CrossRef] [PubMed]
- Kahn, J.L.; Bourjat, P. Les fractures par enfoncement dites « blow-out » de l’orbite. J. Radiol. 2006, 87, 601–605. [Google Scholar] [CrossRef]
- Warwar, R.E.; Bullock, J.D.; Ballal, D.R.; Ballal, R.D. Mechanism of orbital floor fractures: A clinical, experimental, and theoretical study. Ophthalmic Plast. Reconstr. Surg. 2000, 16, 188–200. [Google Scholar] [CrossRef] [PubMed]
- Hirjak, D.; Machoň, V. Traumatologie Skeletu Tváre; Slovensk, s.r.o.: Bratislava, Slovakia, 2013; pp. 99–100. ISBN 978-80-971444-0-1. [Google Scholar]
- Timkovic, J.; Stransky, J.; Janurova, K.; Handlos, P.; Stembirek, J. Role of orthoptics and scoring system for orbital floor blowout fracture: Surgical or conservative treatment. Int. J. Ophthalmol. 2021, 14, 1928–1934. [Google Scholar] [CrossRef] [PubMed]
- Kubíček, J.; Tomanec, F.; Černý, M.; Vilímek, D.; Kalová, M.; Oczka, D. Recent Trends, Technical Concepts and Components of Computer-Assisted Orthopedic Surgery Systems: A Comprehensive Review. Sensor 2019, 19, 5199. [Google Scholar] [CrossRef] [PubMed]
- Eiba, P.; Frydrýšek, K.; Čepica, D.; Halo, T.; Handlos, P.; Timkovič, J.; Štembírek, J.; Stránský, J.; Pleva, L.; Havlíček, M.; et al. Research on splachnocranial injuries due to brachial violence. In Proceedings of the Engineering Mechanics 2022, Milovy, Czech Republic, 9–12 May 2022; pp. 89–92. [Google Scholar]
- Timkovic, J.; Stransky, J.; Handlos, P.; Janosek, J.; Tomaskova, H.; Stembirek, J. Detecting Binocular Diplopia in Orbital Floor Blowout Fractures: Superiority of the Orthoptic Approach. Medicina 2021, 57, 989. [Google Scholar] [CrossRef] [PubMed]
- Klíma, O.; Novobilsky, P.; Madeja, R.; Barina, D.; Chromy, A.; Spanel, M.; Zemcik, P. Intensity-based nonoverlapping area registration supporting “Drop-Outs” in terms of model-based radiostereometric analysis. J. Healthc. Eng. 2018, 2018, 8538125. [Google Scholar] [CrossRef] [PubMed]
- Hudec, M. A new procedure for bleaching bones from ossuaries. Ceskoslovenska Morfol. 1964, 12, 225–228. [Google Scholar]
- White, T. Human Osteology, 3rd ed.; Academic Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Frydrýšek, K.; Šír, M.; Pleva, L.; Szeliga, J.; Stránský, J.; Čepica, D.; Kratochvíl, J.; Koutecký, J.; Madeja, R.; Dědková, K.P.; et al. Stochastic Strength Analyses of Screws for Femoral Neck Fractures. Appl. Sci. 2022, 12, 1015. [Google Scholar] [CrossRef]
- Fastovicz, J.; Grudzinski, M.; Teclaw, M.; Okarma, K. Objective 3D Printed Surface Quality Assessment Based on Entropy of Depth Maps. Entropy 2019, 21, 97. [Google Scholar] [CrossRef] [PubMed]
- Frydrýšek, K. Biomechanika 1: Biomechanics 1; Ostrava: VŠB—Technická Univerzita Ostrava, Fakulta Strojní: Prague, Czech Republic, 2019; ISBN 978-80-248-4263-9. [Google Scholar]
- McElhaney, J.H.; Fogle, J.L.; Melvin, J.W.; Haynes, R.R.; Roberts, V.L.; Alem, N.M. Mechanical properties of cranial bone. J. Biomech. 1970, 3, 495–511. [Google Scholar] [CrossRef] [PubMed]






| Number of Nodes | Number of Elements | Number of DOF |
|---|---|---|
| 3,898,015 | 2,535,958 | 11,694,045 |
| Young’s Modulus | Density | Poisson’s Ratio |
|---|---|---|
| Min. 123.686 MPa | Min. 20.812 kg/m3 | 0.19 |
| Max. 24,552.3 MPa | Max. 4144.3 kg/m3 | 0.19 |
| Mean 12,231.7 MPa | Mean 2064.4 kg/m3 | 0.19 |
| Std. deviation 7166.7 MPa | Std. deviation 1209.6 kg/m3 | 0 |
| Median 12,214.6 MPa | Median 2061.2 kg/m3 | 0.19 |
| Test No. | Initiation Force of Fracture [N] | Max. Loading Force [N] | Age | Sex |
|---|---|---|---|---|
| 1 | 820 | 1229 | 20–30 | Male |
| 2 | 953 | 1403 | 20–30 | Male |
| 3 | 819 | 977 | 20–30 | Male |
| 4 | 404 | 461 | 20–30 | Male |
| 5 | 461 | 885 | 55–65 | Male |
| 6 | 389 | 834 | 55–65 | Male |
| 7 | 129 | 246 | 65–80 | Male |
| 8 | 136 | 143 | 65–80 | Male |
| 9 | 431 | 628 | 55–65 | Male |
| 10 | 455 | 650 | 55–65 | Male |
| 11 | 205 | 242 | 65–80 | Male |
| 12 | 794 | 860 | 65–80 | Male |
| Median | 819 | 1103 | Individuals 20–30 | |
| Maximum | 953 | 1403 | ||
| Minimum | 404 | 461 | ||
| Median | 443 | 742 | Individuals 55–65 | |
| Maximum | 461 | 885 | ||
| Minimum | 389 | 628 | ||
| Median | 170 | 244 | Individuals 65–80 | |
| Maximum | 794 | 860 | ||
| Minimum | 129 | 143 | ||
| Natural Frequency | Young’s Modulus Multiple | Density 95% | Difference from Experiment | Density 100% | Difference from Experiment | Density 105% | Difference from Experiment |
|---|---|---|---|---|---|---|---|
| 95% | 688.3 Hz | 40.8% | 670.9 Hz | 37.2% | 654.7 Hz | 33.9% | |
| Frequency 489 Hz | 100% | 706.2 Hz | 44.4% | 688.3 Hz | 40.8% | 671.7 Hz | 37.4% |
| 105% | 723.6 Hz | 48.0% | 705.3 Hz | 44.2% | 688.3 Hz | 40.8% | |
| 95% | 734.3 Hz | −16.0% | 715.7 Hz | −18.1% | 698.5 Hz | −20.1% | |
| Frequency 874 Hz | 100% | 753.4 Hz | −13.8% | 734.3 Hz | −16.0% | 716.6 Hz | −18.0% |
| 105% | 772.0 Hz | −11.7% | 752.4 Hz | −13.9% | 734.3 Hz | −16.0% | |
| 95% | 1441.7 | −27.3% | 1405.2 | −29.1% | 1371.4 | −30.8% | |
| Frequency 1982 Hz | 100% | 1479.2 | −25.4% | 1441.7 | −27.3% | 1407.0 | −29.0% |
| 105% | 1515.7 | −23.5% | 1477.3 | −25.5% | 1441.7 | −27.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eiba, P.; Frydrysek, K.; Zanganeh, B.; Cepica, D.; Marsalek, P.; Handlos, P.; Timkovic, J.; Stembirek, J.; Cienciala, J.; Onderka, A.; et al. Simulation of Orbital Fractures Using Experimental and Mathematical Approaches: A Pilot Study. J. Funct. Biomater. 2024, 15, 143. https://doi.org/10.3390/jfb15060143
Eiba P, Frydrysek K, Zanganeh B, Cepica D, Marsalek P, Handlos P, Timkovic J, Stembirek J, Cienciala J, Onderka A, et al. Simulation of Orbital Fractures Using Experimental and Mathematical Approaches: A Pilot Study. Journal of Functional Biomaterials. 2024; 15(6):143. https://doi.org/10.3390/jfb15060143
Chicago/Turabian StyleEiba, Patrik, Karel Frydrysek, Behrad Zanganeh, Daniel Cepica, Pavel Marsalek, Petr Handlos, Juraj Timkovic, Jan Stembirek, Jakub Cienciala, Arnost Onderka, and et al. 2024. "Simulation of Orbital Fractures Using Experimental and Mathematical Approaches: A Pilot Study" Journal of Functional Biomaterials 15, no. 6: 143. https://doi.org/10.3390/jfb15060143
APA StyleEiba, P., Frydrysek, K., Zanganeh, B., Cepica, D., Marsalek, P., Handlos, P., Timkovic, J., Stembirek, J., Cienciala, J., Onderka, A., Brezik, M., & Mizera, O. (2024). Simulation of Orbital Fractures Using Experimental and Mathematical Approaches: A Pilot Study. Journal of Functional Biomaterials, 15(6), 143. https://doi.org/10.3390/jfb15060143






