Study of an Additional Layer of Cement Mantle Hip Joints for Reducing Cracks
Abstract
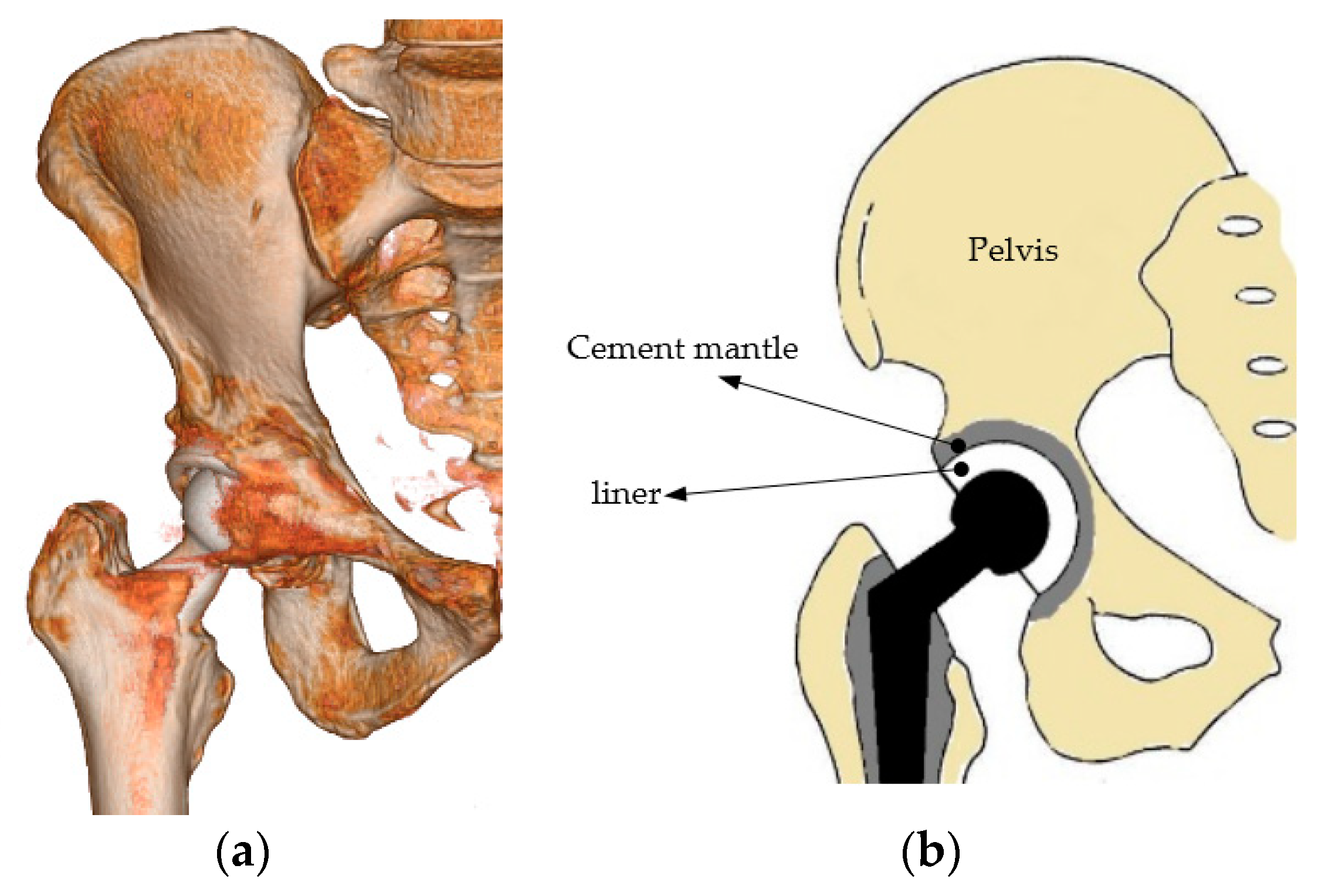
1. Introduction
2. Method
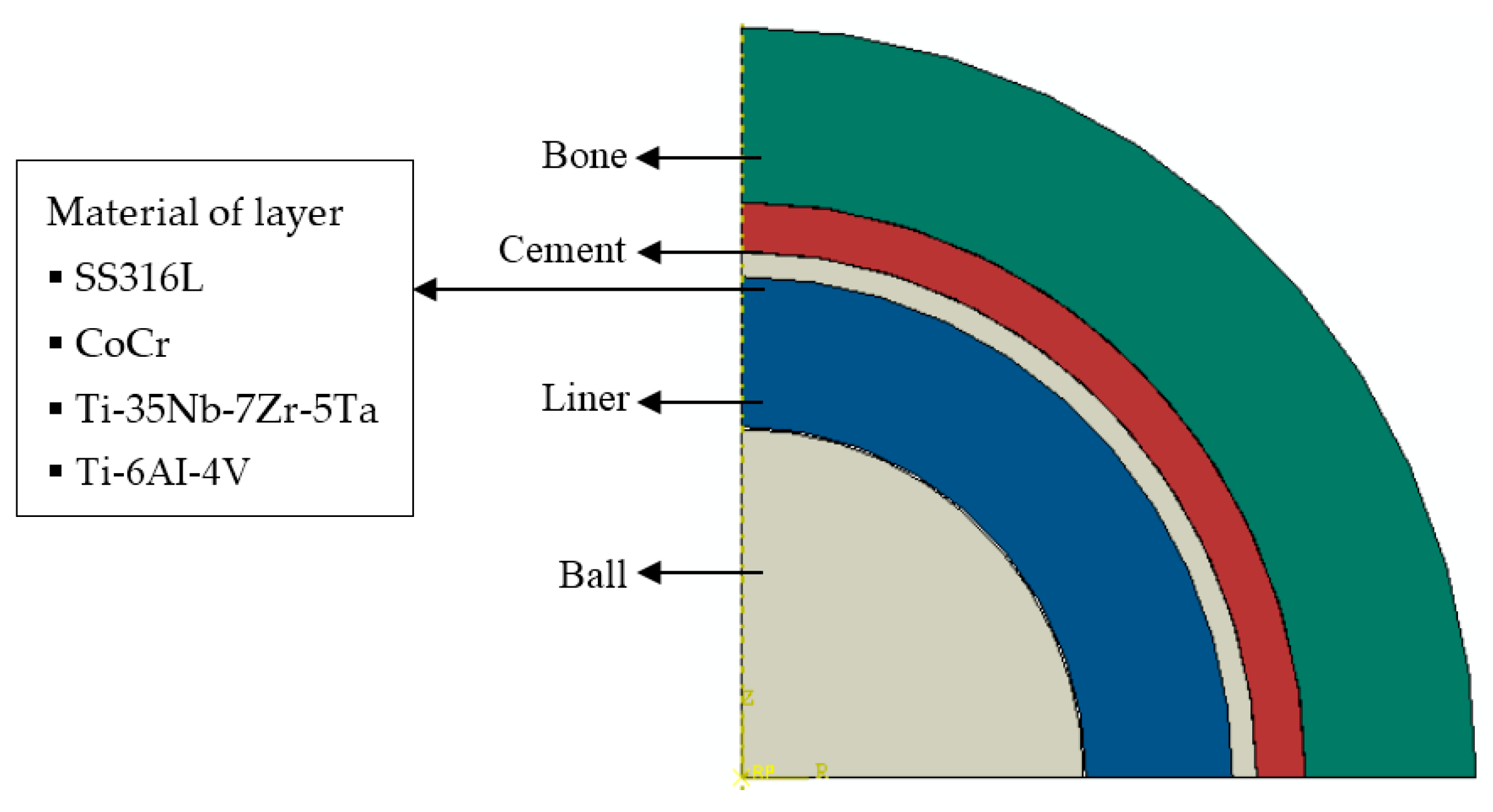
2.1. Model of Geometry and Material
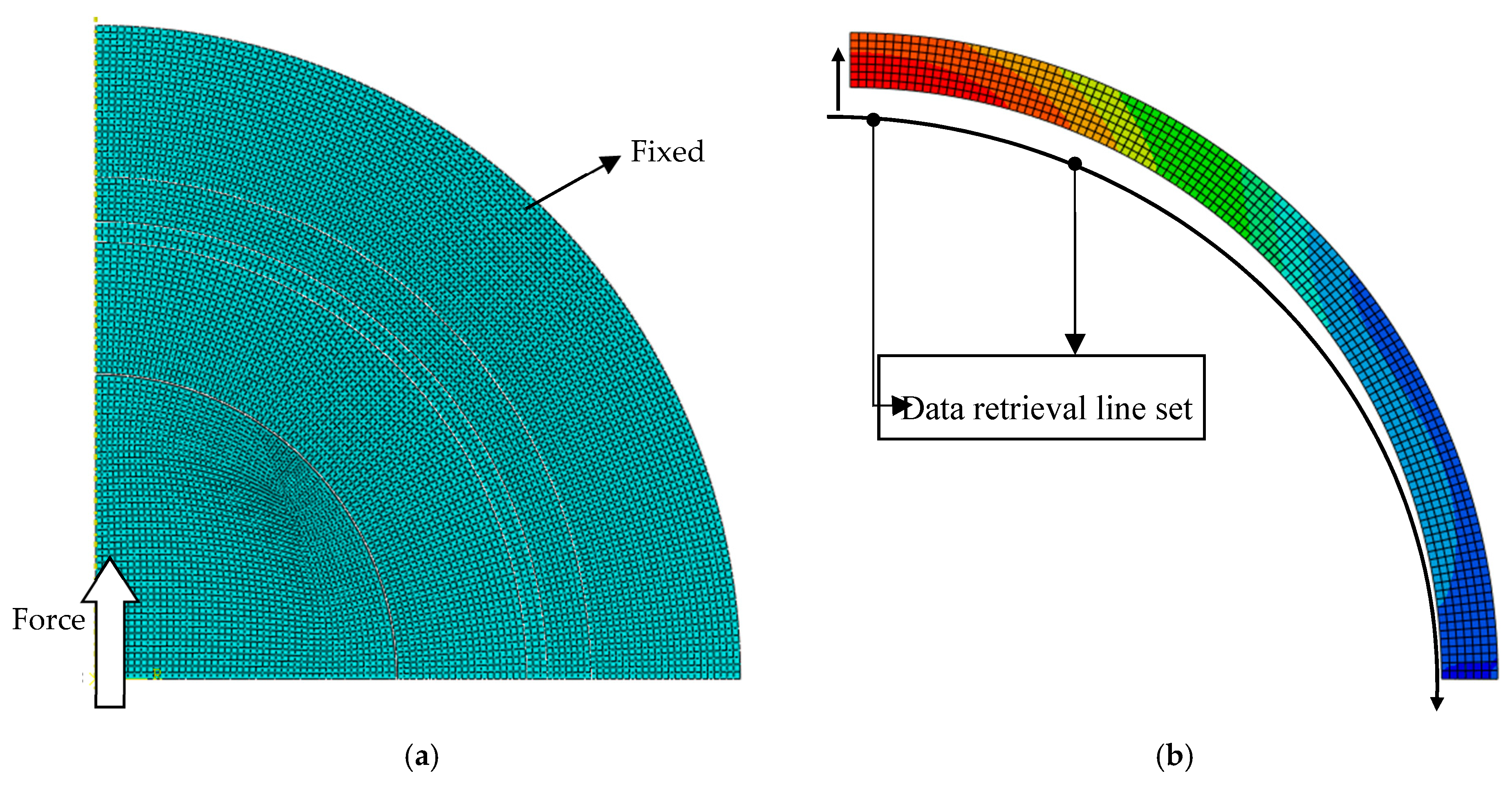
2.2. Simulation Procedure
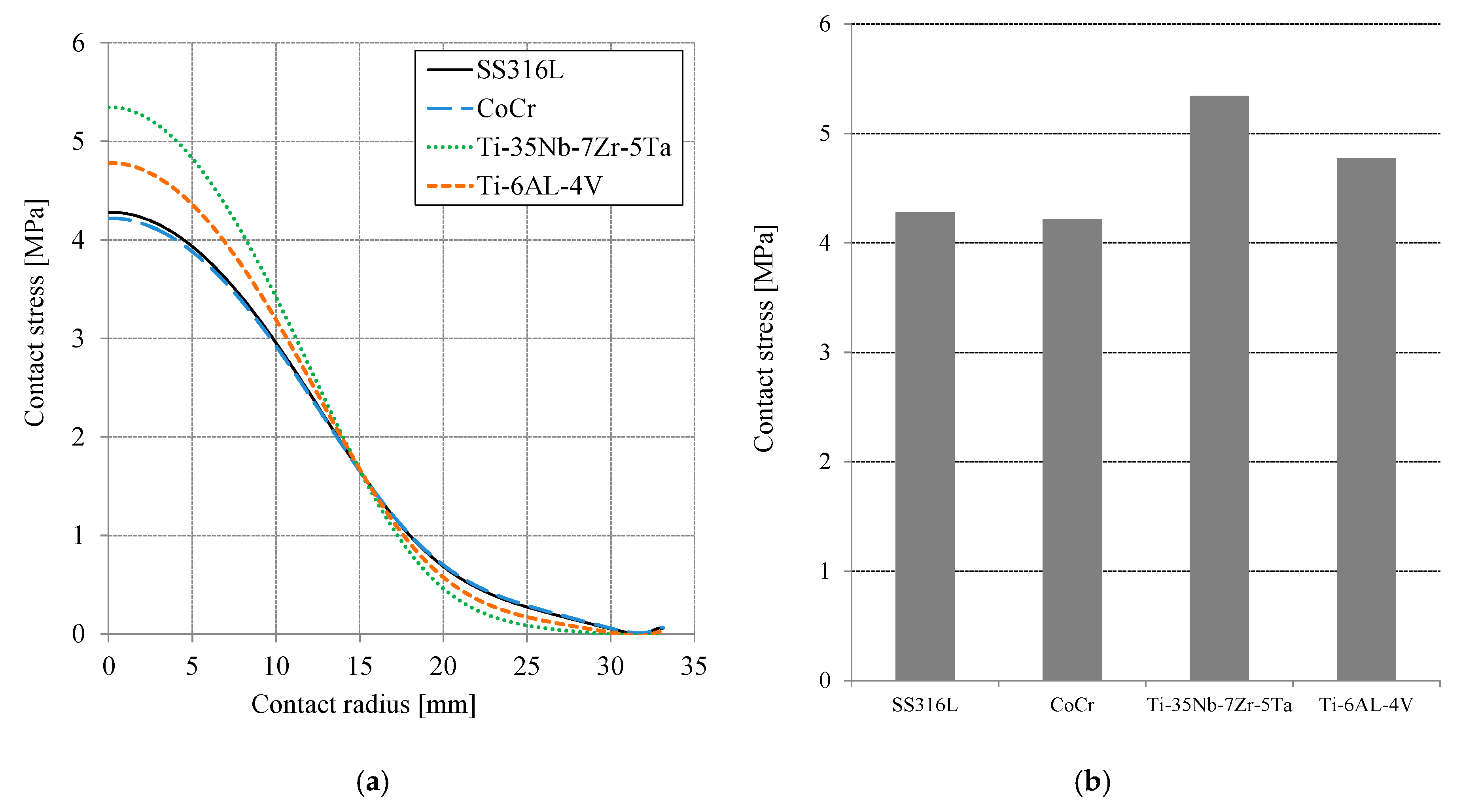
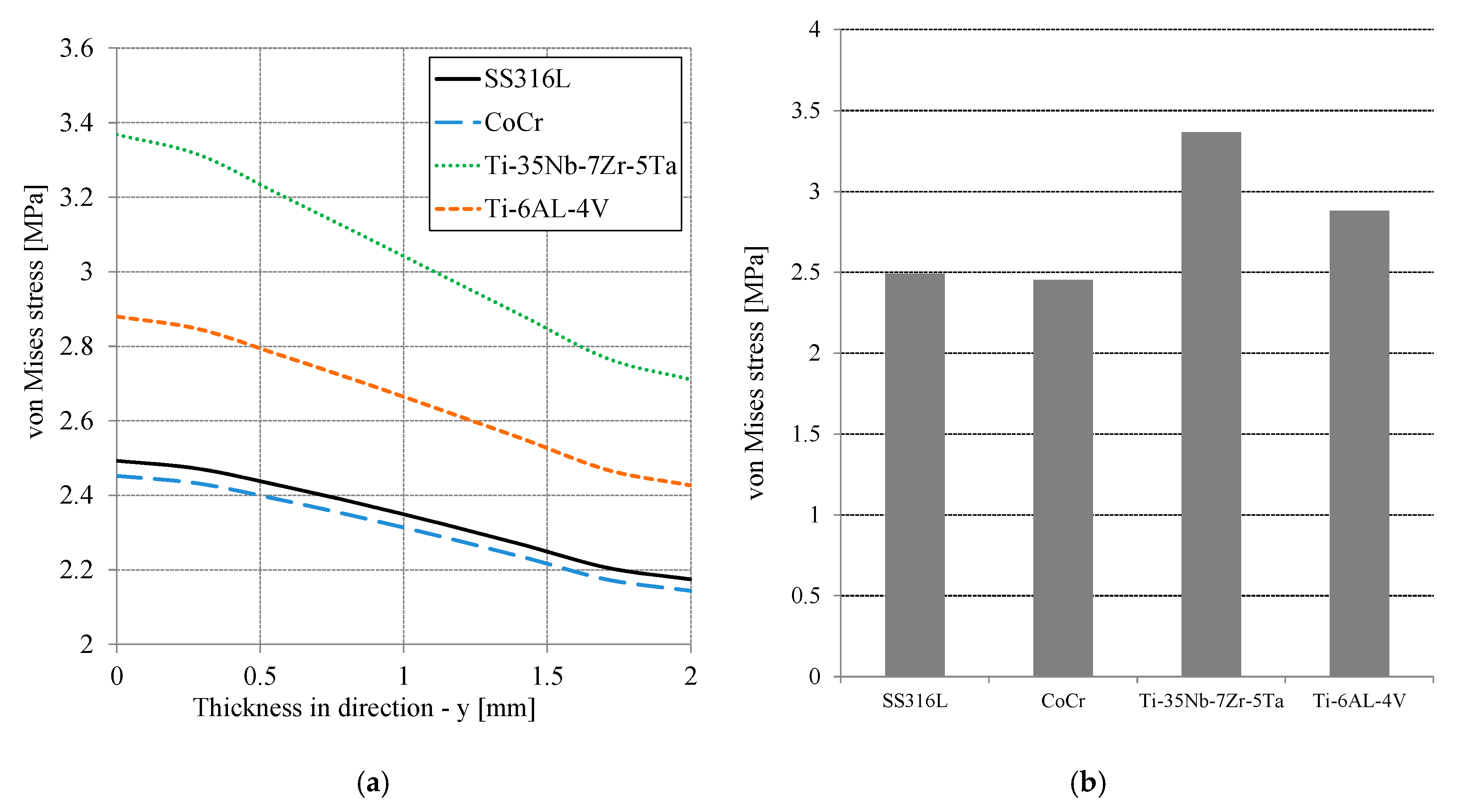
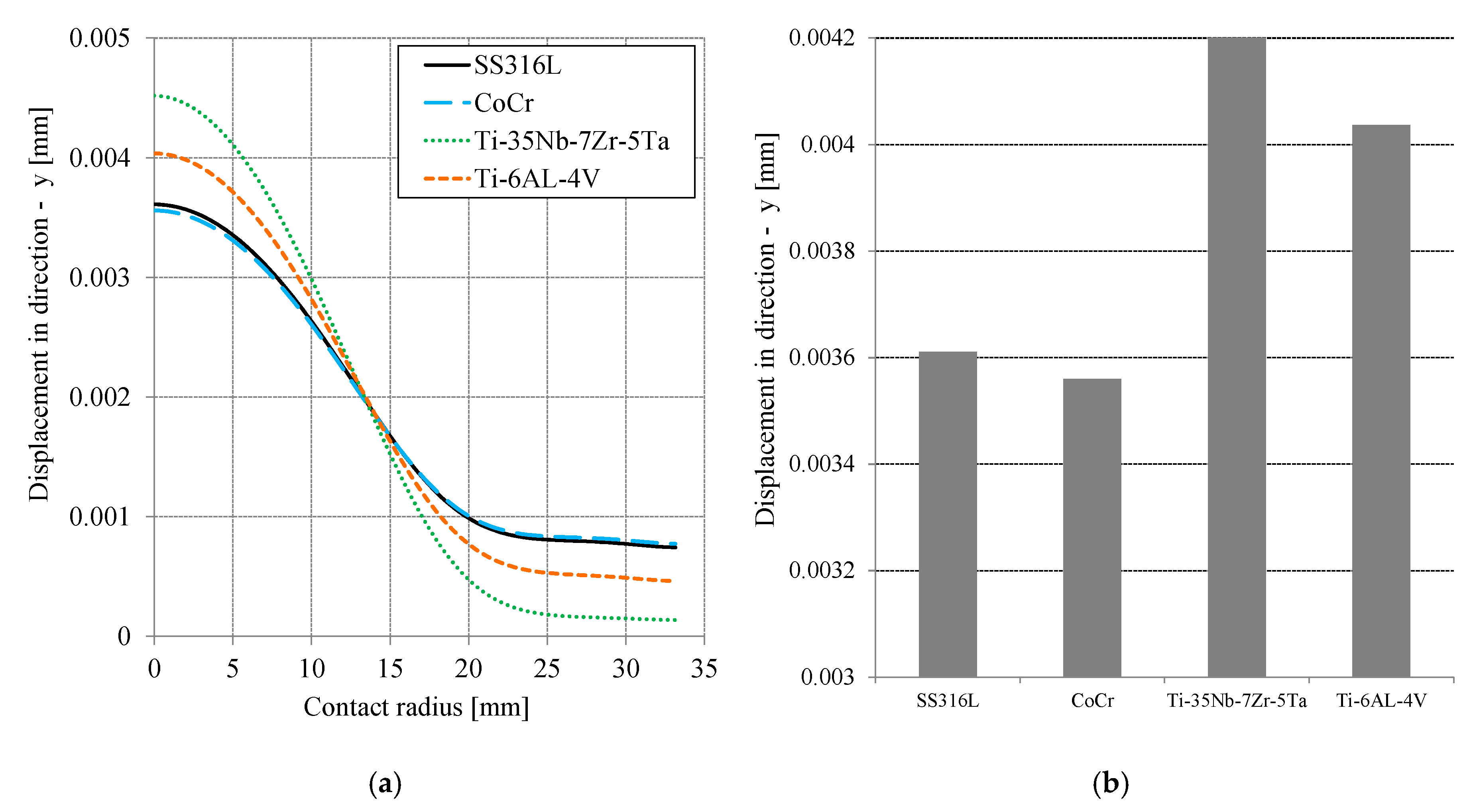
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fisher, D.A.; Tsang, A.C.; Paydar, N.; Milionis, S.; Turner, C.H. Cement-mantle thickness affects cement strains in total hip replacement. J. Biomech. 1997, 30, 1173–1177. [Google Scholar] [CrossRef]
- Jacobs, C.R.; Bechtel, J.B.; Davis, B.R.; Naidu, S.H.; Pellegrini, V.D. Fatigue Lifetime Studies of a New Bone Cement Formulation. Available online: https://usermanual.wiki/Document/97504900700FatigueLifetimeStudiesofa NewBoneCementFormulation.878194870.pdf (accessed on 2 May 2019).
- Letters, T.J.; Higgs, R.J.E.D.; Baillie, C.A. Factors influencing the fatigue life of acrylic bone cements in arthroplasty: An experimental, ex-vivo and finite element analysis. In Proceedings of the 46th Annual Meeting, Orthopaedic Research Society, Orlando, FL, USA, 12–15 March 2000. [Google Scholar]
- Zant, N.P.; Wong, C.K.Y.; Tong, J. Fatigue failure in the cement mantle of a simplified acetabular replacement model. Int. J. Fatigue 2007, 29, 1245–1252. [Google Scholar] [CrossRef]
- National Ortophaedic Hospital Solo. In Internal Report; 2019.
- Ramos, A.; Simoes, J.A. The influence of cement mantle thickness and stem geometry on fatigue damage in two different cemented hip femoral prostheses. J. Biomech. 2009, 42, 2602–2610. [Google Scholar] [CrossRef]
- Lamvohee, J.M.S.; Ingle, P.; Cheah, K.; Dowell, J.; Mootanah, R. Total hip replacement: Tensile stress in bone cement is influenced by cement mantle thickness, acetabular size, bone quality, and body mass index. J. Comput. Sci. Syst. Biol. 2014, 7, 72–78. [Google Scholar] [CrossRef]
- Mann, K.; Hertzler, J. Crack growth rate in cemented total hip replacement does not depend on cement mantle thickness. In Proceedings of the 47th Annual Meeting, Orthopaedic Research Society, San Francisco, CA, USA, 25–28 February 2001. [Google Scholar]
- Hertzler, J.; Miller, M.A.; Mann, K.A. Fatigue crack growth rate does not depend on mantle thickness: An idealized cemented stem construct under torsional loading. J. Orthop. Res. 2002, 20, 676–682. [Google Scholar] [CrossRef]
- Jamari, J.; Han, A.L.; Saputra, E.; Anwar, I.B.; van der Heide, E. The Effect of Additional Layer between Liner and PMMA on Reducing Cracks of Cement Mantle Hip Joints. Int. J. Eng. Tech. Innov. 2018, 8, 99–106. [Google Scholar]
- Saputra, E.; Anwar, I.B.; Jamari, J.; van der Heide, E. Finite element analysis of artificial hip joint movement during human activities. Proced. Eng. 2013, 68, 102–108. [Google Scholar] [CrossRef]
- Jamari, J.; Ismail, R.; Saputra, E.; Sugiyanto, S.; Anwar, I.B. The effect of repeated impingement on UHMWPE material in artificial hip joint during salat activities. Adv. Mater. Res. 2014, 896, 272–275. [Google Scholar] [CrossRef]
- Saputra, E.; Anwar, I.B.; Ismail, R.; Jamari, J.; van der Heide, E. Numerical simulation of artificial hip joint movement for Western and Japanese-style activities. J. Teknol. 2014, 66, 53–58. [Google Scholar] [CrossRef]
- ABAQUS 6.12 Documentation; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2012.
- Gunn, E.; Gundapaneni, D.; Goswami, T. Effect of cement fill ratio in loosening of hip implants. Biomatter 2012, 2, 87–93. [Google Scholar] [CrossRef]
- Anderson, A.E.; Peters, C.L.; Tuttle, B.D.; Weiss, J.A. A subject-specific finite element model of the pelvis: Development, validation and sensitivity studies. J. Biomech. Eng. 2005, 127, 364–373. [Google Scholar] [CrossRef]
- Sahli, A.; Benbareka, S.; Wayneb, S.; Bouiadjraa, B.A.B.; Seriera, B. 3D crack behavior in the orthopedic cement mantle of a total hip replacement. Appl. Bionics. Biomech. 2014, 11, 135–147. [Google Scholar] [CrossRef]
- Ouinas, D.; Flliti, A.; Sahnoun, M.; Benbarek, S.; Taghezout, N. Fracture behavior of the cement mantle of reconstructed acetabulum in the presence of a microcrack emanating from a microvoid. IJMSE 2012, 2, 90–104. [Google Scholar] [CrossRef]
- Achour, T.; Tabeti, M.S.H.; Bouziane, M.M.; Benbarek, S.; Bouiadjra, B.B.; Mankour, A. Finite element analysis of interfacial crack behaviour in cemented total hip arthroplasty. Comput. Mater. Sci. 2010, 47, 672–677. [Google Scholar] [CrossRef]
- Eichmiller, F.C.; Tesk, J.A.; Croarkin, C.M. Mechanical properties of ultra-high molecular weight polyethylene NIST reference material RM 8456. SFB 2001, 22, 472. [Google Scholar]
- Yildiz, F.; Yetim, A.F.; Alsaran, A.; Celik, A.; Kaymaz, I. Fretting fatigue properties of plasma nitrided AISI 316L stainless steel: Experiments and finite element analysis. Tribol. Int. 2011, 44, 1979–1986. [Google Scholar] [CrossRef]
- Navarro, M.; Michiardi, A.; Castano, O.; Planell, J.A. Biomaterials in orthopaedics. J. R. Soc. Interf. 2008, 5, 1137–1158. [Google Scholar] [CrossRef]
- Niinomi, M. Recent metallic materials for biomedical applications. Metal. Mater. Trans. A 2002, 33A, 477–486. [Google Scholar] [CrossRef]
- Bergmann, G.; Deuretzbacher, G.; Heller, G.; Graichen, F.; Rohlmann, A.; Strauss, J.; Duda, G.N. Hip contact forces and gait patterns from routine activities. J. Biomech. 2001, 34, 859–871. [Google Scholar] [CrossRef]
- Wang, J.; Meng, F.; Li, Z.; Li, J.; Yao, K. Research on interface bonding energy of multi-layer on ZChSnSb/FeSn2/Steel. Tribol. Int. 2018, 123, 37–42. [Google Scholar] [CrossRef]
- Xia, Q.; Wang, J.; Yao, K.; Hou, D.; Li, Z. Interface bonding properties of multi-layered metal composites using material composition method. Tribol. Int. 2019, 131, 251–257. [Google Scholar] [CrossRef]
- Lord, J.K.; Langton, D.J.; Nargol, A.V.F.; Meek, R.M.D.; Joyce, J.J. The tribology of explanted hip resurfacings following early fracture of the femur. J. Funct. Biomater. 2015, 6, 1021–1035. [Google Scholar] [CrossRef]
- Keegan, G.M.; Learmonth, I.D.; Case, C.P. Orthopaedic metals and their potential toxicity in the arthroplasty patient: A review of current knowledge and future strategies. J. Bone Joint Surg. 2007, 89-B, 567–573. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamari, J.; Saputra, E.; Anwar, I.B.; van der Heide, E. Study of an Additional Layer of Cement Mantle Hip Joints for Reducing Cracks. J. Funct. Biomater. 2019, 10, 40. https://doi.org/10.3390/jfb10030040
Jamari J, Saputra E, Anwar IB, van der Heide E. Study of an Additional Layer of Cement Mantle Hip Joints for Reducing Cracks. Journal of Functional Biomaterials. 2019; 10(3):40. https://doi.org/10.3390/jfb10030040
Chicago/Turabian StyleJamari, J., Eko Saputra, Iwan Budiwan Anwar, and Emile van der Heide. 2019. "Study of an Additional Layer of Cement Mantle Hip Joints for Reducing Cracks" Journal of Functional Biomaterials 10, no. 3: 40. https://doi.org/10.3390/jfb10030040
APA StyleJamari, J., Saputra, E., Anwar, I. B., & van der Heide, E. (2019). Study of an Additional Layer of Cement Mantle Hip Joints for Reducing Cracks. Journal of Functional Biomaterials, 10(3), 40. https://doi.org/10.3390/jfb10030040





