We Can Boost IQ: Revisiting Kvashchev’s Experiment
Abstract
1. Introduction
2. Theoretical Background
2.1. The Effect of Cognitive Training on Intelligence
2.2. Kvashchev’s Experiment
“I was captured by a band of outlaws—said a famous explorer—and their leader had my hands and legs tied up so that 1could not move. They did not gag me up though, and I was able to use my mouth freely. The leader of the gang hung a piece of bread exactly five centimetres away from my mouth. He then laughed and said: "If you manage to eat this piece of bread, I’II set you free. He knew that I could get no help. Also, in order to ensure that I cannot roll over or move closer to bread, they tied me to a tree. Nevertheless, I managed to free myself. How?”
3. Methodology and Results
New Insights and Proposed Reanalysis
4. Changes in Fluid (Gf) and Crystallized (Gc) Intelligence
5. Conclusions and Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
| IQ Tests | Control Group | Experimental Group | Difference (Experimental–Control) in IQ Units | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial (Age 15) | 2nd Retest (Age 19) | Effect Size in IQ Units | Initial (Age 15) | 2nd Retest (Age 19) | Effect Size in IQ Units | ||||||
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | ||||
| 1. Essential Features (Gc) | 30.76 | 5.45 | 37.49 | 4.21 | 20.90 | 28.41 | 6.72 | 39.42 | 2.83 | 34.59 | 13.69 |
| 2. Word Classification (Gc) | 10.84 | 2.52 | 12.84 | 3.51 | 9.95 | 10.05 | 2.76 | 14.29 | 1.56 | 29.44 | 19.49 |
| 3. Number Series | 10.61 | 2.37 | 12.46 | 2.14 | 12.31 | 9.87 | 2.44 | 13.77 | 1.81 | 27.53 | 15.22 |
| 4. Consequences (Gc) | 34.90 | 4.92 | 38.33 | 3.29 | 12.53 | 31.91 | 6.41 | 39.21 | 3.38 | 22.37 | 9.84 |
| 5. Relations (Gc) | 12.56 | 2.63 | 14.87 | 1.66 | 16.15 | 10.59 | 3.04 | 15.15 | 1.21 | 32.19 | 16.03 |
| 6. Word Meanings | 28.78 | 6.83 | 37.32 | 5.02 | 21.62 | 26.63 | 7.48 | 39.20 | 4.25 | 32.15 | 10.53 |
| 7. Unbalanced Structures (Gc) | 10.28 | 2.53 | 13.19 | 2.08 | 18.94 | 8.85 | 2.62 | 13.66 | 1.73 | 33.17 | 14.24 |
| 8. Numeric | 14.08 | 2.01 | 14.88 | 1.11 | 7.69 | 13.60 | 2.07 | 15.12 | 1.11 | 14.34 | 6.65 |
| 9. Pictorial Poly-profile | 23.00 | 6.67 | 33.01 | 6.33 | 23.10 | 20.53 | 6.00 | 35.33 | 5.23 | 39.54 | 16.44 |
| 10. Meaningful Memory | 12.96 | 4.55 | 21.72 | 8.59 | 20.00 | 13.81 | 5.53 | 25.91 | 8.63 | 25.64 | 5.64 |
| 11. Word Classification “S” | 14.29 | 2.79 | 18.59 | 2.97 | 22.40 | 15.46 | 2.79 | 20.82 | 2.26 | 31.84 | 9.45 |
| 12. Proverbs (Gc) | 9.50 | 3.93 | 16.22 | 4.00 | 25.42 | 9.46 | 3.95 | 17.81 | 2.92 | 36.46 | 11.04 |
| 13. Verbal Analogies (Gc) | 19.51 | 5.11 | 24.73 | 3.25 | 18.73 | 20.06 | 4.76 | 26.11 | 2.66 | 24.46 | 5.73 |
| 14. Disarranged Sentences (Gc) | 10.42 | 4.12 | 16.84 | 3.62 | 24.88 | 10.11 | 3.88 | 17.38 | 3.52 | 29.47 | 4.59 |
| 15. Proverbs Interpretation | 6.71 | 2.36 | 9.44 | 2.06 | 18.53 | 6.93 | 2.37 | 9.89 | 1.98 | 20.41 | 1.88 |
| 16. Arithmetic | 6.85 | 3.09 | 11.76 | 4.34 | 19.83 | 7.20 | 4.43 | 13.62 | 5.42 | 19.55 | −0.27 |
| 17. Perceptual Reason. (Gf) | 23.84 | 5.28 | 33.84 | 4.43 | 30.90 | 22.54 | 6.62 | 35.05 | 4.00 | 35.34 | 4.44 |
| 18. Pictorial Unbalanced Structure | 41.36 | 9.64 | 49.94 | 9.28 | 13.60 | 38.18 | 8.16 | 53.24 | 6.08 | 31.73 | 18.12 |
| 19. Combined Solutions | 39.99 | 10.1 | 45.73 | 8.95 | 9.04 | 37.47 | 9.44 | 49.17 | 7.41 | 20.83 | 11.79 |
| 20. Multiple Solutions (Gf) | 44.54 | 6.55 | 50.68 | 4.81 | 16.21 | 42.55 | 7.15 | 51.91 | 3.70 | 25.88 | 9.67 |
| 21. Pictorial Poly-profile (Gf) | 38.68 | 6.17 | 45.44 | 5.83 | 16.90 | 38.03 | 5.99 | 48.28 | 4.46 | 29.43 | 12.53 |
| 22. Dominoes D-48 (Gf) | 26.12 | 4.99 | 32.82 | 4.96 | 20.20 | 28.09 | 4.41 | 34.62 | 4.65 | 21.72 | 1.52 |
| 23. Figure Classification (Gf) | 6.62 | 2.39 | 9.89 | 2.20 | 21.37 | 6.40 | 2.41 | 10.89 | 2.14 | 29.60 | 8.23 |
| 24. Projection in Water (Gf) | 7.22 | 1.62 | 8.12 | 1.23 | 9.47 | 7.00 | 1.69 | 8.43 | 0.92 | 16.44 | 6.96 |
| 25. Figure Series (Gf) | 9.95 | 2.68 | 12.31 | 2.20 | 14.51 | 9.42 | 3.29 | 13.38 | 2.32 | 21.18 | 6.67 |
| 26. Matrices I (Gf) | 8.25 | 1.46 | 9.34 | 0.94 | 13.63 | 7.85 | 1.54 | 9.56 | 0.74 | 22.50 | 8.88 |
| 27. Matrices II (Gf) | 9.23 | 1.52 | 9.99 | 1.15 | 8.54 | 8.24 | 1.82 | 10.50 | 0.79 | 25.98 | 17.44 |
| 28. Matrices III (Gf) | 5.46 | 2.72 | 7.51 | 2.07 | 12.84 | 5.46 | 2.64 | 8.90 | 1.66 | 24.00 | 11.16 |
| AVERAGE | 18.48 | 4.18 | 23.19 | 3.79 | 17.70 | 17.67 | 4.37 | 24.67 | 3.19 | 27.78 | 10.08 |
References
- Cohen, Jacob. 1988. Statistical Power Analysis for the Behavioral Sciences, 2nd ed. Hillsdale: Lawrence Erlbaum Associates. [Google Scholar]
- Cumming, Geoff. 2012. Understanding the New Statistics: Effect Sizes, Confidence Intervals, and Meta-Analysis. New York: Routledge. [Google Scholar]
- Eysenck, Hans. 1971. Race, Intelligence and Education. London: Maurice Temple Smith. [Google Scholar]
- Fogarty, Gerard, and Lazar Stankov. 1982. Competing tasks as an index of intelligence. Personality and Individual Differences 3: 407–22. [Google Scholar] [CrossRef]
- Fogarty, Gerard, and Lazar Stankov. 1988. Abilities involved in performance on competing tasks. Personality and Individual Differences 9: 35–49. [Google Scholar] [CrossRef]
- Gignac, Gilles. 2015. Raven’s is not a pure measure of general intelligence: Implications for g factor theory and the brief measurement of g. Intelligence 52: 71–79. [Google Scholar] [CrossRef]
- Haier, Richard. 2014. Increased intelligence is a myth (so far). Frontiers in Systems Neuroscience 8: 1–3. [Google Scholar] [CrossRef]
- Harvey, Philip, Susan McGurk, Henry Mahncke, and Til Wykes. 2018. Review: Controversies in Computerized Cognitive Training. Biological Psychiatry: Cognitive Neuroscience and Neuroimaging 3: 907–15. [Google Scholar]
- Hegelund, Emilie Rune, Marie Grønkjær, Merete Osler, Jesper Dammeyer, Trine Flensborg-Madsen, and Erik Lykke Mortensen. 2020. The influence of educational attainment on intelligence. Intelligence 78: 101419. [Google Scholar] [CrossRef]
- Jensen, Arthur. 1969. How much can we boost IQ and scholastic achievement? Harvard Educational Review 39: 1–123. [Google Scholar] [CrossRef]
- Kovacs, Kristof, and Andrew Conway. 2019. A unified cognitive/differential approach to human intelligence: Implications for IQ testing. Journal of Applied Research on Memory and Cognition 8: 255–72. [Google Scholar] [CrossRef]
- Kvashchev, Radivoj. 1980. Mogucnosti I Granice Razvoja Intelligencije [The Feasibility and Limits of Intelligence Training]. Belgrade: Nolit. [Google Scholar]
- Lakens, Daniel. 2013. Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t-tests and ANOVAs. Frontiers in Psychology 4: 863. [Google Scholar] [CrossRef] [PubMed]
- Ma, Hsen-Hsing. 2009. The effect size of variables associated with creativity: A meta-analysis. Creativity Research Journal 21: 30–42. [Google Scholar] [CrossRef]
- Novick, Jared, Michael Bunting, Randall Engle, and Michael Dougherty, eds. 2020. Cognitive and Working Memory Training: Perspectives from Psychology, Neuroscience and Human Development. New York: Oxford University Press. [Google Scholar]
- Plomin, Robert, and Ian Deary. 2015. Genetics and intelligence differences: Five special findings. Molecular Psychiatry 20: 98–108. [Google Scholar] [CrossRef] [PubMed]
- Plomin, Robert, John DeFries, Valerie Knopik, and Jenae Neiderhiser. 2014. Behavioral Genetics, 6th ed. New York: Worth Publishers. [Google Scholar]
- Ritchie, Stuart, and Elliot Tucker-Drob. 2018. How much does education improve intelligence? A meta-analysis. Psychological Science 29: 1358–69. [Google Scholar] [CrossRef]
- Sauce, Bruno, and Louis Matzel. 2018. The paradox of intelligence: Heritability and malleability coexist in hidden gene-environment interplay. Psychological Bulletin 144: 26–47. [Google Scholar] [CrossRef] [PubMed]
- Selita, Fatos, and Yulia Kovas. 2019. Genes and Gini: What inequality means for heritability? Journal of Biosocial Science 51: 18–47. [Google Scholar] [CrossRef] [PubMed]
- Simons, Daniel, Walter Boot, Neil Charness, Susan Gathercole, Christopher Chabris, David Hambrick, and Elizabeth Stine-Morrow. 2016. Do “brain-training” programs work? Psychological Science in the Public Interest 17: 103–86. [Google Scholar] [CrossRef] [PubMed]
- Stankov, Lazar. 1986. Kvashchev’s Experiment: Can we boost intelligence? Intelligence 10: 209–30. [Google Scholar] [CrossRef]
- Stankov, Lazar. 1991. The effects of training and practice on human abilities. In Intelligence: Reconceptualization and Measurement. Edited by Helga Rowe. Hove: Psychology Press Ltd., pp. 97–117. [Google Scholar]
- Stankov, Lazar. 2019a. Diminished ‘g’: Fluid and crystallized intelligence and cognitive abilities linked to sensory modalities. In General and Specific Mental Abilities. Edited by Dennis McFarland. Newcastle upon Tyne: Cambridge Scholars Publishing, pp. 359–86. [Google Scholar]
- Stankov, Lazar. 2019b. Working memory, attention and g as a weak formative construct. (Commentary on Kovacs and Conway’s “A Unified Cognitive/Differential Approach to Human Intelligence: Implications for IQ Testing”). Journal of Applied Research in Memory and Cognition 8: 284–87. [Google Scholar] [CrossRef]
- Stankov, Lazar, and Kuei Chen. 1988a. Training and changes in fluid and crystallized intelligence. Contemporary Educational Psychology 13: 382–96. [Google Scholar] [CrossRef]
- Stankov, Lazar, and Kuei Chen. 1988b. Can we boost fluid and crystallized intelligence? A structural modeling approach. Australian Journal of Psychology 40: 363–76. [Google Scholar] [CrossRef]
- Weiss, Lawrence, and Donald Saklofske. 2020. Mediators of IQ test score differences across racial and ethnic groups: The case for environmental and social justice. Personality and Individual Differences 161: 109962. [Google Scholar] [CrossRef]
| 1 | |
| 2 | We also calculated effect sizes using standard deviations from the initial testing session, reported in the Stankov and Chen (1988a, 1988b) studies, i.e., in the way it was done on the first row of Table 1. This showed the overall 10 IQ points superiority of the experimental group on the Gc factor and 16 points superiority on the Gf factor. |
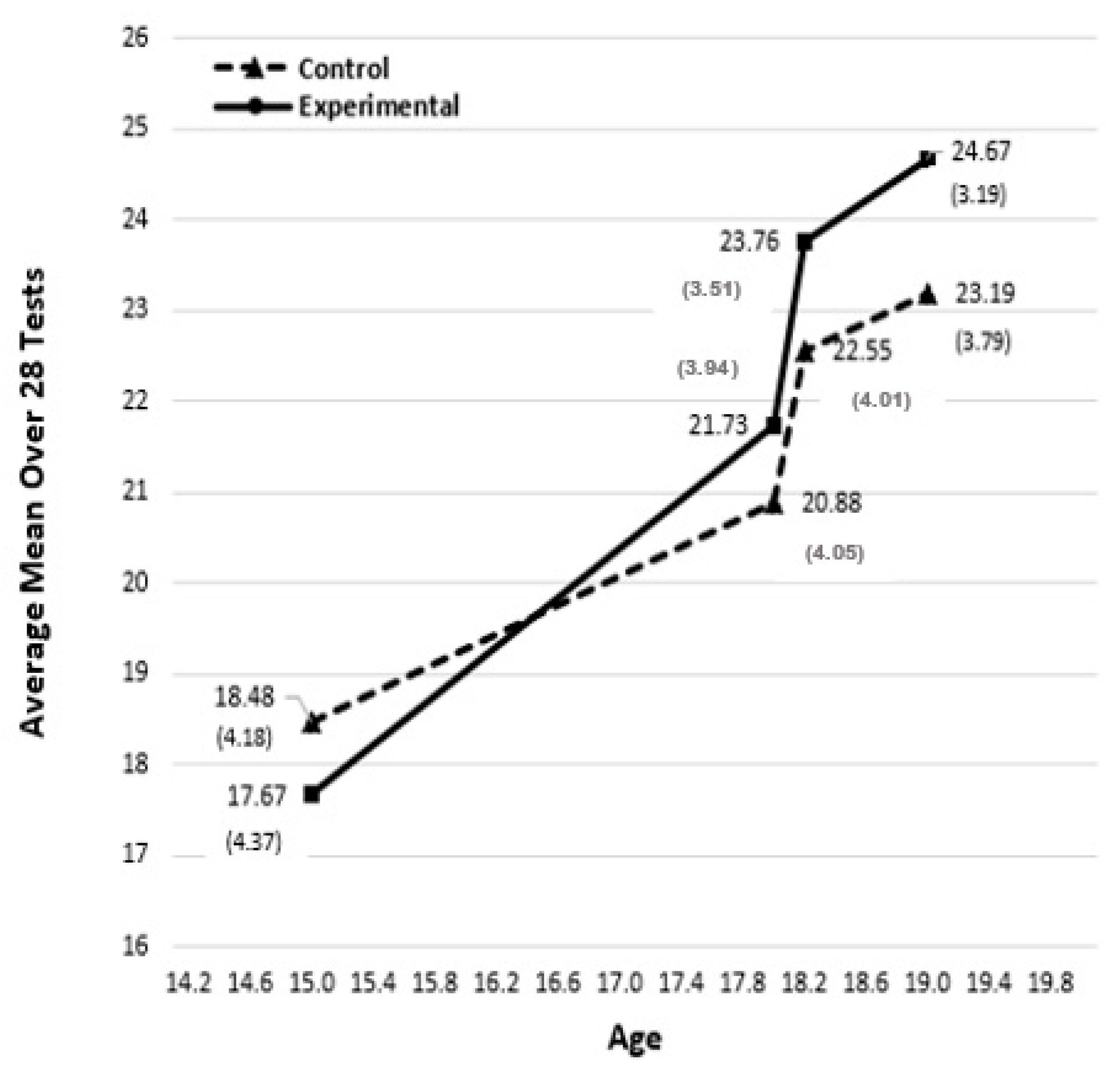
| Analytic Approach | Group | Difference between the Means at Initial & 2nd Retest | Standard Deviation | Training Effect Size in Cohen’s dav | Group Difference in Terms of Cohen’s dav | Training Effect Size × 15 in IQ Units | Group Difference in IQ Units |
|---|---|---|---|---|---|---|---|
| Stankov (1986) | Experim. | 7.00 (24.67–17.67) | 4.37 | 1.60 | 0.47 | 24.00 | 7.13 |
| Control | 4.71 (23.19–18.48) | 4.18 | 1.13 | 16.90 | |||
| Recalculation using 2nd Retest standard deviations | Experim. | 7.00 | 3.19 | 2.19 | 0.95 | 32.92 | 14.28 |
| Control | 4.71 | 3.79 | 1.24 | 18.64 | |||
| Recalculation using the average of pretest–post-test standard deviations (Cumming 2012; Lakens 2013) | Experim. | 7.00 | 3.78 (4.37 + 3.19)/2 | 1.85 | 0.67 | 27.78 | 10.08 |
| Control | 4.71 | 3.99 (4.18 + 3.79)/2 | 1.18 | 17.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stankov, L.; Lee, J. We Can Boost IQ: Revisiting Kvashchev’s Experiment. J. Intell. 2020, 8, 41. https://doi.org/10.3390/jintelligence8040041
Stankov L, Lee J. We Can Boost IQ: Revisiting Kvashchev’s Experiment. Journal of Intelligence. 2020; 8(4):41. https://doi.org/10.3390/jintelligence8040041
Chicago/Turabian StyleStankov, Lazar, and Jihyun Lee. 2020. "We Can Boost IQ: Revisiting Kvashchev’s Experiment" Journal of Intelligence 8, no. 4: 41. https://doi.org/10.3390/jintelligence8040041
APA StyleStankov, L., & Lee, J. (2020). We Can Boost IQ: Revisiting Kvashchev’s Experiment. Journal of Intelligence, 8(4), 41. https://doi.org/10.3390/jintelligence8040041






