Analysing Standard Progressive Matrices (SPM-LS) with Bayesian Item Response Models
Abstract
1. Introduction
2. Bayesian IRT Models
2.1. Bayesian IRT Models for Binary Data
2.2. IRT Models as Regression Models
2.3. Model Priors and Identification
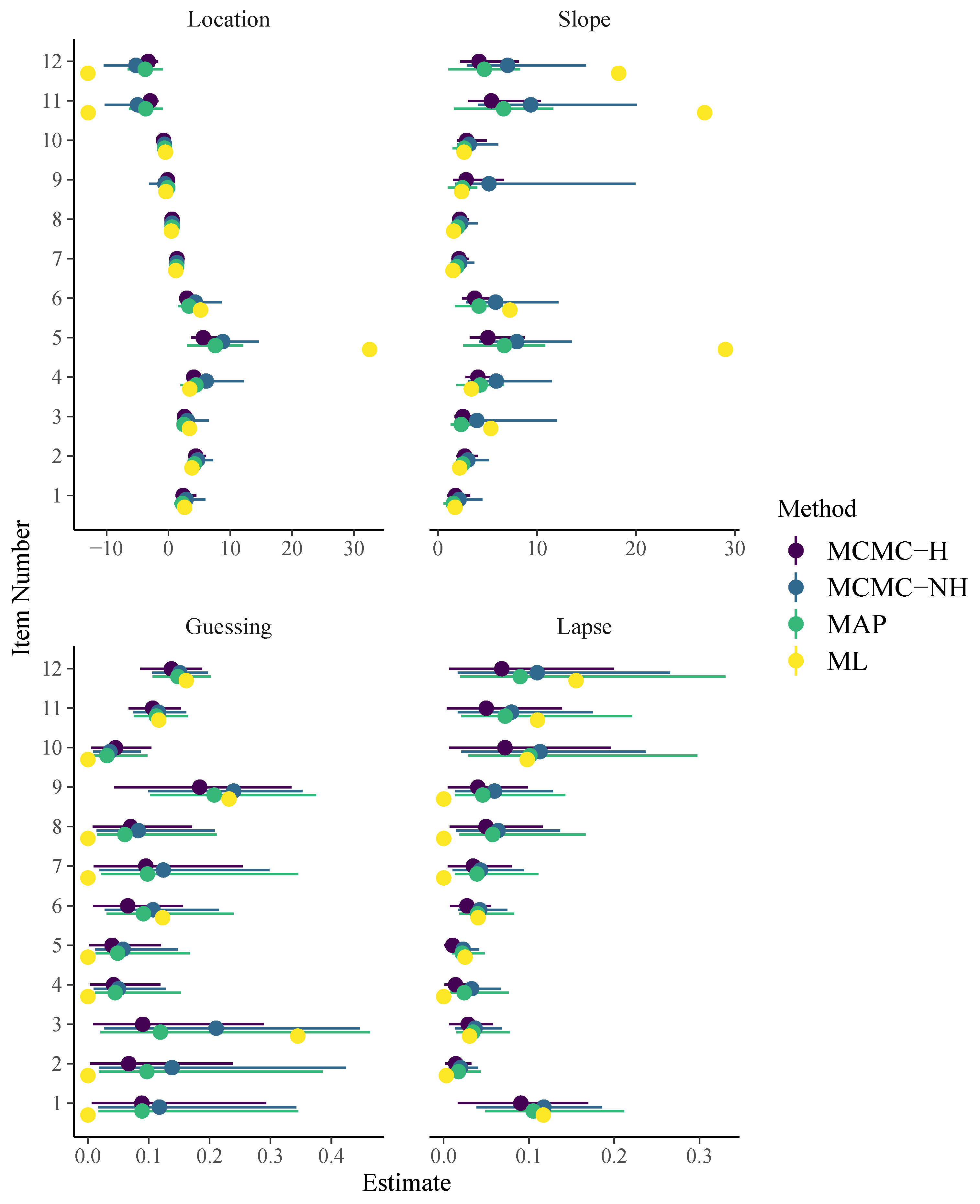
3. Analysis of the SPM-LS Data
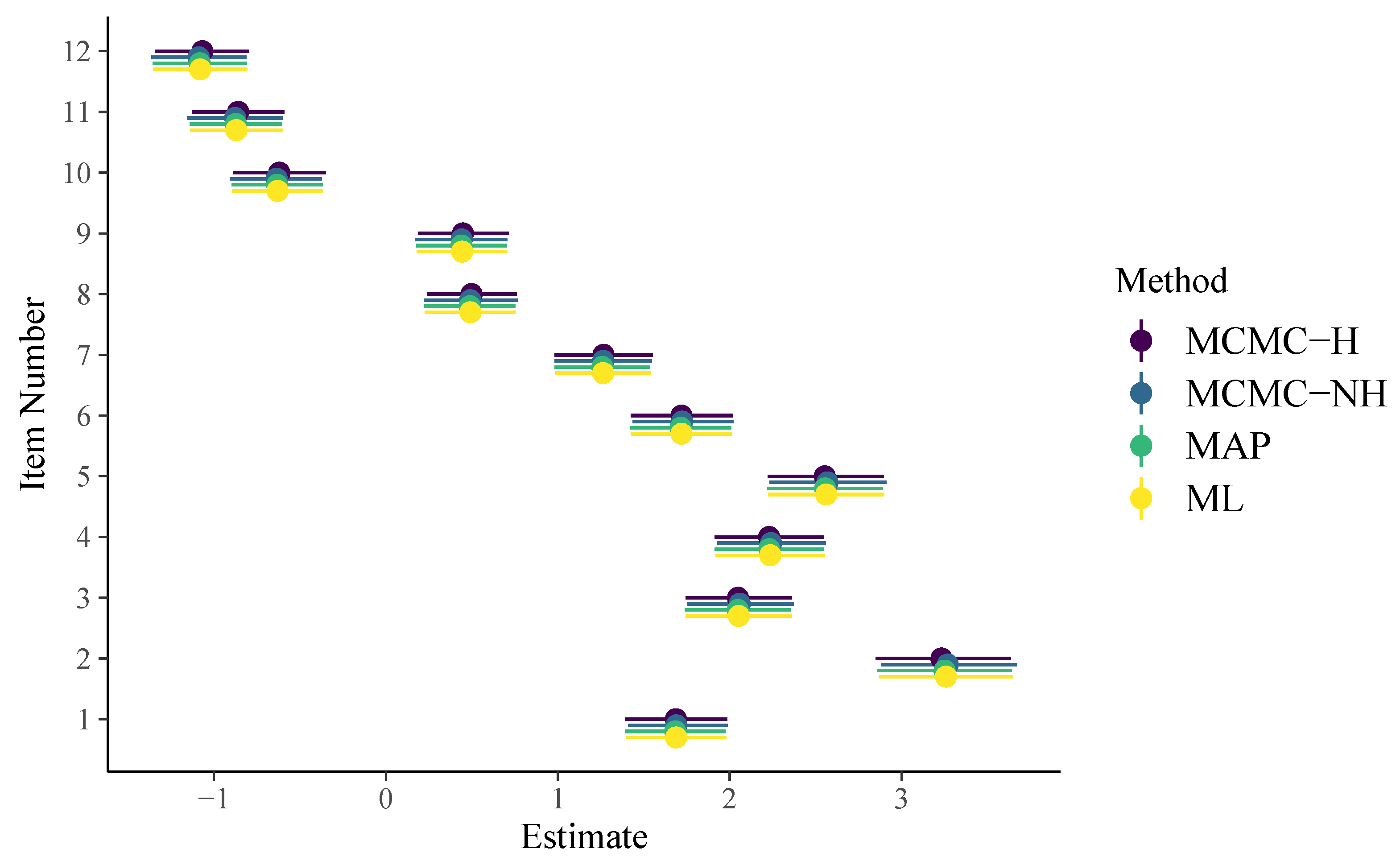
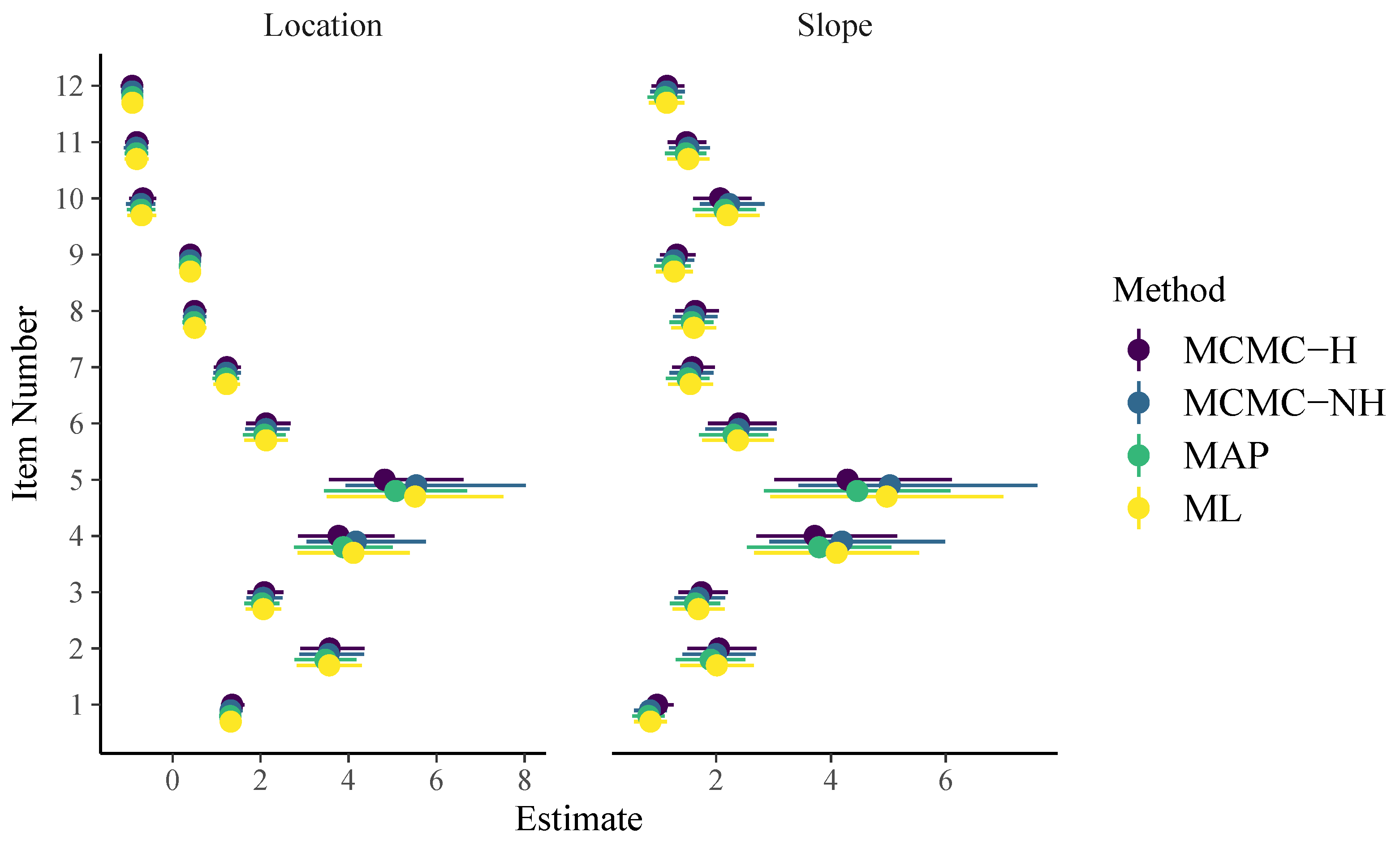
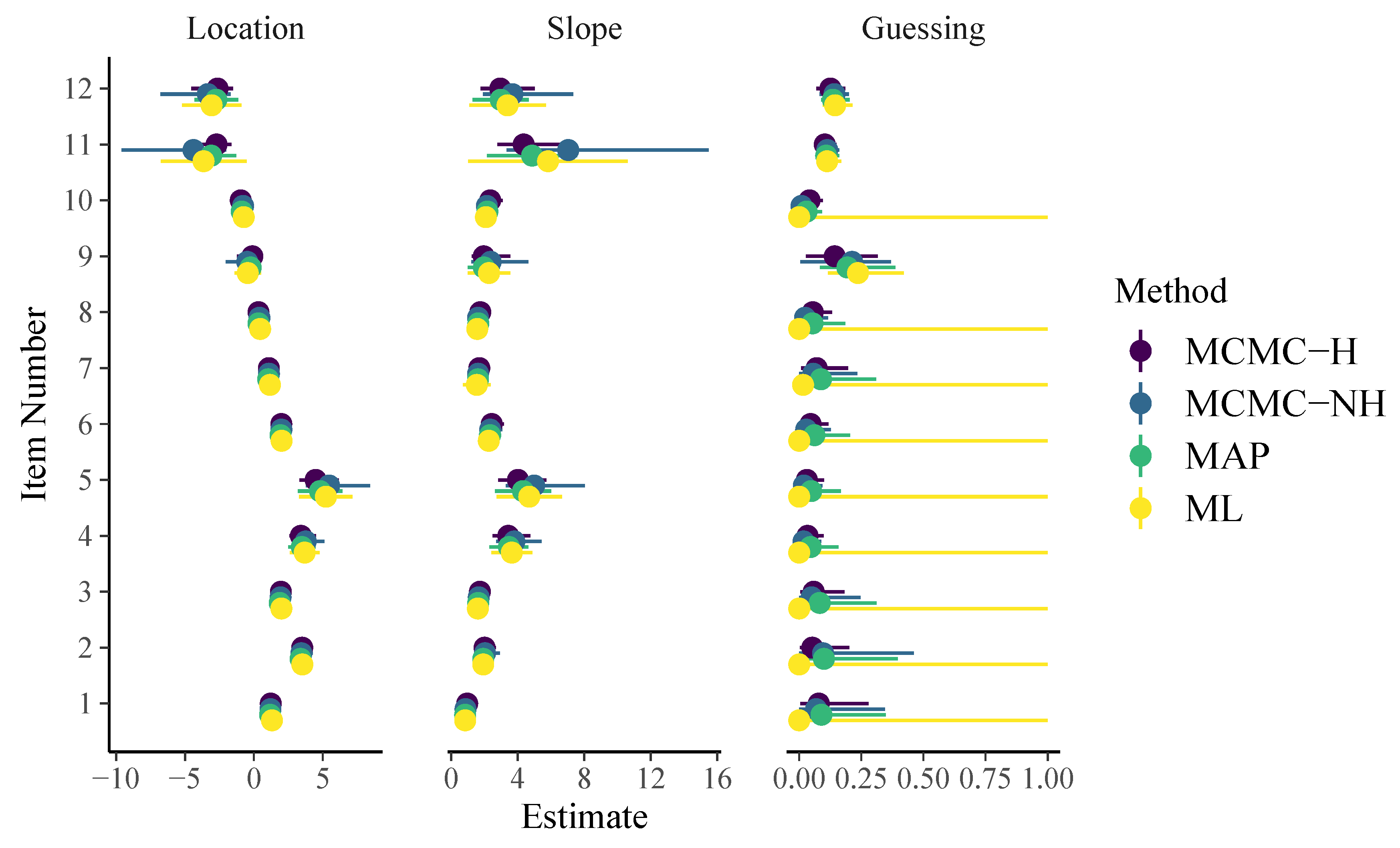
3.1. Model Estimation




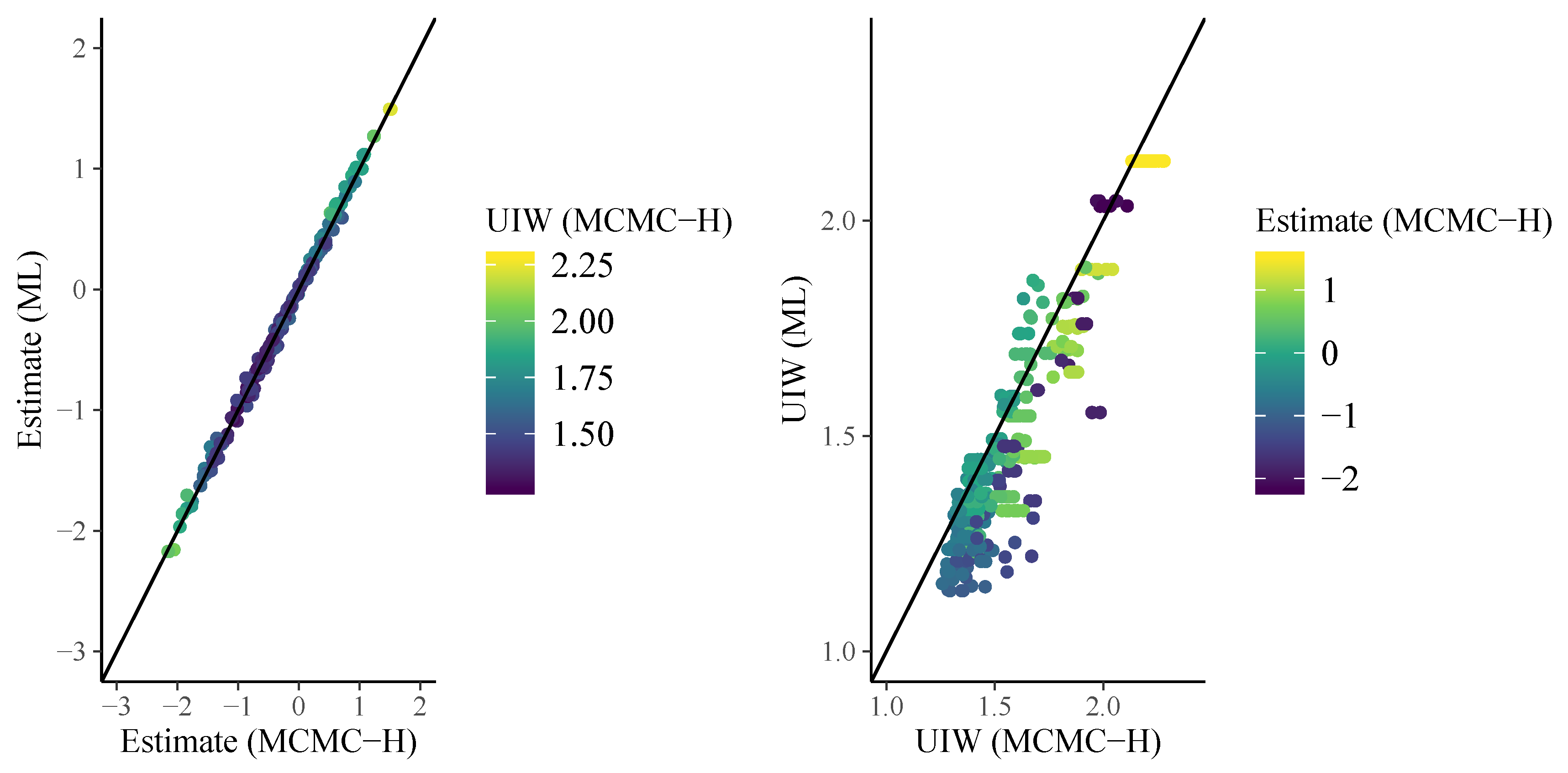
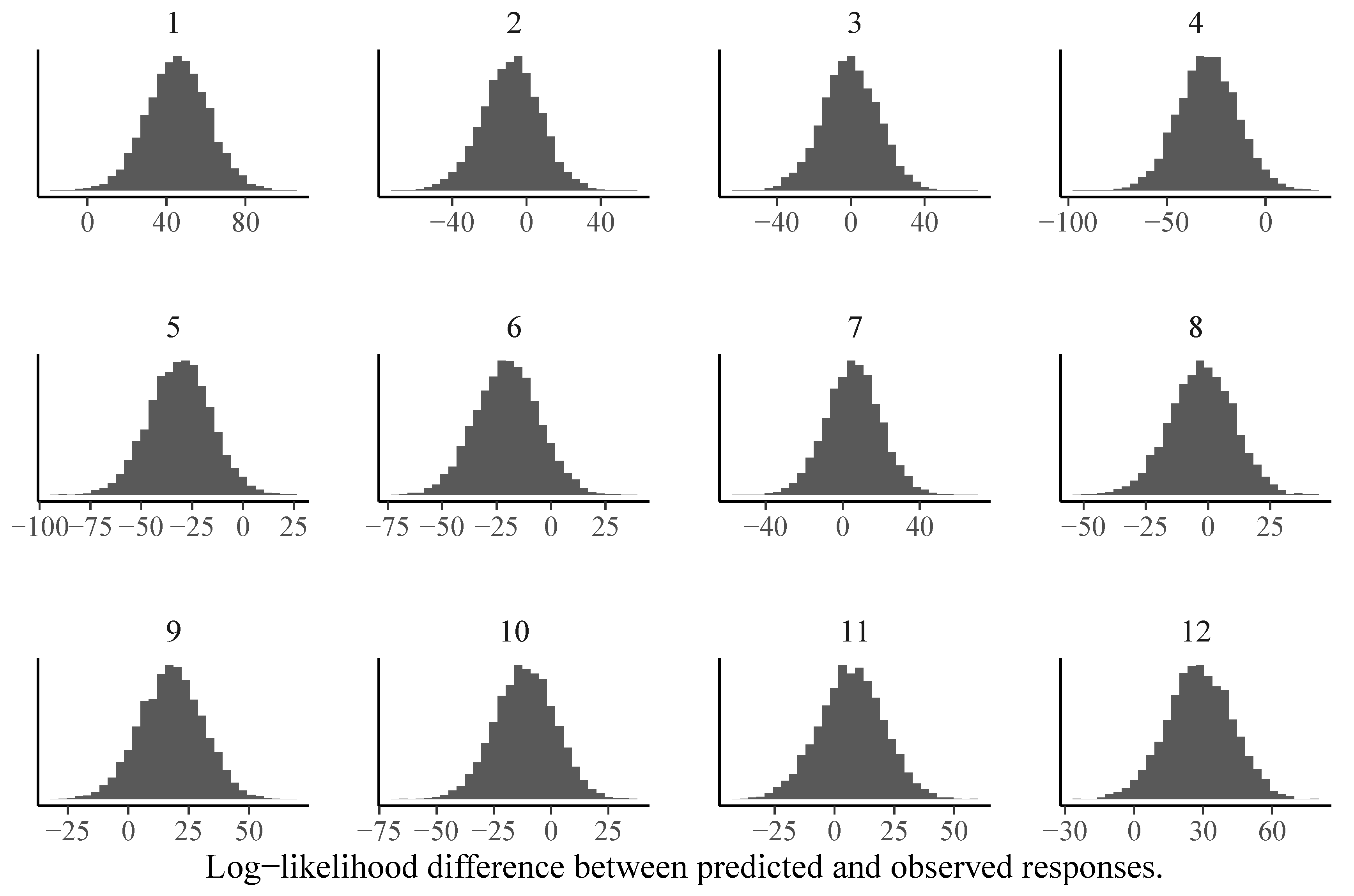
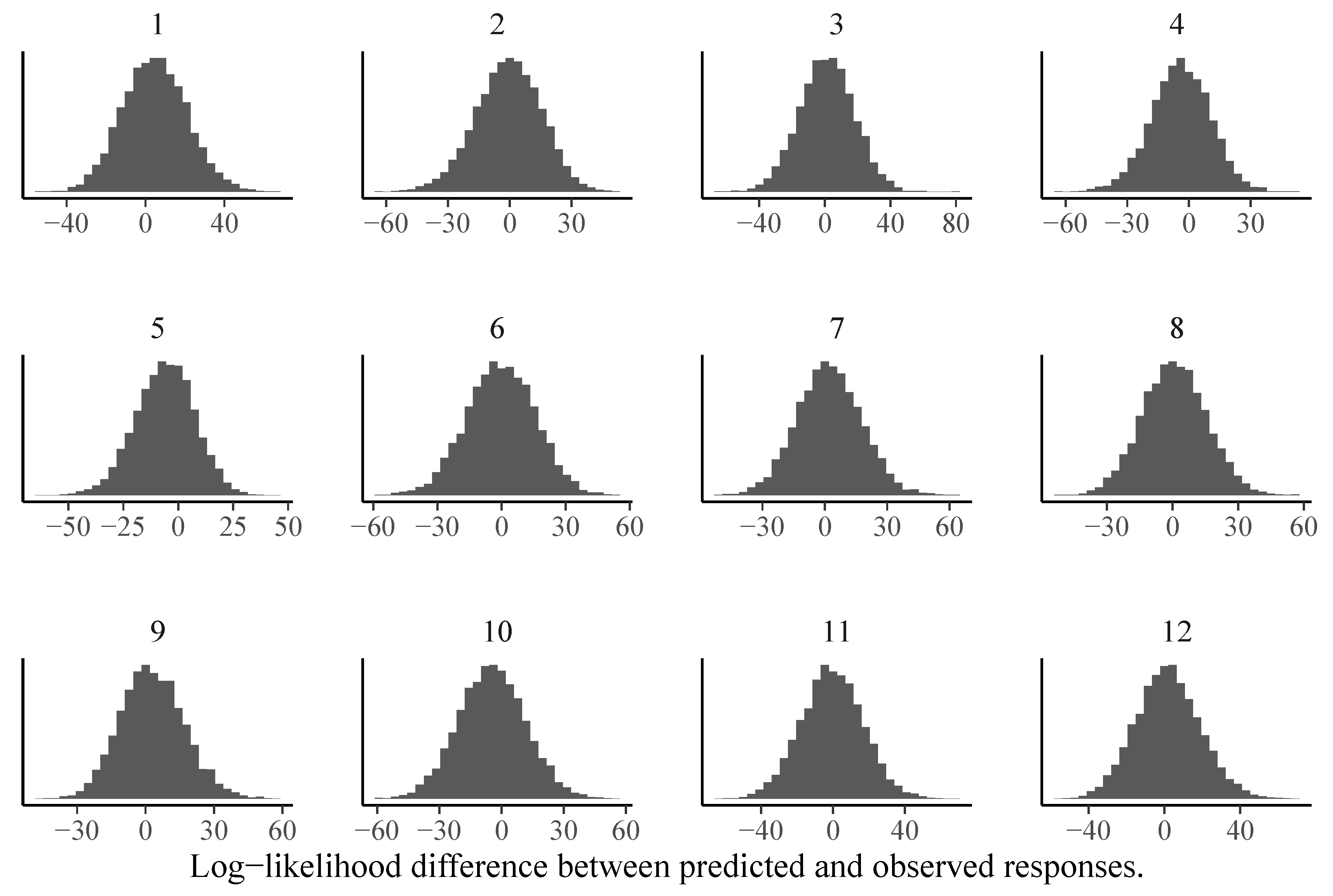
3.2. Model Comparison
4. Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Ackerman, Phillip L., and Ruth Kanfer. 2009. Test length and cognitive fatigue: An empirical examination of effects on performance and test-taker reactions. Journal of Experimental Psychology: Applied 15: 163. [Google Scholar] [CrossRef]
- Allison, J. Ames, and Chi Hang Au. 2018. Using Stan for item response theory models. Measurement: Interdisciplinary Research and Perspectives 16: 129–34. [Google Scholar]
- Aust, F., and M. Barth. 2018. Papaja: Create APA Manuscripts with R Markdown. Available online: https://github.com/crsh/papaja (accessed on 3 February 2020).
- Bates, Douglas, Martin Mächler, Ben Bolker, and Steve Walker. 2015. Fitting linear mixed-effects models using lme4. Journal of Statistical Soft-Ware 67: 1–48. [Google Scholar] [CrossRef]
- Betancourt, Michael. 2017. A conceptual introduction to Hamiltonian Monte Carlo. arXiv arXiv:1701.02434. [Google Scholar]
- Bürkner, Paul-Christian. 2017. brms: An R package for bayesian multilevel models using Stan. Journal of Statistical Software 80: 1–28. [Google Scholar] [CrossRef]
- Bürkner, Paul-Christian. 2018. Advanced Bayesian multilevel modeling with the R package brms. The R Journal 10: 395–411. [Google Scholar] [CrossRef]
- Bürkner, Paul-Christian. 2019. Bayesian item response modelling in R with brms and Stan. arXiv arXiv:1905.09501. [Google Scholar]
- Carpenter, Bob, Andrew Gelman, Matthew D. Hoffman, Daniel Lee, Ben Goodrich, Michael Betancourt, Marcus Brubaker, Jiqiang Guo, Peter Li, and Allen Riddell. 2017. Stan: A probabilistic programming language. Journal of Statistical Software 76: 1–32. [Google Scholar] [CrossRef]
- Chalmers, R. Philip. 2012. mirt: A multidimensional item response theory package for the R environment. Journal of Statistical Software 48: 1–29. [Google Scholar] [CrossRef]
- Culpepper, Steven Andrew. 2016. Revisiting the 4-parameter item response model: Bayesian estimation and application. Psychometrika 81: 1142–63. [Google Scholar] [CrossRef]
- Culpepper, Steven Andrew. 2017. The prevalence and implications of slipping on low-stakes, large-scale assessments. Journal of Educational and Behavioral Statistics 42: 706–25. [Google Scholar] [CrossRef]
- Curtis, S. McKay. 2010. BUGS code for item response theory. Journal of Statistical Software 36: 1–34. [Google Scholar] [CrossRef]
- Depaoli, Sarah, James P. Clifton, and Patrice R. Cobb. 2016. Just another Gibbs sampler (JAGS) flexible software for MCMC implementation. Journal of Educational and Behavioral Statistics 41: 628–49. [Google Scholar] [CrossRef]
- Do, Chuong B., and Serafim Batzoglou. 2008. What is the expectation maximization algorithm? Nature Biotechnology 26: 897. [Google Scholar] [CrossRef] [PubMed]
- Embretson, Susan E., and Steven P. Reise. 2013. Item Response Theory. Hove: Psychology Press. [Google Scholar]
- Fox, Jean-Paul. 2010. Bayesian Item Response Modeling: Theory and Applications. Berlin/Heidelberg: Springer. [Google Scholar]
- Freedman, David A. 1981. Bootstrapping regression models. The Annals of Statistics 9: 1218–28. [Google Scholar] [CrossRef]
- Gelman, Andrew, John B. Carlin, Hal S. Stern, David B. Dunson, Aki Vehtari, and Donald B. Rubin. 2013. Bayesian Data Analysis, 3rd ed. Boca Raton: Chapman Hall/CRC. [Google Scholar] [CrossRef]
- Gelman, Andrew, Daniel Simpson, and Michael Betancourt. 2017. The prior can often only be understood in the context of the likelihood. Entropy 19: 555–67. [Google Scholar] [CrossRef]
- Glas, Cees A. W., and Rob R. Meijer. 2003. A Bayesian approach to person fit analysis in item response theory models. Applied Psychological Measurement 27: 217–33. [Google Scholar] [CrossRef]
- Jensen, Arthur R., Dennis P. Saccuzzo, and Gerald E. Larson. 1988. Equating the standard and advanced forms of the Raven progressive matrices. Educational and Psychological Measurement 48: 1091–95. [Google Scholar] [CrossRef]
- Junker, Brian W., and Klaas Sijtsma. 2001. Nonparametric item response theory in action: An overview of the special issue. Applied Psychological Measurement 25: 211–20. [Google Scholar] [CrossRef]
- Levy, Roy, and Robert J. Mislevy. 2017. Bayesian Psychometric Modeling. Boca Raton: Chapman Hall/CRC. [Google Scholar]
- Loken, Eric, and Kelly L. Rulison. 2010. Estimation of a four-parameter item response theory model. British Journal of Mathematical and Statistical Psychology 63: 509–25. [Google Scholar] [CrossRef]
- Lord, Frederic M. 2012. Applications of Item Response Theory to Practical Testing Problems. Milton Park: Routledge. [Google Scholar]
- Lunn, David, David Spiegelhalter, Andrew Thomas, and Nicky Best. 2009. The BUGS project: Evolution, critique and future directions. Statistics in Medicine 28: 3049–67. [Google Scholar] [CrossRef] [PubMed]
- Luo, Yong, and Hong Jiao. 2018. Using the Stan program for bayesian item response theory. Educational and Psychological Measurement 78: 384–408. [Google Scholar] [CrossRef] [PubMed]
- Maydeu-Olivares, Alberto. 2013. Goodness-of-fit assessment of item response theory models. Measurement: Interdisciplinary Research and Perspectives 11: 71–101. [Google Scholar] [CrossRef]
- Mooney, Christopher F., Christopher L. Mooney, Christopher Z. Mooney, Robert D. Duval, and Robert Duvall. 1993. Bootstrapping: A Nonparametric Approach to Statistical Inference. Thousand Oaks: Sage. [Google Scholar]
- Myszkowski, Nils, and Martin Storme. 2018. A snapshot of g? Binary and polytomous item-response theory investigations of the last series of the standard progressive matrices (SPM-LS). Intelligence 68: 109–16. [Google Scholar] [CrossRef]
- Nalborczyk, Ladislas, Cédric Batailler, Hélène Lœvenbruck, Anne Vilain, and Paul-Christian Bürkner. 2019. An introduction to bayesian multilevel models using brms: A case study of gender effects on vowel variability in standard indonesian. Journal of Speech, Language, and Hearing Research 62: 1225–42. [Google Scholar] [CrossRef]
- Pedersen, Thomas Lin. 2017. Patchwork: The Composer of Ggplots. Available online: https://github.com/thomasp85/patchwork (accessed on 3 February 2020).
- Pind, Jörgen, Eyrún K. Gunnarsdóttir, and Hinrik S. Jóhannesson. 2003. Raven’s standard progressive matrices: New school age norms and a study of the test’s validity. Personality and Individual Differences 34: 375–86. [Google Scholar] [CrossRef]
- Plummer, Martyn. 2013. JAGS: Just Another Gibbs Sampler. Available online: http://mcmc-jags.sourceforge.net/ (accessed on 3 February 2020).
- Rasch, Georg. 1961. On general laws and the meaning of measurement in psychology. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability. Berkeley: University of California Press, vol. 4, pp. 321–33. [Google Scholar]
- Raven, John C. 1941. Standardization of progressive matrices, 1938. British Journal of Medical Psychology 19: 137–50. [Google Scholar] [CrossRef]
- R Core Team. 2019. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 3 February 2020).
- Robitzsch, Alexander. 2019. Sirt: Supplementary Item Response Theory Models. Available online: https://CRAN.R-project.org/package=sirt (accessed on 3 February 2020).
- Robitzsch, Alexander, Thomas Kiefer, and Margaret Wu. 2019. TAM: Test Analysis Modules. Available online: https://CRAN.R-project.org/package=TAM (accessed on 3 February 2020).
- R Studio Team. 2018. RStudio: Integrated Development for R. Boston: RStudio, Inc., vol. 42. [Google Scholar]
- Rupp, Andre A., Dipak K. Dey, and Bruno D. Zumbo. 2004. To Bayes or not to Bayes, from whether to when: Applications of Bayesian methodology to modeling. Structural Equation Modeling 11: 424–51. [Google Scholar] [CrossRef]
- Schloerke, Barret, Jason Crowley, Di Cook, Heike Hofmann, Hadley Wickham, François Briatte, Moritz Marbach, Edwin Thoen, Amos Elberg, and Joseph Larmarange. 2018. GGally: Extension to ’ggplot2’. Available online: https://CRAN.R-project.org/package=GGally (accessed on 3 February 2020).
- van der Linden, Wim J., and Ronald K. Hambleton, eds. 1997. Handbook of Modern Item Response Theory. Berlin/Heidelberg: Springer. [Google Scholar]
- Vehtari, Aki, Daniel Simpson, Andrew Gelman, Yuling Yao, and Jonah Gabry. 2019. Pareto smoothed importance sampling. arXiv arXiv:1507.02646. [Google Scholar]
- Vehtari, Aki, Andrew Gelman, and Jonah Gabry. 2017. Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Statistics and Computing 27: 1413–32. [Google Scholar] [CrossRef]
- Vehtari, Aki, Andrew Gelman, and Jonah Gabry. 2018. Loo: Efficient Leave-One-Out Cross-Validation and WAIC for Bayesian Models. Available online: https://github.com/stan-dev/loo (accessed on 3 February 2020).
- Vehtari, Aki, Andrew Gelman, Daniel Simpson, Bob Carpenter, and Paul-Christian Bürkner. 2019. Rank-normalization, folding, and localization: An improved for assessing convergence of MCMC. arXiv arXiv:1903.08008. [Google Scholar]
- Waller, Niels G., and Leah Feuerstahler. 2017. Bayesian modal estimation of the four-parameter item response model in real, realistic, and idealized datasets. Multivariate Behavioral Research 52: 350–70. [Google Scholar] [CrossRef] [PubMed]
- Wickham, Hadley. 2016. Ggplot2: Elegant Graphics for Data Analysis. New York: Springer. Available online: http://ggplot2.org (accessed on 3 February 2020).
- Wickham, Hadley, Romain Francois, Lionel Henry, and Kirill Müller. 2019. Dplyr: A Grammar of Data Manipulation. Available online: https://CRAN.R-project.org/package=dplyr (accessed on 3 February 2020).
- Wickham, H., and L. Henry. 2019. Tidyr: Tidy Messy Data. Available online: https://CRAN.R-project.org/package=tidyr (accessed on 3 February 2020).
- Xie, Yihui. 2015. Dynamic Documents with R and Knitr, 2nd ed. Boca Raton: Chapman Hall/CRC. Available online: https://yihui.name/knitr/ (accessed on 3 February 2020).
- Xie, Yihui, Joseph J. Allaire, and Garrett Grolemund. 2018. R Markdown: The Definitive Guide. Boca Raton: Chapman Hall/CRC. Available online: https://bookdown.org/yihui/rmarkdown (accessed on 3 February 2020).
- Zhan, Peida, Hong Jiao, Kaiwen Man, and Lijun Wang. 2019. Using JAGS for Bayesian cognitive diagnosis modeling: A tutorial. Journal of Educational and Behavioral Statistics. [Google Scholar] [CrossRef]
- Zhu, Hao. 2019. kableExtra: Construct Complex Table with ’Kable’ and Pipe Syntax. Available online: https://CRAN.R-project.org/package=kableExtra (accessed on 3 February 2020).
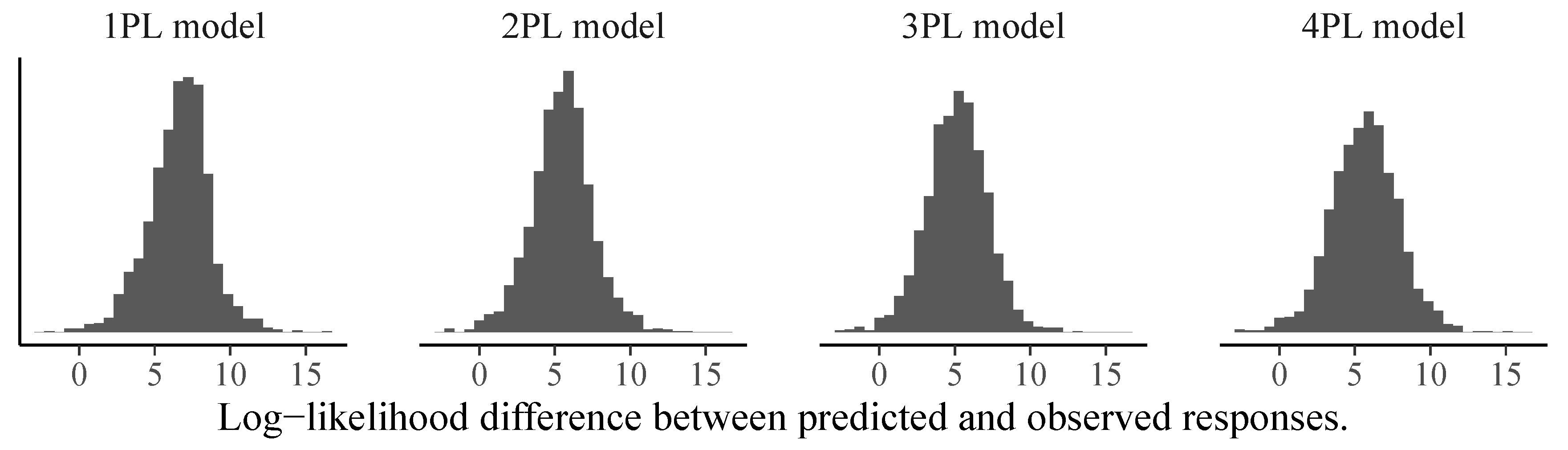

| Model | ELPD | SE(ELPD) | ELPD-Difference | SE(ELPD-Difference) |
|---|---|---|---|---|
| 4PL | −2544.7 | 42.6 | 0.0 | 0.0 |
| 3PL | −2547.8 | 42.8 | −3.1 | 5.1 |
| 2PL | −2588.7 | 42.9 | −44.0 | 9.5 |
| 1PL | −2655.0 | 43.8 | −110.3 | 15.0 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bürkner, P.-C. Analysing Standard Progressive Matrices (SPM-LS) with Bayesian Item Response Models. J. Intell. 2020, 8, 5. https://doi.org/10.3390/jintelligence8010005
Bürkner P-C. Analysing Standard Progressive Matrices (SPM-LS) with Bayesian Item Response Models. Journal of Intelligence. 2020; 8(1):5. https://doi.org/10.3390/jintelligence8010005
Chicago/Turabian StyleBürkner, Paul-Christian. 2020. "Analysing Standard Progressive Matrices (SPM-LS) with Bayesian Item Response Models" Journal of Intelligence 8, no. 1: 5. https://doi.org/10.3390/jintelligence8010005
APA StyleBürkner, P.-C. (2020). Analysing Standard Progressive Matrices (SPM-LS) with Bayesian Item Response Models. Journal of Intelligence, 8(1), 5. https://doi.org/10.3390/jintelligence8010005





