The Impact of Situational Test Anxiety on Retest Effects in Cognitive Ability Testing: A Structural Equation Modeling Approach
Abstract
1. Introduction
1.1. Explanations for Retest Effects
1.2. Definition of Test Anxiety
1.3. Test Anxiety and Test Performance: Interference and Deficit Hypotheses
1.4. A Psychological Theory for the Impact of Situational Test Anxiety on Retest Effects
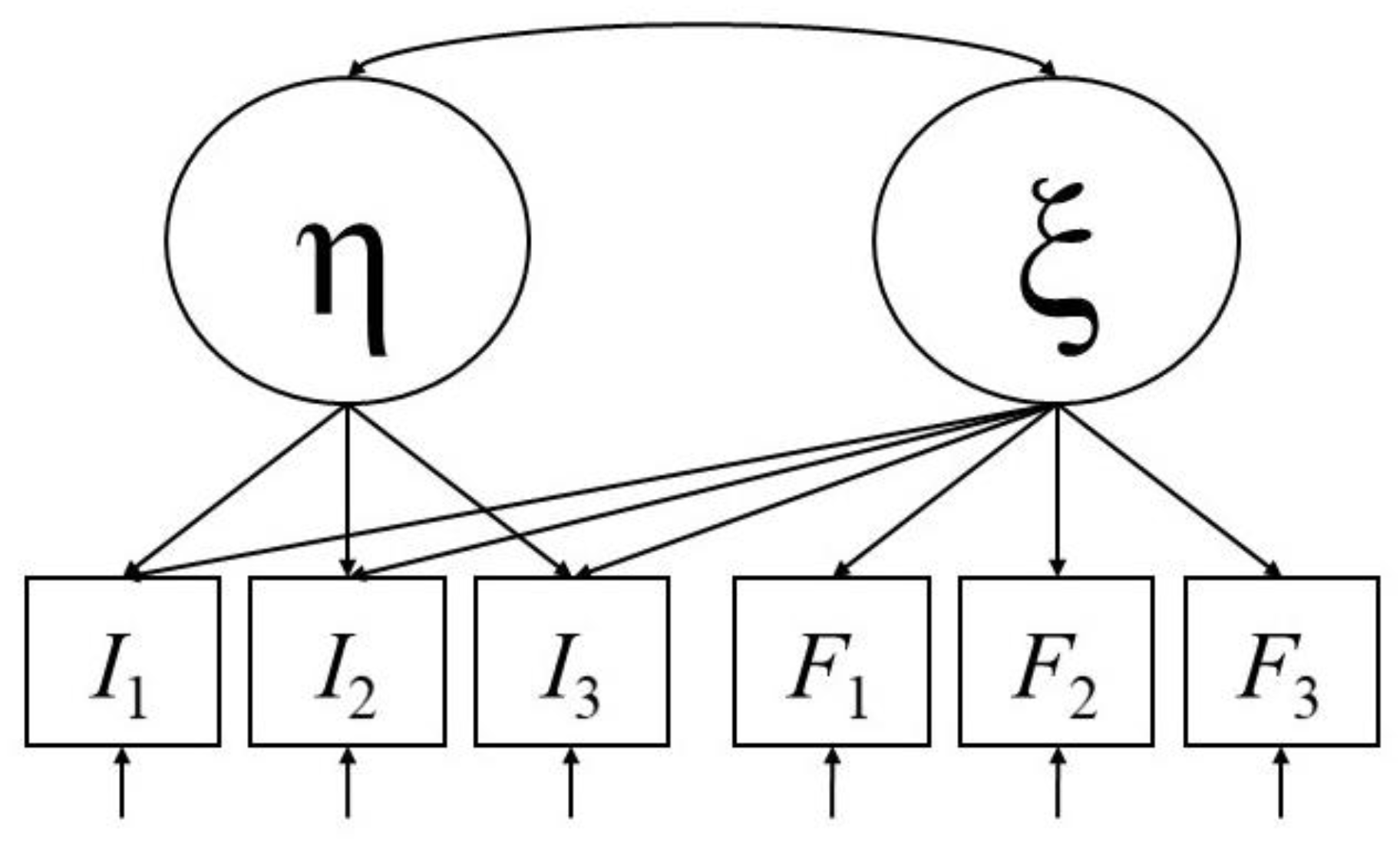
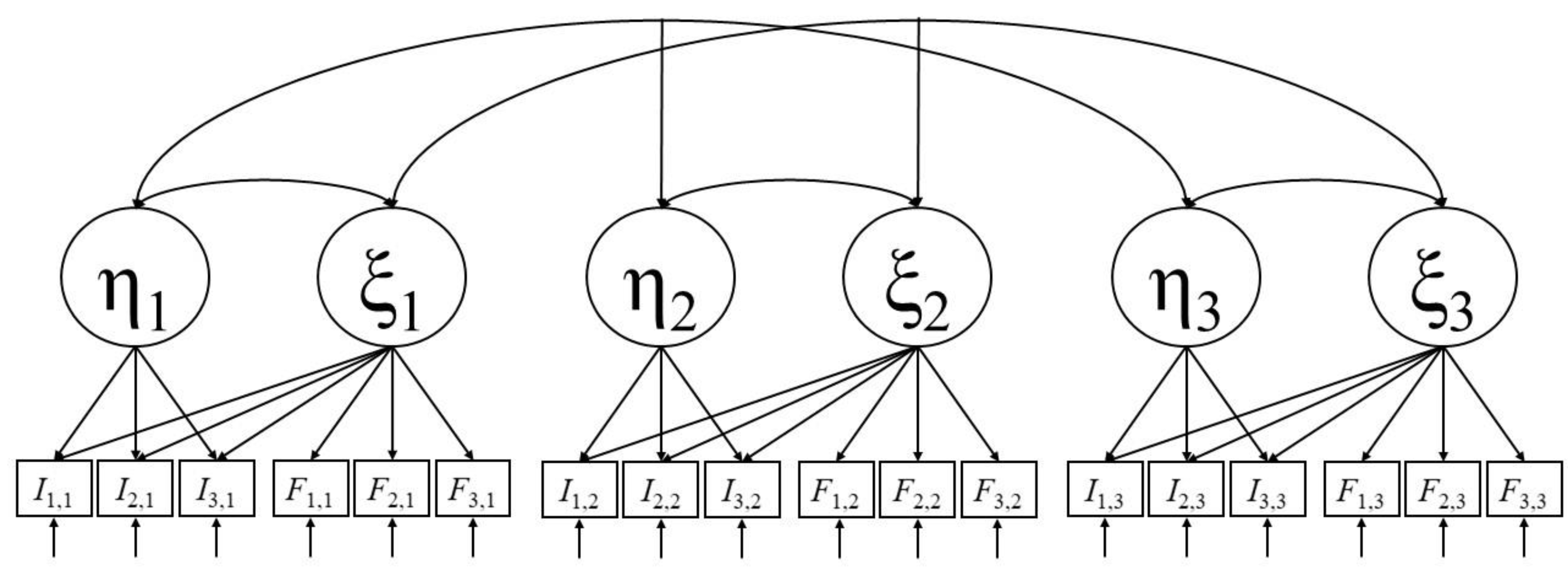
2. A Statistical Model for the Impact of Situational Test Anxiety on Retest Effects
3. An Empirical Study
3.1. Method
3.1.1. Sample
3.1.2. Measures
Figural Matrices Test
Situational Test Anxiety
3.1.3. Procedure
3.1.4. Analytic Strategy
3.2. Results
3.2.1. Descriptive Statistics
3.2.2. Ability-CFA
3.2.3. STA-CFA
3.2.4. Retest Effects
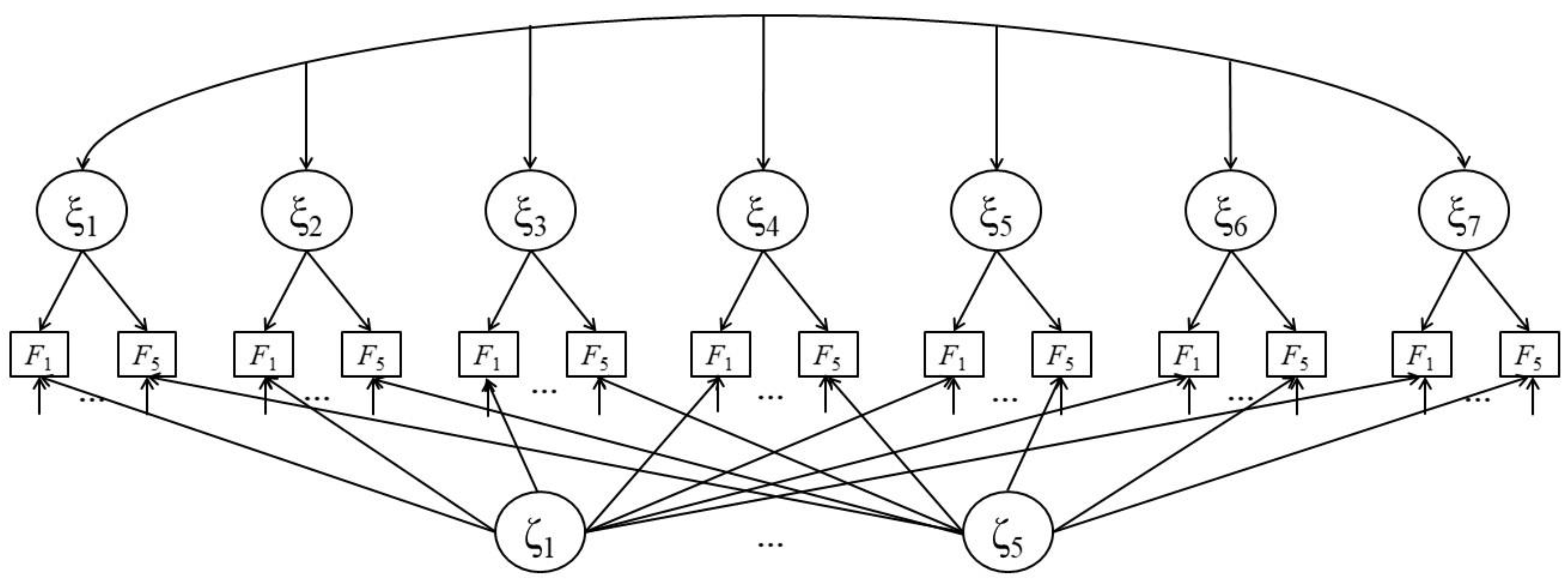
3.2.5. Interference Reduction
4. Discussion
4.1. Implications and Future Research
4.2. Limitations and Future Research
4.3. Deliberations on Measurement Invariance in Multiple Test Administrations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lievens, F.; Reeve, C.L.; Heggestad, E.D. An examination of psychometric bias due to retesting on cognitive ability tests in selection settings. J. Appl. Psychol. 2007, 92, 1672–1682. [Google Scholar] [CrossRef] [PubMed]
- Hausknecht, J.P.; Halpert, J.A.; Di Paolo, N.T.; Moriarty Gerrard, M.O. Retesting in selection: A meta-analysis of coaching and practice effects for tests of cognitive ability. J. Appl. Psychol. 2007, 92, 373–385. [Google Scholar] [CrossRef] [PubMed]
- Calamia, M.; Markon, K.; Tranel, D. Scoring Higher the Second Time Around: Meta-Analyses of Practice Effects in Neuropsychological Assessment. Clin. Neuropsychol. 2012, 26, 543–570. [Google Scholar] [CrossRef] [PubMed]
- Scharfen, J.; Blum, D.; Holling, H. Response Time Reduction Due to Retesting in Mental Speed Tests: A Meta-Analysis. J. Intell. 2018, 6, 6. [Google Scholar] [CrossRef] [PubMed]
- Scharfen, J.; Jansen, K.; Holling, H. Retest effects in working memory capacity tests: A meta-analysis. Psychon. Bull. Rev. 2018, 25, 2175–2199. [Google Scholar] [CrossRef] [PubMed]
- Scharfen, J.; Peters, J.M.; Holling, H. Retest effects in cognitive ability tests: A meta-analysis. Intelligence 2018, 67, 44–66. [Google Scholar] [CrossRef]
- Gignac, G.E. Raven’s is not a pure measure of general intelligence: Implications for g factor theory and the brief measurement of g. Intelligence 2015, 52, 71–79. [Google Scholar] [CrossRef]
- Jensen, A.R. The g factor: The science of mental ability. In Human Evolution, Behavior, and Intelligence; Praeger Publishers/Greenwood Publishing Group: Westport, CT, USA, 1998. [Google Scholar]
- Albers, F.; Höft, S. Do it again and again. And again? Diagnostica 2009, 55, 71–83. [Google Scholar] [CrossRef]
- Bartels, C.; Wegrzyn, M.; Wiedl, A.; Ackermann, V.; Ehrenreich, H. Practice effects in healthy adults: A longitudinal study on frequent repetitive cognitive testing. BMC Neurosci. 2010, 11–22. [Google Scholar] [CrossRef]
- Collie, A.; Maruff, P.; Darby, D.G.; McStephen, M. The effects of practice on the cognitive test performance of neurologically normal individuals assessed at brief test–retest intervals. J. Int. Neuropsychol. Soc. 2003, 9, 419–428. [Google Scholar] [CrossRef]
- Falleti, M.G.; Maruff, P.; Collie, A.; Darby, D.G. Practice Effects Associated with the Repeated Assessment of Cognitive Function Using the CogState Battery at 10-minute, One Week and One Month Test-retest Intervals. J. Clin. Exp. Neuropsychol. 2006, 28, 1095–1112. [Google Scholar] [CrossRef] [PubMed]
- Ferrer, E.; Salthouse, T.A.; McArdle, J.J.; Stewart, W.F.; Schwartz, B.S. Multivariate Modeling of Age and Retest in Longitudinal Studies of Cognitive Abilities. Psychol. Aging 2005, 20, 412–422. [Google Scholar] [CrossRef] [PubMed]
- Fredrickson, J.; Maruff, P.; Woodward, M.; Moore, L.; Fredrickson, A.; Sach, J.; Darby, D. Evaluation of the Usability of a Brief Computerized Cognitive Screening Test in Older People for Epidemiological Studies. Neuroepidemiology 2010, 34, 65–75. [Google Scholar] [CrossRef] [PubMed]
- Kaminski, T.W.; Groff, R.M.; Glutting, J.J. Examining the stability of Automated Neuropsychological Assessment Metric (ANAM) baseline test scores. J. Clin. Exp. Neuropsychol. 2009, 31, 689–697. [Google Scholar] [CrossRef] [PubMed]
- Puddey, I.B.; Mercer, A.; Andrich, D.; Styles, I. Practice effects in medical school entrance testing with the undergraduate medicine and health sciences admission test (UMAT). BMC Med. Educ. 2014, 14, 48–62. [Google Scholar] [CrossRef] [PubMed]
- Rogers, J.M.; Fox, A.M.; Donnelly, J. Impaired practice effects following mild traumatic brain injury: An event-related potential investigation. Brain Inj. 2014, 29, 343–351. [Google Scholar] [CrossRef] [PubMed]
- Verhaeghen, P.; Cerella, J.; Basak, C. A Working Memory Workout: How to Expand the Focus of Serial Attention from One to Four Items in 10 Hours or Less. J. Exp. Psychol. Learn. Mem. Cogn. 2004, 30, 1322–1337. [Google Scholar] [CrossRef] [PubMed]
- Wilson, B.A.; Watson, P.C.; Baddeley, A.D.; Emslie, H.; Evans, J.J. Improvement or simply practice? The effects of twenty repeated assessments on people with and without brain injury. J. Int. Neuropsychol. Soc. 2000, 6, 469–479. [Google Scholar] [CrossRef] [PubMed]
- Wilson, R.S.; Li, Y.; Bienias, L.; Bennett, D.A. Cognitive decline in old age: Separating retest effects from the effects of growing older. Psychol. Aging 2006, 21, 774–789. [Google Scholar] [CrossRef]
- Coyle, T.R. Non-g Factors Predict Educational and Occupational Criteria: More than g. J. Intell. 2018, 6, 43. [Google Scholar] [CrossRef]
- Lievens, F.; Buyse, T.; Sackett, P.R. Retest effects in operational selection settings: Development and test of a framework. Pers. Psychol. 2005, 58, 981–1007. [Google Scholar] [CrossRef]
- Randall, J.G.; Villado, A.J. Take two: Sources and deterrents of score change in employment retesting. Hum. Resour. Manag. Rev. 2017, 27, 536–553. [Google Scholar] [CrossRef]
- Van Iddekinge, C.H.; Arnold, J.D. Retaking Employment Tests: What We Know and What We Still Need to Know. Annu. Rev. Organ. Psychol. Organ. Behav. 2017, 4, 445–471. [Google Scholar] [CrossRef]
- Millman, J.; Bishop, C.H.; Ebel, R. An analysis of test-wiseness. Educ. Psychol. Meas. 1965, 25, 707–726. [Google Scholar] [CrossRef]
- Freund, P.A.; Holling, H. How to get really smart: Modeling retest and training effects in ability testing using computer-generated figural matrix items. Intelligence 2011, 39, 233–243. [Google Scholar] [CrossRef]
- Olenick, J.; Bhatia, S.; Ryan, A.M. Effects of g-Loading and Time Lag on Retesting in Job Selection. Int. J. Sel. Assess. 2016, 24, 324–336. [Google Scholar] [CrossRef]
- Te Nijenhuis, J.; van Vianen, A.E.M.; van der Flier, H. Score gains on g-loaded tests: No g. Intelligence 2007, 35, 283–300. [Google Scholar] [CrossRef]
- Villado, A.J.; Randall, J.G.; Zimmer, C.U. The Effect of Method Characteristics on Retest Score Gains and Criterion-Related Validity. J. Bus. Psychol. 2015, 31, 233–248. [Google Scholar] [CrossRef]
- Knowles, E.S.; Coker, M.C.; Scott, R.A.; Cook, D.A.; Neville, J.W. Measurement-induced improvement in anxiety: Mean shifts with repeated assessment. J. Personal. Soc. Psychol. 1996, 71, 352–363. [Google Scholar] [CrossRef]
- Windle, C. Test-Retest Effect on Personality Questionnaires. Educ. Psychol. Meas. 1954, 14, 617–633. [Google Scholar] [CrossRef]
- Matton, N.; Vautier, S.; Raufaste, É. Situational effects may account for gain scores in cognitive ability testing: A longitudinal SEM approach. Intelligence 2009, 37, 412–421. [Google Scholar] [CrossRef][Green Version]
- Reeve, C.L.; Lam, H. The psychometric paradox of practice effects due to retesting: Measurement invariance and stable ability estimates in the face of observed score changes. Intelligence 2005, 33, 535–549. [Google Scholar] [CrossRef]
- Reeve, C.L.; Heggestad, E.D.; Lievens, F. Modeling the impact of test anxiety and test familiarity on the criterion-related validity of cognitive ability tests. Intelligence 2009, 37, 34–41. [Google Scholar] [CrossRef]
- Sarason, S.B.; Mandler, G. Some correlates of test anxiety. J. Abnorm. Soc. Psychol. 1952, 47, 810–817. [Google Scholar] [CrossRef] [PubMed]
- Halpin, P.F.; da-Silva, C.; De Boeck, P.A. Confirmatory Factor Analysis Approach to Test Anxiety. Struct. Equ. Model. A Multidiscip. J. 2014, 21, 455–467. [Google Scholar] [CrossRef]
- Putwain, D.W. Deconstructing test anxiety. Emot. Behav. Diffic. 2008, 13, 141–155. [Google Scholar] [CrossRef]
- Sommer, M.; Arendasy, M.E. Comparing different explanations of the effect of test anxiety on respondents’ test scores. Intelligence 2014, 42, 115–127. [Google Scholar] [CrossRef]
- Zeidner, M. Test Anxiety: The State of the Art; Springer: New York, NY, USA, 1998. [Google Scholar]
- Hong, E. Differential stability of individual differences in state and trait test anxiety. Learn. Individ. Differ. 1998, 10, 51–69. [Google Scholar] [CrossRef]
- Keith, N.; Hodapp, V.; Schermelleh-engel, K.; Moosbrugger, H. Cross-sectional and longitudinal confirmatory factor models for the german test anxiety inventory: A construct validation. Anxiety Stress Coping 2003, 16, 251–270. [Google Scholar] [CrossRef]
- Meijer, J.; Oostdam, R. Effects of instruction and stage-fright on intelligence testing. Eur. J. Psychol. Educ. 2010, 26, 143–161. [Google Scholar] [CrossRef]
- Dew, K.H.; Galassi, J.P.; Galassi, M.D. Math anxiety: Relation with situational test anxiety, performance, physiological arousal, and math avoidance behavior. J. Couns. Psychol. 1984, 31, 580–583. [Google Scholar] [CrossRef]
- Reeve, C.L.; Bonaccio, S. Does test anxiety induce measurement bias in cognitive ability tests? Intelligence 2008, 36, 526–538. [Google Scholar] [CrossRef]
- Moriya, J.; Tanno, Y. Dysfunction of attentional networks for non-emotional processing in negative affect. Cogn. Emot. 2009, 23, 1090–1105. [Google Scholar] [CrossRef]
- Ng, E.; Lee, K. Effects of trait test anxiety and state anxiety on children’s working memory task performance. Learn. Individ. Differ. 2015, 40, 141–148. [Google Scholar] [CrossRef]
- Pacheco-Unguetti, A.P.; Acosta, A.; Callejas, A.; Lupiáñez, J. Attention and Anxiety. Psychol. Sci. 2010, 21, 298–304. [Google Scholar] [CrossRef] [PubMed]
- Quigley, L.; Nelson, A.L.; Carriere, J.; Smilek, D.; Purdon, C. The effects of trait and state anxiety on attention to emotional images: An eye-tracking study. Cogn. Emot. 2012, 26, 1390–1411. [Google Scholar] [CrossRef] [PubMed]
- Freund, P.A.; Holling, H. Who wants to take an intelligence test? Personality and achievement motivation in the context of ability testing. Personal. Individ. Differ. 2011, 50, 723–728. [Google Scholar] [CrossRef]
- Freund, P.A.; Kuhn, J.T.; Holling, H. Measuring current achievement motivation with the QCM: Short form development and investigation of measurement invariance. Personal. Individ. Differ. 2011, 51, 629–634. [Google Scholar] [CrossRef]
- Gogol, K.; Brunner, M.; Goetz, T.; Preckel, F.; Martin, R. Structural models of achievement motivation. Personal. Individ. Differ. 2014, 60, 70. [Google Scholar] [CrossRef]
- Rheinberg, F.; Vollmeyer, R.; Burns, B.D. FAM: Ein Fragebogen zur Erfassung aktuller Motivation in Lern-und Leistungssituationen. Diagnostica 2001, 47, 57–66. [Google Scholar] [CrossRef]
- Hembree, R. Correlates, Causes, Effects, and Treatment of Test Anxiety. Rev. Educ. Res. 1988, 58, 47–77. [Google Scholar] [CrossRef]
- Lang, J.W.B.; Lang, J. Priming Competence Diminishes the Link Between Cognitive Test Anxiety and Test Performance. Psychol. Sci. 2010, 21, 811–819. [Google Scholar] [CrossRef] [PubMed]
- Sawyer, T.P., Jr.; Hollis-Sawyer, L.A. Predicting Stereotype Threat, Test Anxiety, and Cognitive Ability Test Performance: An Examination of Three Models. Int. J. Test. 2005, 5, 225–246. [Google Scholar] [CrossRef]
- Sommer, M.; Arendasy, M.E. Does trait test anxiety compromise the measurement fairness of high-stakes scholastic achievement tests? Learn. Individ. Differ. 2016, 50, 1–10. [Google Scholar] [CrossRef]
- Eysenck, M.W.; Calvo, M.G. Anxiety and Performance: The Processing Efficiency Theory. Cogn. Emot. 1992, 6, 409–434. [Google Scholar] [CrossRef]
- Eysenck, M.W.; Derakshan, N. New perspectives in attentional control theory. Personal. Individ. Differ. 2011, 50, 955–960. [Google Scholar] [CrossRef]
- Eysenck, M.W.; Derakshan, N.; Santos, R.; Calvo, M.G. Anxiety and cognitive performance: Attentional control theory. Emotion 2007, 7, 336–353. [Google Scholar] [CrossRef]
- Bishop, S.J. Trait anxiety and impoverished prefrontal control of attention. Nat. Neurosci. 2008, 12, 92–98. [Google Scholar] [CrossRef] [PubMed]
- Cassady, J.C. The impact of cognitive test anxiety on text comprehension and recall in the absence of external evaluative pressure. Appl. Cogn. Psychol. 2004, 18, 311–325. [Google Scholar] [CrossRef]
- Klinger, E. A consciousness-sampling analysis of test anxiety and performance. J. Personal. Soc. Psychol. 1984, 47, 1376–1390. [Google Scholar] [CrossRef]
- Paulman, R.G.; Kennelly, K.J. Test anxiety and ineffective test taking: Different names, same construct? J. Educ. Psychol. 1984, 76, 279–288. [Google Scholar] [CrossRef]
- Smith, T.W.; Snyder, C.R.; Handelsman, M.M. On the self-serving function of an academic wooden leg: Test anxiety as a self-handicapping strategy. J. Personal. Soc. Psychol. 1982, 42, 314–321. [Google Scholar] [CrossRef]
- Sommer, M.; Arendasy, M.E. Further evidence for the deficit account of the test anxiety–test performance relationship from a high-stakes admission testing setting. Intelligence 2015, 53, 72–80. [Google Scholar] [CrossRef]
- Strohbeck-Kühner, P. Testangst bei Fahreignungsbegutachtungen: Die Angst-Leistung-Relation. Z. Differ. Diagn. Psychol. 1999, 20, 39–57. [Google Scholar] [CrossRef]
- Tobias, S. Test Anxiety: Interference, Defective Skills, and Cognitive Capacity. Educ. Psychol. 1985, 20, 135–142. [Google Scholar] [CrossRef]
- Zeidner, M. Test anxiety and aptitude test performance in an actual college admissions testing situation: Temporal considerations. Personal. Individ. Differ. 1991, 12, 101–109. [Google Scholar] [CrossRef]
- Kirkland, K.; Hollandsworth, J.G. Effective test taking: Skills-acquisition versus anxiety-reduction techniques. J. Consult. Clin. Psychol. 1980, 48, 431–439. [Google Scholar] [CrossRef] [PubMed]
- Musch, J.; Broder, A. Test anxiety versus academic skills: A comparison of two alternative models for predicting performance in a statistics exam. Br. J. Educ. Psychol. 1999, 69, 105–116. [Google Scholar] [CrossRef] [PubMed]
- Naveh-Benjamin, M.; McKeachie, W.J.; Lin, Y.; Holinger, D.P. Test anxiety: Deficits in information processing. J. Educ. Psychol. 1981, 73, 816–824. [Google Scholar] [CrossRef]
- Grissom, N.; Bhatnagar, S. Habituation to repeated stress: Get used to it. Neurobiol. Learn. Mem. 2009, 92, 215–224. [Google Scholar] [CrossRef]
- Lader, M.H.; Wing, L. Habituation of the psycho-galvanic reflex in patients with anxiety states and in normal subjects. J. Neurol. Neurosurg. Psychiatry 1964, 27, 210–218. [Google Scholar] [CrossRef] [PubMed]
- Oostdam, R.; Meijer, J. Influence of Test Anxiety on Measurement of Intelligence. Psychol. Rep. 2003, 92, 3–20. [Google Scholar] [CrossRef] [PubMed]
- McArdle, J.J. Dynamic but structural equation modeling of repeated measures data. In Handbook of Multivariate Experimental Psychology; Nesselroade, J.R., Cattell, R.B., Eds.; Springer: Boston, MA, USA, 1988; pp. 561–614. [Google Scholar]
- McArdle, J.J.; Hamagami, F. Latent difference score structural models for linear dynamic analyses with incomplete longitudinal data. In New Methods for the Analysis of Change; Collins, L.M., Sayer, A.G., Eds.; American Psychological Association: Washington, DC, USA, 2001; pp. 137–175. [Google Scholar]
- Steyer, R.; Eid, M.; Schwenkmezger, P. Modeling true intraindividual change: True change as a latent variable. Methods Psychol. Res. Online 1997, 2, 21–33. [Google Scholar]
- Steyer, R.; Partchev, I.; Shanahan, M. Modeling true intra-individual change in structural equation models: The case of poverty and children’s psychological adjustment. In Modeling Longitudinal and Multiple-Group Data: Practical Issues, Applied Approaches, and Specific Examples; Little, T.D., Schnabel, K.U., Baumert, J., Eds.; Erlbaum: Hillsdale, NJ, USA, 2000; pp. 109–126. [Google Scholar]
- Geiser, C. Data Analysis with Mplus; The Guilford Press: New York, NY, USA, 2013. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Lawrence Erlbaum: Hillsdale, NJ, USA, 1988. [Google Scholar]
- Freund, P.A.; Hofer, S.; Holling, H. Explaining and Controlling for the Psychometric Properties of Computer-Generated Figural Matrix Items. Appl. Psychol. Meas. 2008, 32, 195–210. [Google Scholar] [CrossRef]
- Irvine, S.H.; Kyllonen, P.C. Item Generation for Test Development; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2002. [Google Scholar]
- Gierl, M.J.; Haladyna, T.M. Automatic Item Generation: Theory and Practice; Routledge: New York, NY, USA, 2012. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2008; ISBN 3-900051-07-0. [Google Scholar]
- Rosseel, Y. Lavaan: An R Package for Structural Equation Modeling. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef]
- Jöreskog, K.G.; Sörbom, D. LISREL 8: User’s Referenceguide; Scientific Software: Chicago, IL, USA, 1996. [Google Scholar]
- Flora, D.B.; Curran, P.J. An Empirical Evaluation of Alternative Methods of Estimation for Confirmatory Factor Analysis with Ordinal Data. Psychol. Methods 2004, 9, 466–491. [Google Scholar] [CrossRef] [PubMed]
- West, S.G.; Taylor, A.B.; Wu, W. Model fit and model selection in structural equation modeling. In Handbook of Structural Equation Modeling; Hoyle, H., Ed.; Guilford: New York, NY, USA, 2012; pp. 209–231. [Google Scholar]
- Satorra, A. Scaled and adjusted restricted tests in multi-sample analysis of moment structures. In Innovations in Multivariate Statistical Analysis. A Festschrift for Heinz Neudecker; Heijmans, R.D.H., Pollock, D.S.G., Satorra, A., Eds.; Kluwer Academic Publishers: London, UK, 2000; pp. 233–247. [Google Scholar]
- Satorra, A.; Bentler, P.M. A scaled difference chi-square test statistic for moment structure analysis. Psychometrika 2001, 66, 507–514. [Google Scholar] [CrossRef]
- Cheung, G.W.; Rensvold, R.B. Evaluating Goodness-of-Fit Indexes for Testing Measurement Invariance. Struct. Equ. Model. A Multidiscip. J. 2002, 9, 233–255. [Google Scholar] [CrossRef]
- Steyer, R.; Ferring, D.; Schmitt, M.J. States and traits in psychological assessment. Eur. J. Psychol. Assess. 1992, 8, 79–98. [Google Scholar]
- Marsh, H.W.; Grayson, D. Longitudinal confirmatory factor analysis: Common, time-specific, item-specific, and residual-error components of variance. Struct. Equ. Model. A Multidiscip. J. 1994, 1, 116–145. [Google Scholar] [CrossRef]
- Eid, M. Longitudinal confirmatory factor analysis for polytomous item responses: Model definition and model selection on the basis of stochastic measurement theory. Methods Psychol. Res. Online 1996, 1, 65–85. [Google Scholar]
- Meredith, W. Measurement invariance, factor analysis and factorial invariance. Psychometrika 1993, 58, 525–543. [Google Scholar] [CrossRef]
- Vandenberg, R.J.; Lance, C.E. A Review and Synthesis of the Measurement Invariance Literature: Suggestions, Practices, and Recommendations for Organizational Research. Organ. Res. Methods 2000, 3, 4–70. [Google Scholar] [CrossRef]
- Chen, F.; Curran, P.J.; Bollen, K.A.; Kirby, J.; Paxton, P. An Empirical Evaluation of the Use of Fixed Cutoff Points in RMSEA Test Statistic in Structural Equation Models. Sociol. Methods Res. 2008, 36, 462–494. [Google Scholar] [CrossRef] [PubMed]
- Newell, A.; Rosenbloom, P.S. Mechanisms of skill acquisition and the law of practice. In Cognitive Skills and Their Acquisition; Anderson, J.R., Ed.; Psychology Press: Hillsdale, NJ, USA, 2015. [Google Scholar]
- Kane, M.J.; Hambrick, D.Z.; Tuholski, S.W.; Wilhelm, O.; Payne, T.W.; Engle, R.W. The Generality of Working Memory Capacity: A Latent-Variable Approach to Verbal and Visuospatial Memory Span and Reasoning. J. Exp. Psychol. 2004, 133, 189–217. [Google Scholar] [CrossRef] [PubMed]
- Kyllonen, P.C.; Christal, R.E. Reasoning ability is (little more than) working-memory capacity?! Intelligence 1990, 14, 389–433. [Google Scholar] [CrossRef]
- Süß, H.M.; Oberauer, K.; Wittmann, W.W.; Wilhelm, O.; Schulze, R. Working-memory capacity explains reasoning ability—And a little bit more. Intelligence 2002, 30, 261–288. [Google Scholar] [CrossRef]
- Bishop, S.J.; Jenkins, R.; Lawrence, A.D. Neural Processing of Fearful Faces: Effects of Anxiety are Gated by Perceptual Capacity Limitations. Cereb. Cortex 2006, 17, 1595–1603. [Google Scholar] [CrossRef]
- Davey, H.M.; Barratt, A.L.; Butow, P.N.; Deeks, J.J. A one-item question with a Likert or Visual Analog Scale adequately measured current anxiety. J. Clin. Epidemiol. 2007, 60, 356–360. [Google Scholar] [CrossRef]
- McGrew, K.S. CHC theory and the human cognitive abilities project: Standing on the shoulders of the giants of psychometric intelligence research. Intelligence 2009, 37, 1–10. [Google Scholar] [CrossRef]
- Cattell, R.B. Intelligence: Its Structure, Growth and Action; Elsevier Science Publishers B.V.: Amsterdam, The Netherlands, 1987; p. 115. [Google Scholar]



| Descriptive Statistics | Correlations | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FM | FOF | ||||||||||||||||||
| Measure | Test session | Mean | SD | Min | Max | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| FM | 1 | 7.658 | 3.11 | 1 | 13 | 0.776 | |||||||||||||
| 2 | 9.187 | 2.63 | 0 | 13 | 0.700 *** | 0.711 | |||||||||||||
| 3 | 9.631 | 2.69 | 0 | 13 | 0.640 *** | 0.684 *** | 0.761 | ||||||||||||
| 4 | 9.938 | 2.621 | 1 | 13 | 0.584 *** | 0.705 *** | 0.660 *** | 0.754 | |||||||||||
| 5 | 9.782 | 3.043 | 0 | 13 | 0.579 *** | 0.616 *** | 0.738 *** | 0.687 *** | 0.819 | ||||||||||
| 6 | 9.791 | 3.058 | 0 | 13 | 0.619 *** | 0.690 *** | 0.695 *** | 0.681 *** | 0.714 *** | 0.819 | |||||||||
| 7 | 9.822 | 2.905 | 0 | 13 | 0.594 *** | 0.639 *** | 0.707 *** | 0.643 *** | 0.736 *** | 0.768 *** | 0.798 | ||||||||
| FOF | 1 | 16.582 | 6.2 | 5 | 31 | −0.157 * | −0.104 | −0.088 | −0.05 | −0.042 | −0.067 | −0.054 | 0.84 | ||||||
| 2 | 15.116 | 6.352 | 5 | 34 | −0.197 ** | −0.094 | −0.087 | −0.032 | 0.023 | −0.033 | −0.037 | 0.785 *** | 0.881 | ||||||
| 3 | 13.569 | 6.001 | 5 | 32 | −0.177 ** | −0.131 | −0.099 | −0.062 | 0.005 | −0.033 | −0.057 | 0.729 *** | 0.864 *** | 0.868 | |||||
| 4 | 12.929 | 5.95 | 5 | 28 | −0.148 * | −0.058 | −0.04 | −0.035 | 0.02 | −0.013 | −0.002 | 0.700 *** | 0.826 *** | 0.888 *** | 0.867 | ||||
| 5 | 12.48 | 6.15 | 5 | 28 | −0.148 * | −0.11 | −0.085 | −0.1 | −0.013 | −0.011 | −0.014 | 0.633 *** | 0.812 *** | 0.882 *** | 0.891 *** | 0.878 | |||
| 6 | 12.36 | 6.005 | 5 | 30 | −0.159 * | −0.124 | −0.107 | −0.116 | −0.068 | −0.069 | −0.077 | 0.574 *** | 0.759 *** | 0.826 *** | 0.838 *** | .906 *** | 0.875 | ||
| 7 | 11.889 | 6.014 | 5 | 28 | −0.133 * | −0.106 | −0.057 | −0.072 | −0.013 | −0.057 | −0.04 | 0.594 *** | 0.749 *** | 0.851 *** | 0.853 *** | 0.861 *** | 0.864 *** | 0.877 | |
| Implemented Invariance | Δχ2 (df) | p | χ2 (df) | p | χ2/df | RMSEA [90% CI] | CFI | TLI |
|---|---|---|---|---|---|---|---|---|
| Configural | - | - | 3283.490 (3983) | 1 | 0.824 | 0.000 [0.000, 0.000] | 1.000 | 1.000 |
| Weak | 168.960 (72) | <0.001 | 6038.581 (4055) | <0.001 | 1.489 | 0.047 [0.044, 0.049] | 0.960 | 0.960 |
| Strong | 727.390 (71) | <0.001 | 6712.612 (4126) | <0.001 | 1.627 | 0.053 [0.051, 0.055] | 0.948 | 0.948 |
| Implemented Invariance | Δχ2 (df) | p | χ2 (df) | p | χ2/df | RMSEA [90% CI] | CFI | TLI |
|---|---|---|---|---|---|---|---|---|
| Configural | - | - | 845.657 (504) | <0.001 | 1.678 | 0.055 [0.049, 0.061] | 0.945 | 0.935 |
| Weak | 74.082 (24) | <0.001 | 913.722 (528) | <0.001 | 1.731 | 0.057 [0.051, 0.063] | 0.938 | 0.930 |
| Test Session | Item | rη,ξ | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ||
| 1 | −0.300 ** | 0.088 | −0.272 * | 0.041 | −0.095 | −0.377 *** | −0.347 *** | −0.340 *** | −0.159 | −0.395 *** | −0.188 | −0.106 | −0.116 | −0.060 |
| 2 | −0.041 | 0.064 | −0.302 ** | −0.074 | −0.168 | −0.014 | −0.037 | −0.014 | −0.254 ** | −0.236 ** | −0.127 | 0.022 | −0.229 ** | 0.134 |
| 3 | −0.039 | −0.178 | −0.274 * | −0.118 | −0.129 | −0.137 | −0.290 ** | −0.153 | −0.087 | 0.065 | 0.032 | −0.071 | 0.021 | −0.006 |
| 4 | −0.039 | −0.170 | −0.196 | −0.094 | −0.042 | −0.246 * | 0.026 | −0.339 ** | −0.133 | −0.041 | −0.038 | 0.120 | −0.166 | 0.132 ** |
| 5 | −0.109 | −0.049 | −0.21 | −0.100 | −0.065 | −0.012 | −0.037 | −0.003 | −0.195 * | −0.024 | 0.053 | 0.067 | 0.047 | 0.031 |
| 6 | −0.194 | 0.016 | −0.078 | 0.009 | 0.052 | −0.237 * | −0.168 | 0.002 | −0.037 | −0.007 | −0.148 | −0.015 | −0.021 | −0.032 |
| 7 | −0.046 | 0.117 | −0.188 | 0.034 | −0.215 * | 0.010 | 0.017 | −0.048 | −0.315 ** | −0.144 | −0.078 | 0.059 | −0.086 | −0.035 |
| Threshold | −1.019 | −0.933 | −1.062 | −0.702 | −0.760 | −0.821 | −0.536 | −0.493 | −0.549 | −0.447 | −0.248 | 0.059 | 0.025 | |
| Test Sessions with Modeled Interference Effects | Δχ2 (df) | p | χ2 (df) | p | χ2/df | RMSEA (90% CI) | CFI | TLI |
|---|---|---|---|---|---|---|---|---|
| 1 to 7 | - | - | 9766.433 (7753) | <0.001 | 1.230 | 0.034 [0.032, 0.036] | 0.971 | 0.971 |
| 1 to 6 | 16.882 (13) | 0.205 | 10,079.649 (7766) | <0.001 | 1.300 | 0.036 [0.034, 0.038] | 0.967 | 0.966 |
| 1 to 5 | 11.459 (13) | 0.572 | 10,272.688 (7779) | <0.001 | 1.321 | 0.038 [0.036, 0.040] | 0.964 | 0.964 |
| 1 to 4 | 9.749 (13) | 0.714 | 10,423.506 (7792) | <0.001 | 1.338 | 0.039 [0.037, 0.041] | 0.962 | 0.962 |
| 1 to 3 | 20.410 (13) | 0.085 | 10,790.511 (7805) | <0.001 | 1.383 | 0.041 [0.039, 0.043] | 0.957 | 0.957 |
| 1 and 2 | 18.128 (13) | 0.153 | 11,126.464 (7818) | <0.001 | 1.423 | 0.043 [0.042, 0.045] | 0.952 | 0.952 |
| 1 | 24.432 (13) | 0.027 | 11,581.707 (7831) | <0.001 | 1.479 | 0.046 [0.044, 0.048] | 0.946 | 0.946 |
| None | 46.045 (13) | <0.001 | 12,525.000 (7844) | <0.001 | 1.597 | 0.052 [0.050, 0.053] | 0.932 | 0.932 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jendryczko, D.; Scharfen, J.; Holling, H. The Impact of Situational Test Anxiety on Retest Effects in Cognitive Ability Testing: A Structural Equation Modeling Approach. J. Intell. 2019, 7, 22. https://doi.org/10.3390/jintelligence7040022
Jendryczko D, Scharfen J, Holling H. The Impact of Situational Test Anxiety on Retest Effects in Cognitive Ability Testing: A Structural Equation Modeling Approach. Journal of Intelligence. 2019; 7(4):22. https://doi.org/10.3390/jintelligence7040022
Chicago/Turabian StyleJendryczko, David, Jana Scharfen, and Heinz Holling. 2019. "The Impact of Situational Test Anxiety on Retest Effects in Cognitive Ability Testing: A Structural Equation Modeling Approach" Journal of Intelligence 7, no. 4: 22. https://doi.org/10.3390/jintelligence7040022
APA StyleJendryczko, D., Scharfen, J., & Holling, H. (2019). The Impact of Situational Test Anxiety on Retest Effects in Cognitive Ability Testing: A Structural Equation Modeling Approach. Journal of Intelligence, 7(4), 22. https://doi.org/10.3390/jintelligence7040022





