1.1. Mental Speed and Its Relation with Intelligence
A classical definition of mental speed tasks is that they are simple enough so that anyone can solve them given sufficient time [
1]. According to Kyllonen and Christal [
2], a broad range of elementary processes can be subsumed under this definition. This comprises the encoding of stimuli into working memory as well as the recall of information stored in long-term memory, even the execution of a motor response. Consequently, a multitude of tasks qualifies as measures of mental speed, as the construct has been conceptualized as multi-faceted and hierarchical, comprising several group factors [
3]. This has been confirmed both for paper-and-pencil tests of mental speed [
4] as well as for computerized equivalents [
5]. However, one central aspect pertains to almost all measures of mental speed: They are moderately correlated with measures of general intelligence. According to a reductionist perspective, mental speed is correlated with intelligence, because speed of processing causally contributes to higher cognitive processes [
6], e.g., by constituting a good neural efficacy see also [
7]. Other theoretical accounts postulate working memory capacity (WMC) as the major basis of fluid intelligence and reasoning ability [
2,
8,
9,
10]. However, it has been argued, too, that mental speed contributes to WMC, as processing and rehearsal rely on a shared, time-dependent resource [
11]. In contrast to the former, not all authors conceive mental speed as a causal basis of intelligence or WMC. In line with hierarchical conceptualizations of mental abilities, it was argued instead that mental speed is one important group factor among others [
12].
Whatever the reason, mental speed is moderately correlated with intelligence, which has been demonstrated in large scale population-based studies [
13] and meta analyses [
14,
15]. However, a number of moderating factors have been identified. For instance, it is a well-known finding that task complexity moderates the validity of mental speed tasks predicting intelligence [
16,
17]. The more complex the task, e.g., in terms of response alternatives; [
17], the slower are response times (RT) on average, and the higher the correlation with measures of intelligence [
14,
15].
After focusing almost exclusively on mean response times for a long time, research conducted in the last decades has addressed alternative performance indicators derived from speed tasks. It has been postulated that inter-trial variability (
SDRT) would be more strongly related with intelligence than mean RT (
MRT) [
18]. This notion builds on the assumption that increased variability of the response times indicates an impaired functioning of their underlying mental process. This prediction can be reconciled with the finding that the developmental trajectory of
SDRT resembles that of cognitive ability.
SDRT has been shown [
19] to be lowest in young adults whose cognitive functioning is high, whereas higher
SDRT have been reported for both younger children and older adults whose cognitive functioning is lower relative to that of young adults. A recent meta analysis conducted across 27 independent samples has confirmed that response time variability is moderately related with intelligence, however, not consistently more highly than mean response times [
14]. Additionally,
MRT and
SDRT have been shown to be highly collinear (
r ≈ 0.90) across participants [
20]. In part, slow extreme values may contribute to this correlation, as they affect both mean and variability of responding in the speed tasks. Additionally, they may contribute to the relations of both metrics with intelligence. In support of this notion, it has been shown that the mean RT (
MRT) is more strongly related with intelligence than the median RT (
MdnRT) [
21,
22], where the former is affected but not the latter is affected by slow extreme values.
Further evidence for the validity of slow response times has been obtained in a classical study conducted by Larson and Alderton [
23]. They divided responses times into a number of RT bands, and found that validity for intelligence has been the higher the slower the response band. This finding constituted the worst performance rule (WPR) which has been confirmed in many studies see [
24] for a review. Building on these findings, the differential development model [
25] postulates that besides the general speed of processing, lapses of attention mediate the relationship of age with intelligence.
However, the WPR has not been supported in all studies, and some research has revealed that all portions of the RT distribution contain comparable validity for assessing individual differences in ability [
26,
27]. It has been suggested that the WPR is moderated by task complexity, as it should rather occur in complex tasks compared to simpler ones [
28]. In fact, recent research using experimental manipulations of task complexity in speed tasks confirmed this assumption. It has been demonstrated that validity of slow responses increased with complexity of the speed task [
29], and it has been ruled likely that WMC requirements in the speed tasks are responsible for the increase in validity for intelligence [
30].
1.2. Modeling of Response Times
Typically observed RT distributions are one-peak functions that are heavily skewed to the right, i.e., they possess a heavy tail to the right side with slow responses. A number of statistical models have been suggested that can be used to approximate the empirically observed shape of the RT distribution. The ex-Gaussian parameterization is a two-component model of response times resulting from folding a Gaussian normal distribution with an exponential distribution. Therefore, it yields three parameters,
μ and
σ for the mean and the standard deviation of the Gaussian normal component, and
τ as the parameter (mean and standard deviation) of the exponential component. The ex-Gaussian model has been shown to be useful in RT research [
31,
32,
33]. The
μ parameter can be used as a bias-corrected estimate of the mean RT, whereas
σ corresponds with the general variability of the response times. In contrast, the
τ parameter characterizes the skew of the distribution, and is, hence, sensitive to the proportion of slow extreme values.
In spite of the model’s descriptive nature, some authors have used parameter estimates to infer theoretically postulated processes. Although there is no consensus which processes are captured by the ex-Gaussian parameters, most authors agree that
τ is the most relevant parameter for cognitive functioning. Traditionally, the exponential component has been argued to represent the actual decision process, whereas the Gaussian component reflects the non-decision component [
34]. Others have argued that the exponential component, which corresponds to the proportion of slow RT values, indexes lapses of attention, and other interruptions in cognitive processes [
35,
36]. In turn, the Gaussian component has been suggested to subsume multiple sources of noise during stimulus processing, or to correspond with motor processes [
37].
In line with these predictions, most studies have confirmed that the ex-Gaussian
τ parameter is consistently related with intelligence and working memory capacity [
27,
30,
38,
39], at least when modeling RT distributions obtained with adults performing elementary cognitive tasks. In contrast to these findings, a recent study conducted with children and adolescents that completed arguably simple RT tasks [
40] revealed a significant relation only for the Gaussian
σ parameter.
Using its three parameters the ex-Gaussian model offers richer information than most conventional RT scores. However, like most other RT scores, only correct responses are considered. Additionally no information is provided concerning the accuracy of responding, so a possible speed-accuracy trade-off cannot be detected.
The diffusion model [
41,
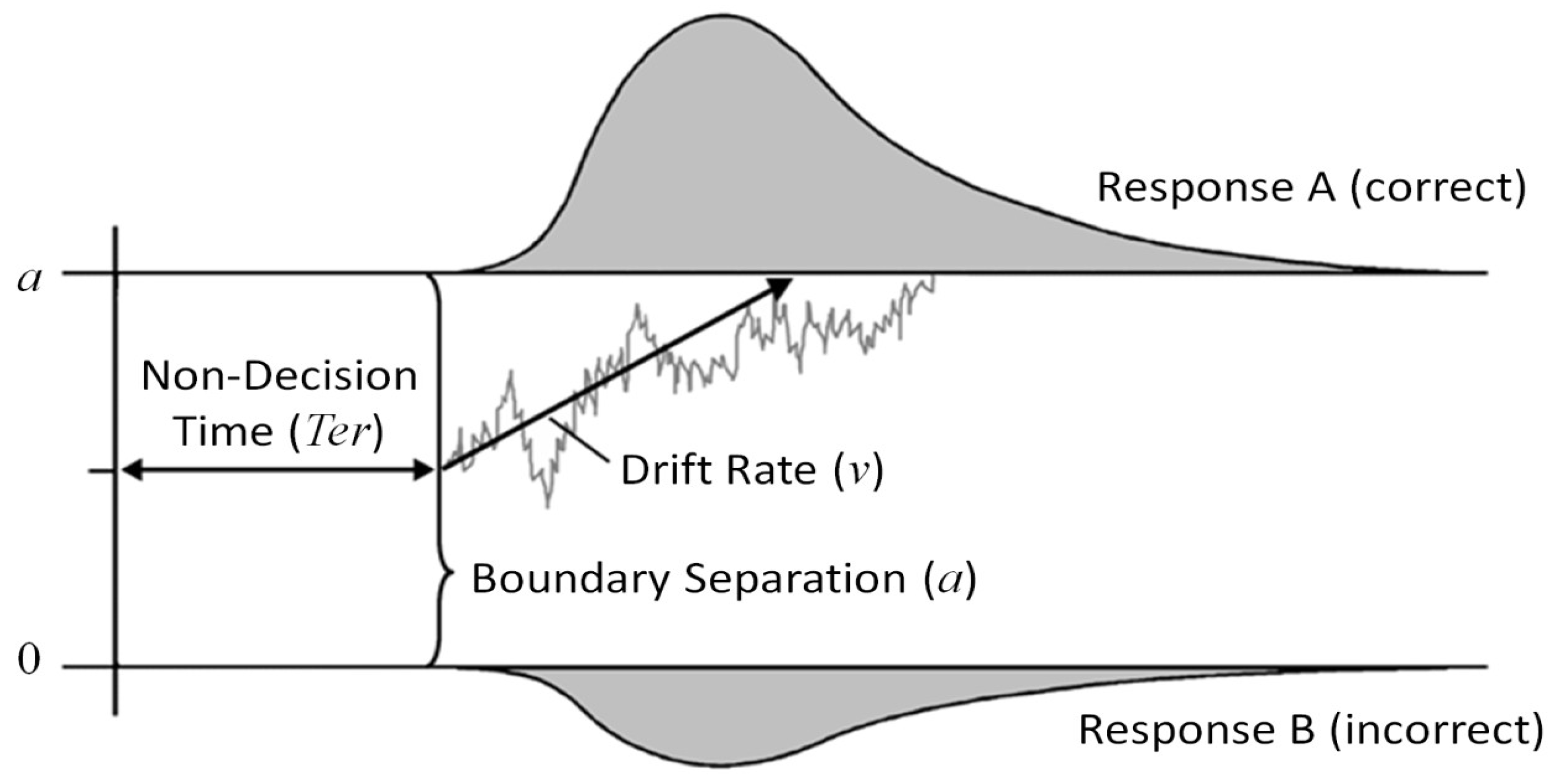
42] can better cope with these challenges. Encompassing a parsimonious account of a binary decision process, the model allows for a dissociation of the efficacy of information processing from the setting of the speed-accuracy compromise, among others. Specifically, the model conceptualizes a binary decision as a random walk process which originates from a starting point between two response thresholds corresponding to the two response options (see
Figure 1). Systematic information and random noise contribute to fluctuation of the decision process across time (see the gray line as a hypothetical sample path in one trial). As soon as the process hits one of the decision thresholds (0 or
a), the corresponding response is elicited. The mean slope of the decision process, i.e., the rate of evidence accumulation across time, is called the drift rate (
ν), and was shown to reflect task easiness [
43] or ability of the participant [
38,
39,
40,
44]. The distance of the two response thresholds denotes the response criterion (
a). Large distances correspond with cautious information processing [
41]: The risk that random fluctuations of the decision process accidently hit the wrong threshold is small, however, the decision will take more time to reach the correct response threshold on average. Consequently, the setting of the response criterion corresponds with the speed-accuracy trade-off. Additionally, a non-decision parameter (
Ter) captures time for processes outside the actual decision phase, such as encoding of stimuli or executing motor responses. The full diffusion model [
42] comprises additional parameters such as a bias in starting point towards one of the response options, and the inter-trial variabilities of all afore-mentioned parameters.
The diffusion model has been suggested as a theoretical explanation for a number of replicated findings in RT research. Using simulations, it has been demonstrated that variation in the diffusion model’s parameters can account for the typical right-skewed shape of the RT distribution, for the theoretically predicted higher validity of
SDRT over
MRT, the higher validity of
MRT over
MdnRT, and the linear correlation of
MRT and
SDRT, among others [
45,
46]. Interestingly, these phenomena can be parsimoniously accounted for by individual differences in the diffusion model’s drift rate that is also responsible for the relation of these observed effects with intelligence. It has to be discussed, though, that the theoretically predicted superiority of
SDRT over
MRT has not been approved meta-analytically on the basis of empirical studies [
14], and the superiority of the
MRT over
MdnRT shown in some studies [
21,
22] has been found to be rather marginal in others [
39].
As the diffusion model offers a theoretical explanation of the observed shape of the RT distribution, it has been argued that the diffusion model should be preferred to the more descriptive ex-Gaussian parameterization [
34,
38]. That said, a combination of diffusion model parameters can explain findings in ex-Gaussian parameters. However, there is no one-to-one correspondence of the parameters in both models. In fact, their correlations have been shown to be moderate [
34,
38,
47], even when all relations are estimated as correlations between latent factors [
39], thereby removing the problem of insufficient reliability of the parameter estimates. This suggests that parameters estimated in both models possess specificity that could lead to differential validity of specific processes and abilities. However, this has to be demonstrated empirically.
For the purpose of individual differences research, it is a vital question whether model-based parameters can be conceived as “measures of trait-like cognitive styles and abilities” [
48] (p. 4). Relevant prerequisites to this end include sufficiently high temporal stability and a certain breadth across a set of different tasks. In fact, temporal stability across a period of eight months has been demonstrated for the most relevant diffusion model parameters, i.e., for the drift rate, for the response criterion, and for the non-decision parameter [
49]. However, research has also shown that parameters modeled in different tasks possess considerable specificity [
39,
49]. Hence, the only moderate correlations between parameters do not result only from insufficient reliability of the estimates, but also from task specificity. Of course, this issue is not confined to modeling approaches, and confirms the hierarchical nature of the speed construct [
3,
4,
5].
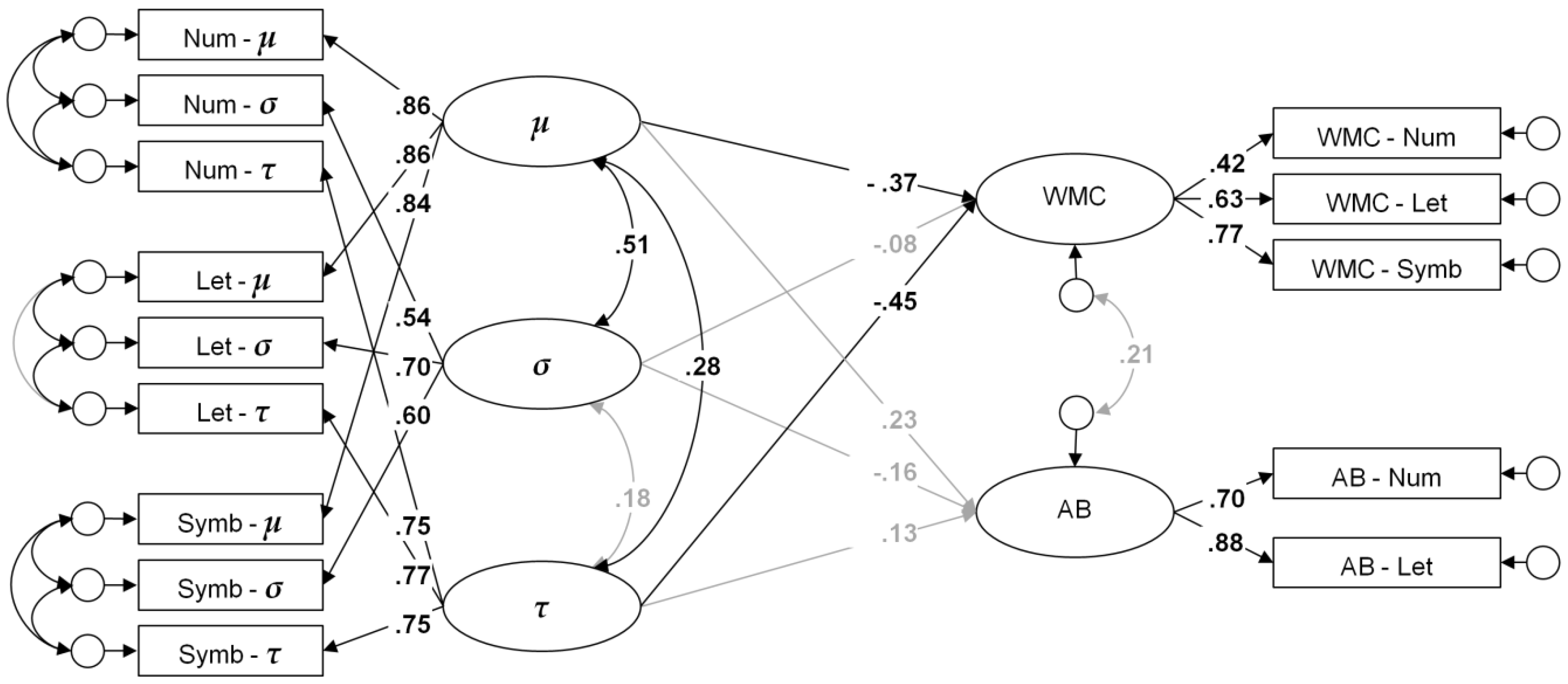
However, a particular challenge when fitting models with several parameters concurrently to data is to cope with computational dependencies. This means, an over- or underestimation of one parameter can be compensated by another parameter, resulting in a comparable model fit. This complicates the identification of the true parameters and can, occasionally, result in relatively extreme parameter estimates that are detrimental in correlative research. Such trade-offs have been demonstrated for the ex-Gaussian model [
38,
47] and for the diffusion model [
50]. In their influential study, Schmiedek et al. [
38] suggested structural equation modeling to overcome this problem. Potentially error-prone parameter estimates obtained from several indicator tasks are treated as observed variables in a confirmatory factor analyses. Parameters of the same kind (e.g., drift rates) are specified as loadings on a common factor that accounts for their communality. In turn, these factors can be used to test the validity of the “true” parameter variances. Meanwhile, the method of combining parameter estimates with structure equation modeling was successfully applied in a couple of studies [
39,
40].
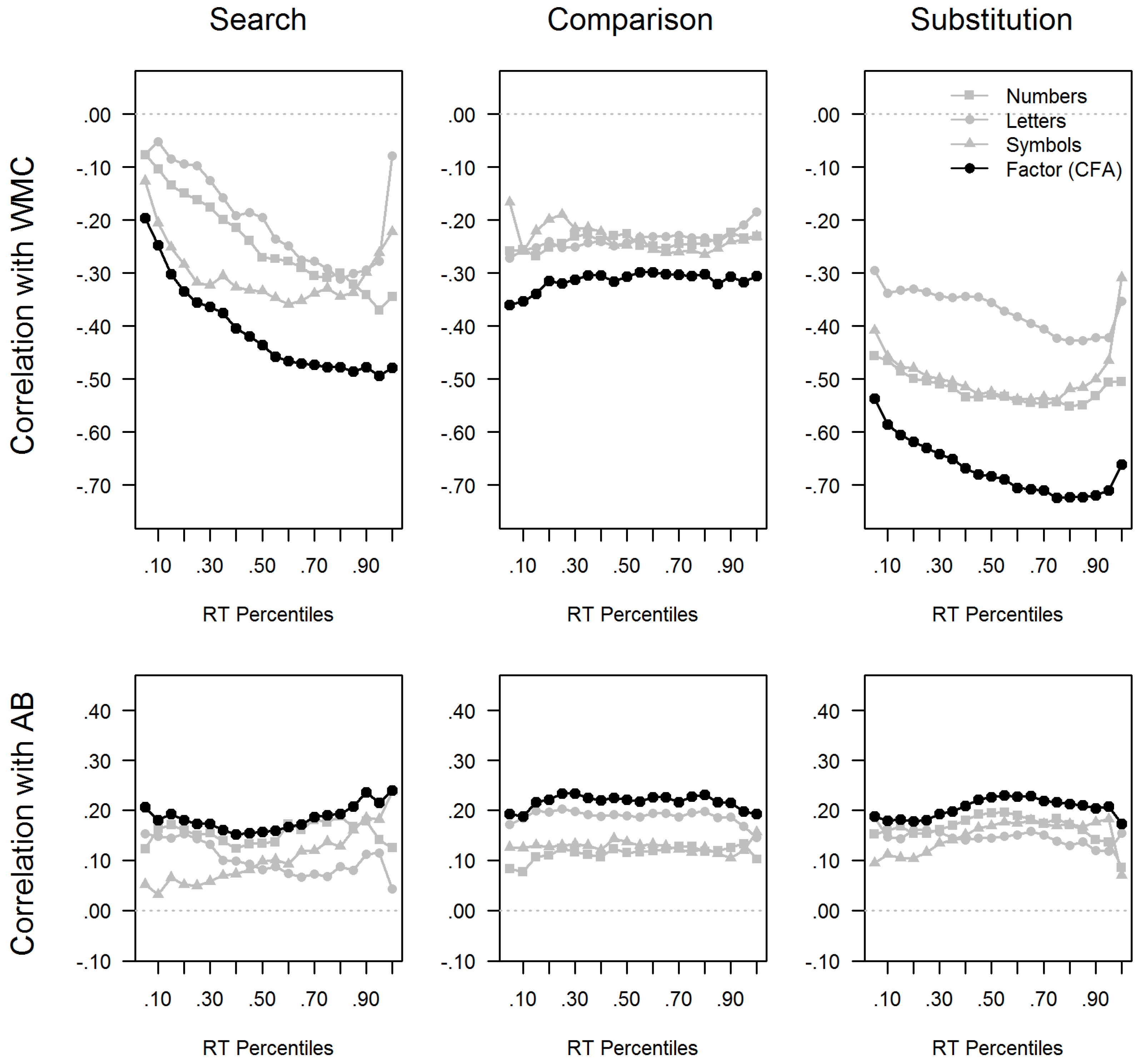
Finally, we would like to discuss the possibility of differential parameter validity when complexity of speed tasks varies. Classical research shows that speed tasks discriminate better between persons of different ability when complexity is increased [
16,
17]. Given that ability is primarily reflected in the diffusions model’s drift rate [
38], a number of drift rate associated effects [
45] can be predicted to covary more strongly with intelligence at higher task difficulty, including the position of the RT distribution, its skew, and its proportion of slow extreme values.
Accordingly, task complexity can be expected to moderate the validity of the ex-Gaussian parameters for ability, although differentially [
20], cf. [
45]. When tasks are very simple, individual RT distributions can be expected to largely overlap, and only the
τ parameter would reliably discriminate between persons of different ability. With increasing task complexity, these differences would become even larger and possibly gain validity. Additionally, the location of the RT distributions would vary more strongly at high task difficulty. Consequently, the
μ parameter would reflect individual differences more reliably and would possibly gain validity with increasing task difficulty. Additionally, both location (
μ) and skew (
τ) would contribute to better discrimination of slow response bands with increasing task complexity. This has been confirmed in previous research [
28,
29].
Only limited research has addressed differential validity of model parameters across levels of task complexity. Indirect evidence comes from a study [
29] in which complexity was manipulated in a Hick paradigm using 0, 1, and 2-bit conditions. Correlations with intelligence were computed for 6 RT bands, and were found to increase across RT bands in all complexity conditions, confirming the WPR [
23,
24]. However, the increase across RT bands was steepest in the simplest 0-bit condition. Correlations were generally much stronger in the most complex 2-bit condition, but the increase across RT bands was attenuated. From an ex-Gaussian perspective, this pattern suggest that the skew of the RT distribution (corresponding with
τ) is most predictive of intelligence in simple tasks (in relative terms), whereas the mean (corresponding with
μ) that contributes to the position of all RT bands gains predictive validity with increasing task complexity. There is only limited direct evidence for differential parameter validity across levels of task complexity. Two studies reported stronger relations with intelligence for the
τ parameter at higher task complexity, at least descriptively [
30,
39]. However, results were mixed for the
μ parameter, either showing the predicted increase [
39] or a decrease [
30]. In one of these studies [
39], results were reported as well for the diffusion model. Relations with intelligence and working memory capacity were parsimoniously accounted for by variation in drift rate, and these relations were slightly stronger at higher task complexity.
1.3. Mental Speed, WMC, and the Attentional Blink Effect
Intelligence tests and WMC paradigms have been extensively employed as criterion variables in previous research addressing the validity of alternative speed scores and modeling approaches [
30,
38,
39,
40]. Also the current study comprised a set of WMC paradigms. This was motivated by the finding that mental speed and WMC are correlated in a mean magnitude [
38,
39], so that range restrictions in either direction are unlikely to occur when the validity of alternative scores is investigated. In fact, previous research has revealed somewhat lower relations of speed with intelligence than that obtained with WMC [
39], arguably an artifact of the narrow measurement model in that study that only comprised one type of reasoning task. Relations of speed with WMC and intelligence were highly comparable in other research using broader measurement models of intelligence incorporating a battery of sufficiently heterogeneous tasks [
38]. The latter could be expected given that WMC constitutes a basis of intelligence [
8,
10,
51]. Facing the time constraints in the current study, we decided to use the same WMC tasks as in previous research [
39] that have been shown to possess highly satisfactory measurement models and validity for intelligence [
52], and that were still brief enough to be included in this battery.
As a novel correlate, we additionally included two rapid serial visual presentation (RSVP) paradigms that have been used in the literature to estimate an attentional blink (AB) effect [
53,
54]. This effect could be of interest as it was theorized to reflect an attentional bottleneck at encoding into working memory. Given this is a processing-speed driven limitation in working memory, it could be predicted to be related with both, mental speed and working memory capacity. Moreover, it could be hypothesized that some of the mental speed scores are more strongly related with the AB effect than others. The latter would depend on the kind of—supposedly—speed-driven limitation that drives the AB effect. For instance, if general speed of processing had an effect, a pronounced relation with RT mean could be predicted. Conversely, if the AB effect was driven by occasional lapses of attention, slow RTs or errors would be most predictive.
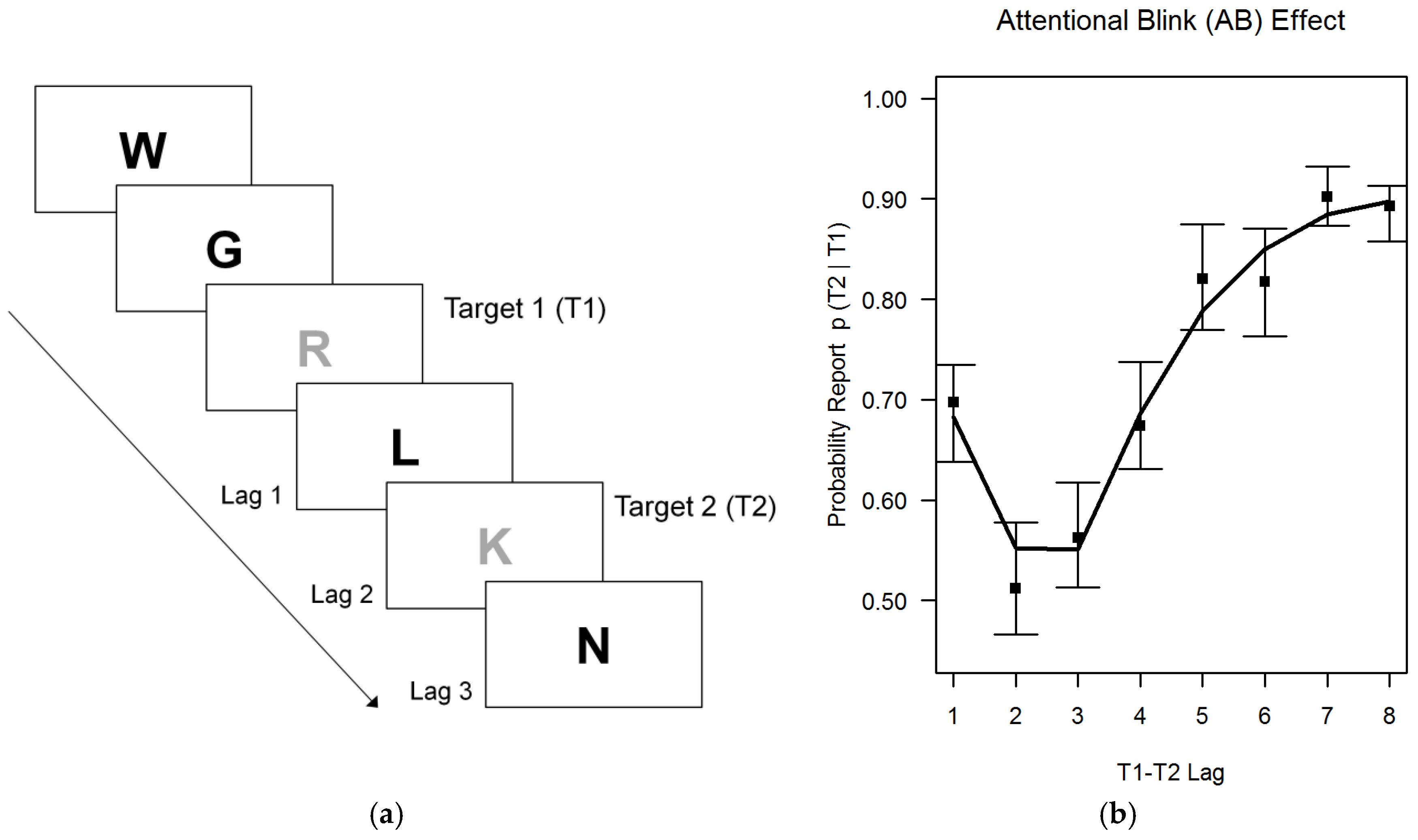
In the RSVP paradigm, a stream of stimuli is presented in short succession (e.g., each 100 ms one stimulus), while participants are asked to report 2 target stimuli marked by a different font color (see
Figure 2, left side). The probability of correctly reporting the second stimulus depends on the lag (target-to-target interval) between target 1 and target 2. Typically, participants can report both stimuli accurately when they are separated by a sufficiently long lag (e.g., 800 ms). However, when the second stimulus is presented shortly (e.g., 200–500 ms) after the first, recall probability is substantially reduced. This effect is known as the attentional blink (AB) effect. The average AB effect observed in this study is depicted on the right side of
Figure 2 (median proportion of correctly recalled target 2 stimuli with 99% bootstrapped CI and a loess smoothed curve). Interestingly, previous research has revealed a high probability that participants can report the second stimulus, when it is presented directly (e.g., 100 ms) after the first stimulus. This effect is known as “lag-1 sparing” [
55], and it speaks against an account in terms of perceptual impairments. Therefore, the AB effect has been classically interpreted as reflecting a capacity limitation when stimuli are encoded into working memory [
56,
57,
58].
As can be seen in
Figure 2, the AB effect observed in this study had a typical shape: After a lag-1 sparring (i.e., 100 ms after T1 presentation), a minimum of correctly recalled T2 stimuli is passed at lag 2 and 3 (i.e., 200–300 ms after T1 presentation). Then, the probability of correctly recalling T2 increases again, and reaches an asymptotic level again at lag 7 and 8 (i.e., 700–800 ms after T1 presentation). A number of alternative scores have been suggested to quantify the AB effect. Typically, only trials are used in which T1 could be correctly recalled, as it implies that T1 was processed. The commonly employed “AB magnitude” score denotes the difference between the minimum recall probability for T2 and the maximum recall probability for T2 [
59], and has been shown to be a robust measure [
60] that could be used to infer individual differences.
A couple of individual differences studies were conducted to test correlates of the AB effect with performance measures. Some research supports the notion that the AB effect reflects capacity limitations in working memory. For instance, in one study [
59] WMC was inversely related with the magnitude of the AB effect. However, intelligence was only related with overall accuracy in that task. In another study [
61], the probability of reporting the second target after correctly reporting the first target was correlated with WMC and intelligence. Yet another study [
62] confirmed moderate relations of AB with WMC and processing speed. However, inverse relations of WMC with the AB effect were not supported in all studies [
60]. The relationship of mental speed with WMC suggested in some studies [
62] was not supported in other research, where the latter study actually comprised a set of different response time tasks [
63]. Finally, inverse relations were reported for the AB effect with executive functions [
61,
64]. In summary, most studies addressing individual differences in AB magnitude investigated correlations with WMC or intelligence, supposedly because the task was classically conceptualized as a marker of capacity limitations. Additionally, executive functions were investigated as correlates. However, in spite of its obvious speediness only few studies addressed mental speed as a possible correlate. Another challenge arises from the fact that the AB magnitude is computed as a contrast score which tends to be unreliable in case of correlated constituents [
65]. Consequently, some of the inconsistencies obtained in previous research may be due to insufficient reliability of the AB score. Please note that some studies used different variants of scoring the AB effect, which may have contributed to the apparent discrepancies of the observed relations.