Using Standardized Test Scores to Include General Cognitive Ability in Education Research and Policy
Abstract
1. Introduction
1.1. What Does the SAT Measure?
1.2. What Is the Impact of Teachers and Classrooms after Accounting for g?
1.3. The Fallacy of the Neglected Aspect
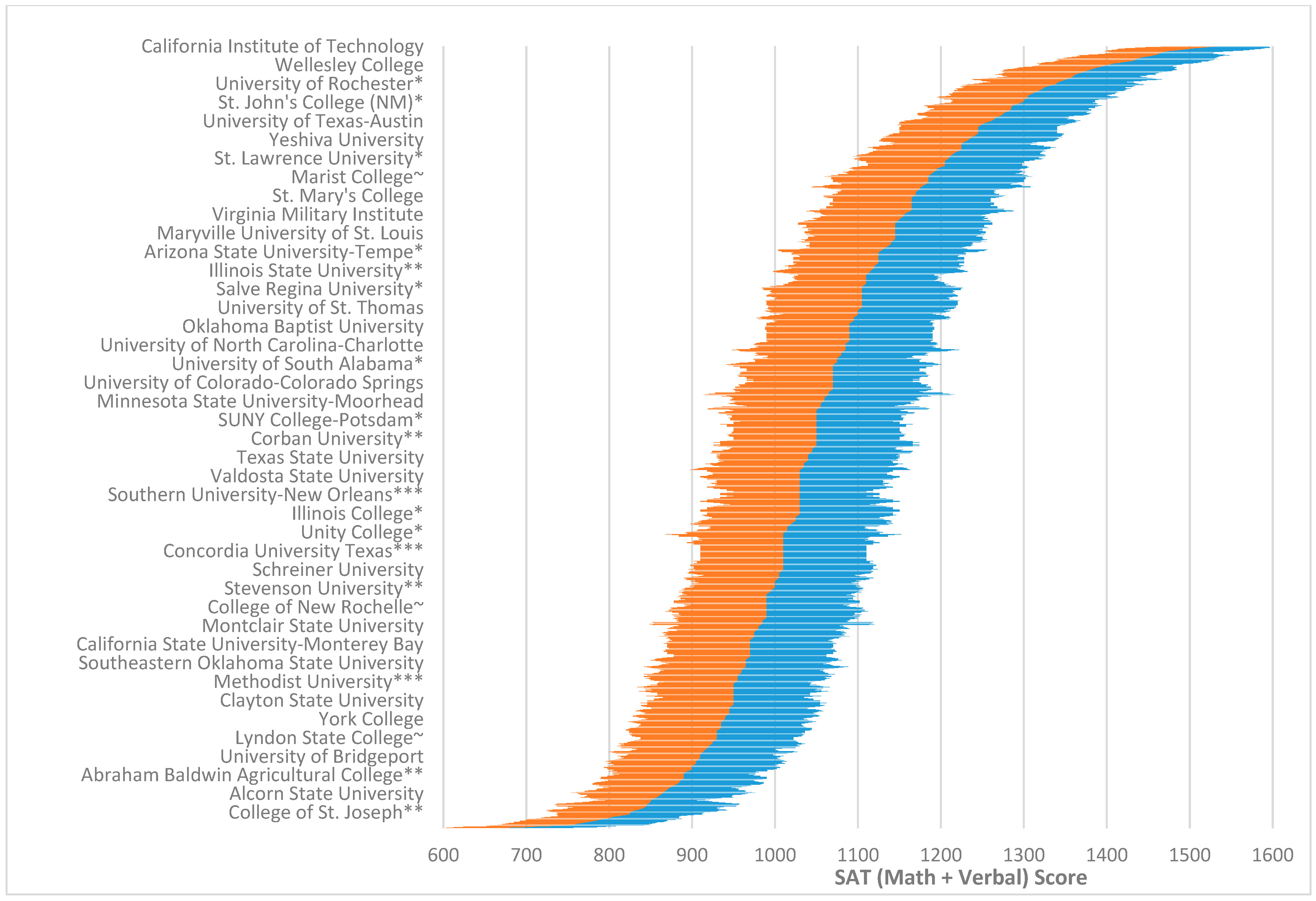
2. Study 1: A Higher Education “g Vector”: Colleges Distributed by General Ability
2.1. Sample 1: U.S. News & World Report SAT and ACT Scores for Colleges and Universities
2.2. Results
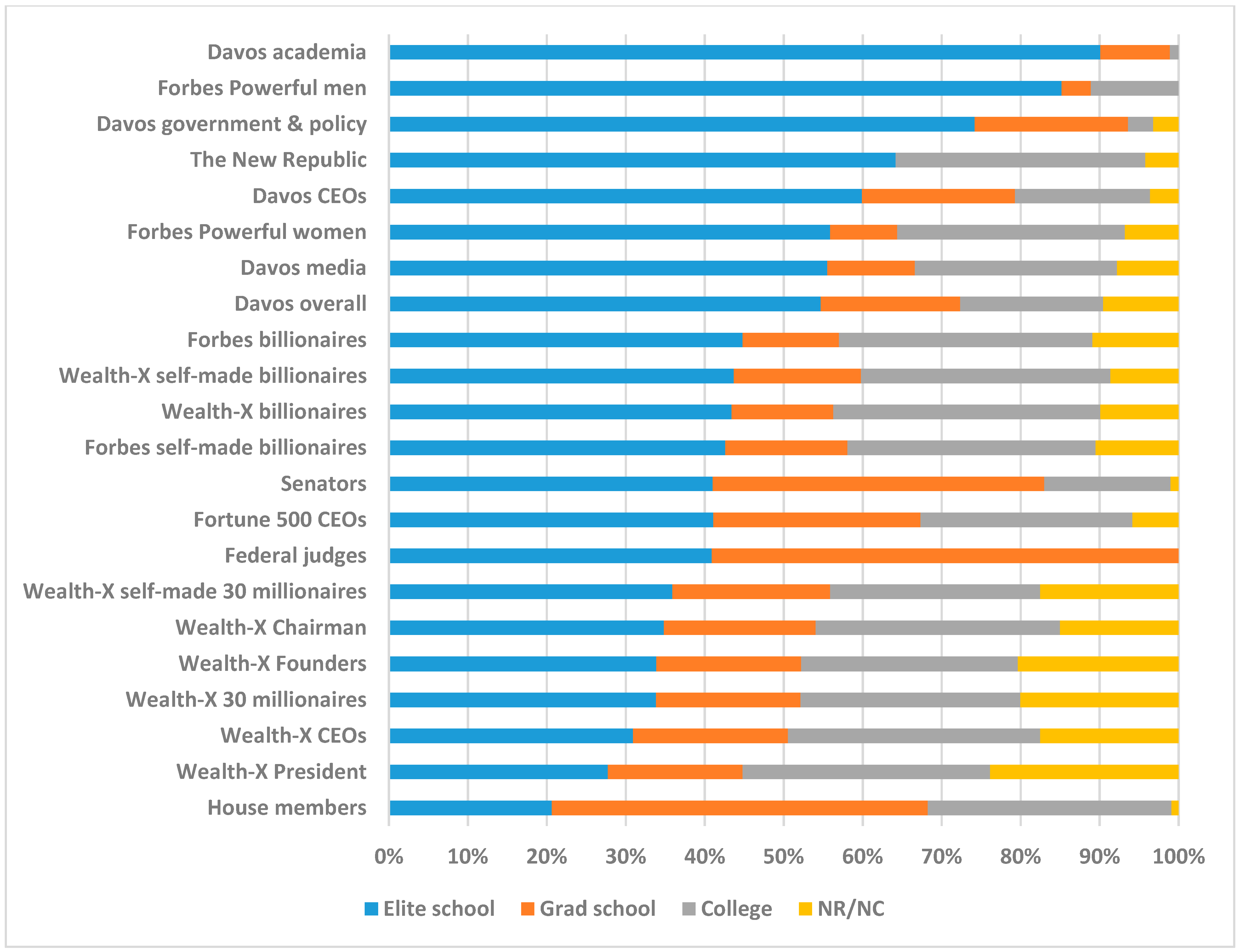
3. Study 2: College Attendance as a Proxy for General Ability to Study Other Groups
3.1. Sample 2: U.S. Occupationally Select Groups and the SAT and ACT Scores of the Colleges and Universities They Attended
3.2. Results
4. Limitations
4.1. Study 1
4.2. Study 2
5. Discussion
5.1. Standardized Tests Throughout Education as Proxy Measures of g
5.2. Cognitive Segregation in Higher Education and Society
5.3. Standardized Tests, When Used to Test all Students, Improves the Identification of Disadvantaged Students
5.4. The Importance of Other Individual Differences Beyond g
5.5. Accounting for g in Educational Observational Studies and Interventions
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Kelley, T.L. Interpretation of Educational Measurements; World Book Company: Yonkers, NY, USA, 1927. [Google Scholar]
- Coleman, W.; Cureton, E.E. Intelligence and achievement: The “jangle fallacy” again. Educ. Psychol. Meas. 1954, 14, 347–351. [Google Scholar] [CrossRef]
- Gottfredson, L.S. Schools and the g factor. Wilson Quart. 2004, 28, 35–45. [Google Scholar]
- Jensen, A.R. Straight Talk about Mental Tests; The Free Press: New York, NY, USA, 1981. [Google Scholar]
- Murray, C. Real Education: Four Simple Truths for Bringing America’s Schools Back to Reality; Crown Forum: New York, NY, USA, 2008. [Google Scholar]
- National Research Council. Ability Testing: Uses, Consequences, and Controversies; The National Academies Press: Washington, DC, USA, 1982. [Google Scholar]
- Zwick, R. Is the SAT a ‘wealth test’? Phi Delta Kappan 2002, 84, 307–311. [Google Scholar] [CrossRef]
- Kohn, A. Two Cheers for an End to the SAT. Chronicle Higher Educ. 2011. Available online: https://www.chronicle.com/article/Two-Cheers-for-an-End-to-the/15930 (accessed on 27 July 2018).
- Colvin, R.L. Q & A: Should UC do away with the SAT? Los Angeles Times. 1997. Available online: http://articles.latimes.com/1997/oct/01/local/me-38061 (accessed on 27 July 2018).
- Frey, M.C.; Detterman, D.K. Scholastic assessment or g? The relationship between the Scholastic Assessment Test and general cognitive ability. Psychol. Sci. 2004, 15, 373–378. [Google Scholar] [CrossRef] [PubMed]
- Koenig, K.A.; Frey, M.C.; Detterman, D.K. ACT and general cognitive ability. Intelligence 2008, 36, 153–160. [Google Scholar] [CrossRef]
- Beaujean, A.A.; Firmin, M.W.; Knoop, A.J.; Michonski, J.D.; Berry, T.P.; Lowrie, R.E. Validation of the Frey and Detterman (2004) IQ prediction equations using the Reynolds Intellectual Assessment Scales. Personal. Individ. Differ. 2006, 41, 353–357. [Google Scholar] [CrossRef]
- Hsu, S.D.H.; Schombert, J. Data mining the university: College GPA predictions from SAT scores. arXiv, 2010; arXiv:1004.2731v1. [Google Scholar] [CrossRef]
- Angoff, W.H.; Johnson, E.G. The differential impact of curriculum on aptitude test scores. J. Educ. Meas. 1990, 27, 291–305. [Google Scholar] [CrossRef]
- Hunt, E. Teaching intelligence: Why, why it is hard and perhaps how to do it. Intelligence 2014, 42, 156–165. [Google Scholar] [CrossRef]
- Kuncel, N.R.; Hezlett, S.A.; Ones, D.S. Academic performance, career potential, creativity, and job performance. Can one construct predict them all? J. Person. Soc. Psychol. 2004, 86, 148–161. [Google Scholar] [CrossRef] [PubMed]
- Lubinski, D. Cognitive epidemiology: With emphasis on untangling cognitive ability and socioeconomic status. Intelligence 2009, 37, 625–633. [Google Scholar] [CrossRef]
- Strauss, V. Why the new SAT scores are meaningless. The Washington Post. 2013. Available online: https://www.washingtonpost.com/news/answer-sheet/wp/2013/09/26/why-the-new-sat-scores-are-meaningless/?utm_term=.25ad351d4551 (accessed on 27 July 2018).
- Hoxby, C.; Avery, C. The missing “one-offs”: The hidden supply of high-achieving low-income students. Brook. Papers Econ. Act. Spring 2013, 1–65. [Google Scholar] [CrossRef]
- Card, D.; Giuliano, L. Universal screening increases the representation of low-income and minority students in gifted education. Proc. Natl. Acad. Sci. USA 2016, 113, 13678–13683. [Google Scholar] [CrossRef] [PubMed]
- Dynarski, S.M. ACT/Sat for all: A cheap, effective way to narrow income gaps in college. Brookings 2018. Available online: https://www.brookings.edu/research/act-sat-for-all-a-cheap-effective-way-to-narrow-income-gaps-in-college/ (accessed on 27 July 2018).
- Grissom, J.A.; Redding, C. Discretion and disproportionality: Explaining the underrepresentation of high-achieving students of color in gifted programs. AERA Open 2016, 2, 1–25. [Google Scholar] [CrossRef]
- McBee, M.T.; Peters, S.J.; Miller, E.M. The impact of the nomination stage on gifted program identification. Gifted Child. Quart. 2016, 60, 258–278. [Google Scholar] [CrossRef]
- Carroll, J.B. Human Cognitive Abilities: A Survey of Factor Analytic Studies; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Detterman, D.K. Education and intelligence: Pity the poor teacher because student characteristics are more significant than teachers or schools. Span. J. Psychol. 2016, 19, E93. [Google Scholar] [CrossRef] [PubMed]
- Chabris, C.F. Cognitive and neurobiological mechanisms of the law of general intelligence. In Integrating the Mind: Domain General Versus Domain Specific Processes in Higher Cognition; Roberts, M.J., Ed.; Psychology Press: New York, NY, USA, 2007; pp. 449–491. [Google Scholar]
- Jensen, A.R. The g Factor: The Science of Mental Ability; Praeger: Westport, CT, USA, 1998. [Google Scholar]
- Spearman, C. The Abilities of Man: Their Nature and Measurement; Macmillan: New York, NY, USA, 1927. [Google Scholar]
- Ree, M.J.; Earles, J.A. The stability of g across different methods of estimation. Intelligence 1991, 15, 271–278. [Google Scholar] [CrossRef]
- Johnson, W.; Bouchard, T.J.; Krueger, R.F.; McGue, M.; Gottesman, I.I. Just one g: Consistent results from three test batteries. Intelligence 2004, 32, 95–107. [Google Scholar] [CrossRef]
- Schult, J.; Sparfeldt, J.R. Do non-g factors of cognitive ability tests align with specific academic achievements? A combined bifactor modeling approach. Intelligence 2016, 59, 96–102. [Google Scholar] [CrossRef]
- Kaufman, S.B.; Reynolds, M.R.; Liu, X.; Kaufman, A.S.; McGrew, K.S. Are cognitive g and academic achievement g one and the same g? An exploration on the Woodcock-Johnson and Kaufman tests. Intelligence 2012, 40, 123–138. [Google Scholar] [CrossRef]
- Chetty, R.; Friedman, J.N.; Hilger, N.; Saez, E.; Schanzenbach, D.W.; Yagan, D. How does your kindergarten classroom affect your earnings? Evidence from Project Star. Quart. J. Econ. 2011, 126, 1593–1660. [Google Scholar] [CrossRef]
- Rivkin, S.G.; Hanushek, E.A.; Kain, J.F. Teachers, schools, and academic achievement. Econometrica 2005, 73, 417–458. [Google Scholar] [CrossRef]
- The 74 Million Staff. Flashcards: Test scores and Teacher Evals: A Complex Controversy Explained. The 74 Million. Available online: https://www.the74million.org/article/test-scores-and-teacher-evals-a-complex-controversy-explained/ (accessed on 27 July 2018).
- Ioannidis, J.P.A. Why most published research findings are false. Chance 2005, 18, 40–47. [Google Scholar] [CrossRef]
- Open Science Collaboration. Estimating the reproducibility of psychological science. Science 2015, 349, aac4716. [Google Scholar] [CrossRef] [PubMed]
- Simmons, J.P.; Nelson, L.D.; Simonsohn, U. False-positive psychology: Undisclosed flexibility in data collection and analysis allows presenting anything as significant. Psychol. Sci. 2011, 22, 1359–1366. [Google Scholar] [CrossRef] [PubMed]
- Makel, M.C.; Plucker, J.A. Facts are more important than novelty: Replication in the education sciences. Educ. Res. 2014, 43, 304–316. [Google Scholar] [CrossRef]
- Schmidt, F.L. Beyond questionable research methods: The role of omitted relevant research in the credibility of research. Arch. Sci. Psychol. 2017, 5, 32–41. [Google Scholar] [CrossRef]
- Ellis, R.S. The Psychology of Individual Differences; D. Appleton and Co.: New York, NY, USA, 1928. [Google Scholar]
- Carnap, R. Logical Foundations of Probability; University of Chicago Press: Chicago, IL, USA, 1950. [Google Scholar]
- Lubinski, D. Scientific and social significance of assessing individual differences: “Sinking shafts at a few critical points”. Annu. Rev. Psychol. 2000, 51, 405–444. [Google Scholar] [CrossRef] [PubMed]
- America’s Best Colleges. 2015. Available online: http://colleges.usnews.rankingsandreviews.com/best-colleges (accessed on 27 July 2018).
- American College Test. ACT-SAT Concordance. 2011. Available online: http://www.act.org/aap/concordance/pdf/reference.pdf (accessed on 27 July 2018).
- Avery, C.N.; Glickman, M.E.; Hoxby, C.M.; Metrick, A. A revealed preference ranking of U.S. colleges and universities. Quart. J. Econ. 2013, 128, 425–467. [Google Scholar] [CrossRef]
- Times Higher Education. World University Rankings. Available online: https://www.timeshighereducation.com/world-university-rankings (accessed on 27 July 2018).
- Sternberg, D.A. Lumosity’s Smartest Colleges. 2013. Available online: https://www.scribd.com/document/184980304/America-s-Smartest-Colleges-2013 (accessed on 27 July 2018).
- Belkin, D. Exclusive test data: Many colleges fail to improve critical-thinking skills. Wall Street J. 2017. Available online: https://www.wsj.com/articles/exclusive-test-data-many-colleges-fail-to-improve-critical-thinking-skills-1496686662 (accessed on 27 July 2018).
- Shaw, E.J.; Marini, J.P.; Beard, J.; Shmueli, D.; Young, L.; Ng, H. The Redesigned SAT Pilot Predictive Validity Study: A First Look; College Board Research Report; College Board: New York, NY, USA, 2016. [Google Scholar]
- College Board. SAT: Understanding Scores. 2017. Available online: https://collegereadiness.collegeboard.org/pdf/understanding-sat-scores.pdf (accessed on 27 July 2018).
- Simons, D.J.; Boot, W.R.; Charness, N.; Gathercole, S.E.; Chabris, C.F.; Hambrick, D.Z.; Stine-Morrow, E.A.L. Do “brain-training” programs work? Psychol. Sci. Public Int. 2016, 17, 103–186. [Google Scholar] [CrossRef] [PubMed]
- Wai, J. Investigating the world’s rich and powerful: Education, cognitive ability, and sex differences. Intelligence 2014, 46, 54–72. [Google Scholar] [CrossRef]
- Wai, J. Investigating America’s elite: Cognitive ability, education, and sex differences. Intelligence 2013, 41, 203–211. [Google Scholar] [CrossRef]
- Wai, J.; Kell, H.J. How Important is Intelligence in the Development of Professional Expertise? Combining Prospective and Retrospective Longitudinal Data Provides an Answer. In The Science of Expertise: Behavioral, Neural, and Genetics Approaches to Complex Skill; Hambrick, D.Z., Campitelli, G., Macnamara, B., Eds.; Routledge: New York, NY, USA, 2017. [Google Scholar]
- Wai, J.; Lincoln, D. Investigating the right tail of wealth: Education, cognitive ability, giving, network power, gender, ethnicity, leadership, and other characteristics. Intelligence 2016, 54, 1–32. [Google Scholar] [CrossRef]
- Wai, J.; Rindermann, H.R. The path and performance of a company leader: An historical examination of the education and cognitive ability of Fortune 500 CEOs. Intelligence 2015, 53, 102–107. [Google Scholar] [CrossRef]
- Murray, C. Coming Apart: The State of White America, 1960–2010; Crown Forum: New York, NY, USA, 2012. [Google Scholar]
- Pinker, S. The trouble with Harvard: The Ivy League is broken and only standardized tests can fix it. The New Republic. 2014. Available online: http://www.newrepublic.com/article/119321/harvard-ivy-league-should-judge-students-standardized-tests (accessed on 27 July 2018).
- Espenshade, T.J.; Radford, A.W. No Longer Separate, Not Yet Equal: Race and Class in Elite College Admission and Campus Life; Princeton University Press: Princeton, NJ. USA, 2009. [Google Scholar]
- Golden, D. The Price of Admission; Three Rivers Press: New York, NY, USA, 2006. [Google Scholar]
- Sander, R.H. A systemic analysis of affirmative action in American law schools. Stanf. Law Rev. 2004, 57, 367–483. [Google Scholar]
- Schmidt, F.L.; Hunter, J.E. General mental ability in the world of work: Occupational attainment and job performance. J. Pers. Soc. Psychol. 2004, 86, 162–173. [Google Scholar] [CrossRef] [PubMed]
- Gottfredson, L.S. G, Jobs, and Life. In The Scientific Study of General Intelligence: Tribute to Arthur R. Jensen; Nyborg, H., Ed.; Pergamon: New York, NY, USA, 2003; pp. 293–342. [Google Scholar]
- Pascarella, E.T.; Cruce, T.; Umbach, P.D.; Wolniak, G.C.; Kuh, G.D.; Carini, R.M.; Hayek, J.C.; Gonyea, R.M.; Zhao, C.-M. Institutional Selectivity and Good Practices in Undergraduate Education: How Strong is the Link? J. High. Educ. 2006, 77, 251–285. [Google Scholar] [CrossRef]
- Lubinski, D.; Benbow, C.P. Study of mathematically precocious youth after 35 years: Uncovering antecedents for the development of math-science expertise. Perspect. Psychol. Sci. 2006, 1, 316–345. [Google Scholar] [CrossRef] [PubMed]
- Wai, J.; Putallaz, M.; Makel, M.C. Studying intellectual outliers: Are there sex differences, and are the smart getting smarter? Curr. Dir. Psychol. Sci. 2012, 21, 382–390. [Google Scholar] [CrossRef]
- Rindermann, H.R.; Thompson, J. The effect of cognitive ability on wealth, as mediated through scientific achievement and economic freedom. Psychol. Sci. 2011, 22, 754–763. [Google Scholar] [CrossRef] [PubMed]
- Hyman, J. ACT for all: The effect of mandatory college entrance exams on postsecondary attainment and choice. Educ. Financ. Policy 2017, 12, 281–311. [Google Scholar] [CrossRef]
- Hambrick, D.Z.; Campitelli, G.; Macnamara, B. (Eds.) The Science of Expertise: Behavioral, Neural, and Genetics Approaches to Complex Skill; Routledge: New York, NY, USA, 2017. [Google Scholar]
- Vansteenkiste, M.; Sierens, E.; Soenens, B.; Luyckx, K.; Lens, W. Motivational profiles from a self-determination perspective: The quality of motivation matters. J. Educ. Psychol. 2009, 101, 671–688. [Google Scholar] [CrossRef]
- Kovas, Y.; Garon-Carrier, G.; Boivin, M.; Petrill, S.A.; Plomin, R.; Malykh, S.B.; Spinath, F.; Murayama, K.; Ando, K.; Bogdanova, O.Y.; et al. Why children differ in motivation to learn: Insights from over 13,000 twins from 6 countries. Person. Individ. Differ. 2015, 80, 51–63. [Google Scholar] [CrossRef] [PubMed]
- Revelle, W.; Wilt, J.; Condon, D.M. Individual differences and differential psychology. In The Wiley-Blackwell Handbook of Individual Differences; Chamorro-Premuzic, T., von Stumm, S., Furnham, A., Eds.; Wiley-Blackwell: Hoboken, NJ, USA, 2013. [Google Scholar]
- Wai, J.; Worrell, F.C.; Chabris, C.F. The Consistent Influence of General Cognitive Ability in College, Career, and Lifetime Achievement. In Preparing Students for College and Careers: Theory, Measurement, and Educational Practice; McClarty, K., Mattern, K., Gaertner, M., Eds.; Routledge: New York, NY, USA, 2018. [Google Scholar]
- Rogers, W.T.; Hopkins, K.D. Power estimates in the presence of a covariate and measurement error. Educ. Psychol. Meas. 1988, 48, 647–656. [Google Scholar] [CrossRef]
- Van Breukelen, G.J.P. ANCOVA versus change from baseline had more power in randomized studies and more bias in nonrandomized studies. J. Clin. Epidemiol. 2006, 59, 920–925. [Google Scholar] [CrossRef] [PubMed]
- Borm, G.F.; Fransen, J.; Lemmens, W.A.J.G. A simple sample size formula for analysis of covariance in randomized clinical trials. J. Clin. Epidemiol. 2007, 60, 1234–1238. [Google Scholar] [CrossRef] [PubMed]
- Gottfredson, L.S. Intelligence: Is it the epidemiologists’ elusive “fundamental cause” of social class inequalities in health? J. Personal. Soc. Psychol. 2004, 86, 174–199. [Google Scholar] [CrossRef] [PubMed]
- Wainer, H. Uneducated Guesses: Using Evidence to Uncover Misguided Education Policies; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
| Times Higher Education World Rank | Average SAT (Math + Verbal) | Number of Institutions |
|---|---|---|
| 1 to 10 | 1499 | 7 |
| 11 to 25 | 1406 | 11 |
| 26 to 50 | 1343 | 8 |
| 51 to 100 | 1281 | 17 |
| 101 to 150 | 1326 | 7 |
| 151 to 200 | 1249 | 12 |
| 201 to 300 | 1205 | 21 |
| 301 to 400 | 1182 | 26 |
| 401 to 500 | 1146 | 15 |
| 501 to 600 | 1151 | 14 |
| 601 to 1000 | 1104 | 20 |
| Effect Size | |||||
|---|---|---|---|---|---|
| ρ | d = 0.1 | d = 0.2 | d = 0.3 | d = 0.4 | d = 0.5 |
| 0.0 | 3142 | 788 | 352 | 200 | 128 |
| 0.1 | 3111 | 780 | 348 | 198 | 127 |
| 0.3 | 2859 | 717 | 320 | 182 | 116 |
| 0.5 | 2357 | 591 | 264 | 150 | 96 |
| 0.7 | 1602 | 402 | 180 | 102 | 65 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wai, J.; Brown, M.I.; Chabris, C.F. Using Standardized Test Scores to Include General Cognitive Ability in Education Research and Policy. J. Intell. 2018, 6, 37. https://doi.org/10.3390/jintelligence6030037
Wai J, Brown MI, Chabris CF. Using Standardized Test Scores to Include General Cognitive Ability in Education Research and Policy. Journal of Intelligence. 2018; 6(3):37. https://doi.org/10.3390/jintelligence6030037
Chicago/Turabian StyleWai, Jonathan, Matt I. Brown, and Christopher F. Chabris. 2018. "Using Standardized Test Scores to Include General Cognitive Ability in Education Research and Policy" Journal of Intelligence 6, no. 3: 37. https://doi.org/10.3390/jintelligence6030037
APA StyleWai, J., Brown, M. I., & Chabris, C. F. (2018). Using Standardized Test Scores to Include General Cognitive Ability in Education Research and Policy. Journal of Intelligence, 6(3), 37. https://doi.org/10.3390/jintelligence6030037





