1. Introduction
Intelligence researchers have investigated the correlation of mental speed with measures of intelligence since the mid-20th century [
1]. In fact, large-scale studies and meta-analyses have documented a moderate relation of intelligence with inspection time, reaction time, and other measures of speed of processing [
1,
2,
3].
Reductionist theories posit that mental speed constitutes a fundamental of fluid intelligence (
gf) [
4]. Similarly, some accounts of working memory capacity (WMC) assume a causal role of mental speed. For instance, the time-based resource-sharing model [
5,
6] assumes some executive resource is responsible for processing and rehearsal. The faster processing is completed, the more time is available for the rehearsal of decaying memory traces. In turn, it was suggested that WMC constitutes a basis of
gf [
7,
8]. However, the notion that speed plays a causal role for intelligence is not unequivocal. It was emphasized that mental speed should not be considered the basis of intelligence, but as one important factor among others [
9]. Additionally, it was argued that speed requirements in measures of WMC or
gf may contribute to the observed correlation [
10].
Nevertheless, a moderate relation of mental speed with cognitive ability is empirically well supported in large scale population-based studies [
3] and in different age groups [
11]. However, a meta-analysis [
1] suggests that this relation is moderated by characteristics of the speed tasks. Specifically, choice reaction time tasks show a trend towards higher correlations with increasing complexity. Early evidence in this respect dates back to the work of Hick [
12], who demonstrated that response times increase with the number of response alternatives. Additionally, this increase was found to be steeper for persons with lower intelligence [
13]. This implies that tasks discriminate better between persons as complexity increases [
2].
Interestingly, classical studies suggest the standard deviation of the RT distribution (
SDRT) is slightly more correlated with
gf than the mean (
MRT) [
2]. Variability in task performance is of interest as it may indicate impaired stability of the cognitive system. It was shown that
SDRT is lowest in young adults and is higher in both younger children and older adults [
14]. Thereby, the developmental trajectory of
SDRT as an inverse marker of cognitive functioning resembles that of cognitive ability. A recent meta-analysis on the basis of 27 independent samples [
15] confirms a moderate relation between
SDRT and intelligence, but does not support the previously held notion [
2] that variability is a better predictor of intelligence than mean RT. Generally,
MRT and
SDRT are highly collinear across participants (i.e.,
r ≈ 0.9; [
16]). Additionally, both scores are affected by extreme values, which can be expected to contribute to their correlation. Therefore, the common practice in some RT measures to scale means by the individual’s variability may function as a pragmatic remedy [
17]. Theoretically, more satisfactory modeling approaches are discussed below. Since
MRT,
SDRT, and
gf are highly related, it was suggested that, from a psychometric perspective, a common factor could account for their relation [
18].
Other lines of research suggest that not mean and variability of the RT distribution, but the slowest RT values of a person are the most predictive score of cognitive ability. In a classic study, Larson and Alderton [
19] sorted responses in increasing order and investigated relations with ability for different RT bands. They found that the slower the RT, the higher the relation with ability, which is now known as the
worst performance rule (WPR). The WPR was confirmed in many studies (see [
20], for a review), both for fluid intelligence and for executive functions [
21]. Additionally, the WPR was shown across different age groups [
11]. However, the evidence is not unequivocal, as some studies revealed that all portions of the reaction time distribution contain similar individual difference information [
22] (see also [
23]). It was argued that WPR only holds for complex but not for simple tasks [
24]. It should be noted that the WPR can be considered a paradigm shift in experimental research: Traditionally, researchers were interested in mean response times, and they tried to reduce the potentially biasing effects of extreme values by excluding or winsorizing outliers, by log-transforming individual RTs, or by computing their median. Of course, such treatments only make sense if they help remove contaminants but not meaningful information. In fact, some studies revealed that cognitive ability is slightly more correlated with the mean (
MRT) than with the median (
MdnRT) RT [
18,
25], where the former but not the latter is known to be biased by extreme values.
A more elegant way to dissociate components that contribute to an RT distribution is to fit an explicit RT model. The most popular approaches include the ex-Gaussian model [
26,
27,
28] and the diffusion model [
29,
30]. Additionally, growth curve modeling was recently suggested as an alternative to model task demands and WPR simultaneously [
31].
The ex-Gaussian approach offers a parsimonious parameterization that effectively describes the shape of a typical RT distribution, which resembles a normal distribution but with heavy right tail. Technically, the ex-Gaussian model assumes that RT distributions can be approximated by folding a Gaussian normal distribution, with parameters
μ and
σ for the mean and the standard deviation, with an exponential decay function with parameter
τ. The ex-Gaussian parameters are informative because they offer a bias-corrected estimate of the location of the RT distribution (
μ), of its variability (
σ), and of the proportion of exponential contaminants (
τ). Parameter
μ is conventionally interpreted as the average time required for a (correct) response in most of the trials (as an inverse indicator of mental speed), while the parameter
τ is sensitive to the proportion of occasional, but extreme, RT outliers. Therefore, the
τ parameter has been interpreted as an indicator of attentional/cognitive lapses—or other interruptions in information processing [
21,
32]. The ex-Gaussian model is a good descriptive approximation of the RT distribution [
27,
28] and has been shown to be a useful tool in RT research [
26,
33]. Its parameters have been used to test theories (e.g.,
τ as an indicator of cognitive lapses [
21,
32], among others). However, the model itself is descriptive and lacks an explicit theoretical basis. Additionally, the ex-Gaussian model only uses the information in correct responses and cannot adequately cope with speed-accuracy trade-offs.
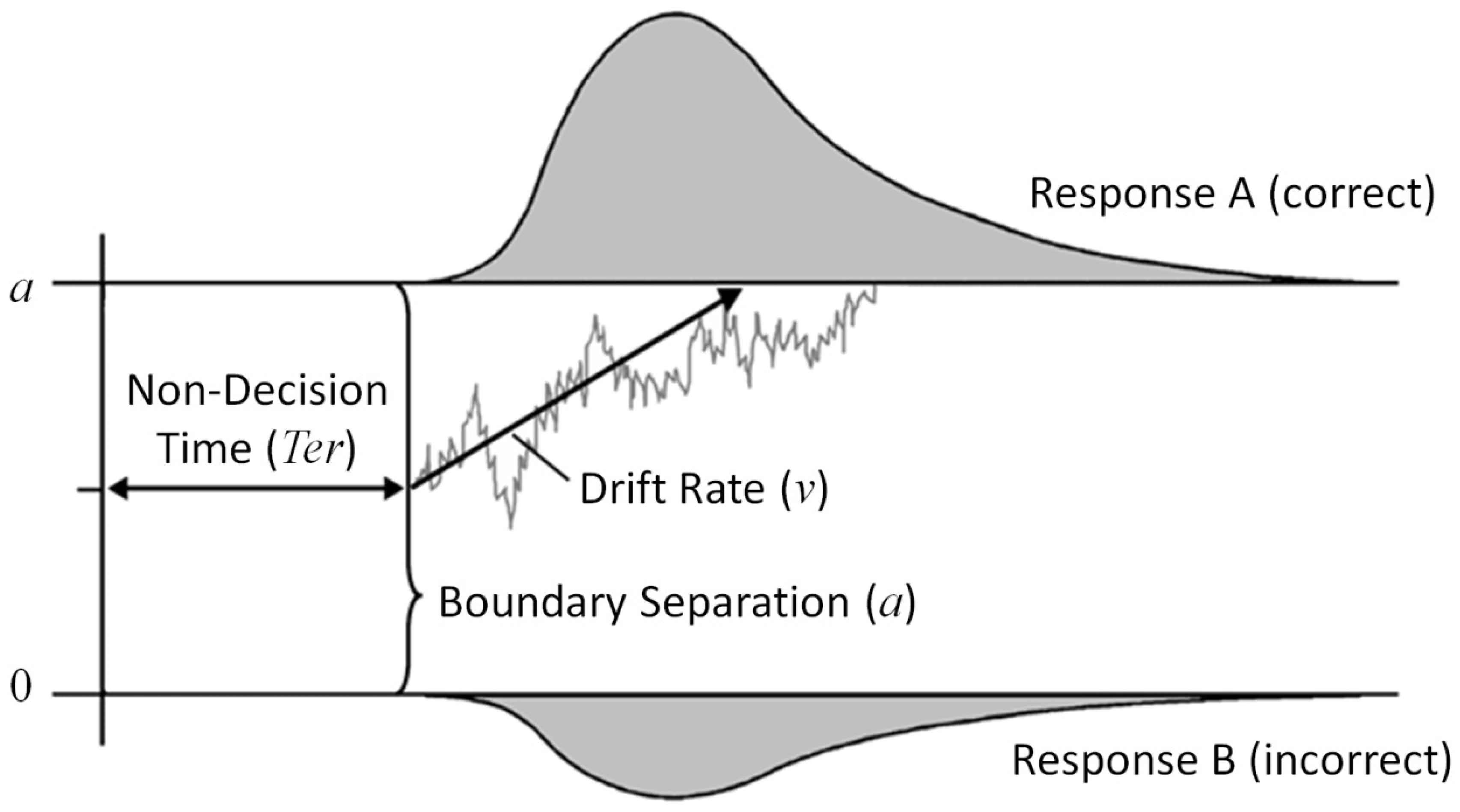
The diffusion model [
29,
34] is a better alternative in both respects since it offers a psychologically plausible yet parsimonious model of a binary decision process. In addition, it helps dissociate task–performance from speed–accuracy settings among other components. Specifically, the diffusion model (see
Figure 1) decomposes a decision process into non-decision time and the actual decision process. Non-decision time (
Ter) subsumes processes before and after the actual decision phase (encoding of stimuli and execution of the motor response). In turn, the actual decision process is characterized by a continuous sampling of information. A decision process, originating from starting point
z, fluctuates over time as a function of systematic stimulus information and random noise (see gray sample path). When it hits either the lower or the upper response boundary (at 0 or
a, respectively), the according response is elicited. The mean slope of the decision process across trials denotes the drift rate (
ν).
Thus, the diffusion model dissociates some components of the decision process. The boundary separation indexes the setting of the speed–accuracy trade-off, while the drift rate is an estimate of the efficiency of information processing (i.e., the speed of evidence accumulation for the correct response per time). An advantage over conventional RT scores is that the simultaneous estimation of parameters should result in more adequate estimates of task performance with a reduced bias of speed-accuracy setting. It was demonstrated on theoretical grounds, as well as simulations [
35,
36], that the diffusion model can account for a number of replicated phenomena in RT research, including the right skew of the RT distribution, the WPR, the higher ability correlations of
SDRT over
MRT and the latter over
MdnRT, and the linear correlation of
MRT and
SDRT. All these effects were argued to be driven by a single latent relation between individual differences in drift rate and individual differences in general intelligence.
One challenge pertaining to parameter estimation is to cope with computational dependencies. These can arise from trade-offs between parameter estimates in the data-fitting process and would result in correlated deviations of the estimated values from the true parameter values. Such trade-offs have been demonstrated for the ex-Gaussian model [
37,
38] and for the diffusion model [
34]. In the ex-Gaussian model, dependencies are positive for
μ and
σ, but negative for both Gaussian parameters with the
τ parameter of the exponential component. In the diffusion model, positive correlations are frequently observed between all parameters (
a,
ν, and
Ter). These can result from the by-chance occurrence of a few extra slow error response times that would bias all parameters jointly in the same direction [
34]. Additionally, estimating drift rate (
ν) and response caution (
a) can be a challenge in case of only few errors values, as different combinations of both parameters (both jointly increasing) could account for the observed distribution of correct RT values.
Schmiedek et al. [
38] suggested an elegant way of circumventing these problems of parameter dependencies, combining the parameterization of RT distributions and structural equation modeling. Specifically, they fitted the ex-Gaussian model and the diffusion model independently to the RT data obtained in eight elementary tasks. Variability in these parameter estimates can be expected to contain true parameter variance as well as estimation error/biases. These parameter estimates were entered, technically, as observed variables in a CFA model, with latent parameter factors accounting for the reliable (shared) portion of the variance in the parameter estimates. Residuals of parameters simultaneously estimated from the same data were allowed to be correlated and would reflect covariance in the deviations of parameter estimates. This approach reduced problems with parameter dependencies and with unreliability of the parameter estimates. The parameter factors, which captured the reliable portion of parameter variance, were used as predictors of WMC and
gf.
In spite of estimating parameters from relatively simple tasks, substantial relations with ability were obtained for the
τ parameter in the ex-Gaussian model and for the drift rate (
ν) in the diffusion model. The observed relations with the
τ parameter can be reconciled with an account on lapses of attention (or at any other processing stage) that would result in occasional delayed responses. However, Schmiedek et al. [
38] argued in favor of the theoretically more satisfactory diffusion model, and they offered a simulation study showing that assuming a diffusion process as the “true” underlying mechanism generates RT data that can account for the relations of the ex-Gaussian parameters. The ability of the diffusion model to account for relations of the
τ parameter or the WPR, respectively, has been confirmed in recent simulation studies [
35,
36].
As all elementary tasks in the Schmiedek et al. study [
38] were relatively simple; the previously well-documented moderating effect of task complexity [
1,
2] could not be tested in their study. It can be hypothesized, though, that task complexity affects the shape and location of the RT distribution, and consequently derived model parameters. Most elementary tasks require maintaining a number of task relevant bits of information, e.g., S-R mapping rules, in working memory. Presented stimuli have to be compared with these rules until an appropriate rule is found and the response can be selected. Building on the seminal finding that search in working memory is serial and exhaustive [
39,
40], a linear relation of the number of task-relevant bits of information maintained in working memory and response times can be expected. In turn, this would result in a shift of the entire RT distribution towards slower RT values as complexity increases. Such an effect would be reflected in the
μ parameter of the ex-Gaussian model. Additionally, variability and skew of the RT distribution may be increased, as longer processing requirements usually result in higher variability, too [
34,
41]. These effects would be reflected in increased
σ and
τ in the ex-Gaussian model, while all these effects could be parsimoniously accounted for by lower drift rate (
ν) in the diffusion model [
35]. In turn, individual differences associated with an increase in task complexity would be reflected in these parameters (i.e.,
μ additionally to
τ in the ex-Gaussian model; and drift rate
ν in the diffusion model).
What is the status of individual differences in these parameter estimates? How are the reliable portions of individual differences in parameter values related across models and with the conventionally computed RT and accuracy scores? First, if parameter estimates are considered “measures of trait-like cognitive styles and abilities” ([
42], p. 4), sufficiently high temporal stability is required. Further prerequisites comprise their generality (at least across a set of tasks assigned to one processing domain) and validity with other parameters and criterion variables (e.g., shown in [
38]); Second, with respect to relations across the diffusion model and the ex-Gaussian model, it has been consistently shown that correlations are only moderate [
37,
38,
43] in spite of sufficiently high (parallel test) reliability [
38] and temporal stability [
42]. This situation suggests that parameters of different models may, at most, simply tap different processes. In fact, most of the studies specifically addressing parameter relations across diffusion model and ex-Gaussian model may have yielded inflated relation estimates at the upper boundary. For instance, some of these studies investigated relations by means of simulating RT distributions based on parameters of the one model (with many trials and without contamination), and subsequently used the simulated RT data to estimate parameters of the other model [
37,
38,
43]. These simulations were supplemented by analyses of moderately sized experimental datasets that were jointly fitted by both models [
38,
43]. In the latter case, even random fluctuations or contaminants that do not correspond with stable personality dispositions may contribute to parameter relations. However, parameter relations across models were only moderate and were not very specific in most studies. Nevertheless, their patterns appear to be comparable across studies [
37,
38,
43]: response caution (
a) is positively related with all ex-Gaussian parameters, in particular with
μ and
τ. The drift rate (
ν) is moderately negatively correlated with
μ, somewhat more negatively correlated with
σ, and the strongest negative correlation is with
τ. Finally, non-decision time (
Ter) is positively related with
μ but not with the other ex-Gaussian parameters.
Relations of model parameters with conventional RT and accuracy scores are hardly ever reported (but see [
35,
38]), although these relations may be potentially informative as they offer a first insight into which processes may be reflected in the scores conventionally reported in the literature. In fact, Schmiedek et al. [
38] report correlations of model parameters with some RT scores in an appendix of their paper. Since these correlations were estimated as pairwise latent correlations on the basis of identical RT data, most correlations were mediocre to high. It could be predicted on theoretical/computational grounds that they found drift rate (
ν) to be inversely correlated with RT scores, in particular with those indexing slow response times (slower quantiles) and with variability (
SDRT). In contrast, non-decision time (
Ter) was most highly correlated with the faster quantiles of the RT distribution. Analogous correlations were obtained for
μ and
τ of the ex-Gaussian distribution, respectively. Unfortunately, the authors did not report these correlations with accuracy. Nevertheless, these findings are definitely informative with respect to the correspondence of parameters with observable scores. However, since identical RT distributions were entered, this does not distinguish between state/contamination and the stable/generalizable portions of parameters as (indicators of) trait-like dispositions (cf. [
42]) that can be predicted to be considerably more moderate. Another challenge is that the correlations of parameters with observed RT scores were shown to depend on the variance in the other parameters, as demonstrated in simulation studies [
35]. Therefore, observed correlations in experimental datasets can be expected to vary as a function of the variance in the other parameters. The resulting range of relationship estimates is therefore an empirical question.
To summarize, previous research has shown moderate but not unique correlations between parameters of the diffusion model and of the ex-Gaussian model [
37,
38,
43]. Differential correlations with conventional RT scores can be predicted on theoretical grounds and for computational reasons [
34,
41]. However, there is only limited evidence of how the reliable portion of parameter variance (i.e., on the level of latent factors; [
38]) is correlated with conventional RT scores. To arrive at a more realistic estimate of parameter correlations conceived of as trait-like dispositions, it is desirable to model correlations across non-overlapping RT data.
Goals and Hypotheses of the Present Study
This study was conducted to test correlations of RT scores and parameters in elementary cognitive tasks with WMC and
gf. A set of conventionally employed scores and model-based parameters found in the RT literature was investigated as predictors of cognitive ability. The design was inspired by the Schmiedek et al. [
38] study, but we employed tasks with different levels of complexity to test possible moderation effects on parameter correlations. Additionally, correlations of parameters across models and with conventional RT and accuracy scores will be reported using non-overlapping raw RT data. Specifically, the following hypotheses were tested:
H1: Correlations of mental speed with WMC and gf: Building on previous research, we predicted that mental speed is moderately correlated with WMC and
gf [
1,
2,
3]. Such a correlation was predicted by theoretical accounts that postulate a contribution of speed to WMC [
5,
6] and
gf [
4]. Additionally, such correlations were expected to result if the cognitive measures require speedy processing as a confounding factor [
10].
H2: Differential validity of RT scores: Higher validity of some RT scores over others could be postulated on theoretical grounds [
35], as well as on the basis of previous findings [
2,
18,
19,
25]. Given that the slowest RT values are the most predictive of cognitive ability (i.e., the worst performance rule, [
19]), validity of RT scores were expected to increase with their sensitivity to slow RT values. For instance, slower RT bands were predicted to be more highly correlated with ability than fast RT bands. Additionally, location scores that can be biased by extreme values (e.g.,
MRT) were expected to be somewhat more highly correlated with ability than with their robust counterparts (e.g.,
MdnRT or
Mlog(RT)) [
18,
25]. However, in line with the current meta-analysis, we did not predict RT variability to be consistently more highly correlated with ability than with mean RT [
15]. Error scores were less frequently employed in the literature, supposedly because of their reduced variability and, consequently, their reduced reliability and validity. We still included them in this study and investigated their correlations with model parameters and cognitive ability to uncover possible speed-accuracy trade-offs.
H3: Validity of parameters sensitive to the right tail of the distribution: Relatedly, we predicted that the exponential component
τ in the ex-Gaussian model and the drift rate
ν in the diffusion model are correlated with ability, since both parameters are affected by the slow tail of the RT distribution [
35,
38].
H4: Moderation of the WPR by task complexity: Since very simple tasks do not require much mental work, hardly any differences were expected in the mean response times [
2,
24]. Only occasional slow outliers (e.g., attentional, cognitive, or other lapses or interruptions in information processing [
21,
32]) could account for the relation with ability [
19,
38], and correlations would be confined to the
τ parameter in the ex-Gaussian model, replicating previous findings [
38]. However, given that processing time increases with task-relevant information maintained in working memory [
39,
40], the location of the RT distribution was expected to be shifted towards slower response times. In turn, individual differences would be additionally reflected in
μ in the ex-Gaussian model as task complexity increases. In the diffusion model, these effects in location and skew [
34,
41] with increasing task complexity should be accounted for by decreased drift rate (
ν) [
34,
35,
43].
H5: Testing model parameters as trait-like dispositions: Given that model parameters may serve as indicators of trait-like dispositions [
42], they were expected to possess sufficient generality. In other words, individual differences in parameter estimates should be replicable across different tasks—at least if tasks are comparable in their cognitive requirements. Additionally, parameter estimates were expected to possess consist relations (with other parameters and scores), even when estimated from independent experimental data. We expected model parameters to display a pattern of relations comparable to that observed in previous studies [
37,
38,
43]. However, the magnitude of relationships was predicted to be attenuated when estimated across different task classes, even when modeling the reliable portion of parameter variance (as in [
38]). Nevertheless, reducing possible confounding factors and contamination as well as computational dependencies, was considered as more adequate to arrive at better estimates of parameters as trait-like dispositions.
2. Experimental Section
2.1. Sample
The study was advertised in a local newspaper, by means of flyers, and in electronic media. Inclusion criteria were an age of 18 to 40 years old and sufficient knowledge of the German language. N = 200 participants (n = 144 female) completed the battery comprising mental speed tests, as well as measures of working memory capacity and of fluid intelligence. Testing was conducted in small groups of up to six people per testing session. Participants were 25.7 years old on average (SD = 5.2). The educational level of the sample was above average, as a majority of the participants (n = 130) had completed high school, and they were working in various occupational fields. All participants signed informed consent before participating and received compensation.
2.2. Speed Tasks
We used a computerized version of typical clerical speed tasks, namely Search, Comparison, and Substitution tasks [
44]. Following a matrix construction format, all three tasks were administered with numbers, letters, and symbols as stimuli. The different classes of tasks can be expected to differ in complexity. Additionally, with three tasks (stimulus materials) per class, the measurement models for the latent ex-Gaussian and diffusion model parameter factors had sufficient degrees of freedom (
df = 15) to be testable. The computerized administration required a few procedural changes so that individual RTs could be recorded that would be used for the RT modeling (see
Figure 2).
The original paper-and-pencil Search task consisted of a printed matrix of stimuli: participants were asked to go through the matrix line by line and to mark all target stimuli (but not distractors) they saw in the given time. In the computerized version, single stimuli were presented sequentially on screen and participants indicated whether the displayed stimulus was the target or not by pressing a right or left button, respectively. In the version with letters as stimuli, the target was an ‘A’, in the version with numbers, it was the digit ‘3’, and in the version with symbols as stimuli, it was a smiley among other emoticons. For each stimulus material, participants completed two blocks of 40 trials each (and two warm-up trials each that were discarded from the analyses). Note that the computerized version of the “Search” task could be formally classified as a one-bit choice reaction time (CRT) task.
In the Comparison task, two strings of three elements each were presented horizontally on the screen. Participants indicated whether the strings of stimuli were identical or different by pressing a left or a right button, respectively. In the case of a difference, only one of the elements was randomly exchanged. The presented elements could either be numbers, letters, or symbols. Again, there were two blocks with 40 trials each (plus two warm-up trials) for each stimulus domain.
In the original paper-and-pencil Substitution tasks, there is a coding table presenting how stimuli of one stimulus domain (e.g., numbers) are mapped onto the stimuli of another domain (e.g., symbols). Below this table, participants see lines of stimuli from the first domain, and they are asked to draw the corresponding stimulus from the second domain. In the computerized version, the coding table was permanently visible on screen and stimuli of the first domain appeared sequentially. We used special keyboards with keys labeled with the corresponding second stimulus, and participants were instructed to press the according key. There were three different combinations of stimulus domains in the Substitution tasks: numbers to symbols, symbols to letters, and letters to numbers. For each combination, participants completed two blocks with 30 trials each (plus two warm-up trials).
Note that the three task classes differ markedly in complexity, i.e., in the number of task-relevant bits of information that have to be maintained in working memory in order to solve the task correctly. The Search tasks require keeping just one target stimulus in mind for the duration of the entire task and to decide in each trial whether a presented stimulus matches it or not. The Comparison tasks are more demanding. They necessitate the comparison of two three-item sets in each trial. Finally, Substitution tasks are by far the most complex, since they require operating with nine arbitrary S-R mapping rules in order to select the appropriate response for the presented stimulus in each trial. The number of mapping rules exceeds what people can reliably keep in mind at one time (so they need to look up the mapping rules repeatedly).
2.3. WMC and gf Measures
Three recall-one-back tasks [
45] with different stimuli were included in this study. This design allowed for modeling WMC as a latent factor, thereby removing problems associated with compromised reliability and task specificity. The tasks were constructed following a matrix design balancing memory load (two, three, and four stimuli) and an updating requirement (six and nine updates). In the numerical WMC task, two to four boxes appeared on a screen aligned horizontally (see
Figure 2D). Each run started by presenting numbers in all boxes. Then, all numbers disappeared and one number was shown unpredictably in one of the boxes for 3000 ms. Participants were asked to type in the number shown in that box the time before and to remember the new number. After an inter-trial interval of 500 ms the next trial started. The task version with letters as stimuli was analogous, only with consonants instead of numbers. In the figural task version, all stimuli were shown at unpredictable positions in a 3 × 3 grid. At the beginning of each run, all stimuli appeared simultaneously (i.e., either 2, 3, or 4 stimuli) at different positions in the grid. Then, all stimuli were removed and only one of these stimuli would appear randomly in one the cells for 3000 ms. Participants were asked to indicate, by mouse-click, the cell where this stimulus was shown last and to remember the actual position of the stimulus. After an inter-trial interval of 500 ms, the next stimulus was shown until the 6 or 9 updates of the current run were completed. The tasks were scored following a partial credit scheme [
46], i.e., the proportion of correct responses in all trials.
Fluid intelligence was assessed with a figural sequence reasoning test from the BEFKI [
47]. The scale is comprised of 16 items in which two consecutive pictures have to be selected from a set of distractors that complete a sequence in a logical way. The individual items were aggregated into three parcels so that
gf could be modeled as a latent factor. The paper-and-pencil version of the BEFKI was administered.
2.4. Scoring and Modeling of Response Times
We computed a number of conventional scores used in research with elementary cognitive tasks [
26,
28], including speed of responding, response times, quartiles, variability, and errors. Most of the scores are highly correlated, since they all use information in the RT distribution. However, given they are differentially sensitive to the shape of the RT distribution and to extreme RT values, it can be predicted that the scores are also differentially correlated to cognitive ability. Data were analyzed with R [
48], using retimes [
49] for the ex-Gaussian analyses, EZ for the simplified diffusion model [
50], and the psych package [
51] for psychometric analyses. Mplus [
52] was used for structural equation modeling.
Speed of responding: Mental speed is conventionally scored as correct responses in the given time in most paper-and-pencil tests. We averaged reciprocal response times (1/RT) for correct responses as an approximation. Although this method is less common in laboratory research, it corresponds with standard scoring in psychometric tests. As an additional benefit, the distribution of reciprocal response times across participants is approximately normal, a requirement for some correlational analyses.
Response Time: The most frequently used score in laboratory research is the mean latency of correct responses. The arithmetic mean (MRT) is frequently used, but it can be biased towards higher values by a few extreme RT values. Therefore, the mean of individually log-transformed RTs (Mlog(RT)) or the Median of the RT distribution (MdnRT) are frequently computed when a more robust estimate of the location of the distribution is desired. Distributions of mean response times across participants can be positively skewed.
Quartiles: The Worst Performance Rule was originally discovered by inspecting RT bands (i.e., quantiles of the RT distribution). Given the available trial numbers per task in the current study, we computed the mean for four quartiles (Q1–Q4).
Variability: Variability of responding may correspond with impaired stability of cognitive processes. We computed the within-person standard deviation (SDRT) and the interquartile range (IQRRT) of the response times as two conventional scores. The first can be biased by just a few outliers, whereas the second may be a more robust estimate of the spread of the RT distribution.
Errors: Cognitive impairments can also manifest in erroneous responses. Additionally, individuals may differ in their speed-accuracy trade-offs, either sacrificing speed for accuracy or the other way round. Errors may be informative, but they are usually rare events, thereby characterized by low variability and low reliability. Additionally, they are heavily skewed to the right. We computed the error rate as well as the probit of the error rate, which compresses the positive skew.
Additionally, we fit the ex-Gaussian and a simplified diffusion model to the RT data. Since parameter dependencies can result in trade-offs in the estimates of parameter values, we used a two-step maximum likelihood (ML) procedure to estimate the ex-Gaussian parameters [
53], as is implemented in the retimes R package [
49]: The
μ and
σ parameters of the normal distribution are estimated from the RT distribution in a first step; then, the exponential τ parameter is determined with help of a bootstrapping procedure. We computed parameters of the EZ diffusion model [
50], which is a simplified closed-form expression yielding equivalents of the three most important parameters of the diffusion model, i.e., boundary separation (
a), drift rate (
ν), and non-decision time (
Ter). Dependencies are less of a problem using EZ, since parameters are not estimated, but their respective equivalents are directly computed from moments of the RT distribution and accuracy. Additionally, a number of simulation studies converge in showing that EZ estimates are robust for the purpose of modeling individual differences [
54,
55], even when only a moderate number of trials are available [
56]. Since the diffusion model is only suited for binary choice tasks, it could only be fitted to the data from the Search and Comparison tasks.
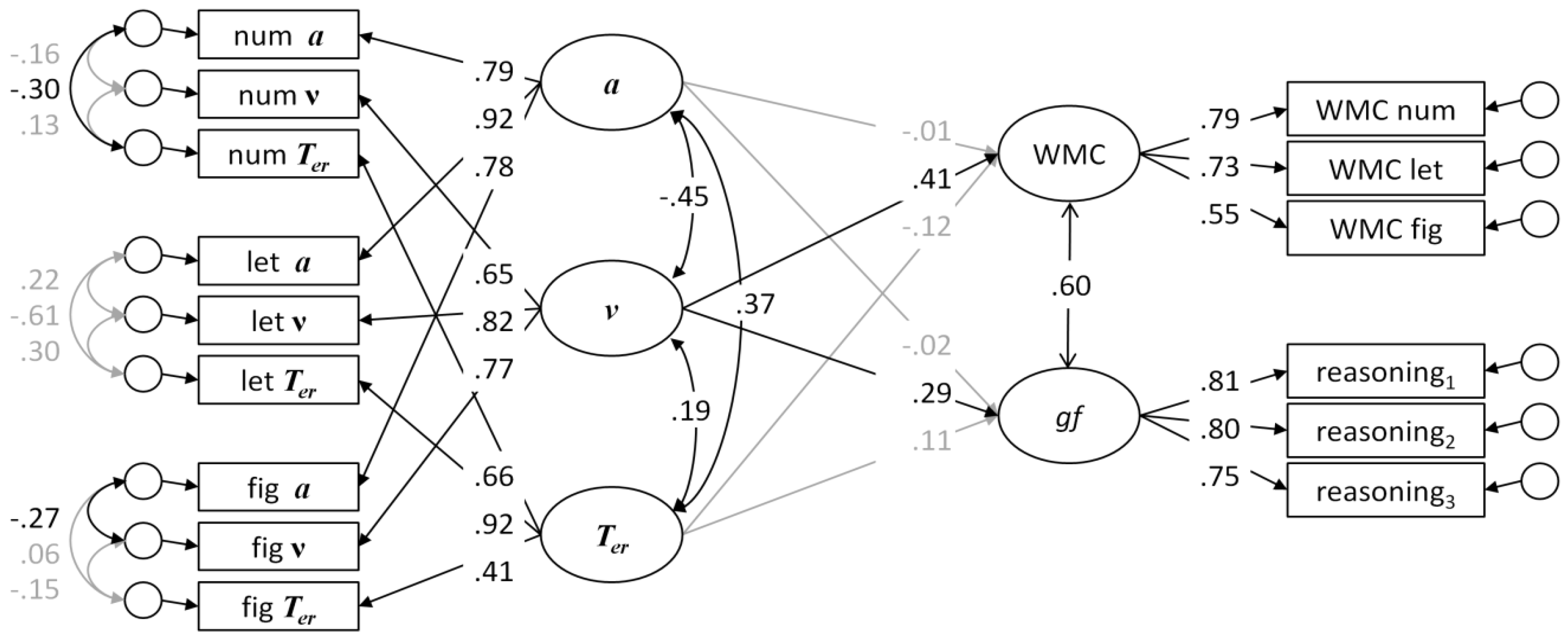
To estimate the relations between parameters as trait-like dispositions, we modeled their reliable portions of variance analogously to what was done by Schmiedek et al. [
38]: first fitting models independently to each task, and then modeling the communality of these parameter estimates as latent factors, while allowing residuals of the parameters estimated from the same data to be correlated (see Figure 4). These measurement models were used to investigate latent correlations of model parameters across task classes—within and across models and with conventional scores. For testing relations with conventional RT and accuracy scores, the reliable portion of variance was modeled as one factor accounting for the communality in the scores of one task class. In order to avoid adverse effects of random fluctuation, contamination, and computational dependency, relations were estimated across different task classes. As the diffusion model could be fitted only to the binary choice Search and Comparison tasks, there was only one cross-task correlation for each combination of parameters. The ex-Gaussian model could be fitted to all task classes; consequently, three independent correlations could be estimated across task classes. Finally, four correlations could be estimated across task classes for the parameters of diffusion model with the ex-Gaussian parameters (i.e., Search–comparison, Comparison–search, Search–substitution, and Comparison–substitution). The same combinations of task classes were also used to compute correlations with conventional scores.
2.5. Data Preparation and Descriptive Analyses
All RT data were carefully screened and a limited number of potentially invalid trials were removed prior to conducting the analyses. The two warm-up trials at the beginning of each block were removed because of re-start costs. All trials directly following an error were discarded because post-error control processes may affect RTs independent of task requirements [
57] (ca. 4%, see
Table 1 for details). Extreme RTs (ca. 1%) were removed by applying the liberal Tukey criterion [
58], individually adjusted to person and task. Specifically, the criteria were set at three interquartile ranges below the 25th percentile (but not below 200 ms) and above the 75th percentile of the RT distribution.
As expected, descriptive statistics of task performance and corresponding model parameters were relatively homogeneous within task classes, but differed considerably across task classes (see
Table 1). In general, accuracy was high and comparable across tasks, but different response times across task classes confirmed differential task complexity. The Comparison tasks were most comparable with the tasks used by Schmiedek et al. [
38] in terms of response times. The Search/CRT tasks had considerable faster response times, suggesting that they were simpler. Conversely, the Substitution tasks had considerably longer response times, suggesting that they were more complex. The differences in mean RT were paralleled by a corresponding increase in the variability of RT, replicating previous findings [
16,
18].
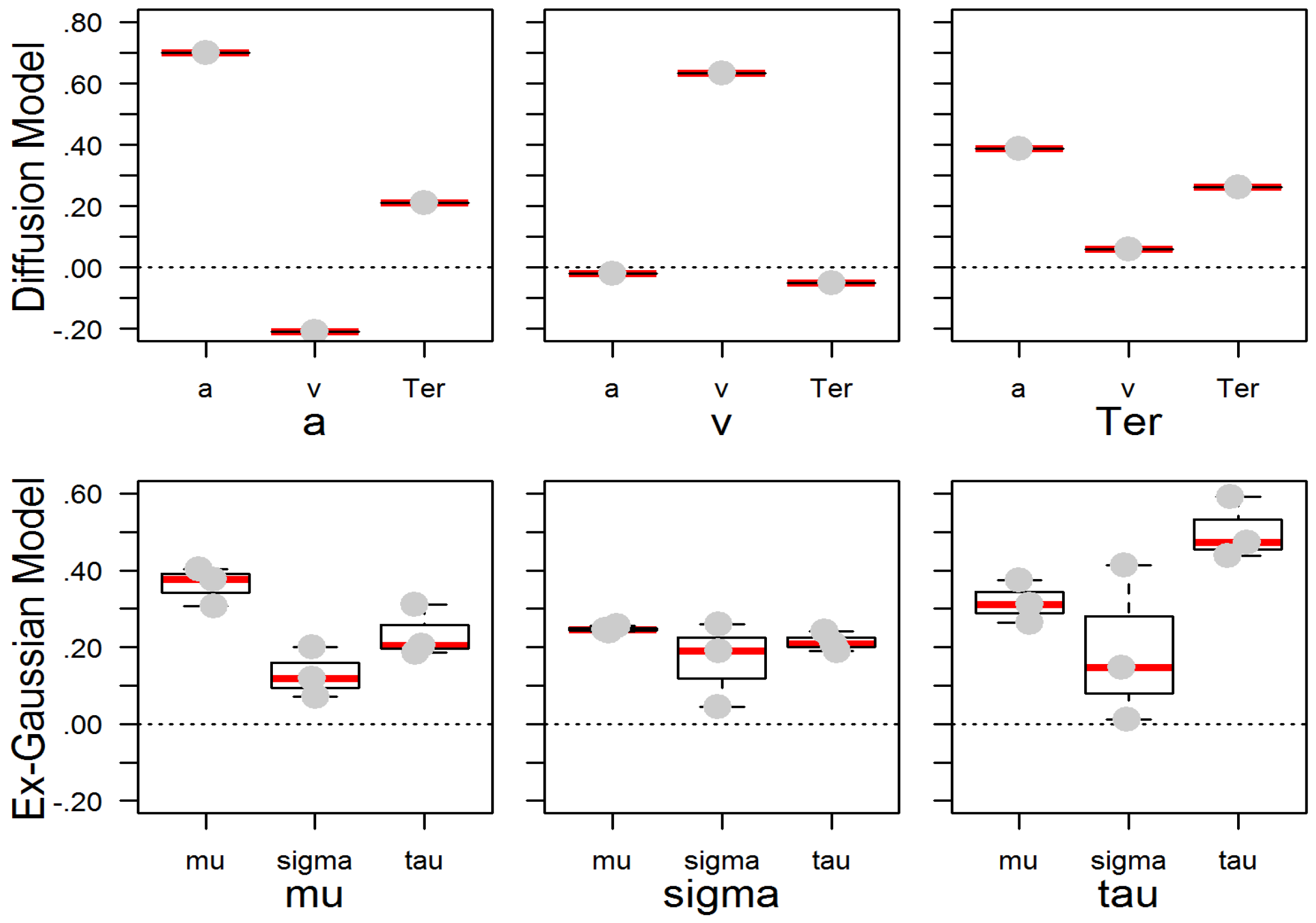
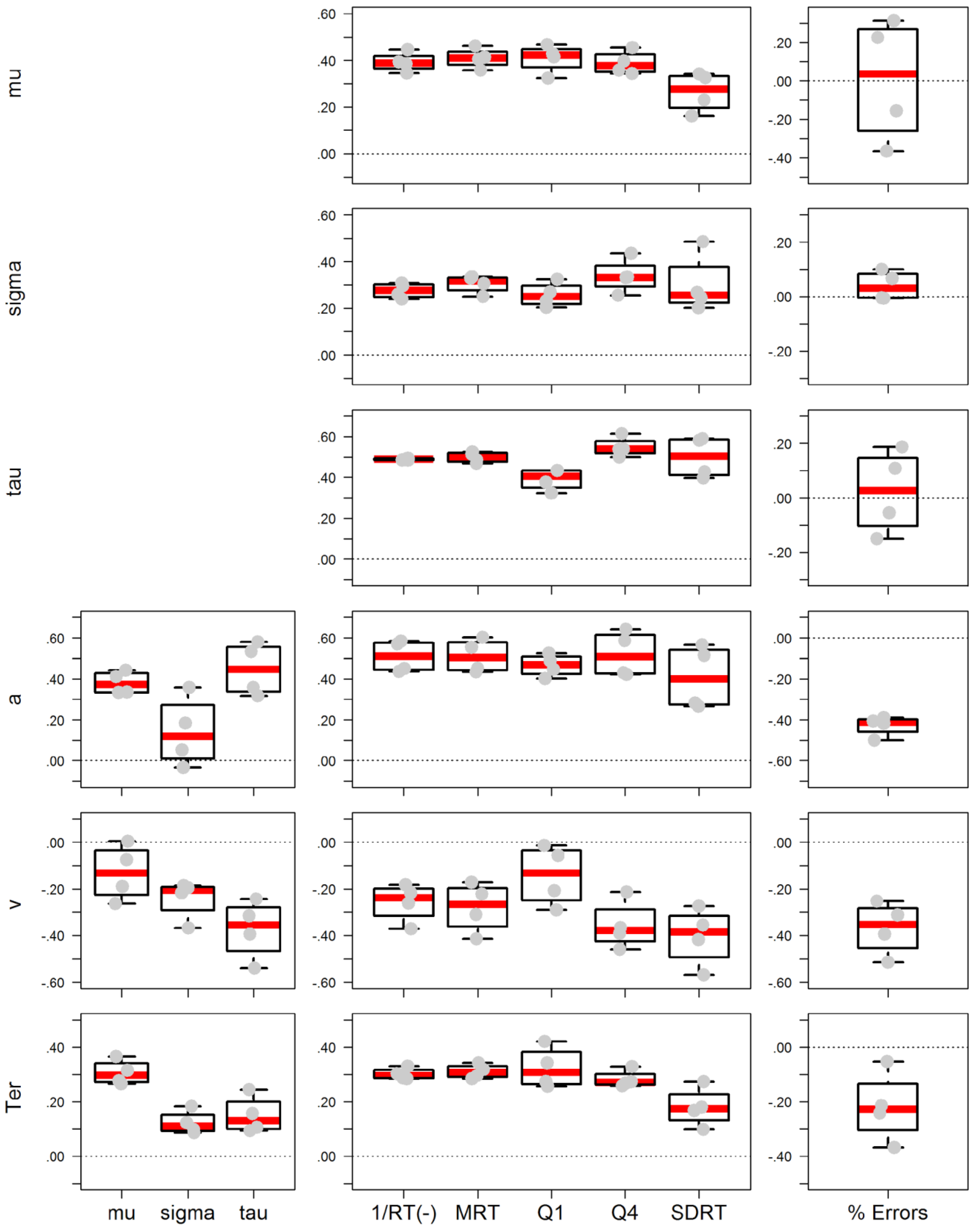
Analogous results were observed in the parameters of the ex-Gaussian model. As expected, all parameters yielded larger values with slower mean response times. The marked increase in the exponential τ parameter, in addition to the standard deviation parameter σ, suggests that the increase in the conventional SDRT score is in part driven by extreme values from the right tail of the RT distribution. The same holds for the MRT, which appears to be biased towards higher values compared with the μ parameter.
The diffusion model could only be fitted to the Search/CRT and the Comparison tasks with binary response values. The reduced drift rates ν in the Comparison tasks relative to the Search/CRT tasks confirm their higher task difficulty. Additionally, generally increased estimates of the a parameter indicate that participants exercised higher response caution, which quite likely reflects that they perceived Comparison tasks as more difficult. Finally, non-decision time (Ter) was higher in the Comparison tasks, possibly indicating longer encoding time of the more complex stimuli.
In order to model fluid intelligence as a latent factor, individual items of the matrix test were aggregated into three parcels by sorting them according to a systematic ABC scheme. It was tested whether parcels were strictly parallel: loadings, intercepts, and residuals did not differ significantly across parcels. (Constraining these parameters to be equal across parcels did not deteriorate the model fit relative to the configural model, Δχ2(6) = 10.03, p = 0.12.)
4. Discussion
We conducted this study to test the correlation of response times in elementary cognitive tasks with WMC and gf. A set of frequently used scores and model-based parameters derived from RT distributions was investigated in tasks of varying complexity.
Correlations of mental speed with WMC and gf (H1): In line with previous research [
1,
2,
3], we predicted that mental speed is moderately correlated with WMC and
gf. This hypothesis was confirmed in the current study: the faster participants completed elementary cognitive tasks, the higher their WMC. The same was also found for
gf, although to a lesser extent. The correlative relation of mental speed with WMC can be reconciled with both theories that consider mental speed a causal constituent of WMC [
5], as well as with a more technical interpretation in terms of overlapping task requirements, such as a speed requirement in WMC or in the
gf tasks as a confounding factor [
10]. In fact, the somewhat larger correlation of speed with WMC compared to
gf could result from the faster presentation of stimuli and response deadlines in the recall-one-back tasks employed in the current study.
However, other mechanisms could also contribute to the higher correlation of speed with WMC. Given that the correlation was largely driven by the exponential component (
τ) of the RT distribution, an account in terms of attentional lapses could hold: Stimuli are continuously presented in the recall-one-back task, and if participants do not pay attention for a short moment, they can miss a stimulus, thereby losing credit points. The situation is different for the figural reasoning test. Since the task is largely self-paced, participants can easily restart the solution process and still arrive at the correct response in time. Therefore, task performance in
gf tests can be predicted to be less strongly correlated with attentional lapses. In fact, previous research has shown that increasing speed pressure in a reasoning task (used as a
gf measure) increases the correlation of
gf with WMC [
60]. Further, the narrow scope of the
gf factor, which is identified only by items of a single test, could contribute to the reduced correlation with the speed factor. Finally, and in line with the notion that WMC constitutes the basis of
gf [
7,
8], indirect effects of mental speed via WMC could explain the lower correlation. At the same time, reasoning ability likely requires more than capacity of working memory alone (e.g., knowledge of rules and their application). Thereby, a speed-related mechanism will only explain some of the total variance in reasoning tasks.
Differential validity of RT scores (H2): We predicted that alternative scores derived from RT data are differentially related with cognitive ability. This second hypothesis was motivated on theoretical grounds and simulations [
35], as well as on the basis of previous findings [
2,
18,
19,
25]. In line with the Worst Performance Rule [
19], we predicted that scores reflecting or biased by slow RTs are more highly related with cognitive ability than those scores that are less affected by extreme values. In fact, there was a descriptive increase in the magnitude of the correlation across RT bands, although the increase was only small in magnitude and appeared to be confined to the correlation with WMC, but not with
gf. We additionally tested whether mean RT (
MRT), which is potentially biased by extreme RT values, is more highly correlated with cognitive ability than those location scores that are less affected by extreme RT values (
MdnRT,
Mlog(RT)) [
18,
25]. However, there was virtually no difference in their correlations. Apparently, a few outlier values did not distort the rank order of participants. This finding suggests that all of the conventional mean RT scores can be used as predictors of cognitive ability and none of them is clearly superior over the others. In addition, scores of RT variability (
SDRT) were not found to be more strongly related with ability than with mean RT (
MRT), confirming findings from a recent meta-analysis [
15]. As expected, the error scores were less reliable than the RT scores. Not surprisingly, their correlations obtained with WMC and
gf were low. The fit of the error score model was still good. Consequently, the probit transformation did not considerably improve the fit of the model, but slightly decreased validity of the scores. This result suggests that the correlations in error variables are largely driven by participants with more extreme error proportions.
Validity of parameters sensitive to the right tail of the distribution (H3): We predicted that the effects of extreme RT values are more clearly related to model-based parameters that either reflect the tail of the RT distribution (
τ in the ex-Gaussian model) or are sensitive to the tail of the RT distribution (such as the drift rate
ν in the diffusion model) [
20,
21,
35,
38]. Confirming these predictions, the relations of the ex-Gaussian
τ parameter and of the diffusion model drift rate
ν with WMC and
gf were generally replicated across task classes.
While the pattern of observed parameter correlations was replicated, the magnitude of the correlations was only moderate in strength compared with the Schmiedek et al. study [
38]. In part, this result may be due to differences in task characteristics that affect the level and distribution of parameter estimates: our task-homogeneous measurement models likely reflect, in part, task-specific parameter effects. The more heterogeneous measurement model in the Schmiedek et al. [
38] study may capture communality across all paradigms, and thus the so-obtained parameter factors may reflect correlations with ability at a higher level.
Generally, parameter estimates were not as highly correlated with ability as conventional RT scores. One reason for this can be that the information in empirical data is “distributed” across parameters, whereas it is “aggregated” in the conventional scores. In that sense, reliability may be traded for theoretical clarity in the models. Additionally, some of the modeling benefits may not come into play in the current study: the error rate was generally low and there was only limited variance in the errors. Consequently, there may not have been much of a speed-accuracy trade-off that would have distorted the rank order of participants in RT scores. Therefore, the diffusion model had only a limited chance to demonstrate its inherent advantage.
Moderation of the WPR by task complexity (H4): We predicted that individual differences in simple, elementary cognitive tasks are largely reflected in the proportion of extreme values [
2,
24]. However, the average response time was expected to gain predictive validity as task complexity increased. Confirming these predictions, the exponential parameter
τ showed moderate relations in all tasks, whereas the mean response time (
μ) was correlated with ability only in the most complex task class. These effects were parsimoniously reflected by individual differences in drift rate
ν in the diffusion model.
At first glance, these effects in mean RT (
μ) appear to contradict previous findings of increased WPR effects (i.e., higher correlations of slow RT bands) with increasing task complexity [
2,
13,
19]. However, it needs to be considered that WPR effects have been traditionally investigated by analyzing RT bands. In turn, individual differences in RT bands are not only determined by the skew of the individual RT distributions, but also by individual differences in their locations. We believe the ex-Gaussian decomposition is a more adequate data description, since it helps dissociate components that are confounded in RT bands. This interpretation is supported by the differential parameter correlations observed in the current study, as well as in previous research using the ex-Gaussian model [
21,
38].
Testing model parameters as trait-like dispositions (H5): Cross-task correlations of parameters within models were moderate to high (but far from unity). Generally, there appeared to be a better correspondence of diffusion model parameters than those of the ex-Gaussian decomposition across different task classes. It is of note that these correlations were only moderate, given that correlations were estimated across latent factors capturing the reliable portion of parameter variance and that measurement models were generally satisfactory (see
Appendix A). In part, the only moderate and not very specific parameter correlations in the ex-Gaussian model may result from the fact that all parameters are estimated from the same distribution of correct RT values. The diffusion model surely profits from also using error rate for the estimation of boundary separation (
a), while drift rate (
ν) largely accounts for location, skew, and variability of the correct RT distribution in the absence of competing performance parameters. Some of the problems in non-decision time may result from the computational procedure in EZ [
50], where non-decision time is computed as a residual after removing decision time (as function of
ν and
a) from
MRT. However, comparably moderate retest correlations were also observed using other estimation procedures [
42].
Nevertheless, the pattern of parameter correlations closely replicated that previously observed in other studies [
37,
38,
43], although relationships were generally attenuated if computed across task classes. This result was somewhat expected, as correlations across different experimental tasks remove adverse effects of random variation, contamination, and computational dependencies. In part, this result may reflect previously demonstrated moderating effects in the variation of other parameters [
35] and specificity of task requirements in the different task classes. Confirming previous findings, the drift rate was more highly correlated with variability of responding (
SDRT) than with mean response times (
MRT) [
35], even when correlations were estimated across non-overlapping data sets. Still then,
SDRT was not more highly related with ability than
MRT, in line with the recent meta-analysis on RT and intelligence [
15]. This finding suggests that drift rate is not the only “determinant” of a high task score. It is of note for the assessment of mental speed that the correlations of the response caution (
a) parameter with virtually all location scores suggests the setting of speed-accuracy trade-off contributes as well to the observed RT scores in elementary tasks. The virtual null correlations of the ex-Gaussian parameters with error rate might be due to the constraint that ex-Gaussian parameters are estimated from the distribution of correct response times only. This observation suggests that errors contain independent (possibly incremental) information to RT scores. However, the null relations could also be the result of an artifact from the joint effects of processing efficiency (which would result in a positive relation of RT and error rate) and of the speed–accuracy trade-off (which would result in a negative relation of RT and error rate). The diffusion model is better suited to dissociate both components.
Equivalence with paper-and-pencil tests: In this study, we tested different RT scoring and modeling approaches that can be employed for data obtained with computerized elementary tasks. Most of these scores meet the psychometric criteria in terms of reliability (factor saturation) and validity (of cognitive ability), and a few of them may be particularly informative from a theoretical perspective. However, with the exception of (non-corrected) mean RT (or 1/RT) and the error rate, the computation of virtually all other scores requires individual RT data. The latter are typically not available in paper-and-pencil tests. Therefore, the equivalence of computer and paper versions cannot be tested for all scores. Fitting diffusion models is not possible in paper tests either, making it more difficult to quantify and compensate possible speed–accuracy trade-offs. In turn, the possibility of modeling task performance, thereby dissociating components of the decision process, makes chronometric tasks and their data analyses an appealing domain of their own. In this study, we demonstrated the validity of the derived scores in terms of correlations with WMC and gf. What still needs to be tested is the equivalence of paper and computerized speed tests using aggregate scores that can be computed in both versions analogously.
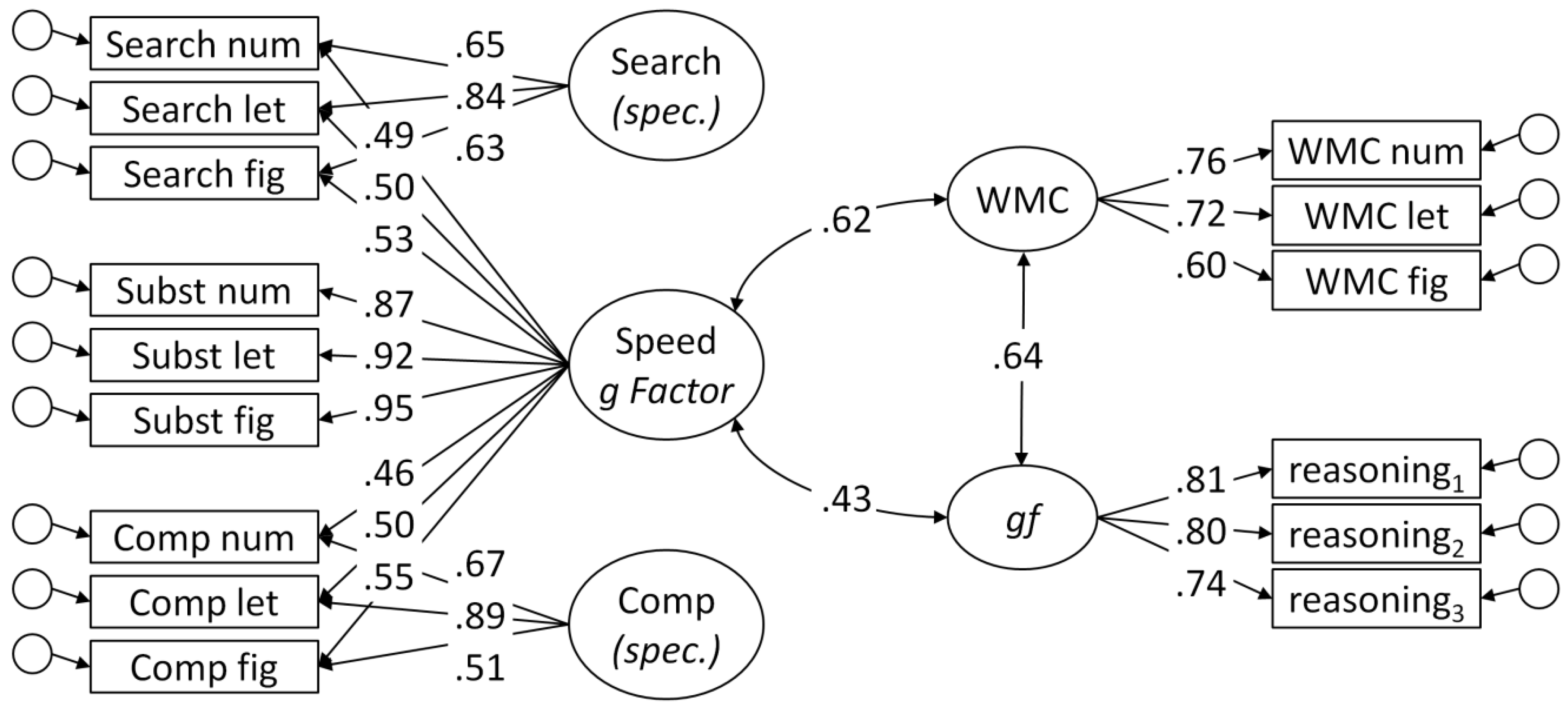
Structure of mental speed: In the present study, we administered typical clerical speed tasks [
44]. Although all of them are conventionally considered to be elementary cognitive tasks, they differed considerably in complexity, as was indicated by the time required to produce a correct response. Psychometrically, a bifactor model [
59] best described the structure of the speed tasks, with a
g factor of mental speed and task class-specific nested factors. This model confirms previous findings of mental speed as a hierarchical construct [
61,
62]. In this study, we additionally showed that the pattern of correlations of model-based parameters differed across task classes (with
μ contributing to ability correlations only in the most complex task). This finding suggests that different cognitive operations are involved in the tasks, and that task specificity could be more than method-related variance. Still, the high communality of all tasks justifies the extraction of a
g factor in a hierarchical model for psychometric purposes.