Use of Response Time for Measuring Cognitive Ability
Abstract
:1. Introduction
2. Speed-Level Distinction
3. Dimensions of Speed and Level in the Structure of Human Cognitive Abilities
4. Speed–Accuracy Tradeoff
4.1. Deadline Method (Time Limits)
4.2. A Posteriori Deadlines
- Time data: coded 1 if the observed response time (regardless of right or wrong) is shorter than the posterior time limit, 0 otherwise;
- Time-accuracy data: coded 1 if a correct answer is given within the posterior time limit, 0 otherwise;
- Accuracy data: coded 1 if a correct answer is given within the posterior time limit, 0 if a wrong answer is given within the posterior time limit, and missing if no response is given within the posterior time limit.
4.3. Instructions & Scoring Rules
4.3.1. Test-Level Deadlines
4.3.2. Item-Level Deadlines
4.3.3. CUSUM
4.3.4. The Countdown Scoring Rule
- The item response function (the probability of answering an item correctly as a function of ability) is a 2PL model where the item discrimination parameter is the time limit. This implies that an increase of the time limit makes the item better distinguish high and low ability examinees.
- Item response time function is the same for the same distance between the person ability and the difficulty of the item, while the sign of the distance does not matter. Examinees with ability equal to item difficulty (i.e., with a 50% chance of answering the item correctly) have the longest expected response time, while examinees with ability levels much higher or lower than the item difficulty spend less time.
- In terms of speed–accuracy tradeoff, given the same time limit, for examinees with ability higher than the item difficulty, as response time increases, the probability of correctness decreases from 1 to 0.5; for examinees with ability lower than the item difficulty, as response time increases, the probability of correctness increases from 0 to 0.5.
4.4. Summary of Methods for Controlling Speed–Accuracy Tradeoff
5. Process Models of Response Time
5.1. The Ex-Gaussian Function
5.2. The Diffusion Model
5.3. Relevance to Studying Abilities
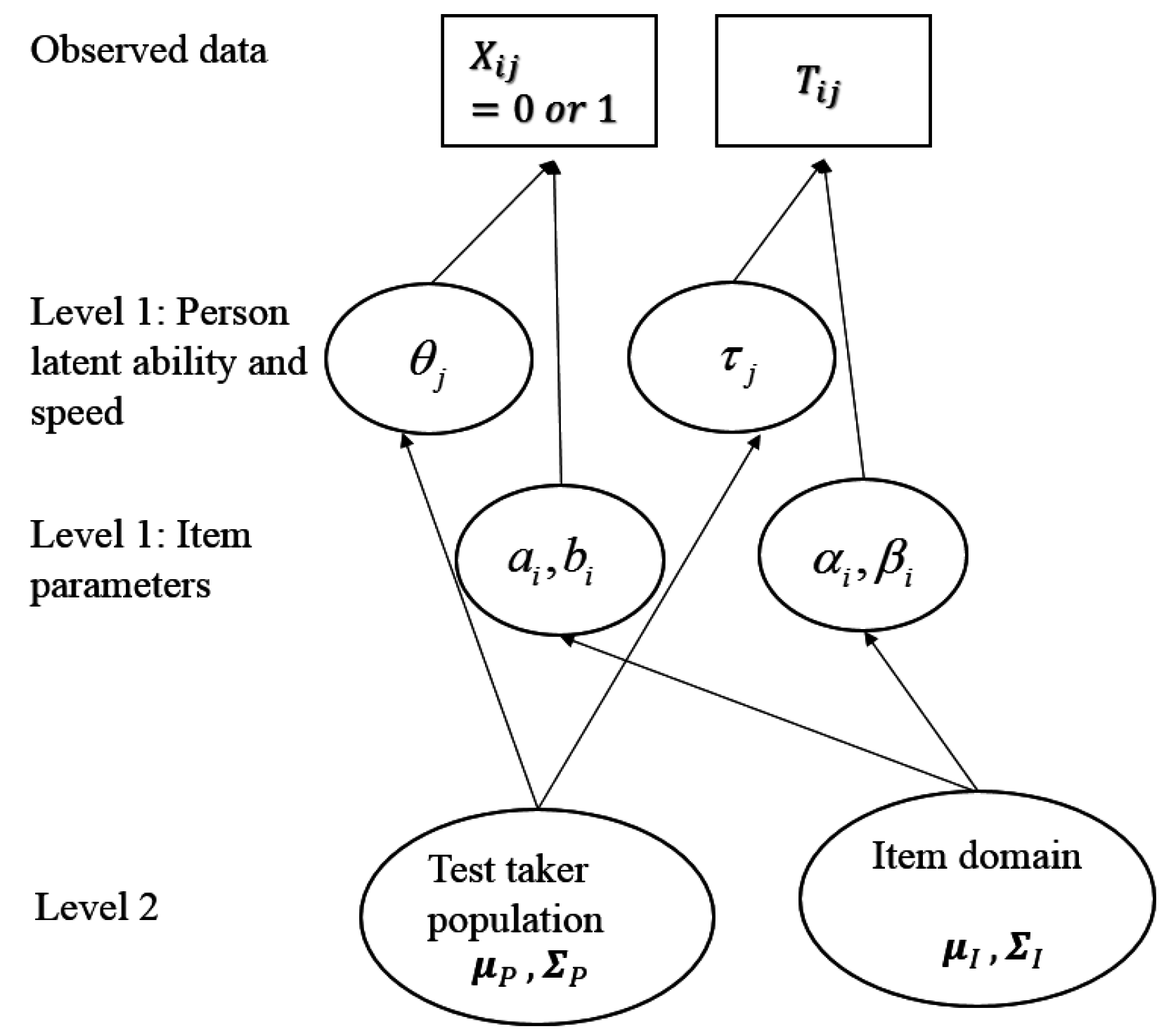
6. Joint Modeling of Time and Accuracy with Item Response Theory (IRT) Methods
6.1. Regression-Type Models
6.2. Hierachical Models
6.3. Cognitive Components
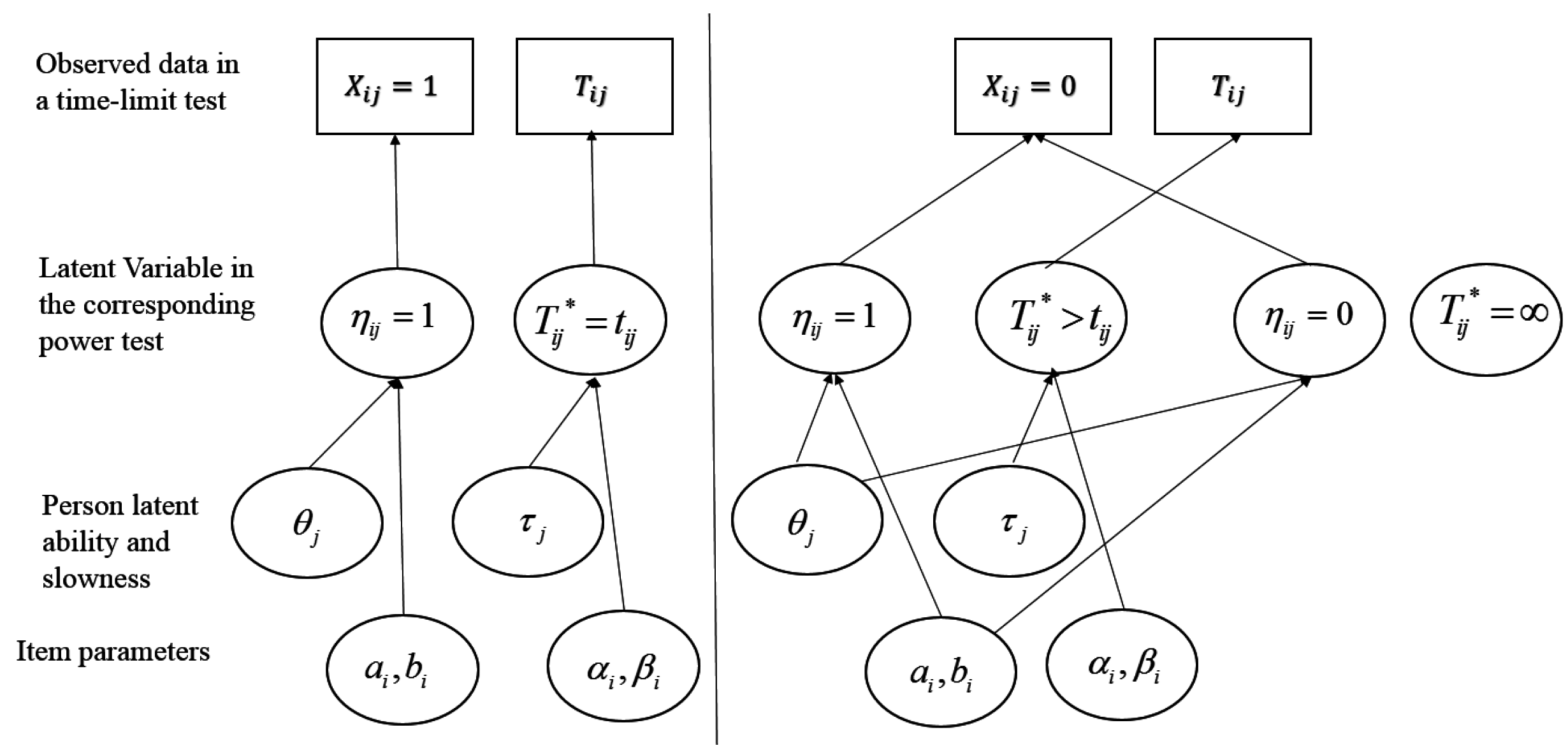
6.4. Assessing Ability and Speed in Power Tests with Observations from Time-Limit Tests
- If an examinee responds correctly within the time limit, then it is assumed that the examinee would get it correct in unlimited time (), and power time () for that item is the same as observed time (tij) for that item (the model assumes no guessing); log power time (log[]) is a function of person slowness (), item time-intensity (), a random variable () with mean 0, and a scale parameter (, analogous to the time discrimination parameter in [98]).
- If an examinee responds incorrectly within the time limit, then they might or might not have gotten it correct with unlimited time, depending on ability and item difficulty. Censoring time is the time an examinee chooses to give up working on an item and is equal to observed time tij:
- For those examinees expected to answer correctly with unlimited time (), log power time (log[])) is modeled as in the first case and tij is a lower bound of power time;
- For those not expected to answer correctly with unlimited time (), power time is infinity.
6.5. Diffusion-Based IRT models
7. Fast vs. Slow Responding = Fast vs. Slow Thinking?
8. Other Uses of Response Time
9. Discussion
Acknowledgments
Conflicts of Interest
Abbreviations
| ETS | Educational Testing Service |
| PISA | Program for International Student Assessment |
| NAEP | National Assessment for Educational Progress |
| IRT | Item Response Theory |
| CUSUM | Cumulative Sum |
| ms | millisecond |
| PIAAC | Program for International Assessment of Adult Competencies |
| ASVAB | Armed Services Vocational Aptitude Battery |
| SAT | Scholastic Aptitude Test (formerly) |
| GRE | Graduate Record Examination |
| TOEFL | Test of English as a Foreign Language |
| Gs | General cognitive speediness (on paper-and-pencil tests) |
| Gt | General cognitive speed (on computer-based memory-retrieval and decision-making tests) |
Appendix A
Thissen [94]
Van der Linden [96]
Van der Linden [95]
Lee and Ying [116]
References
- Jensen, A.R. Galton’s Legacy to Research on Intelligence. J. Biosoc. Sci. 2002, 34, 145–172. [Google Scholar] [CrossRef] [PubMed]
- Spearman, C. General Intelligence, Objectively Determined and Measured. Am. J. Psychol. 1904, 15, 201–292. [Google Scholar] [CrossRef]
- Goldhammer, F. Measuring ability, speed, or both? Challenges, psychometric solutions, and what can be gained from experimental control. Meas. Interdiscip. Res. Perspect. 2015, 13, 133–164. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.-H.; Chen, H. A review of recent response-time analyses in educational testing. Psychol. Test Assess. Model. 2011, 53, 359–379. [Google Scholar]
- Schnipke, D.L.; Scrams, D.J. Exploring issues of examinee behavior: Insights gained from response-time analyses. In Computer-Based Testing: Building the Foundation for Future Assessments; Mills, C.N., Potenza, M., Fremer, J.J., Ward, W., Eds.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 2002; pp. 237–266. [Google Scholar]
- Van der Linden, W.J. Conceptual issues in response-time modeling. J. Educ. Meas. 2009, 46, 247–272. [Google Scholar] [CrossRef]
- Thorndike, E.L.; Bregman, E.O.; Cobb, M.V.; Woodyard, E.; The Staff of the Division of Psychology of the Institute of Educational Research at Teachers College, Columbia University. The Measurement of Intelligence; Teachers College, Columbia University: New York, NY, USA, 1926; Available online: https://archive.org/details/measurementofint00thoruoft (accessed on 10 September 2016).
- Cronbach, L.J.; Warrington, W.G. Time-limit tests: Estimating their reliability and degree of speeding. Psychometrika 1951, 6, 167–188. [Google Scholar] [CrossRef]
- Helmstadter, G.C.; Ortmeyer, D.H. Some techniques for determining the relative magnitude of speed and power components of a test. Educ. Psychol. Meas. 1953, 8, 280–287. [Google Scholar] [CrossRef]
- Swineford, F. The Test Analysis Manual; ETS SR 74-06; Educational Testing Service: Princeton, NJ, USA, 1974. [Google Scholar]
- Rindler, S.E. Pitfalls in assessing test speededness. J. Educ. Meas. 1979, 16, 261–270. [Google Scholar] [CrossRef]
- Bridgeman, B.; Trapani, C.; Curley, E. Impact of fewer questions per section on SAT I scores. J. Educ. Meas. 2004, 41, 291–310. [Google Scholar] [CrossRef]
- Davidson, W.M.; Carroll, J.B. Speed and level components of time limit scores: A factor analysis. Educ. Psychol. Meas. 1945, 5, 411–427. [Google Scholar]
- Dwyer, P.S. The determination of the factor loadings of a given test from the known factor loadings of other tests. Psychometrika 1937, 2, 173–178. [Google Scholar] [CrossRef]
- Neisser, U. Cognitive Psychology; Prentice-Hall: Englewood Cliffs, NJ, USA, 1967. [Google Scholar]
- Shepard, R.; Metzler, J. Mental rotation of three-dimensional objects. Science 1971, 171, 701–703. [Google Scholar] [CrossRef] [PubMed]
- Lohman, D.F. Spatial Ability: Individual Differences in Speed and Level; Technical Report No. 9; Stanford University, Aptitude Research Project, School of Education (NTIS NO. AD-A075 973): Stanford, CA, USA, 1979. [Google Scholar]
- Kyllonen, P.C.; Tirre, W.C.; Christal, R.E. Knowledge and processing speed as determinants of associative learning. J. Exp. Psychol. Gen. 1991, 120, 89–108. [Google Scholar] [CrossRef]
- Carroll, J.B. Human Cognitive Abilities: A Survey of Factor Analytic Studies; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar]
- Cattell, R.B. Abilities: Their Structure, Growth, and Action; Houghton Mifflin: Boston, MA, USA, 1971. [Google Scholar]
- Horn, J.L.; Cattell, R.B. Refinement and test of the theory of fluid and crystallized general intelligences. J. Educ. Psychol. 1966, 57, 253–270. [Google Scholar] [CrossRef] [PubMed]
- Kyllonen, P.C. Human cognitive abilities: Their organization, development, and use. In Handbook of Educational Psychology, 3rd ed.; Routledge: New York, NY, USA, 2015; pp. 121–134. [Google Scholar]
- McGrew, K. CHC theory and the human cognitive abilities project: Standing on the shoulders of the giants of psychometric intelligence research. Intelligence 2009, 37, 1–10. [Google Scholar] [CrossRef]
- Schneider, W.J.; McGrew, K. The Cattell-Horn-Carroll model of intelligence. In Contemporary Intellectual Assessment: Theories, Tests, and Issues, 3rd ed.; Flanagan, D., Harrison, P., Eds.; Guilford: New York, NY, USA, 2012; pp. 99–144. [Google Scholar]
- Danthiir, V.; Wilhelm, O.; Roberts, R.D. Further evidence for a multifaceted model of mental speed: Factor structure and validity of computerized measures. Learn. Individ. Differ. 2012, 22, 324–335. [Google Scholar] [CrossRef]
- Roberts, R.D.; Stankov, L. Individual differences in speed of mental processing and human cognitive abilities: Towards a taxonomic model. Learn. Individ. Differ. 1999, 11, 1–120. [Google Scholar] [CrossRef]
- Sheppard, L.D.; Vernon, P.A. Intelligence and speed of information-processing: A review of 50 years of research. Personal. Individ. Differ. 2008, 44, 535–551. [Google Scholar] [CrossRef]
- Dodonova, Y.A.; Dodonov, Y.S. Faster on easy items, more accurate on difficult ones: Cognitive ability and performance on a task of varying difficulty. Intelligence 2013, 41, 1–10. [Google Scholar] [CrossRef]
- Goldhammer, F.; Entink, R.H.K. Speed of reasoning and its relation to reasoning ability. Intelligence 2011, 39, 108–119. [Google Scholar] [CrossRef]
- Wilhelm, O.; Schulze, R. The relation of speeded and unspeeded reasoning with mental speed. Intelligence 2002, 30, 537–554. [Google Scholar] [CrossRef]
- Ferrando, P.J.; Lorenzo-Seva, U. An item-response model incorporating response time data in binary personality items. Appl. Psychol. Meas. 2007, 31, 525–543. [Google Scholar] [CrossRef]
- White, P.O. Individual differences in speed, accuracy, and persistence: A mathematical model of problem solving. In A Model for Intelligence; Eysenck, H.J., Ed.; Springer: Berlin, Germany, 1973; pp. 44–90. [Google Scholar]
- Heitz, R.P. The speed–accuracy tradeoff: History physiology, methodology, and behavior. Front. Neurosci. 2014, 8, 150. [Google Scholar] [CrossRef] [PubMed]
- Henmon, V. The relation of the time of a judgment to its accuracy. Psychol. Rev. 1911, 18, 186–201. [Google Scholar] [CrossRef]
- Bridgeman, B.; Cline, F.; Hessinger, J. Effect of Extra Time on GRE® Quantitative and Verbal Scores; ETS RR-03-13; Educational Testing Service: Princeton, NJ, USA, 2003. [Google Scholar]
- Evans, F.R. A Study of the Relationships among Speed and Power Aptitude Test Score, and Ethnic Identity; ETS RR 80-22; Educational Testing Service: Princeton, NJ, USA, 1980. [Google Scholar]
- Wild, C.L.; Durso, R.; Rubin, D.B. Effects of increased test-taking time on test scores by ethnic group, years out of school, and sex. J. Educ. Meas. 1982, 19, 19–28. [Google Scholar] [CrossRef]
- Lohman, D.F. The effect of speed–accuracy tradeoff on sex differences in mental rotation. Percept. Psychophys. 1986, 39, 427–436. [Google Scholar] [CrossRef] [PubMed]
- Sternberg, S. The discovery of processing stages: Extensions of Donders’ method. Acta Psychol. 1969, 30, 276–315. [Google Scholar] [CrossRef]
- Shiffrin, R.M.; Schneider, W. Controlled and automatic human information processing: II. Perceptual learning, automatic attending, and a general theory. Psychol. Rev. 1977, 84, 127–190. [Google Scholar] [CrossRef]
- Wickegren, W. Speed–accuracy tradeoff and information processing dynamics. Acta Psychol. 1977, 41, 67–85. [Google Scholar] [CrossRef]
- Lohman, D.F. Individual differences in errors and latencies on cognitive tasks. Learn. Individ. Differ. 1989, 1, 179–202. [Google Scholar] [CrossRef]
- Reed, A.V. List length and the time course of recognition in human memory. Mem. Cogn. 1976, 4, 16–30. [Google Scholar] [CrossRef] [PubMed]
- Wright, D.E.; Dennis, I. Exploiting the speed-accuracy trade-off. In Learning and Individual Differences: Process, Trait, and Content Determinants; Ackerman, P.L., Kyllonen, P.C., Roberts, R.D., Eds.; American Psychological Association: Washington, DC, USA, 1999. [Google Scholar]
- Irvine, S. Computerised Test Generation for Cross-National Military Recruitment; IOS Press: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Lewis, C. Expected response functions. In Essays on Item Response Theory; Boomsma, A., van Duijn, M.A.J., Snijders, T.A.B., Eds.; Springer: New York, NY, USA, 2001; Volume 157, pp. 163–171. [Google Scholar]
- Fischer, G.H. The linear logistic test model as an instrument in educational research. Acta Psychol. 1973, 37, 359–374. [Google Scholar] [CrossRef]
- Irvine, S.; Kyllonen, P.C. Item Generation for Test Development; Erlbaum: Mahwah, NJ, USA, 2002. [Google Scholar]
- Gierl, M.J.; Haladyna, T. Automatic Item Generation: Theory and Practice; Routledge: New York, NY, USA, 2013. [Google Scholar]
- Beilock, S.L.; Bertenthal, B.I.; Hoerger, M.; Carr, T.H. When does haste make waste? Speed–accuracy tradeoff, skill level, and the tools of the trade. J. Exp. Psychol. Appl. 2008, 14, 340–352. [Google Scholar] [CrossRef] [PubMed]
- Lohman, D.F. Estimating individual differences in information processing using speed-accuracy models. In Abilities, Motivation, Methodology: The Minnesota Symposium on Learning and Individual Differences; Kanfer, R., Ackerman, P.L., Cudeck, R., Eds.; Psychology Press: New York, NY, USA, 1990; pp. 119–163. [Google Scholar]
- Evans, J.S.B.T.; Wright, D.E. The Properties of Fixed-Time Tests: A Simulation Study; Technical Report 3-1993, Army Personnel Research Establishment; Human Assessment Laboratory, University of Plymouth: Plymouth, UK, 1993. [Google Scholar]
- Partchev, I.; De Boeck, P.; Steyer, R. How much power and speed is measured in this test? Assessment 2013, 20, 242–252. [Google Scholar] [CrossRef] [PubMed]
- Birnbaum, A. Some latent trait models and their use in inferring an examinee’s ability. In Statistical Theories of Mental Test Scores; Lord, F.M., Novick, M.R., Eds.; Addison-Wesley: Reading, MA, USA, 1968. [Google Scholar]
- Way, W.D.; Gawlick, L.A.; Eignor, D.R. Scoring Alternatives for Incomplete Computerized Adaptive Tests; Research Report No. RR-01-20; Educational Testing Service: Princeton, NJ, USA, 2001. [Google Scholar]
- Weeks, J.P.; Kyllonen, P.C.; Bertling, M.; Bertling, J.P. General Fluid/Inductive Reasoning Battery for a High-Ability Population; Unpublished manuscript; Educational Testing Service: Princton, NJ, USA, 2016. [Google Scholar]
- Wright, D.E. BARB and the Measurement of Individual Differences, Departing from Traditional Models. In Proceedings of the 35th International Military Testing Association Conference, Williamsburg, VA, USA, 15–18 November 1993; pp. 391–395.
- Ali, U.S.; Rijn, P.W. Psychometric quality of scenario-based tasks to measure learning outcomes. In Proceedings of the 2nd International Conference for Assessment and Evaluation, Riyadh, Saudi Arabia, 1–3 December 2015; Available online: http://ica.qiyas.sa/Presentations/Usama%20Ali.pdf (accessed on 10 September 2016).
- Maris, G.; van der Maas, H. Speed-accuracy response models: Scoring rules based on response time and accuracy. Psychometrika 2012, 77, 615–633. [Google Scholar] [CrossRef]
- Dennis, I.; Evans, J.S.B.T. The speed-error trade-off problem in psychometric testing. Br. J. Psychol. 1996, 87, 105–129. [Google Scholar] [CrossRef]
- Van der Maas, H.L.J.; Wagenmakers, E.-J. A psychometric analysis of chess expertise. Am. J. Psychol. 2005, 118, 29–60. [Google Scholar] [PubMed]
- Luce, R.D.; Bush, R.R.; Galanter, E. Handbook of Mathematical Psychology. Vol 1; John Wiley & Sons: New York, NY, USA, 1963. [Google Scholar]
- Newell, A. You can’t play 20 questions with nature and win. In Visual Information Processing; Chase, W.G., Ed.; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Luce, R.D. Response Times; Oxford University Press: New York, NY, USA, 1986. [Google Scholar]
- Hunt, E.B.; Davidson, J.; Lansman, M. Individual differences in long-term memory access. Mem. Cogn. 1981, 9, 599–608. [Google Scholar] [CrossRef]
- Kyllonen, P.C. Aptitude testing inspired by information processing: A test of the four-sources model. J. Gen. Psychol. 1993, 120, 375–405. [Google Scholar] [CrossRef]
- Faust, M.E.; Balota, D.A.; Spieler, D.H.; Ferraro, F.R. Individual differences in information processing rate and amount: Implications for group differences in response latency. Psychol. Bull. 1999, 125, 777–799. [Google Scholar] [CrossRef] [PubMed]
- Pieters, L.P.M.; van der Ven, A.H.G.S. Precision, speed, and distraction in time limit-tests. Appl. Psychol. Meas. 1982, 6, 93–109. [Google Scholar] [CrossRef]
- Schmiedek, F.; Oberauer, K.; Wilhelm, O.; Süß, H.M.; Wittmann, W.W. Individual differences in components of reaction time distributions and their relations to working memory and intelligence. J. Exp. Psychol. Gen. 2007, 136, 414–429. [Google Scholar] [CrossRef] [PubMed]
- Tuerlinckx, F.; De Boeck, P. Two interpretations of the discrimination parameter. Psychometrika 2005, 70, 629–650. [Google Scholar] [CrossRef]
- Van der Maas, H.L.; Molenaar, D.; Maris, G.; Kievit, R.A.; Borsboom, D. Cognitive psychology meets psychometric theory: On the relation between process models for decision making and latent variable models for individual differences. Psychol. Rev. 2011, 118, 339–177. [Google Scholar] [CrossRef] [PubMed]
- Underwood, B.J. Individual differences as a crucible in theory construction. Am. Psychol. 1975, 30, 128–134. [Google Scholar] [CrossRef]
- Murre, J.M.J.; Chessa, A.G. Power laws from individual differences in learning and forgetting: mathematical analyses. Psychon. Bull. Rev. 2011, 18, 592–597. [Google Scholar] [CrossRef] [PubMed]
- Newell, A.; Rosenbloom, P.S. Mechanisms of skill acquisition and the law of practice. In Cognitive Skills and Their Acquisition; Anderson, J.R., Ed.; Erlbaum: Hillsdale, NJ, USA, 1981; pp. 1–55. [Google Scholar]
- Heathcote, A.; Brown, S.; Mewhort, D.J. The power law repealed: the case for an exponential law of practice. Psychon. Bull. Rev. 2000, 7, 185–207. [Google Scholar] [CrossRef] [PubMed]
- Furneaux, W.D. Intellectual abilities and problem solving behavior. In Handbook of Abnormal Psychology; Eysenck, H.J., Ed.; Pitman Medical: London, UK, 1960; pp. 167–192. [Google Scholar]
- Lacouture, Y.; Cousineau, D. How to use MATLAB to fit the ex-Gaussian and other probability functions to a distribution of response times. Tutor. Quant. Methods Psychol. 2008, 4, 35–45. [Google Scholar] [CrossRef]
- R Core Team R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014; Available online: http://www.R-project.org/ (accessed on 10 September 2016).
- Massidda, D. Retimes: Reaction Time Analysis; R Package Version 0.1-2; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Ratcliff, R. A theory of memory retrieval. Psychol. Rev. 1978, 85, 59–108. [Google Scholar] [CrossRef]
- Ratcliff, R.; Smith, P.L.; Brown, S.D.; McKoon, G. Diffusion decision model: Current issues and history. Trends Cogn. Sci. 2016, 20, 260–281. [Google Scholar] [CrossRef] [PubMed]
- Donkin, C.; Brown, S.; Heathcote, A.; Wagenmakers, E.J. Diffusion versus linear ballistic accumulation: Different models but the same conclusions about psychological processes? Psychon. Bull. Rev. 2011, 18, 61–69. [Google Scholar] [CrossRef] [PubMed]
- Ratcliff, R.; Thapar, A.; Gomez, P.; McKoon, G. A diffusion model analysis of the effects of aging in the lexical-decision task. Psychol. Aging 2004, 19, 278–289. [Google Scholar] [CrossRef] [PubMed]
- Ratcliff, R.; Tuerlinckx, F. Estimating parameters of the diffusion model: Approaches to dealing with contaminant reaction times and parameter variability. Psychon. Bull. Rev. 2002, 9, 438–481. [Google Scholar] [CrossRef] [PubMed]
- Ratcliff, R.; Childers, C. Individual differences and fitting methods for the two-choice diffusion model of decision making. Decision 2015, 4, 237–279. [Google Scholar] [CrossRef] [PubMed]
- Held, J.D.; Carretta, T.R. Evaluation of Tests of Processing Speed, Spatial Ability, and Working Memory for Use in Military Occupational Classification; Technical Report NPRST-TR-14-1 (ADA589951); Navy Personnel Research, Studies, and Technology (Navy Personnel Command): Millington, TN, USA, 2013. [Google Scholar]
- Caplin, A.; Martin, D. The dual-process drift diffusion model: Evidence from response times. Econ. Inq. 2016, 54, 1274–1282. [Google Scholar] [CrossRef]
- Lord, F.M.; Novick, M.R. Statistical Theories of Mental Test Scores; Addison-Wesley: Reading, MA, USA, 1968. [Google Scholar]
- Roskam, E.E. Toward a psychometric theory of intelligence. In Progress in Mathematical Psychology; Roskam, E.E., Suck, R., Eds.; North Holland: Amsterdam, The Netherlands, 1987; pp. 151–171. [Google Scholar]
- Roskam, E.E. Models for speed and time-limit tests. In Handbook of Modern Item Response Theory; van der Linden, W.J., Hambleton, R.K., Eds.; Springer: New York, NY, USA, 1997; pp. 187–208. [Google Scholar]
- Verhelst, N.D.; Verstralen, H.H.F.M.; Jansen, M.G.H. A logistic model for time-limit tests. In Handbook of Modern Item Response Theory; van der Linden, W.J., Hambleton, R.K., Eds.; Springer: New York, NY, USA, 1997; pp. 169–186. [Google Scholar]
- Wang, T.; Hanson, B.A. Development and calibration of an item response model that incorporates response time. Appl. Psychol. Meas. 2005, 29, 323–339. [Google Scholar] [CrossRef]
- Gaviria, J.-L. Increase in precision when estimating parameters in computer assisted testing using response times. Qual. Quant. 2005, 39, 45–69. [Google Scholar] [CrossRef]
- Thissen, D. Timed testing: An approach using item response theory. In New Horizons in Testing: Latent Trait Test Theory and Computerized Adaptive Testing; Weiss, D.J., Ed.; Academic Press: New York, NY, USA, 1983; pp. 179–203. [Google Scholar]
- Van der Linden, W.J. A hierarchical framework for modeling speed and accuracy on test items. Psychometrika 2007, 72, 287–308. [Google Scholar] [CrossRef]
- Van der Linden, W.J. A lognormal model for response times on test items. J. Educ. Behav. Stat. 2006, 31, 181–204. [Google Scholar] [CrossRef]
- Van der Linden, W.; Guo, F. Bayesian procedures for identifying aberrant response time patterns in adaptive testing. Psychometrika 2008, 73, 365–384. [Google Scholar] [CrossRef]
- Van der Linden, W.J.; Breithaupt, K.; Chuah, S.C.; Zhang, Y. Detecting differential speededness in multistage testing. J. Educ. Meas. 2007, 44, 117–130. [Google Scholar] [CrossRef]
- Van der Linden, W.J.; Klein Entink, R.H.; Fox, J.-P. IRT parameter estimation with response time as collateral information. Appl. Psychol. Meas. 2010, 34, 327–347. [Google Scholar] [CrossRef]
- Glas, C.A.; van der Linden, W.J. Marginal likelihood inference for a model for item responses and response times. Br. J. Math. Stat. Psychol. 2010, 63, 603–626. [Google Scholar] [CrossRef] [PubMed]
- Klein Entink, R.H.; Fox, J.-P.; van der Linden, W.J. A multivariate multilevel approach to the modeling of accuracy and speed of test takers. Psychometrika 2009, 74, 21–48. [Google Scholar] [CrossRef] [PubMed]
- Klein Entink, R.H.; van der Linden, W.J.; Fox, J.-P. A Box-Cox normal model for response times. Br. J. Math. Stat. Psychol. 2009, 62, 621–640. [Google Scholar] [CrossRef] [PubMed]
- Ranger, J.; Ortner, T. The case of dependence of responses and response time: A modeling approach based on standard latent trait models. Psychol. Test Assess. Model. 2012, 54, 128–148. [Google Scholar]
- Meng, X.-B.; Tao, J.; Chang, H.-H. A conditional joint modeling approach for locally dependent item responses and response times. J. Educ. Meas. 2015, 52, 1–27. [Google Scholar] [CrossRef]
- Molenaar, D.; Tuerlinckx, F.; van der Maas, H.L.J. A generalized linear factor model approach to the hierarchical framework for responses and response times. Br. J. Math. Stat. Psychol. 2014, 68, 197–219. [Google Scholar] [CrossRef] [PubMed]
- Pellegrino, J.W.; Glaser, R. Cognitive components and correlates in the analysis of individual differences. Intelligence 1979, 3, 187–214. [Google Scholar] [CrossRef]
- Sternberg, R.J. Component processes in analogical reasoning. Psychol. Rev. 1977, 84, 353–378. [Google Scholar] [CrossRef]
- DiBello, L.V.; Roussos, L.A.; Stout, W. 31A Review of cognitively diagnostic assessment and a summary of psychometric models. In Handbook of Statistics; Elsevier: Amsterdam, The Netherlands, 2006; pp. 979–1030. [Google Scholar]
- DiBello, L.V.; Stout, W.F.; Roussos, L.A. Unified cognitive/psychometric diagnostic assessment likelihood-based classification techniques. In Cognitively Diagnostic Assessment; Nichols, P.D., Chipman, S.F., Brennan, R.L., Eds.; Erlbaum: Hillsdale, NJ, USA, 1995; pp. 361–389. [Google Scholar]
- Tatsuoka, K.K. Rule space: An approach for dealing with misconceptions based on item response theory. J. Educ. Meas. 1983, 20, 345–354. [Google Scholar] [CrossRef]
- Embretson, S.E. A cognitive design system approach to generating valid tests: Application to abstract reasoning. Psychol. Methods 1998, 3, 380–396. [Google Scholar] [CrossRef]
- Primi, R. Complexity of geometric inductive reasoning tasks: Contribution to the understanding of fluid intelligence. Intelligence 2001, 30, 41–70. [Google Scholar] [CrossRef]
- Gorin, J.S. Manipulating processing difficulty of reading comprehension questions: The feasibility of verbal item generation. J. Educ. Meas. 2005, 42, 351–373. [Google Scholar] [CrossRef]
- Klien Entink, R.H.; Kuhn, J.-T.; Hornke, L.F.; Fox, J.-P. Evaluating cognitive theory: A joint modeling approach using responses and response times. Psychol. Methods 2009, 14, 54–75. [Google Scholar] [CrossRef] [PubMed]
- Hornke, L.F.; Habon, M.W. Rule-based item bank construction and evaluation within the linear logistic framework. Appl. Psychol. Meas. 1986, 10, 369–380. [Google Scholar] [CrossRef]
- Lee, Y.-H.; Ying, Z. A mixture cure-rate model for responses and response times in time-limit tests. Psychometrika 2015, 80, 748–775. [Google Scholar] [CrossRef] [PubMed]
- Eisenberg, P.; Wesman, A.G. Consistency in response and logical interpretation of psychoneurotic inventory items. J. Educ. Psychol. 1941, 32, 321–338. [Google Scholar] [CrossRef]
- Molenaar, D.; Tuerlinckx, F.; van der Maas, H.L.J. Fitting diffusion item response theory models for responses and response times using the R package diffIRT. J. Stat. Softw. 2015, 66, 1–34. [Google Scholar] [CrossRef]
- Evans, J.S.B.T.; Stanovich, K.E. Dual-process theories of higher cognition: Advancing the debate. Perspect. Psychol. Sci. 2013, 8, 223–241. [Google Scholar] [CrossRef] [PubMed]
- Kahneman, D. Thinking Fast and Slow; Farrar, Straus, and Giroux: New York, NY, USA, 2011. [Google Scholar]
- Stanovich, K.E. Individual differences in reasoning: Implications for the rationality debate? Behav. Brain Sci. 2000, 23, 645–726. [Google Scholar] [CrossRef] [PubMed]
- Stanovich, K.E.; West, R.F. Individual differences in rational thought. J. Exp. Psychol. Gen. 1998, 127, 161–188. [Google Scholar] [CrossRef]
- Larson, G.E.; Alderton, D.L. Reaction time variability and intelligence: A “worst performance” analysis of individual differences. Intelligence 1990, 14, 309–325. [Google Scholar] [CrossRef]
- Coyle, T.R. A review of the worst performance rule: Evidence, theory, and alternative hypotheses. Intelligence 2003, 31, 567–587. [Google Scholar] [CrossRef]
- Wang, C.; Xu, G. A mixture hierarchical model for response times and response accuracy. Br. J. Math. Stat. Psychol. 2015, 68, 456–477. [Google Scholar] [CrossRef] [PubMed]
- Chaiken, S.R. Test-proximity effects in a single-session individual-differences study of learning ability: The case of activation savings. Intelligence 1993, 17, 173–190. [Google Scholar] [CrossRef]
- Kane, M.J.; Brown, L.H.; McVay, J.C.; Silvia, P.J.; Myin-Germeys, I.; Kwapil, T.R. For who the mind wanders, and when: An experience-sampling study of working memory and executive control in daily life. Psychol. Sci. 2007, 18, 614–621. [Google Scholar] [CrossRef] [PubMed]
- Partchev, I.; De Boeck, P. Can fast and slow intelligence be differentiated? Intelligence 2012, 40, 23–32. [Google Scholar] [CrossRef]
- De Boeck, P.; Partchev, I. IRTrees: Tree-based item response models of the GLMM family. J. Stat. Softw. 2012, 48, 1–28. [Google Scholar]
- DiTrapani, J.; Jeon, M.; De Boeck, P.; Partchev, I. Attempting to differentiate fast and slow intelligence: Using generalized item response trees to examine the role of speed on intelligence tests. Intelligence 2016, 56, 82–92. [Google Scholar] [CrossRef]
- Coomans, F.; Hofman, A.; Brinkhuis, M.; van der Maas, H.L.J.; Maris, G. Distinguishing fast and slow processes in accuracy-response time data. PLoS ONE 2016, 11, e0155149. [Google Scholar] [CrossRef] [PubMed]
- Finn, B. Measuring Motivation in Low-Stakes Stakes Assessments; Research Report No. RR-15; Educational Testing Service: Princeton, NJ, USA, 2015. [Google Scholar]
- Lee, Y.-H.; Jia, Y. Using response time to investigate students’ test-taking behaviors in a NAEP computer-based study. Large-Scale Assess. Educ. 2014, 2, 8. [Google Scholar] [CrossRef]
- Wise, S.; Pastor, D.A.; Kong, X. Correlates of rapid-guessing behavior in low stakes testing: Implications for test development and measurement practice. Appl. Meas. Educ. 2009, 22, 185–205. [Google Scholar] [CrossRef]
- Kyllonen, P.C.; Lohman, D.F.; Woltz, D.J. Componential modeling of alternative strategies for performing spatial tasks. J. Educ. Psychol. 1984, 76, 1325–1345. [Google Scholar] [CrossRef]
- Molenaar, D.; Bolsinova, M.; Rozsa, S.; De Boeck, P. Response mixture modeling of intraindividual differences in responses and response times to the Hungarian WISC-IV Block Design test. J. Intell. 2016, 4, 10. [Google Scholar] [CrossRef]
- Lee, Y.-H.; Haberman, S.J. Investigating test-taking behaviors using timing and process data. Int. J. Test. 2015, 16, 240–267. [Google Scholar] [CrossRef]
- Van der Linden, W.J. Linear Models for Optimal Test Assembly; Springer: New York, NY, USA, 2005. [Google Scholar]
- Van der Linden, W.J. Using response times for item selection in adaptive testing. J. Educ. Stat. 2008, 33, 5–20. [Google Scholar] [CrossRef]
- Van der Linden, W.J.; Scrams, D.J.; Schnipke, D.L. Using response-time constraints to control for differential speededness in computerized adaptive testing. Appl. Psychol. Meas. 1999, 23, 195–210. [Google Scholar] [CrossRef]
- American Educational Research Association; American Psychological Association; National Council on Measurement in Education. Standards for Educational and Psychological Testing; American Educational Research Association: Washington, DC, USA, 2014. [Google Scholar]
- Bridgeman, B.; Cline, F. Variations in Mean Response Times for Questions on the Computer-Adaptive GRE General Test: Implications for Fair Assessment; ETS RR-00-7; Educational Testing Service: Princeton, NJ, USA, 2000. [Google Scholar]
- Bridgeman, B.; Cline, F. Effects of differentially time-consuming tests on computer-adaptive test scores. J. Educ. Meas. 2004, 41, 137–148. [Google Scholar] [CrossRef]
- Ranger, J. Modeling responses and response times in personality tests with rating scales. Psychol. Test Assess. Model. 2013, 55, 361–382. [Google Scholar]
- Ranger, J.; Ortner, T. Assessing personality traits through response latencies using item response theory. Educ. Psychol. Meas. 2011, 71, 389–406. [Google Scholar] [CrossRef]
- Williams, M.D.; Hollan, J.D. The process of retrieval from very long-term memory. Cogn. Sci. 1981, 5, 87–119. [Google Scholar] [CrossRef]
- Fox, J.P.; Klein Entink, R.; van der Linden, W. Modeling of responses and response times with the package CIRT. J. Stat. Softw. 2007, 20, 1–14. [Google Scholar] [CrossRef]
- 1Thorndike et al. (p. 33 in [7]) proposed that the time to complete a test is “a mixture of (1) time spent in doing some tasks correctly; (2) the time spent in doing other tasks incorrectly and (3) the time spent in inspecting other tasks and deciding not to attempt them.”
- 2The soundness of this definition of unspeededness depends on respondents answering questions in order; if a respondent skips early questions to work on later ones the test might still be speeded even though it would not be so by this definition [12].
- 3It has been common practice in the cognitive psychology literature to exclude incorrect items when computing response time, and often to re-administer wrong items until the participant got them right, then to use that response time in the analysis.
- 5The authors credit Dan Segall as their source for a similar approach he developed for the ASVAB, but do not provide a citation.
- 7In this literature, the term “response” typically refers to whether the item response was correct or not, with 1 indicating a correct response and 0 indicating an incorrect response; we also use the term “correctness” to mean the same thing.
- 8The cognitive psychology literature typically refers to an item as a stimulus, given its behavioral (stimulus-response) roots; here we use the terms stimulus and item interchangeably. The term trial is also used synonymously with item.
- 9A transformation, such as the reciprocal of response time (1/T), or better, the log of response time (log T) tends to create a normally distributed variable that is more practical for analysis.
- 10The mean of the exponential function is commonly referred to as tau, τ, also, but here we use beta, β, instead, because we use τ as a time parameter in response time models.
- 11Item analysis is a routine part of classical test theory methodology, but primarily as a means for identifying poorly performing items that can be modified or deleted in order to obtain better test scores, per se.
- 12Van der Linden [95] later popularized the term time intensity, which is now commonly used, but it is the same concept as Thissen’s βj. Time intensity refers to the amount of time an item tends to require, analogous to item difficulty in modeling accuracy.
- 14They point out that this was already noted [103].
- 15It is a generalized linear factor model rather than a linear factor model because indicators for the first factor are categorical (right-wrong, true-false, or Likert) responses.
- 16The importance of comparable meaning across alternate sets of items is addressed in the AERA, NCME, APA Test Standards [141]; Standard 5.16; p. 106).
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kyllonen, P.C.; Zu, J. Use of Response Time for Measuring Cognitive Ability. J. Intell. 2016, 4, 14. https://doi.org/10.3390/jintelligence4040014
Kyllonen PC, Zu J. Use of Response Time for Measuring Cognitive Ability. Journal of Intelligence. 2016; 4(4):14. https://doi.org/10.3390/jintelligence4040014
Chicago/Turabian StyleKyllonen, Patrick C., and Jiyun Zu. 2016. "Use of Response Time for Measuring Cognitive Ability" Journal of Intelligence 4, no. 4: 14. https://doi.org/10.3390/jintelligence4040014
APA StyleKyllonen, P. C., & Zu, J. (2016). Use of Response Time for Measuring Cognitive Ability. Journal of Intelligence, 4(4), 14. https://doi.org/10.3390/jintelligence4040014




