The Relationship of Need for Cognition and Typical Intellectual Engagement with Intelligence and Executive Functions: A Multi-Level Meta-Analysis
Abstract
1. Introduction
1.1. Cognitive Motivation
1.2. Intelligence
1.3. Executive Functions
1.4. Relating NFC/TIE to Intelligence and Executive Functions
1.5. The Present Study
2. Materials and Methods
2.1. Transparency and Openness
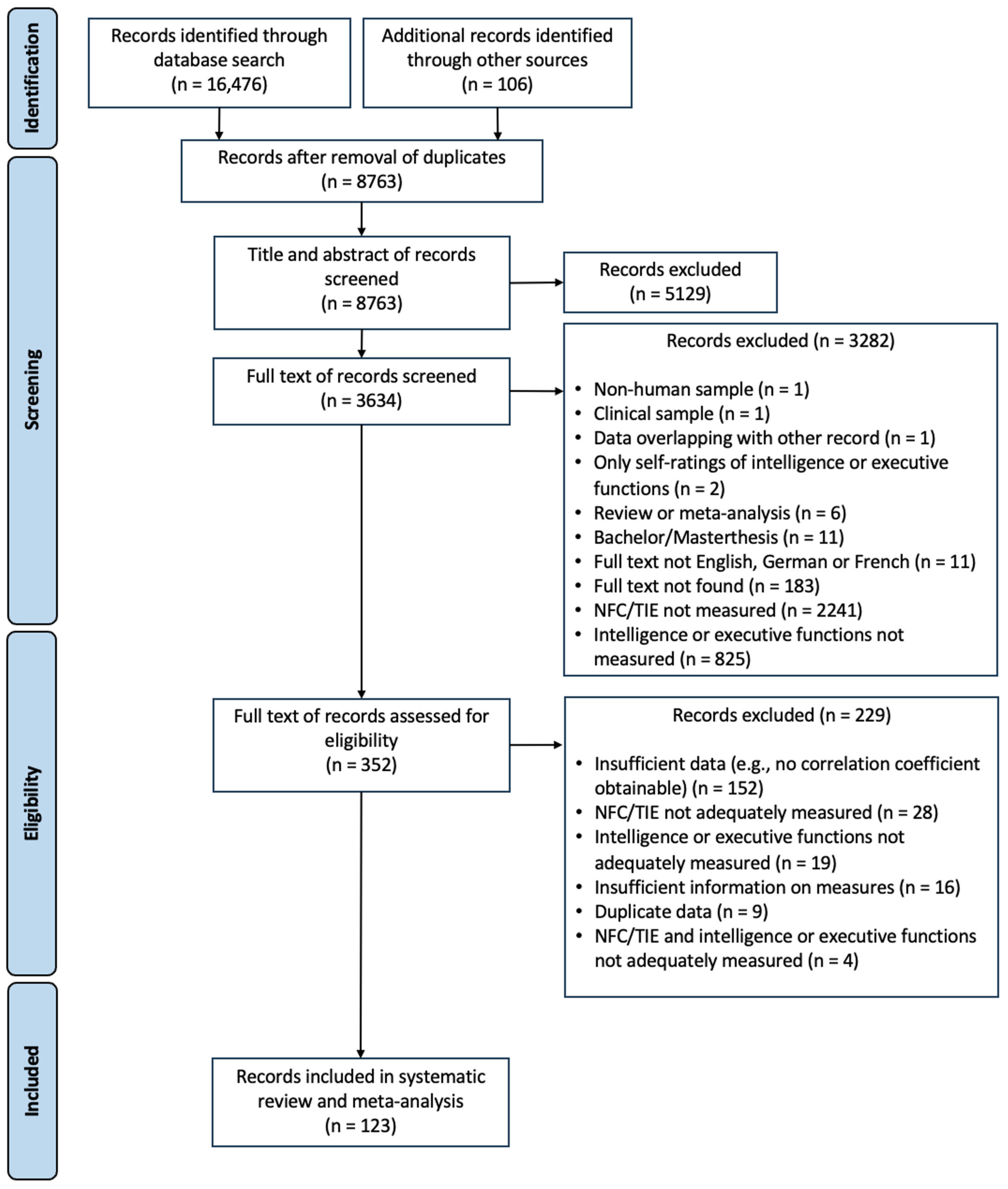
2.2. Literature Search
2.3. Inclusion and Exclusion Criteria
- (a)
- The publication was written in English, German, or French.
- (b)
- The publication examined NFC or TIE.
- (c)
- (d)
- The publication was not itself a review or meta-analysis. If this criterion was not met but the publication was considered relevant to our research questions, it was later screened for relevant references.
- (e)
- The publication sample was not drawn exclusively from clinical populations, including those characterized by psychiatric or physical disorders and diseases. We considered a publication eligible regarding this criterion if it examined data from, for example, a healthy control arm in a clinical study design.
- (f)
- The publication quantitatively analyzed the data to obtain effect sizes such as correlation coefficients, regression coefficients, or data transferable into a Pearson correlation coefficient for the association of NFC/TIE and the respective cognitive function.
2.4. Screening and Coding
2.5. Data Analysis
2.5.1. General Models
2.5.2. Outliers and Influential Cases
2.5.3. Moderator and Meta-Regression Analyses
2.5.4. Assessment of Publication Bias
3. Results
3.1. Intelligence, Executive Functions, and NFC/TIE
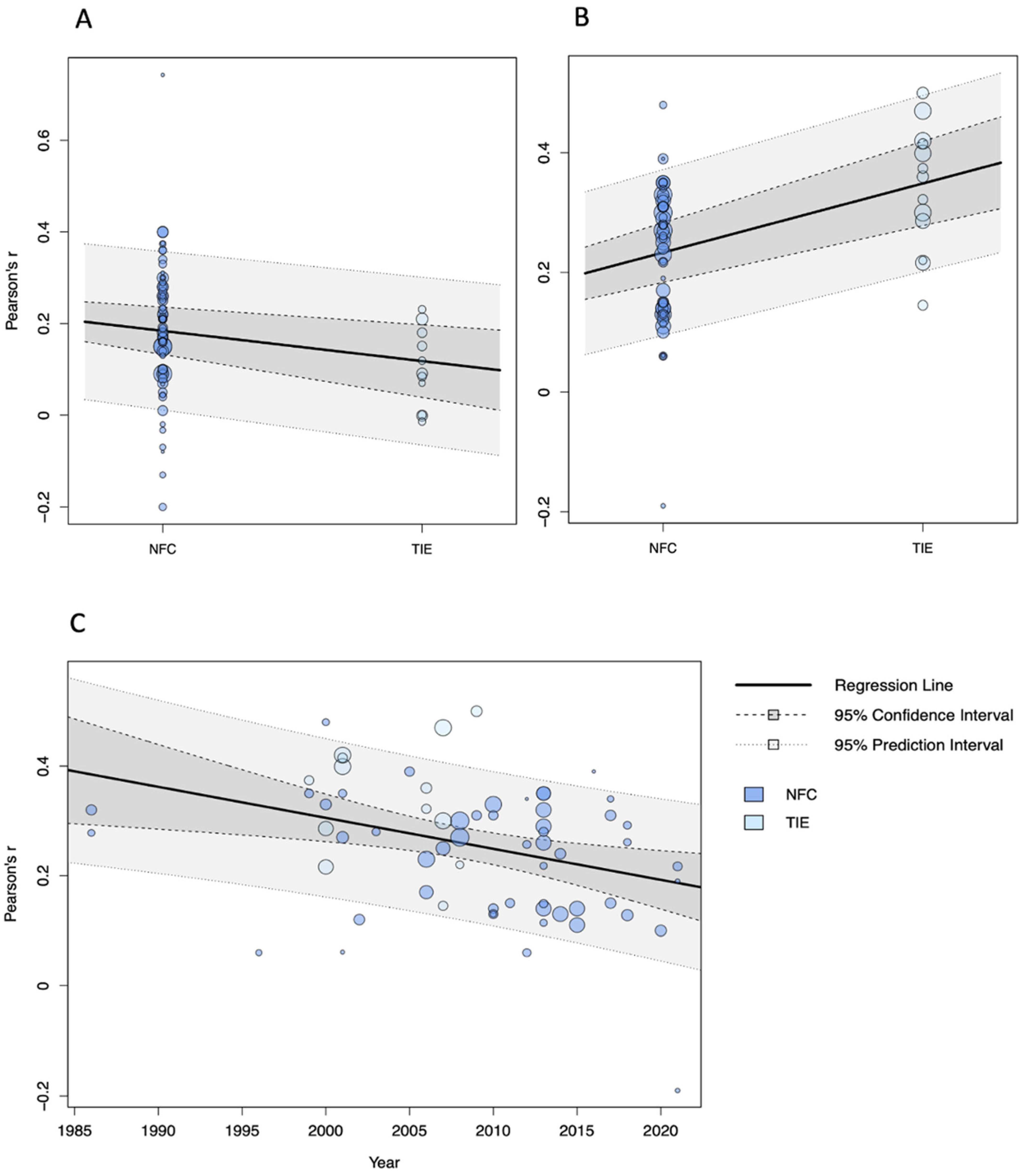
3.2. Moderator Analyses
3.3. Publication Bias
4. Discussion
4.1. Main Findings
4.2. Moderator Analyses
4.3. Longitudinal Relationships Between NFC/TIE and Intelligence
4.4. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NFC | need for cognition |
| TIE | typical intellectual engagement |
| NFC/TIE | need for cognition/typical intellectual engagement |
| WM | working memory |
| Gc | crystallized intelligence |
| Gf | fluid intelligence |
| Gen. know. | general knowledge |
| Verb. know | verbal knowledge |
| Resp. inhib. | response inhibition |
| Interf. cont. | interference control |
| Red. model | model without moderators with missing cases removed |
| OFCI | Openness-Fluid-Crystallized-Intelligence |
| PET-PEESE | precision-effect test and precision-effect estimate with standard errors |
| CHC | Cattell-Horn-Carroll |
| RVE | robust variance estimation |
| ROBUST | Risk of Bias Utilized for Surveys Tool |
| REML | restricted maximum likelihood |
| CI | confidence interval |
| PI | prediction interval |
| SE | standard error |
| k | number of publications |
| s | number of studies |
| t | number of tasks |
| e | number of effects |
| DGPs | Deutsche Gesellschaft für Psychologie |
| 1 | The direction of the effect reflects lower theta power in high-NFC individuals in simple compared to complex tasks. |
| 2 | We originally intended to focus only on Gf and Gc. However, the inspection of the literature following preregistration revealed several studies using broad measures of intelligence that can be considered proxies for general intelligence. Although the scope of this analysis is smaller than that for Gf and Gc, we decided to include these effects in a separate analysis. Similarly to the processing of the literature on general intelligence in Anglim et al. (2022), the included measures had to be sufficiently broad – either targeting at least two ability domains or consisting of a single broad measure with tasks covering several different abilities, such as the Wonderlic Personnel Test (Wonderlic Inc. 1999) or Wechsler Adult Intelligence Scale (WAIS–III; Wechsler 1997). We will refer to this as general intelligence, although arguably not every measure found in the literature perfectly aligns with a general g-factor (Spearman 1904). |
| 3 | Similarly, we identified many studies examining the associations of NFC/TIE with WM capacity and not specifically updating. Meta-analytic results from these data are also presented below for the interested reader. |
| 4 | For simplicity we refer to this moderator as “publication year” in the following. |
References
- Ackerman, Phillip L. 1996. A theory of adult intellectual development: Process, personality, interests, and knowledge. Intelligence 22: 227–57. [Google Scholar] [CrossRef]
- Ackerman, Phillip L. 2000. Domain-specific knowledge as the “dark matter” of adult intelligence: Gf/Gc, personality and interest correlates. The Journals of Gerontology Series B: Psychological Sciences and Social Sciences 55: 69–84. [Google Scholar] [CrossRef]
- Ackerman, Phillip L., and Eric D. Heggestad. 1997. Intelligence, personality, and interests: Evidence for overlapping traits. Psychological Bulletin 121: 219–45. [Google Scholar] [CrossRef]
- Ackerman, Phillip L., and Margaret E. Beier. 2006. Determinants of domain knowledge and independent study learning in an adult sample. Journal of Educational Psychology 98: 366–81. [Google Scholar] [CrossRef]
- Ackerman, Phillip L., and Maynard Goff. 1994. Typical intellectual engagement and personality: Reply to Rocklin 1994. Journal of Educational Psychology 86: 150–53. [Google Scholar] [CrossRef]
- Ackerman, Phillip L., Kristy R. Bowen, Margaret E. Beier, and Ruth Kanfer. 2001. Determinants of individual differences and gender differences in knowledge. Journal of Educational Psychology 93: 797–825. [Google Scholar] [CrossRef]
- Ackerman, Phillip L., Margaret E. Beier, and Mary O. Boyle. 2005. Working memory and intelligence: The same or different constructs? Psychological Bulletin 131: 30–60. [Google Scholar] [CrossRef]
- Ackerman, Phillip L., Ruth Kanfer, and Maynard Goff. 1995. Cognitive and noncognitive determinants and consequences of complex skill acquisition. Journal of Experimental Psychology: Applied 1: 270–304. [Google Scholar] [CrossRef]
- Amabile, Teresa M., Karl G. Hill, Beth A. Hennessey, and Elizabeth M. Tighe. 1995. The work preference inventory: Assessing intrinsic and extrinsic motivational orientations. Journal of Personality and Social Psychology 66: 950–67. [Google Scholar] [CrossRef]
- Amthauer, Rudolf, Burkhard Brocke, Detlev Liepmann, and Andre Beauducel. 2001. Intelligenz-Struktur-Test 2000 R (I-S-T 2000 R). Seattle: Hogrefe. [Google Scholar]
- Anglim, Jeromy, Patrick D. Dunlop, Serena Wee, Sharon Horwood, Joshua K. Wood, and Andrew Marty. 2022. Personality and intelligence: A meta-analysis. Psychological Bulletin 148: 301–36. [Google Scholar] [CrossRef]
- Arteche, Adriane, Tomas Chamorro–Premuzic, Philipp Ackerman, and Adrian Furnham. 2009. Typical intellectual engagement as a byproduct of openness, learning approaches, and self–assessed intelligence. Educational Psychology 29: 357–67. [Google Scholar] [CrossRef]
- Assink, Mark, and Carlijn J. M. Wibbelink. 2016. Fitting three-level meta-analytic models in R: A step-by-step tutorial. The Quantitative Methods for Psychology 12: 154–74. [Google Scholar] [CrossRef]
- Bagby, Michael, Graeme J. Taylor, and David Ryan. 1986. Toronto Alexithymia Scale: Relationship with personality and psychopathology measures. Psychotherapy and Psychosomatics 45: 207–15. [Google Scholar] [CrossRef]
- Beauducel, André, Burkhard Brocke, and Detlev Liepmann. 2001. Perspectives on fluid and crystallized intelligence: Facets for verbal, numerical, and figural intelligence. Personality and Individual Differences 30: 977–94. [Google Scholar] [CrossRef]
- Beier, Margaret E., and Phillip L. Ackerman. 2001. Current-events knowledge in adults: An investigation of age, intelligence, and nonability determinants. Psychology and Aging 16: 615–28. [Google Scholar] [CrossRef]
- Bergold, Sebastian, and Ricarda Steinmayr. 2024. The interplay between investment traits and cognitive abilities: Investigating reciprocal effects in elementary school age. Child Development 95: 780–99. [Google Scholar] [CrossRef] [PubMed]
- Bergold, Sebastian, Anke Hufer-Thamm, Katharina Abad Borger, Maike Luhmann, and Ricarda Steinmayr. 2023. Does intelligence predict development of investment traits from mid to late adolescence? Evidence from a 3-year longitudinal study. Journal of Adolescence 95: 553–65. [Google Scholar] [CrossRef]
- Bertrams, Alex, and Oliver Dickhäuser. 2012. Passionate thinkers feel better: Self-control capacity as mediator of the relationship between Need for Cognition and affective adjustment. Journal of Individual Differences 33: 69–75. [Google Scholar] [CrossRef]
- Bless, Herbert, Michaela Wänke, Gerd Bohner, Roland F. Fellhauer, and Norbert Schwarz. 1994. Need for Cognition: Eine Skala zur Erfassung von Engagement und Freude bei Denkaufgaben. Zeitschrift für Sozialpsychologie 25: 147–154. [Google Scholar]
- Borenstein, Michael. 2019. Common Mistakes in Meta-Analysis and How to Avoid Them. Englewood: Biostat, Inc. [Google Scholar]
- Borenstein, Michael, Larry V. Hedges, Julian P. T. Higgins, and Hannah R. Rothstein. 2009. Introduction to Meta-Analysis. Hoboken: John Wiley & Sons. [Google Scholar]
- Brocki, Karin C., and Gunilla Bohlin. 2004. Executive functions in children aged 6 to 13: A dimensional and developmental study. Developmental Neuropsychology 26: 571–93. [Google Scholar] [CrossRef]
- Buecker, Susanne, Marlies Maes, Jaap J. A. Denissen, and Maike Luhmann. 2020. Loneliness and the Big Five personality traits: A meta-analysis. European Journal of Personality 34: 8–28. [Google Scholar] [CrossRef]
- Burkolter, Dina, and Annette Kluge. 2012. Process control and risky decision-making: Moderation by general mental ability and need for cognition. Ergonomics 55: 1285–97. [Google Scholar] [CrossRef]
- Cacioppo, John T., and Richard E. Petty. 1982. The need for cognition. Journal of Personality and Social Psychology 42: 116–31. [Google Scholar] [CrossRef]
- Cacioppo, John T., Richard E. Petty, and Chuan Feng Kao. 1984. The efficient assessment of need for cognition. Journal of Personality Assessment 48: 306–7. [Google Scholar] [CrossRef]
- Cacioppo, John T., Richard E. Petty, Chuan Feng Kao, and Regina Rodriguez. 1986. Central and peripheral routes to persuasion: An individual difference perspective. Journal of Personality and Social Psychology 51: 1032–43. [Google Scholar] [CrossRef]
- Cacioppo, John T., Richard E. Petty, Jeffrey A. Feinstein, and W. Blair G. Jarvis. 1996. Dispositional differences in cognitive motivation: The life and times of individuals varying in need for cognition. Psychological Bulletin 119: 197–253. [Google Scholar] [CrossRef]
- Carroll, John B. 1993. Human Cognitive Abilities: A Survey of Factor-Analytic Studies. Cambridge: Cambridge University Press. [Google Scholar] [CrossRef]
- Carson, Kenneth P., Chester A. Schriesheim, and Angelo J. Kinicki. 1990. The usefulness of the “fail-safe” statistic in meta-analysis. Educational and Psychological Measurement 50: 233–43. [Google Scholar] [CrossRef]
- Cattell, Raymond B. 1987. Intelligence: Its Structure, Growth and Action. Amsterdam: North-Holland. [Google Scholar]
- Chevalier, Nicolas. 2018. Willing to think hard? The subjective value of cognitive effort in children. Child Development 89: 1283–95. [Google Scholar] [CrossRef]
- Collins, Anne, and Etienne Koechlin. 2012. Reasoning, learning, and creativity: Frontal lobe function and human decision-making. PLoS Biology 10: e1001293. [Google Scholar] [CrossRef]
- Costa, Paul T., and Robert R. McCrae. 1992. Normal personality assessment in clinical practice: The NEO Personality Inventory. Psychological Assessment 4: 5–13. [Google Scholar] [CrossRef]
- Cowan, Nelson. 2008. What are the differences between long-term, short-term, and working memory? Progress in Brain Research 169: 323–38. [Google Scholar] [CrossRef]
- Craig Aulisi, Lydia, Hannah M. Markell-Goldstein, Jose M. Cortina, Carol M. Wong, Xue Lei, and Cyrus K. Foroughi. 2023. Detecting gender as a moderator in meta-analysis: The problem of restricted between-study variance. Psychological Methods 30: 687–719. [Google Scholar] [CrossRef]
- Day, Eric Anthony, Jazmine Espejo, Vanessa Kowollik, Paul R. Boatman, and Lauren E. McEntire. 2007. Modeling the links between need for cognition and the acquisition of a complex skill. Personality and Individual Differences 42: 201–12. [Google Scholar] [CrossRef]
- Deák, Gedeon O., and Gayathri Narasimham. 2003. Is perseveration caused by inhibition failure? Evidence from preschool children’s inferences about word meanings. Journal of Experimental Child Psychology 86: 194–222. [Google Scholar] [CrossRef][Green Version]
- Dellenbach, Myriam, and Daniel Zimprich. 2008. Typical intellectual engagement and cognition in old age. Aging, Neuropsychology, and Cognition 15: 208–31. [Google Scholar] [CrossRef]
- DeYoung, Colin G. 2020. Intelligence and personality. In The Cambridge Handbook of Intelligence, 2nd ed. Edited by Robert J. Sternberg. Cambridge: Cambridge University Press, pp. 1011–47. [Google Scholar] [CrossRef]
- Diamond, Adele. 2013. Executive functions. Annual Review of Psychology 64: 135–68. [Google Scholar] [CrossRef]
- Dornic, Stan, Bo Ekehammar, and Tarja Laaksonen. 1991. Tolerance for mental effort: Self-ratings related to perception, performance and personality. Personality and Individual Differences 12: 313–19. [Google Scholar] [CrossRef]
- Duggan, Emily C., and Mauricio A. Garcia-Barrera. 2015. Executive functioning and intelligence. In Handbook of Intelligence: Evolutionary Theory, Historical Perspective, and Current Concepts. Edited by Sam Goldstein, Dana Princiotta and Jack A. Naglieri. Berlin and Heidelberg: Springer, pp. 435–58. [Google Scholar] [CrossRef]
- Duncan, John, Roger Johnson, and Michaela Swales. 1997. Frontal lobe deficits after head injury: Unity and diversity of function. Cognitive Neuropsychology 14: 713–41. [Google Scholar] [CrossRef]
- Duval, Sue. 2005. The trim and fill method. In Publication Bias in Meta-Analysis: Prevention, Assessment and Adjustments. Edited by Hannah R. Rothstein, Alexander J. Sutton and Michael Borenstein. Hoboken: John Wiley & Sons, pp. 127–44. [Google Scholar] [CrossRef]
- Duval, Sue, and Richard Tweedie. 2000. A nonparametric “trim and fill” method of accounting for publication bias in meta-analysis. Journal of the American Statistical Association 95: 89–98. [Google Scholar] [CrossRef] [PubMed]
- Egger, Matthias, George Davey Smith, Matthias Schneider, and Christoph Minder. 1997. Bias in meta-analysis detected by a simple, graphical test. BMJ 315: 629–34. [Google Scholar] [CrossRef] [PubMed]
- Enge, Sören, Monika Fleischhauer, Burkhard Brocke, and Alexander Strobel. 2008. Neurophysiological measures of involuntary and voluntary attention allocation and dispositional differences in need for cognition. Personality and Social Psychology Bulletin 34: 862–74. [Google Scholar] [CrossRef] [PubMed]
- Enge, Sören, Monika Fleischhauer, Klaus-Peter Lesch, and Alexander Strobel. 2011. On the role of serotonin and effort in voluntary attention: Evidence of genetic variation in N1 modulation. Behavioural Brain Research 216: 122–28. [Google Scholar] [CrossRef]
- Engle, Randall W. 2018. Working memory and executive attention: A revisit. Perspectives on Psychological Science 13: 190–93. [Google Scholar] [CrossRef]
- Fleischhauer, Monika, Robert Miller, Magdalena Katharina Wekenborg, Marlene Penz, Clemens Kirschbaum, and Sören Enge. 2019. Thinking against burnout? An individual’s tendency to engage in and enjoy thinking as a potential resilience factor of burnout symptoms and burnout-related impairment in executive functioning. Frontiers in Psychology 10: 420. [Google Scholar] [CrossRef] [PubMed]
- Fleischhauer, Monika, Robert Miller, Sören Enge, and Thorsten Albrecht. 2014. Need for cognition relates to low-level visual performance in a metacontrast masking paradigm. Journal of Research in Personality 48: 45–50. [Google Scholar] [CrossRef]
- Fleischhauer, Monika, Sören Enge, Burkhard Brocke, Johannes Ullrich, Alexander Strobel, and Anja Strobel. 2010. Same or different? Clarifying the relationship of need for cognition to personality and intelligence. Personality and Social Psychology Bulletin 36: 82–96. [Google Scholar] [CrossRef]
- Friedman, Naomi P., and Akira Miyake. 2004. The relations among inhibition and interference control functions: A latent-variable analysis. Journal of Experimental Psychology: General 133: 101–35. [Google Scholar] [CrossRef]
- Friedman, Naomi P., and Akira Miyake. 2017. Unity and diversity of executive functions: Individual differences as a window on cognitive structure. Cortex 86: 186–204. [Google Scholar] [CrossRef]
- Furnham, Adrian, and Jeremy D. Thorne. 2013. Need for Cognition: Its dimensionality and personality and intelligence correlates. Journal of Individual Differences 34: 230–40. [Google Scholar] [CrossRef]
- Furnham, Adrian, Jeremy Monsen, and Gorkan Ahmetoglu. 2009. Typical intellectual engagement, Big Five personality traits, approaches to learning and cognitive ability predictors of academic performance. British Journal of Educational Psychology 79: 769–82. [Google Scholar] [CrossRef]
- Gardner, Howard. 1999. Intelligence Reframed: Multiple Intelligences for the 21st Century. New York: Basic Books. [Google Scholar]
- Garlick, Dennis. 2002. Understanding the nature of the general factor of intelligence: The role of individual differences in neural plasticity as an explanatory mechanism. Psychological Review 109: 116–36. [Google Scholar] [CrossRef]
- Gärtner, Anne, Julia Grass, Max Wolff, Thomas Goschke, Anja Strobel, and Alexander Strobel. 2021. No relation of Need for Cognition to basic executive functions. Journal of Personality 89: 1113–25. [Google Scholar] [CrossRef]
- Gilpin, Andrew R. 1993. Table for conversion of Kendall’s Tau to Spearman’s Rho within the context of measures of magnitude of effect for meta-analysis. Educational and Psychological Measurement 53: 87–92. [Google Scholar] [CrossRef]
- Godefroy, Olivier, Maryline Cabaret, Violaine Petit-Chenal, Jean-Pierre Pruvo, and Marc Rousseaux. 1999. Control functions of the frontal lobes. Modularity of the central-supervisory system? Cortex 35: 1–20. [Google Scholar] [CrossRef]
- Goff, Maynard, and Phillip L. Ackerman. 1992. Personality-intelligence relations: Assessment of typical intellectual engagement. Journal of Educational Psychology 84: 537–52. [Google Scholar] [CrossRef]
- Grass, Julia, Florian Krieger, Philipp Paulus, Samuel Greiff, Anja Strobel, and Alexander Strobel. 2019. Thinking in action: Need for cognition predicts self-control together with action orientation. PLoS ONE 14: e0220282. [Google Scholar] [CrossRef]
- Harrer, Mathias, Pim Cuijpers, Toshi A. Furukawa, and David D. Ebert. 2022. Doing Meta-Analysis with R: A Hands-on Guide. Boca Raton: Chapman & Hall/CRC. [Google Scholar]
- Hedges, Larry V., Elizabeth Tipton, and Matthew C. Johnson. 2010. Robust variance estimation in meta-regression with dependent effect size estimates. Research Synthesis Methods 1: 39–65. [Google Scholar] [CrossRef] [PubMed]
- Higgins, Julian P. T., and Simon G. Thompson. 2002. Quantifying heterogeneity in a meta-analysis. Statistics in Medicine 21: 1539–58. [Google Scholar] [CrossRef] [PubMed]
- Hill, Benjamin D., Joshua D. Foster, Emily M. Elliott, Jill Talley Shelton, Jessica McCain, and Wm. Drew Gouvier. 2013. Need for cognition is related to higher general intelligence, fluid intelligence, and crystallized intelligence, but not working memory. Journal of Research in Personality 47: 22–25. [Google Scholar] [CrossRef]
- Hofmann, Wilhelm, Brandon J. Schmeichel, and Alan D. Baddeley. 2012. Executive functions and self-regulation. Trends in Cognitive Sciences 16: 174–80. [Google Scholar] [CrossRef]
- Horn, John L., and Raymond B. Cattell. 1966. Refinement and test of the theory of fluid and crystallized intelligence. Journal of Educational Psychology 57: 253–70. [Google Scholar] [CrossRef]
- Hox, Joop J. 2010. Multilevel analysis: Techniques and applications. New York: Routledge. [Google Scholar]
- Hufer-Thamm, Anke, Sebastian Bergold, and Ricarda Steinmayr. 2025. The Role of Need for Cognition and Its Interaction with Fluid Intelligence in the Prediction of School Grades in Primary School Children. Journal of Intelligence 13: 94. [Google Scholar] [CrossRef]
- Hunter, John E., and Frank L. Schmidt. 1990. Methods of Meta-Analysis: Correcting Error and Bias in Research Findings. Newbury Park: Sage. [Google Scholar]
- Hupe, Meghan. 2019. EndNote X9. Journal Of Electronic Resources in Medical Libraries 16: 117–19. [Google Scholar] [CrossRef]
- Hülür, Gizem, Fidan Gasimova, Alexander Robitzsch, and Oliver Wilhelm. 2018. Change in fluid and crystallized intelligence and student achievement: The role of intellectual engagement. Child Development 89: 1074–87. [Google Scholar] [CrossRef]
- Kane, Michael J., David Z. Hambrick, and Andrew R. A. Conway. 2005. Working memory capacity and fluid intelligence are strongly related constructs: Comment on Ackerman, Beier, and Boyle 2005. Psychological Bulletin 131: 66–71. [Google Scholar] [CrossRef]
- Kaufman, James C., Scott Barry Kaufman, and Jonathan A. Plucker. 2013. Contemporary theories of intelligence. In The Oxford Handbook of Cognitive Psychology. Edited by Daniel Reisberg. New York: Oxford University Press, pp. 811–22. [Google Scholar] [CrossRef]
- Knapp, Guido, and Joachim Hartung. 2003. Improved tests for a random effects meta-regression with a single covariate. Statistics in Medicine 22: 2693–710. [Google Scholar] [CrossRef] [PubMed]
- Kramer, Anne-Wil, Anna C. K. Van Duijvenvoorde, Lydia Krabbendam, and Hilde M. Huizenga. 2021. Individual differences in adolescents’ willingness to invest cognitive effort: Relation to need for cognition, motivation and cognitive capacity. Cognitive Development 57: 100978. [Google Scholar] [CrossRef]
- Krumpal, Ivar. 2013. Determinants of social desirability bias in sensitive surveys: A literature review. Quality & Quantity 47: 2025–47. [Google Scholar] [CrossRef]
- Ksiazkiewicz, Aleksander J. 2015. Genetic Links Among Ideology, Cognitive Style, Big Five Personality, and Executive Functions. Ph.D. dissertation, Rice University, Houston, TX, USA. Available online: https://www.proquest.com/dissertations-theses/genetic-links-among-ideology-cognitive-style-big/docview/1993464625/se-2 (accessed on 15 January 2023).
- Langan, Dean, Julian P. T. Higgins, Dan Jackson, Jack Bowden, Areti Angeliki Veroniki, Evangelos Kontopantelis, Wolfgang Viechtbauer, and Mark Simmonds. 2019. A comparison of heterogeneity variance estimators in simulated random-effects meta-analyses. Research Synthesis Methods 10: 83–98. [Google Scholar] [CrossRef]
- Lassiter, G. Daniel, Michael A. Briggs, and R. David Slaw. 1991. Need for cognition, causal processing, and memory for behavior. Personality and Social Psychology Bulletin 17: 694–700. [Google Scholar] [CrossRef]
- Laube, Corinna, Wouter Van Den Bos, and Yana Fandakova. 2020. The relationship between pubertal hormones and brain plasticity: Implications for cognitive training in adolescence. Developmental Cognitive Neuroscience 42: 100753. [Google Scholar] [CrossRef]
- Lavrijsen, Jeroen, Franzis Preckel, and Karine Verschueren. 2023. Seeking, mastering, and enjoying cognitive effort: Scrutinizing the role of need for cognition in academic achievement. Learning and Individual Differences 107: 102363. [Google Scholar] [CrossRef]
- Levin, Irwin P., Mary E. Huneke, and J. D. Jasper. 2000. Information processing at successive stages of decision making: Need for cognition and inclusion-exclusion effects. Organizational Behavior and Human Decision Processes 82: 171–93. [Google Scholar] [CrossRef]
- Li, Shi-jun, Hua Jiang, Hao Yang, Wei Chen, Jin Peng, Ming-wei Sun, Charles Damien Lu, Xi Peng, and Jun Zeng. 2015. The dilemma of heterogeneity tests in meta-analysis: A challenge from a simulation study. PLoS ONE 10: e0127538. [Google Scholar] [CrossRef]
- Liepmann, Dirk, André Beauducel, Bettina Brocke, and Rudolf Amthauer. 2007. Intelligenz-Struktur-Test 2000 R, 2nd ed. Seattle: Hogrefe. [Google Scholar]
- Litman, Jordan A. 2008. Interest and deprivation dimensions of epistemic curiosity. Personality and Individual Differences 44: 1585–95. [Google Scholar] [CrossRef]
- Litman, Jordan A., and Charles D. Spielberger. 2003. Measuring epistemic curiosity and its diversive and specific components. Journal of Personality Assessment 80: 75–86. [Google Scholar] [CrossRef] [PubMed]
- Litman, Jordan A., Tiffany Hutchins, and Ryan Russon. 2005. Epistemic curiosity, feeling-of-knowing, and exploratory behaviour. Cognition & Emotion 19: 559–82. [Google Scholar] [CrossRef]
- Liu, Shijie, Qian Yu, Zaimin Li, Paolo Marcello Cunha, Yanjie Zhang, Zhaowei Kong, Wang Lin, Sitong Chen, and Yujun Cai. 2020. Effects of acute and chronic exercises on executive function in children and adolescents: A systemic review and meta-analysis. Frontiers in Psychology 11: 554915. [Google Scholar] [CrossRef] [PubMed]
- Logan, Gordon D., Russell J. Schachar, and Rosemary Tannock. 1997. Impulsivity and inhibitory control. Psychological Science 8: 60–64. [Google Scholar] [CrossRef]
- Luo, Xiaohui, Yan Ge, and Weina Qu. 2023. The association between the Big Five personality traits and driving behaviors: A systematic review and meta-analysis. Accident Analysis & Prevention 183: 106968. [Google Scholar] [CrossRef]
- Mashburn, Cody A., Mariel K. Barnett, and Randall W. Engle. 2024. Processing speed and executive attention as causes of intelligence. Psychological Review 131: 664–94. [Google Scholar] [CrossRef]
- McGrew, Kevin S. 2009. CHC theory and the human cognitive abilities project: Standing on the shoulders of the giants of psychometric intelligence research. Intelligence 37: 1–10. [Google Scholar] [CrossRef]
- Miyake, Akira, and Naomi P. Friedman. 2012. The nature and organization of individual differences in executive functions: Four general conclusions. Current Directions in Psychological Science 21: 8–14. [Google Scholar] [CrossRef] [PubMed]
- Miyake, Akira, Naomi P. Friedman, Michael J. Emerson, Alexander H. Witzki, Amy Howerter, and Tor D. Wager. 2000. The unity and diversity of executive functions and their contributions to complex “frontal lobe” tasks: A latent variable analysis. Cognitive Psychology 41: 49–100. [Google Scholar] [CrossRef]
- Monsell, Stephen. 2003. Task switching. Trends in Cognitive Sciences 7: 134–40. [Google Scholar] [CrossRef]
- Moriguchi, Yusuke. 2014. The early development of executive function and its relation to social interaction: A brief review. Frontiers in Psychology 5: 388. [Google Scholar] [CrossRef] [PubMed]
- Mozuraitis, Mindaugas, Craig G. Chambers, and Meredyth Daneman. 2016. Verbal ability, argument order, and attitude formation. Frontiers in Psychology 7: 1374. [Google Scholar] [CrossRef]
- Mussel, Patrick. 2010. Epistemic curiosity and related constructs: Lacking evidence of discriminant validity. Personality and Individual Differences 49: 506–10. [Google Scholar] [CrossRef]
- Mussel, Patrick. 2013. Intellect: A theoretical framework for personality traits related to intellectual achievements. Journal of Personality and Social Psychology 104: 885–906. [Google Scholar] [CrossRef] [PubMed]
- Mussel, Patrick, and Maik Spengler. 2015. Investigating intellect from a trait activation perspective: Identification of situational moderators for the correlation with work-related criteria. Journal of Research in Personality 55: 51–60. [Google Scholar] [CrossRef]
- Mussel, Patrick, Natalie Ulrich, John J. B. Allen, Roman Osinsky, and Johannes Hewig. 2016. Patterns of theta oscillation reflect the neural basis of individual differences in epistemic motivation. Scientific Reports 6: 29245. [Google Scholar] [CrossRef]
- Nee, Derek Evan, and John Jonides. 2008. Dissociable interference-control processes in perception and memory. Psychological Science 19: 490–500. [Google Scholar] [CrossRef] [PubMed]
- Nudelman, Gabriel, and Kathleen Otto. 2020. The development of a new generic risk-of-bias measure for systematic reviews of surveys. Methodology 16: 278–98. [Google Scholar] [CrossRef]
- Oberauer, Klaus, Heinz-Martin Süß, Ralf Schulze, Oliver Wilhelm, and Werner W. Wittmann. 2000. Working memory capacity—Facets of a cognitive ability construct. Personality and Individual Differences 29: 1017–45. [Google Scholar] [CrossRef]
- Page, Matthew J., Joanne E. McKenzie, Patrick M. Bossuyt, Isabelle Boutron, Tammy C. Hoffmann, Cynthia D. Mulrow, Larissa Shamseer, Jennifer M. Tetzlaff, Elie A. Akl, Sue E. Brennan, and et al. 2021. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 372: n71. [Google Scholar] [CrossRef]
- Parry, Robert, and Ian Stuart-Hamilton. 2010. Animism begins at forty: Evidence that animism and other naive beliefs are established before the onset of old age. Educational Gerontology 36: 1043–50. [Google Scholar] [CrossRef]
- Peterson, Robert A., and Steven P. Brown. 2005. On the use of beta coefficients in meta-analysis. Journal of Applied Psychology 90: 175–81. [Google Scholar] [CrossRef]
- Petty, Richard E., and John T. Cacioppo. 1986. The Elaboration Likelihood Model of Persuasion. Advances in Experimental Social Psychology 19: 123–205. [Google Scholar] [CrossRef]
- Posit Team. 2024. RStudio: Integrated Development Environment for R, Version 2024.4.2.764. [Computer software]. Boston: Posit Software. Available online: http://www.posit.co/ (accessed on 21 December 2024).
- Powell, Christopher, and Ted Nettelbeck. 2014. Intellectual curiosity may not incrementally predict academic success. Personality and Individual Differences 64: 7–11. [Google Scholar] [CrossRef]
- Pustejovsky, James E. 2020. Weighting in Multivariate Meta-Analysis. June 9. James E. Pustejovsky. Available online: https://jepusto.com/posts/weighting-in-multivariate-meta-analysis/ (accessed on 12 November 2024).
- Pustejovsky, James E. 2021a. Synthesis of Dependent Effect Sizes: Versatile Models Through Clubsandwich and Metafor. Paper presented at ESMARConf2021, Online, January 18–22. [Google Scholar] [CrossRef]
- Pustejovsky, James E. 2021b. Synthesis of Dependent Effect Sizes: Robust Variance Estimation with Clubsandwich. Paper presented at OSLO R User Group Meetup, Oslo, Norway (virtual), February 16; Available online: https://jepusto.com/files/Oslo-RUG-RVE-with-clubSandwich.pdf (accessed on 12 November 2024).
- Pustejovsky, James E. 2024. ClubSandwich: Cluster-Robust (Sandwich) Variance Estimators with Small-Sample Corrections, Version 0.5.11. [R package clubSandwich]. Available online: https://cran.r-project.org/package=clubSandwich (accessed on 4 December 2024).
- Pustejovsky, James E, and Elizabeth Tipton. 2022. Meta-analysis with robust variance estimation: Expanding the range of working models. Prevention Science 23: 425–38. [Google Scholar] [CrossRef]
- Raven, John. 2000. Manual for Raven’s Progressive Matrices and Vocabulary Scales. Research Supplement no. 3 (2nd ed.): A Compendium of International and North American Normative and Validity Studies Together with a Review of the Use of the RPM in Neuropsychological Assessment by Court, Drebing, and Hughes. London: Oxford Psychologists Press. [Google Scholar]
- R Core Team. 2024. R: A Language and Environment for Statistical Computing, Version 4.4.1. [Computer software]. Vienna: R Foundation for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 4 December 2024).
- Reinhard, Marc-André, and Oliver Dickhäuser. 2009. Need for cognition, task difficulty, and the formation of performance expectancies. Journal of Personality and Social Psychology 96: 1062–76. [Google Scholar] [CrossRef]
- Rey-Mermet, Alodie, Miriam Gade, and Klaus Oberauer. 2018. Should we stop thinking about inhibition? Searching for individual and age differences in inhibition ability. Journal of Experimental Psychology: Learning, Memory, and Cognition 44: 501–26. [Google Scholar] [CrossRef]
- Rodríguez-Nieto, Geraldine, Caroline Seer, Justina Sidlauskaite, Lore Vleugels, Anke Van Roy, Robert Hardwick, and Stephan Swinnen. 2022. Inhibition, shifting and updating: Inter and intra-domain commonalities and differences from an executive functions activation likelihood estimation meta-analysis. NeuroImage 264: 119665. [Google Scholar] [CrossRef]
- Rogers, Robert D., and Stephen Monsell. 1995. The costs of a predictable switch between simple cognitive tasks. Journal of Experimental Psychology: General 124: 207–31. [Google Scholar] [CrossRef]
- Rolfhus, Eric L., and Phillip L. Ackerman. 1999. Assessing individual differences in knowledge: Knowledge, intelligence, and related traits. Journal of Educational Psychology 91: 511–26. [Google Scholar] [CrossRef]
- Ruch, Floyd L., and William W. Ruch. 1980. Technical Report for the Employee Aptitude Survey. Los Angeles: Psychological Services. [Google Scholar]
- Rudolph, Julia, Samuel Greiff, Anja Strobel, and Franzis Preckel. 2018. Understanding the link between need for cognition and complex problem solving. Contemporary Educational Psychology 55: 53–62. [Google Scholar] [CrossRef]
- Ruhr, Torben W. 2024. Lernagilität als Eignungsdiagnostischer Indikator. Ph.D. dissertation, Ruhr Universität Bochum, Bochum, Germany. Available online: https://hss-opus.ub.ruhr-uni-bochum.de/opus4/frontdoor/index/index/docId/10840 (accessed on 10 September 2024).
- Salthouse, Timothy A. 1990. Working memory as a processing resource in cognitive aging. Developmental Review 10: 101–24. [Google Scholar] [CrossRef]
- Salthouse, Timothy A., Diane E. Berish, and James D. Miles. 2002. The role of cognitive stimulation on the relations between age and cognitive functioning. Psychology and Aging 17: 548–57. [Google Scholar] [CrossRef]
- Salthouse, Timothy A., Jeffrey E. Pink, and Elliot M. Tucker-Drob. 2008. Contextual analysis of fluid intelligence. Intelligence 36: 464–86. [Google Scholar] [CrossRef] [PubMed]
- Sandra, Dasha A., and A. Ross Otto. 2018. Cognitive capacity limitations and Need for Cognition differentially predict reward-induced cognitive effort expenditure. Cognition 172: 101–6. [Google Scholar] [CrossRef] [PubMed]
- Santarnecchi, Emiliano, Davide Momi, Lucia Mencarelli, Franziska Plessow, Sadhvi Saxena, Simone Rossi, Alessandro Rossi, Santosh Mathan, and Alvaro Pascual-Leone. 2021. Overlapping and dissociable brain activations for fluid intelligence and executive functions. Cognitive, Affective, & Behavioral Neuroscience 21: 327–46. [Google Scholar] [CrossRef]
- Schäfer, Jonas, Timo Reuter, Miriam Leuchter, and Julia Karbach. 2024. Executive functions and problem-solving—The contribution of inhibition, working memory, and cognitive flexibility to science problem-solving performance in elementary school students. Journal of Experimental Child Psychology 244: 105962. [Google Scholar] [CrossRef] [PubMed]
- Scherrer, Vsevolod, Moritz Breit, and Franzis Preckel. 2024. Crystallized intelligence, fluid intelligence, and need for cognition: Their longitudinal relations in adolescence. Journal of Intelligence 12: 104. [Google Scholar] [CrossRef]
- Schwarzer, Guido, James R. Carpenter, and Gerta Rücker. 2015. Meta-Analysis with R. Berlin and Heidelberg: Springer. [Google Scholar]
- Shi, Linyu, and Lifeng Lin. 2019. The trim-and-fill method for publication bias: Practical guidelines and recommendations based on a large database of meta-analyses. Medicine 98: e15987. [Google Scholar] [CrossRef]
- Simonsohn, Uri, Joseph P. Simmons, and Leif D. Nelson. 2015. Better P-curves: Making P-curve analysis more robust to errors, fraud, and ambitious P-hacking, a reply to Ulrich and Miller. Journal of Experimental Psychology: General 144: 1146–52. [Google Scholar] [CrossRef]
- Simonsohn, Uri, Leif D. Nelson, and Joseph P. Simmons. 2014. P-curve: A key to the file-drawer. Journal of Experimental Psychology: General 143: 534–47. [Google Scholar] [CrossRef]
- Soubelet, Andrea, and Timothy A. Salthouse. 2010. The role of activity engagement in the relations between Openness/Intellect and cognition. Personality and Individual Differences 49: 896–901. [Google Scholar] [CrossRef]
- Spearman, Charles. 1904. ‘General intelligence,’ objectively determined and measured. The American Journal of Psychology 15: 201–93. [Google Scholar] [CrossRef]
- Spearman, Charles. 1927. The Abilities of Man. Basingstoke: Macmillan. [Google Scholar]
- Spiegel, Jamie A., J. Marc Goodrich, Brittany M. Morris, Colleen M. Osborne, and Christopher J. Lonigan. 2021. Relations between executive functions and academic outcomes in elementary school children: A meta-analysis. Psychological Bulletin 147: 329–51. [Google Scholar] [CrossRef]
- Stanek, Kevin C., and Deniz S. Ones. 2023. Meta-analytic relations between personality and cognitive ability. Psychological and Cognitive Sciences 120: e2212794120. [Google Scholar] [CrossRef] [PubMed]
- Stanley, T. D. 2017. Limitations of PET-PEESE and other meta-analysis methods. Social Psychological and Personality Science 8: 581–91. [Google Scholar] [CrossRef]
- Stanley, T. D., and Hristos Doucouliagos. 2014. Meta-regression approximations to reduce publication selection bias. Research Synthesis Methods 5: 60–78. [Google Scholar] [CrossRef]
- Stern, Chadly, and Jordan Axt. 2021. Ideological differences in race and gender stereotyping. Social Cognition 39: 259–94. [Google Scholar] [CrossRef]
- Sternberg, Robert J. 1997. Successful Intelligence. New York: Plume. [Google Scholar]
- Sternberg, Robert J. 2003. Contemporary theories of intelligence. In Handbook of Psychology: Educational Psychology. Edited by William M. Reynolds and Gloria E. Miller. Hoboken: John Wiley and Sons, vol. 7, pp. 23–45. [Google Scholar] [CrossRef]
- Stuart-Hamilton, Ian, and Lorraine McDonald. 2001. Do we need intelligence? Some reflections on the perceived importance of “g”. Educational Gerontology 27: 399–407. [Google Scholar] [CrossRef]
- Svedholm, Annika M., and Marjaana Lindeman. 2013. The separate roles of the reflective mind and involuntary inhibitory control in gatekeeping paranormal beliefs and the underlying intuitive confusions. British Journal of Psychology 104: 303–19. [Google Scholar] [CrossRef]
- Tanner-Smith, Emily E., Elizabeth Tipton, and Joshua R. Polanin. 2016. Handling complex meta-analytic data structures using robust variance estimates: A tutorial in R. Journal of Developmental and Life-Course Criminology 2: 85–112. [Google Scholar] [CrossRef]
- Terrin, Norma, Christopher H. Schmid, Joseph Lau, and Ingram Olkin. 2003. Adjusting for publication bias in the presence of heterogeneity. Statistics in Medicine 22: 2113–26. [Google Scholar] [CrossRef] [PubMed]
- Thurstone, Louis L. 1938. Primary Mental Abilities. Chicago: University of Chicago Press. [Google Scholar]
- Tidwell, Pamela S., Cyril J. Sadowski, and Lia M. Pate. 2000. Relationships between need for cognition, knowledge, and verbal ability. The Journal of Psychology 134: 634–44. [Google Scholar] [CrossRef] [PubMed]
- Vandenberg, Steven G., and Allan R. Kuse. 1978. Mental rotations, a group test of three-dimensional spatial visualization. Perceptual and Motor Skills 47: 599–604. [Google Scholar] [CrossRef]
- Vermeylen, Luc, Senne Braem, and Wim Notebaert. 2019. The affective twitches of task switches: Task switch cues are evaluated as negative. Cognition 183: 124–30. [Google Scholar] [CrossRef]
- Veroniki, Areti Angeliki, Dan Jackson, Wolfgang Viechtbauer, Ralf Bender, Jack Bowden, Guido Knapp, Oliver Kuss, Julian P. T. Higgins, Dean Langan, and Georgia Salanti. 2016. Methods to estimate the between-study variance and its uncertainty in meta-analysis. Research Synthesis Methods 7: 55–79. [Google Scholar] [CrossRef]
- Viechtbauer, Wolfgang. 2005. Bias and efficiency of meta-analytic variance estimators in the random-effects model. Journal of Educational and Behavioral Statistics 30: 261–93. [Google Scholar] [CrossRef]
- Viechtbauer, Wolfgang. 2010. Conducting meta-analyses in R with the metafor package. Journal of Statistical Software 36: 1–48. [Google Scholar] [CrossRef]
- Viechtbauer, Wolfgang. 2024. Weights in Models Fitted with the rma.mv() Function. The Metafor Package. Available online: https://www.metafor-project.org/doku.php/tips:weights_in_rma.mv_models (accessed on 13 November 2024).
- Viechtbauer, Wolfgang, and Mike W. -L. Cheung. 2010. Outlier and influence diagnostics for meta-analysis. Research Synthesis Methods 1: 112–25. [Google Scholar] [CrossRef]
- Von Stumm, Sophie. 2013. Investment traits and intelligence in adulthood. Journal of Individual Differences 34: 82–89. [Google Scholar] [CrossRef]
- Von Stumm, Sophie, and Phillip L. Ackerman. 2013. Investment and intellect: A review and meta-analysis. Psychological Bulletin 139: 841–69. [Google Scholar] [CrossRef] [PubMed]
- Walker, David A. 2003. JMASM9: Converting Kendall’s tau for correlational or meta-analytic analyses. Journal of Modern Applied Statistical Methods 2: 525–30. [Google Scholar] [CrossRef]
- Wechsler, David. 1997. WAIS-III/WMS-III Technical Manual. San Antonio: The Psychological Corporation. [Google Scholar]
- Westbrook, Andrew, Daria Kester, and Todd S. Braver. 2013. What is the subjective cost of cognitive effort? Load, trait, and aging effects revealed by economic preference. PLoS ONE 8: e68210. [Google Scholar] [CrossRef] [PubMed]
- Wittmann, Werner W., and Heinz-Martin Süß. 1999. Investigating the paths between working memory, intelligence, knowledge, and complex problem-solving performances via Brunswik symmetry. In Learning and Individual Differences: Process, Trait, and Content Determinants. Edited by Phillip Lawrence Ackerman, Patrick C. Kyllonen and Richard D. Roberts. Washington, DC: American Psychological Association, pp. 77–108. [Google Scholar] [CrossRef]
- Wolff, Max, Klaus-Martin Krönke, John Venz, Anja Kräplin, Gerhard Bühringer, Michael N. Smolka, and Thomas Goschke. 2016. Action versus state orientation moderates the impact of executive functioning on real-life self-control. Journal of Experimental Psychology: General 145: 1635–53. [Google Scholar] [CrossRef]
- Wonderlic Inc. 1999. Wonderlic’s Personnel Test Manual and Scoring Guide. Vernon Hills: Wonderlic. [Google Scholar]
- Woo, Sang Eun, Peter D. Harms, and Nathan R. Kuncel. 2007. Integrating personality and intelligence: Typical intellectual engagement and need for cognition. Personality and Individual Differences 43: 1635–39. [Google Scholar] [CrossRef]
- Zhang, Qian, and Qi Wang. 2024. Correcting for measurement error under meta-analysis of z-transformed correlations. British Journal of Mathematical and Statistical Psychology 77: 261–88. [Google Scholar] [CrossRef]
- Zhang, Ying, Eric Klopp, Heike Dietrich, Roland Brünken, Ulrike-Marie Krause, Birgit Spinath, Robin Stark, and Frank M. Spinath. 2018. Reexamining the factorial validity of the 16-Item scale measuring Need for Cognition. European Journal of Psychological Assessment 36: 212–15. [Google Scholar] [CrossRef]
- Ziegler, Matthias, Erik Danay, Moritz Heene, Jens Asendorpf, and Markus Bühner. 2012. Openness, fluid intelligence, and crystallized intelligence: Toward an integrative model. Journal of Research in Personality 46: 173–83. [Google Scholar] [CrossRef]

| Cognitive Function | k | s | t | e | N | r | 95% CI | p | τlevel 5 | τlevel 4 | τlevel 3 | τlevel 2 | I2level 5 | I2level 4 | I2level 3 | I2level 2 | Q(df) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intelligence | ||||||||||||||||||
| Gf | 61 | 69 | 76 | 76 | 25,367 | 0.18 | [0.15, 0.20] | <.001 | 0.000 | 0.094 | 0.000 | 0.00 | 72.89 | 0.00 | Q(75) = 232.81 *** | |||
| Gc | 51 | 56 | 65 | 65 | 14,651 | 0.26 | [0.23, 0.29] | <.001 | 0.086 | 0.000 | 0.030 | 58.19 | 0.00 | 6.70 | Q(64) = 179.71 *** | |||
| General intelligence | 24 | 24 | 24 | 24 | 8479 | 0.23 | [0.18, 0.28] | <.001 | 0.108 *** | 78.10 | Q(23) = 78.99 *** | |||||||
| Executive functions | ||||||||||||||||||
| WM | 36 | 41 | 45 | 50 | 7005 | 0.14 | [0.10, 0.18] | <.001 | 0.058 | 0.078 | 0.000 | 0.000 | 19.83 | 36.13 | 0.00 | 0.00 | Q(49) = 93.16 *** | |
| Inhibition | 12 | 13 | 19 | 21 | 2895 | 0.04 | [−0.01, 0.09] | .077 | 0.000 | 0.018 | 0.040 | 0.000 | 0.00 | 3.56 | 16.91 | 0.00 | Q(20) = 27.92 | |
| Shifting | 8 | 9 | 10 | 13 | 1727 | 0.01 | [−0.05, 0.07] | .642 | 0.000 | 0.019 | 0.000 | 0.000 | 0.00 | 4.42 | 0.00 | 0.00 | Q(12) = 9.95 | |
| Moderator | Comparison | r | 95% CI | p | b1 | β1 | 95% CI | p | F(df1, df2) | Q(df) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Publication year | 0.16 | [0.04, 0.27] | .010 | 0.001 | 0.01 | [−0.03, 0.04] | .699 | Q(74) = 232.24 *** | |||
| Publication | Q(74) = 231.81 *** | ||||||||||
| Journal | Dissertation | 0.17 | [0.14, 0.20] | <.001 | F(1, 8.58) = 0.73 | ||||||
| Dissertation | 0.21 | [0.10, 0.32] | .003 | ||||||||
| Mean age | 0.14 | [0.08, 0.19] | <.001 | 0.002 | 0.02 | [−0.01, 0.06] | .158 | Q(60) = 192.95 *** | |||
| Red. model | 0.17 | [0.14, 0.20] | <.001 | Q(61) = 199.64 *** | |||||||
| % female | 0.16 | [0.05, 0.27] | .009 | 0.000 | 0.00 | [−0.03, 0.03] | .919 | Q(69) = 208.73 *** | |||
| Red. model | 0.17 | [0.14, 0.20] | <.001 | Q(70) = 210.80 *** | |||||||
| Risk of bias | 0.11 | [0.02, 0.18] | .011 | 0.027 | 0.03 | [0.00, 0.06] | .070 | Q(74) = 232.11 *** | |||
| College | Q(74) = 215.20 *** | ||||||||||
| No | Yes | 0.19 | [0.14, 0.24] | <.001 | F(1, 47.10) = 0.97 | ||||||
| Yes | 0.16 | [0.13; .20] | <.001 | ||||||||
| Controlled | Q(69) = 194.85 *** | ||||||||||
| No | Yes | 0.18 | [0.12, 0.24] | <.001 | F(1, 24.70) = 0.03 | ||||||
| Yes | 0.17 | [0.14, 0.21] | <.001 | ||||||||
| Red. model | 0.17 | [0.15, 0.20] | <.001 | Q(70) = 198.02 *** | |||||||
| Simultaneous | Q(70) = 194.68 *** | ||||||||||
| No | Yes | 0.17 | [0.09, 0.25] | <.001 | F(1, 21.50) = 0.05 | ||||||
| Yes | 0.18 | [0.15, 0.21] | <.001 | ||||||||
| Red. model | 0.17 | [0.14, 0.20] | <.001 | Q(71) = 196.29 *** | |||||||
| Aspect | Q(72) = 214.35 *** | ||||||||||
| Inductive | 0.19 | [0.15, 0.23] | <.001 | ||||||||
| Deductive | F(1, 6.57) = 5.39 | ||||||||||
| Spatial | F(1, 10.72) = 0.80 | ||||||||||
| Mixed | F(1, 18.88) = 0.00 | ||||||||||
| Deductive | 0.10 | [0.02, 0.19] | .024 | ||||||||
| Spatial | F(1, 9.42) = 1.82 | ||||||||||
| Mixed | F(1, 9.77) = 3.63 | ||||||||||
| Spatial | 0.16 | [0.10, 0.23] | <.001 | ||||||||
| Mixed | F(1, 18.70) = 0.45 | ||||||||||
| Mixed | 0.19 | [0.12, 0.26] | <.001 | ||||||||
| Content | Q(73) = 208.74 *** | ||||||||||
| Figural | 0.19 | [0.15, 0.22] | <.001 | ||||||||
| Verbal | F(1, 4.65) = 11.15 | ||||||||||
| Mixed | F(1, 10.02) = 0.00 | ||||||||||
| Verbal | 0.11 | [0.05, 0.16] | .005 | ||||||||
| Mixed | F(1, 4.29) = 8.96 | ||||||||||
| Mixed | 0.18 | [0.13, 0.24] | <.001 | ||||||||
| NFC/TIE scale | Q(74) = 232.68 *** | ||||||||||
| NFC | TIE | 0.19 | [0.16, 0.22] | <.001 | F(1, 12.10) = 5.04 * | ||||||
| TIE | 0.12 | [0.05, 0.18] | .003 | ||||||||
| Moderator | Comparison | r | 95% CI | p | b1 | β1 | 95% CI | p | F(df1, df2) | Q(df) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Publication year | 0.38 | [0.28, 0.48] | <.001 | −0.006 | −0.04 | [−0.08, −0.01] | .010 | Q(63) = 153.39 *** | |||
| Mean age | 0.30 | [0.24, 0.35] | <.001 | −0.002 | −0.03 | [−0.07, 0.01] | .113 | Q(55) = 161.84 *** | |||
| Red. model | 0.26 | [0.22, 0.30] | <.001 | Q(56) = 164.87 *** | |||||||
| % female | 0.27 | [0.10, 0.43] | .004 | 0.000 | 0.00 | [−0.04, 0.04] | .860 | Q(59) = 175.57 *** | |||
| Red. model | 0.26 | [0.23, 0.29] | <.001 | Q(60) = 175.58 *** | |||||||
| Risk of bias | 0.29 | [0.18, 0.39] | <.001 | −0.010 | −0.01 | [−0.05, 0.03] | .557 | Q(63) = 174.00 *** | |||
| College | Q(63) = 178.64 *** | ||||||||||
| No | Yes | 0.25 | [0.20, 0.30] | <.001 | F(1, 24.90) = 0.29 | ||||||
| Yes | 0.27 | [0.23, 0.31] | <.001 | ||||||||
| Controlled | Q(63) = 178.61 *** | ||||||||||
| No | Yes | 0.27 | [0.19, 0.34] | <.001 | F(1, 19.80) = 0.13 | ||||||
| Yes | 0.26 | [0.22, 0.30] | <.001 | ||||||||
| Red. model | 0.26 | [0.23, 0.30] | <.001 | Q(64) = 179.71 *** | |||||||
| Simultaneous | Q(57) = 161.57 *** | ||||||||||
| No | Yes | 0.24 | [0.16, 0.30] | <.001 | F(1, 24.20) = 0.45 | ||||||
| Yes | 0.26 | [0.22, 0.30] | <.001 | ||||||||
| Red. model | 0.25 | [0.22, 0.29] | <.001 | Q(58) = 166.35 *** | |||||||
| Aspect | Q(61) = 170.75 *** | ||||||||||
| Gen. know. | 0.29 | [0.23, 0.35] | <.001 | ||||||||
| Verb. know. | F(1, 18.70) = 1.46 | ||||||||||
| Verb. know. + | F(1, 8.54) = 1.10 | ||||||||||
| reasoning | |||||||||||
| Mixed | F(1, 10.50) = 0.67 | ||||||||||
| Verb. know. | 0.25 | [0.21, 0.29] | <.001 | ||||||||
| Verb. know. + | F(1, 7.57) = 0.05 | ||||||||||
| reasoning | |||||||||||
| Mixed | F(1, 11.92) = 0.10 | ||||||||||
| Verb. know. | 0.24 | [0.14, 0.34] | .001 | ||||||||
| +reasoning | Mixed | F(1, 9.89) = 0.17 | |||||||||
| Mixed | 0.26 | [0.20, 0.34] | <.001 | ||||||||
| NFC/TIE scale | Q(63) = 144.89 *** | ||||||||||
| NFC | TIE | 0.24 | [0.20, 0.27] | <.001 | F(1, 13.10) = 10.70 ** | ||||||
| TIE | 0.35 | [0.28, 0.42] | <.001 | ||||||||
| Moderator | Comparison | r | 95% CI | p | b1 | β1 | 95% CI | p | F(df1, df2) | Q(df) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Publication year | 0.30 | [0.12, 0.48] | .002 | −0.003 | −0.03 | [−0.08, 0.03] | .390 | Q(22) = 75.48 *** | |||
| Mean age | 0.13 | [−0.10, 0.35] | .270 | 0.006 | 0.03 | [−0.03, 0.09] | .323 | Q(19) = 71.68 *** | |||
| Red. model | 0.23 | [0.17, 0.30] | <.001 | Q(20) = 78.32 *** | |||||||
| % female | 0.29 | [−0.04, 0.61] | .080 | −0.001 | −0.01 | [−0.08, 0.06] | .758 | Q(17) = 77.26 *** | |||
| Red. model | 0.24 | [0.17, 0.31] | <.001 | Q(18) = 77.38 *** | |||||||
| Risk of bias | 0.24 | [0.11, 0.36] | .001 | −0.002 | 0.00 | [−0.06, 0.06] | .941 | Q(22) = 78.67 *** | |||
| College | Q(22) = 76.02 *** | ||||||||||
| No | Yes | 0.21 | [0.13, 0.29] | <.001 | F(1, 22) = 0.43 | ||||||
| Yes | 0.25 | [0.17, 0.32] | <.001 | ||||||||
| Controlled | Q(20) = 78.75 *** | ||||||||||
| No | Yes | 0.21 | [0.06, 0.34] | .006 | F(1, 20) = 0.24 | ||||||
| Yes | 0.24 | [0.17, 0.31] | <.001 | ||||||||
| Red. model | 0.24 | [0.18, 0.29] | <.001 | Q(21) = 78.78 *** | |||||||
| Simultaneous | Q(20) = 66.85 *** | ||||||||||
| No | Yes | 0.24 | [0.14, 0.34] | <.001 | F(1, 20) = 0.00 | ||||||
| Yes | 0.24 | [0.16, 0.32] | <.001 | ||||||||
| Red. model | 0.24 | [0.18, 0.30] | <.001 | Q(21) = 67.77 *** | |||||||
| NFC/TIE scale | Q(22) = 76.30 *** | ||||||||||
| NFC | TIE | 0.22 | [0.16, 0.29] | <.001 | F(1, 22) = 0.32 | ||||||
| TIE | 0.26 | [0.15, 0.36] | <.001 | ||||||||
| Moderator | Comparison | r | 95% CI | p | b1 | β1 | 95% CI | p | F(df1, df2) | Q(df) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Publication year | 0.30 | [0.09, 0.51] | .015 | −0.007 | −0.05 | [−0.10, 0.01] | .099 | Q(48) = 82.75 *** | |||
| Publication | Q(48) = 90.90 *** | ||||||||||
| Journal | Dissertation | 0.13 | [0.08, 0.18] | <.001 | F(1, 5.29) = 1.65 | ||||||
| Dissertation | 0.19 | [0.07, 0.31] | .012 | ||||||||
| Mean age | 0.11 | [0.02, 0.20] | .016 | 0.001 | 0.01 | [−0.08, 0.10] | .752 | Q(39) = 81.22 *** | |||
| Red. model | 0.12 | [0.07, 0.18] | <.001 | Q(40) = 81.33 *** | |||||||
| % female | 0.04 | [−0.16, 0.24] | .668 | 0.002 | 0.03 | [−0.03, 0.09] | .363 | Q(41) = 81.99 *** | |||
| Red. model | 0.13 | [0.08, 0.18] | <.001 | Q(42) = 84.10 *** | |||||||
| Risk of bias | 0.23 | [0.06, 0.38] | .011 | −0.028 | −0.03 | [−0.06, 0.01] | .175 | Q(48) = 89.65 *** | |||
| College | Q(48) = 92.73 *** | ||||||||||
| No | Yes | 0.14 | [0.07, 0.21] | <.001 | F(1, 29.30) = 0.01 | ||||||
| Yes | 0.14 | [0.07, 0.20] | <.001 | ||||||||
| Controlled | Q(46) = 91.71 *** | ||||||||||
| No | Yes | 0.12 | [0.00, 0.24] | .056 | F(1, 6.49) = 0.31 | ||||||
| Yes | 0.15 | [0.10, 0.20] | <.001 | ||||||||
| Red. model | 0.14 | [0.10, 0.19] | <.001 | Q(47) = 91.71 *** | |||||||
| Simultaneous | Q(39) = 83.80 *** | ||||||||||
| No | Yes | 0.10 | [−0.10, 0.30] | .217 | F(1, 4.48) = 0.46 | ||||||
| Yes | 0.15 | [0.10, 0.20] | <.001 | ||||||||
| Red. model | 0.14 | [0.09, 0.19] | <.001 | Q(40) = 85.37 *** | |||||||
| Function | Q(48) = 92.90 *** | ||||||||||
| Updating | Capacity | 0.08 | [−0.03, 0.18] | .111 | F(1, 6.81) = 2.91 | ||||||
| Capacity | 0.15 | [0.10, 0.20] | <.001 | ||||||||
| Moderator | Comparison | r | 95% CI | p | b1 | β1 | 95% CI | p | F(df1, df2) | Q(df) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Publication year | 0.05 | [−0.11, 0.21] | .363 | −0.001 | 0.00 | [−0.06, 0.05] | .795 | Q(19) = 27.87 | |||
| Mean age | 0.01 | [−0.06, 0.08] | .640 | 0.005 | 0.02 | [−0.10, 0.14] | .596 | Q(17) = 22.66 | |||
| Red. model | 0.03 | [−0.03, 0.09] | .208 | Q(18) = 23.03 | |||||||
| % female | −0.17 | [−0.65, 0.31] | .422 | 0.003 | 0.03 | [−0.05, 0.12] | .360 | Q(17) = 22.60 | |||
| Red. model | 0.03 | [−0.03, 0.09] | .208 | Q(18) = 23.03 | |||||||
| Risk of bias | 0.10 | [−0.11, 0.31] | .218 | −0.021 | −0.02 | [−0.10, 0.06] | .428 | Q(19) = 26.60 | |||
| College | Q(19) = 27.85 | ||||||||||
| No | Yes | 0.06 | [−0.08, 0.20] | .347 | F(1, 7.67) = 0.23 | ||||||
| Yes | 0.03 | [−0.04, 0.10] | .217 | ||||||||
| Simultaneous | Q(17) = 26.03 | ||||||||||
| No | Yes | 0.03 | [−0.28, 0.32] | .614 | F(1, 2.57) = 0.33 | ||||||
| Yes | 0.06 | [−0.01, 0.13] | .098 | ||||||||
| Red. model | 0.05 | [−0.01, 0.11] | .087 | Q(18) = 26.03 | |||||||
| Function | Q(18) = 23.71 | ||||||||||
| Interf. cont. | Resp. inhib. | 0.07 | [0.00, 0.15] | .054 | F(1, 3.36) = 5.13 | ||||||
| Resp. inhib. | 0.01 | [−0.04, 0.06] | .465 | ||||||||
| Red. model | 0.05 | [0.00, 0.10] | .041 | Q(19) = 25.72 | |||||||
| Moderator | Comparison | r | 95% CI | p | b1 | β1 | 95% CI | p | F(df1, df2) | Q(df) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Publication year | 0.06 | [−0.14, 0.25] | .228 | −0.007 | −0.02 | [−0.10, 0.05] | .325 | Q(11) = 8.59 | |||
| Mean age | −0.06 | [−0.12, 0.00] | .059 | 0.005 | 0.05 | [−0.01, 0.10] | .068 | Q(10) = 5.00 | |||
| Red. model | 0.00 | [−0.07, 0.07] | .957 | Q(11) = 9.30 | |||||||
| % female | 0.04 | [−0.22, 0.30] | .671 | −0.001 | −0.01 | [−0.07, 0.04] | .424 | Q(9) = 6.76 | |||
| Red. model | −0.02 | [−0.09, 0.05] | .473 | Q(10) = 6.96 | |||||||
| Risk of bias | −0.03 | [−0.24, 0.18] | .614 | 0.013 | 0.01 | [−0.05, 0.08] | .482 | Q(11) = 9.66 | |||
| College | Q(11) = 7.67 | ||||||||||
| No | Yes | 0.06 | [−0.04, 0.16] | .138 | F(1, 4.67) = 3.28 | ||||||
| Yes | −0.01 | [−0.12, 0.09] | .668 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schweitzer, F.M.; Lindenberg, N.M.; Fleischhauer, M.; Enge, S. The Relationship of Need for Cognition and Typical Intellectual Engagement with Intelligence and Executive Functions: A Multi-Level Meta-Analysis. J. Intell. 2025, 13, 142. https://doi.org/10.3390/jintelligence13110142
Schweitzer FM, Lindenberg NM, Fleischhauer M, Enge S. The Relationship of Need for Cognition and Typical Intellectual Engagement with Intelligence and Executive Functions: A Multi-Level Meta-Analysis. Journal of Intelligence. 2025; 13(11):142. https://doi.org/10.3390/jintelligence13110142
Chicago/Turabian StyleSchweitzer, Felix M., Nele M. Lindenberg, Monika Fleischhauer, and Sören Enge. 2025. "The Relationship of Need for Cognition and Typical Intellectual Engagement with Intelligence and Executive Functions: A Multi-Level Meta-Analysis" Journal of Intelligence 13, no. 11: 142. https://doi.org/10.3390/jintelligence13110142
APA StyleSchweitzer, F. M., Lindenberg, N. M., Fleischhauer, M., & Enge, S. (2025). The Relationship of Need for Cognition and Typical Intellectual Engagement with Intelligence and Executive Functions: A Multi-Level Meta-Analysis. Journal of Intelligence, 13(11), 142. https://doi.org/10.3390/jintelligence13110142




