Factorial Validity of the German KABC-II at Ages 7 to 12 in a Clinical Sample: Four Factors Fit Better than Five
Abstract
1. Introduction
1.1. Theoretical Background and Structure of the KABC-II
1.2. Confirmatory Factor Analyses of the CHC Test Structure at Ages 7 to 12
1.3. Purpose
2. Materials and Methods
2.1. Participants
2.2. Instrument
2.3. Statistical Analyses and Models
- Model 1: A first-order model with all core subtests loading on a single-factor (g-factor). To achieve identifiability, one subtest loading was fixed to one.
- Model 2: A second-order (three-stratum) model reflecting the standard test structure with one second-order factor and five first-order factors. One loading of each factor was fixed to one. Model 2 was used as a baseline model for comparisons with modified models allowing cross-loadings of subtests. These models were selected based on the CHC narrow-ability classifications (Table 1) and previous research:
- ○
- 2a: Riddles allowed to load on Planning/Gf
- ○
- 2b: Story Completion allowed to load on Knowledge/Gc
- ○
- 2c: Story Completion allowed to load on Simultaneous/Gv
- ○
- 2d: Rover allowed to load on Planning/Gf
- ○
- 2e: Pattern Reasoning allowed to load on Simultaneous/Gv
- ○
- 2f: A model including all significant cross-loadings from models 2a to 2e
- Model 3: A bifactor model with all subtests loading on a general factor and five orthogonal group factors corresponding to the scales of the KABC-II. To achieve identifiability, loadings of all subtests on group factors and of one subtest on the general factor were fixed to one.
- Model 5: A four-factor bifactor model, with four group factors, including a combined Gf/Gv factor.
3. Results
3.1. Preliminary Analyses
3.2. Confirmatory Factor Analyses of Core Subtests (With Time Points)
3.3. Confirmatory Factor Analyses of Core Subtests (Without Time Points)
4. Discussion
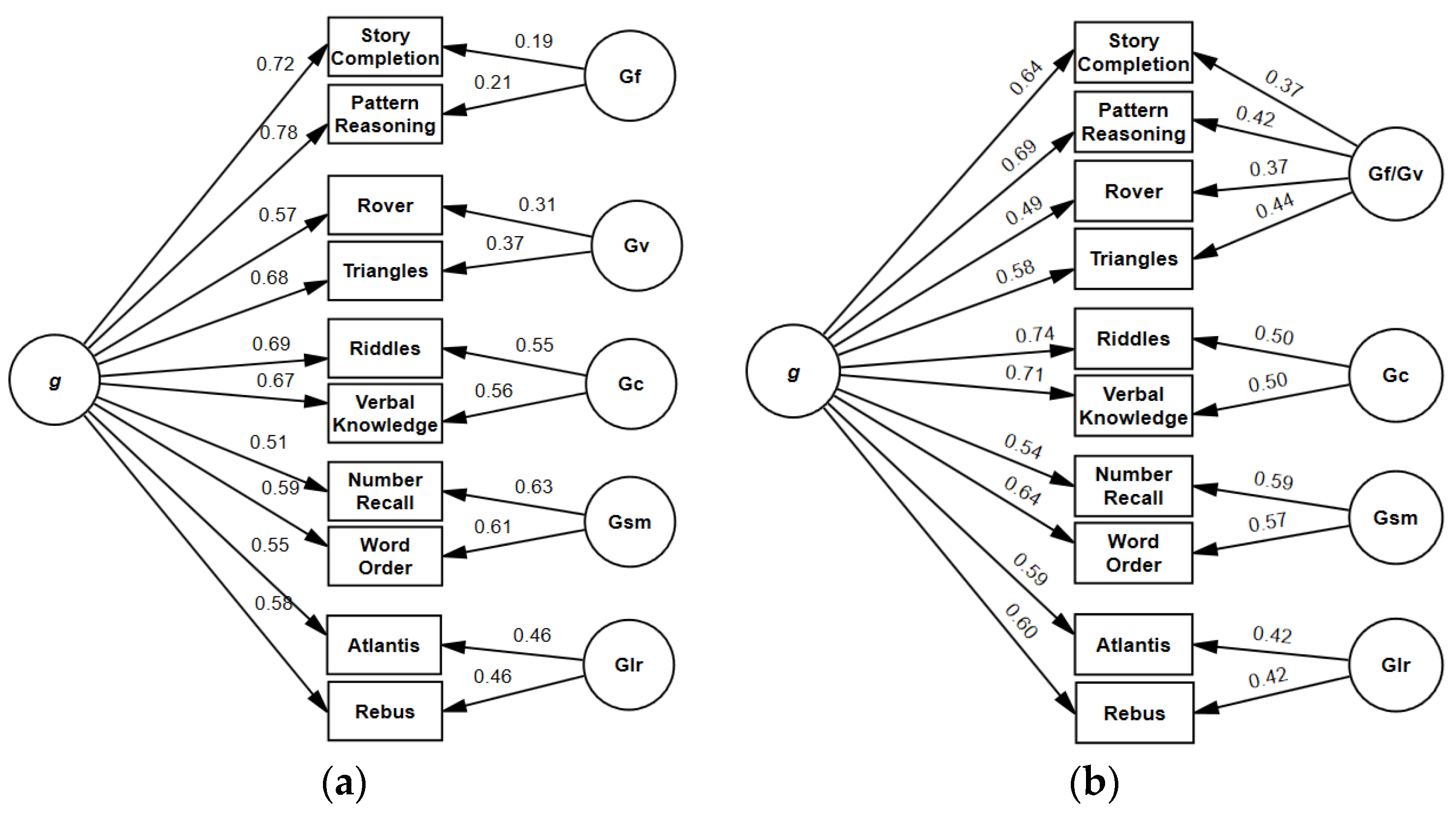
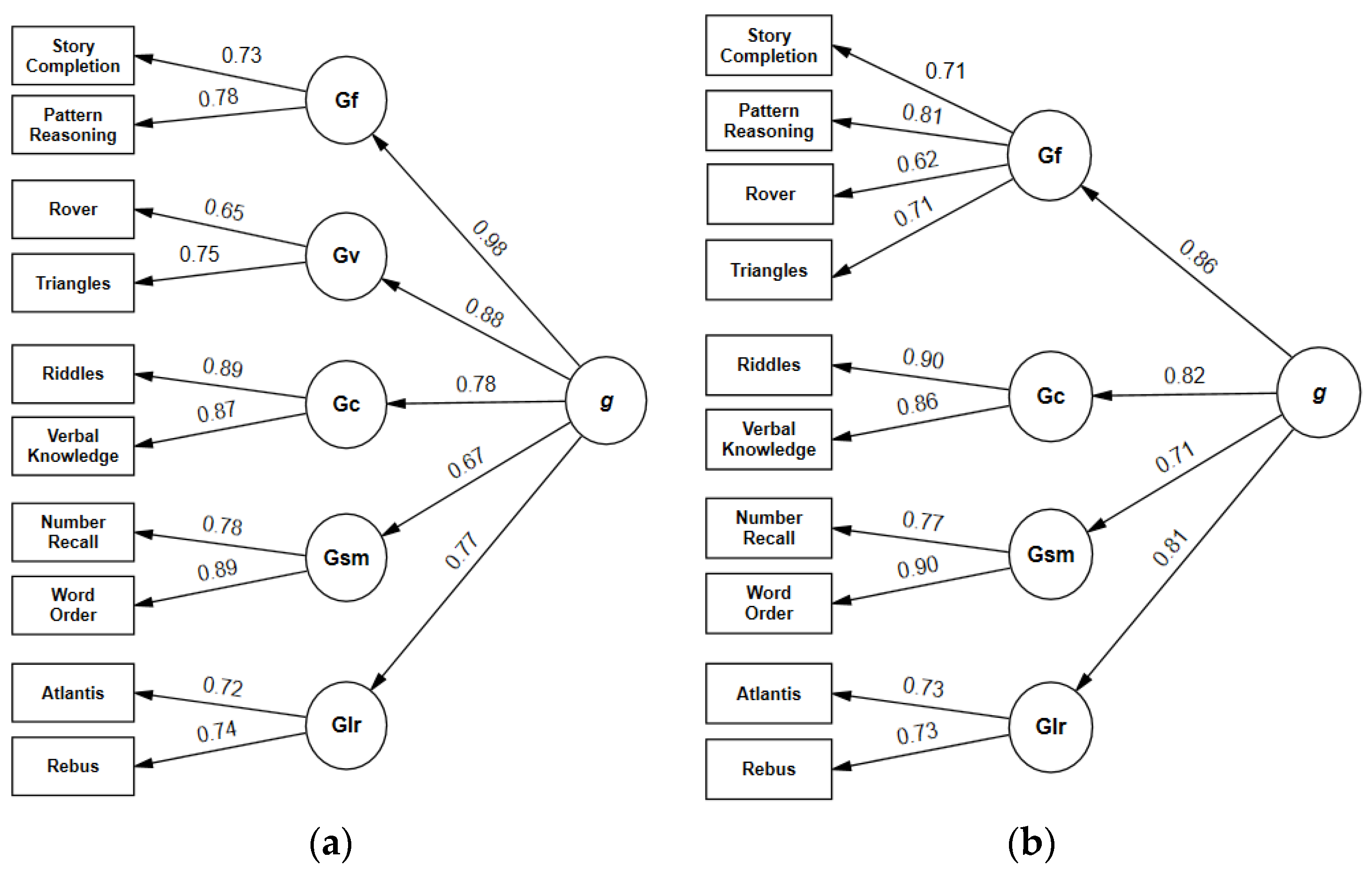
4.1. Standard Higher-Order Model of KABC-II Subtests
4.2. Bifactor vs. Higher-Order Structure Models
4.3. Effects of Time Points
4.4. Limitations
5. Conclusions
- Our data showed that the scales of the KABC-II cannot be interpreted as dimensions independent of the general factor. Therefore, focusing mainly on the interpretation of scales and disregarding the influence of general intelligence on all scales is not recommended. At the same time, a general factor model that would support an interpretive strategy based solely on the total score was inferior to four- and five-factorial solutions.
- As in previous research, the distinction between Planning/Gf and Simultaneous/Gv is questionable. These scales seem to measure both visual and fluid abilities. Consequently, we caution against interpreting normative and intraindividual strengths and weaknesses in these scales as strong indicators of strengths and weaknesses in fluid intelligence, and respectively, visual processing. Accurate differentiation of fluid and visual abilities may require the use of additional tests that provide a purer measure of these intelligence factors.
- The strong additional loading of Pattern Reasoning on Simultaneous/Gv precludes an unequivocal interpretation of this subtest as measuring Planning/Gf. The cross-loading between Story Completion and Knowledge/Gc points to the influence of verbal processes in this subtest.
- Some subtests, notably Rover, Number Recall, and Atlantis, showed a large portion of unique variance. When used separately or as part of a cross-battery assessment, they should not be interpreted as strong measures of general intelligence or the presumed CHC factors.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- American Educational Research Association, American Psychological Association, and National Council on Measurement in Education. 2014. Standards for Educational and Psychological Testing. Washington, DC: American Educational Research Association. [Google Scholar]
- Arbuckle, James L. 2021. Amos (Version 28.0.0). Chicago: IBM SPSS. [Google Scholar]
- Benson, Nicholas F., John H. Kranzler, and Randy G. Floyd. 2016. Examining the integrity of measurement of cognitive abilities in the prediction of achievement: Comparisons and contrasts across variables from higher-order and bifactor models. Journal of School Psychology 58: 1–19. [Google Scholar] [CrossRef]
- Bollen, Kenneth A., and Robert A. Stine. 1992. Bootstrapping goodness-of-fit measures in structural equation models. Sociological Methods & Research 21: 205–29. [Google Scholar] [CrossRef]
- Brunner, Martin, Gabriel Nagy, and Oliver Wilhelm. 2012. A tutorial on hierarchically structured constructs. Journal of Personality 80: 796–846. [Google Scholar] [CrossRef] [PubMed]
- Burnham, Kenneth P., and David R. Anderson. 2004. Multimodel inference. Sociological Methods & Research 33: 261–304. [Google Scholar] [CrossRef]
- Canivez, Gary L., Ryan J. McGill, Stefan C. Dombrowski, Marley W. Watkins, and Alison E. Pritchard. 2020. Construct validity of the WISC-V in clinical cases: Exploratory and confirmatory factor analyses of the 10 primary subtests. Assessment 27: 274–96. [Google Scholar] [CrossRef]
- Canivez, Gary L., Silvia Grieder, and Anette Buenger. 2021. Construct validity of the German Wechsler Intelligence Scale for Children-Fifth Edition: Exploratory and confirmatory factor analyses of the 15 primary and secondary subtests. Assessment 28: 327–52. [Google Scholar] [CrossRef] [PubMed]
- Cucina, Jeffrey, and Kevin Byle. 2017. The bifactor model fits better than the higher-order model in more than 90% of comparisons for mental abilities test batteries. Journal of Intelligence 5: 27. [Google Scholar] [CrossRef]
- Decker, Scott L. 2021. Don’t use a bifactor model unless you believe the true structure is bifactor. Journal of Psychoeducational Assessment 39: 39–49. [Google Scholar] [CrossRef]
- Dombrowski, Stefan C., Gary L. Canivez, and Marley W. Watkins. 2018. Factor structure of the 10 WISC-V primary subtests across four standardization age groups. Contemporary School Psychology 22: 90–104. [Google Scholar] [CrossRef]
- Dombrowski, Stefan C., Ryan J. McGill, Gary L. Canivez, Marley W. Watkins, and A. Alexander Beaujean. 2021. Factor analysis and variance partitioning in intelligence test research: Clarifying misconceptions. Journal of Psychoeducational Assessment 39: 28–38. [Google Scholar] [CrossRef]
- Ehrich, Jochen, Ulrike Grote, Andreas Gerber-Grote, and Michael Strassburg. 2016. The child health care system of Germany. Journal of Pediatrics 177S: S71–S86. [Google Scholar] [CrossRef]
- Flanagan, Dawn P., and Samuel O. Ortiz. 2001. Essentials of Cross-Battery Assessment. New York: Wiley. [Google Scholar]
- Flanagan, Dawn P., Samuel O. Ortiz, and Vincent C. Alfonso. 2013. Essentials of Cross-Battery Assessment, 3rd ed. Hoboken: Wiley. [Google Scholar]
- Gernsbacher, Morton Ann, Raechel N. Soicher, and Kathryn A. Becker-Blease. 2020. Four empirically based reasons not to administer time-limited tests. Translational Issues in Psychological Science 6: 175–90. [Google Scholar] [CrossRef]
- Gignac, Gilles E., and André Kretzschmar. 2017. Evaluating dimensional distinctness with correlated-factor models: Limitations and suggestions. Intelligence 62: 138–47. [Google Scholar] [CrossRef]
- Hair, Joseph F., William C. Black, Barry J. Babin, and Rolph E. Anderson. 2014. Multivariate Data Analysis, 7th ed. Harlow: Pearson. [Google Scholar]
- Hollmann, Helmut, Christoph Kretzschmar, and Ronald G. Schmid. 2014. Das Altöttinger Papier. Mehrdimensionale Bereichsdiagnostik Sozialpädiatrie. Qualität in der Sozialpädiatrie 1. Altötting: Bundesarbeitsgemeinschaft Sozialpädiatrischer Zentren—RS Verlag. [Google Scholar]
- Hu, Li-tze, and Peter M. Bentler. 1999. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling 6: 1–55. [Google Scholar] [CrossRef]
- IBM Corp. 2020. SPSS Statistics for Windows. Armonk: IBM Corp. [Google Scholar]
- Irblich, Dieter, Anne Schroeder, and Gerolf Renner. 2020. Psychometrische Eigenschaften der “Kaufman Assessment Battery for Children-II” (KABC-II) bei 5- und 6-jährigen Kindern [Psychometric properties of the “Kaufman-Assessment Battery for Children-II” (KABC-II) in a clinical sample of 5- and 6-year-old children]. Frühförderung interdisziplinär 39: 137–50. [Google Scholar]
- Jennrich, Robert I., and Peter M. Bentler. 2011. Exploratory Bi-factor Analysis. Psychometrika 76: 537–49. [Google Scholar] [CrossRef] [PubMed]
- Joél, Torsten. 2021. Die Anwendung von Intelligenztests im sonderpädagogischen Kontext [The Use of Intelligence Tests in the Context of Special Education]. Weinheim: Beltz Juventa. [Google Scholar]
- Kaufman, Alan S., and Nadeen L. Kaufman. 2004a. KABC-II. Kaufman Assessment Battery for Children, Second Edition. Circle Pines: American Guidance Service. [Google Scholar]
- Kaufman, Alan S., and Nadeen L. Kaufman. 2004b. Kaufman Test of Educational Achievement, 2nd ed. Circle Pines: American Guidance Service. [Google Scholar]
- Kaufman, Alan S., and Nadeen L. Kaufman. 2018. (KABC-II NU) Kaufman Assessment Battery for Children, Second Edition Normative Update. Bloomington: Pearson. [Google Scholar]
- Kaufman, Alan S., Elizabeth O. Lichtenberger, Elaine Fletcher-Janzen, and Nadeen L. Kaufman. 2005. Essentials of KABC-II Assessment. Essentials of Psychological Assessment Series. New York: John Wiley & Sons. [Google Scholar]
- Kaufman, Scott Barry, Matthew R. Reynolds, Xin Liu, Alan S. Kaufman, and Kevin S. McGrew. 2012. Are cognitive g and academic achievement g one and the same g? An exploration on the Woodcock-Johnson and Kaufman tests. Intelligence 40: 123–38. [Google Scholar] [CrossRef]
- Keith, Timothy Z., and Matthew R. Reynolds. 2018. Using confirmatory factor analysis to aid in understanding the constructs measured by intelligence tests. In Contemporary Intellectual Assessment. Edited by Dawn Flanagan and Erin M. McDonough. New York: Guilford, pp. 853–900. [Google Scholar]
- Kline, Rex B. 2016. Principles and Practice of Structural Equation Modeling, 4th ed. New York: Guilford. [Google Scholar]
- Lai, Keke, and Samuel B. Green. 2016. The problem with having two watches: Assessment of fit when RMSEA and CFI disagree. Multivariate Behavioral Research 51: 220–39. [Google Scholar] [CrossRef]
- Lazaridis, Alexandros, Marco Vetter, and Jakob Pietschnig. 2022. Domain-specificity of Flynn effects in the CHC-model: Stratum II test score changes in Germanophone samples (1996–2018). Intelligence 95: 101707. [Google Scholar] [CrossRef]
- Lecerf, Thierry, and Gary L. Canivez. 2018. Complementary exploratory and confirmatory factor analyses of the French WISC-V: Analyses based on the standardization sample. Psychological Assessment 30: 793–808. [Google Scholar] [CrossRef]
- Lüdeke, Sören, Friedrich Linderkamp, Andrea Weidenfeld, and Peter Borusiak. 2015. Die Einflüsse des Migrationshintergrundes und psychischer Störungen auf kognitive Leistungsdaten einer SPZ-Inanspruchnahmepopulation [The impact of migration background and psychiatric disorders on cognitive achievement of a pediatric outpatient sample]. Kindheit und Entwicklung 24: 236–42. [Google Scholar] [CrossRef]
- Luria, Aleksandr Roimanovic. 1966. Human Brain and Psychological Processes. New York: Harper & Row. [Google Scholar]
- MacCallum, Robert C., Mary Roznowski, and Lawrence B. Necowitz. 1992. Model modifications in covariance structure analysis: The problem of capitalization on chance. Psychological Bulletin 111: 490–504. [Google Scholar] [CrossRef]
- MacCallum, Robert C., Michael W. Brown, and Hazuki M. Sugawara. 1996. Power analysis and determination of sample for covariance structure modeling. Psychological Methods 1: 130–49. [Google Scholar] [CrossRef]
- Malda, M., Fons J. R. van de Vijver, Krishnamachari Srinivasan, Catherine Transler, and Prathima Sukumar. 2010. Traveling with cognitive tests: Testing the validity of a KABC-II adaptation in India. Assessment 17: 107–15. [Google Scholar] [CrossRef] [PubMed]
- Markon, Kristian E. 2019. Bifactor and hierarchical models: Specification, inference, and interpretation. Annual Review of Clinical Psychology 15: 51–69. [Google Scholar] [CrossRef] [PubMed]
- McGill, Ryan J. 2017. Exploring the latent structure of the Luria model for the KABC-II at school age: Further insights from confirmatory factor analysis. Psychology in the Schools 54: 1004–18. [Google Scholar] [CrossRef]
- McGill, Ryan J. 2020. An instrument in search of a theory: Structural validity of the Kaufman assessment battery for children-second edition normative update at school-age. Psychology in the Schools 57: 247–64. [Google Scholar] [CrossRef]
- McGrew, Kevin S. 1997. Analysis of the Major Intelligence Batteries According to a Proposed Comprehensive Gf-Gc Framework. In Contemporary Intellectual Assessment. Edited by Dawn P. Flanagan, Judy L. Genshaft and Patti. L. Harrison. New York: Guilford Press, pp. 155–79. [Google Scholar]
- McNeish, Daniel, Ji An, and Gregory R. Hancock. 2018. The thorny relation between measurement quality and fit index cutoffs in latent variable models. Journal of Personality Assessment 100: 43–52. [Google Scholar] [CrossRef] [PubMed]
- Melchers, Peter, and Martin Melchers. 2015. KABC-II. Kaufman Assessment Battery for Children-II von Alan S. Kaufman & Nadeen L. Kaufman. Deutschsprachige Fassung. [Kaufman Assessment Battery for Children-II by Alan S. Kaufman & Nadeen L. Kaufman. German Adaptation]. Frankfurt a.M.: Pearson. [Google Scholar]
- Miezah, Daniel, Melanie Porter, Adriana Rossi, Christina Kazzi, Jennifer Batchelor, and Jessica Reeve. 2021. Cognitive profile of young children with Williams syndrome. Journal of Intellectual Disability Research 65: 784–94. [Google Scholar] [CrossRef]
- Mitchell, Joanie M., Mark Tomlinson, Ruth M. Bland, Brian Houle, Alan Stein, and Tamsen J. Rochat. 2018. Confirmatory factor analysis of the Kaufman assessment battery in a sample of primary school-aged children in rural South Africa. South African Journal of Psychology 48: 434–52. [Google Scholar] [CrossRef]
- Nevitt, Jonathan, and Gregory Hancock. 2001. Performance of bootstrapping approaches to model test statistics and parameter standard error estimation in structural equation modeling. Structural Equation Modeling 8: 353–77. [Google Scholar] [CrossRef]
- Pauls, Franz, and Monika Daseking. 2021. Revisiting the factor structure of the German WISC-V for clinical interpretability: An exploratory and confirmatory approach on the 10 primary subtests. Frontiers in Psychology 12: 710929. [Google Scholar] [CrossRef] [PubMed]
- Pietschnig, Jakob, Pia Deimann, Nicole Hirschmann, and Ursula Kastner-Koller. 2021. The Flynn effect in Germanophone preschoolers (1996–2018): Small effects, erratic directions, and questionable interpretations. Intelligence 86: 101544. [Google Scholar] [CrossRef]
- Reise, Steven P., Tyler M. Moore, and Mark G. Haviland. 2010. Bifactor models and rotations: Exploring the extent to which multidimensional data yield univocal scale scores. Journal of Personality Assessment 92: 544–59. [Google Scholar] [CrossRef] [PubMed]
- Reise, Steven P., Wes E. Bonifay, and Mark G. Haviland. 2013. Scoring and modeling psychological measures in the presence of multidimensionality. Journal of Personality Assessment 95: 129–40. [Google Scholar] [CrossRef]
- Renner, Gerolf, Dieter Irblich, and Anne Schroeder. 2019. Die WISC-IV in der klinisch-psychologischen Anwendung bei 6- bis 13-Jährigen in einer sozialpädiatrischen Stichprobe [The WISC-IV in clinical psychological practice in a social-pediatric sample of 6- to 13-year-olds]. Kindheit und Entwicklung 37: 182–89. [Google Scholar] [CrossRef]
- Renner, Gerolf, Dieter Irblich, and Anne Schroeder. 2022. Factor structure of the KABC-II at ages 5 and 6: Is it valid in a clinical sample? Children 9: 645. [Google Scholar] [CrossRef]
- Reynolds, Matthew R., Timothy Z. Keith, Jodene Goldenring Fine, Melissa E. Fisher, and Justin A. Low. 2007. Confirmatory factor structure of the Kaufman Assessment Battery for Children—Second Edition: Consistency with Cattell-Horn-Carroll theory. School Psychology Quarterly 22: 511–39. [Google Scholar] [CrossRef]
- Riccio, Cynthia A., Stephanie M. Vidrine, Morris J. Cohen, Delmaris Acosta-Cotte, and Yong Park. 2017. Neurocognitive and behavioral profiles of children with Landau-Kleffner syndrome. Applied Neuropsychology: Child 6: 345–54. [Google Scholar] [CrossRef]
- Scheiber, Caroline. 2016. Do the Kaufman tests of cognitive ability and academic achievement display construct bias across a representative sample of Black, Hispanic, and Caucasian school-age children in grades 1 through 12? Psychological Assessment 28: 942–52. [Google Scholar] [CrossRef]
- Scheiber, Caroline, and Alan S. Kaufman. 2015. Which of the three KABC-II global scores is the least biased? Journal of Pediatric Neuropsychology 1: 21–35. [Google Scholar] [CrossRef]
- Schermelleh-Engel, Karin, Helfried Moosbrugger, and Hans Müller. 2003. Evaluating the fit of structural equation models: Tests of significance and descriptive goodness-of-fit measures. Methods of Psychological Research Online 8: 23–74. Available online: https://www.psycharchives.org/en/item/1a8dea48-0285-4dac-a612-9dc0ff2532f6 (accessed on 1 June 2023).
- Schneider, W. Joel, and Kevin S. McGrew. 2018. The Cattell-Horn-Carroll theory of cognitive abilities. In Contemporary Intellectual Assessment. Edited by Dawn Flanagan and Erin M. McDonough. New York: Guilford, pp. 73–163. [Google Scholar]
- Takayanagi, Mizuho, Yoko Kawasaki, Mieko Shinomiya, Hoshino Hiroshi, Satoshi Okada, Tamiko Ino, Kazuko Sakai, Kimiko Murakami, Rie Ishida, Kaoru Mizuno, and et al. 2022. Review of cognitive characteristics of autism spectrum disorder using performance on six subtests on four versions of the Wechsler Intelligence Scale for Children. Journal of Autism and Developmental Disorders 52: 240–53. [Google Scholar] [CrossRef] [PubMed]
- Tomarken, Andrew J., and Niels G. Waller. 2003. Potential problems with “well fitting” models. Journal of Abnormal Psychology 112: 578–98. [Google Scholar] [CrossRef] [PubMed]
- Villeneuve, Ethan F., Daniel B. Hajovsky, Benjamin A. Mason, and Brittany M. Lewno. 2019. Cognitive ability and math computation developmental relations with math problem solving: An integrated, multigroup approach. School Psychology 34: 96–108. [Google Scholar] [CrossRef]
- Wagenmakers, Eric-Jan, and Simon Farrell. 2004. AIC model selection using Akaike weights. Psychonomic Bulletin & Review 11: 192–96. [Google Scholar]
- Watkins, Marley W. 2013. Omega. Phoenix: Ed & Psych Associates. [Google Scholar]
- Watkins, Marley W., and A. Alexander Beaujean. 2014. Bifactor structure of the Wechsler Preschool and Primary Scale of Intelligence—Fourth Edition. School Psychology Quarterly 29: 52–63. [Google Scholar] [CrossRef]
- Wechsler, David. 2014. WISC-V. Wechsler Intelligence Scale for Children, 5th ed. San Antonio: Pearson. [Google Scholar]
- West, Stephen G., John F. Finch, and Patrick J. Curran. 1995. Structural equation models with nonnormal variables: Problems and remedies. In Structural Equation Modeling. Edited by Rick H. Hoyle. Thousand Oaks: Sage, pp. 56–75. [Google Scholar]
- Zhang, Bo, Jing Luo, Tianjun Sun, Mengyang Cao, and Fritz Drasgow. 2021. Small but nontrivial: A comparison of six strategies to handle cross-loadings in bifactor predictive models. Multivariate Behavioral Research 58: 115–32. [Google Scholar] [CrossRef]


| Scale Subtest | CHC Narrow Abilities Measured |
|---|---|
| Planning/Fluid Reasoning (Gf) | |
| Pattern Reasoning | Gf: Induction Gv: Visualization |
| Story Completion | Gf: Induction Gf: General Sequential Reasoning Gc: General Information Gv: Visualization |
| Simultaneous Processing/Visual Processing (Gv) | |
| Rover | Gv: Spatial Scanning Gf: General Sequential Reasoning Gq: Math Achievement |
| Triangles | Gv: Spatial Relations Gv: Visualization |
| Crystallized Ability (Gc) | |
| Riddles | Gc: Lexical Knowledge Gc: Language Development Gf: General Sequential Reasoning |
| Verbal Knowledge | Gc: Lexical Knowledge Gc: General Information |
| Sequential Processing/Short-Term Memory (Gsm) | |
| Number Recall | Gsm: Memory Span |
| Word Order | Gsm: Memory Span (without color interference) Gsm: Working Memory (with color interference) |
| Learning Ability/Long-Term Storage and Retrieval (Glr) | |
| Atlantis | Glr: Associative Memory |
| Rebus | Glr: Associative Memory |
| Variable | n (%) |
|---|---|
| Age | |
| 7;0–7;11 | 154 (24.6%) |
| 8;0–8;11 | 168 (26.8%) |
| 9;0–9;11 | 131 (20.9%) |
| 10;0–10;11 | 85 (13.6%) |
| 11;0–11;11 | 57 (9.1%) |
| 12;0–12;11 | 32 (5.1%) |
| Sex | |
| Male | 425 (67.8%) |
| Female | 202 (32.2%) |
| Family structure | |
| Two-parent family | 411 (65.6%) |
| Single-parent family | 121 (19.3%) |
| Step-family | 59 (9.4%) |
| Foster and residential care | 31 (4.9%) |
| Other/unknown | 5 (0.8%) |
| Migration | |
| None | 466 (74.3%) |
| Parents only | 124 (19.8%) |
| Child | 25 (4.0%) |
| Other/unknown | 12 (1.9%) |
| Most common psychological diagnoses (ICD-10, Chapter 5) | |
| Specific developmental disorders of scholastic skills (F81.x) | 305 (48.6%) |
| Attention-deficit hyperactivity disorders (F90.x) | 156 (24.9%) |
| Specific developmental disorders of speech and language (F80.x) | 149 (23.8) |
| Emotional disorders with onset specific to childhood (F93.x) | 116 (18.5%) |
| Other/Unspecified disorders of psychological development (F88.x, F89.x) | 110 (17.5%) |
| Other behavioral and emotional disorders (F98.x) | 103 (16.4%) |
| Conduct disorders (F91.x) | 50 (8.0%) |
| Reaction to severe stress, and adjustment disorders (F43.x) | 47 (7.5%) |
| Intellectual disabilities (F7x.x) | 35 (5.6%) |
| Most common somatic diagnoses (ICD-10) | |
| Congenital malformations, deformations, and chromosomal abnormalities (Q00–Q99) | 79 (12.6%) |
| Diseases of the nervous system (G00–G99) | 65 (10.4%) |
| Symptoms, signs, and abnormal clinical and laboratory findings, not elsewhere classified (R00–R99) | 63 (10.0%) |
| Endocrine, nutritional, and metabolic diseases (E00–E99) | 47 (7.5%) |
| Diseases of the eye (H00–H59) | 39 (6.2%) |
| Certain conditions originating in the perinatal period (P00–P96) | 26 (4.1%) |
| Model | SC | PR | ROV | TRI | RID | VK | NR | WO | ATL | REB | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | unidimensional | g | g | g | g | g | g | g | g | g | g |
| 2 | second-order | Gf | Gf | Gv | Gv | Gc | Gc | Gsm | Gsm | Glr | Glr |
| 2a | second-order | Gf | Gf | Gv | Gv | Gc + Gf | Gc | Gsm | Gsm | Glr | Glr |
| 2b | second-order | Gf + Gc | Gf | Gv | Gv | Gc | Gc | Gsm | Gsm | Glr | Glr |
| 2c | second-order | Gf + Gv | Gf | Gv | Gv | Gc | Gc | Gsm | Gsm | Glr | Glr |
| 2d | second-order | Gf | Gf | Gv + Gf | Gv | Gc | Gc | Gsm | Gsm | Glr | Glr |
| 2e | second-order | Gf | Gf + Gv | Gv | Gv | Gc | Gc | Gsm | Gsm | Glr | Glr |
| 2f | second-order | Gf + Gv | Gf + Gv | Gv | Gv | Gc | Gc | Gsm | Gsm | Glr | Glr |
| 3 | bifactor | g, Gf | g, Gf | g, Gv | g, Gv | g, Gc | g, Gc | g, Gsm | g, Gsm | g, Glr | g, Glr |
| 4 | second-order | Gf/Gv | Gf/Gv | Gf/Gv | Gf/Gv | Gc | Gc | Gsm | Gsm | Glr | Glr |
| 4a | second-order | Gf/Gv | Gf/Gv | Gf/Gv | Gf/Gv | Gc, Gf/Gv | Gc | Gsm | Gsm | Glr | Glr |
| 4b | second-order | Gf/Gv, Gc | Gf/Gv | Gf/Gv | Gf/Gv | Gc | Gc | Gsm | Gsm | Glr | Glr |
| 5 | bifactor | g, Gf/Gv | g, Gf/Gv | g, Gf/Gv | g, Gf/Gv | g, Gc | g, Gc | g, Gsm | g, Gsm | g, Glr | g, Glr |
| Model | χ2 | df | p | CFI | RMSEA | 90% CI RMSEA | SRMR | AIC | ΔAIC | wi AIC |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 g-factor | 609.238 | 35 | 0.000 | 0.795 | 0.162 | [0.151, 0.173] | 0.076 | 649.238 | 548.107 | 0.000 |
| 2 second-order | 106.166 | 30 | 0.000 | 0.973 | 0.064 | [0.051, 0.077] | 0.038 | 156.166 | 55.035 | 0.000 |
| 2a (Gf -> RID) | Inadmissible solution | |||||||||
| 2b (Gc -> SC) | 97.873 | 29 | 0.000 | 0.975 | 0.062 | [0.048, 0.075] | 0.038 | 149.873 | 48.742 | 0.000 |
| 2c (Gv -> SC) | 106.152 | 29 | 0.000 | 0.973 | 0.065 | [0.052, 0.079] | 0.039 | 158.152 | 57.021 | 0.000 |
| 2d (Gf -> ROV) | Inadmissible solution | |||||||||
| 2e (Gv -> PR) | 64.498 | 29 | 0.002 | 0.987 | 0.044 | [0.030, 0.059] | 0.027 | 116.498 | 15.367 | 0.001 |
| 2f (Gc -> SC, Gv -> PR) | 106.152 | 29 | 0.001 | 0.988 | 0.044 | [0.030, 0.059] | 0.028 | 116.388 | 15.257 | 0.001 |
| 3 bifactor | 64.498 | 29 | 0.000 | 0.973 | 0.064 | [0.051, 0.077] | 0.038 | 156.166 | 55.035 | 0.000 |
| 4 second-order (Gf/Gv) | 72.868 | 31 | 0.000 | 0.985 | 0.046 | [0.033, 0.060] | 0.029 | 120.868 | 19.737 | 0.000 |
| 4a (Gf/Gv -> RID) | 72.468 | 30 | 0.001 | 0.985 | 0.048 | [0.034, 0.062] | 0.028 | 122.868 | 21.337 | 0.000 |
| 4b (Gc -> SC) | 51.131 | 30 | 0.025 | 0.992 | 0.034 | [0.017, 0.049] | 0.022 | 101.131 | 0.000 | 0.998 |
| 5 Bifactor (Gf/Gv) | 66.487 | 31 | 0.003 | 0.987 | 0.043 | [0.029, 0.057] | 0.026 | 114.487 | 13.356 | 0.001 |
| Time Points | No Time Points | |
|---|---|---|
| Story Completion | 0.70 | 0.69 |
| Pattern Reasoning | 0.74 | 0.73 |
| Rover | 0.56 | 0.55 |
| Triangles | 0.64 | 0.63 |
| Riddles | 0.77 | 0.77 |
| Verbal Knowledge | 0.75 | 0.76 |
| Number Recall | 0.57 | 0.57 |
| Word Order | 0.64 | 0.64 |
| Atlantis | 0.58 | 0.58 |
| Rebus | 0.59 | 0.58 |
| Factor | Model 2 | Model 4 | ||
|---|---|---|---|---|
| ω | AVE | ω | AVE | |
| Planning/Gf | 0.75 | 0.60 | 0.81 | 0.53 |
| Simultaneous/Gv | 0.67 | 0.51 | ||
| Knowledge/Gc | 0.87 | 0.77 | 0.87 | 0.77 |
| Sequential/Gsm | 0.82 | 0.70 | 0.82 | 0.70 |
| Learning/Glr | 0.69 | 0.53 | 0.69 | 0.52 |
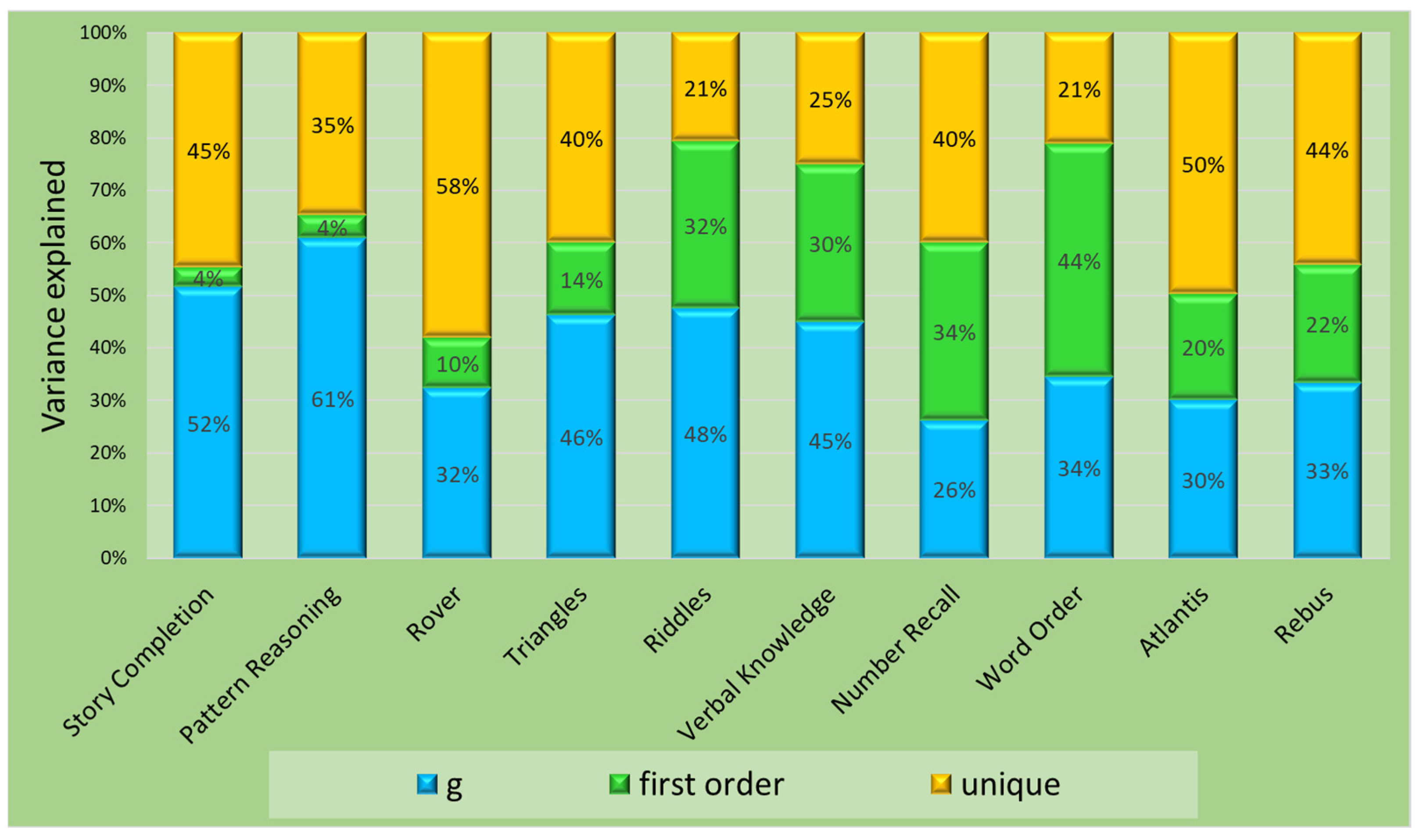
| Subtest | General | Gf | Gv | Gc | Gsm | Glr | Unique Var | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λ | Var | λ | Var | λ | Var | λ | Var | λ | Var | λ | Var | ||
| Story Completion | 0.72 | 0.52 | 0.19 | 0.04 | 0.45 | ||||||||
| Pattern Reasoning | 0.78 | 0.61 | 0.22 | 0.05 | 0.35 | ||||||||
| Rover | 0.57 | 0.32 | 0.32 | 0.10 | 0.58 | ||||||||
| Triangles | 0.68 | 0.46 | 0.37 | 0.14 | 0.40 | ||||||||
| Riddles | 0.69 | 0.48 | 0.55 | 0.31 | 0.22 | ||||||||
| Verbal Knowledge | 0.67 | 0.45 | 0.56 | 0.31 | 0.24 | ||||||||
| Number Recall | 0.51 | 0.26 | 0.61 | 0.38 | 0.36 | ||||||||
| Word Order | 0.59 | 0.35 | 0.63 | 0.40 | 0.26 | ||||||||
| Atlantis | 0.55 | 0.30 | 0.46 | 0.21 | 0.49 | ||||||||
| Rebus | 0.58 | 0.33 | 0.47 | 0.22 | 0.45 | ||||||||
| ECV | 0.66 | 0.01 | 0.04 | 0.10 | 0.13 | 0.07 | |||||||
| ω/ωS | 0.92 | 0.75 | 0.67 | 0.87 | 0.82 | 0.69 | |||||||
| ωH/ωHS | 0.83 | 0.05 | 0.16 | 0.35 | 0.46 | 0.28 | |||||||
| Subtest | General | Gf/Gv | Gc | Gsm | Glr | Unique Var | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| λ | Var | λ | Var | λ | Var | λ | Var | λ | Var | ||
| Story Completion | 0.64 | 0.41 | 0.37 | 0.14 | 0.45 | ||||||
| Pattern Reasoning | 0.69 | 0.48 | 0.42 | 0.18 | 0.34 | ||||||
| Rover | 0.49 | 0.24 | 0.37 | 0.14 | 0.62 | ||||||
| Triangles | 0.58 | 0.34 | 0.44 | 0.19 | 0.47 | ||||||
| Riddles | 0.74 | 0.55 | 0.50 | 0.25 | 0.21 | ||||||
| Verbal Knowledge | 0.71 | 0.50 | 0.50 | 0.25 | 0.25 | ||||||
| Number Recall | 0.55 | 0.30 | 0.59 | 0.35 | 0.35 | ||||||
| Word Order | 0.64 | 0.41 | 0.44 | 0.19 | 0.40 | ||||||
| Atlantis | 0.59 | 0.35 | 0.42 | 0.18 | 0.48 | ||||||
| Rebus | 0.60 | 0.36 | 0.42 | 0.18 | 0.46 | ||||||
| ECV | 0.66 | 0.11 | 0.08 | 0.09 | 0.06 | ||||||
| ω/ωS | 0.92 | 0.82 | 0.87 | 0.77 | 0.69 | ||||||
| ωH/ωHS | 0.81 | 0.25 | 0.28 | 0.33 | 0.23 | ||||||
| Model | χ2 | df | p | CFI | RMSEA | 90% CI RMSEA | SRMR | AIC | ΔAIC | wi AIC | ΔAIC Time Points a |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 second-order | 90.50 | 30 | <.001 | 0.978 | 0.057 | [0.044, 0.070] | 0.035 | 140.495 | 48.31 | 0.000 | 15.671 |
| 2e (Gv → PR) | 47.53 | 29 | .016 | 0.993 | 0.032 | [0.014, 0.048] | 0.023 | 99.526 | 7.34 | 0.025 | 16.972 |
| 3 bifactor | 90.50 | 30 | <.001 | 0.978 | 0.057 | [0.044, 0.070] | 0.035 | 140.495 | 48.31 | 0.000 | 15.671 |
| 4 second-order (Gf/Gv) | 61.81 | 31 | .001 | 0.989 | 0.040 | [0.025, 0.054] | 0.028 | 109.807 | 17.62 | 0.000 | 11.061 |
| 4b (Gc → SC) | 42.19 | 30 | .069 | 0.996 | 0.025 | [0.026, 0.055] | 0.021 | 92.190 | 0.00 | 0.972 | 8.941 |
| 5 bifactor (Gf/Gv) | 55.79 | 31 | .004 | 0.991 | 0.036 | [0.020, 0.051] | 0.025 | 103.794 | 11.60 | 0.003 | 10.693 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Renner, G.; Schroeder, A.; Irblich, D. Factorial Validity of the German KABC-II at Ages 7 to 12 in a Clinical Sample: Four Factors Fit Better than Five. J. Intell. 2023, 11, 148. https://doi.org/10.3390/jintelligence11070148
Renner G, Schroeder A, Irblich D. Factorial Validity of the German KABC-II at Ages 7 to 12 in a Clinical Sample: Four Factors Fit Better than Five. Journal of Intelligence. 2023; 11(7):148. https://doi.org/10.3390/jintelligence11070148
Chicago/Turabian StyleRenner, Gerolf, Anne Schroeder, and Dieter Irblich. 2023. "Factorial Validity of the German KABC-II at Ages 7 to 12 in a Clinical Sample: Four Factors Fit Better than Five" Journal of Intelligence 11, no. 7: 148. https://doi.org/10.3390/jintelligence11070148
APA StyleRenner, G., Schroeder, A., & Irblich, D. (2023). Factorial Validity of the German KABC-II at Ages 7 to 12 in a Clinical Sample: Four Factors Fit Better than Five. Journal of Intelligence, 11(7), 148. https://doi.org/10.3390/jintelligence11070148





