Phenomenology, Quantity, and Numerosity
Abstract
1. Introduction
2. Qualities
3. Current Theories
4. The Phenomenal Experience of Numerosity
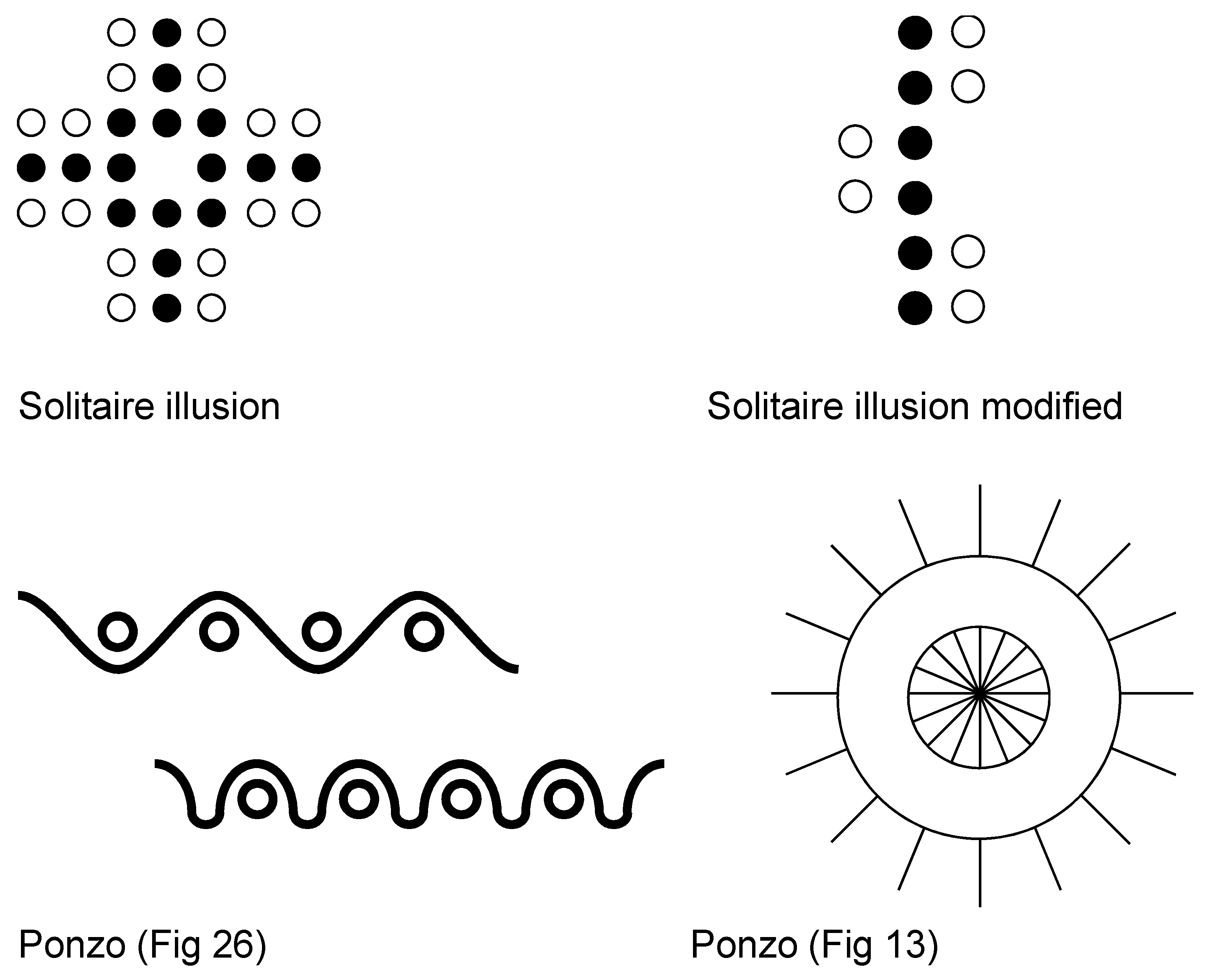
5. Two Illusions of Numerosity
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Agostini, Tiziano, and Riccardo Luccio. 1994. Müller-Lyer Illusion and Perception of Numerosity. Perceptual & Motor Skills 78: 937–38. [Google Scholar] [CrossRef]
- Alam, Seemen, Riccardo Luccio, and Fulvia Vardabasso. 1986. Regularity, exposure time and perception of numerosity. Perceptual & Motor Skills 63: 883–88. [Google Scholar] [CrossRef]
- Alexander, Samuel. 1933. Beauty and Other Forms of Value. London: Macmillan. [Google Scholar]
- Anobile, Giovanni, Guido Marco Cicchini, and David C. Burr. 2014. Separate mechanisms for perception of numerosity and density. Psychological Science 25: 265–70. [Google Scholar] [CrossRef] [PubMed]
- Anobile, Giovanni, Marco Turi, Guido Marco Cicchini, and David C. Burr. 2015. Mechanisms for perception of numerosity or texture-density. Journal of Vision 15: 1–12. [Google Scholar] [CrossRef]
- Apthorp, Deborah, and Jason Bell. 2015. Symmetry is less than meets the eye. Current Biology 25: 267–68. [Google Scholar] [CrossRef]
- Balas, Benjamin. 2016. Seeing number using texture: How summary statistics account for reductions in perceived numerosity in the visual periphery. Attention, Perception, & Psychophysics 78: 2313–19. [Google Scholar] [CrossRef]
- Bertamini, Marco, and Nicholas J. Wade. 2023. Mario Ponzo (1928) on perception of numerosity: A translation and commentary. Perception 52: 545–75. [Google Scholar] [CrossRef]
- Bertamini, Marco, Martin Guest, Giorgio Vallortigara, Rosa Rugani, and Regolin Lucia. 2018. The Effect of Clustering on Perceived Quantity in Humans (Homo sapiens) and in Chicks (Gallus gallus). Journal of Comparative Psychology 132: 280–93. [Google Scholar] [CrossRef]
- Bertamini, Marco, Martin Guest, Giulio Contemori, and Michele Zito. 2023. What the Solitaire illusion tells us about perception of numerosity. British Journal of Psychology 114: 393–414. [Google Scholar] [CrossRef]
- Bertamini, Marco, Michele Zito, Nicholas E. Scott-Samuel, and Johan Hulleman. 2016. Spatial clustering and its effect on perceived clustering, numerosity, and dispersion. Attention, Perception, and Psychophysics 78: 1460–71. [Google Scholar] [CrossRef]
- Bianchi, Ivana, and Richard Davies, eds. 2019. Paolo Bozzi’s Experimental Phenomenology, 1st ed. London: Routledge. [Google Scholar]
- Blackburn, Simon. 2008. Simon. Oxford: Oxford University Press. [Google Scholar]
- Bobbio, A., and E. Giora. 2023. Cesare Musatti e Silvia De Marchi allievi di Vittorio Benussi. In Cesare Musatti Intellettuale del Novecento. Edited by Mauro Antonelli and Aurelio Molaro. Milan: Edizioni Cortina. [Google Scholar]
- Bozzi, Paolo. 1990. Fisica Ingenua [Naïve Physics]. Milan: Garzanti. [Google Scholar]
- Brannon, Elizabeth M., and Herbert S. Terrace. 1998. Ordering of the numerosities 1 to 9 by monkeys. Science 282: 746–49. [Google Scholar] [CrossRef]
- Burr, David C., Giovanni Anobile, and Roberto Arrighi. 2018. Psychophysical evidence for the number sense. Philosophical Transactions of the Royal Society B: Biological Sciences 373: 20170045. [Google Scholar] [CrossRef]
- Burr, David, and John Ross. 2008. A visual sense of number. Current Biology 18: 425–28. [Google Scholar] [CrossRef] [PubMed]
- Butterworth, Brian, Sashank Varma, and Diana Laurillard. 2011. Dyscalculia: From brain to education. Science 332: 1049–53. [Google Scholar] [CrossRef] [PubMed]
- Cantlon, Jessica F., and Elizabeth M. Brannon. 2006. Shared system for ordering small and large numbers in monkeys and humans. Psychological Science 17: 401–6. [Google Scholar] [CrossRef] [PubMed]
- Chakravarthi, Ramakrishna, and Marco Bertamini. 2020. Clustering leads to underestimation of numerosity, but crowding is not the cause. Cognition 198: 104195. [Google Scholar] [CrossRef] [PubMed]
- Cretenoud, Aline F., Arthur Barakat, Alain Milliet, Oh-Hyeon Choung, Marco Bertamini, Christophe Constantin, and Michael H. Herzog. 2021. How do visual skills relate to action video game performance? Journal of Vision 21: 10. [Google Scholar] [CrossRef]
- Cretenoud, Aline F., Lukasz Grzeczkowski, Marco Bertamini, and Michael H. Herzog. 2020. Individual differences in the Müller-Lyer and Ponzo illusions are stable across different contexts. Journal of Vision 20: 4. [Google Scholar] [CrossRef]
- Dakin, Steven C., Marc S. Tibber, John A. Greenwood, Frederick A. A. Kingdom, and Michael J. Morgan. 2011. A common visual metric for approximate number and density. Proceedings of the National Academy of Sciences of the United States of America 108: 19552–57. [Google Scholar] [CrossRef]
- De Marchi, Silvia. 1924. Contributi alla psicologia giudiziaria [Contributions to Forensic Psychology]. University thesis, Università degli Studi di Padova, Facoltà di Lettere e Filosofia, Padua, Italy. Available online: https://phaidra.cab.unipd.it/detail/o:283146 (accessed on 28 September 2023).
- De Marchi, Silvia. 1929. Le valutazioni numeriche di collettività. [Numerical judgments of quantities]. Archivio Italiano di Psicologia 7: 177–225. [Google Scholar]
- Dehaene, Stanislas. 2011. The Number Sense: How the Mind Creates Mathematics, Rev. and updated ed. Oxford: Oxford University Press. [Google Scholar]
- Dehaene, Stanislas, Manuela Piazza, Philippe Pinel, and Laurent Cohen. 2003. Three parietal circuits for number processing. Cognitive Neuropsychology 20: 487–506. [Google Scholar] [CrossRef] [PubMed]
- DeWind, Nicholas K., Michael F. Bonner, and Elizabeth M. Brannon. 2020. Similarly oriented objects appear more numerous. Journal of Vision 20: 4. [Google Scholar] [CrossRef]
- Dobias, Joshua J., Thomas V. Papathomas, and Anuja Sarwate. 2016. Ponzo’s illusion in 3D: Perspective gradients dominate differences in retinal size. Multisensory Research 29: 421–38. [Google Scholar] [CrossRef]
- Fisher, Gerald H. 1969. Towards a new explanation for the geometrical illusions: I. The properties of contours which induce illusory distortion. British Journal of Psychology 60: 179–85. [Google Scholar] [CrossRef] [PubMed]
- Frith, Christopher D., and Uta Frith. 1972. The solitaire illusion: An illusion of numerosity. Perception & Psychophysics 11: 409–10. [Google Scholar] [CrossRef]
- Gebuis, Titia, Roi Cohen Kadosh, and Wim Gevers. 2016. Sensory-integration system rather than approximate number system underlies numerosity processing: A critical review. Acta Psychologica 171: 17–35. [Google Scholar] [CrossRef]
- Ginsburg, Norman. 1976. Effect of item arrangement on perceived numerosity: Randomness vs. regularity. Perceptual & Motor Skills 43: 663–68. [Google Scholar] [CrossRef]
- Ginsburg, Norman. 1980. The regular-random numerosity illusion: Rectangular patterns. The Journal of General Psychology 103: 211–16. [Google Scholar] [CrossRef] [PubMed]
- Ginsburg, Norman. 1991. Numerosity estimation as a function of stimulus organization. Perception 20: 681–86. [Google Scholar] [CrossRef]
- Ginsburg, Norman, and Andrea Nicholls. 1988. Perceived numerosity as a function of item size. Perceptual & Motor Skills 67: 656–58. [Google Scholar] [CrossRef]
- Gregory, Richard L. 1963. Distortion of visual space as inappropriate constancy scaling. Nature 199: 678–80. [Google Scholar] [CrossRef] [PubMed]
- Guest, Martin, Michele Zito, Johan Hulleman, and Marco Bertamini. 2022. On the usefulness of graph-theoretic properties in the study of perceived numerosity. Behavior Research Methods 54: 2381–97. [Google Scholar] [CrossRef] [PubMed]
- Harvey, Ben M., and Serge O. Dumoulin. 2017. Can responses to basic non-numerical visual features explain neural numerosity responses? Neuroimage 149: 200–9. [Google Scholar] [CrossRef]
- He, Lixia, Ke Zhou, Tiangang Zhou, Sheng He, and Lin Chen. 2015. Topology-defined units in numerosity perception. Proceedings of the National Academy of Sciences of the United States of America 112: E5647–55. [Google Scholar] [CrossRef] [PubMed]
- Izard, Véronique, Coralie Sann, Elizabeth S. Spelke, and Arlette Streri. 2009. Newborn infants perceive abstract numbers. Proceedings of the National Academy of Sciences of the United States of America 106: 10382–85. [Google Scholar] [CrossRef]
- Jevons, W. Stanley. 1871. The power of numerical discrimination. Nature 3: 281–82. [Google Scholar] [CrossRef]
- Kanizsa, G., and R. Luccio. 1981. Stima del Numero e Impressione di Numerosità due Processi di Natura Diversa. Trieste: University of Trieste. [Google Scholar]
- Kaufman, Edna L., M. W. Lord, T. W. Reese, and J. Volkmann. 1949. The Discrimination of Visual Number. The American Journal of Psychology 62: 498–525. [Google Scholar] [CrossRef]
- Köhler, Wolfgang. 1947. Gestalt Psychology. London: Liveright Publishing. First published in 1929. [Google Scholar]
- Libertus, Melissa E., and Elizabeth M. Brannon. 2010. Stable individual differences in number discrimination in infancy. Developmental Science 13: 900–6. [Google Scholar] [CrossRef]
- Liebenberg, Richard. 1914. Über das Schätzen von Mengen [On the Estimate of Numerosity]. Leipzig: J.A. Barth. [Google Scholar]
- Locke, John. 1690. Essay Concerning Human Understanding. London: Printed by Eliz. Holt, for Thomas Basset. [Google Scholar]
- Masin, Sergio. 2006. Le Valutazioni Numeriche di Collettività di Silvia De Marchi. Padova: University of Padova. Available online: https://web.archive.org/web/20060515052212 (accessed on 28 September 2023).
- Piaget, Jean. 1952. The Child’s Conception of Number. London: Routledge & Paul. [Google Scholar]
- Piazza, Manuela, Andrea Facoetti, Anna Noemi Trussardi, Ilaria Berteletti, Stefano Conte, Daniela Lucangeli, Stanislas Dehaene, and Marco Zorzi. 2010. Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition 116: 33–41. [Google Scholar] [CrossRef]
- Piazza, Manuela, Véronique Izard, Philippe Pinel, Denis Le Bihan, and Stanislas Dehaene. 2004. Tuning curves for approximate numerosity in the human intraparietal sulcus. Neuron 44: 547–55. [Google Scholar] [CrossRef]
- Piffer, Laura, Maria Elena Miletto Petrazzini, and Christian Agrillo. 2013. Large number discrimination in newborn fish. PLoS ONE 8: e62466. [Google Scholar] [CrossRef] [PubMed]
- Ponzo, Mario. 1912. Rapports entre quelques illusions visuelles de contraste angulaire et l’appréciation de grandeur des astres à l’horizon. Archives Italiennes de Biologie 58: 327–29. [Google Scholar]
- Ponzo, Mario. 1928. Urteilstäuschungen über Mengen [Illusions of judgments of numbers]. Archiv Für Die Gesamte Psychologie 65: 129–62. [Google Scholar]
- Ponzo, Mario. 1929. Illusioni negli apprezzamenti di collettività. Archivio Italiano Di Psicologia 7: 1–37. [Google Scholar]
- Poom, Leo, Marcus Lindskog, Anders Winman, and Ronald van den Berg. 2019. Grouping effects in numerosity perception under prolonged viewing conditions. PLoS ONE 14: e0207502. [Google Scholar] [CrossRef] [PubMed]
- Prado, Jérome, Rachna Mutreja, Hongchuan Zhang, Rucha Mehta, Amy S. Desroches, Jennifer E. Minas, and James R. Booth. 2011. Distinct representations of subtraction and multiplication in the neural systems for numerosity and language. Human Brain Mapping 32: 1932–47. [Google Scholar] [CrossRef]
- Prpic, Valter, and Riccardo Luccio. 2016. Do you hear more piano or drum sounds? An auditory version of the solitaire illusion. Perception 45: 1433–38. [Google Scholar] [CrossRef]
- Raphael, Sabine, and Michael J. Morgan. 2016. The computation of relative numerosity, size and density. Vision Research 124: 15–23. [Google Scholar] [CrossRef][Green Version]
- Raphael, Sabine, Barbara Dillenburger, and Michael Morgan. 2013. Computation of relative numerosity of circular dot textures. Journal of Vision 13: 17. [Google Scholar] [CrossRef][Green Version]
- Robinson, James Outram. 1972. The Psychology of Visual Illusion. London: Hutchinson. [Google Scholar]
- Rugani, Rosa, Annachiara Cavazzana, Giorgio Vallortigara, and Lucia Regolin. 2013. One, two, three, four, or is there something more? Numerical discrimination in day-old domestic chicks. Animal Cognition 16: 557–64. [Google Scholar] [CrossRef]
- Schneider, Michael, Kassandra Beeres, Leyla Coban, Simon Merz, S. Susan Schmidt, Johannes Stricker, and Bert De Smedt. 2017. Associations of non-symbolic and symbolic numerical magnitude processing with mathematical competence: A meta-analysis. Developmental Science 20: e12372. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, Arthur G., and Dejan Todorovic. 2017. The Oxford Compendium of Visual Illusions. Oxford: Oxford University Press. [Google Scholar]
- Shuman, Miles, and Elizabeth Spelke. 2006. Area and element size bias numerosity perception. Journal of Vision 6: 777. [Google Scholar] [CrossRef]
- Sinico, Michele. 2015. Tertiary qualities, from Galileo to Gestalt psychology. History of the Human Sciences 28: 68–79. [Google Scholar] [CrossRef]
- Solomon, Joshua A., and Michael J. Morgan. 2018. Calculation Efficiencies for Mean Numerosity. Psychological Science 29: 1824–31. [Google Scholar] [CrossRef] [PubMed]
- Stancher, G., R. Rugani, L. Regolin, and G. Vallortigara. 2015. Numerical discrimination by frogs (Bombina orientalis). Animal Cognition 18: 219–29. [Google Scholar] [CrossRef]
- Tokita, Midori, and Akira Ishiguchi. 2010. How might the discrepancy in the effects of perceptual variables on numerosity judgment be reconciled? Attention, Perception & Psychophysics 72: 1839–53. [Google Scholar] [CrossRef]
- Valsecchi, Matteo, Matteo Toscani, and Karl R. Gegenfurtner. 2013. Perceived numerosity is reduced in peripheral vision. Journal of Vision 13: 7. [Google Scholar] [CrossRef]
- van den Berg, Ronald, Marcus Lindskog, Leo Poom, and Anders Winman. 2017. Recent is more: A negative time-order effect in nonsymbolic numerical judgment. Journal of Experimental Psychology: Human Perception and Performance 43: 1084–97. [Google Scholar] [CrossRef]
- Vicario, Giovanni Bruno. 2011. Illusioni ottico-Geometriche. Una Rassegna di Problemi [Optocal-Geometric Illusions. A Review of Problems]. Venezia: Istituto Veneto di Scienze, Lettere ed Arte. [Google Scholar]
- Vos, Piet G., Michiel P. van Oeffelen, Hein J. Tibosch, and Jüri Allik. 1988. Interactions between area and numerosity. Psychological Research 50: 148–54. [Google Scholar] [CrossRef]
- Yildiz, Gizem Y., Irene Sperandio, Christine Kettle, and Philippe A. Chouinard. 2022. A review on various explanations of Ponzo-like illusions. Psychonomic Bulletin & Review 29: 293–320. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bertamini, M. Phenomenology, Quantity, and Numerosity. J. Intell. 2023, 11, 197. https://doi.org/10.3390/jintelligence11100197
Bertamini M. Phenomenology, Quantity, and Numerosity. Journal of Intelligence. 2023; 11(10):197. https://doi.org/10.3390/jintelligence11100197
Chicago/Turabian StyleBertamini, Marco. 2023. "Phenomenology, Quantity, and Numerosity" Journal of Intelligence 11, no. 10: 197. https://doi.org/10.3390/jintelligence11100197
APA StyleBertamini, M. (2023). Phenomenology, Quantity, and Numerosity. Journal of Intelligence, 11(10), 197. https://doi.org/10.3390/jintelligence11100197





