Stop Worrying about Multiple-Choice: Fact Knowledge Does Not Change with Response Format
Abstract
1. Introduction
1.1. Declarative Knowledge as an Indicator of Crystallized Intelligence
1.2. Assessment Methods of Declarative Knowledge
1.3. MC Format Items vs. CR Format Items
1.4. Cognitive Processes Underlying Different Response Formats
1.5. The Present Studies
2. Methods and Materials: Study 1
2.1. Participants and Procedure
2.2. Measures
- MC-format items included a knowledge question (e.g., “What is the capital of Sweden?”) and four response alternatives with exactly one veridical response;
- For open-ended format items, participants were only presented with the knowledge question and a text box for typing in the response;
- The same was true for the cued open-ended format items, although in this particular response format, participants were additionally provided with a cue (the first letter of the correct response, or a restriction as to the range of the correct number).
2.3. Data Preparation
2.4. Statistical Analysis
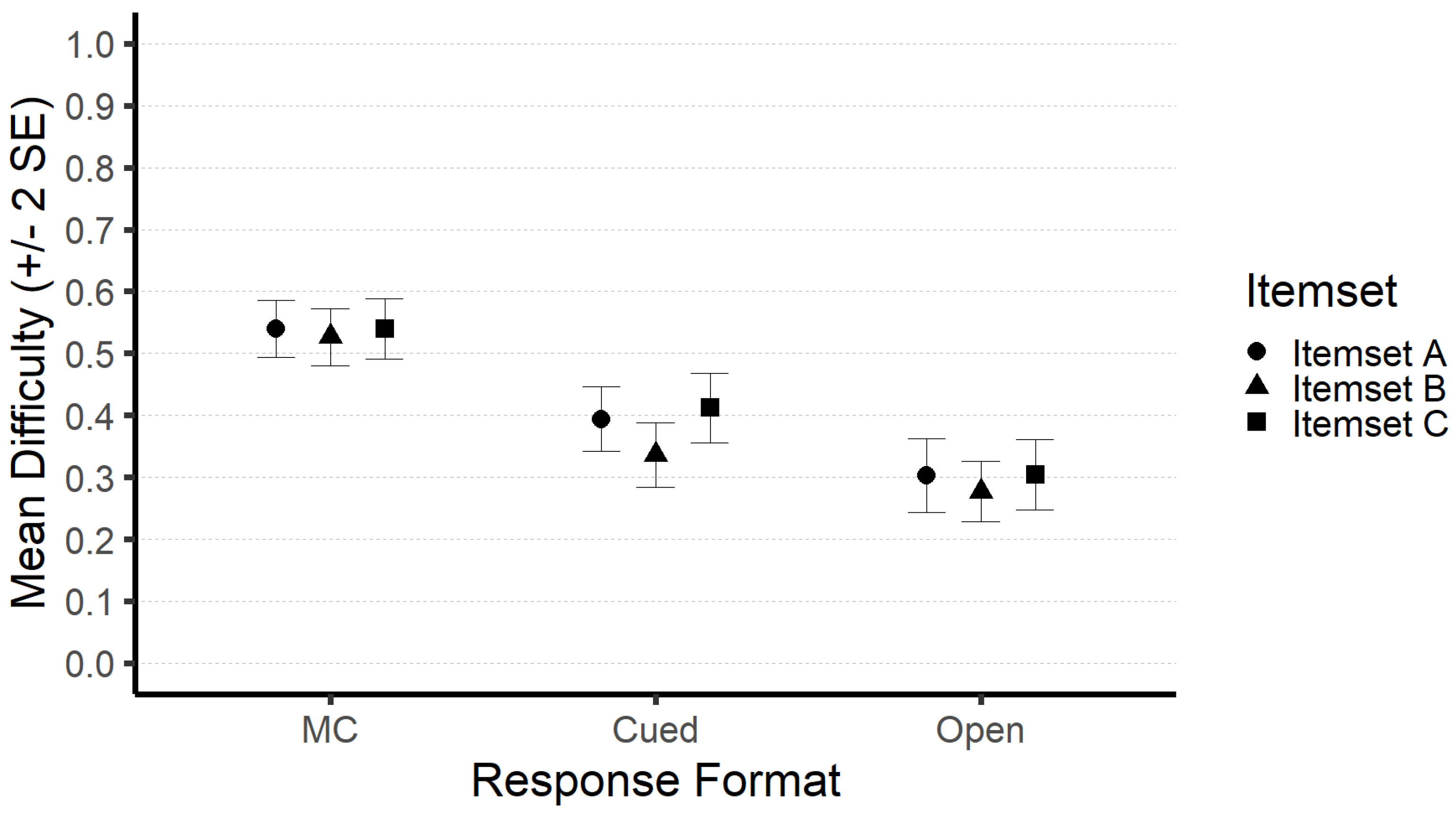
3. Results: Study 1
4. Discussion: Study 1
5. Methods and Materials: Study 2
5.1. Participants and Procedure
5.2. Measures
5.3. Data Preparation
5.4. Statistical Analysis
6. Results: Study 2
Modeling Declarative Knowledge and Accounting for Response Formats
7. Discussion: Study 2
8. General Discussion
8.1. Response Formats as Means to an End
8.2. Recognition, Recall, or What to Study Next
8.3. Limitations
9. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abu-Zaid, Ahmed, and Tehreem A. Khan. 2013. Assessing Declarative and Procedural Knowledge Using Multiple-Choice Questions. Medical Education Online 18: 21132. [Google Scholar] [CrossRef] [PubMed]
- Ackerman, Phillip L. 1996. A Theory of Adult Intellectual Development: Process, Personality, Interests, and Knowledge. Intelligence 22: 227–57. [Google Scholar] [CrossRef]
- Ackerman, Phillip L. 2000. Domain-Specific Knowledge as the ‘Dark Matter’ of Adult Intelligence: Gf/Gc, Personality and Interest Correlates. The Journals of Gerontology Series B: Psychological Sciences and Social Sciences 55: 69–84. [Google Scholar] [CrossRef] [PubMed]
- Ackerman, Phillip L., and David Z. Hambrick. 2020. A Primer on Assessing Intelligence in Laboratory Studies. Intelligence 80: 101440. [Google Scholar] [CrossRef]
- Amthauer, Rudolf, Burkhard Brocke, Detlev Liepmann, and André Beauducel. 2001. Intelligenz-Struktur-Test 2000 R Manual [Manual of the Intelligence Structure Test 2000 R]. Göttingen: Hogrefe. [Google Scholar]
- Anderson, John R., and Gordon H. Bower. 1972. Recognition and Retrieval Processes in Free Recall. Psychological Review 79: 97–123. [Google Scholar] [CrossRef]
- Beauducel, André, and Martin Kersting. 2002. Fluid and Crystallized Intelligence and the Berlin Model of Intelligence Structure (BIS). European Journal of Psychological Assessment 18: 97–112. [Google Scholar] [CrossRef]
- Beauducel, Andre, and Philipp Yorck Herzberg. 2006. On the Performance of Maximum Likelihood Versus Means and Variance Adjusted Weighted Least Squares Estimation in CFA. Structural Equation Modeling: A Multidisciplinary Journal 13: 186–203. [Google Scholar] [CrossRef]
- Becker, Nicolas, Florian Schmitz, Anke Falk, Jasmin Feldbrügge, Daniel Recktenwald, Oliver Wilhelm, Franzis Preckel, and Frank Spinath. 2016. Preventing Response Elimination Strategies Improves the Convergent Validity of Figural Matrices. Journal of Intelligence 4: 2. [Google Scholar] [CrossRef]
- Becker, Nicolas, Franzis Preckel, Julia Karbach, Nathalie Raffel, and Frank M. Spinath. 2015. Die Matrizenkonstruktionsaufgabe: Validierung eines distraktorfreien Aufgabenformats zur Vorgabe figuraler Matrizen. Diagnostica 61: 22–33. [Google Scholar] [CrossRef]
- Becker, William E., and Carol Johnston. 1999. The Relationship between Multiple Choice and Essay Response Questions in Assessing Economics Understanding. Economic Record 75: 348–57. [Google Scholar] [CrossRef]
- Bentler, Peter M. 1990. Comparative Fit Indexes in Structural Models. Psychological Bulletin 107: 238–46. [Google Scholar] [CrossRef] [PubMed]
- Browne, Michael W., and Robert Cudeck. 1992. Alternative Ways of Assessing Model Fit. Sociological Methods & Research 21: 230–58. [Google Scholar]
- Brunner, Martin, Gabriel Nagy, and Oliver Wilhelm. 2012. A Tutorial on Hierarchically Structured Constructs. Journal of Personality 80: 796–846. [Google Scholar] [CrossRef]
- Buckles, Stephen, and John J. Siegfried. 2006. Using Multiple-Choice Questions to Evaluate In-Depth Learning of Economics. The Journal of Economic Education 37: 48–57. [Google Scholar] [CrossRef]
- Campbell, Donald T., and Donald W. Fiske. 1959. Convergent and Discriminant Validation by the Multitrait-Multimethod Matrix. Psychological Bulletin 56: 81–105. [Google Scholar] [CrossRef] [PubMed]
- Carroll, John B. 1993. Human Cognitive Abilities: A Survey of Factor-Analytic Studies, 1st ed. Cambridge: Cambridge University Press. [Google Scholar] [CrossRef]
- Cattell, Raymond B. 1957. Personality and Motivation Structure and Measurement. Chicago: World Book. [Google Scholar]
- Cattell, Raymond B. 1971. Abilities: Their Structure, Growth, and Action. Boston: Houghton Mifflin. [Google Scholar]
- Cattell, Raymond B. 1987. Intelligence: Its Structure, Growth, and Action. Advances in Psychology 35. Amsterdam and New York: Elsevier Science Pub. Co. [Google Scholar]
- Chan, Nixon, and Peter E. Kennedy. 2002. Are Multiple-Choice Exams Easier for Economics Students? A Comparison of Multiple-Choice and ‘Equivalent’ Constructed-Response Exam Questions. Southern Economic Journal 68: 957–71. [Google Scholar] [CrossRef]
- Chapelle, Carol A. 1999. Construct Definition and Validity Inquiry in SLA Research. In Interfaces between Second Language Acquisition and Language Testing Research, 1st ed. Edited by Lyle F. Bachman and Andrew D. Cohen. Cambridge: Cambridge University Press, pp. 32–70. [Google Scholar] [CrossRef]
- Chittooran, Mary M., and Dorothy D. Miles. 2001. Test-Taking Skills for Multiple-Choice Formats: Implications for School Psychologists. Washington, DC: Education Resources Information Center, p. 23. [Google Scholar]
- Cohen, Jacob. 1960. A Coefficient of Agreement for Nominal Scales. Educational and Psychological Measurement 20: 37–46. [Google Scholar] [CrossRef]
- Cohen, Jacob. 1969. Statistical Power Analysis for the Behavioral Sciences. San Diego: Academic Press. [Google Scholar]
- Cole, David A., Corinne E. Perkins, and Rachel L. Zelkowitz. 2016. Impact of Homogeneous and Heterogeneous Parceling Strategies When Latent Variables Represent Multidimensional Constructs. Psychological Methods 21: 164–74. [Google Scholar] [CrossRef]
- Coleman, Chris, Jennifer Lindstrom, Jason Nelson, William Lindstrom, and K. Noël Gregg. 2010. Passageless Comprehension on the Nelson-Denny Reading Test: Well Above Chance for University Students. Journal of Learning Disabilities 43: 244–49. [Google Scholar] [CrossRef]
- Daneman, Meredyth, and Brenda Hannon. 2001. Using Working Memory Theory to Investigate the Construct Validity of Multiple-Choice Reading Comprehension Tests Such as the SAT. Journal of Experimental Psychology: General 130: 208–23. [Google Scholar] [CrossRef]
- Diedenhofen, Birk, and Jochen Musch. 2017. PageFocus: Using Paradata to Detect and Prevent Cheating on Online Achievement Tests. Behavior Research Methods 49: 1444–59. [Google Scholar] [CrossRef] [PubMed]
- Downing, Steven M., and Thomas M. Haladyna, eds. 2006. Handbook of Test Development. Mahwah: L. Erlbaum. [Google Scholar]
- Enders, Craig K., ed. 2010. Applied Missing Data Analysis. New York: Guilford Press. [Google Scholar]
- Fazio, Lisa K., Pooja K. Agarwal, Elizabeth J. Marsh, and Henry L. Roediger. 2010. Memorial Consequences of Multiple-Choice Testing on Immediate and Delayed Tests. Memory & Cognition 38: 407–18. [Google Scholar] [CrossRef]
- Flake, Jessica Kay, and Eiko I. Fried. 2020. Measurement Schmeasurement: Questionable Measurement Practices and How to Avoid Them. Advances in Methods and Practices in Psychological Science 3: 456–65. [Google Scholar] [CrossRef]
- Fowler, Bill, and Barry M. Kroll. 1978. Verbal Skills as Factors in the Passageless Validation of Reading Comprehension Tests. Perceptual and Motor Skills 47: 335–38. [Google Scholar] [CrossRef]
- Gillund, Gary, and Richard M. Shiffrin. 1984. A Retrieval Model for Both Recognition and Recall. Psychological Review 91: 67. [Google Scholar] [CrossRef]
- Haist, Frank, Arthur P. Shimamura, and Larry R. Squire. 1992. On the Relationship Between Recall and Recognition Memory. Journal of Experimental Psychology: Learning, Memory, and Cognition 18: 691–702. [Google Scholar] [CrossRef] [PubMed]
- Hakstian, A. Ralph, and Raymond B. Cattell. 1978. Higher-Stratum Ability Structures on a Basis of Twenty Primary Abilities. Journal of Educational Psychology 70: 657–69. [Google Scholar] [CrossRef]
- Hancock, Gregory R. 1994. Cognitive Complexity and the Comparability of Multiple-Choice and Constructed-Response Test Formats. The Journal of Experimental Education 62: 143–58. [Google Scholar] [CrossRef]
- Harke, Douglas J., J. Dudley Herron, and Ralph W. Leffler. 1972. Comparison of a Randomized Multiple Choice Format with a Written One-Hour Physics Problem Test. Science Education 56: 563–65. [Google Scholar] [CrossRef]
- Hartung, Johanna, Selina Weiss, and Oliver Wilhelm. 2017. Individual Differences in Performance on Comprehension and Knowledge Tests with and without Passages and Questions. Learning and Individual Differences 56: 143–50. [Google Scholar] [CrossRef]
- Hickson, Stephen, and Bob Reed. 2011. More Evidence on the Use of Constructed-Response Questions in Principles of Economics Classes. International Review of Economics Education 10: 28–49. [Google Scholar] [CrossRef][Green Version]
- Hohensinn, Christine, and Klaus D. Kubinger. 2011. Applying Item Response Theory Methods to Examine the Impact of Different Response Formats. Educational and Psychological Measurement 71: 732–46. [Google Scholar] [CrossRef]
- Horn, John L. 1965. Fluid and Crystallized Intelligence: A Factor Analytic Study of the Structure among Primary Mental Abilities. Ph.D. dissertation, University of Illinois, Urbana, IL, USA. [Google Scholar]
- Horn, John L. 1966. Some Characteristics of Classroom Examinations. Journal of Educational Measurement 3: 293–95. [Google Scholar] [CrossRef]
- Hu, Li-tze, and Peter M. Bentler. 1999. Cutoff Criteria for Fit Indexes in Covariance Structure Analysis: Conventional Criteria versus New Alternatives. Structural Equation Modeling: A Multidisciplinary Journal 6: 1–55. [Google Scholar] [CrossRef]
- Jewsbury, Paul A., and Stephen C. Bowden. 2017. Construct Validity of Fluency and Implications for the Factorial Structure of Memory. Journal of Psychoeducational Assessment 35: 460–81. [Google Scholar] [CrossRef]
- Katz, Stuart, A. Boyd Blackburn, and Gary J. Lautenschlager. 1991. Answering Reading Comprehension Items without Passages on the SAT When Items Are Quasi-Randomized. Educational and Psychological Measurement 51: 747–54. [Google Scholar] [CrossRef]
- Katz, Stuart, Gary J. Lautenschlager, A. Boyd Blackburn, and Felicia H. Harris. 1990. Answering Reading Comprehension Items without Passages on the SAT. Psychological Science 1: 122–27. [Google Scholar] [CrossRef]
- Kennedy, Peter, and William B. Walstad. 1997. Combining Multiple-Choice and Constructed-Response Test Scores: An Economist’s View. Applied Measurement in Education 10: 359–75. [Google Scholar] [CrossRef]
- Kesselman-Turkel, Judi, and Franklynn Peterson. 2004. Test-Taking Strategies. Madison: University of Wisconsin Press. [Google Scholar]
- Krathwohl, David R. 2002. A Revision of Bloom’s Taxonomy: An Overview. Theory Into Practice 41: 212–18. [Google Scholar] [CrossRef]
- Krieg, Randall G., and Bulent Uyar. 2001. Student Performance in Business and Economics Statistics: Does Exam Structure Matter? Journal of Economics and Finance 25: 229–41. [Google Scholar] [CrossRef]
- Li, Shu-Chen, Ulman Lindenberger, Bernhard Hommel, Gisa Aschersleben, Wolfgang Prinz, and Paul B. Baltes. 2004. Transformations in the Couplings among Intellectual Abilities and Constituent Cognitive Processes across the Life Span. Psychological Science 15: 155–63. [Google Scholar] [CrossRef] [PubMed]
- Lindner, Marlit Annalena, Jörn R. Sparfeldt, Olaf Köller, Josef Lukas, and Detlev Leutner. 2021. Ein Plädoyer zur Qualitätssicherung schriftlicher Prüfungen im Psychologiestudium. Psychologische Rundschau 72: 93–105. [Google Scholar] [CrossRef]
- Little, Todd D., William A. Cunningham, Golan Shahar, and Keith F. Widaman. 2002. To Parcel or Not to Parcel: Exploring the Question, Weighing the Merits. Structural Equation Modeling: A Multidisciplinary Journal 9: 151–73. [Google Scholar] [CrossRef]
- Lukhele, Robert, David Thissen, and Howard Wainer. 1994. On the Relative Value of Multiple-Choice, Constructed Response, and Examinee-Selected Items on Two Achievement Tests. Journal of Educational Measurement 31: 234–50. [Google Scholar] [CrossRef]
- Lynn, Richard, and Paul Irwing. 2002. Sex Differences in General Knowledge, Semantic Memory and Reasoning Ability. British Journal of Psychology 93: 545–56. [Google Scholar] [CrossRef]
- Lynn, Richard, Paul Irwing, and Thomas Cammock. 2001. Sex Differences in General Knowledge. Intelligence 30: 27–39. [Google Scholar] [CrossRef]
- Martinez, Michael E. 1999. Cognition and the Question of Test Item Format. Educational Psychologist 34: 207–18. [Google Scholar] [CrossRef]
- McDonald, Roderick P. 1999. Test Theory: A Unified Treatment. Hillsdale: Erlbaum. [Google Scholar]
- McGrew, Kevin S. 2005. The Cattell-Horn-Carroll Theory of Cognitive Abilities: Past, Present, and Future. In Contemporary Intellectual Assessment: Theories, Tests, and Issues. New York: The Guilford Press, pp. 136–81. [Google Scholar]
- McGrew, Kevin S. 2009. CHC Theory and the Human Cognitive Abilities Project: Standing on the Shoulders of the Giants of Psychometric Intelligence Research. Intelligence 37: 1–10. [Google Scholar] [CrossRef]
- Millman, Jason, Carol H. Bishop, and Robert Ebel. 1965. An Analysis of Test-Wiseness. Educational and Psychological Measurement 25: 707–26. [Google Scholar] [CrossRef]
- Mullis, Ina V. S., Michael O. Martin, and Pierre Foy. 2008. TIMSS 2007 International Mathematics Report: Findings from IEA’s Trends in International Mathematics and Science Study at the Fourth and Eighth Grades. Chestnut Hill: TIMSS & PIRLS International Study Center, Boston College. [Google Scholar]
- Mullis, Ina V. S., Michael O. Martin, Ann M. Kennedy, and Pierre Foy. 2007. IEA’s Progress in International Reading Literacy Study in Primary School in 40 Countries. Chestnut Hill: TIMSS & PIRLS International Study Center, Boston College. [Google Scholar]
- Nakagawa, Shinichi, Paul C. D. Johnson, and Holger Schielzeth. 2017. The Coefficient of Determination R2 and Intra-Class Correlation Coefficient from Generalized Linear Mixed-Effects Models Revisited and Expanded. Journal of the Royal Society 14: 11. [Google Scholar]
- Oberauer, Klaus, Ralf Schulze, Oliver Wilhelm, and Heinz-Martin Süß. 2005. Working Memory and Intelligence—Their Correlation and Their Relation: Comment on Ackerman, Beier, and Boyle (2005). Psychological Bulletin 131: 61–65. [Google Scholar] [CrossRef] [PubMed]
- Pornprasertmanit, Sunthud, Patrick Miller, Alexander Schoemann, and Terrence D. Jorgensen. 2021. Simsem: SIMulated Structural Equation Modeling. R Package. Available online: https://CRAN.Rproject.org/package=simsem (accessed on 1 January 2022).
- R Core Team. 2022. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 1 January 2022).
- Raykov, Tenko, and George A. Marcoulides. 2011. Classical Item Analysis Using Latent Variable Modeling: A Note on a Direct Evaluation Procedure. Structural Equation Modeling: A Multidisciplinary Journal 18: 315–24. [Google Scholar] [CrossRef]
- Rodriguez, Michael C. 2003. Construct Equivalence of Multiple-Choice and Constructed-Response Items: A Random Effects Synthesis of Correlations. Journal of Educational Measurement 40: 163–84. [Google Scholar] [CrossRef]
- Rosen, Virginia M., and Randall W. Engle. 1997. The Role of Working Memory Capacity in Retrieval. Journal of Experimental Psychology: General 126: 211–27. [Google Scholar] [CrossRef]
- Rosseel, Yves. 2012. Lavaan: An R Package for Structural Equation Moeling. Journal of Statistical Software 48: 1–36. [Google Scholar] [CrossRef]
- Rost, Detlef H., and Jörn R. Sparfeldt. 2007. Leseverständnis ohne Lesen?: Zur Konstruktvalidität von multiple-choice-Leseverständnistestaufgaben. Zeitschrift für Pädagogische Psychologie 21: 305–14. [Google Scholar] [CrossRef]
- Sabers, Darrell. 1975. Test-Taking Skills. Tucson: The University of Arizona. [Google Scholar]
- Sam, Amir H., Emilia Peleva, Chee Yeen Fung, Nicki Cohen, Emyr W. Benbow, and Karim Meeran. 2019. Very Short Answer Questions: A Novel Approach To Summative Assessments In Pathology. Advances in Medical Education and Practice 10: 943–48. [Google Scholar] [CrossRef]
- Sam, Amir H., Samantha M. Field, Carlos F. Collares, Colin Melville, Joanne Harris, and Karim Meeran. 2018. Very-short-answer Questions: Reliability, Discrimination and Acceptability. Medical Education 52: 447–55. [Google Scholar] [CrossRef]
- Schafer, Joseph L., and John W. Graham. 2002. Missing Data: Our View of the State of the Art. Psychological Methods 7: 147–77. [Google Scholar] [CrossRef]
- Schipolowski, Stefan, Oliver Wilhelm, and Ulrich Schroeders. 2014. On the Nature of Crystallized Intelligence: The Relationship between Verbal Ability and Factual Knowledge. Intelligence 46: 156–68. [Google Scholar] [CrossRef]
- Schneider, W. Joel, and Kevin S. McGrew. 2018. The Cattell–Horn–Carroll Theory of Cognitive Abilities. In Contemporary Intellectual Assessment: Theories, Tests and Issues. New York: Guilford Press, p. 91. [Google Scholar]
- Schroeders, Ulrich, Oliver Wilhelm, and Gabriel Olaru. 2016. The Influence of Item Sampling on Sex Differences in Knowledge Tests. Intelligence 58: 22–32. [Google Scholar] [CrossRef]
- Schroeders, Ulrich, Stefan Schipolowski, and Oliver Wilhelm. 2020. Berliner Test Zur Erfassung Fluider Und Kristalliner Intelligenz Für Die 5. Bis 7. Klasse (BEFKI 5-7). Göttingen: Hogrefe Verlag. [Google Scholar]
- Schult, Johannes, and Jörn R. Sparfeldt. 2018. Reliability and Validity of PIRLS and TIMSS: Does the Response Format Matter? European Journal of Psychological Assessment 34: 258–69. [Google Scholar] [CrossRef]
- Scouller, Karen. 1998. The Influence of Assessment Method on Students’ Learning Approaches: Multiple Choice Question Examination versus Assignment Essay. Higher Education 35: 453–72. [Google Scholar] [CrossRef]
- Scully, Darina. 2017. Constructing Multiple-Choice Items to Measure Higher-Order Thinking. Practical Assessment, Research, and Evaluation Practical Assessment, Research, and Evaluation 22: 4. [Google Scholar] [CrossRef]
- Sparfeldt, Jörn R., Rumena Kimmel, Lena Löwenkamp, Antje Steingräber, and Detlef H. Rost. 2012. Not Read, but Nevertheless Solved? Three Experiments on PIRLS Multiple Choice Reading Comprehension Test Items. Educational Assessment 17: 214–32. [Google Scholar] [CrossRef]
- Steger, Diana, Ulrich Schroeders, and Oliver Wilhelm. 2019. On the Dimensionality of Crystallized Intelligence: A Smartphone-Based Assessment. Intelligence 72: 76–85. [Google Scholar] [CrossRef]
- Steger, Diana, Ulrich Schroeders, and Oliver Wilhelm. 2020. Caught in the Act: Predicting Cheating in Unproctored Knowledge Assessment. Assessment 28: 1004–17. [Google Scholar] [CrossRef] [PubMed]
- Thissen, David, Howard Wainer, and Xiang-Bo Wang. 1994. Are Tests Comprising Both Multiple-Choice and Free-Response Items Necessarily Less Unidimensional Than Multiple-Choice Tests? An Analysis of Two Tests. Journal of Educational Measurement 31: 113–23. [Google Scholar] [CrossRef]
- Traub, Ross E. 1993. On the Equivalence of the Traits Assessed by Multiple-Choice and Constructed-Response Tests. In Construction Versus Choice in Cognitive Measurement. Issues in Constructed Response, Performance Testing, and Portfolio Assessment. New York: Routledge, pp. 29–44. [Google Scholar]
- Traub, Ross E., and Charles W. Fisher. 1977. On the Equivalence of Constructed- Response and Multiple-Choice Tests. Applied Psychological Measurement 1: 355–69. [Google Scholar] [CrossRef]
- Tulving, Endel, and Michael J. Watkins. 1973. Continuity between Recall and Recognition. The American Journal of Psychology 86: 739. [Google Scholar] [CrossRef]
- Unsworth, Nash, and Gene A. Brewer. 2009. Examining the Relationships among Item Recognition, Source Recognition, and Recall from an Individual Differences Perspective. Journal of Experimental Psychology: Learning, Memory, and Cognition 35: 1578–85. [Google Scholar] [CrossRef]
- Unsworth, Nash, Gregory J. Spillers, and Gene A. Brewer. 2011. Variation in Verbal Fluency: A Latent Variable Analysis of Clustering, Switching, and Overall Performance. The Quarterly Journal of Experimental Psychology 64: 447–66. [Google Scholar] [CrossRef] [PubMed]
- Unsworth, Nash. 2019. Individual Differences in Long-Term Memory. Psychological Bulletin 145: 79–139. [Google Scholar] [CrossRef] [PubMed]
- Veloski, J. Jon, Howard K. Rabinowitz, Mary R. Robeson, and Paul R. Young. 1999. Patients Don’t Present with Five Choices: An Alternative to Mulitple-Choice Tests in Assessing Physicians’ Competence. Academic Medicine 74: 539–46. [Google Scholar] [CrossRef] [PubMed]
- Vernon, Philip E. 1962. The Determinants of Reading Comprehension. Educational and Psychological Measurement 22: 269–86. [Google Scholar] [CrossRef]
- von Stumm, Sophie, and Phillip L. Ackerman. 2013. Investment and Intellect: A Review and Meta-Analysis. Psychological Bulletin 139: 841–69. [Google Scholar] [CrossRef]
- Walstad, William B. 2001. Improving Assessment in University Economics. The Journal of Economic Education 32: 281–94. [Google Scholar] [CrossRef]
- Ward, William C. 1982. A Comparison of Free-Response and Multiple-Choice Forms of Verbal Aptitude Tests. Applied Psychological Measurement 6: 1–11. [Google Scholar] [CrossRef]
- Watrin, Luc, Ulrich Schroeders, and Oliver Wilhelm. 2022. Structural Invariance of Declarative Knowledge across the Adult Lifespan. Psychology and Aging 37: 283–97. [Google Scholar] [CrossRef]
- Wilhelm, Oliver, and Patrick Kyllonen. 2021. To Predict the Future, Consider the Past: Revisiting Carroll (1993) as a Guide to the Future of Intelligence Research. Intelligence 89: 101585. [Google Scholar] [CrossRef]
- Wilhelm, Oliver, and Ulrich Schroeders. 2019. Intelligence. In The Psychology of Human Thought: An Introduction. Edited by Robert Sternberg and Joachim Funke. Heidelberg: Heidelberg University Publishing, pp. 257–77. [Google Scholar]


| Study | Group (N) | n (Items) + Itemset | Total Items | ||
|---|---|---|---|---|---|
| MC | Cued Open-Ended | Open-Ended | |||
| 1 | 1 (N = 46) | 24 A | 24 C | 24 B | 72 |
| 2 (N = 50) | 24 B | 24 A | 24 C | 72 | |
| 3 (N = 46) | 24 C | 24 B | 24 A | 72 | |
| 2 | 1 (N = 300) | 24 | 24 | 24 | 72 |
| Model | With Defocusing | |||
|---|---|---|---|---|
| MC Reference | Fixed Effects | Estimate (SE) | OR | p |
| (Intercept) | .22 (.15) | 1.25 | .15 | |
| Cued | −.98 (.06) | .38 | <.001 | |
| Open | −1.55 (.07) | .21 | <.001 | |
| Defocusing | .65 (.18) | 1.91 | <.001 | |
| Defocusing*Cued | .24 (.21) | 1.28 | .24 | |
| Defocusing*Open | .61 (.21) | 1.85 | <.01 | |
| Random effect | Variance (SD) | |||
| (Intercept of Person) | .76 (.87) | |||
| (Intercept of Item) | 1.20 (1.10) | |||
| Measurement Model | χ2 | df | CFI | RMSEA | [90% CI] | SRMR | |
|---|---|---|---|---|---|---|---|
| A | 3 Correlated Factors Response Formats | 148.7 | 51 | .917 | .080 | [.065; .095] | .045 |
| B | g-factor | 150.90 | 54 | .918 | .077 | [.063; .092] | .045 |
| C | 4 Correlated Factors Knowledge Domains | 57.87 | 48 | .992 | .026 | [.000; .048] | .026 |
| D | Higher-Order Knowledge Domains | 62.98 | 50 | .989 | .029 | [.000; .050] | .029 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goecke, B.; Staab, M.; Schittenhelm, C.; Wilhelm, O. Stop Worrying about Multiple-Choice: Fact Knowledge Does Not Change with Response Format. J. Intell. 2022, 10, 102. https://doi.org/10.3390/jintelligence10040102
Goecke B, Staab M, Schittenhelm C, Wilhelm O. Stop Worrying about Multiple-Choice: Fact Knowledge Does Not Change with Response Format. Journal of Intelligence. 2022; 10(4):102. https://doi.org/10.3390/jintelligence10040102
Chicago/Turabian StyleGoecke, Benjamin, Marlena Staab, Catherine Schittenhelm, and Oliver Wilhelm. 2022. "Stop Worrying about Multiple-Choice: Fact Knowledge Does Not Change with Response Format" Journal of Intelligence 10, no. 4: 102. https://doi.org/10.3390/jintelligence10040102
APA StyleGoecke, B., Staab, M., Schittenhelm, C., & Wilhelm, O. (2022). Stop Worrying about Multiple-Choice: Fact Knowledge Does Not Change with Response Format. Journal of Intelligence, 10(4), 102. https://doi.org/10.3390/jintelligence10040102





