Shaky Student Growth? A Comparison of Robust Bayesian Learning Progress Estimation Methods
Abstract
1. Introduction
1.1. Estimation of Learning Progress
1.2. Factors That Influence the Quality of Learning Progress Estimates
1.3. Aim of the Current Study
- Research Question 1: Do robust Bayesian latent growth models outperform a simple Bayesian latent growth model based on the Gaussian distribution in terms of learning progress estimation?
- Research Question 2: Which robust Bayesian latent growth model performs best in terms of learning progress estimation?
2. Materials and Methods
2.1. Dataset
2.2. Analytical Approach
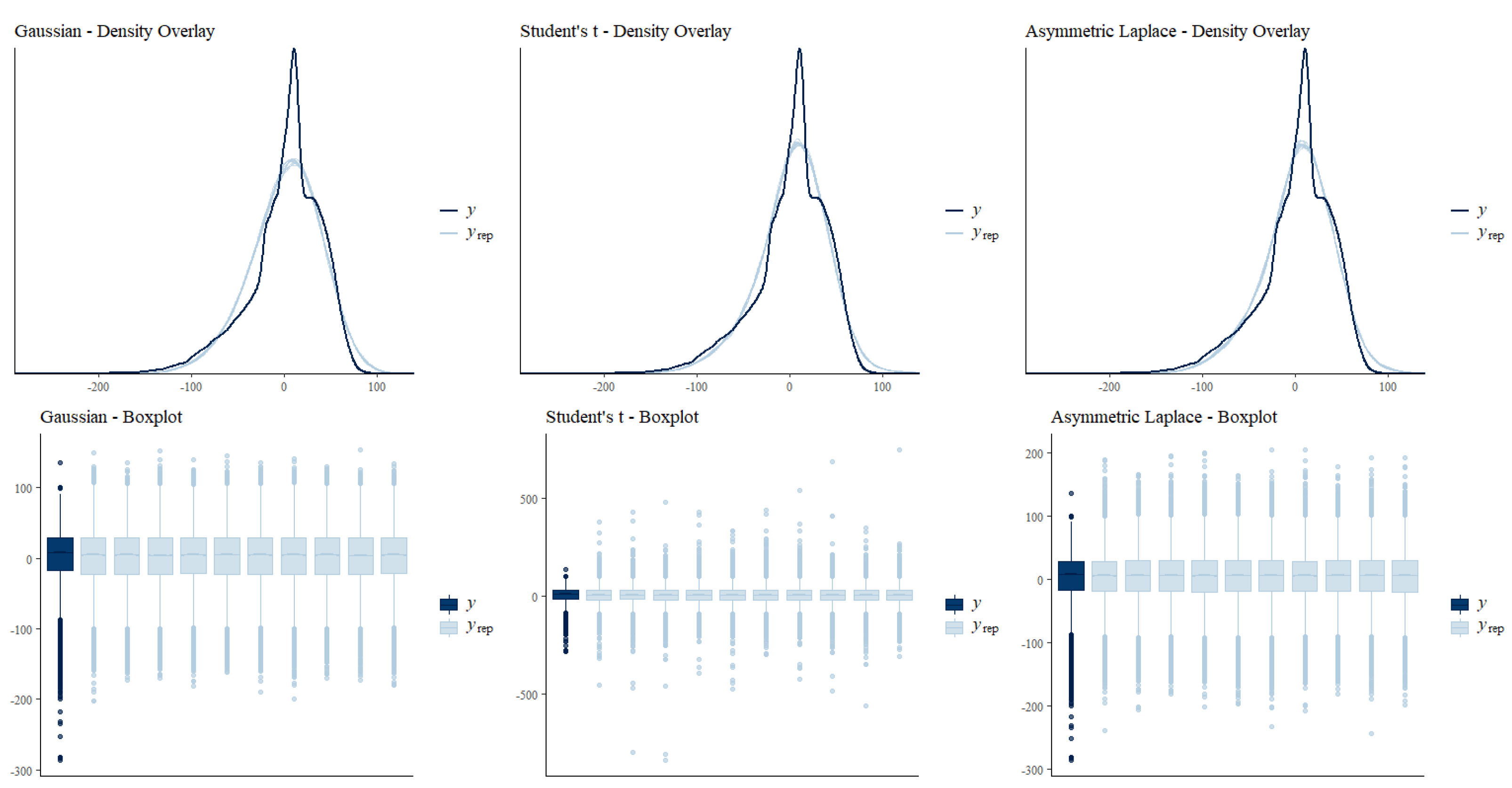
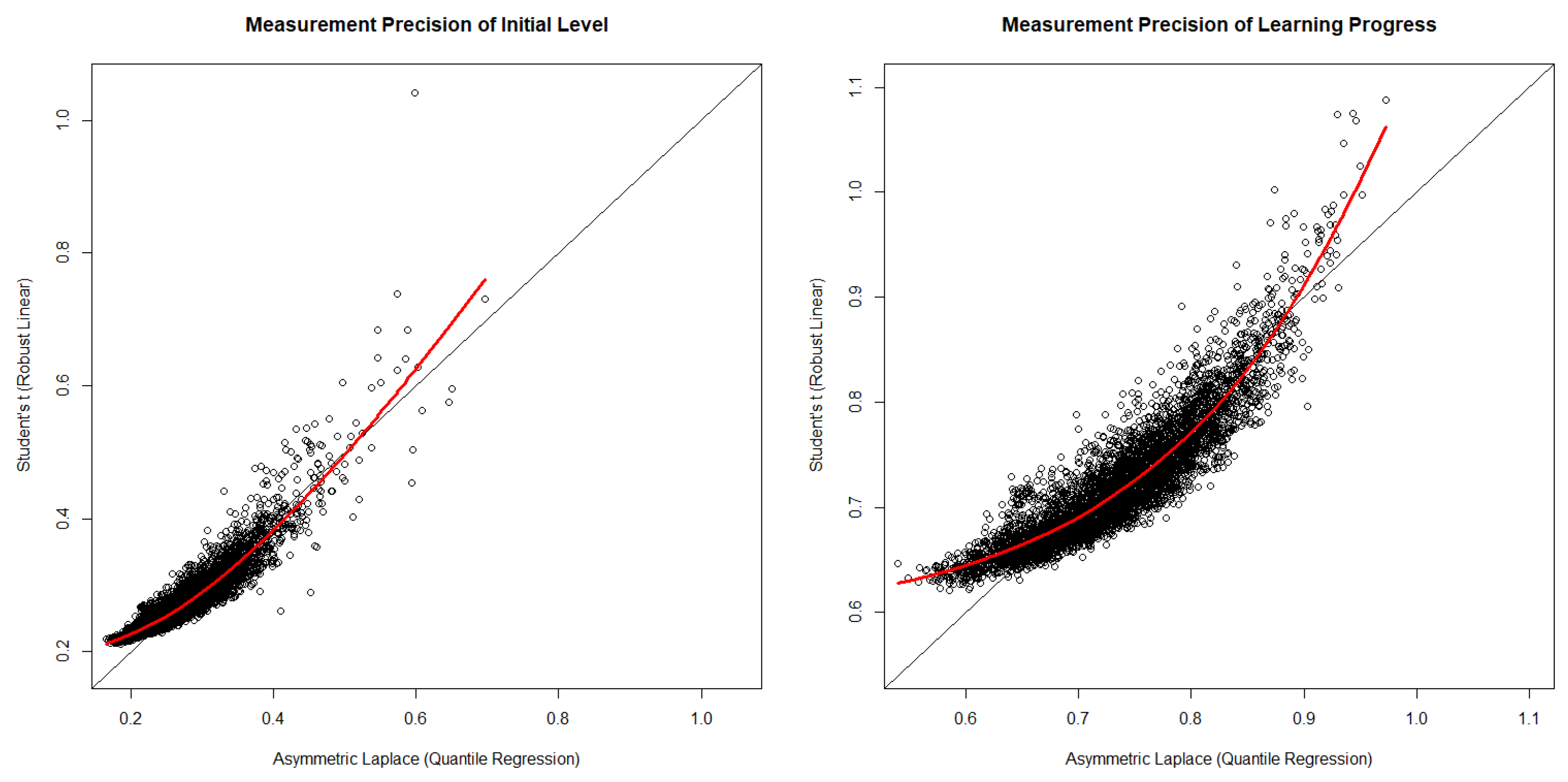
3. Results
3.1. Model Comparison and Model Parameter Findings
3.2. Exploring Differences between the Models
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ardoin, Scott P., Theodore J. Christ, Laura S. Morena, Damien C. Cormier, and David A. Klingbeil. 2013. A systematic review and summarization of the recommendations and research surrounding Curriculum-Based Measurement of oral reading fluency (CBM-R) decision rules. Journal of School Psychology 51: 1–18. [Google Scholar] [CrossRef]
- Asendorpf, Jens B., Rens van de Schoot, Jaap J. A. Denissen, and Roos Hutteman. 2014. Reducing bias due to systematic attrition in longitudinal studies: The benefits of multiple imputation. International Journal of Behavioral Development 38: 453–60. [Google Scholar] [CrossRef]
- Bollen, Kenneth A. 1980. Issues in the Comparative Measurement of Political Democracy. American Sociological Review 45: 370. [Google Scholar] [CrossRef]
- Boorse, Jaclin, and Ethan R. Van Norman. 2021. Modeling within-year growth on the Mathematics Measure of Academic Progress. Psychology in the Schools 58: 2255–68. [Google Scholar] [CrossRef]
- Bulut, Okan, and Damien C. Cormier. 2018. Validity Evidence for Progress Monitoring With Star Reading: Slope Estimates, Administration Frequency, and Number of Data Points. Frontiers in Education 3. [Google Scholar] [CrossRef]
- Bürkner, Paul-Christian. 2017. brms: An R Package for Bayesian Multilevel Models Using Stan. Journal of Statistical Software 80: 1–28. [Google Scholar] [CrossRef]
- Bürkner, Paul-Christian. 2018. Advanced Bayesian Multilevel Modeling with the R Package brms. The R Journal 10: 395. [Google Scholar] [CrossRef]
- Carpenter, Bob, Andrew Gelman, Matthew D. Hoffman, Daniel Lee, Ben Goodrich, Miachael Betancourt, Marcus Brubaker, Jiqiang Guo, Peter Li, and Allen Riddell. 2017. Stan: A probabilistic programming language. Journal of Statistical Software 76: 1–32. [Google Scholar] [CrossRef]
- Chen, Fang F. 2007. Sensitivity of Goodness of Fit Indexes to Lack of Measurement Invariance. Structural Equation Modeling: A Multidisciplinary Journal 14: 464–504. [Google Scholar] [CrossRef]
- Christ, Theodore J., and Christopher D. Desjardins. 2018. Curriculum-Based Measurement of Reading: An Evaluation of Frequentist and Bayesian Methods to Model Progress Monitoring Data. Journal of Psychoeducational Assessment 36: 55–73. [Google Scholar] [CrossRef]
- Christ, Theodore J., and Scott P. Ardoin. 2009. Curriculum-based measurement of oral reading: Passage equivalence and probe-set development. Journal of School Psychology 47: 55–75. [Google Scholar] [CrossRef]
- Christ, Theodore J., Cengiz Zopluoglu, Barbara D. Monaghen, and Ethan R. Van Norman. 2013. Curriculum-Based Measurement of Oral Reading: Multi-study evaluation of schedule, duration, and dataset quality on progress monitoring outcomes. Journal of School Psychology 51: 19–57. [Google Scholar] [CrossRef]
- Christ, Theodore J., Cengiz Zopluoglu, Jeffery D. Long, and Barbara D. Monaghen. 2012. Curriculum-Based Measurement of Oral Reading: Quality of Progress Monitoring Outcomes. Exceptional Children 78: 356–73. [Google Scholar] [CrossRef]
- Christ, Theodore J., Kristin N. Johnson-Gros, and John M. Hintze. 2005. An examination of alternate assessment durations when assessing multiple-skill computational fluency: The generalizability and dependability of curriculum-based outcomes within the context of educational decisions. Psychology in the Schools 42: 615–22. [Google Scholar] [CrossRef]
- Cronbach, Lee J. 1951. Coefficient alpha and the internal structure of tests. Psychometrika 16: 297–334. [Google Scholar] [CrossRef]
- Cummings, Kelli D., Yonghan Park, and Holle A. Bauer Schaper. 2013. Form Effects on DIBELS Next Oral Reading Fluency Progress-Monitoring Passages. Assessment for Effective Intervention 38: 91–104. [Google Scholar] [CrossRef]
- Deno, Stanley L. 1985. Curriculum-Based Measurement: The Emerging Alternative. Exceptional Children 52: 219–32. [Google Scholar] [CrossRef] [PubMed]
- Deno, Stanley L., and Phyllis K. Mirkin. 1977. Data-Based Program Modification: A Manual. Minneapolis: Leadership Training Institute for Special Education. [Google Scholar]
- DiStefano, Christine, Min Zhu, and Diana Mîndrilã. 2009. Understanding and Using Factor Scores: Considerations for the Applied Researcher. Practical Assessment, Research, and Evaluation 14: 20. [Google Scholar] [CrossRef]
- Espin, Christine A., Miya M. Wayman, Stanley L. Deno, Kristen L. McMaster, and Mark de Rooij. 2017. Data-Based Decision-Making: Developing a Method for Capturing Teachers’ Understanding of CBM Graphs. Learning Disabilities Research & Practice 32: 8–21. [Google Scholar] [CrossRef]
- Ferrando, Pere J., and Urbano Lorenzo-Seva. 2018. Assessing the Quality and Appropriateness of Factor Solutions and Factor Score Estimates in Exploratory Item Factor Analysis. Educational and Psychological Measurement 78: 762–80. [Google Scholar] [CrossRef]
- Finch, W. Holmes, and J. E. Miller. 2019. The Use of Incorrect Informative Priors in the Estimation of MIMIC Model Parameters with Small Sample Sizes. Structural Equation Modeling: A Multidisciplinary Journal 26: 497–508. [Google Scholar] [CrossRef]
- Förster, Natalie, and Elmar Souvignier. 2014. Learning progress assessment and goal setting: Effects on reading achievement, reading motivation and reading self-concept. Learning and Instruction 32: 91–100. [Google Scholar] [CrossRef]
- Förster, Natalie, and Jörg-Tobias Kuhn. 2021. Ice is hot and water is dry: Developing equivalent reading tests using rule-based item design. European Journal of Psychological Assessment. [Google Scholar] [CrossRef]
- Förster, Natalie, Mathis Erichsen, and Boris Forthmann. 2021. Measuring Reading Progress in Second Grade: Psychometric Properties of the quop-L2 Test Series. European Journal of Psychological Assessment. [Google Scholar] [CrossRef]
- Forthmann, Boris, Natalie Förster, and Elmar Souvignier. 2021. Empirical Reliability: A Simple-to-Calculate Alternative for Reliability Estimation of Growth in Progress Monitoring. Manuscript Submitted for Publication. [Google Scholar]
- Forthmann, Boris, Rüdiger Grotjahn, Philipp Doebler, and Purya Baghaei. 2020. A Comparison of Different Item Response Theory Models for Scaling Speeded C-Tests. Journal of Psychoeducational Assessment 38: 692–705. [Google Scholar] [CrossRef]
- Fuchs, Lynn S. 2004. The Past, Present, and Future of Curriculum-Based Measurement Research. School Psychology Review 33: 188–92. [Google Scholar] [CrossRef]
- Gelman, Andrew, John B. Carlin, Hal S. Stern, David B. Dunson, Aki Vehtari, and Donald B. Rubin. 2013. Bayesian Data Analysis, 3rd ed. New York: Chapman and Hall/CRC. [Google Scholar]
- Jenkins, Joseph R., J. Jason Graff, and Diana L. Miglioretti. 2009. Estimating Reading Growth Using Intermittent CBM Progress Monitoring. Exceptional Children 75: 151–63. [Google Scholar] [CrossRef]
- Jorgensen, Terrence D., Sunthud Pornprasertmanit, Alexander M. Schoemann, and Yves Rosseel. 2021. semTools: Useful Tools for Structural Equation Modeling (R Package Version 0.5-4). Available online: https://cran.r-project.org/package=semTools (accessed on 18 February 2022).
- Juul, Holger, Mads Poulsen, and Carsten Elbro. 2014. Separating speed from accuracy in beginning reading development. Journal of Educational Psychology 106: 1096–106. [Google Scholar] [CrossRef]
- Keller-Margulis, Milena A., and Sterett H. Mercer. 2014. R-CBM in spanish and in english: Differential relations depending on student reading performance. Psychology in the Schools 51: 677–92. [Google Scholar] [CrossRef]
- Kruschke, John K. 2015. Doing Bayesian Data Analysis: A Tutorial with R, JAGS, and Stan, 2nd ed. New York: Academic Press. [Google Scholar]
- Maris, Gunter, and Han van der Maas. 2012. Speed-Accuracy Response Models: Scoring Rules based on Response Time and Accuracy. Psychometrika 77: 615–33. [Google Scholar] [CrossRef]
- Raykov, Tenko. 2001. Estimation of congeneric scale reliability using covariance structure analysis with nonlinear constraints. British Journal of Mathematical and Statistical Psychology 54: 315–23. [Google Scholar] [CrossRef]
- R Core Team. 2021. R: A Language and Environment for Statistical Computing (4.1.2). Vienna: R Foundation for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 18 February 2022).
- Rosseel, Yves. 2012. lavaan: An R Package for Structural Equation Modeling. Journal of Statistical Software 48: 2. [Google Scholar] [CrossRef]
- Salaschek, Martin, and Eelmar Souvignier. 2014. Web-Based Mathematics Progress Monitoring in Second Grade. Journal of Psychoeducational Assessment 32: 710–24. [Google Scholar] [CrossRef]
- Schatschneider, Christopher, Richard K. Wagner, and Elizabetz C. Crawford. 2008. The importance of measuring growth in response to intervention models: Testing a core assumption. Learning and Individual Differences 18: 308–15. [Google Scholar] [CrossRef][Green Version]
- Schurig, Michael, Jana Jungjohann, and Markus Gebhardt. 2021. Minimization of a Short Computer-Based Test in Reading. Frontiers in Education 6: 684595. [Google Scholar] [CrossRef]
- Silberglitt, Benjamin, and John M. Hintze. 2007. How Much Growth Can We Expect? A Conditional Analysis of R—CBM Growth Rates by Level of Performance. Exceptional Children 74: 71–84. [Google Scholar] [CrossRef]
- Sivula, Tuomas, Måns Magnusson, and Aki Vehtari. 2020. Uncertainty in Bayesian Leave-One-Out Cross-Validation Based Model Comparison. arXiv arXiv:2008.10296. [Google Scholar]
- Solomon, Benjamin G., and Ole J. Forsberg. 2017. Bayesian asymmetric regression as a means to estimate and evaluate oral reading fluency slopes. School Psychology Quarterly 32: 539–51. [Google Scholar] [CrossRef]
- Souvignier, Elmar, Natalie Förster, Karin Hebbecker, and Birgit Schütze. 2021. Using digital data to support teaching practice—Quop: An effective web-based approach to monitor student learning progress in reading and mathematics in entire classrooms. In International Perspectives on School Settings, Education Policy and Digital Strategies. A Transatlantic Discourse in Education Research. Edited by Sieglinde Jornitz and Annika Wilmers. Opladen: Budrich, pp. 283–98. [Google Scholar]
- Tabachnick, Barbara G., and Linda S. Fidell. 2005. Using Multivariate Statistics, 5th ed. Boston: Pearson/Allyn and Bacon. [Google Scholar]
- Van Norman, Ethan R., and David C. Parker. 2018. A Comparison of Split-Half and Multilevel Methods to Assess the Reliability of Progress Monitoring Outcomes. Journal of Psychoeducational Assessment 36: 616–27. [Google Scholar] [CrossRef]
- Vandenberg, Robert J., and Charles E. Lance. 2000. A Review and Synthesis of the Measurement Invariance Literature: Suggestions, Practices, and Recommendations for Organizational Research. Organizational Research Methods 3: 4–70. [Google Scholar] [CrossRef]
- Vannest, Kimberly J., Richard I. Parker, John L. Davis, Denise A. Soares, and Stacey L. Smith. 2012. The Theil–Sen Slope for High-Stakes Decisions from Progress Monitoring. Behavioral Disorders 37: 271–80. [Google Scholar] [CrossRef][Green Version]
- Vehtari, Aki, Andrew Gelman, Daniel Simpson, Bob Carpenter, and Paul-Christian Bürkner. 2021. Rank-Normalization, Folding, and Localization: An Improved Rˆ for Assessing Convergence of MCMC (with Discussion). Bayesian Analysis 16: 2. [Google Scholar] [CrossRef]
- Vehtari, Aki, Andrew Gelman, and Jonah Gabry. 2017. Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Statistics and Computing 27: 1413–32. [Google Scholar] [CrossRef]
- West, Stephen G., Aaron B. Taylor, and Wei Wu. 2012. Model fit and model selection in structural equation modeling. In Handbook of Structural Equation Modeling. Edited by Rick H. Hoyle. New York: The Guilford Press, pp. 209–31. [Google Scholar]
- Wise, Steven L. 2017. Rapid-Guessing Behavior: Its Identification, Interpretation, and Implications. Educational Measurement: Issues and Practice 36: 52–61. [Google Scholar] [CrossRef]
- Wise, Steven L., and Christine E. DeMars. 2010. Examinee Noneffort and the Validity of Program Assessment Results. Educational Assessment 15: 27–41. [Google Scholar] [CrossRef]
- Yeo, Seungsoo, Jamie Y. Fearrington, and Theodore J. Christ. 2012. Relation Between CBM-R and CBM-mR Slopes. Assessment for Effective Intervention 37: 147–58. [Google Scholar] [CrossRef]
- Yu, Keming, and Rana A. Moyeed. 2001. Bayesian quantile regression. Statistics & Probability Letters 54: 437–47. [Google Scholar] [CrossRef]
- Zitzmann, Steffen, and Martin Hecht. 2019. Going Beyond Convergence in Bayesian Estimation: Why Precision Matters Too and How to Assess It. Structural Equation Modeling: A Multidisciplinary Journal 26: 646–61. [Google Scholar] [CrossRef]
- Zitzmann, Steffen, Oliver Lüdtke, Alexander Robitzsch, and Martin Hecht. 2021. On the Performance of Bayesian Approaches in Small Samples: A Comment on Smid, McNeish, Miocevic, and van de Schoot. Structural Equation Modeling: A Multidisciplinary Journal 28: 40–50. [Google Scholar] [CrossRef]


| Model | Gaussian | Student’s t | Asymmetric Laplace |
|---|---|---|---|
| Response Distribution | |||
| Linear Predictor | |||
| Latent Variable Distribution | |||
| Improper flat prior | Improper flat prior | Improper flat prior | |
| Prior for correlation matrices | |||
| Prior for σ | |||
| Prior for ν | - | - |
| Model | Gaussian | Student’s t | Asymmetric Laplace | |||
|---|---|---|---|---|---|---|
| Estimate | 95% CI | Estimate | 95% CI | Estimate | 95% CI | |
| Person Level (Latent Variables) | ||||||
| 34.10 | [33.32, 34.90] | 34.28 | [33.48, 35.06] | 34.17 | [33.38, 34.98] | |
| 2.79 | [2.65, 2.94] | 2.41 | [2.28, 2.54] | 2.29 | [2.15, 2.42] | |
| ) | −0.55 | [−0.58, −0.52] | −0.63 | [−0.67, −0.60] | −0.63 | [−0.66, −0.59] |
| Population Level | ||||||
| −13.98 | [−15.00, −12.96] | −12.79 | [−13.79, −11.75] | −12.70 | [−13.74, −11.68] | |
| 4.52 | [4.40, 4.64] | 4.59 | [4.49, 4.70] | 4.57 | [4.46, 4.67] | |
| σ | 21.90 | [21.73, 22.08] | 14.55 | [14.31, 14.80] | 7.67 | [7.59, 7.76] |
| ν | - | - | 3.22 | [3.08, 3.36] | - | - |
| Quantile | - | - | - | - | 0.50 | - |
| LOO Comparison | ||||||
| ELPD Difference | −2600.60 | 0.00 | −32.50 | |||
| ELPD Difference SE | 154.00 | 0.00 | 30.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forthmann, B.; Förster, N.; Souvignier, E. Shaky Student Growth? A Comparison of Robust Bayesian Learning Progress Estimation Methods. J. Intell. 2022, 10, 16. https://doi.org/10.3390/jintelligence10010016
Forthmann B, Förster N, Souvignier E. Shaky Student Growth? A Comparison of Robust Bayesian Learning Progress Estimation Methods. Journal of Intelligence. 2022; 10(1):16. https://doi.org/10.3390/jintelligence10010016
Chicago/Turabian StyleForthmann, Boris, Natalie Förster, and Elmar Souvignier. 2022. "Shaky Student Growth? A Comparison of Robust Bayesian Learning Progress Estimation Methods" Journal of Intelligence 10, no. 1: 16. https://doi.org/10.3390/jintelligence10010016
APA StyleForthmann, B., Förster, N., & Souvignier, E. (2022). Shaky Student Growth? A Comparison of Robust Bayesian Learning Progress Estimation Methods. Journal of Intelligence, 10(1), 16. https://doi.org/10.3390/jintelligence10010016





